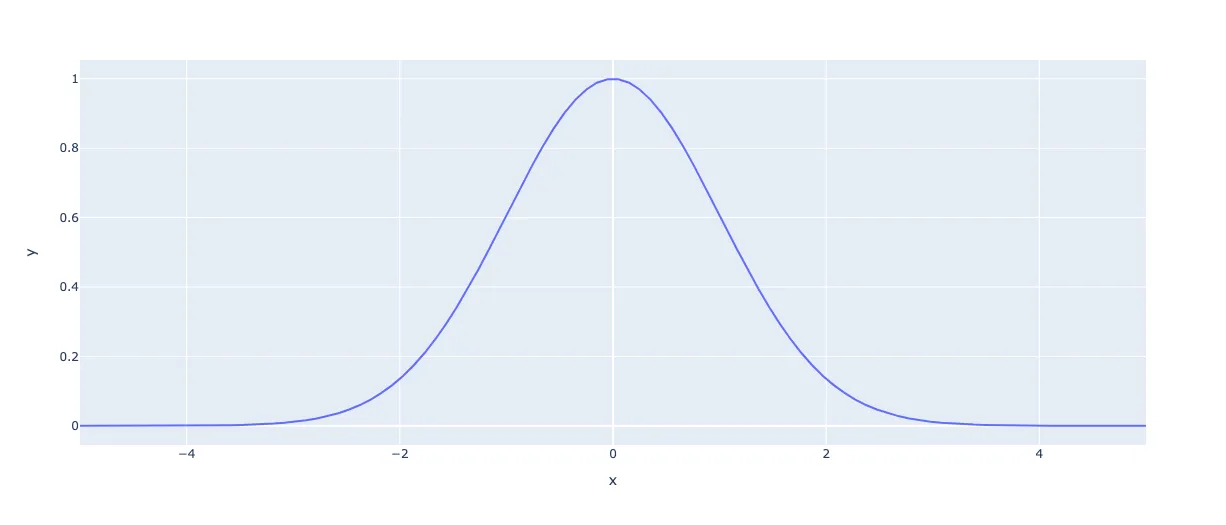
| Нормальное распределение | |
|---|---|
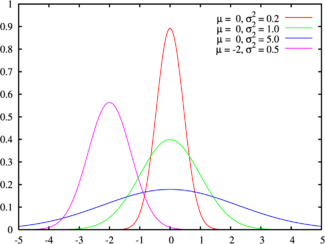 Зеленая линия соответствует стандартному нормальному распределениюПлотность вероятности |
|
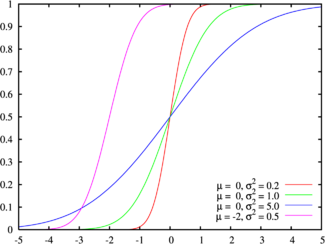 Цвета на этом графике соответствуют графику наверхуФункция распределения |
|
| Обозначение |
 |
| Параметры |
μ — коэффициент сдвига (вещественный) σ > 0 — коэффициент масштаба (вещественный, строго положительный) |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
![{frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sqrt {2sigma ^{2}}}}right)right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/04670b14acb4ddb796469f3812ead9d9cccec275) |
| Математическое ожидание |
 |
| Медиана |
 |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Норма́льное распределе́ние[1][2], также называемое распределением Гаусса или Гаусса — Лапласа[3], или колоколообразная кривая — непрерывное распределение вероятностей с пиком в центре и симметричными боковыми сторонами, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
,
- где параметр
— математическое ожидание (среднее значение), медиана и мода распределения, а параметр
— среднеквадратическое отклонение,
— дисперсия распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений[4]. Многомерный случай описан в статье «Многомерное нормальное распределение».
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 

Общие сведения[править | править код]
Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.
Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце XIX века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.
Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.
Определения[править | править код]
Стандартное нормальное распределение[править | править код]
Наиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда 

Множитель 






Гаусс называл стандартным нормальным распределение с 
Нормальное распределение с параметрами μ, σ[править | править код]
Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем 



Если 







Если в экспоненте плотности вероятности раскрыть скобки и учитывать, что 
Таким образом, плотность вероятности каждого нормального распределения представляет собой экспоненту квадратичной функции:
- где
Отсюда можно выразить среднее значение как 




Обозначение[править | править код]
Плотность вероятности стандартного нормального распределения (с нулевым средним и единичной дисперсией) часто обозначается греческой буквой 

Нормальное распределение часто обозначается 




Функция распределения[править | править код]
Функция распределения стандартного нормального распределения (нормальное интегральное распределение) обычно обозначается заглавной греческой буквой 
С ней связана функция ошибок (интеграл вероятности) 
![{displaystyle [-x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23c41ff0bd6f01a0e27054c2b85819fcd08b762)
Эти интегралы не выражаются в элементарных функциях и называются специальными функциями. Многие их численные приближения известны. См. ниже.
Функции связаны, в частности, соотношением:
.
Нормальное распределение с плотностью 


Можно использовать функцию 


.
График стандартной нормальной функции распределения 

Функция распределения стандартной нормальной случайной величины может быть разложена с помощью метода интегрирования по частям в ряд:
где знак 
Асимптотическое разложение функции распределения для больших 
Стандартное отклонение[править | править код]

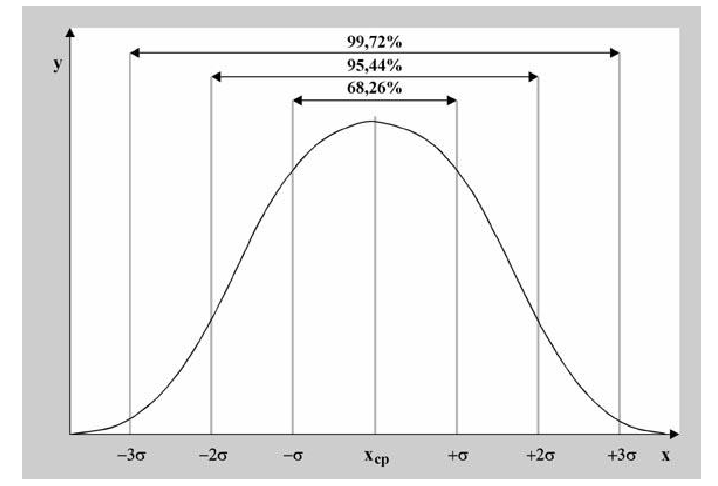
Правило 68-95-99,7.
Для нормального распределения количество значений, отличающихся от среднего на число, меньшее чем одно стандартное отклонение, составляют 68,27 % выборок. В то же время количество значений, отличающиеся от среднего на два стандартных отклонения, составляют 95,45 %, а на три стандартных отклонения — 99,73 %.
Около 68 % значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх. Этот факт является частным случаем правила 3 сигм для нормальной выборки.
Более точно, вероятность получить нормальное число в интервале между 

С точностью до 12 значащих цифр значения для 
 |
 |
 |
 |
OEIS |
|---|---|---|---|---|
| 1 | 0,682689492137 | 0,317310507863 |
3,15148718753 |
A178647 |
| 2 | 0,954499736104 | 0,045500263896 |
21,9778945080 |
A110894 |
| 3 | 0,997300203937 | 0,002699796063 |
370,398347345 |
A270712 |
| 4 | 0,999936657516 | 0,000063342484 |
15787.1927673 |
|
| 5 | 0,999999426697 | 0,000000573303 |
1744277,89362 |
|
| 6 | 0,999999998027 | 0,000000001973 |
506797345,897 |
Свойства[править | править код]
Моменты[править | править код]
Моментами и абсолютными моментами случайной величины 




Если 


Здесь 




Центральные абсолютные моменты для неотрицательных целых 
Последняя формула справедлива также для произвольных 
Преобразование Фурье и характеристическая функция[править | править код]
Преобразование Фурье нормальной плотности вероятности 


- где
есть мнимая единица.
Если математическое ожидание 


В теории вероятности, преобразование Фурье плотности распределения действительной случайной величины 




Бесконечная делимость[править | править код]
Нормальное распределение является бесконечно делимым.
Если случайные величины 








Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.
Максимальная энтропия[править | править код]
Нормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину[11][12].
Правило трёх сигм для гауссовской случайной величины[править | править код]

График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.
Правило трёх сигм (
- где
— математическое ожидание и параметр нормальной случайной величины.
Более точно — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.
Моделирование нормальных псевдослучайных величин[править | править код]
При компьютерном моделировании, особенно при применении метода Монте-Карло, желательно использовать величины, распределенные по нормальному закону. Многие алгоритмы дают стандартные нормальные величины, так как нормальную величину 
- где Z — стандартная нормальная величина.
Алгоритмы также используют различные преобразования равномерных величин.
Простейшие приближённые методы моделирования основываются на центральной предельной теореме. Если сложить достаточно большое количество независимых одинаково распределённых величин с конечной дисперсией, то сумма будет иметь распределение, близкое к нормальному. Например, если сложить 100 независимых стандартно равномерно распределённых случайных величин, то распределение суммы будет приближённо нормальным.
Для программного генерирования нормально распределённых псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределённую величину на базе одной равномерно распределённой.
Также существует алгоритм Зиккурат, который работает даже быстрее преобразования Бокса — Мюллера. Тем не менее, сложнее в реализации, но его применение оправдано в случаях, когда требуется генерирование очень большого числа неравномерно распределённых случайных чисел.
Нормальное распределение в природе и приложениях[править | править код]
Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
- отклонение при стрельбе;
- погрешности измерений (однако погрешности некоторых измерительных приборов имеют иное распределение);
- некоторые характеристики живых организмов в популяции.
Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например биномиальное и пуассоновское. Этим распределением моделируются многие недетерминированные физические процессы[13].
Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование параметров личности человека в психологии и психиатрии.
Связь с другими распределениями[править | править код]
- Отношение квадратов двух стандартных нормальных случайных величин имеет распределение Фишера со степенями свободы
История[править | править код]
Впервые нормальное распределение как предел биномиального распределения при 
См. также[править | править код]
- Аддитивный белый гауссовский шум
- Логнормальное распределение
- Равномерное распределение
- Центральная предельная теорема
- Двумерное нормальное распределение
- Многомерное нормальное распределение
- Распределение хи-квадрат
- Статистический критерий
- Частотное распределение
Примечания[править | править код]
- ↑ Вентцель Е. С. Теория вероятностей. — 10-е изд., стереотипное.. — М.: Academia, 2005. — 576 с. — ISBN 5-7695-2311-5.
- ↑ Ширяев А. Н. Вероятность. — М.: Наука, 1980.
- ↑ 1 2 Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 139—140.
- ↑ Wasserman L. All of Statistics. — New York, NY: Springer, 2004. — С. 142. — 433 с. — ISBN 978-1-4419-2322-6.
- ↑ Доказательство см. Гауссов интеграл
- ↑ Halperin, Hartley & Hoel, 1965, item 7.
- ↑ McPherson (1990)
- ↑ Wolfram|Alpha: Computational Knowledge Engine. Wolframalpha.com. Дата обращения: 3 марта 2017.
- ↑ Bryc (1995, p. 23)
- ↑ Bryc (1995, p. 24)
- ↑ Cover, Thomas M.; Thomas, Joy A. Elements of Information Theory. — John Wiley and Sons, 2006. — С. 254.
- ↑ Park, Sung Y.; Bera, Anil K. Maximum Entropy Autoregressive Conditional Heteroskedasticity Model (англ.) // Journal of Econometrics (англ.) (рус. : journal. — Elsevier, 2009. — P. 219—230. Архивировано 7 марта 2016 года.
- ↑ Талеб Н. Н. Чёрный лебедь. Под знаком непредсказуемости = The Black Swan: The Impact of the Highly Improbable. — КоЛибри, 2012. — 525 с. — ISBN 978-5-389-00573-0.
- ↑ Королюк, 1985, с. 135.
- ↑ Галкин В. М., Ерофеева Л. Н., Лещева С. В. Оценки параметра распределения Коши // Труды Нижегородского государственного технического университета им. Р. Е. Алексеева. — 2014. — № 2(104). — С. 314—319. — УДК 513.015.2(G).
- ↑ Lukacs, Eugene. A Characterization of the Normal Distribution (англ.) // The Annals of Mathematical Statistics (англ.) (рус. : journal. — 1942. — Vol. 13, no. 1. — P. 91—3. — ISSN 0003-4851. — doi:10.1214/aoms/1177731647. — JSTOR 2236166.
- ↑ Lehmann, E. L.ruen. Testing Statistical Hypotheses. — 2nd. — Springer (англ.) (рус., 1997. — С. 199. — ISBN 978-0-387-94919-2.
- ↑ The doctrine of chances; or, a method of calculating the probability of events in play, L., 1718, 1738, 1756; L., 1967 (репродуцир. изд.); Miscellanea analytica de scriebus et quadraturis, L., 1730.
Литература[править | править код]
- Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
- Halperin, Max; Hartley, Herman O.; Hoel, Paul G. Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation (англ.) // The American Statistician (англ.) (рус. : journal. — 1965. — Vol. 19, no. 3. — P. 12—14. — doi:10.2307/2681417. — JSTOR 2681417.
- McPherson, Glen. Statistics in Scientific Investigation: Its Basis, Application and Interpretation (англ.). — Springer-Verlag, 1990. — ISBN 978-0-387-97137-7.
- Bryc, Wlodzimierz. The Normal Distribution: Characterizations with Applications (англ.). — Springer-Verlag, 1995. — ISBN 978-0-387-97990-8.
Ссылки[править | править код]
- Таблица значений функции стандартного нормального распределения
- Онлайн расчёт вероятности нормального распределения
Содержание:
Нормальный закон распределения:
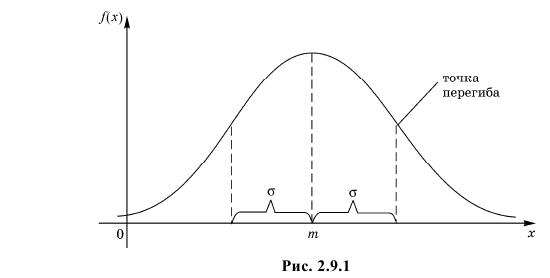
Нормальный закон распределения имеет плотность вероятности
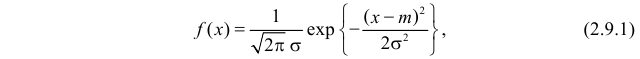
где 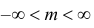
График функции плотности вероятности (2.9.1) имеет максимум в точке 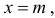 а точки перегиба отстоят от точки
а точки перегиба отстоят от точки 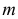 на расстояние
на расстояние 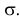 При
При 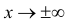 функция (2.9.1) асимптотически приближается к нулю (ее график изображен на рис. 2.9.1).
функция (2.9.1) асимптотически приближается к нулю (ее график изображен на рис. 2.9.1).
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр  равен математическому ожиданию нормально распределенной случайной величины, а дисперсия
равен математическому ожиданию нормально распределенной случайной величины, а дисперсия  Если
Если  т.е. X имеет нормальный закон распределения с параметрами
т.е. X имеет нормальный закон распределения с параметрами 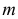 и
и 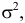 то
то 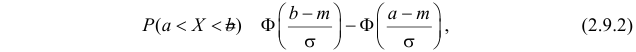
где 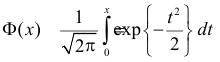 – функция Лапласа
– функция Лапласа
Значения функции 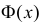 можно найти по таблице (см. прил., табл. П2). Функция Лапласа нечетна, т.е.
можно найти по таблице (см. прил., табл. П2). Функция Лапласа нечетна, т.е. 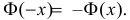 Поэтому ее таблица дана только для неотрицательных
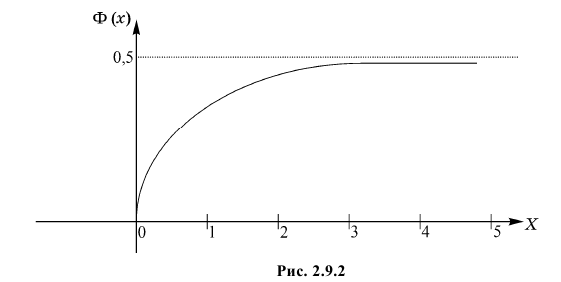
Поэтому ее таблица дана только для неотрицательных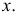 График функции Лапласа изображен на рис. 2.9.2. При значениях
График функции Лапласа изображен на рис. 2.9.2. При значениях 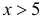 она практически остается постоянной. Поэтому в таблице даны значения функции только для
она практически остается постоянной. Поэтому в таблице даны значения функции только для 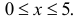 При значениях
При значениях 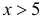 можно считать, что
можно считать, что 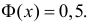
Если 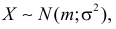 то
то
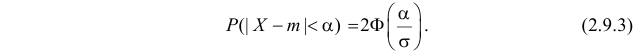
Пример:
Случайная величина X имеет нормальный закон распределения 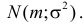 Известно, что
Известно, что 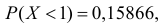 а
а 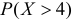
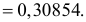 Найти значения параметров
Найти значения параметров 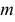 и
и 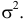
Решение. Воспользуемся формулой (2.9.2): 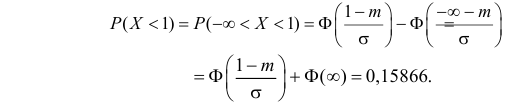
Так как 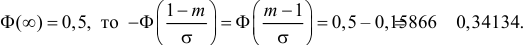 По таблице функции Лапласа (см. прил., табл. П2) находим, что
По таблице функции Лапласа (см. прил., табл. П2) находим, что 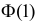
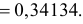 Поэтому
Поэтому 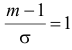 или
или 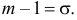
Аналогично 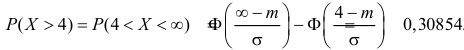 Так как
Так как 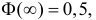 то
то 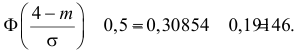 По таблице функции Лапласа (см. прил., табл. П2) находим, что
По таблице функции Лапласа (см. прил., табл. П2) находим, что 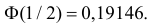 Поэтому
Поэтому 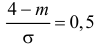 или
или 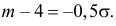 Из системы двух уравнений
Из системы двух уравнений 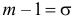 и
и 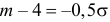 находим, что
находим, что 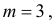 а
а 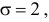 т.е.
т.е.  Итак, случайная величина X имеет нормальный закон распределения N(3;4).
Итак, случайная величина X имеет нормальный закон распределения N(3;4).
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
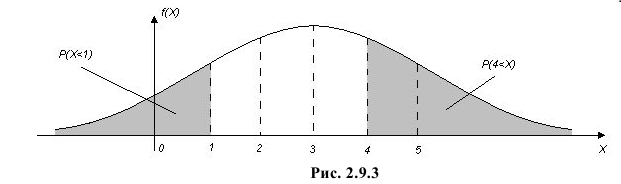
Ответ. 
Пример:
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 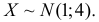 Вычислим сначала вероятность того, что в одном измерении ошибка не превзойдет 2 мк. По формуле (2.9.2)
Вычислим сначала вероятность того, что в одном измерении ошибка не превзойдет 2 мк. По формуле (2.9.2)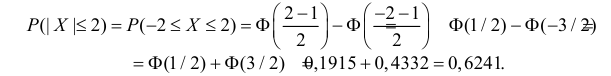
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
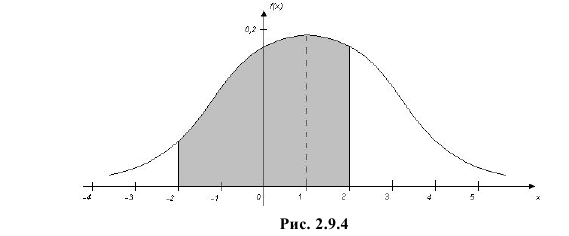
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна 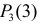
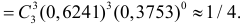
Ответ. 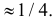
Пример:
Функция плотности вероятности случайной величины X имеет вид 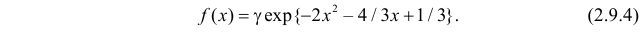
Требуется определить коэффициент 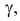 найти
найти 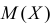 и
и 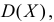 определить тип закона распределения, нарисовать график функции
определить тип закона распределения, нарисовать график функции 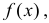 вычислить вероятность
вычислить вероятность 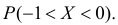
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 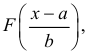 где
где 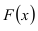 – фиксированная функция распределения, a
– фиксированная функция распределения, a 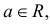
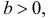 то говорят, что эти законы распределения принадлежат к одному виду или типу распределений. Параметр
то говорят, что эти законы распределения принадлежат к одному виду или типу распределений. Параметр 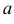 называют параметром сдвига,
называют параметром сдвига, 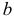 – параметром масштаба.
– параметром масштаба.
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице: 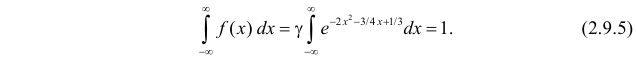
Преобразуем выражение в показателе степени, выделяя полный квадрат: 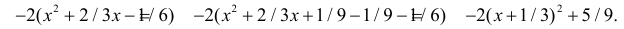
Тогда (2.9.5) можно записать в виде 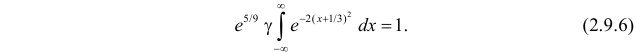
Сделаем замену переменных так, чтобы 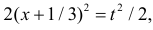 т.е.
т.е. 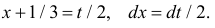 Пределы интегрирования при этом останутся прежними. Тогда (2.9.6) преобразуется к виду
Пределы интегрирования при этом останутся прежними. Тогда (2.9.6) преобразуется к виду

Умножим и разделим левую часть равенства на 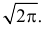 Получим равенство
Получим равенство 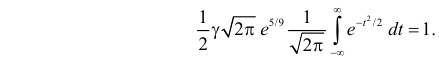
Так как 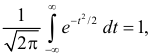 как интеграл по всей числовой оси от функции плотности вероятности стандартного нормального закона распределения N(0,1), то приходим к выводу, что
как интеграл по всей числовой оси от функции плотности вероятности стандартного нормального закона распределения N(0,1), то приходим к выводу, что

Поэтому
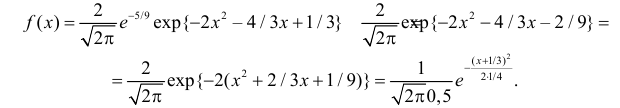
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 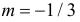 и
и 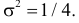 График функции плотности вероятности этого закона изображен на рис. 2.9.5. Распределение случайной величины X принадлежит к семейству нормальных законов распределения. По формуле (2.9.2)
График функции плотности вероятности этого закона изображен на рис. 2.9.5. Распределение случайной величины X принадлежит к семейству нормальных законов распределения. По формуле (2.9.2)
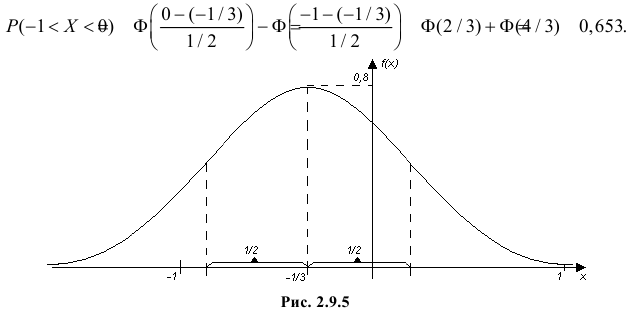
Ответ. 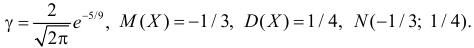
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 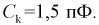 Сколько транзисторов попадет в группу
Сколько транзисторов попадет в группу 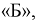 если в нее попадают транзисторы с емкостью коллекторного перехода от 1,80 до 2,00 пФ. Цех выпустил партию в 1000 штук.
если в нее попадают транзисторы с емкостью коллекторного перехода от 1,80 до 2,00 пФ. Цех выпустил партию в 1000 штук.
Решение.
Статистическими исследованиями в цеху установлено, что 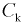 можно трактовать как случайную величину, подчиняющуюся нормальному закону.
можно трактовать как случайную величину, подчиняющуюся нормальному закону.
Чтобы вычислить количество транзисторов, попадающих в группу  необходимо учитывать, что вся партия транзисторов имеет разброс параметров, накрывающий всю (условно говоря) числовую ось. То есть кривая Гаусса охватывает всю числовую ось, центр ее совпадает с
необходимо учитывать, что вся партия транзисторов имеет разброс параметров, накрывающий всю (условно говоря) числовую ось. То есть кривая Гаусса охватывает всю числовую ось, центр ее совпадает с  (т. к. все установки в цеху настроены на выпуск транзисторов именно с этой емкостью). Вероятность попадания отклонений параметров всех транзисторов на всю числовую ось равна 1. Поэтому нам необходимо фактически определить вероятность попадания случайной величины
(т. к. все установки в цеху настроены на выпуск транзисторов именно с этой емкостью). Вероятность попадания отклонений параметров всех транзисторов на всю числовую ось равна 1. Поэтому нам необходимо фактически определить вероятность попадания случайной величины 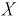 в интервал
в интервал 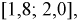 а затем пересчитать количество пропорциональной вероятности.
а затем пересчитать количество пропорциональной вероятности.
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения 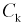
дает 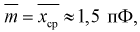 оценка среднего квадратического отклонения
оценка среднего квадратического отклонения 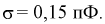
Обозначая 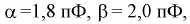 подставим приведенные значения в (6.3):
подставим приведенные значения в (6.3):
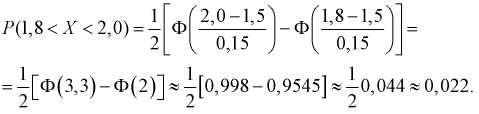
Тогда количество транзисторов 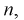 попавших в интервал [1,8; 2,0] пФ, можно найти так:
попавших в интервал [1,8; 2,0] пФ, можно найти так: 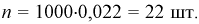 Таким образом можно планировать и рассчитывать количество транзисторов, попадающих в ту или иную группу.
Таким образом можно планировать и рассчитывать количество транзисторов, попадающих в ту или иную группу.
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, “от 180 до 181 включительно”.
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
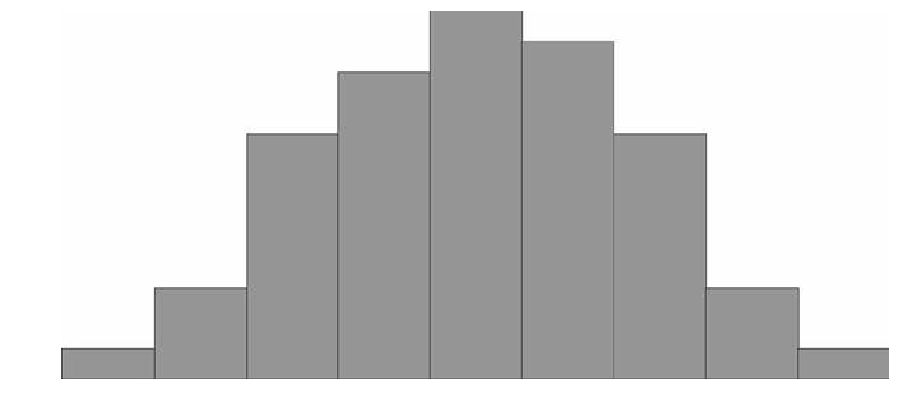
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, “оплывет” вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади “ломтика” кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста – достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона – чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько “популярен” выбранный нами рост. Напомним, что мода – самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 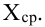 и отклонение s. Кроме того, любой житель города с вероятностью 68% попадет в диапазон роста
и отклонение s. Кроме того, любой житель города с вероятностью 68% попадет в диапазон роста 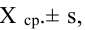 с вероятностью 95% – в диапазон
с вероятностью 95% – в диапазон 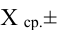
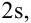 и с вероятностью 99,7% – в диапазон
и с вероятностью 99,7% – в диапазон 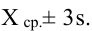
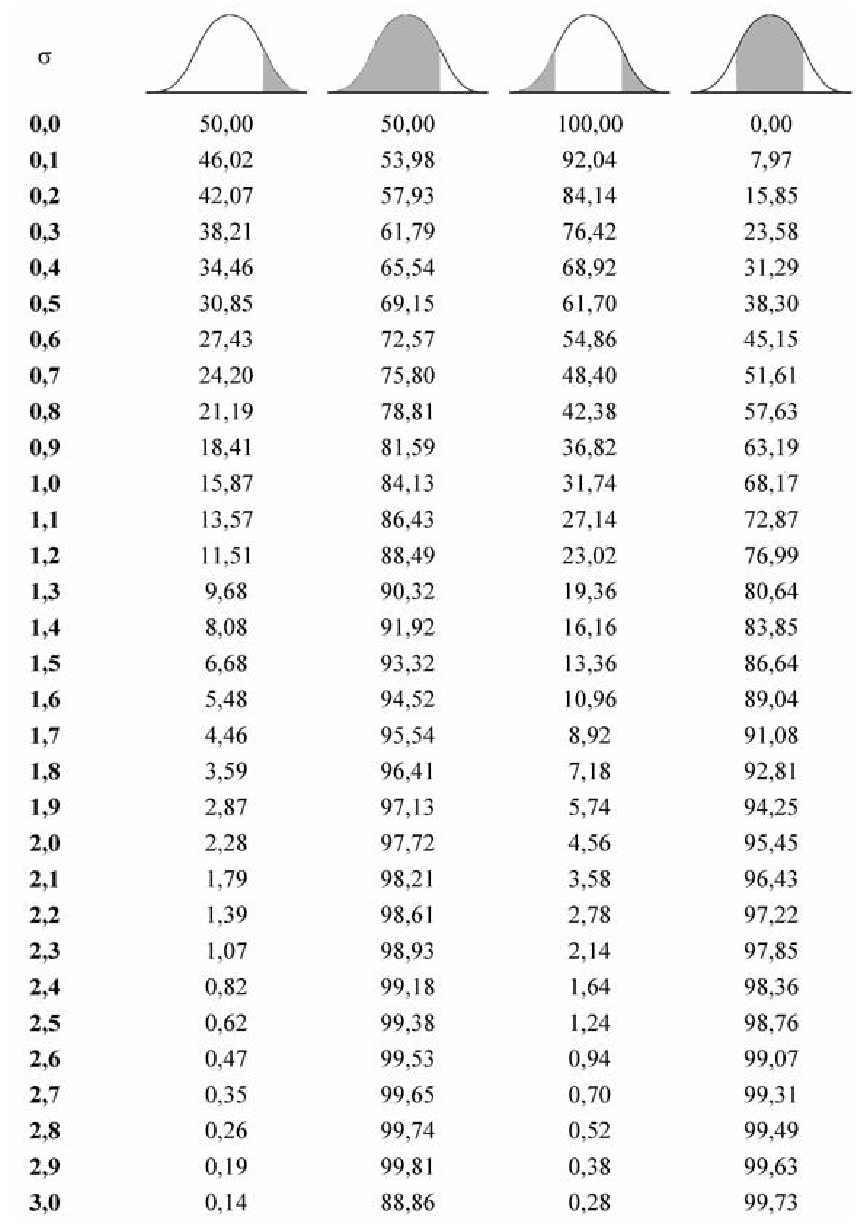
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой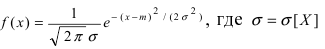 – средне-квадратичное отклонение, a m = М[Х] – математическое ожидание.
– средне-квадратичное отклонение, a m = М[Х] – математическое ожидание.
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
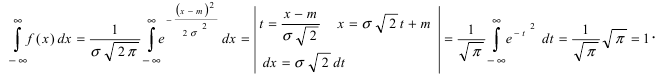
Выясним геометрический смысл параметров  Зафиксируем параметр
Зафиксируем параметр  и будем изменять параметр m. Построим графики соответствующих кривых (Рис. 8).
и будем изменять параметр m. Построим графики соответствующих кривых (Рис. 8). 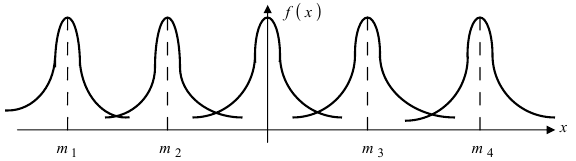
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 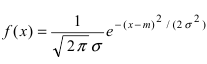 получается путем смещения кривой
получается путем смещения кривой 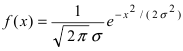 вдоль оси абсцисс на величину m, поэтому параметр m определяет центр тяжести данного распределения. Кроме того, из рисунка видно, что функция
вдоль оси абсцисс на величину m, поэтому параметр m определяет центр тяжести данного распределения. Кроме того, из рисунка видно, что функция 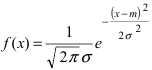 достигает своего максимального значения в точке
достигает своего максимального значения в точке 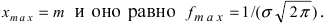 Из этой формулы видно, что при уменьшении параметра
Из этой формулы видно, что при уменьшении параметра 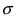 значение максимума возрастает. Так как площадь под кривой плотности распределения всегда равна 1, то с уменьшением параметра
значение максимума возрастает. Так как площадь под кривой плотности распределения всегда равна 1, то с уменьшением параметра 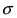 кривая вытягивается вдоль оси ординат, а с увеличением параметра
кривая вытягивается вдоль оси ординат, а с увеличением параметра 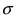 кривая прижимается к оси абсцисс. Построим график нормальной плотности распределения при m = 0 и разных значениях параметра
кривая прижимается к оси абсцисс. Построим график нормальной плотности распределения при m = 0 и разных значениях параметра 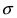 (Рис. 9):
(Рис. 9): 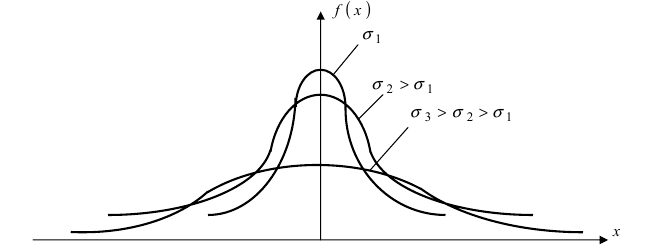
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
Интегральная функция нормального распределения имеет вид: 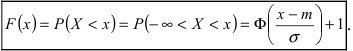
График функции распределения имеет вид (Рис. 10): 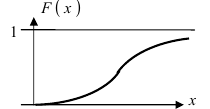
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 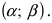 Согласно определению
Согласно определению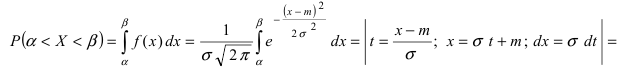 пересчитаем пределы интегрирования
пересчитаем пределы интегрирования 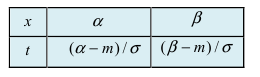
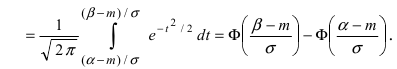 Следовательно,
Следовательно,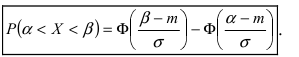
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 – график функции Лапласа проходит через начало координат.
- Ф (-х) = – Ф(х) – функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
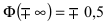 – график функции Лапласа имеет горизонтальные асимптоты
– график функции Лапласа имеет горизонтальные асимптоты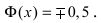
Следовательно, график функции Лапласа имеет вид (Рис. 11): 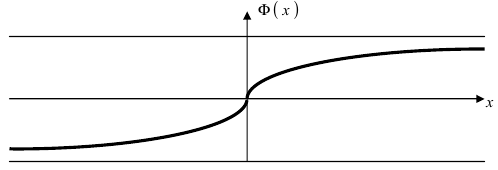
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 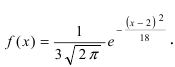 Определить вероятность попадания случайной величины X в интервал (-1;8).
Определить вероятность попадания случайной величины X в интервал (-1;8).
Решение:
Согласно условиям задачи 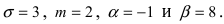 Поэтому искомая вероятность равна:
Поэтому искомая вероятность равна: 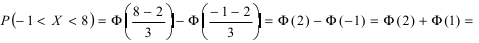 0,4772 + 0,3413 = 0,8185.
0,4772 + 0,3413 = 0,8185.
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 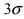 .
.
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 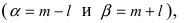 то, используя свойство нечетности функции Лапласа, получим
то, используя свойство нечетности функции Лапласа, получим
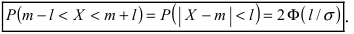
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 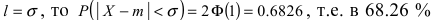 случаях нормальная случайная величина X отличается от своего математического ожидания на величину равную среднему квадратичному отклонению. Если
случаях нормальная случайная величина X отличается от своего математического ожидания на величину равную среднему квадратичному отклонению. Если 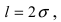 то вероятность отклонения равна
то вероятность отклонения равна 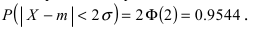 Наконец, в случае
Наконец, в случае 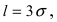 то вероятность отклонения равна
то вероятность отклонения равна 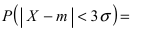
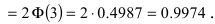 Из последнего равенства видно, что только приблизительно в 0.3 % случаях отклонение нормальной случайной величины X от своего математического ожидания превышает
Из последнего равенства видно, что только приблизительно в 0.3 % случаях отклонение нормальной случайной величины X от своего математического ожидания превышает 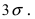 Это свойство нормальной случайной величины X называется правилом “трех сигм”. На практике это правило применяется следующим образом: если отклонение случайной величины X от своего математического ожидания не превышает
Это свойство нормальной случайной величины X называется правилом “трех сигм”. На практике это правило применяется следующим образом: если отклонение случайной величины X от своего математического ожидания не превышает 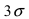 то эта случайная величина распределена по нормальному закону.
то эта случайная величина распределена по нормальному закону.
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
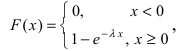 называется экспоненциальным или показательным.
называется экспоненциальным или показательным.
График экспоненциального закона распределения имеет вид (Рис. 12): 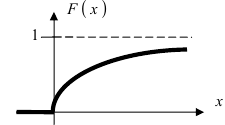
Рис. 12. График функции распределения для случая экспоненциального закона.
Дифференциальная функция распределения (плотность вероятности) имеет вид: 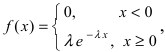 а ее график показан на (Рис. 13):
а ее график показан на (Рис. 13): 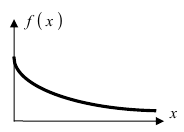
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 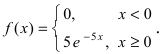 Найти вероятность того, что случайная величина X попадет в интервал (2; 4), математическое ожидание M[Х], дисперсию D[X] и среднее квадратичное отклонение
Найти вероятность того, что случайная величина X попадет в интервал (2; 4), математическое ожидание M[Х], дисперсию D[X] и среднее квадратичное отклонение 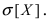 Проверить выполнение правила “трех сигм” для показательного распределения.
Проверить выполнение правила “трех сигм” для показательного распределения.
Решение:
Интегральная функция распределения 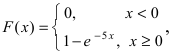 следовательно, вероятность того, что случайная величина X попадет в интервал (2; 4), равна:
следовательно, вероятность того, что случайная величина X попадет в интервал (2; 4), равна: 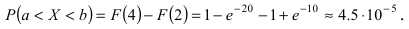 Математическое ожидание
Математическое ожидание 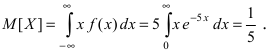 Вычислим значение величины М
Вычислим значение величины М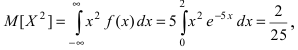 тогда дисперсия случайной величины X равна
тогда дисперсия случайной величины X равна 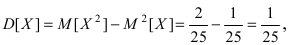 а средне-квадратичное
а средне-квадратичное
отклонение 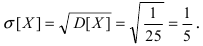 Для проверки правила “трех сигм” вычислим вероятность заданного отклонения:
Для проверки правила “трех сигм” вычислим вероятность заданного отклонения:
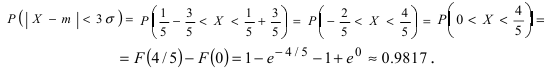
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Нормально разбираемся в Нормальном распределении
Уровень сложности
Средний
Время на прочтение
6 мин
Количество просмотров 12K
Всем привет. Это пост про интуитивное понимание Нормального распределения.
Обычный курс теории вероятностей проходит следующим образом. Сначала вам даются понятные и относительно простые концепции. Все легко объясняется “на пальцах”: подбрасывание монеток, красные и белые шары в урнах, кролики в клетках и так далее.
Но в следующей теме вас бросают в яму к этому монстру:
Внезапно больше нет ни монет, ни урн, ни шаров. Вам только говорят запомнить эту функцию плотности вероятности Нормального распределения, что это очень важно и что график похож на колокол. В остальном вы предоставлены сами себе.
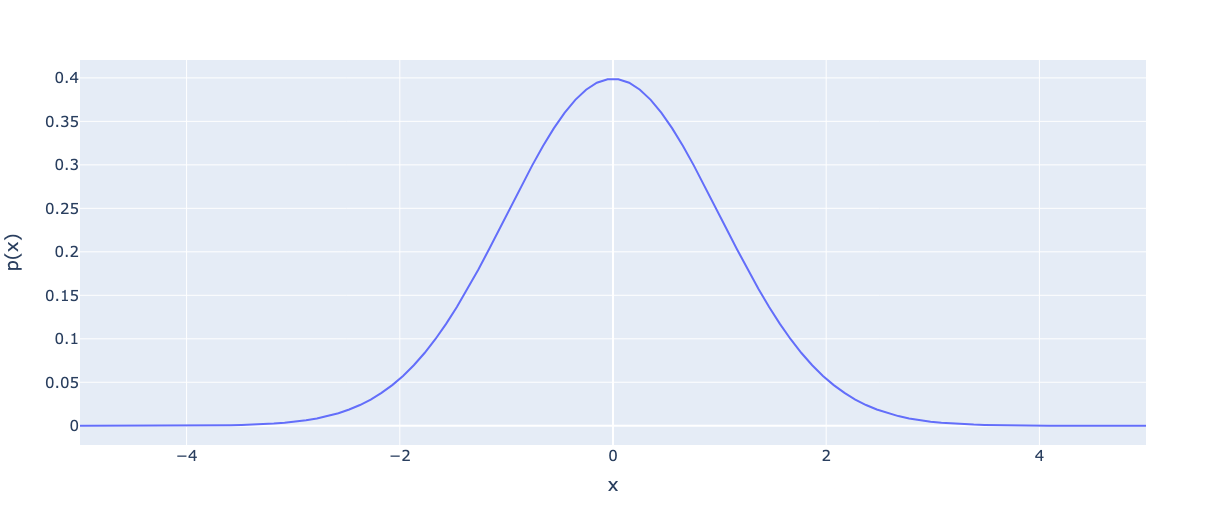
Но что это такое? Почему там экспонента? Почему минус? Зачем делить на 2 сигма-квадрат? Откуда взялось число Пи? Куда делись монеты, шары, урны и кролики? Почему мы от интуитивных объяснений перешли к тупому запоминанию?
Каждая формула несет некоторую идею. В этом посте мы будем препарировать нормальное распределение, пока не поймем, что оно в себе несет. В конце мы выведем функцию плотности вероятности, чтобы понять, откуда она берется.
Я покажу, что, несмотря на пугающий вид, Нормальное распределение это не конь в вакууме. Это все еще про броски монеток, урны и другие вещи из реального мира.
Самореклама
Эта статья является переводом моей статьи из Substack Understanding the Normal Distribution for Real. Переходите туда если вам удобнее читать на английском или хочется получать такой контент по почте.
Так же у меня есть телеграм канал @boris_again
Препарируем монстра
Начнем изнутри. Разберемся в идеях, стоящих за этим куском:
Режем монстра на части.
Где это среднее, один из параметров распределения.
Посмотрим на график функции при
:
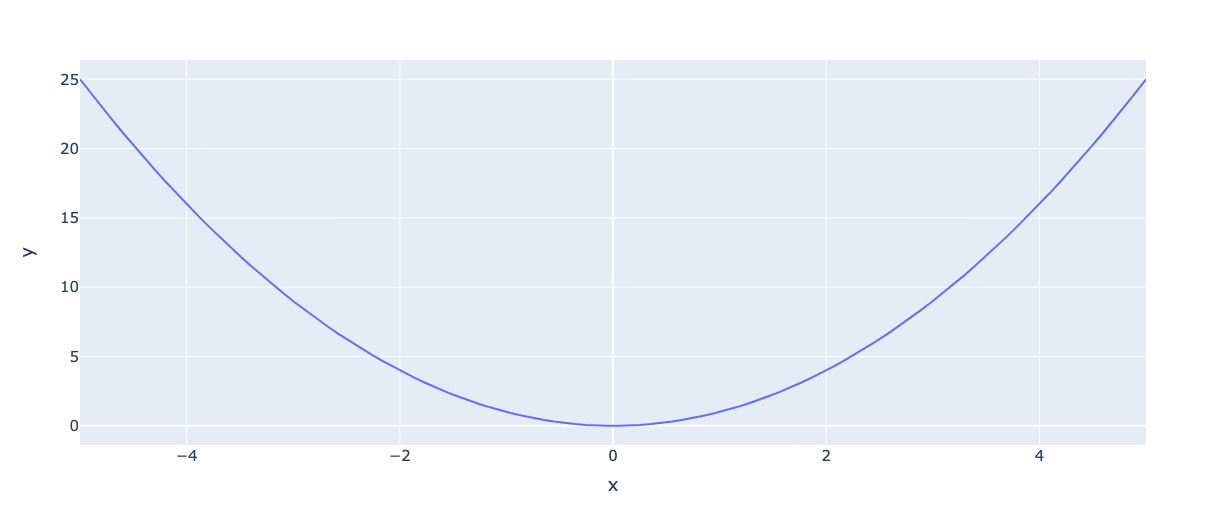
Мы видим параболу. Она похожа на форму колокола, но перевернутую. Также заметьте, что ось произвольна, а не находится в диапазоне
, так что это пока не распределение.
Обратите внимание, что чем дальше от среднего значения, тем больше значение функции. Во-вторых, квадрат позволяет нам одинаково относиться к отрицательным и положительным значениям. Он делает форму колокола симметричной.
Идея: определяет местоположение вершины колокола, и распределение становится симметричным.

Наконец-то, форма колокола! Но значения y отрицательны. Естественно у нас не может быть отрицательных вероятностей.
Что будет если менять ?
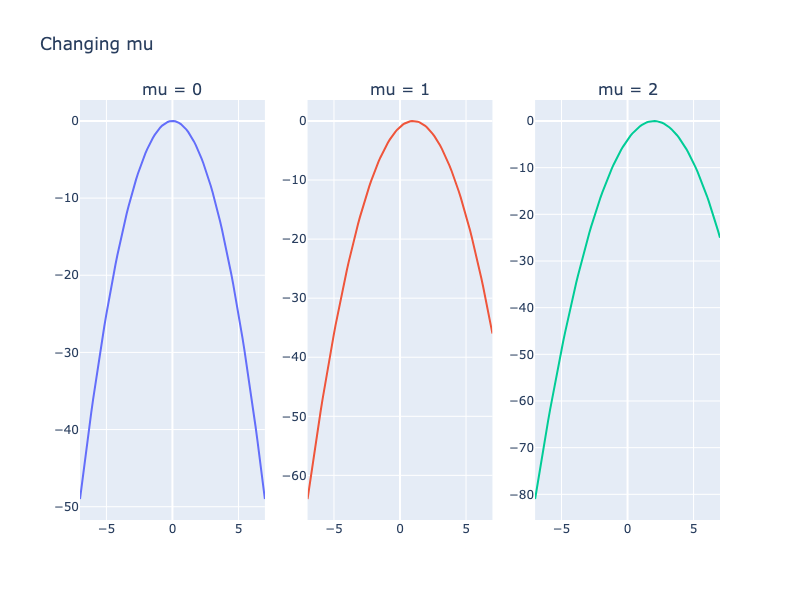
Вывод: Изменение перемещает пик колокола в другое место.
Добавим следующий кусок, деление на сигма квадрат:
Здесь сигма — это второй параметр распределения: стандартное отклонение. Квадрат сигмы — это дисперсия. Что это дает нашему распределению?
Попробуем поменять ее:
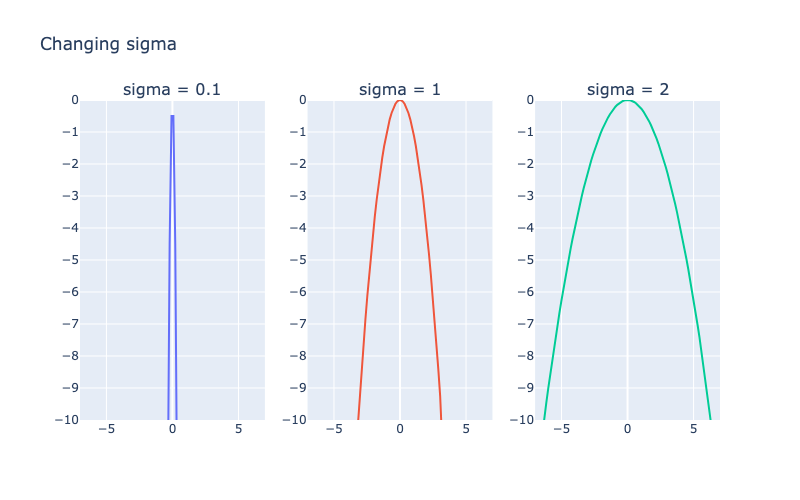
Идея: знаменатель с сигмой задает скорость изменения значения функции по мере удаления от среднего. Меньшие сигмы создают более узкие колоколообразные формы.
Мы можем рассматривать сигму как меру неопределенности. Малые сигмы указывают на то, что среднее значение более вероятно. Большие сигмы распределяют вероятность по более широкому диапазону.
Сигма возводится в квадрат, чтобы показать: неопределенность возрастает квадратично (быстро), а не линейно (медленно). Другими словами, небольшая вариация данных сильно меняет колоколообразную кривую.
Отлично, у нас есть колоколообразная кривая. Но она не похожа на распределение вероятностей. Чтобы это было распределение, выходы должны находиться в пределах и в сумме равняться 1. Вот здесь и появляется экспонента.
Давайте построим на график около нуля:
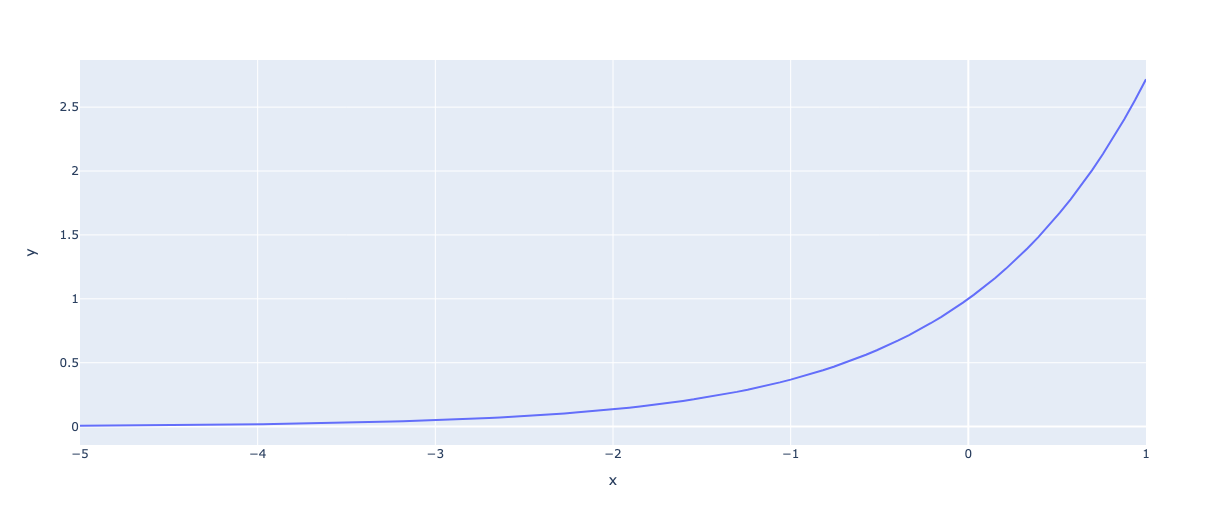
Обратите внимание: экспонента отображает любой отрицательный вход в значение между 0 и 1. В нашем случае аргумент всегда отрицательный.
Отлично! Теперь все значения находятся между , и у нас получилась нужная нам колоколообразная кривая. Мы закончили.
На самом деле нет. Это прекрасная колоколообразная кривая, но в сумме значения не равны 1. Один только пик почти равен 1.
Как сделать так, чтобы сумма была равна 1? Нормализовать!
Как бы вы нормализовали такую последовательность чисел, как: ? Легко: разделить на сумму.
В нашем случае функция — это не просто последовательность чисел. Она непрерывна. Тем не менее, идея та же. Чтобы получить сумму давайте проинтегрируем:
Теперь, когда у нас есть сумма, давайте разделим функцию на нее:
Наконец, мы собрали все части, чтобы получить нормальное распределение.
Если вм нужны подробности вычисления интеграла, то я рекомендую это видео:
Связь с Биномиальным распределением
Нормальное распределение тесно связано с биномиальным. Давайте отвлечемся и рассмотрим биномиальное распределение поближе. Это поможет нам получить полное представление о нормальном распределении.
Представьте, что у вас есть Substack рассылка, и вы собираетесь запустить рекламную кампанию, нацеленную на 100 человек. Вы знаете свою конверсию в подписку: 10%. Какова вероятность того, что подпишутся ровно 5 человек?
Давайте представим каждого пользователя в виде броска монеты. Он либо регистрируются с вероятностью , либо нет. Это может быть описано распределением Bernoulli(n, p), которое имеет следующую функцию массы вероятности:
Идея: это бросок монеты, есть два возможных исхода, и с вероятностью выпадает орел.
Это распределение позволяет отвечать на вопросы типа “Какова вероятность выпадения орла для этой монеты?” или, более практично, “Какова вероятность того, что пользователь подпишется?”.
Мы можем сложить несколько случайных величин Бернулли и получить Биномиальное распределение . Оно говорит нам о вероятности получения
успехов из
независимых испытаний Бернулли с вероятностью
.
Биномиальное распределение объединяет все независимые испытания, чтобы ответить на новые вопросы: “Какова вероятность выпадения 3 орлов из 3 бросков?” или “Сколько пользователей мы можем ожидать при регистрации?”
Вот PMF Биномиального распределения:
Где это Биномиальный коэффициент.
Биномиальный коэффициент используется для того, чтобы учесть множество способов регистрации человек. Например, при наличии четырех посетителей существует шесть способов зарегистрироваться двум из них.
Давайте подставим наши значения, чтобы найти вероятность того, что зарегистрируются ровно пять человек:
Ожидаемое количество подписчиков среди 5 пользователей равно просто умноженное на
, то есть 3.387. Мы также можем получить вероятность регистрации хотя бы 5 подписчиков, просуммировав по
и получим 0.94242.
Теперь давайте посмотрим, что происходит по мере роста числа испытаний.

Обратите внимание: с ростом результирующая PMF приближается к знакомой колоколообразной форме Нормального распределения.
Оказывается, что Нормальное распределение является предельным случаем биномиального распределения. Биномиальное распределение отвечает на вопрос: “Насколько вероятно получить k орлов из n бросков монеты?” Нормальное распределение имеет ту же идею, но дает приблизительный результат.
Нас интересует это приближение, потому что вычисление коэффициентов биномиального распределения для больших значений требует огромных вычислительных затрат. Факториалы в формуле являются самой большой проблемой. Например, для биномиальный коэффициент равен 75287520. Это очень дорогое вычисление, особенно если вам нужно суммировать по многим
.
Вместо вычисления биномиальной PMF мы можем аппроксимировать его вычислением PDF нормального распределения. Это гораздо быстрее: нужно только подставить несколько чисел в формулу. Этот подход часто используется в опросах.
Основная идея нормального распределения: число успехов в большом количестве независимых испытаний типа “да или нет” распределено симметрично вокруг среднего значения, а форма распределения описывается функцией Гаусса.
Надеюсь, теперь PMF нормального распределения больше не является просто страшной формулой в вакууме. Она по-прежнему связана с подбрасыванием монет и реальной жизнью, как и Биномиальное распределение
Выводим Нормальное распределение
Почему именно такая функция позволяет нам аппроксимировать Биномиальное распределение? Чтобы ответить на этот вопрос, нам нужно будет вывести PMF нормального распределения. Есть несколько способов сделать это, но мы будем использовать наши знания о том, что нормальное распределение является предельным случаем биномиального распределения. Я опишу только основные шаги, так как детали вывода довольно длинные, но вы можете найти полный вывод в этой статье.
Нормальное распределение является предельным случаем Биномиального, если не очень мало, и выполняется условие:
Если это не так, мы получаем распределение Пуассона, что тоже круто, но выходит за рамки этого поста.
Помните биномиальный PMF? Предположим, у нас есть последовательность испытаний Бернулли, каждое с вероятностью успеха , и мы повторяем этот эксперимент
раз. Пусть
— количество успехов в n испытаниях. Тогда
имеет биномиальное распределение с параметрами
. Функция массы вероятности
определяется как:
Самая тяжелая часть — факториал. Давайте воспользуемся приближением Cтирлинга, чтобы вычислить факториалы быстрее:
Подставив это в Биномиальный коэффициент мы получаем:
Это может выглядеть пугающе, но на самом деле это просто замена и некоторая перестановка терминов.
Подставляя это приближение в PMF Биномиального распределения, мы получаем:
Это функция плотности вероятности нормального распределения при , и квадратом
:
Вывод: гауссиана появляется, когда мы заменяем вычисления факториалов в биномиальном приближении.
Завершение
Мы разобрали нормальное распределение на его компоненты, исследовали связь между биномиальным и нормальным распределением и, наконец, получили нормальную PDF. Надеюсь, теперь для вас это не столько таинственный монстр, сколько прекрасный способ описания явлений реального мира.
Код для графиков вы можете найти в этом коллабе.
Спасибо за внимание! Если вам нравится такой контент, то подписывайтесь на мой телеграм канал @boris_again и substack.
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы – случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
Нормальный закон распределения и его параметры:
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.
Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.
Нормальный закон распределения характеризуется плотностью вероятности вида:
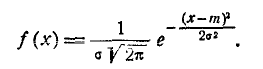 (6.1.1)
(6.1.1)
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная  , соответствует точке х = m по мере удаления от точки m плотность распределения падает, и при
, соответствует точке х = m по мере удаления от точки m плотность распределения падает, и при  кривая асимптотически приближается к оси абсцисс.
кривая асимптотически приближается к оси абсцисс.
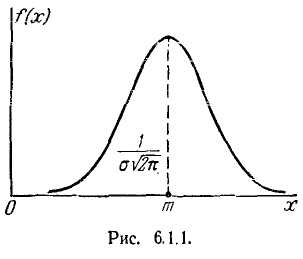
Выясним смысл численных параметров т и о, входящих в выражение нормального закона (5.1.1); докажем, что величина m есть не что иное, как математическое ожидание, а величина 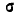 — среднее квадратическое отклонение величины X. Для этого вычислим основные числовые характеристики величины X — математическое ожидание и дисперсию.
— среднее квадратическое отклонение величины X. Для этого вычислим основные числовые характеристики величины X — математическое ожидание и дисперсию.
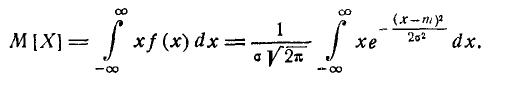
Применяя замену переменной
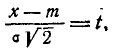
имеем:
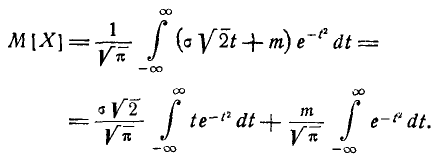 (6.1.2)
(6.1.2)
Нетрудно убедиться, что первый из двух интервалов в формуле (5.1.2) равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:
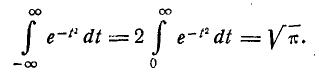 (6.1.3)
(6.1.3)
Следовательно, М[Х] = m
т. е. параметр m представляет собой математическое ожидание вели- величины X. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно — ц. р.). Вычислим дисперсию величины X:
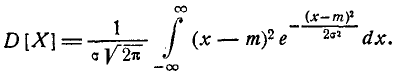
Применив снова замену переменной
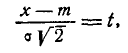
имеем:
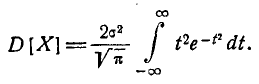
Интегрируя по частям, получим:
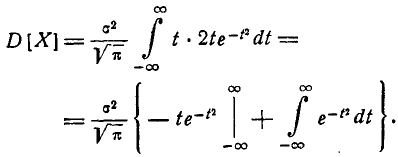
Первое слагаемое в фигурных скобках равно нулю (так как 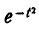 При
При 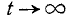 убывает быстрее, чем возрастает любая степень f), второе слагаемое по формуле 5.1.3) равно
убывает быстрее, чем возрастает любая степень f), второе слагаемое по формуле 5.1.3) равно 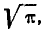 откуда
откуда 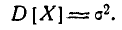
Следовательно, параметр о в формуле 5.1.1) есть не что иное, как среднее квадратическое отклонение величины X.
Выясним смысл параметров m и 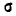 нормального распределения. Непосредственно из формулы 5.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (х — m) на обратный выражение 5.1.1) не меняется. Если изменять центр рассеивания т. кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
нормального распределения. Непосредственно из формулы 5.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (х — m) на обратный выражение 5.1.1) не меняется. Если изменять центр рассеивания т. кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
Размерность центра рассеивания—та же, что размерность случайной величины X.
Параметр о характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна 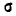 ; при увеличении
; при увеличении 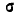 максимальная ордината уменьшается. Так как площадь
максимальная ордината уменьшается. Так как площадь
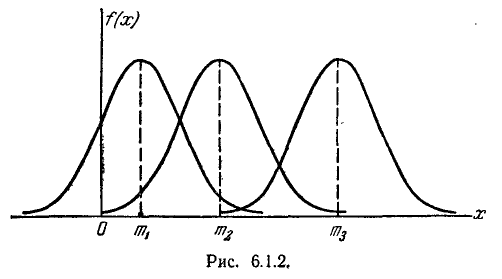
кривой распределения всегда должна оставаться равной единице, то при увеличении о кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении  кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (/, //, ///) при m=0; из них кривая l соответствует
кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (/, //, ///) при m=0; из них кривая l соответствует 
самому большому, а кривая /// — самому малому значению 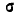 . Изменение параметра
. Изменение параметра 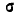 равносильно изменению масштаба кривой распределения— увеличению масштаба по одной оси и такому же уменьшению по другой.
равносильно изменению масштаба кривой распределения— увеличению масштаба по одной оси и такому же уменьшению по другой.
Размерность параметра 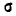 , естественно, совпадает с раpмерноcтью случайной величины X.
, естественно, совпадает с раpмерноcтью случайной величины X.
В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению 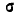 :
: 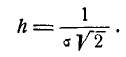
Размерность меры точности обратна размерности случайной величины.
Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности h, можно записать нормальный закон в виде: 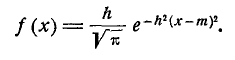

Моменты нормального распределения
Выше мы доказали, что математическое ожидание случайной вели- величины, подчиненной нормальному закону 6.1.1), равно m, а среднее квадратическое отклонение равно 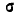 .
.
Выведем общие формулы для центральных моментов любого порядка.
По определению:
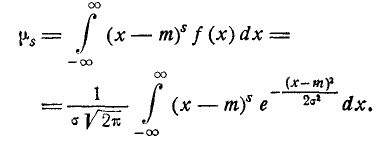
Делая замену переменной
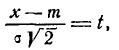
получим:
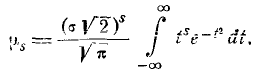 (6.2.1)
(6.2.1)
Применим к выражению (6.2.1) формулу интегрирования по частям: 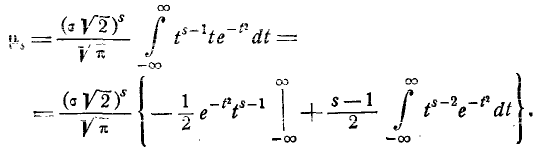
Имея в виду, что первый член внутри скобок равен нулю, получим: 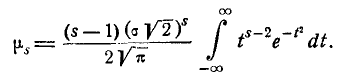 (6.2.2)
(6.2.2)
Из формулы (6.2.1) имеем следующее выражение для 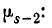
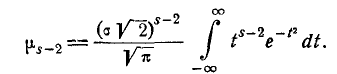 (6.2.3)
(6.2.3)
Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем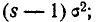 следовательно,
следовательно,
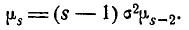 (6.2.4)
(6.2.4)
Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 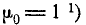 и
и  можно вычислить центральные моменты всех порядков. Так как
можно вычислить центральные моменты всех порядков. Так как  то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.
то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.
Для четных s из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:
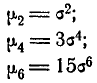
и т. д. Общая формула для момента s-гo порядка при любом четном s имеет вид:
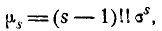
где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s— 1. Так как для нормального закона  то асимметрия его также равна нулю:
то асимметрия его также равна нулю:
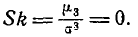
Из выражения четвертого момента
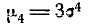
имеем:
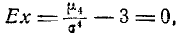
‘) Нулевой момент любой случайной величины равен единице как математическое ожидание нулевой степени этой величины.
т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса — характеризовать сравнительную крутость данного закона по сравнению с нормальным.
Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m,  , на участок от а до
, на участок от а до  Для вычисления этой вероятности воспользуемся общей формулой
Для вычисления этой вероятности воспользуемся общей формулой
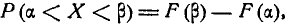 (6.3.1)
(6.3.1)
где F (х)— функция распределения величины X.
Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, 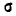 . Плот- Плотность распределения величины X равна:
. Плот- Плотность распределения величины X равна:
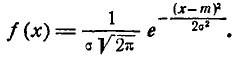 (6.3.2)
(6.3.2)
Отсюда находим функцию распределения
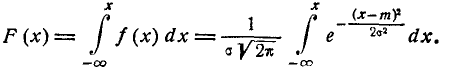 (6.3.3)
(6.3.3)
Сделаем в интеграле (6.3.3) замену переменной
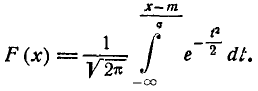 (6.3.4)
(6.3.4)
и приведем его к виду:
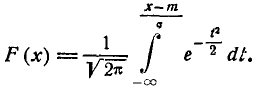 (6.3.4)
(6.3.4)
Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения  или
или (так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:
(так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:
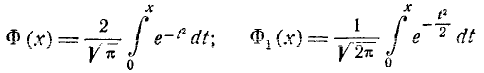
и т. д. Какой из этих функций пользоваться — вопрос вкуса. Мы выберем в качестве такой функции
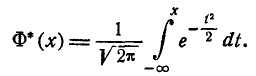 (6.3.5)
(6.3.5)
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами от m = 0, 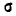 =1.
=1.
Условимся называть функцию Ф*(х) нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции Ф*(х)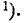
Выразим функцию распределения (6.3.3) величины X с пара- параметрами m и 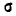 через нормальную функцию распределения Ф*(х). Очевидно,
через нормальную функцию распределения Ф*(х). Очевидно,
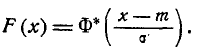 (6.3.6)
(6.3.6)
Теперь найдем вероятность попадания случайной величины X на участок от а до 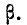 Согласно формуле (6.3.1)
Согласно формуле (6.3.1)
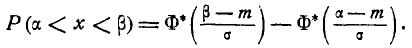 (6.3.7)
(6.3.7)
Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф* (х), соответствующую простейшему нормальному . закону с параметрами 0,1. Заметим, что аргументы функции Ф* в фор- формуле (6.3.7) имеют очень простой смысл: 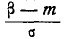 есть расстояние от правого конца участка
есть расстояние от правого конца участка 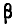 до центра рассеивания, выраженное в средних квадратических отклонениях;
до центра рассеивания, выраженное в средних квадратических отклонениях; 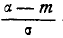 — такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания , и отрицательным, если слева.
— такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания , и отрицательным, если слева.
Как и всякая функция распределения,, функция Ф*(х) обладает свойствами:
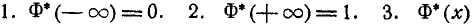 -неубывающая функция
-неубывающая функция
Кроме того, из симметричности нормального распределения с параметрами m = 0,  =1 относительно начала координат следует, что
=1 относительно начала координат следует, что
ф* (— х)=1— Ф* (х). (6.3.8)
 Для облегчения интерполяции в таблицах рядом со значениями функции приведены ее приращения за один шаг таблиц
Для облегчения интерполяции в таблицах рядом со значениями функции приведены ее приращения за один шаг таблиц 
Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения Ф(х) как для положительных, так и для отрицательных аргументов.
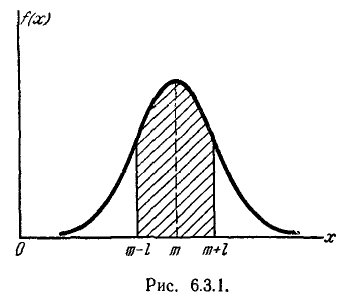
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m. Рассмотрим такой участок длины 2l (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7): 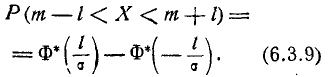
Учитывая свойство (6.3.8) функции Ф*(х) и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:
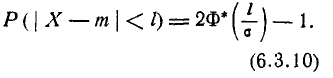
Решим следующую задачу. Отложим от центра рассеивания m последовательные отрезки длиной  (рис. 6.3.2) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.
(рис. 6.3.2) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.
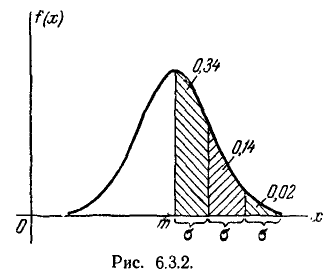
По формуле (6.3.7) находим:
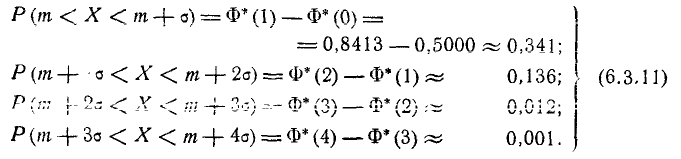
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.
Округляя вероятности попадания в отрезки до 0,01 (до 1%). получим три числа, которые легко запомнить: 0,34; 0,14; 0,02.
Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке m± З .
.
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма«. Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения  .
.
Пример:
Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м) среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).
Решение:
Ошибка измерения есть случайная величина X, подчинен- подчиненная нормальному закону с параметрами m= 1,2 и  = 0,8. Нужно найти вероятность попадания этой величины на участок от а =—1,6 до
= 0,8. Нужно найти вероятность попадания этой величины на участок от а =—1,6 до 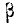 = + 1,6. По формуле (6.3.7) имеем:
= + 1,6. По формуле (6.3.7) имеем:
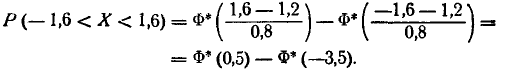
Пользуясь таблицами функции Ф* (х) (приложение, табл. 1), найдем:
Ф* (0,5) = 0,6915; Ф* (—3,5) = 0,0002,
откуда Р (—1,6 < X < 1,6) = 0,6915 — 0,0002 = 0,6913  0,691.
0,691.
Пример:
Найти ту же вероятность, что в предыдущем примере, но при условии, что систематической ошибки нет.
Решение:
По формуле (6.3.10), полагая l=1.6, найдем:
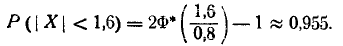
Пример:
По цели, имеющей вид полосы (автострада), ширина которой равна 20 м, ведется стрельба в направлении, перпендикулярном автостраде, прицеливание ведется по средней линии автострады. Среднее квадратическое отклонение в направлении стрельбы равно 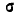 = 8 м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.
= 8 м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.
Решение:
Выберем начало координат в любой точке на средней линии автострады (рис. 6.3.3) и направим ось абсцисс перпендикулярно автостраде. Попадание или непопадание снаряда в автостраду определяется значением только одной координаты точки падения X (другая координата Y нам безразлична). Случайная величина X распределена по нормальному закону
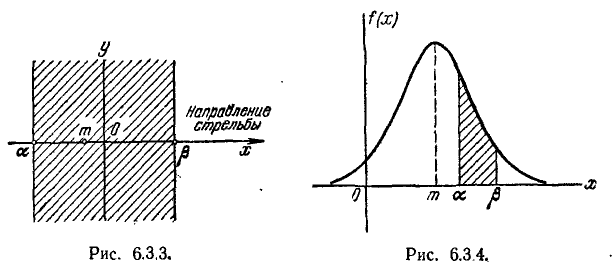
с параметрами m = —3,  = 8. Попадание снаряда в автостраду соответствует попаданию величины X на участок от а = — 10 до
= 8. Попадание снаряда в автостраду соответствует попаданию величины X на участок от а = — 10 до 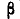 = 4-10. Применяя формулу (6.3.7), имеем:
= 4-10. Применяя формулу (6.3.7), имеем:
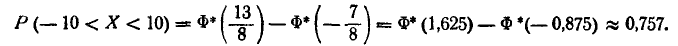
Пример:
Имеется случайная величина Х, нормально распределенная, с центром рассеивания m (рис. 6.3.4) и некоторый участок 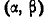 оси абсцисс. Каково должно быть среднее квадратическое отклонение о случайной величины X для того, чтобы вероятность попадания р на участок
оси абсцисс. Каково должно быть среднее квадратическое отклонение о случайной величины X для того, чтобы вероятность попадания р на участок 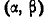 достигала максимума?
достигала максимума?
Решение:
Имеем:
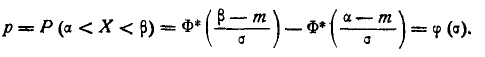
Продифференцируем эту функцию величины 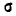 :
:
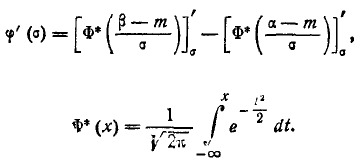
Применяя правило дифференцирования интеграла по переменной, входящей в его предел, получим:
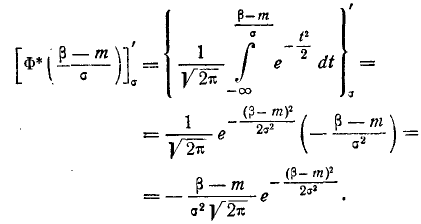
Аналогично
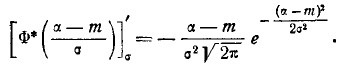
Для нахождения экстремума положим:
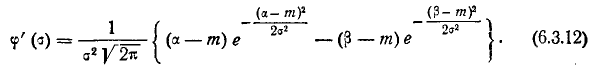
При 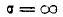 это выражение обращается в нуль и вероятность р достигает минимума. Максимум р получим из условия
это выражение обращается в нуль и вероятность р достигает минимума. Максимум р получим из условия 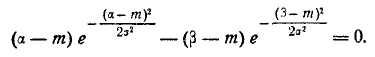 (6.3.13)
(6.3.13)
Уравнение (6.3.13) можно решить численно или графически.
6.4. Вероятное (срединное) отклонение
В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой Е (иногда В).
Вероятным (срединным) отклонением случайной величины X, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение Е — это половина длины участка оси абсцисс, симметричного относительно точки m, на кото- который опирается половина площади кривой распределения.
Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».
Рассмотрим случайную величину X, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания m меньше чем на Е, по определению вероятного отклонения Е, равна 
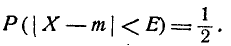 (6.4.1)
(6.4.1)
Вероятность того, что она отклонится от m больше чем на Е, тоже равна 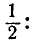
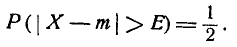
Таким образом, при большом числе опытов в среднем половина значений случайной величины X отклонится от m больше чем на Е, а половина — меньше. Отсюда и термины «срединная ошибка», «срединное отклонение».
Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего rвадратического отклонения  . Установим эту зависимость. Вычислим вероятность события | X — m | < Е в уравнении (6.4.1) по формуле (6.3.10). Имеем:
. Установим эту зависимость. Вычислим вероятность события | X — m | < Е в уравнении (6.4.1) по формуле (6.3.10). Имеем:
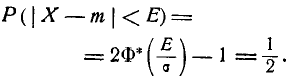
Отсюда
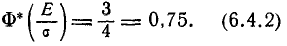
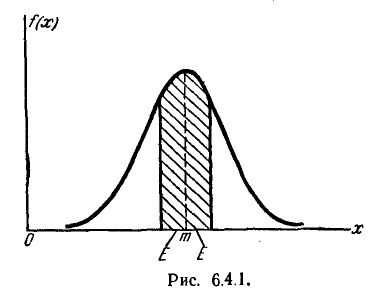
По таблицам функции Ф* (х) можно найти такое значение аргумента х, при котором она равна 0,75. Это значение аргумента приближенно равно 0,674; отсюда
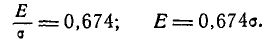 (6.4.3)
(6.4.3)
Таким образом, зная значение 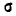 , можно сразу найти пропорциональное ему значение Е. Часто пользуются еще такой формой записи этой зависимости:
, можно сразу найти пропорциональное ему значение Е. Часто пользуются еще такой формой записи этой зависимости:
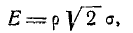 (6.4.4)
(6.4.4)
где р — такое значение аргумента, при котором одна из форм интеграла вероятностей — так называемая функция Лапласа 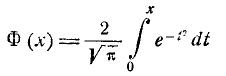
— равна половине. Численное значение величины р приближенно равно 0,477.
В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой 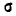 . В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
. В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
Если в качестве характеристики рассеивания принято вероятное отклонение Е, то плотность нормального распределения записывается в виде:
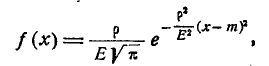 (6.4.5)
(6.4.5)
а вероятность попадания на участок от а до  чаще всего записывается в виде:
чаще всего записывается в виде:
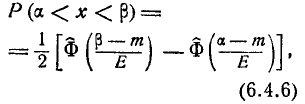
где
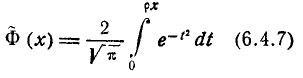 — так называемая приведенная функция Лапласа.
— так называемая приведенная функция Лапласа. 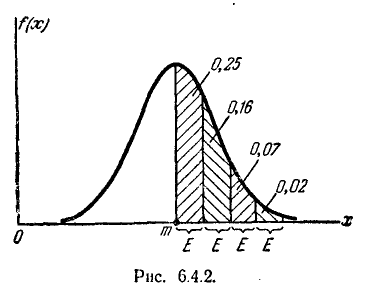
Сделаем подсчет, аналогичный выполненному в предыдущем п° для среднего квадратического отклонения  : отложим от центра рассеивания т. последовательные отрезки длиной в одно вероятное отклонение Е (рис. 6.4.2) и подсчитаем вероятности попа- попадания в эти отрезки с точностью до 0,01. Получим:
: отложим от центра рассеивания т. последовательные отрезки длиной в одно вероятное отклонение Е (рис. 6.4.2) и подсчитаем вероятности попа- попадания в эти отрезки с точностью до 0,01. Получим: 
Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке 
Пример:
Самолет-штурмовик производит обстрел колонны войск противника, ширина которой’ равна 8 м. Полет — вдоль колонны, прицеливание— по средней линии колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо но направлению полета. Главные вероятные отклонения: по направлению полета 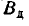 = 15 м, в боковом направлении
= 15 м, в боковом направлении 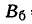 = 5 М. Не имея в своем распоряжении никаких таблиц интеграла вероятностей, а зная только числа:
= 5 М. Не имея в своем распоряжении никаких таблиц интеграла вероятностей, а зная только числа:
25%, 16%, 7%, 2%,
оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.
Решение:
Для решения задачи достаточно рассмотреть одну координату точки попадания — абсциссу X в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания m = 2 и вероятным отклонением 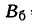 =Е = 5 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
=Е = 5 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
0,4-25% =0,1.
Влево от центра рассеивания цель занимает участок б м. Это — целое вероятное отклонение E м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна: 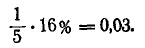
Таким образом, вероятность попадания в колонну приближенно равна:
0,1+0,25 + 0,03 = 0,38.
Вероятность хотя бы одного попадания при трех выстрелах равна: 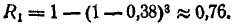
Закон нормального распределения случайных величин




Смотрите также:
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность










![{displaystyle F(x)=Phi left({frac {x-mu }{sigma }}right)={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a75caa2df3861960f6c6a5ac91f0b0fa6d79504)

![{displaystyle Phi (x)={frac {1}{2}}+{frac {1}{sqrt {2pi }}}cdot e^{-x^{2}/2}left[x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+cdots +{frac {x^{2n+1}}{(2n+1)!!}}+cdots right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b755fcac449fe404b290943b01b01eab9c50440a)


![{displaystyle mathbb {E} left[X^{p}right]={begin{cases}0&p=2n+1,\sigma ^{p},left(p-1right)!!&p=2n.end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39f9a1d5eadfbc872b3cd41f8135576e3123bc4)
![{displaystyle mathbb {E} left[left|Xright|^{p}right]=sigma ^{p},left(p-1right)!!cdot left.{begin{cases}{sqrt {frac {2}{pi }}}&p=2n+1,\1&p=2n.end{cases}}right}=sigma ^{p}cdot {frac {2^{frac {p}{2}}Gamma left({frac {p+1}{2}}right)}{sqrt {pi }}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45215d47f1e0fc958abfae9a8d7137995cf90a8)




![{displaystyle t={frac {{overline {X}}-mu }{S/{sqrt {n}}}}={frac {{frac {1}{n}}(X_{1}+cdots +X_{n})-mu }{sqrt {{frac {1}{n(n-1)}}left[(X_{1}-{overline {X}})^{2}+cdots +(X_{n}-{overline {X}})^{2}right]}}}sim t_{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ff0d3c79a0504e8f259ef99192b825357914d7)


