| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Найти плотность распределения вероятностей площади ромба
|
|||
|
Значение острого угла ромба со стороной a распределены равномерно в интервале (0,pi/2). Найти плотность распределения вероятностей площади ромба.
|
||
| Вернуться к началу |
|
||
|
Azgral |
Заголовок сообщения: Re: Найти плотность распределения вероятностей площади ромба
|
|
AGN писал(а): Запишите формулу для площади ромба и найдите плотность распределения СВ [math]Y = sin{ alpha }[/math], где [math]alpha[/math] – СВ, равномерно распределенная на [math]left( 0;frac{ pi }{ 2 } right)[/math] можно еще слегка поподробнее? если более конкретно помогите записать функцию распределения площади ромба , у меня получилось что это P{a^2*sinA<x}=P{sinA<x/a^2}=P{A<arcsin(x/a^2)} а дальше что? вот как исходя из этого составить функцию распределения площади ромба? потому что если я беру 0, x<0 ; arcsin(x/a^2) при 0<x<a^2; 1 при x>a^2 и беру от этого производную для плотности распределения вероятности то у меня получается что интеграл от 0 до a^2 от проивзодной arcsin(x/a^2) больше 1 такого быть не может там получается pi/2, значит где-то в составлении функции распределения я совершил ошибку и вероятнее всего потерял 2/pi
|
|
| Вернуться к началу |
|
|
Azgral |
Заголовок сообщения: Re: Найти плотность распределения вероятностей площади ромба
|
|
AGN писал(а): Почитайте “функции от случайных величин”. если бы я не прочитал, то не обращался бы сюда, я с этой задачей просидел уже пару дней и попросил помощи потому что у самого не получается, но спасибо за дельный совет
|
|
| Вернуться к началу |
|
|
AGN |
Заголовок сообщения: Re: Найти плотность распределения вероятностей площади ромба
|
|
Azgral писал(а): AGN писал(а): Почитайте “функции от случайных величин”. если бы я не прочитал, то не обращался бы сюда, я с этой задачей просидел уже пару дней и попросил помощи потому что у самого не получается, но спасибо за дельный совет Открываем книжку Е.С.Вентцель “Теория вероятностей” М, Наука, 1964, стр. 263, и читаем: В нашем случае [math]x = psi left( y right) = arcsin{frac{ Y }{ a^{2} } }[/math].
|
|
| Вернуться к началу |
|
Закажите у меня новую работу, просто написав мне в чат!
Значения острого угла ромба со стороной а распределены равномерно в интервале (0, П/2). Найти плотность распределения вероятностей площади ромба.
Пусть – случайная величина – острый угол ромба. Так как имеет равномерное распределение, то на интервале , вне этого интервала . Площадь рома с углом и стороной равна При изменении от до функция равномерно , так как – остается постоянной, а на указанном интервале . Закон распределения случайной величины находится по формуле: , где – обратная функция к Так как , то Найдем производную : ОТВЕТ:
теория-вероятностей – Плотность распределения функции случайной величины
|
Значения острого угла ромба со стороной a распределены равномерно в интервале (0,π/2). Найти плотность распределения вероятностей площади ромба. |
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Задача 1
На шести карточках написаны буквы Е, И,
С, С, С, Я. Тщательно перемешав карточки,
извлекают их одну за другой и кладут в
порядке извлечения. Найти вероятность
того, что составится слово “сессия”.
Решение:
Введем события:
А1 – на первой выбранной карточке
написана буква С
А2 – на первой выбранной карточке
написана буква Е
А3 – на первой выбранной карточке
написана буква С
А4 – на первой выбранной карточке
написана буква С
А5 – на первой выбранной карточке
написана буква И
А6 – на первой выбранной карточке
написана буква Я
А – получится слово “сессия”.
P(A)=P(А1
А2 А3 А4 А5 А6)=
P(А1) P(А2|А1)
P(А2|А1) P(А2|А1)
P(А2|А1) P(А3|А1А2)
P(А3|А1А2) P(А4|А1А2А3)
P(А4|А1А2А3) P(А5|А1
P(А5|А1
А2 А3 А4) P(А6|А1А2А3А4А5).
P(А6|А1А2А3А4А5).








Задача 2
В группе из 20 человек имеются 5 отличных,
9 хороших и 6 посредственных стрелков.
При одном выстреле отличный стрелок
попадает в мишень с вероятностью 0,9;
хороший – с вероятностью 0,8; посредственный
– с вероятностью 0,7. Наугад выбранный
стрелок выстрелил дважды, в результате
отмечено одно попадание и один промах.
Какой вероятнее всего был стрелок:
отличный, хороший или посредственный?
Решение:
Пусть событие А – попадание в мишень
Гипотеза H1 –
стрелок отличный
H2 – стрелок
хороший
H3 – стрелок
посредственный

Вероятности попадания в мишень:









Т.к.

Ответ: хороший стрелок.
Задача 3
Значение острого угла ромба со стороной
a распределены
равномерно в интервале ( ).
).
Найти плотность распределения вероятностей
площади ромба.
Решение:



Ответ:

Задача 4
Математическое ожидание скорости ветра
у земли в данной местности составляет
8 км/ч. Найти вероятность того, что
скорость ветра превысит 20 км/ч и что она
будет меньше 50 км/ч. Как изменятся искомые
вероятности, если будет известно, что
среднее квадратичное отклонение скорости
ветра равно 2 км/ч?
Решение:
-
Используя первое неравенство Чебышева:





-
Используя второе неравенство Чебышева:







Задача 5
Случайная величина ( )
)
распределена по нормальному закону с
математическим ожиданием ( )
)
и ковариационной матрицей:
 .
.
Найти: P{
> a}. ( )=(-0,15;
)=(-0,15;
0);

Решение:
P{
> 0}
Рассмотрим
 ;
;





P{
> 0} =
Задача 6
Для заданной выборки:
-
постройте:
а) статистический ряд; б)интервальный
статистический ряд, предварительно
определив число интервалов; -
найдите
значения точечных оценок математического
ожидания и дисперсии -
постройте
гистограмму -
на
основе анализа результатов наблюдений
выдвинете гипотезу о виде закона
распределения генеральной совокупности
Решение:
-
а)
|
Статистический |
||||||||||||||||||
|
12,6 |
14,4 |
15 |
17,4 |
19 |
19,2 |
19,4 |
19,9 |
20 |
20,4 |
20,5 |
20,6 |
20,7 |
20,8 |
21 |
21,2 |
21,4 |
21,5 |
21,6 |
|
1 |
1 |
1 |
1 |
3 |
1 |
1 |
1 |
3 |
1 |
1 |
3 |
2 |
1 |
6 |
1 |
1 |
3 |
5 |
|
21,8 |
21,9 |
22 |
22,2 |
22,6 |
22,7 |
22,8 |
23 |
23,1 |
23,2 |
23,4 |
23,5 |
23,6 |
23,8 |
24 |
24,1 |
24,2 |
24,3 |
24,4 |
|
1 |
4 |
2 |
2 |
5 |
3 |
1 |
7 |
3 |
4 |
7 |
1 |
1 |
3 |
5 |
1 |
6 |
1 |
2 |
|
24,5 |
24,6 |
25 |
25,1 |
25,2 |
25,4 |
25,6 |
25,8 |
25,9 |
26 |
26,2 |
26,4 |
26,6 |
26,9 |
27 |
27,2 |
27,3 |
27,6 |
27,7 |
|
1 |
3 |
10 |
2 |
6 |
2 |
1 |
3 |
5 |
3 |
4 |
1 |
1 |
3 |
8 |
4 |
1 |
2 |
1 |
|
27,8 |
28 |
28,5 |
28,6 |
28,8 |
29 |
29,2 |
29,4 |
29,7 |
30 |
30,2 |
31 |
31,2 |
32,6 |
33,4 |
34 |
37,5 |
39,2 |
|
|
3 |
4 |
1 |
1 |
1 |
4 |
5 |
1 |
1 |
7 |
3 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
б)
Интервальный статистический ряд
|
[10;14) |
[14;18) |
[18;22) |
[22;26) |
[26;30) |
[30;34) |
[34;38) |
[38;42] |
|
1 |
3 |
38 |
87 |
49 |
15 |
2 |
1 |
2)
 24,84
24,84

3)

4)
Полигон
частот

Построив полигон частот, можно
предположить, что генеральная совокупность
распределена по нормальному закону.
Задача 7
До наладки станка была проверена точность
изготовления 10-ти втулок и оценено
значение дисперсии диаметра втулок
 ,
,
которое характеризует точность станка.
После наладки станка контролировалось
еще 25 втулок и получено новое значение
дисперсии
 .
.
Есть ли основания считать, что в результате
наладки станка точность изготовления
на нем деталей не изменилась? Проверку
гипотезы осуществлять на уровне
значимости

в предположении, что ошибка изготовления
распределена по нормальному закону.
Решение:
Проверим гипотезу

(о равенстве дисперсий) при альтернативной
гипотезе
 .
.

распределение Фишера со степенями
свободы

и
 .
.
По таблице квантилей распределения
Фишера находим
 .
.


Гипотезу

принимаем, т.к.

Задача 8
Оценка значений сопротивления для
большой партии однотипных резисторов,
определенная по результатам измерений
100 случайно отобранных экземпляров,

Считая, что СКО ошибки измерений
сопротивления известно ( ),
),
найти вероятность того, что для резисторов
всей партии значения сопротивления
лежит в пределах 10 ±
0,1 кОм.
Решение:
Обозначим

оценку математического ожидания, а

= 10 математическое ожидание для всей
партии. Тогда


Значение функции Лапласа найдём по
таблице Ф(1)=0,841345. Отсюда, вероятность
того, что среднее сопротивления значение
находится в указанном интервале, равна
0,68269.
Соседние файлы в папке 02
- #
- #
- #

{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
Формула площади ромба через сторону и угол

S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту

S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
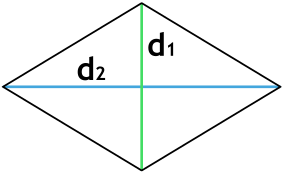
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
Формула площади ромба через угол и диагональ из угла
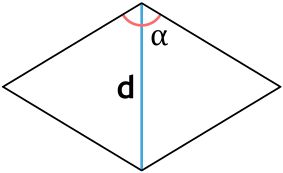
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ

S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и угол
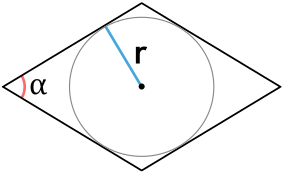
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и сторону
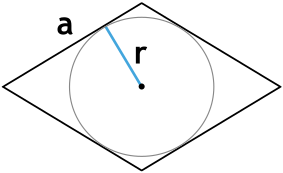
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .






