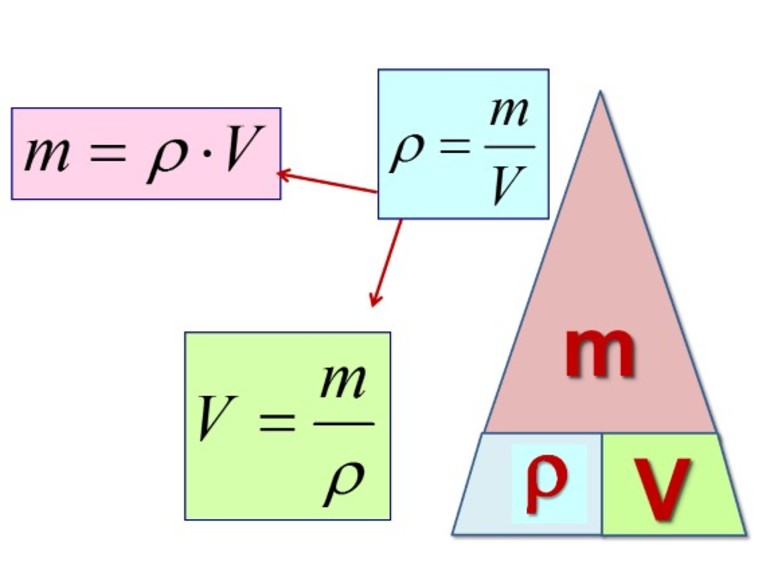
Как найти плотность соединения

Как найти плотность смеси

Смесь состоит минимум из двух компонентов, перемешанных в хаотичном порядке без определенной системы. Каждый из них имеет свою плотность. Для определения плотности смеси нужно знать массы или объемы веществ, которые смешиваются. Плотность жидких смесей измеряется ареометром.

Вам понадобится

• – ареометр;
• – таблица плотностей веществ;
• – весы;
• – мерный цилиндр.

Инструкция

Для измерения плотности жидкой смеси возьмите ареометр. Погрузите его в жидкость, чтобы он свободно плавал в ней. В верхней части ареометра находится шкала. Определите плотность смеси, совмещая шкалу с нижним краем мениска жидкости, в которую он погружен.

Для расчета плотности смеси взвесьте ее на весах. Значение массы m получите в граммах. С помощью мерного цилиндра, или другим способом, определите объем взвешенного количества смеси V. Измерение произведите в см³. Рассчитайте плотность смеси, поделив ее массу на объем, ρ=m/V. Результат получите в г/см³. Чтобы перевести его в кг/м³, результат умножьте на 1000.

ПримерПри переплавке двух металлов получили 400 г сплава, объемом 50 см³. Определите его плотность. Рассчитайте значение плотности по формуле ρ=400/50=8 г/ см³ или 8000 кг/м³.

Если известны плотности веществ, которые будут смешиваться, и их объемы, как это часто встречается при смешивании жидкостей, рассчитайте плотность получившейся смеси. Измерьте объем смеси. Он может несколько отличаться от суммарного объема смешиваемых жидкостей. Например, при смешивании 1 литра спирта и 1 литра воды объем смеси окажется меньше 2-х литров. Это связанно с особенностями строения молекул этих двух жидкостей.

Если плотности смешиваемых жидкостей неизвестны, найдите их значение в специальной таблице. Для расчета найдите сумму произведений плотности каждой из жидкостей на ее объем ρ1∙V1+ ρ2∙V2+ ρ3∙V3+… и т.д. Полученное значение поделите на общий объем смеси V, ρ=(ρ1∙V1+ ρ2∙V2+ ρ3∙V3+…)/V.

ПримерПри смешивании 1 л воды и 1 л этилового спирта получили 1,9 л смеси. Определите ее плотность. Плотность воды равна 1 г/ см³, спирта – 0,8 г/см³. Переведите единицы объема: 1 л=1000 см³, 1,9=1900 см³. Рассчитайте плотность смеси по формуле для двух компонентов ρ=(ρ1∙V1+ ρ2∙V2)/V=(1∙1000+ 0,8∙1000)/1900≈0,947 г/см³.

Источники:

• Изменение объёма при нагревании

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.

Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.

Сегодня мы познакомимся с такой характеристикой как плотность. Она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.

Связь массы, объема и вещества, из которого состоит тело

Рассмотрим опыт, представленный на рисунке 1.

Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.

Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.

В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.

Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.

На рисунке изображены 2 тела массой $100 space г$: лед, железо и золото.

Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.

Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.

Определение плотности вещества

Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.

Рассмотрим два тела объемом $1 space м^3$ каждое. Если они будут состоять из разных веществ, то их массы тоже будут разными.

Итак, алюминий такого объема будет иметь массу 2700 кг, а свинец такого же объема ( $1 space м^3$) будет имеет массу 11 300 кг.

На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.

Плотность показывает, чему равна масса вещества, взятого в объеме  $1 space м^3$ (или  $1 space см^3$). Чтобы найти плотность вещества, нужно массу тела разделить на его объем.

По какой формуле можно рассчитать плотность вещества? Дадим определение.

Плотность  — это физическая величина, которая равна отношению массы тела к его объему:
$плотность = frac{масса}{объем}$
или
$rho = frac{m}{V}$,
где $rho$ (“ро”) — плотность вещества, $m$ — масса тела, $V$ — объем тела.

Единицы измерения плотности

Какова единица плотности в СИ?
В СИ плотность вещества измеряется в килограммах на кубический метр ($1 frac{кг}{м^3}$).

Какие еще единицы плотности вам известны?
Часто используется другая единица измерения — граммы на кубический сантиметр ($1 frac{г}{см^3}$) (рисунок 4).

Иногда нам потребуется переводить плотность веществ, выраженную в $frac{кг}{м^3}$ в $ frac{г}{см^3}$.

Давайте выразим плотность мрамора ($2700 frac{кг}{м^3}$) в $frac{г}{см^3}$:

$$rho = 2700 cdot frac{1 space кг}{1 space м^3} = 2700 cdot frac{1000 space г}{1 space 000 space 000 space см^3} = frac{2700}{1000} cdot frac{г}{см^3} = 2.7 frac{г}{см^3}$$

Таблицы плотности некоторых тел и веществ

Плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна. 

Например, плотность воды составляет $1000 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, водяного пара — $0.590 frac{кг}{м^3}$ (рисунок 5).

Плотности различных твердых тел

Твердое тело	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$	Твердое тело	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$
Осмий	22 600	22,6	Мрамор	2700	2,7
Иридий	22 400	22,4	Стекло	2500	2,5
Платина	21 500	21,5	Фарфор	2300	2,3
Золото	19 300	19,3	Бетон	2300	2,3
Свинец	11 300	11,3	Кирпич	1800	1,8
Серебро	10 500	10,5	Сахар	1600	1,6
Медь	8900	8,9	Оргстекло	1200	1,2
Латунь	8500	8,5	Капрон	1100	1,1
Сталь, железо	7800	7,8	Полиэтилен	920	0,92
Олово	7300	7,3	Парафин	900	0,90
Цинк	7100	7,1	Лед	900	0,90
Чугун	7000	7,0	Дуб сухой	700	0,70
Корунд	4000	4,0	Сосна сухая	400	0,40
Алюминий	2700	2,7	Пробка	240	0,24

Плотности различных жидкостей

Жидкость	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$	Жидкость	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$
Ртуть	13 600	13,60	Керосин	800	0,80
Серная кислота	1800	1,80	Спирт	800	0,80
Мед	1350	1,35	Нефть	800	0,80
Вода морская	1030	1,03	Ацетон	790	0,79
Молоко цельное	1030	1,03	Эфир	710	0,41
Вода чистая	1000	1,00	Бензин	710	0,71
Масло подсолнечное	930	0,93	Жидкое олово (при $400^{circ}$)	6800	6,80
Масло машинное	900	0,90	Жидкий воздух (при $-194^{circ}$)	860	0,86

Плотности различных газов

Газ	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$	Газ	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$
Хлор	3,210	0,00321	Угарный газ	1,250	0,00125
Углекислый газ	1,980	0,00198	Природный газ	0,800	0,0008
Кислород	1,430	0,00143	Водяной пар (при $100^{circ}$)	0,590	0,00059
Воздух (при $0^{circ}C$	1,290	0,00129	Гелий	0,180	0,00018
Азот	1,250	0,00125	Водород	0,090	0,00009

Примеры задач на расчет плотности вещества

Посмотреть ответ

Скрыть

Переведем литры в кубические метры ($1 space л = 0.001 space м^3$): 
$30 cdot 0.001 = 0.03 space м^3$.

Дано:
$V = 30 space л$
$m =  21.3 space кг$

$rho -?$

Показать решение и ответ

Скрыть

Дано:
$а = 3 space м$
$b = 10 space см$
$c = 50 space см$
$m = 75 space кг$

$rho -?$

Показать решение и ответ

Скрыть

Больше задач с подробными решениями смотрите в отдельном уроке.

Упражнения

Посмотреть ответ

Скрыть

Показать ответ

Скрыть

Показать ответ

Скрыть

Дано:
$m = 12 space г$
$V = 100 space см^3$

$rho — ?$

Показать решение и ответ

Скрыть

Дано:
$а = 2.5 space см$
$b = 1 space см$
$с = 0.7 space см$
$m = 0.32 space г$

$rho — ?$

Показать решение и ответ

Скрыть

Взвесим шарик, мы узнаем его массу. Чтобы определить его объем, мы можем использовать измерительный цилиндр с водой. Для этого нужно опустить шарик в воду, и посмотреть, до какого уровня теперь поднялась воды. Разность этого объема и первоначального объема жидкости будет равна объему шарику.

Зная его массу и объем, мы сможем рассчитать его плотность по формуле: $rho = frac{m}{V}$.

Что такое плотность? Определение
Плотность – это мера того, сколько “материала” находится в заданном объеме пространства. Например, блок более тяжелого элемента свинца (Pb) будет плотнее, чем более мягкий и легкий элемент золота (Au). Блок из пенополистирола менее плотный, чем кирпич. Она определяется как масса на единицу объема.

Вы можете думать об этом, как о том, насколько плотно или свободно упаковано вещество, или насколько оно компактно. Твердые вещества, как правило, плотнее жидкостей, а жидкости плотнее газов, но есть много исключений.

Является ли плотность физическим свойством?
Это физическое свойство, определяемое превышением массы над объемом. Физические свойства можно наблюдать без изменения химического состава вещества. Другие физические свойства включают температуру плавления и температуру кипения. Каждое вещество, элемент и соединение имеют уникальную плотность, связанную с ним.

Единицы измерения плотности
Давайте обсудим “обычные” единицы плотности и “официальные” единицы. Все единицы измерения указаны в некоторых для веса на объем. Наиболее распространенной единицей измерения плотности является грамм на кубический сантиметр, или г / см3. Например, плотность воды составляет один грамм на кубический сантиметр, а свинца – 3,42 г / см3. Официальными единицами измерения плотности, известными как единицы СИ (Международная система единиц), являются килограмм на кубический метр (кг / см3). Другими эквивалентами являются граммы на миллилитр, г / мЛ и килограммы на литр, кг / л.

Что такое плотность?
Пенополистирол менее плотный примерно на 1 г / см3. Он обычно используется в качестве легкого материала для защиты упаковок во время транспортировки. Кирпич примерно в два раза больше пенополистирола при 2 г / см3. Он достаточно вынослив, чтобы противостоять стихиям в качестве строительного материала.

Формула плотности вещества р = m/V р — плотность вещества [кг/м 3] m — масса вещества [кг] V — объем вещества [м 3].

Как рассчитать плотность
Чтобы рассчитать это свойство, мы помним, что оно определяется как масса на объем. Масса обычно обозначается буквой “m”, объем – буквой “V”, а плотность – буквой “ρ” или прописной буквой “D.” Общая формула выглядит следующим образом:

Формула / уравнение плотности

Измерение Переменная
Плотность  ρ
D
Масса        m
Объем       V

Переменные в уравнении
Если вы знаете массу и плотность вещества, вы можете рассчитать объем. Если вы знаете, что плотность и объем, вы можете рассчитать массу. И последнее, но не менее важное: если вы знаете массу и объем, вы можете рассчитать плотность.

Практика
Вот несколько примеров расчетов, основанных на некоторых важных элементах и молекулах.

Рассчитайте плотность ртути (Hg), если ее масса составляет 28 г, а объем – 2 см3.

Если квадратный кусок железа (Fe) с длиной стороны 2 см весит 64 г. Насколько плотным является железо?

Вода примерно равна d = 1 г / мЛ, сколько весит 5 мл воды в граммах?

Решения:
Для ртути d =14 г/см3. Чтобы получить это значение, 28 г делят на 2 см3.
Для железа d=8 г / см3. Мы уже знаем вес (64 г). Объем составляет 2 см x 2 см x 2 см, потому что в вопросе говорится, что кусок представляет собой квадрат. Таким образом, объем составляет 8 см3. Тогда 64 г / 8 см3 приводит нас к ответу 8 г / см3.
5 мл воды весит 5 г. Чтобы получить этот ответ, мы умножаем 1 г / мЛ на интересующий нас объем (5 мл).

Плотность – Интересные факты
Самым плотным элементом является осмий.
Наименее плотным элементом (или любым газом) является водород.
Одним из самых плотных известных нам астрономических объектов является черная дыра.

Золото и вольфрам, оба с плотностью 19,3 грамма на кубический сантиметр, являются самыми плотными из всех легкодоступных материалов. Маленький вольфрамовый кубик невероятно тяжелый.

Наименее плотным твердым веществом в мире является графеновый аэрогель с плотностью 0,16 мг / см3, разработанный в лаборатории полимерной науки и техники в Китае.

Ртуть – это жидкий металл, который плотнее большинства твердых веществ.
Самый плотный газ, гексафторид вольфрама, все еще примерно в 45 раз плотнее, чем одна из наименее плотных жидкостей, изопентан.

Предмет утонет в воде только в том случае, если он более плотный, чем вода. Попробуйте найти предмет домашнего обихода плотнее воды – это сложнее, чем вы думаете!

Окружающие тела состоят из веществ, масса каждого зависит от размера, объема и других критериев.

Плотность вещества показывает численное выражение массы тела в определенном объеме.

Существуют разные виды скалярной физической величины.

Общая характеристика

Каждый элемент занимает индивидуальную величину. Определение плотности может обозначаться греческой буквой ρ, D или d. Если объемы двух тел одинаковы, а массы различны, тогда плотности не идентичны.

Основные понятия

Определения и характеристики показателя известны с 7 класса школьной программы химии. Плотность представляет собой физическую величину о свойствах вещества. Это удельный вес любого элемента. Существует средняя и относительная плотность. Последняя классификация — это отношение плотности (П) вещества к П эталонного вещества. Часто за эталон принимают дистиллированную воду. Единица измерения П- кг/м3 в интернациональной системе.

Формула нахождения плотности:

P = m/V

Обозначения:

• m — масса.
• V — объем.

Кроме стандартной формулы плотности, применяемой для твердых состояний веществ, имеется формула для газообразных элементов в нормальных условиях.

ρ (газа) = M/Vm M

Расшифровка:

• М — молярная масса газа [г/моль].
• Vm — объем газа (в норме 22,4 л/моль).

Для сыпучих и пористых тел различают истинную плотность, вычисляемую без учета пустот, и удельную плотность, рассчитываемую как отношение массы вещества ко всему объему. Истинную П получают через коэффициент пористости — доли объема пустот в занимаемом объеме. Для сыпучих тел удельная П называется насыпной.

Низкие показатели П имеет среда между Галактиками (1033 кг/м3).

Способы измерения:

• Пикнометр. Измеряет истинную П.
• Ареометр, денсиметр, плотномер. Используется для жидкого состояния.
• Бурик. Измеряет П почвы.

Вещества состоят из молекулярных структур, масса тела формируется из скопления молекул. Аналогично вес пакета с карамелью складывается из масс всех конфет в мешке. Если все сладости одинаковые, то массу упаковки определяют умножением веса одной конфеты на количество штук.

Молекулярные частицы чистого вещества одинаковы, поэтому вес капли воды равен произведению массы 1 молекулы Н2О на число составляющих молекул в капле. Плотность вещества показывает, чему равна масса одного кубического метра.

Плотность воды – 1000 кг/м³, а масса 1 м³ Н2О равна 1000 килограмм. Это число можно вычислить, умножив массу 1 молекулы воды на количество молекулярных частиц, содержащихся в 1 м3 объема.

П льда составляет 900 кг/м³, это значит, что вес кубического метра льда равна 900 кг. Употребляют единицу измерения плотности г/см3.

При равнозначности физических масс двух тел их объемы различаются. Например, объём льда в девять раз больше объема бруска из металлического сплава. Масса тела распределяется неодинаково, устанавливает П в каждой точке тела.

Влияние факторов

П зависит от давления и температуры. При высоком давлении молекулы плотно прилегают друг к другу, поэтому вещество обладает значительной плотностью.

Зависимость показателей учитывается при расчете П. При повышении температуры П снижается из-за термического расширения, при котором объем вырастает, а масса остается прежней. Если температура снижается, П увеличивается, хотя имеются вещества, П которых при некоторых условиях температурного режима ведет себя иначе. Это вода, бронза, чугун. При фазовом переходе, модифицировании агрегатного состояния П меняется скачками. Условия вычисления зависят от свойств веществ, молекулярных элементов. Для разных природных объектов П изменяется в широком диапазоне.

П воды ниже П льда из-за молекулярной структуры твердой формы жидкости. Вещество, переходя из жидкой в твердую форму, изменяет молекулярную структуру, расстояние между составными частицами сужается и плотность увеличивается. Зимой, если забыть слить воду из труб, их разрывает на части после замерзания. На П Н2О влияют примеси. У морской воды знак П выше, чем у пресной. При соединении в одном стакане двух типов жидкости пресная останется на поверхности. Чем выше концентрация соли, тем больше П воды.

Когда плотность вещества больше П воды, оно полностью погрузится в воду. Предметы, сделанные из материала по низкой П, будут плавать на поверхности воды. На практике эти свойства используются человеком. Сооружая суда, инженеры-проектировщики применяют материалы с высокой П. Корабли, теплоходы, яхты смогут затонуть во время плавания, в корпусах суден создают специальные полости, наполненные воздухом, ведь его П ниже плотности воды.

Чтобы наживка для рыбалки погрузилась в воду, ее обременяют тяжелым по плотности материалом, например, грузиком из металла (чаще свинца). Плотность сплава выше, чем у Н2О.

Жирные пятна масла, нефти, бензина остаются на поверхности воды из-за низкой П маслянистых веществ.

Практическое применение

Из учебников химии и физики вычисляют уровень плотности по формуле. Но также это можно сделать, используя онлайн-систему.

Значение показателя

Окружающий мир состоит из разных веществ.

Скамейка в парке или баня за городом сооружены из древесины, подошва утюга, сковорода выполнены из металла, покрышка колеса, велосипеда — из резины. Каждый предмет имеет свой вес.

Черные дыры Вселенной составляют наибольшую плотность 1014 кг/м3. Самый низкий показатель имеет область между Галактиками (2•10−31—5•10−31 кг/м³).

Таблица плотности веществ

Вещество	Плотность (кг/м3)
Сухой воздух	1,293
Металлы
Осмий	22,61
Родий	12,41
Иридий	22,56
Плутоний	19,84
Палладий	12,02
Свинец	11,35
Платина	19,59
Золото	19,30
Сталь	7,8
Алюминий	2,7
Медь	8,94
Газы
Азот	1,25
Аммиак	0,771
Аргон	1,784
Жидкий водород	70
Гелий в жидком состоянии	130
Водород	0,09
Водяной пар	0,598
Воздух	1,293
Хлор	3,214
О2	1,429
Углекислый газ	1,977
Остальные вещества
Тело человека	На вдохе 940-990, при выдохе – 1010-1070
Пресная вода	1000
Солнце	1410
Гранит	2600
Земля	5520
Железо	7874
Бензин	710
Керосин	820
Молоко	1040
Этанол	789
Ацетон	792
Морская вода	1030
Древесина
Пихта	0,39
Ива	0,46
Ель	0,45
Сосна	0,52
Дуб	0,69

П металлов изменяется от минимального значения у лития, который легче Н2О, до максимального значения у осмия, который тяжелее драгоценных металлов.

Способы расчета и примеры

В сети Интернет существует множество приложений для онлайн-расчета плотности веществ или материалов. В стандартные поля калькулятора вводится основная информация: масса, объем, единицы измерения. Плотность вычисляется автоматически по заданным параметрам и выводится на экран интерфейса. Можно перевести информативные данные в нужную единицу измерения.

Без использования учебной информации показатель П можно определить через физические опыты. Для лабораторных изучений нужны весы, сантиметр, если исследуемое тело находится в твердом состоянии. Для жидкости необходима колба.

Сначала измеряют объем тела, записывая результат по цифровой шкале (в сантиметрах или миллилитрах).

Вычисляя объем деревянного бруска квадратной формы, параметр стороны возводится в третью степень. Измеряя объемные характеристики, тело ставят на весы и записывают значение массы. Рассчитывая жидкое состояние, учитывают массу сосуда, куда помещено исследуемое. В формулу подставляют данные и рассчитывают показатель.

Поскольку П измеряется в кг/л или в г/см³, то иногда приходится пересчитывать одни величины в другие.

В одном грамме содержится 0,001 кг, а один кубический сантиметр (см³) — это 0,000001 м³. В 1 г/(см)³ содержится 1000кг/м³.

Пример 1:

Необходимо найти плотность молока, если 350 г занимают 100 см³. Для решения используют формулу, где масса делится на объем.

Решение: P=m/V = 350/100= 3,5 г/см³.

Пример 2:

Необходимо определить П мела, если масса большого куска объемом 20 см³ составляет 48 грамм. П выразить в кг/м³ и вг/см³.

Решение:

Нужно перевести см³ в кубические метры, а граммы — в килограммы.

V = 20см³= 0,00002 м³.

M= 48 г = 0,048 кг.

Плотность мела составляет 0,048 кг/0,00002 м³ = 2400 кг/м³.

Выражаем в г/см³: 2400 кг/м³ = 2400*1000/1000000 см³ = 2,4 г/см³.

Один килограмм равен 1000 грамм, один кубический метр (1м³) содержит 1000000 см ³. Плотность получится 2,4 г/см³или 2400 кг/м³.

Показатель имеет большое значение в разных сферах жизни и деятельности. Он определяется по таблице или высчитывается расчетным путем.

Решение
задач на нахождение плотности смесей и сплавов,

средней
плотности неоднородных тел (7 класс)

Ларионов Вадим Сергеевич,

 учитель физики МБОУ Лицея №
15 г.Сарова, larionvadim@yandex.ru

Ларионова Наталья Валентиновна,

к.п.н., учитель физики МБОУ Лицея № 15
г.Сарова, nvlarionova@yandex.ru

В статье сформулированы методические рекомендации по
организации факультативного занятия по решению задач на нахождение плотности
смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме,
структурированные по уровню сложности.

Задачи на
нахождение плотности смеси или сплава, средней плотности неоднородного
(«составного»)  тела являются базовыми при изучении темы «Плотность»  и
достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно
поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие,
структура которого соответствует принципу «от простого к сложному» и содержит последовательные
блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см.
приложение).

Средняя плотность
неоднородного («составного») тела, плотность смеси или сплава рассчитывается по
формуле

где m₁, m₂, m₃… -массы отдельных частей тела
(компонентов смеси или сплава), а V₁, V₂, V₃ … – их объёмы.

Для решения задач
по данной теме,  необходимо составить систему уравнений, в основе которой лежат
следующие положения:

1.       Определительная формула
плотности

2.       Свойство аддитивности массы
(масса смеси или сплава равна сумме масс его составных частей)

m=m₁+ m₂+ m₃+…

3.       Как правило, в таких задачах
полагают, что объём сплава (смеси) равен сумме объёмов его составных частей

V=V₁+V₂+V₃ …

В задачах, предложенных ниже,
исключением является задача № 6 из блока олимпиадных задач (задача о смешивании
спирта и воды).

Ключевые задачи,
представленные в занятии, в зависимости от подготовки учащихся могут быть
решены непосредственно на уроке при изучении темы «Плотность». В этом случае на
факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам
предлагаются задачи для самостоятельного решения, которые, как правило,
составляют домашнее задание. В этом случае удобно дифференцировать домашнее
задание учеников, предложив не более трёх обязательных задач в зависимости от
уровня подготовленности учеников. Учитель может дополнить списки олимпиадных
задач и задач для самостоятельного решения, используя материалы последних
олимпиад.

Приложение

Плотность смесей, сплавов, «составных» тел

Цель:  Научиться решать задачи
на нахождение плотности смесей и сплавов, а также средней плотности
неоднородных тел («составных») тел.

Ключевые задачи

1.       Какова плотность сплава из
300г олова и 100г свинца? (8г/см³)

2.                    
Сплав
изготовлен из меди объёмом 0,4 м³  и цинка массой 710 кг. Какова
плотность сплава? (8540 кг/м³)

3.       Для приготовления вишнёвого
сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали.
Какова плотность сиропа, если плотность варенья 1300 кг/м³? (1100
кг/м³)

4.       Какова плотность смеси из
глицерина и спирта, если объём спирта составляет половину объёма смеси? Как
изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг/м³, 980 кг/м³)

Олимпиадные задачи

1.       Масса первого изделия в 2
раза больше массы второго изделия, а их объёмы находятся в отношении V₁:V₂=1:3. Плотность первого изделия ρ₁=4г/см³.
Какова будет средняя плотность «составного» тела, если два изделия склеить?
Массой и объёмом клея пренебречь. (1,5 г/см³)

2.       Изделие, склеенное из трёх
различных частей, имеет объём V=600см³.
Объёмы частей находятся в соотношении V₁:V₂:V₃=2:3:5, а их плотности – в соотношении ρ₁:ρ₂:ρ₃=4:3:1.
Чему равна масса изделия, если плотность первой части ρ₁=2000кг/м³?
(660 г)

3.       Ученик измерил плотность
деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м³. Но на
самом деле брусок состоит из двух частей, равных по массе, плотность одной из
которых в два раза больше плотности другой. Найдите плотности обеих частей
бруска. Массой краски можно пренебречь. (450 кг/м³, 900 кг/м³)

4.       В дистиллированную воду
аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρ_р=1200
кг/м³ и массу m=120г. Объём раствора равен
сумме объёмов воды и кислоты. Плотность воды ρ_в=1000 кг/м³,
плотность кислоты ρ_к=1800 кг/м³.  Какова масса кислоты,
влитой в воду? (45 г)

5.       Однородный кубик со стороной
a и плотностью ρ поместили внутрь куска глины с плотностью 4ρ, которому придали
форму куба со стороной 2a. Получившийся куб облепили пластилином плотностью 2ρ,
в результате чего получился куб со стороной 3a (см. рисунок). Определите
среднюю плотность получившейся системы. (67ρ/27≈2,5ρ)

6.       Плотностью вещества называют
отношение массы тела из этого вещества к его объёму. Например, масса 1 см³
воды составляет 1 г, поэтому плотность воды 1 г/см³. Представим, что
смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см³, и
при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова
плотность полученного раствора? (ρ=18/19 г/cм³≈0,95г/cм³)

Задачи
для самостоятельного решения

1.   Какую плотность имеет сплав
из 270г алюминия и 445г меди? (≈4,77
г/cм³)

2.   Сплав золота и серебра массой
400 г имеет плотность 1,4·10⁴ кг/м³. Полагая объём сплава
равным сумме объёмов его составных частей, определите массу золота в сплаве? (220
г)

3.   Масса первого изделия в 3
раза меньше массы второго изделия, а их объёмы находятся в соотношении V₁:V₂=2:1. Плотность первого тела ρ₁=1,8 г/см³.
Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой
и объёмом клея пренебречь. (4,8 г/см³)

4.   Изделие, склеенное из трёх
различных частей, имеет объём V=900см³.
Объёмы частей находятся в соотношении V₁:V₂:V₃=5:3:1, а их плотности – в соотношении ρ₁:ρ₂:ρ₃=1:2:5.
Чему равна масса изделия, если плотность первой части ρ₁=500кг/м³?
(800 г)

5.       Кубик с ребром a=20см сделан из материала с
плотностью ρ=3000кг/м³. Однако внутри кубика имеется воздушная
полость, поэтому его средняя плотность ρ_ср=1200кг/м³.
Определите объём этой воздушной полости. Во сколько раз изменится средняя
плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри
полости можно пренебречь. (4800 см³, 1,5)

Литература к занятию

1.     Генденштейн Л.Э., Кирик Л.А.,
Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова.
– М.: Илекса, 2009. – 416 с.

2.       Бажанский И.И., Гой В.А.,
Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное
пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.

3.       Олимпиады 2008-2009. Физика.
Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.:
МЦНМО, 2009. – 70 с.

4.       400 физических этюдов.
Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.

5.       
Борисов
С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009.  –
100 с.