Корабли бывают разные, большие и малые, пассажирские, грузовые, военные. Все они имеют свои базовые технические характеристики. В частности, среди базовых показателей для каждого судна фигурирует его вес. Это важный показатель, исходя из которого необходимо подбирать двигатель, его мощность, ходовые и другие элементы. Возможная нагрузка на водный транспорт, другие эксплуатационные характеристики также высчитываются с учетом его веса. Таким образом, подсчет данного показателя необходимо осуществлять с максимальной точностью. Но как взвесить корабль?
Можно представить себе поставленную на весы моторную лодку, но даже небольшую яхту едва ли удастся взвесить таким образом. А ведь корабли бывают очень большими по размеру. Представить себе огромный авианосец, стоящий на весах, уже не получится. Так каким же образом осуществляется подсчет веса судов? Многие любознательные люди задаются этим вопросом. Ответ на него предоставить не сложно.
Вытесненная вода и закон Архимеда
На самом деле, все не так уж сложно. Взвесить авианосец или любое другое судно смог бы еще Архимед в свои древние века. Ведь именно он открыл закон, согласно которому вес тела равен весу воды, которая была вытеснена при его погружении. Таким образом, получить результат можно, просто спустив судно на воду. Едва только построив корабль, поместив его в родную среду, можно узнать, сколько именно он весит, с максимальной точностью.
Как осуществляется подсчет объема вытесненной воды?
Но вода – это очень пластичная стихия, тот объем, который был вытеснен при погружении объекта в открытом водоеме, определить крайне проблематично. Разумеется, что объекты для взвешивания помещаются не в открытое море, а в специальный док. Но это актуально только в случае с небольшими по размерам объектами, которые можно поместить в док методом погрузки. Вода при этом поднимется до той или иной отметки, что позволит вычислить вес, учитывая, что все габариты дока в точности известны.
Если рассматривать вариант, при котором корабль будет заходить в шлюз или док своим ходом, будет очевидно, что некоторая часть воды покинет док при входе судна в его ворота. Подход окажется нецелесообразным, данные окажутся неточными. Такая ситуация вынуждает использовать кардинально другой подход. Приходится производить сложные расчеты, учитывая целый ряд конструкторских аспектов, учитывая при этом корпус и особенности его формы, величину его осадки от ватерлинии.
Бывает так, что сведений о той части корабля, что находится под водой, просто нет. Это актуально в первую очередь для военных судов. И в этой ситуации можно рассчитать только приблизительный вес водного транспорта, прояснить точные данные по нему не получится. Результатом сможет стать только приблизительный его тоннаж.
Узнать вес корабля можно до его строительства!
Есть еще более простой способ узнать вес корабля. Причем его общая масса при таком подходе будет известна до того, как его спустят на воду, даже до его создания. Каждый из элементов, входящих в состав судна. Имеет собственный вес. Учитывая массу каждой детали, сложив показатели, можно узнать точный вес судна с минимальной погрешностью.
Интересный факт: современные инженеры узнают другие показатели корабля еще до его строительства – известны заранее его водоизмещение, тот объем, который приходится на подводную часть. Проведенные заранее вычисления исключают ошибки при строительстве судна, позволяют сделать его максимально эффективным в эксплуатации.
Но стоит помнить, что базовый вес корабля, рассчитанный до его строительства инженерами за счет суммирования массы оборудования и деталей – это еще не все. Для обеспечения судну устойчивого положения на воде используется балласт, а кроме того, корабль всегда имеет на борту дополнительные грузы. Стоит помнить о весе членов команды и пассажиров, если таковые есть, мебели и вещах, находящихся на борту, перевозимых грузах, и так далее. Перегружать корабль нельзя, при этом его посадка понижается, возникают проблемы с управлением, риск затопления.
Плотность воды и другие нюансы
А еще стоит помнить, что вода в разных водоемах имеет различную плотность. Ведь соленость водоемов варьирует, разница есть не только между реками и морями, но и между разными участками океанов. В зависимости от плотности воды масса корабля, разумеется, не изменяется, однако осадка варьирует, и этот фактор необходимо иметь в виду.
Таким образом, вес корабля определяют преимущественно расчетами. Каких-то особенных приспособлений, весов или иного оборудования для этого не существует. Зная вес каждой из деталей, можно получить общий показатель для всего корабля. Но также необходимо иметь в виду вес команды, погруженных вещей, чтобы иметь максимально точную для текущего момента цифру.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
38.1. Условия плавучести и равновесия судна
Плавучестью (floatation) судна – называется способность судна находиться на плаву по определенной осадке (по определенную ватерлинию) неся всю положенную нагрузку (т.е. при заданном количестве находящихся на нем грузов).
На судно, как на плавающее тело, постоянно действуют две категории сил: силы тяжести (вес судна) и силы давления воды (гидростатические силы).
Атмосферное давление действует как на надводную часть судна, так и на подводную (через объем воды). Учитывая незначительный перепад этого давления по высоте судна, влиянием аэростатического давления на посадку судна пренебрегают.
Вертикально вниз на плавающее судно действуют силы веса (тяжести), пропорциональные нагрузке масс судна, а вертикально вверх – силы гидростатические, пропорциональные массе вытесненной воды.
Результирующая сил веса Р равна сумме сил веса (тяжести) самого судна и всех грузов, находящихся на нем, приложена в центре тяжести (ЦТ) судна (Centre of gravity) в точке G.
Сила веса при любых положениях судна всегда направлена вертикально вниз.
Равнодействующая гидростатических сил является результирующей всех сил, возникающих вследствие давления воды на поверхность корпуса судна.
Согласно закону Архимеда, вес, или водоизмещение (масса), плавающего тела равны весу или массе вытесненной им воды:
P=yV или D = ρV,
где V – объем подводной части судна, м3;
у – удельный вес воды, н/м3 или тс/м3;
D – масса судна, т;
ρ – плотность воды, т/м3;
P – вес судна в целом, кН или тс.
Cила поддержания yV приложена в центре тяжести подводного объема – точке С, которую называют центром величины (ЦВ).
Объем V называется объемным водоизмещением и служит мерой плавучести.
Следует различать понятия веса и массы судна.
Масса выражает инерционные и гравитационные свойства судна, является скалярной величиной и измеряется в тоннах (т).
Вес судна является векторной величиной и измеряется в килоньютонах (кН) или тонна-силах (тс).
Масса судна в тоннах
численно равна
его весу в тонна-силах.
Результирующая гидростатических сил, определяемых давлением воды на поверхность судна, приводится к вертикальной силе ɣV, направленной вверх и называемой силой поддержания, или силой плавучести.
Сила плавучести направлена по вертикали вверх.
Так как под действием сил Р и yV судно находится в равновесии, то необходимо, чтобы эти силы были равны и действовали по одной прямой в противоположные стороны.
Точка приложения силы плавучести называется центром величины (Centre of buoyancy).
Эта точка обозначается буквой С или B и находится в центре тяжести подводного объема корпуса.
Рис. 1. Сила тяжести
Сила плавучести D’, согласно закону Архимеда, равна весу вытесненной воды в объеме, равном погруженной в жидкость части тела (корпуса):
D’ = у • V
Для равновесия тела, на которое действует две системы сил, необходимо и достаточно, чтобы равнодействующие этих сил были равны по величине и направлены по одной прямой в противоположные стороны.
На основании этого правила для равновесия судна необходимо и достаточно, чтобы сила плавучести равнялась весу судна, а центр тяжести G и центр величины С – лежали на одной вертикали.
Если обозначить координаты точек G и С по длине, ширине и высоте судна соответственно хg и хc, yg и ус, zg и zc, то условия равновесия плавающего судна можно выразить следующими уравнениями:
P=yV или D = ρV;
xg=xс;
yg=yс.
Так как судно симметрично ДП, то точки G и С должны лежать в этой плоскости, т. е.
уg=yс=0
Аппликаты Zg и Zс, характеризующие положение центра величины и центра тяжести по высоте, не связаны какой-либо зависимостью, но практически всегда у плавающего судна
Zс< Zg,
т. е. центр величины всегда лежит ниже центра тяжести.
Удельный вес воды у является переменной величиной.
При выполнении расчетов, связанных с проектированием судов, обычно принимают
у = 10,05 кн/м3 для морской воды и
у = 9,81 кн/м3 для пресной.
Водоизмещение (масса) судна равна массе вытесняемой им воды:
D=ρ⋅V,
где V – объемное водоизмещение судна, м3;
ρ – плотность забортной воды.
Для пресной воды ρ = 1,0 т/м3,
для морской ρ = 1,025 т/м3.
Для конкретных морских бассейнов плотность воды можно найти в гидрологических справочниках и атласах.
При их отсутствии можно воспользоваться для некоторых морей следующими значениями, имея в виду, что зимой плотность воды возрастет по отношению к указанной на 0,001–0,002 т/м3
|
Море |
Плотность воды, т/м3 |
|---|---|
| Азовское | 1,008– 1,009 |
| Балтийское | 1,010– 1,015 |
| Баренцево | 1,025– 1,026 |
| Белое | 1,019– 1,026 |
| Берингово | 1,021– 1,024 |
| Каспийское | 1,011– 1,012 |
| Охотское | 1,021– 1,025 |
| Черное | 1,013– 1,016 |
| Японское | 1,021– 1,027 |
Приведенные формулы представляют собой математическое выражение условий равновесия судна.
Уравнения:
называются основными уравнениями плавучести,
т. к. они устанавливают связь соответственно между водоизмещением (массой) или весом судна и массой или весом вытесняемой им воды.
При наличии у судна крена и дифферента условие P=yV остается неизменным, а второе (xg=xc ) и третье (yg = yc) условия меняются и принимают более сложный вид.
Действительно, в случае посадки судна на ровный киль, но с креном, условие расположения Ц.Т. и Ц.В. на одной вертикали запишется в виде:
Xg = XcYc—Yg=(Zg—Zc)⋅tgθ
Рис.2.Ц.Т.судна
При посадке судна прямо, но с дифферентом это условие будет иметь вид:
Рис.3. Плоскости мидель-шпангоута
Содержание:
- § 1 Условия плавания судов. Характеристики судна
- § 2 Как плавают подводные лодки
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Условия плавания судов. Характеристики судна
Рассмотрим условия плавания судов по рекам, озерам и морям.
Поставим небольшой опыт. Возьмем деревянный брусочек, положим на стол и подуем на него. Брусочек остается на месте. А теперь опустим его в широкую чашу с водой. Плотность дерева меньше плотности воды, поэтому действующая на него архимедова сила больше силы тяжести, и брусочек плавает на поверхности, частично погрузившись в воду. Подуем на него. Брусок скользит по поверхности воды.
Эту способность движения твердых тел по поверхности воды люди научились использовать тысячелетия назад. Первыми плавательными средствами были стволы деревьев, затем начали строить плоты и лодки. С течением времени размеры судов становились больше, появились парусные суда, пароходы, теплоходы.
В строительстве современных морских и речных судов применяют материалы, плотность которых больше плотности воды. Почему же эти сверхтяжелые корабли, танкеры, лайнеры, изготовленные из металла, держатся на поверхности воды и к тому же перевозят пассажиров и грузы?
Поставим еще один опыт. Возьмем пластинку металлической фольги и опустим в воду. Фольга утонет. Из такого же куска фольги сделаем кораблик. Мы видим, кораблик плавает на поверхности. Что изменилось? Масса фольги осталась прежней, значит, действующая на него сила тяжести не изменилась. Но объем кораблика больше объема куска фольги, поэтому архимедова сила, действующая на него, увеличилась. Если архимедова сила равна силе тяжести, то тело плавает.
Будем нагружать наш кораблик. Он глубже погружается в воду и может даже утонуть, если масса груза окажется очень большой для этого кораблика. Можем сделать вывод, что и на настоящие корабли нельзя помещать слишком много груза.
Известно, что тело плавает, если вес воды, вытесненной его подводной частью, равен весу этого тела в воздухе.
Значит, если вес воды, вытесненной подводной частью судна, равен весу этого судна вместе с грузом в воздухе, то это судно будет плавать.Если же вес судна вместе с грузом окажется больше веса вытесненной воды, то судно утонет.
Чтобы знать, сколько груза можно погрузить на судно, ввели следующие характеристики.
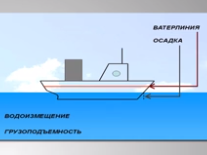
-Осадка – это глубина, на которую судно погружается в воду.
– Ватерлиния – красная линия на корпусе судна, показывающая наибольшую допустимую осадку судна.
– Водоизмещение – вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом.
– Грузоподъемность – вес полезного груза, перевозимого судном.
Нагружать судно можно только до тех пор, пока его осадка ниже ватерлинии.
Чтобы найти грузоподъемность, нужно из веса вытесненной воды (водоизмещения) вычесть вес самого судна. Pгруза = Pвыт.воды – Pсудна
§ 2 Как плавают подводные лодки
А как плавают подводные лодки?
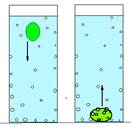
Для объяснения принципа плавания подводных лодок рассмотрим опыт. Нальем в стакан газированную воду и опустим виноградинку. Плотность винограда больше плотности воды, поэтому она утонет. Но через некоторое время виноградинка, вся облепленная пузырьками воздуха, поднимется на поверхность.
Так же и подводные лодки. В них есть специальные балластные отсеки, которые заполняются водой при погружении. Если же нужно подняться на поверхность, то сжатым воздухом вытесняют воду из этих отсеков. Средняя плотность лодки при этом становится меньше плотности воды и лодка всплывает.
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи на плавание судов.
Задача: Судно, погруженное в пресную воду до ватерлинии, вытесняет воду объемом 15 000 м3. Вес судна без груза составляет 5 000 кН. Чему равна грузоподъемность судна? Чему равна масса груза?
Решение: Запишем условие задачи. Объем вытесненной воды, равный объему подводной части судна, обозначим Vвыт.воды., составляет 15 000 м3. Вес судна Pсудна = 5000 кН, в СИ 5 000 000 Н. Плотность воды ρж = 1000 кг/м3. Необходимо определить грузоподъемность, т.е. вес груза Pгруза и массу груза mгруза.
Чтобы найти вес груза, нужно из водоизмещения вычесть вес самого судна. Водоизмещение – это вес воды, вытесненной погруженной частью судна, равный весу судна вместе с грузом, обозначим Pвыт.воды. Тогда Pгруза = Pвыт.воды – Pсудна.
Найдем вес вытесненной воды (водоизмещение) по формуле Pвыт.воды = mвыт.воды.·g, где масса вытесненной воды равна произведению ее плотности на объем.
Тогда Pвыт.воды = g·ρж·Vвыт.воды.
Формула определения веса груза запишется так: Pгруза = g·ρж·Vвыт.воды. – Pсудна. Подставим числовые значения величин, сократим единицы измерения и получим: Pгруза = 10 000 000 Н = 10 000 кН.
Тогда масса груза из формулы веса равна: mгруза = Pгруза :g = 1 000 000 кг = 1000 т.
Ответ: вес груза 10 000 кН, масса груза 1000 т
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
Если вес воды, вытесненной подводной частью судна, равен весу этого судна вместе с грузом в воздухе, то это судно будет плавать.
Осадка – это глубина, на которую судно погружается в воду.
Ватерлиния – красная линия на корпусе судна, показывающая наибольшую допустимую осадку судна.
Водоизмещение – вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом.
Грузоподъемность – вес полезного груза, перевозимого судном.
Нагружать судно можно только до тех пор, пока его осадка ниже ватерлинии. Чтобы найти грузоподъемность, нужно из веса вытесненной воды (водоизмещения) вычесть вес самого судна: Pгруза = Pвыт.воды – Pсудна
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
|
2. |
Мореходными
качествами должны обладать как гражданские
суда, так и военные корабли.
Изучением
этих качеств с применением математического
анализа занимается специальная научная
дисциплина — теория
судна.
Если
математическое решение вопроса
невозможно, то прибегают к опыту, чтобы
найти необходимую зависимость и проверить
выводы теории на практике. Только после
всестороннего изучения и проверки на
опыте всех мореходных качеств судна
приступают к его созданию.
Мореходные
качества в предмете «Теория судна»
изучаются в двух разделах: статике
и динамике судна.
Статика изучает законы равновесия
плавающего судна и связанные с этим
качества: плавучесть, остойчивость и
непотопляемость. Динамика изучает судно
в движении и рассматривает такие его
качества, как управляемость, качку и
ходкость.
Познакомимся с
мореходными качествами судна.
Плавучестью
судна называется
его способность держаться на воде по
определенную осадку, неся предназначенные
грузы в соответствии с назначением
судна.
На плавающее судно всегда
действуют две силы: а) с одной стороны, силы
веса,
равные сумме веса самого судна и всех
грузов на нем (вычисленные в тоннах);
равнодействующая сил веса приложена
в центре
тяжести судна (ЦТ)
в точке G и всегда направлена по вертикали
вниз; б) с другой стороны, силы
поддержания,
ил и силы
плавучести (выраженные
в тоннах), т. е. давление воды на погруженную
часть корпуса, определяемое произведением
объема погруженной части корпуса на
объемный вес воды, в которой судно
плавает. Если эти силы выразить
равнодействующей, приложенной в центре
тяжести подводного объема судна в точке
С, называемой центром
величины (ЦВ),
то эта равнодействующая при всех
положениях плавающего судна всегда
будет направлена по вертикали вверх
(рис. 10).
Объемным
водоизмещением называется
объем погруженной части корпуса,
выраженный в кубических метрах. Объемное
водоизмещение служит мерой плавучести,
а вес вытесняемой им воды называется весовым
водоизмещением D)
и выражается в тоннах.
По закону
Архимеда вес плавающего тела равен весу
объема жидкости, вытесненной этим
телом,
D
= Р = Vy,
где
у — объемный вес забортной воды, т/м3,
принимаемый в расчетах равным 1,000 для
пресной воды и 1,025 — для морской воды.
Рис.
10. Силы, действующие на плавающее судно,
и точки приложения равнодействующих
этих сил.
Так
как вес плавающего судна Р всегда равен
его весовому водоизмещению D, а их
равнодействующие направлены противоположно
друг другу по одной вертикали, и если
обозначить координаты точки G и С по
длине судна соответственно xg и
хc,
по ширине уg и
уc и
по высоте zg и
zc,
то условия равновесия плавающего судна
можно сформулировать следующими
уравнениями:
Р
= D; xg =
хc.
Вследствие
симметрии судна относительно ДП очевидно,
что точки G и С должны лежать в этой
плоскости, тогда
yg =
yc =
0.
Обычно
центр тяжести надводных судов G лежит
выше центра величины С, в таком случае
Zg >
Zc
Иногда
объем подводной части корпуса удобнее
выразить через главные размерения судна
и коэффициент общей полноты, т. е.
V
= LBTб,
тогда
весовое водоизмещение может быть
представлено в виде
D
= LBTбy.
Если
обозначить через Vn полный
объем корпуса до верхней палубы, при
условии водонепроницаемости закрытия
всех бортовых отверстий, то получим
Vn >
V
Разность
Vn —
V, представляющая некоторый объем
водонепроницаемого корпуса выше грузовой
ватерлинии, носит название запаса
плавучести. При аварийном попадании
воды внутрь корпуса судна увеличится
его осадка, но судно останется на плаву,
благодаря запасу плавучести. Таким
образом, запас плавучести будет тем
больше, чем больше высота надводного
непроницаемого борта. Следовательно,
запас плавучести является важной
характеристикой судна, обеспечивающей
его непотопляемость. Он выражается в
процентах от нормального водоизмещения
и имеет следующие минимальные значения:
для речных судов 10—15%, для танкеров
10—25 %, для сухогрузных судов 30—50%, для
ледоколов 80—90%, а для пассажирских судов
80—100%.
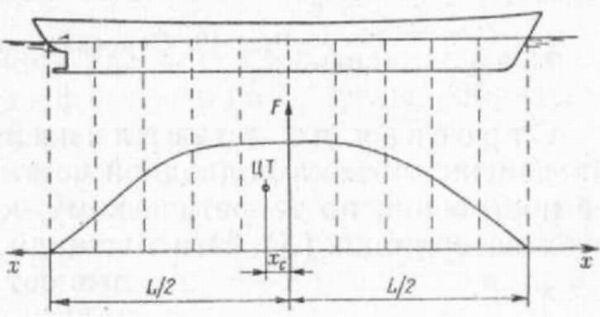
Рис.
11. Строевая по шпангоутам
Вес
судна Р (весовая нагрузка) И координаты
центра тяжести определяются расчетом,
учитывающим вес каждой детали корпуса,
механизмов, предметов оборудования,
снабжения, запасов, грузов, людей, их
багажа и всего находящегося на судне.
Для упрощения вычислений предусматривается
объединение отдельных наименований по
специальности в статьи, подгруппы,
группы и разделы нагрузки. Для каждого
из них подсчитывается вес и статический
момент.
Учитывая, что момент
равнодействующей силы равен сумме
моментов составляющих сил относительно
той же плоскости, после суммирования
по всему судну весов и статических
моментов, определяют координаты центра
тяжести судна G. Объемное водоизмещение,
а также координаты центра величины С
по длине от миделя хc и
по высоте от основной линии zc определяют
по теоретическому чертежу методом
трапеции в табличной форме.
Для
этой же цели пользуются вспомогательными
кривыми, так называемыми строевыми,
вычерченными также по данным теоретического
чертежа.
Различают две кривые:
строевую по шпангоутам и строевую по
ватерлиниям.
Строевая
по шпангоутам (рис.
11) характеризует распределение объема
подводной части корпуса по длине судна.
Она строится следующим способом.
Пользуясь методом приближенных
вычислений, определяют по теоретическому
чертежу площади погруженной части
каждого шпангоута (w). По оси абсцисс
откладывают в выбранном масштабе длину
судна и на нее наносят положение
шпангоутов теоретического чертежа. На
ординатах, восстановленных из этих
точек, откладывают в определенном
масштабе соответствующие площади
вычисленных шпангоутов.
Концы
ординат соединяют плавной кривой,
которая и является строевой по шпангоутам.
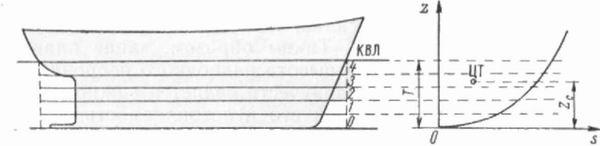
Рис.
12. Строевая по ватерлиниям.
Строевая
по ватерлинии (рис.
12) характеризует распределение объема
подводной части корпуса по высоте судна.
Для ее построения по теоретическому
чертежу подсчитывают площади всех
ватерлиний (5). Эти площади в избранном
масштабе откладывают по соответствующим
горизонталям, расположенным по осадкам
судна, в соответствии с положением
данной ватерлинии. Полученные точки
соединяют плавной кривой, которая и
является строевой по ватерлиниям.
Рис.
13. Кривая грузового размера.
Эти
кривые служат следующими характеристиками:
1)
площади каждой из строевых выражают в
соответствующем масштабе объемное
водоизмещение судна;
2) абсцисса
центра тяжести площади строевой по
шпангоутам, измеренная в масштабе длины
судна, равна абсциссе центра величины
судна хc;
3)
ордината центра тяжести площади строевой
по ватерлиниям, измеренная в масштабе
осадок, равна ординате центра величины
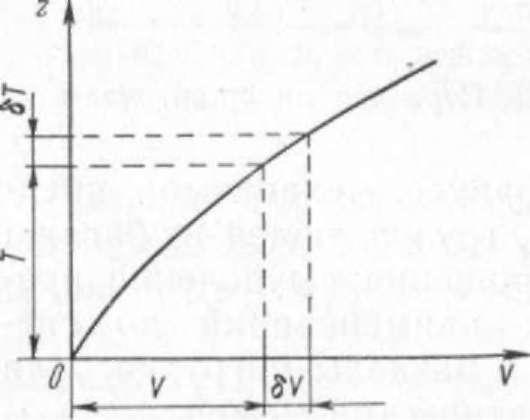
судна zc. Грузовой
размер представляет
собой кривую (рис. 13), характеризующую
объемное водоизмещение судна V в
зависимости от его осадки Т. По этой
кривой можно определить водоизмещение
судна в зависимости от его осадки или
решить обратную задачу.
Эта
кривая строится в системе прямоугольных
координат на основании предварительно
вычисленных объемных водоизмещении по
каждую ватерлинию теоретического
чертежа. На оси ординат в выбранном
масштабе откладывают осадки судна по
каж- дую из ватерлиний и через них
проводят горизонтали, на которых, также
в определенном масштабе, откладывают
значение водоизмещения, полученное для
соответствующих ватерлиний. Концы
полученных отрезков соединяют плавной
кривой, которая и называется грузовым
размером.
Пользуясь грузовым
размером, можно определить изменение
средней осадки от приема или расходования
груза или по заданному водоизмещению
определить осадку судна и т.
п.
Остойчивостью называется
способность судна противостоять, силам,
вызвавшим его наклонение, и после
прекращения действия этих сил возвращаться
в первоначальное положение.
Наклонения
судна возможны по разным причинам: от
действия набегающих волн, из-за
несимметричного затопления отсеков
при пробоине, от перемещения грузов,
давления ветра, из-за приема или
расходования грузов и пр.
Наклонение
судна в поперечной плоскости
называют креном ,
а в продольной плоскости — дифферентом ;
углы, образующиеся при этом, обозначают
соответственно O и y,
Различают
начальную остойчивость ,
т. е. остойчивость при малых углах крена,
при которых кромка верхней палубы
начинает входить в воду (но не более 15°
для высокобортных надводных судов),
и остойчивость
при больших наклонениях .
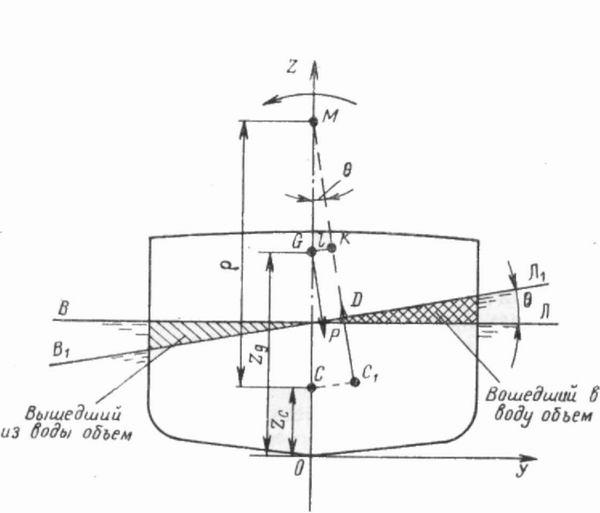
Представим
себе, что под действием внешних сил
судно получило крен на угол 9 (рис. 14).
Вследствие этого объем подводной части
судна сохранил свою величину, но изменил
форму; по правому борту в воду вошел
дополнительный объем, а по левому борту
равновеликий ему объем вышел из воды.
Центр величины переместился из
первоначального положения С в сторону
крена судна, в центр тяжести нового
объема — точку С1.
При наклонном положении судна сила
тяжести Р, приложенная в точке G, и сила
поддержания D, приложенная в точке С,
оставаясь перпендикулярными к новой
ватерлинии В1Л1 образуют
пару сил с плечом GK, являющимся
перпендикуляром, опущенным из точки G
на направление сил поддержания.
Если
продолжить направление силы поддержания
из точки С1 до
пересечения с ее первоначальным
направлением из точки С, то на малых
углах крена, соответствующих условиям
начальной остойчивости, эти два
направления пересекутся в точке М,
называемой поперечным
метацентром .
Расстояние
между метацентром и центром величины
МС называется поперечным
мета центрическим радиусом ,
обозначаемым р, а расстояние между
точкой М и центром тяжести судна G
— поперечной
метацентрической высотой h0 .
На основании данных рис. 14 можно составить
тождество
h0 =
p + zc —
zg.
В
прямоугольном треугольнике GMR угол у
вершины М будет равен углу 0. По его
гипотенузе и противолежащему углу можно
определить катет GK, являющийся плечо
м восстанавливающей судно пары GK=h0 sin
8, а восстанавливающий момент будет
равен Мвосст = DGK. Подставляя значения
плеча, получим выражение
Мвосст
= Dh0 *
sin 0,
Рис.
14. Силы, действующие при крене судна.
Взаимное
положение точек М и G позволяет установить
следующий признак, характеризующий
поперечную остойчивость: если метацентр
расположен выше центра тяжести, то
восстанавливающий момент положителен
и стремится вернуть судно в исходное
положение, т. е. при накренении судно
будет остойчиво, наоборот, если точка
М находится ниже точки G, то при
отрицательном значении h0 момент
отрицателен и будет стремиться увеличивать
крен, т. е. в этом случае судно неостойчиво.
Возможен случай, когда точки М и G
совпадают, силы Р и D действуют по одной
вертикальной прямой, пары сил не
возникает, и восстанавливающий момент
равен нулю: тогда судно надо считать
неостойчивым, так как оно не стремится
вернуться в первоначальное положение
равновесия (рис. 15).
Метацентрическую
высоту для характерных случаев нагрузки
вычисляют в процессе проектирования
судна, и она служит ме- рой остойчивости.
Значение поперечной метацентрической
высоты для основных типов судов лежит
в пределах 0,5—1,2 м и лишь у ледоколов
достигает 4,0 м.
Для увеличения
поперечной остойчивости судна необходимо
снижать его центр тяжести. Это чрезвычайно
важный фактор всегда надо помнить,
особенно при эксплуатации судна, и вести
строгий учет за расходованием топлива
и воды, хранящихся в междудонных
цистернах.
Продольная
метацентрическая высота H0 рассчитывается
аналогично поперечной, но так как ее
величина, выражается в десятках или
даже в сотнях метров, всегда весьма
велика — от одной до полутора длин
судна, то после проверочного расчета
продольную остойчивость судна практически
не рассчитывают, ее величина интересна
только в случае определения осадки
судна носом или кормой при продольных
перемещениях грузов или при затоплении
отсеков по длине судна.
Рис.
15. Поперечная остойчивость судна в
зависимости от расположения грузов: а
— положительная остойчивость; б —
положение равновесия — судно неостойчиво;
в — отрицательная остойчивость.
Вопросам
остойчивости судна придается исключительно
важное значение, и поэтому обычно, кроме
всех теоретических вычислений, после
постройки судна проверяют истинное
положение его центра тяжести путем
опытного кренования, т. е. поперечного
наклонения судна путем перемещения
груза определенного веса,
называемого кренбалластом .
Все
полученные ранее выводы, как уже
упоминалось, практически справедливы
при начальной остойчивости, т. е. при
крене на малые углы.
При расчетах
поперечной остойчивости на больших
углах крена (продольные наклонения на
практике не бывают большими) определяют
переменные положения центра величины,
метацентра, поперечного метацентрического
радиуса и плеча восстанавливающего
момента GK для различных углов крена
судна. Такой расчет делают начиная от
прямого положения через 5— 10° до того
угла крена, когда восстанавливающее
плечо превращается в нуль и судно
приобретает отрицательную остойчивость.
По
данным этого расчета для наглядного
представления об остойчивости судна
на больших углах крена строят диаграмму
статической остойчивости (ее
также называют диаграммой Рида),
показывающую зависимость плеча
статической остойчивости (GK) или
восстанавливающего момента Мвосcт от
угла крена 8 (рис. 16). На этой диаграмме
по оси абсцисс откладывают углы крена,
а по оси ординат — значение восстанавливающих
моментов или плечи восстанавливающей
пары, так как при равнообъемных
наклонениях, при которых водоизмещение
судна D остается постоянным, восстанавливающие
моменты пропорциональны плечам
остойчивости.
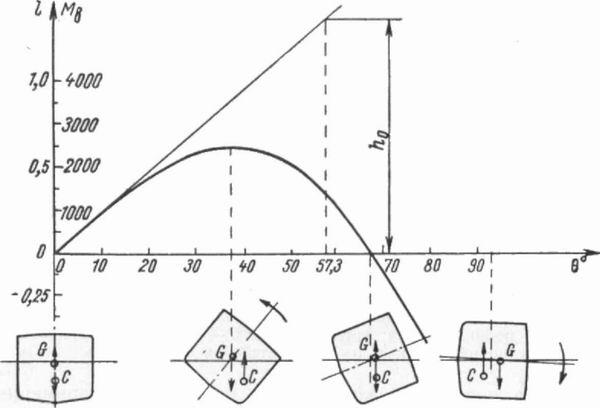
Рис.
16. Диаграмма статической остойчивости.
Диаграмму
статической остойчивости строят для
каждого характерного случая нагрузки
судна, и она следующим образом характеризует
остойчивость судна:
1) на всех
углах, при которых кривая расположена
над осью абсцисс, восстанавливающие
плечи и моменты имеют положительное
значение, и судно имеет положительную
остойчивость. При тех углах крена, когда
кривая расположена под осью абсцисс,
судно будет неостойчивым;
2)
максимум диаграммы определяет предельный
угол крена 0 мах и предельный кренящий
момент при статическом наклонении
судна;
3) угол 8, при котором
нисходящая ветвь кривой пересекает ось
абсцисс, называется углом
заката диаграммы .
При этом угле крена восстанавливающее
плечо становится равным нулю;
4)
если на оси абсцисс отложить угол, равный
1 радиану (57,3°), и из этой точки восставить
перпендикуляр до пересечения с
касательной, проведенной к кривой из
начала координат, то этот перпендикуляр
в масштабе диаграммы будет равен
начальной метацентрической высоте
h0.
Большое
влияние на остойчивость оказывают
подвижные, т. е. незакрепленные, а также
жидкие и сыпучие грузы, имеющие свободную
(открытую) поверхность. При наклонении
судна эти грузы начинают перемещаться
в сторону крена и, как следствие, центр
тяжести всего судна уже не будет
находиться в неподвижной точке G, а
начнет тоже перемещаться в ту же сторону,
вызывая уменьшение плеча поперечной
остойчивости, что равносильно уменьшению
метацентрической высоты со всеми
вытекающими из этого последствиями.
Для предотвращения таких случаев все
грузы на судах должны быть закреплены,
а жидкие или сыпучие должны быть погружены
в емкости, исключающие всякое переливание
или пересыпание грузов.
При
медленном действии сил, создающих
кренящий момент, судно, наклоняясь,
остановится тогда, когда кренящий и
восстанавливающий моменты сравняются.
При внезапном действии внешних сил,
таких, как порыв ветра, натяжение буксира
на борт, качка, бортовой залп из орудий
и т. п., судно, наклоняясь, приобретает
угловую скорость и даже с прекращением
действия этих сил будет продолжать
крениться по инерции на дополнительный
угол до тех пор, пока не израсходуется
вся его кинетическая энергия (живая
сила) вращательного движения судна и
его угловая скорость не превратится в
нуль. Такое наклонение судна под действием
внезапно приложенных сил
называется динамическим
наклонением .
Если при статическом кренящем моменте
судно плавает, имея лишь некоторый крен
0СТ,
то в случае динамического действия того
же кренящего момента оно может
опрокинуться.
При анализе
динамической остойчивости для каждого
водоизмещения судна строят диаграммы
динамической остойчивости,
ординаты которых представляют в
определенном масштабе площади,
образованные кривой моментов статической
остойчивости для соответствующих углов
крена, т. е. выражают работу восстанавливающей
пары при наклонении судна на угол 0,
выраженный в радианах. При вращательном
движении, как известно, работа равна
произведению момента на угол поворота,
выраженный в радианах,
Т1 =
Мkp0.
По
этой диаграмме все вопросы, связанные
с определением динамической остойчивости,
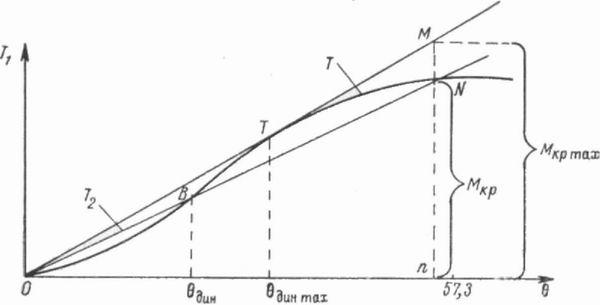
можно решить следующим образом (рис.
17).
Угол крена при динамически
приложенном кренящем моменте можно
найти, нанеся на диаграмму в том же
масштабе график работы кренящей пары;
абсцисса точки пересечения этих двух
графиков дает искомый угол 0ДИН.
Если
в частном случае крепящий момент имеет
постоянное значение, т. е. Мкр =
const, то работа будет выражаться
Т2 =
Мkp0.
а
график будет иметь вид прямой, проходящей
через начало координат.
Для того,
чтобы построить эту прямую на диаграмме
динамической остойчивости, необходимо
отложить по оси абсцисс угол, равный
радиану, и провести из полученной точки
ординату. Отложив на ней в масштабе
ординат величину Мкр в
виде отрезка Nn (рис. 17), надо провести
прямую ON, которая является искомым
графиком работы кренящей пары.
Рис.
17. Определение угла крена и предельного
динамического наклонения по диаграмме
динамической остойчивости.
На
этой же диаграмме показан угол
динамического наклонения 0ДИН,
определяемый как абсцисса точки
пересечения обоих графиков.
С
увеличением момента Мкр секущая
ON может занять предельное положение,
обратившись во внешнюю касательную ОТ,
проведенную из начала координат к
диаграмме динамической остойчивости.
Таким образом, абсцисса точки касания
будет искодинмах мым предельным углом
динамических наклонений 0 Ордината этой
касательной, соответствующая радиану,
выражает предельный кренящий момент
при динамических наклонениях Мкрмах.
При
плавании судно часто подвергается
динамическому воздействию внешних сил.
Поэтому умение определить динамический
кренящий момент при решении вопроса об
остойчивости судна имеет большое
практическое значение.
Изучение
причин гибели судов приводит к выводу,
что в основном суда гибнут из-за потери
остойчивости. Для ограничения потери
остойчивости в соответствии с различными
условиями плавания, Регистром Союза
ССР разработаны Нормы остойчивости
судов транспортного и промыслового
флота. В этих нормах основным показателем
является способность судна сохранять
положительную остойчивость при совместном
действии на него бортовой качки и ветра.
Судно отвечает основному требованию
Норм остойчивости, если при наихудшем
варианте загрузки его МКР остается
меньше MОПР.
При
этом минимальный опрокидывающий момент
судна определяется по диаграммам
статической или динамической остойчивости
с учетом влияния свободной поверхности
жидких грузов, бортовой качки и элементов
расчета парусности судна для различных
случаев нагрузки судна.
Нормами
предусматривается целый ряд требований
к остойчивости, например: MКР <
MОПР,
коэффициент запаса остойчивости
метацентрическая
высота должна иметь положительное
значение, угол заката диаграммы
статической остойчивости должен быть
не менее 60°, а с учетом обледенения —
не менее 55° и т. п. Обязательное соблюдение
этих требований при всех случаях нагрузки
дает право считать судно
остойчивым.
Непотопляемостью
судна называется
его способность сохранять плавучесть
и остойчивость после затопления части
внутренних помещений водой, поступившей
из-за борта.
Непотопляемость
судна обеспечивается запасом плавучести
и сохранением положительной остойчивости
при частично затопленных помещениях.
Если
судно получило пробоину в наружном
корпусе, то количество воды Q, вливающееся
через нее, характеризуется выражением
где
S — площадь пробоины, м²;
g — 9,81
м/сек²
Н — отстояние центра
пробоины от ватерлинии, м.
Даже
при незначительной пробоине количество
воды, поступающее внутрь корпуса, будет
так велико, что справиться с нею отливные
насосы не в состоянии. Поэтому водоотливные
средства ставят на судне исходя из
расчета только удаления воды, поступающей
уже после заделки пробоины или через
неплотности в соединениях.
Чтобы
предотвратить распространение по судну
воды, вливающейся в пробоину, предусматривают
конструктивные мероприятия: корпус
делят на отдельные отсекиводонепроницаемыми
переборками и палубами .
При таком делении в случае получения
пробоины затопится один или несколько
ограниченных отсеков, отчего увеличится
осадка судна и соответственно уменьшится
высота надводного борта и запас плавучести
судна.
Основу
чертежа составляет сетка из линий
теоретических шпангоутов, ватерлиний,
батоксов, рыбин, строевых по шпангоутам
и ватерлиниям и т.д. Кто-то назвал, что
теоретический чертеж – это симфония
линий.
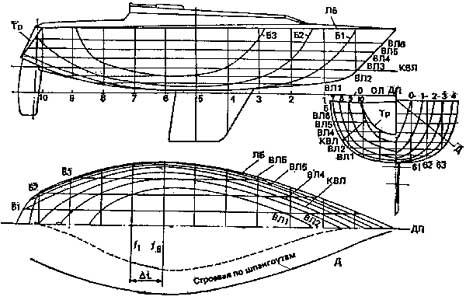
При
проектировании обводов шпангоутов и
ватерлиний конструктор преследует цель
обеспечения самого благоприятного
обтекания корпуса, необходимой
остойчивости формы и эстетического
внешнего вида судна. Абсолютное выполнение
этих условий выражается в точном
совпадении предварительно определенного
центра тяжести с центром величины
подводного объема корпуса по длине, а
также в достижении такого водоизмещения,
которое было получено из расчета массовой
нагрузки.
Распределение
водоизмещения по длине является
критерием, которому при проектировании
быстроходных судов придают все большее
значение. Обводы парусных яхт, кроме
того, должны быть рассчитаны на плавание
судна с креном от 0 до 30°. Необходимо,
чтобы распределение водоизмещения по
длине яхты при изменении крена изменялось
как можно меньше.
Строевая
по шпангоутам, наряду с характерными
очертаниями кормовых ветвей батоксов,
является важным критерием при
проектировании обводов. Она определяет
эффективную длину корпуса. Конструктор
стремится распределить водоизмещение
как можно ближе к окончанию ватерлинии
в носу и корме. У моторного судна эта
тенденция выражается в появлении
бульбовидного носа и такой же кормы. У
парусной яхты применение носового
бульба невозможно из-за плохого поведения
яхты на волне, так как при килевой качке
он создает повышенное сопротивление.
Компромисс был найден в применении
относительно полных сечений по носовым
шпангоутам. В кормовой части, наоборот,
целесообразна концентрация водоизмещения
в корпусе яхты. Так как здесь несложно
обеспечить плавный сток воды.
В
зависимости от плотности воды, в которой
плавает яхта, ее объемное водоизмещение
может изменяться, хотя масса судна
остается постоянной. В пресной воде,
плотность которой близка к единице, для
поддержания судна определенной массы
требуется больший погруженный объем
V, чем в соленой воде, плотность которой
колеблется: 010—1,015 т/м3 в Балтийском
море до 1,023—1,028 т/м3 в океане. Изменение
объемного водоизмещения при переходе
судна из пресной воды (плотность = 1,00) в
морскую и наоборот происходит за счет
изменения осадки. Величина этого
изменения невелика — менее 1 % осадки и
на эксплуатационных качествах судна
практически не сказывается. Однако
влияние солености на осадку следует
учитывать при обмере яхты и вычислении
ее гоночного балла.
Один
из приемов приближенного расчета
водоизмещения и центра величины
выполняется, например, по правилу
Симпсона, вычисляя площади теоретических
шпангоутов. Для этой же цели используют
планиметр, с помощью которого находят
площади шпангоутов и наносят их на
строевую по шпангоутам. Обкатав строевую
планиметром, определяют водоизмещение.
Пользуясь правилом Симпсона, можно
быстро найти положение центра величины
по длине. Довольно точно это можно
сделать, уравновешивая строевую по
шпангоутам, вырезанную из бумаги, на
острие ножа. Проектирование линий
теоретического чертежа с согласованием
точек пересечения ватерлиний, рыбин и
шпангоутов на всех проекциях, а также
получение нужного значения водоизмещения
и положения центра величины требует от
конструктора терпения, сноровки и
опыта.
Объяснение гидроаэромеханики
Отчего плавают рыбы, почему птицы не падают на землю? Как построить корабль, чтобы он не утонул? Может ли машина подняться в воздух, двигаться по небу или зависнуть в небе? Пытаясь найти ответы на эти и на многие другие вопросы, люди создали много разных наук. Их название начинаются со слова гидро, что в переводе означает вода, или аэро, что в переводе означает воздух. Если собрать эти науки вместе, то получится объемная наука – гидроаэромеханика.
Она рассматривает вопросы, связанные с движением жидкостей и воздуха, а также всех тел, которые в них находятся – животных и человека, парусных судов, самолетов и воздушных шаров.
Знакомство с гидромеханикой
Масса современных судов достигает нескольких десятков тысяч тонн. Почему же эти корабли не тонут? Всё дело в том, что их средняя плотность по-прежнему меньше плотности воды, а выталкивающая архимедова сила уравновешивает силу тяжести, и корабль не тонет.
Опыт с корабликом из фольги. Понятие осадки и ватерлинии
Рассмотрим опыт из предыдущего урока: если мы возьмем кусочек фольги и опустим его в воду, то он утонет. Но если из этой же самой фольги сделать кораблик, то он благополучно будет покоиться на поверхности воды. В чем же дело? Дело в том, что любой современный корабль содержит множество отсеков, заполненных воздухом. Если бы корабль был сделан из цельного куска металла, то он, конечно, бы утонул.
Получается, что наличие пустых помещений, заполненных воздухом, приводит к тому, что средняя плотность судна оказывается меньше плотности воды. Глубина, на которую погружается судно, называется осадкой. При полной загрузке судна, оно не должно погружаться в воду ниже определенной линии. Её называют грузовой ватерлинией (рис. 1), то есть линией, с которой соприкасается поверхность воды и корпус судна при его полной загрузке.
Рис. 1 Ватерлиния, нанесенная на корпус корабля (черным)
Постепенно загружая кораблик грузом, увидим, что с ним произойдет: осадка становится всё ниже, и при определенном значении корабль тонет. Вес груза превысил определенное значение, корабль опустился ниже ватерлинии. Хотелось бы обратить ваше внимание, что при погружении корабль вытесняет определенное количество воды.
Водоизмещение, грузоподъемность. Решение задачи
Вес воды, вытесненный кораблем при погружении, называется водоизмещением. Численно водоизмещение равно весу корабля вместе с грузом. Разница между водоизмещением и весом судна называется грузоподъемностью судна.
Решим задачу.
Нам необходимо определить грузоподъемность судна. Судно погружено в пресную воду до ватерлинии и при этом вытесняет воду объемом 15000 кубических метров. Известно, что вес самого судна составляет 5х107 ньютон. Запишем краткое условие задачи:
Дано:
Vв=15000 м3
ϱв=1000 кг/ м3
P0 = 5х107 H
——————-
Pг= ?
Нам необходимо рассчитать грузоподъемность судна. Обозначим грузоподъемность как вес груза. Для этого нам нужно из веса вытесненной воды вычесть вес судна:
Pг= Pвв– Pс , вес вытесненной воды рассчитывается:
Pвв= ϱв ∙ g ∙ Vв , как плотность воды на величину g и на объем вытесненной воды. Подставим это в исходную формулу и получим выражение для расчета:
Pг= ϱв ∙ g ∙ Vв – Pс .
Проведем анализ размерности, при подстановке всех размерных величин и математических преобразованиях, мы получим, что грузоподъемность судна будет измеряться в ньютонах. Pг= кг/м3 х Н/кг х м3 – Н = Н – Н = Н.
Подставим числовые данные:
Pвв = 1000∙10∙15000 – 5∙107 = 150∙106 – 5∙107 = 108 Н.
Т. е. грузоподъемность судна равна 108 Н.
Подводные лодки, эксперимент с газировкой
Суда, способные плавать под водой, называют подводными, а все остальные – надводными. Первая подводная лодка появилась в Англии в 1620 году, в России подводные лодки появились позднее, в 1724 году.
Проведем эксперимент.
В сосуд нальем газированную воду и опустим туда виноградинку. Она опустится на дно, потому что ее плотность больше плотности воды, но, облепленная пузырьками газа, она поднимется на поверхность. Как только пузырьки газа будут постепенно лопаться, она вновь опустится на дно, и так будет продолжаться до тех пор, пока весь газ из газировки не выйдет. Движение виноградинки аналогично тому, как движутся подводные лодки, внутри которых есть специальные балластные цистерны. Когда необходимо, чтобы лодка погрузилась, цистерны открываются и забортная вода устремляется внутрь – лодка опускается на дно. При необходимости поднятия наверх – под давлением сжатый воздух заполняет эти балластные цистерны, вытесняя забортную воду, и облегченная лодка поднимается на поверхность.
Развитие водного транспорта
Развитие водного транспорта имеет огромное значение, так как это достаточно дешевый вид транспорта с огромной грузоподъемностью, и именно благодаря водному транспорту осуществляется торговля со многими зарубежными странами.
Вопросы к конспектам
Что такое гидроаэромеханика?
К чашкам весов подвешены на нитях два одинаковых по объему тела: одно из меди, а другое из алюминия. Весы уравновешены. Нарушится ли равновесие, если тела опустить в воду, и как?
Дать определение водоизмещению и грузоподъемности.