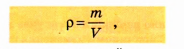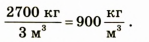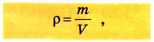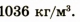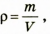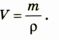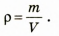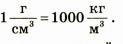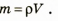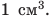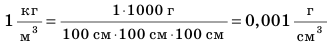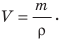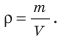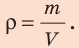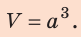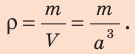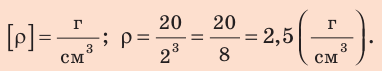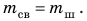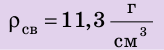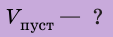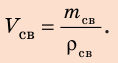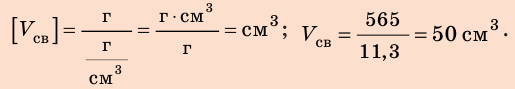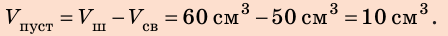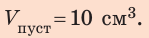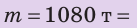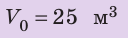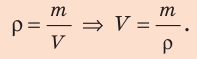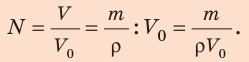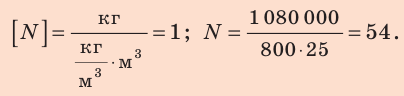| Плотность | |
|---|---|
 |
|
| Размерность | L−3 M |
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
| скалярная величина |
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или как производная массы по объёму:
.
Данные выражения не эквивалентны, и выбор зависит от того, какая именно плотность рассматривается. Различаются:
Для точечной массы плотность является бесконечной. Математически её можно определить или как меру, или как производную Радона — Никодима по отношению к некоторой опорной мере.
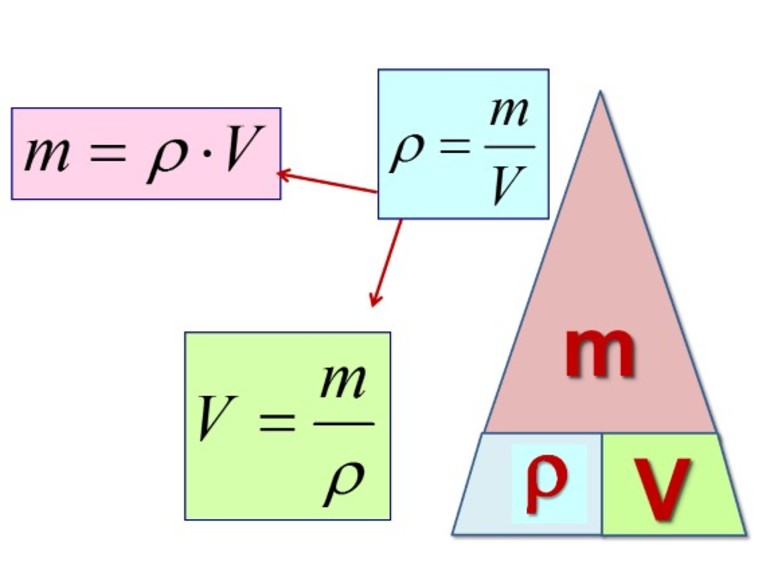
Для обозначения плотности обычно используется греческая буква 
Понятие «плотность» в физике может иметь более широкую трактовку. Существуют поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам. Кроме того, говорят не только о плотности массы, но и о плотности других величин, например энергии, электрического заряда. В таких случаях к термину «плотность» добавляются конкретизирующие слова, скажем «линейная плотность заряда». «По умолчанию» под плотностью понимается вышеуказанная (трёхмерная, кг/м³) плотность массы.
Формула нахождения плотности[править | править код]
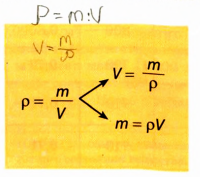
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где M — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.
При вычислении плотности газов при стандартных условиях эта формула может быть записана и в виде:
где 

Плотность тела в точке записывается как
тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как
Случай сыпучих и пористых тел[править | править код]
В случае сыпучих и пористых тел различают
- истинную плотность, определяемую без учёта пустот;
- насыпную плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из насыпной (кажущейся) получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Зависимость плотности от температуры[править | править код]
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Диапазон плотностей в природе[править | править код]
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[2].
- Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
- Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
- Плотность газообразного водорода (самого лёгкого газа) при стандартных условиях равна 0,0899 кг/м³.
- Плотность сухого воздуха при стандартных условиях составляет 1,293 кг/м³.
- Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
- Плотность пресной воды при 4 °C 1000 кг/м³.
- Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
- Гранит имеет плотность 2600 кг/м³.
- Средняя плотность Земли равна 5520 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Плотность металлического урана 19100 кг/м³.
- Плотность золота 19320 кг/м³.
- Плотность нептуния — самого плотного актиноида — 20200 кг/м³.
- Самые плотные вещества при стандартных условиях — металлы платиновой группы шестого периода (осмий, иридий, платина), а также рений. Имеют плотность 21000—22700 кг/м³.
- Плотность атомных ядер приблизительно 2·1017 кг/м³.
- Теоретически верхняя граница плотности по современным[когда?] физическим представлениям — это планковская плотность 5,1⋅1096 кг/м³.
Плотности астрономических объектов[править | править код]
Средняя плотность небесных тел Солнечной
системы (в г/см³)[3][4][5]
- Средние плотности небесных тел Солнечной системы см. на врезке.
- Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше чем у Солнца из-за того, что их радиус в сотни раз больше.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
- Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).
Плотности некоторых газов[править | править код]
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
| Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Радон | 9,81 |
| Гексафторид вольфрама | 12,9 | Углекислый газ | 1,977 |
| Гелий | 0,178 | Хлор | 3,164 |
| Дициан | 2,38 | Этилен | 1,260 |
Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:[6]
,
где:
Плотности некоторых жидкостей[править | править код]
| Бензин | 710 | Молоко | 1040 |
| Вода (4 °C) | 1000 | Ртуть (0 °C) | 13600 |
| Керосин | 820 | Диэтиловый эфир | 714 |
| Глицерин | 1260 | Этанол | 789 |
| Морская вода | 1030 | Скипидар | 860 |
| Масло оливковое | 920 | Ацетон | 792 |
| Масло моторное | 910 | Серная кислота | 1835 |
| Нефть | 550—1050 | Жидкий водород (−253 °C) | 70 |
Плотность некоторых пород древесины[править | править код]
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
| Свитения (Махагони) | 0,70 | Платан | 0,70 |
| Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
| Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,20 |
Плотность некоторых металлов[править | править код]
Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.
| Осмий | 22610[7] | Родий | 12410[8] | Хром | 7190[9] |
| Иридий | 22560[10] | Палладий | 12020[11] | Германий | 5320[12] |
| Плутоний | 19840[13] | Свинец | 11350[14] | Алюминий | 2700[15] |
| Платина | 19590[16] | Серебро | 10500[17] | Бериллий | 1850[18] |
| Золото | 19300[14] | Никель | 8910[19] | Рубидий | 1530[20] |
| Уран | 19050[21] | Кобальт | 8860[22] | Натрий | 970[23] |
| Тантал | 16650[24] | Медь | 8940[25] | Цезий | 1840[26] |
| Ртуть | 13530[27] | Железо | 7870[28] | Калий | 860[29] |
| Рутений | 12450[30] | Марганец | 7440[31] | Литий | 530[32] |
Измерение плотности[править | править код]
Для измерений плотности используются:
- Пикнометр — прибор для измерения истинной плотности
- Различные виды ареометров — измерители плотности жидкостей.
- Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
- Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
- Метод гидростатического взвешивания.
Остеоденситометрия — процедура измерения плотности костной ткани человека.
См. также[править | править код]
Видеоурок: плотность вещества
- Список химических элементов с указанием их плотности
- Удельный вес
- Удельная плотность
- Относительная плотность
- Объёмная плотность
- Конденсация
- Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
- Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
- Концентрация частиц
- Концентрация растворов
- Плотность заряда
- Уравнение неразрывности
Примечания[править | править код]
- ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
- ↑ Агекян Т. А. . Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
- ↑ Planetary Fact Sheet Архивировано 14 марта 2016 года. (англ.)
- ↑ Sun Fact Sheet Архивная копия от 15 июля 2010 на Wayback Machine (англ.)
- ↑ Stern, S. A., et al. The Pluto system: Initial results from its exploration by New Horizons (англ.) // Science : journal. — 2015. — Vol. 350, no. 6258. — P. 249—352. — doi:10.1126/science.aad1815.
- ↑ МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. Учебно-методическое пособие к лабораторным работам № 1-51, 1-61, 1-71, 1-72. Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров (2014). Дата обращения: 4 января 2019. Архивировано 23 ноября 2018 года.
- ↑ Krebs, 2006, p. 158.
- ↑ Krebs, 2006, p. 136.
- ↑ Krebs, 2006, p. 96.
- ↑ Krebs, 2006, p. 160.
- ↑ Krebs, 2006, p. 138.
- ↑ Krebs, 2006, p. 198.
- ↑ Krebs, 2006, p. 319.
- ↑ 1 2 Krebs, 2006, p. 165.
- ↑ Krebs, 2006, p. 179.
- ↑ Krebs, 2006, p. 163.
- ↑ Krebs, 2006, p. 141.
- ↑ Krebs, 2006, p. 67.
- ↑ Krebs, 2006, p. 108.
- ↑ Krebs, 2006, p. 57.
- ↑ Krebs, 2006, p. 313.
- ↑ Krebs, 2006, p. 105.
- ↑ Krebs, 2006, p. 50.
- ↑ Krebs, 2006, p. 151.
- ↑ Krebs, 2006, p. 111.
- ↑ Krebs, 2006, p. 60.
- ↑ Krebs, 2006, p. 168.
- ↑ Krebs, 2006, p. 101.
- ↑ Krebs, 2006, p. 54.
- ↑ Krebs, 2006, p. 134.
- ↑ Krebs, 2006, p. 98.
- ↑ Krebs, 2006, p. 47.
Литература[править | править код]
- Плотность — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
- Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
- Krebs R. E. . The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.
Ссылки[править | править код]
- Онлайн интерактивная таблица плотности веществ Архивная копия от 29 апреля 2011 на Wayback Machine (рус.)
- Подробная таблица значений плотности распространенных жидкостей Архивная копия от 5 октября 2016 на Wayback Machine (рус.)
- Урок по теме “Плотность вещества” Архивная копия от 30 января 2022 на Wayback Machine
Окружающие тела состоят из веществ, масса каждого зависит от размера, объема и других критериев.
Плотность вещества показывает численное выражение массы тела в определенном объеме.
Существуют разные виды скалярной физической величины.
Общая характеристика
Каждый элемент занимает индивидуальную величину. Определение плотности может обозначаться греческой буквой ρ, D или d. Если объемы двух тел одинаковы, а массы различны, тогда плотности не идентичны.
Основные понятия
Определения и характеристики показателя известны с 7 класса школьной программы химии. Плотность представляет собой физическую величину о свойствах вещества. Это удельный вес любого элемента. Существует средняя и относительная плотность. Последняя классификация — это отношение плотности (П) вещества к П эталонного вещества. Часто за эталон принимают дистиллированную воду. Единица измерения П- кг/м3 в интернациональной системе.
Формула нахождения плотности:
P = m/V
Обозначения:
- m — масса.
- V — объем.
Кроме стандартной формулы плотности, применяемой для твердых состояний веществ, имеется формула для газообразных элементов в нормальных условиях.
ρ (газа) = M/Vm M
Расшифровка:
- М — молярная масса газа [г/моль].
- Vm — объем газа (в норме 22,4 л/моль).
Для сыпучих и пористых тел различают истинную плотность, вычисляемую без учета пустот, и удельную плотность, рассчитываемую как отношение массы вещества ко всему объему. Истинную П получают через коэффициент пористости — доли объема пустот в занимаемом объеме. Для сыпучих тел удельная П называется насыпной.
Низкие показатели П имеет среда между Галактиками (1033 кг/м3).
Способы измерения:
- Пикнометр. Измеряет истинную П.
- Ареометр, денсиметр, плотномер. Используется для жидкого состояния.
- Бурик. Измеряет П почвы.
Вещества состоят из молекулярных структур, масса тела формируется из скопления молекул. Аналогично вес пакета с карамелью складывается из масс всех конфет в мешке. Если все сладости одинаковые, то массу упаковки определяют умножением веса одной конфеты на количество штук.
Молекулярные частицы чистого вещества одинаковы, поэтому вес капли воды равен произведению массы 1 молекулы Н2О на число составляющих молекул в капле. Плотность вещества показывает, чему равна масса одного кубического метра.
Плотность воды – 1000 кг/м³, а масса 1 м³ Н2О равна 1000 килограмм. Это число можно вычислить, умножив массу 1 молекулы воды на количество молекулярных частиц, содержащихся в 1 м3 объема.
П льда составляет 900 кг/м³, это значит, что вес кубического метра льда равна 900 кг. Употребляют единицу измерения плотности г/см3.
При равнозначности физических масс двух тел их объемы различаются. Например, объём льда в девять раз больше объема бруска из металлического сплава. Масса тела распределяется неодинаково, устанавливает П в каждой точке тела.
Влияние факторов
П зависит от давления и температуры. При высоком давлении молекулы плотно прилегают друг к другу, поэтому вещество обладает значительной плотностью.
Зависимость показателей учитывается при расчете П. При повышении температуры П снижается из-за термического расширения, при котором объем вырастает, а масса остается прежней. Если температура снижается, П увеличивается, хотя имеются вещества, П которых при некоторых условиях температурного режима ведет себя иначе. Это вода, бронза, чугун. При фазовом переходе, модифицировании агрегатного состояния П меняется скачками. Условия вычисления зависят от свойств веществ, молекулярных элементов. Для разных природных объектов П изменяется в широком диапазоне.
П воды ниже П льда из-за молекулярной структуры твердой формы жидкости. Вещество, переходя из жидкой в твердую форму, изменяет молекулярную структуру, расстояние между составными частицами сужается и плотность увеличивается. Зимой, если забыть слить воду из труб, их разрывает на части после замерзания. На П Н2О влияют примеси. У морской воды знак П выше, чем у пресной. При соединении в одном стакане двух типов жидкости пресная останется на поверхности. Чем выше концентрация соли, тем больше П воды.
Когда плотность вещества больше П воды, оно полностью погрузится в воду. Предметы, сделанные из материала по низкой П, будут плавать на поверхности воды. На практике эти свойства используются человеком. Сооружая суда, инженеры-проектировщики применяют материалы с высокой П. Корабли, теплоходы, яхты смогут затонуть во время плавания, в корпусах суден создают специальные полости, наполненные воздухом, ведь его П ниже плотности воды.
Чтобы наживка для рыбалки погрузилась в воду, ее обременяют тяжелым по плотности материалом, например, грузиком из металла (чаще свинца). Плотность сплава выше, чем у Н2О.
Жирные пятна масла, нефти, бензина остаются на поверхности воды из-за низкой П маслянистых веществ.
Практическое применение
Из учебников химии и физики вычисляют уровень плотности по формуле. Но также это можно сделать, используя онлайн-систему.
Значение показателя
Окружающий мир состоит из разных веществ.
Скамейка в парке или баня за городом сооружены из древесины, подошва утюга, сковорода выполнены из металла, покрышка колеса, велосипеда — из резины. Каждый предмет имеет свой вес.
Черные дыры Вселенной составляют наибольшую плотность 1014 кг/м3. Самый низкий показатель имеет область между Галактиками (2•10−31—5•10−31 кг/м³).
Таблица плотности веществ
| Вещество | Плотность (кг/м3) |
| Сухой воздух | 1,293 |
| Металлы | |
| Осмий | 22,61 |
| Родий | 12,41 |
| Иридий | 22,56 |
| Плутоний | 19,84 |
| Палладий | 12,02 |
| Свинец | 11,35 |
| Платина | 19,59 |
| Золото | 19,30 |
| Сталь | 7,8 |
| Алюминий | 2,7 |
| Медь | 8,94 |
| Газы | |
| Азот | 1,25 |
| Аммиак | 0,771 |
| Аргон | 1,784 |
| Жидкий водород | 70 |
| Гелий в жидком состоянии | 130 |
| Водород | 0,09 |
| Водяной пар | 0,598 |
| Воздух | 1,293 |
| Хлор | 3,214 |
| О2 | 1,429 |
| Углекислый газ | 1,977 |
| Остальные вещества | |
| Тело человека | На вдохе 940-990, при выдохе – 1010-1070 |
| Пресная вода | 1000 |
| Солнце | 1410 |
| Гранит | 2600 |
| Земля | 5520 |
| Железо | 7874 |
| Бензин | 710 |
| Керосин | 820 |
| Молоко | 1040 |
| Этанол | 789 |
| Ацетон | 792 |
| Морская вода | 1030 |
| Древесина | |
| Пихта | 0,39 |
| Ива | 0,46 |
| Ель | 0,45 |
| Сосна | 0,52 |
| Дуб | 0,69 |
П металлов изменяется от минимального значения у лития, который легче Н2О, до максимального значения у осмия, который тяжелее драгоценных металлов.
Способы расчета и примеры
В сети Интернет существует множество приложений для онлайн-расчета плотности веществ или материалов. В стандартные поля калькулятора вводится основная информация: масса, объем, единицы измерения. Плотность вычисляется автоматически по заданным параметрам и выводится на экран интерфейса. Можно перевести информативные данные в нужную единицу измерения.
Без использования учебной информации показатель П можно определить через физические опыты. Для лабораторных изучений нужны весы, сантиметр, если исследуемое тело находится в твердом состоянии. Для жидкости необходима колба.
Сначала измеряют объем тела, записывая результат по цифровой шкале (в сантиметрах или миллилитрах).
Вычисляя объем деревянного бруска квадратной формы, параметр стороны возводится в третью степень. Измеряя объемные характеристики, тело ставят на весы и записывают значение массы. Рассчитывая жидкое состояние, учитывают массу сосуда, куда помещено исследуемое. В формулу подставляют данные и рассчитывают показатель.
Поскольку П измеряется в кг/л или в г/см³, то иногда приходится пересчитывать одни величины в другие.
В одном грамме содержится 0,001 кг, а один кубический сантиметр (см³) — это 0,000001 м³. В 1 г/(см)3 содержится 1000кг/м3.
Пример 1:
Необходимо найти плотность молока, если 350 г занимают 100 см3. Для решения используют формулу, где масса делится на объем.
Решение: P=m/V = 350/100= 3,5 г/см3.
Пример 2:
Необходимо определить П мела, если масса большого куска объемом 20 см3 составляет 48 грамм. П выразить в кг/м3 и вг/см3.
Решение:
Нужно перевести см3 в кубические метры, а граммы — в килограммы.
V = 20см3= 0,00002 м3.
M= 48 г = 0,048 кг.
Плотность мела составляет 0,048 кг/0,00002 м3 = 2400 кг/м3.
Выражаем в г/см3: 2400 кг/м3 = 2400*1000/1000000 см3 = 2,4 г/см3.
Один килограмм равен 1000 грамм, один кубический метр (1м3) содержит 1000000 см 3. Плотность получится 2,4 г/см3или 2400 кг/м3.
Показатель имеет большое значение в разных сферах жизни и деятельности. Он определяется по таблице или высчитывается расчетным путем.
Содержание:
Плотность, единицы плотности:
Мы часто употребляем выражение «легкий, как воздух» или «тяжелый. как свинец». Но знаете ли вы. что воздух внутри, скажем, супермаркета, весит больше 400 кг. а груз такой массы не поднять и силачу. Свинцовое же грузило для удочки легко поднимет даже малыш. Выходит, приведенные выше выражения — неправильные? Подождите делать выводы — давайте разберемся.
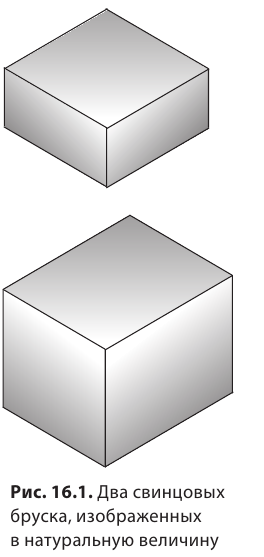
На рис. 2.8 вы видите два бруска, оба бруска изготовлены из одного и того же вещества — свинца, но имеют разные размеры. Наша задача — найти отношение массы каждого бруска к его объему.
Для начала измерьте длину, ширину и высоту брусков и вычислите их объемы. (Если вы правильно выполните измерения и не ошибетесь в расчетах, то вы получите такие результаты: объем меньшего бруска равен 4 см3, большего бруска — 10 см3.)
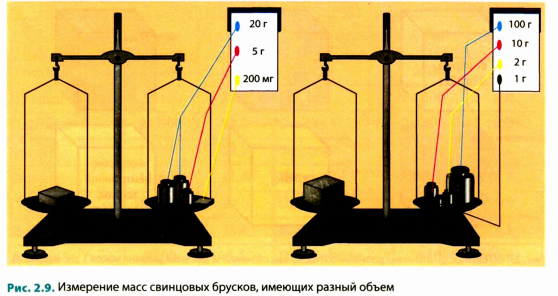
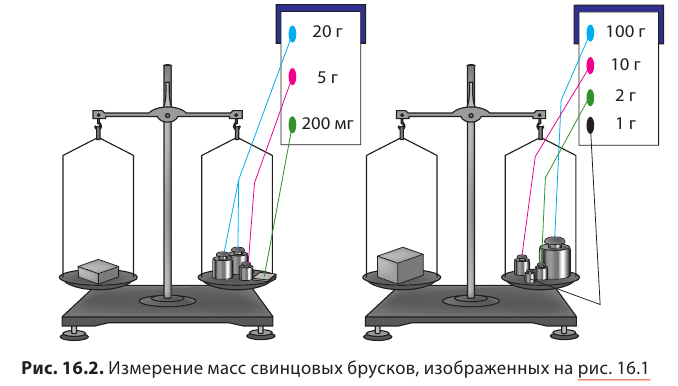
Определив объемы брусков, взвесим их. На левую чашу весов поместим один из брусков, на правую — разновесы (рис. 2.9). Весы находятся в равновесии, ваша задача — сосчитать массу разновесов.
Нам осталось найти отношение массы каждого бруска к его объему, т. е. вычислить, чему равняется масса свинца объемом 1 см3 для меньшего и для большего брусков. Очевидно, что если масса меньшего бруска 45,2 г и он занимает объем 4 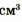
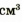
Если теперь взять бруски, изготовленные из другого вещества (например алюминия), и повторить те же действия, то отношение массы алюминиевого бруска к его объему также не будет зависеть от размеров бруска. Мы снова получим постоянное число, но уже другое, чем в опыте со свинцом.
Определение плотности вещества
Физическая величина, характеризующая данное вещество и численно равная массе вещества единичного объема, называется плотностью вещества.
Плотность обозначается символом р и вычисляется по формуле
где V — объем, занятый веществом массой m.
Плотность — это характеристика вещества, не зависящая от массы вещества и его объема. Если увеличить массу вещества, например, в два раза, то объем, который оно займет, также возрастет в два раза*.
Из определения плотности вещества получим единицу плотности. Поскольку в СИ единицей массы является килограмм, а единицей объема — метр кубический, то единицей плотности в СИ будет килограмм на метр кубический (кг/м*).
1 кг/м-* — это плотность такого однородного вещества, масса которого в объеме один кубический метр равняется одному килограмму.
На практике также очень часто применяется единица плотности грамм на сантиметр кубический (г/см*).
Единицы плотности килограмм на метр кубический (кг/м-1) и грамм на сантиметр кубический (г/см3) связаны между собой соотношением:
Плотности разных веществ
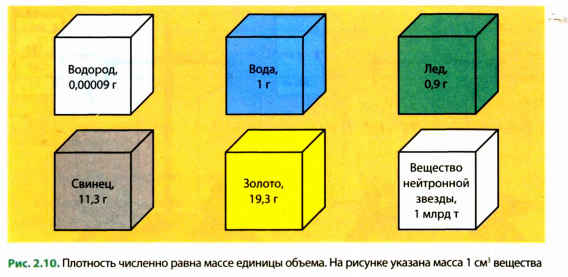
Плотности разных веществ и материалов могут существенно отличаться друг от друга (рис. 2.10). Рассмотрим несколько примеров. Плотность водорода при температуре О С и давлении 760 мм рт. ст. составляет 0,090 кг/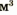
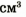
1 м3 имеет массу 11 300 кг, или 11,3 т. Плотность вещества нейтронной звезды достигает 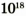
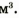
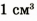

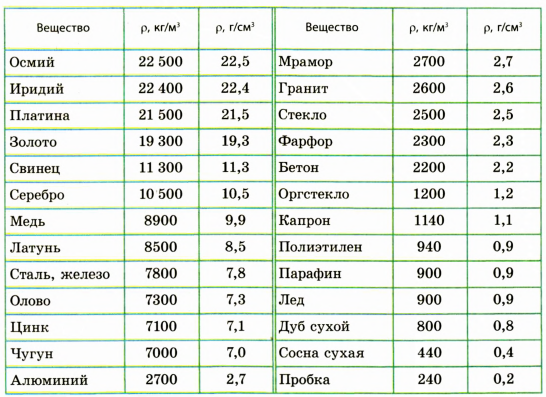
Таблица плотностей некоторых веществ в твердом состоянии
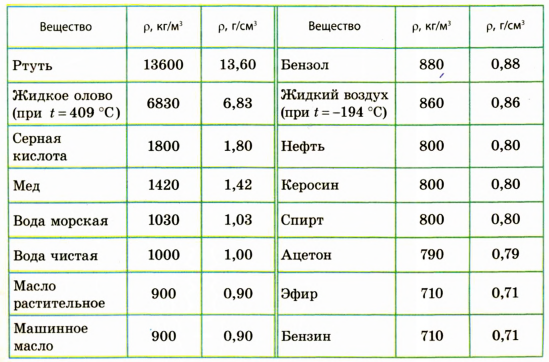
Таблица плотностей некоторых веществ в жидком состоянии
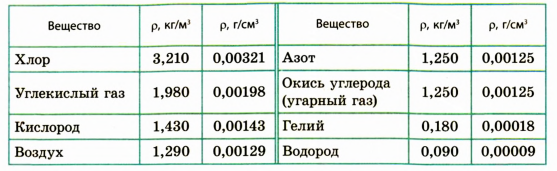
Таблица плотностей некоторых веществ в газообразном состоянии (при температуре О °С и давлении 760 мм рт. ст.)
Вычисление плотности, массы и объема физического тела
На практике часто бывает необходимо определить, из какого вещества состоит то или иное физическое тело. Для этого можно воспользоваться таким способом. Вначале вычислить плотность этого тела, т. е. найти отношение массы тела к его объему. Далее, воспользовавшись данными таблицы плотностей, выяснить, какому веществу соответствует найденное значение плотности.
Например, если глыба объемом 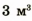
По таблице находим, что глыба состоит из льда.
В приведенных выше примерах мы рассматривали так называемые однородные тела, т. е. тела, не имеющие пустот и состоящие из одного ее щества (ледяная глыба, свинцовый и алюминиевый бруски). В таких случаях плотность тела равна плотности вещества, из которого оно состоит (плотность ледяной глыбы = плотности льда).
Если в теле есть пустоты или оно изготовлено из различных веществ (например, корабль, футбольный мяч, человек), то говорят о средней плотности тела, которая также исчисляется по формуле
где V — объем тела массой m.
Средняя плотность тела человека, например, составляет
Зная плотность вещества, из которого изготовлено тело (или среднюю плотность тела), и объем тела, можно определить массу данного тела без взвешивания. В самом деле, если
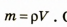
Итоги:
Физическая величина, характеризующая данное вещество и численно равная массе вещества единичного объема, называется плотностью вещества.
Плотность вещества и плотность тела можно рассчитать по формуле
В СИ плотность измеряется в килограммах на метр кубический 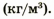
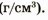
Зная массу тела и его плотность, можно найти объем тела: 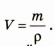
Плотность и единицы плотности
Вы наверняка слышали выражения «легкий, как воздух», «тяжелый, как свинец». При этом воздух внутри, скажем, супермаркета имеет массу более 5000 кг! Поднять груз такой массы не сможет и силач. В то же время свинцовое грузило для удочки легко поднимет даже малыш. Так что же, приведенные выражения ошибочны? Выясним, в чем здесь дело.
На рис. 16.1 изображены два однородных (не имеющих пустот) свинцовых бруска разного объема. Массы брусков тоже разные. Наша задача — найти отношение массы каждого бруска к его объему, то есть определить массу свинца объемом
1)Измерьте длину, ширину, высоту брусков и вычислите их объемы 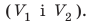
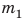
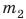
3)Определите отношение массы каждого бруска к его объему 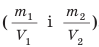
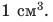
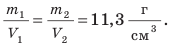
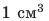
Как вы считаете, изменится ли результат, если для эксперимента взять однородные свинцовые бруски вдвое большей массы? Если изменится, то как?
Определение плотности вещества
Мы провели измерения и расчеты для тел, изготовленных из свинца. Если для эксперимента взять однородные тела, изготовленные из другого вещества, например алюминия, то снова получим одинаковые результаты, но уже другие, чем в опыте со свинцом.
Отношение массы тела к его объему — характеристика не тела, а вещества, из которого это тело изготовлено. Эту величину называют плотность вещества.
Плотность вещества — это физическая величина, которая характеризует вещество и равна отношению массы однородного тела, изготовленного из данного вещества, к объему этого тела: 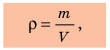
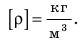
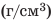
Сравнение плотности разных веществ
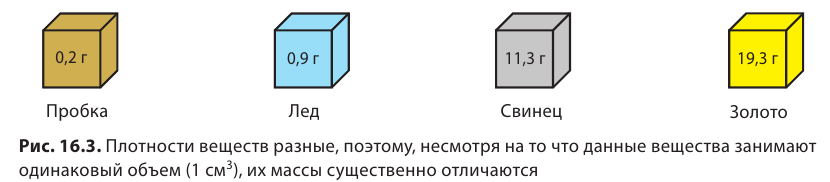
Плотности веществ могут существенно отличаться. Именно поэтому одинаковые по размерам однородные тела, изготовленные из разных веществ, будут иметь разную массу. Приведем несколько примеров.
Кубики на рис. 16.3 изображены в натуральную величину и являются однородными. Объем каждого кубика — 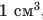
Первый кубик изготовлен из пробки. Плотность пробки составляет 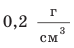
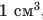
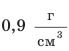
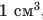
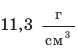
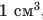
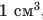
От чего зависит плотность вещества
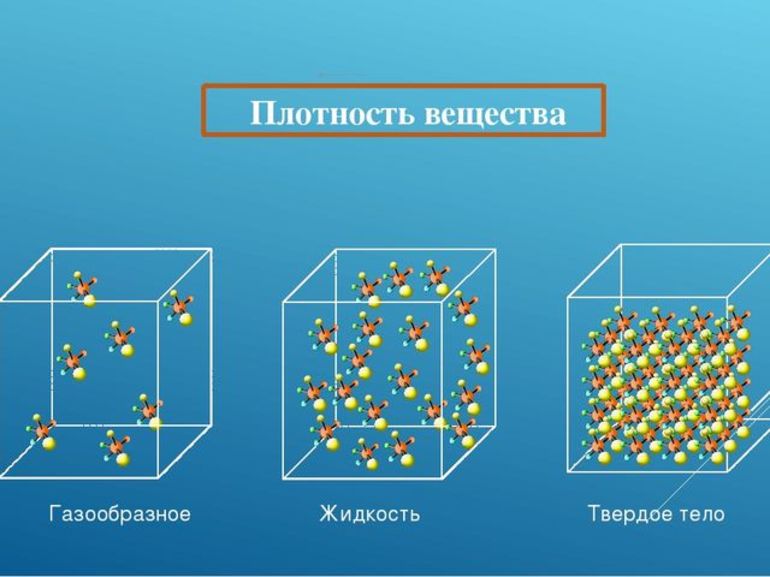
Плотность существенно зависит от агрегатного состояния и температуры вещества. Если вещество изменяет свое агрегатное состояние или температуру, его масса остается неизменной, так как количество частиц (молекул, атомов) и масса каждой из них не изменяются. А вот объем вещества изменяется, поскольку изменяется среднее расстояние между частицами. Так, при переходе вещества из жидкого состояния в газообразное плотность вещества уменьшается, поскольку увеличивается среднее расстояние между частицами, а значит, увеличивается объем, который занимает вещество (рис. 16.4).
С увеличением температуры среднее расстояние между частицами увеличивается, соответственно увеличивается объем вещества и уменьшается его плотность. И наоборот, чем ниже температура вещества, тем меньше межмолекулярные промежутки, а значит, меньше объем вещества и больше — его плотность*. 5
Вычисление и расчёт плотности тела, массы и объем тела
Как выяснить, из какого вещества изготовлено однородное тело? Один из способов — определить плотность этого тела и сравнить полученный результат с данными таблиц плотностей. Чтобы определить плотность тела, достаточно измерить его массу и объем и вычислить отношение массы тела к его объему.
Исключениями являются вода, чугун и некоторые другие вещества. Например, при нагревании воды от О °C до 4 °C ее плотность увеличивается. Плотность — это характеристика вещества, но иногда, например для сокращения записи, употребляют термин «плотность тела».
Например, если однородная фигурка объемом 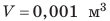
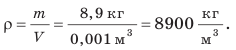
До сих пор речь шла об однородных телах, то есть телах, не имеющих пустот и состоящих из одного вещества (свинцовые бруски, медная фигурка). А вот если в теле есть пустоты или оно состоит из разных веществ (например, корабль, футбольный мяч, человек), то говорят о средней плотности тела; ее вычисляют по формуле: 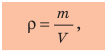
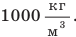
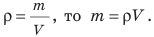
Итоги:
Плотность вещества — это физическая величина, которая характеризует вещество и равна отношению массы однородного тела, изготовленного из данного вещества, к объему этого тела. Плотность можно определить по формуле
Единица плотности в СИ — килограмм на метр кубический 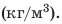
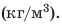
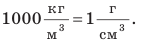
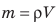
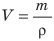
Напомним: приступив к решению задачи по физике, сначала следует несколько раз внимательно прочитать ее условие и понять, какое явление описано в задаче, какое тело рассматривается. Другими словами, нужно четко представить ситуацию, которую описывает задача, а уже потом приступать к поиску ответа. Итак, внимательно читаем, думаем, решаем. Попробуйте сначала поработать над каждой задачей самостоятельно, а уже потом ознакомьтесь с ее решением в учебнике.
- Заказать решение задач по физике
Пример №1
Однородный кубик с ребром 2 см имеет массу 20 г. Из какого вещества изготовлен кубик? Анализ физической проблемы. Для ответа на вопрос определим плотность вещества, из которого изготовлен кубик, а потом воспользуемся таблицей плотностей. Задачу будем решать в единицах, данных в условии.
Дано:

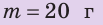
Найти:
Решение:
По определению плотности:
Объем куба вычисляют по формуле:
Следовательно, имеем:
Проверим единицу, найдем значение искомой величины:
Анализ результата. Из таблицы плотностей узнаем, что плотность 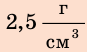
Ответ: кубик, возможно, изготовлен из стекла.
Пример №2
Свинцовый шар объемом 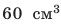
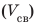
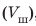
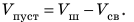
Плотность свинца найдем в таблице плотностей. В данной задаче массу лучше выразить в граммах, объем — в сантиметрах кубических, плотность — в граммах на сантиметр кубический.
Дано:

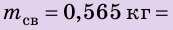

Найти:
Решение:
1. Определим объем свинца.
По определению плотности: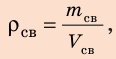
Проверим единицу, найдем значение искомой величины:
Анализ результатов: 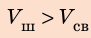
2. Вычислим объем пустоты:
Ответ:
Пример №3
Сколько железнодорожных цистерн емкостью 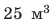
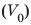
Дано:
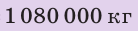
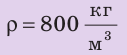
Найти:
Решение:
Из определения плотности найдем общий объем нефти:
Определим общее количество цистерн:
Проверим единицу, найдем значение искомой величины:
Анализ результатов. Количество цистерн, полученное в результате расчетов, вполне реально.
Ответ: N=54.
- Движение молекул в физике в газах, жидкостях и твёрдых телах
- Скорость движения молекул газа
- Газовые законы
- Взаимодействие молекул
- Движение и силы
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.
Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.
Сегодня мы познакомимся с такой характеристикой как плотность. Она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.
Связь массы, объема и вещества, из которого состоит тело
Рассмотрим опыт, представленный на рисунке 1.
Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.
Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.
В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.
Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.
На рисунке изображены 2 тела массой $100 space г$: лед, железо и золото.
Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.
Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.
Определение плотности вещества
Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.
Рассмотрим два тела объемом $1 space м^3$ каждое. Если они будут состоять из разных веществ, то их массы тоже будут разными.
Итак, алюминий такого объема будет иметь массу 2700 кг, а свинец такого же объема ( $1 space м^3$) будет имеет массу 11 300 кг.
На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.
Плотность показывает, чему равна масса вещества, взятого в объеме $1 space м^3$ (или $1 space см^3$). Чтобы найти плотность вещества, нужно массу тела разделить на его объем.
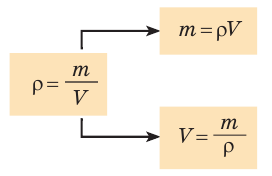
По какой формуле можно рассчитать плотность вещества? Дадим определение.
Плотность — это физическая величина, которая равна отношению массы тела к его объему:
$плотность = frac{масса}{объем}$
или
$rho = frac{m}{V}$,
где $rho$ (“ро”) — плотность вещества, $m$ — масса тела, $V$ — объем тела.
Единицы измерения плотности
Какова единица плотности в СИ?
В СИ плотность вещества измеряется в килограммах на кубический метр ($1 frac{кг}{м^3}$).
Какие еще единицы плотности вам известны?
Часто используется другая единица измерения — граммы на кубический сантиметр ($1 frac{г}{см^3}$) (рисунок 4).
Иногда нам потребуется переводить плотность веществ, выраженную в $frac{кг}{м^3}$ в $ frac{г}{см^3}$.
Давайте выразим плотность мрамора ($2700 frac{кг}{м^3}$) в $frac{г}{см^3}$:
$$rho = 2700 cdot frac{1 space кг}{1 space м^3} = 2700 cdot frac{1000 space г}{1 space 000 space 000 space см^3} = frac{2700}{1000} cdot frac{г}{см^3} = 2.7 frac{г}{см^3}$$
Таблицы плотности некоторых тел и веществ
Плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна.
Например, плотность воды составляет $1000 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, водяного пара — $0.590 frac{кг}{м^3}$ (рисунок 5).
Плотности различных твердых тел
| Твердое тело | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Твердое тело | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Осмий | 22 600 | 22,6 | Мрамор | 2700 | 2,7 |
| Иридий | 22 400 | 22,4 | Стекло | 2500 | 2,5 |
| Платина | 21 500 | 21,5 | Фарфор | 2300 | 2,3 |
| Золото | 19 300 | 19,3 | Бетон | 2300 | 2,3 |
| Свинец | 11 300 | 11,3 | Кирпич | 1800 | 1,8 |
| Серебро | 10 500 | 10,5 | Сахар | 1600 | 1,6 |
| Медь | 8900 | 8,9 | Оргстекло | 1200 | 1,2 |
| Латунь | 8500 | 8,5 | Капрон | 1100 | 1,1 |
| Сталь, железо | 7800 | 7,8 | Полиэтилен | 920 | 0,92 |
| Олово | 7300 | 7,3 | Парафин | 900 | 0,90 |
| Цинк | 7100 | 7,1 | Лед | 900 | 0,90 |
| Чугун | 7000 | 7,0 | Дуб сухой | 700 | 0,70 |
| Корунд | 4000 | 4,0 | Сосна сухая | 400 | 0,40 |
| Алюминий | 2700 | 2,7 | Пробка | 240 | 0,24 |
Плотности различных жидкостей
| Жидкость | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Жидкость | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Ртуть | 13 600 | 13,60 | Керосин | 800 | 0,80 |
| Серная кислота | 1800 | 1,80 | Спирт | 800 | 0,80 |
| Мед | 1350 | 1,35 | Нефть | 800 | 0,80 |
| Вода морская | 1030 | 1,03 | Ацетон | 790 | 0,79 |
| Молоко цельное | 1030 | 1,03 | Эфир | 710 | 0,41 |
| Вода чистая | 1000 | 1,00 | Бензин | 710 | 0,71 |
| Масло подсолнечное | 930 | 0,93 | Жидкое олово (при $400^{circ}$) | 6800 | 6,80 |
| Масло машинное | 900 | 0,90 | Жидкий воздух (при $-194^{circ}$) | 860 | 0,86 |
Плотности различных газов
| Газ | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Газ | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Хлор | 3,210 | 0,00321 | Угарный газ | 1,250 | 0,00125 |
| Углекислый газ | 1,980 | 0,00198 | Природный газ | 0,800 | 0,0008 |
| Кислород | 1,430 | 0,00143 | Водяной пар (при $100^{circ}$) | 0,590 | 0,00059 |
| Воздух (при $0^{circ}C$ | 1,290 | 0,00129 | Гелий | 0,180 | 0,00018 |
| Азот | 1,250 | 0,00125 | Водород | 0,090 | 0,00009 |
Примеры задач на расчет плотности вещества
Задача №1
В таблице 1 указана плотность сахара — $1600 frac{кг}{м^3}$. Что это значит? Какой здесь физический смысл?
Посмотреть ответ
Скрыть
Ответ:
Значение плотности показывает нам, какое количество вещества (его масса) будет находиться в объеме $1 space м^3$. Итак, это означает, что масса сахара объемом $1 space м^3$ будет равна $1600 space кг$.
Задача №2
Канистра объемом 30 л наполнена бензином. Масса полной канистры составляет 21,3 кг. Рассчитайте плотность бензина.
Переведем литры в кубические метры ($1 space л = 0.001 space м^3$):
$30 cdot 0.001 = 0.03 space м^3$.
Дано:
$V = 30 space л$
$m = 21.3 space кг$
$rho -?$
Показать решение и ответ
Скрыть
Решение:
По определению плотности:
$rho = frac{m}{V}$.
$rho = frac{21.3 space кг}{0.03 space м^3} = 710 frac{кг}{м^3}$.
Если мы сравним полученное значение с табличным, то получим подтверждение, что задача решена верно.
Ответ: $rho = 710 frac{кг}{м^3}$.
Задача №3
Деревянный брусок из березы имеет следующие размеры: длину 3 м, высоту 10 см, и ширину 50 см. Масса бруска составляет 75 кг. Найдите плотность березы.
Дано:
$а = 3 space м$
$b = 10 space см$
$c = 50 space см$
$m = 75 space кг$
$rho -?$
Показать решение и ответ
Скрыть
Решение:
Найдем объем бруска:
$V = a cdot b cdot c$,
$V = 3 space м cdot 0.1 space м cdot 0.5 space м = 0.15 space м^3$.
По определению плотности:
$rho = frac{m}{V}$.
$rho = frac{75 space кг}{0.15 space м^3} = 500 frac{кг}{м^3}$.
Ответ: $rho = 500 frac{кг}{м^3}$.
Больше задач с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Плотность редкого металла осмия равна $22 space 600 frac{кг}{м^3}$. Что это означает?
Посмотреть ответ
Скрыть
Ответ:
Значение плотности показывает нам, какое количество вещества (его масса) будет находиться в объеме $1 space м^3$. Итак, это означает, что масса осмия объемом $1 space м^3$ будет равна $22 space 600 space кг$ или $22.6 space т$.
Упражнение №2
Пользуясь таблицами плотностей (таблицы 1, 2), определите, плотность какого вещества больше: цинка или серебра; бетона или мрамора; бензина или спирта.
Показать ответ
Скрыть
Плотность цинка составляет $7100 frac{кг}{м^3}$, а серебра — $10 space 500 frac{кг}{м^3}$. Получается, что плотность серебра больше плотности цинка.
Плотность бетона составляет $2300 frac{кг}{м^3}$, а мрамора — $2700 frac{кг}{м^3}$. Получается, что плотность мрамора больше плотности бетона.
Плотность бензина составляет $710 frac{кг}{м^3}$, а спирта — $800 frac{кг}{м^3}$. Получается, что плотность спирта больше плотности бензина.
Упражнение №3
Три кубика — из мрамора, льда и латуни — имеют одинаковый объем. Какой из них имеет большую массу, а какой — меньшую?
Показать ответ
Скрыть
Выразим массу из формулы плотности:
$rho = frac{m}{V}$,
$m = rho V$.
Объем кубиков у нас одинаковый. Значит, чем больше плотность вещества, из которого изготовлен кубик, тем больше его масса.
Плотность мрамора составляет $2700 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, а латуни — $8500 frac{кг}{м^3}$. У латуни наибольшая плотность, а у льда — наименьшая. Значит, кубик из латуни будет иметь наибольшую массу, а из льда — наименьшую.
Упражнение №4
Самое легкое дерево — бальза. Масса древесины этого дерева равна $12 space г$ при объеме в $100 space см^3$. Определите плотность древесины в $frac{г}{см^3}$ и $frac{кг}{м^3}$.
Дано:
$m = 12 space г$
$V = 100 space см^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Мы не стали переводить единицы измерения в СИ. Сначала мы рассчитаем плотность этой древесины в $frac{г}{см^3}$, а затем переведем в $frac{кг}{м^3}$.
Рассчитаем плотность по известной нам формуле:
$rho = frac{m}{V}$,
$rho = frac{12 space г}{100 space см^3} = 0.12 frac{г}{см^3}$.
Теперь переведем полученное значение в $frac{кг}{м^3}$:
$rho = 0.12 frac{г}{см^3} = 0.12 frac{0.001 space кг}{0.01^3 space м^3} = 0.12 frac{10^{-3} space кг}{10^{-6} space м^3} = 0.12 cdot 10^3 frac{кг}{м^3} = 120 frac{кг}{м^3}$.
Ответ: $rho = 0.12 frac{г}{см^3} = 120 frac{кг}{м^3}$.
Упражнение №5
Кусочек сахара имеет размеры: $а = 2.5 space см$, $b = 1 space см$, $с = 0.7 space см$ (рис. 53). Его масса равна $0.32 space г$. Определите плотность сахара. Проверьте полученный результат по таблице 1.
Дано:
$а = 2.5 space см$
$b = 1 space см$
$с = 0.7 space см$
$m = 0.32 space г$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Чтобы рассчитать плотность сахара, нужно знать его объем. Его мы можем вычислить перемножив друг на друга известные высоту, ширину и длину:
$V = a cdot b cdot c$.
Подставим в формулу плотности и рассчитаем ее:
$rho = frac{m}{V} = frac{m}{a cdot cdot b cdot c}$,
$rho = frac{0.32 space г}{2.5 space см cdot 1 space см cdot 0.7 space см} = frac{0.32 space г}{1.75 space см^3} approx 0.18 frac{г}{см^3}$.
Полученный результат не совпадает с табличным ($rho = 1.6 frac{г}{см^3}$). Расчеты произведены верно, значит ошибка или в условии задачи, или мы наблюдаем очень необычный сахар.
Ответ: $rho approx 0.18 frac{г}{см^3}$.
Задание
В вашем распоряжении имеются весы с разновесами, измерительный цилиндр с водой и металлический шарик на нити. Предложите, как определить плотность шарика.
Взвесим шарик, мы узнаем его массу. Чтобы определить его объем, мы можем использовать измерительный цилиндр с водой. Для этого нужно опустить шарик в воду, и посмотреть, до какого уровня теперь поднялась воды. Разность этого объема и первоначального объема жидкости будет равна объему шарику.
Зная его массу и объем, мы сможем рассчитать его плотность по формуле: $rho = frac{m}{V}$.
Содержание:
- Определение и формула плотности вещества
- Виды плотности вещества
- Единицы измерения плотности вещества
- Примеры решения задач
Определение и формула плотности вещества
Определение
Плотностью вещества (плотностью вещества тела) называют скалярную физическую величину, которая равна отношению массы
(dm) малого элемента тела к его единичному объему (dV). Чаще всего плотность вещества обозначают греческой буквой
$rho$. И так:
$$rho=frac{d m}{d V}$$
Виды плотности вещества
Применяя выражение (1) для определения плотности, говорят о плотности тела в точке.
Плотность тела зависит от материала тела и его термодинамического состояния.
В том случае, если тело можно считать однородным (плотность вещества во всем теле одинакова (
$rho = const$), то $rho$ определяют следующей формулой:
$$rho=frac{m}{V}$$
где m – масса тела, V – объем тела.
Если тело является неоднородным, то иногда пользуются понятием средней плотности
$langlerhorangle$, которая рассчитывается как:
$$langlerhorangle=frac{m}{V}(3)$$
где m – масса тела, V – объем тела. В технике для неоднородных (например, сыпучих) тел используют понятие объемной плотности.
Объемную плотность рассчитывают так же как $langlerhorangle=frac{m}{V}(3)$ (3). Объем определяют,
включая промежутки в сыпучих и рыхлых материалах (таких как: песок, гравий, зерно и т.д.).
При рассмотрении газов, находящихся в нормальных условиях для вычисления плотности применяют формулу:
$$rho=frac{mu}{V_{mu}}(4)$$
где $mu$ – молярная масса газа,
$V_{mu}$ – молярный объем газа, который при нормальных условиях составляет 22,4 л/моль.
Единицы измерения плотности вещества
В соответствии с определением, можно записать, что
единицами измерения плотности в системе СИ служит: [$rho$]=кг/м3
в СГС: [$rho$]=г/(см)3
При этом: 1 кг/м3 = (10)-3 г/(см)3 .
Примеры решения задач
Пример
Задание. Какова плотность воды, если объем, который занимает одна молекула H2O,
примерно равен $Delta V approx 3 cdot 10^{-29}$ м3? Считайте, что молекулы в воде плотно упакованы.
Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как:
$$rho=frac{m_{0}}{Delta V}$$
где m0 – масса молекулы воды. Найдем m0, используя известное соотношение:
$$frac{m}{mu}=frac{N}{N_{A}}$$
где N=1 – количество молекул (в нашем случае одна молекула), m – масса рассматриваемого количества молекул
(в нашем случае m=m0), NА=6,02• 1023 моль-1 – постоянная Авогадро,
$mu$=18•10-3
кг/моль (так как относительная молекулярная масса воды равна Mr=18). Следовательно, применяя выражение (2)
для нахождения массы одной молекулы имеем:
$$m_{0}=frac{mu}{N_{A}}(3)$$
Подставим m0 в выражение (1), получаем:
$$rho=frac{mu}{Delta V N_{A}}(4)$$
Проведем расчет искомой величины:
$rho=frac{18 cdot 10^{-3}}{3 cdot 10^{-29} cdot 6,02 cdot 10^{23}}=10^{3} mathrm{kr} / mathrm{m}^{3}$ кг/м3
Ответ. Плотность воды равна 103 кг/м3 .

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
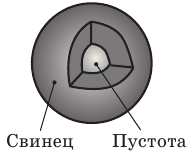
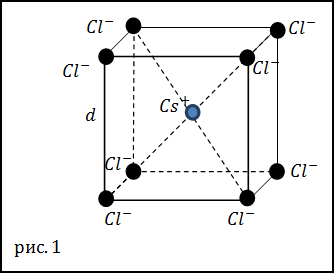
Задание. Какова плотность кристаллов хлорида цезия (CsCl), если кристаллы имеют кубическую кристаллическую
решетку (рис.1) в вершинах которой находятся ионы хлора (Cl–), а в центре расположен ион цезия
(Cs+). Ребро кристаллической решетки считайте равным d=0, 41 нм.
Решение. За основу решения задачи примем выражение:
$$frac{m}{mu}=frac{N}{N_{A}}(2.1)$$
где m – масса вещества (в нашем случае это масса одной молекулы
$left.operatorname{CsCl}left(m_{0}right)right), N=1, N_{A}=6,02 cdot 10^{23}$ – постоянная Авогадро,
$mu=168 cdot 10^{-3}$ кг/моль молярная масса хлорида Цезия
(так как относительная молекулярная хлорида цезия равна $M_r = 168$).
Выражение (2.1) для одной молекулы примет вид:
$$frac{m_{0}}{mu}=frac{1}{N_{A}}$$
В выражении (2.2) массу молекулы можно выразить через ее плотность как:
$$m_{0}=rho V_{m}(2.3)$$
где Vm – объем исследуемой молекулы. Так как кристаллы имеют кубическую кристаллическую решетку, ребро которой нам известно
(и равно d), то вместо объема Vm можно использовать выражение:
$$V_{m}=d^{3}(2.4)$$
Подставим выражения (2.3) и (2.4) в формулу (2.2), получим:
$$frac{rho V_{m}}{mu}=frac{1}{N_{A}}(2.5)$$
Тогда выражение для плотности примет вид:
$$rho=frac{mu}{d^{3} N_{A}}$$
Переведем размер стороны кристаллической решетки в единицы системы СИ, получим d=0,41нм=0, 41•10-9) м. Проведем вычисления:
$rho=frac{168 cdot 10^{-3}}{left(0,41 cdot 10^{-9}right)^{3} cdot 6,02 cdot 10^{23}}=4047,6$ кг/м3
Ответ. $rho=4047,6$ кг/м3
Читать дальше: Формула потенциальной энергии.