Как найти плотность тела в воздухе

Так как чего-то не могу пересылать латинницу, то буду в формулах всё писать русскими буквами.
————————————–

ДАНО:

М1 – масса в воздухе; М2 – масса в воде.

НАЙТИ:

РО – искомая плотность тела.

————————————————

РЕШЕНИЕ:

Формула плотности:

РО = М1/В

где “В” – это объём тела, но он нам неизвестен

Откуда же взять это “В”? Обратимся к силе, котороя облегчает вес тела в воде – СИЛА АРХИМЕДА.

Имеются 2 формулы, по которым она вычисляется .Первая из них:

Фа = Ф1 – Ф2,

где Ф1 = М1*Г; Ф2 = М2*Г;

Теперь вторая формула силы Архимеда:

Фа = РОв * В * Г,

где РОв – плотность воды, Г – гравитационная постоянная (9,8 Н/м) ;

А теперь важный шаг – соеденям две предыдущие формулы в одну:

Ф1 – Ф2 = РОв * В * Г

Упрощаем:

Ф1 – Ф2 = РОв * В * Г;

М1*Г – М2*Г = РОв * В *Г;

М1 – М2 = РОв * В;

Уже близок ответ. Из последней формулы, которую мы получили, вычисляем объём “В”…

В = (М1 – М2) / РОв ;

… И подставляем в самую первую формулу, получая КОНЕЧНЫЙ ОТВЕТ:

РО = (М1*РОв) / (М1 – М2)

Плотность
Размерность	L−3 M
Единицы измерения
СИ	кг/м³
СГС	г/см³
Примечания
скалярная величина

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или как производная массы по объёму:

.

Данные выражения не эквивалентны, и выбор зависит от того, какая именно плотность рассматривается. Различаются:

Для точечной массы плотность является бесконечной. Математически её можно определить или как меру, или как производную Радона — Никодима по отношению к некоторой опорной мере.

Для обозначения плотности обычно используется греческая буква (ро) (происхождение обозначения подлежит уточнению), иногда используются латинские буквы D и d (от лат. densitas «плотность»). Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.

Понятие «плотность» в физике может иметь более широкую трактовку. Существуют поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам. Кроме того, говорят не только о плотности массы, но и о плотности других величин, например энергии, электрического заряда. В таких случаях к термину «плотность» добавляются конкретизирующие слова, скажем «линейная плотность заряда». «По умолчанию» под плотностью понимается вышеуказанная (трёхмерная, кг/м³) плотность массы.

Формула нахождения плотности[править | править код]

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

где M — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.

При вычислении плотности газов при стандартных условиях эта формула может быть записана и в виде:

где  — молярная масса газа,  — молярный объём (при стандартных условиях приближённо равен 22,4 л/моль).

Плотность тела в точке записывается как

тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как

Случай сыпучих и пористых тел[править | править код]

В случае сыпучих и пористых тел различают

• истинную плотность, определяемую без учёта пустот;
• насыпную плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.

Истинную плотность из насыпной (кажущейся) получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.

Зависимость плотности от температуры[править | править код]

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.

Диапазон плотностей в природе[править | править код]

Для различных природных объектов плотность меняется в очень широком диапазоне.

• Самую низкую плотность имеет межгалактическая среда (2·10⁻³¹—5·10⁻³¹ кг/м³, без учёта тёмной материи)^[2].
• Плотность межзвёздной среды приблизительно равна 10⁻²³—10⁻²¹ кг/м³.
• Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
• Плотность газообразного водорода (самого лёгкого газа) при стандартных условиях равна 0,0899 кг/м³.
• Плотность сухого воздуха при стандартных условиях составляет 1,293 кг/м³.
• Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
• Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
• Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
• Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
• Плотность пресной воды при 4 °C 1000 кг/м³.
• Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
• Гранит имеет плотность 2600 кг/м³.
• Средняя плотность Земли равна 5520 кг/м³.
• Плотность железа равна 7874 кг/м³.
• Плотность металлического урана 19100 кг/м³.
• Плотность золота 19320 кг/м³.
• Плотность нептуния — самого плотного актиноида — 20200 кг/м³.
• Самые плотные вещества при стандартных условиях — металлы платиновой группы шестого периода (осмий, иридий, платина), а также рений. Имеют плотность 21000—22700 кг/м³.
• Плотность атомных ядер приблизительно 2·10¹⁷ кг/м³.
• Теоретически верхняя граница плотности по современным^{[когда?]} физическим представлениям — это планковская плотность 5,1⋅10⁹⁶ кг/м³.

Плотности астрономических объектов[править | править код]

• Средние плотности небесных тел Солнечной системы см. на врезке.
• Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10⁻²¹÷10⁻²⁰ кг/м³.
• Плотность межзвёздной среды ~10⁻²³÷10⁻²¹ кг/м³.
• Плотность межгалактической среды 2×10⁻³⁴÷5×10⁻³⁴ кг/м³.
• Средняя плотность красных гигантов на много порядков меньше чем у Солнца из-за того, что их радиус в сотни раз больше.
• Плотность белых карликов 10⁸÷10¹² кг/м³
• Плотность нейтронных звёзд имеет порядок 10¹⁷÷10¹⁸ кг/м³.
• Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:

Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M⁻²). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 10¹⁹ кг/м³, превышающей ядерную плотность (2×10¹⁷ кг/м³), то сверхмассивная чёрная дыра с массой в 10⁹ солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).

Плотности некоторых газов[править | править код]

Плотность газов, кг/м³ при НУ.

Азот	1,250	Кислород	1,429
Аммиак	0,771	Криптон	3,743
Аргон	1,784	Ксенон	5,851
Водород	0,090	Метан	0,717
Водяной пар (100 °C)	0,598	Неон	0,900
Воздух	1,293	Радон	9,81
Гексафторид вольфрама	12,9	Углекислый газ	1,977
Гелий	0,178	Хлор	3,164
Дициан	2,38	Этилен	1,260

Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:^[6]

,

где:

Плотности некоторых жидкостей[править | править код]

Плотность жидкостей, кг/м³

Бензин	710	Молоко	1040
Вода (4 °C)	1000	Ртуть (0 °C)	13600
Керосин	820	Диэтиловый эфир	714
Глицерин	1260	Этанол	789
Морская вода	1030	Скипидар	860
Масло оливковое	920	Ацетон	792
Масло моторное	910	Серная кислота	1835
Нефть	550—1050	Жидкий водород (−253 °C)	70

Плотность некоторых пород древесины[править | править код]

Плотность древесины, г/см³

Бальса	0,15	Пихта сибирская	0,39
Секвойя вечнозелёная	0,41	Ель	0,45
Ива	0,46	Ольха	0,49
Осина	0,51	Сосна	0,52
Липа	0,53	Конский каштан	0,56
Каштан съедобный	0,59	Кипарис	0,60
Черёмуха	0,61	Лещина	0,63
Грецкий орех	0,64	Берёза	0,65
Вишня	0,66	Вяз гладкий	0,66
Лиственница	0,66	Клён полевой	0,67
Тиковое дерево	0,67	Бук	0,68
Груша	0,69	Дуб	0,69
Свитения (Махагони)	0,70	Платан	0,70
Жостер (крушина)	0,71	Тис	0,75
Ясень	0,75	Слива	0,80
Сирень	0,80	Боярышник	0,80
Пекан (кария)	0,83	Сандаловое дерево	0,90
Самшит	0,96	Эбеновое дерево	1,08
Квебрахо	1,21	Бакаут	1,28
Пробка	0,20

Плотность некоторых металлов[править | править код]

Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.

Плотность металлов, кг/м³

Осмий	22610[7]	Родий	12410[8]	Хром	7190[9]
Иридий	22560[10]	Палладий	12020[11]	Германий	5320[12]
Плутоний	19840[13]	Свинец	11350[14]	Алюминий	2700[15]
Платина	19590[16]	Серебро	10500[17]	Бериллий	1850[18]
Золото	19300[14]	Никель	8910[19]	Рубидий	1530[20]
Уран	19050[21]	Кобальт	8860[22]	Натрий	970[23]
Тантал	16650[24]	Медь	8940[25]	Цезий	1840[26]
Ртуть	13530[27]	Железо	7870[28]	Калий	860[29]
Рутений	12450[30]	Марганец	7440[31]	Литий	530[32]

Измерение плотности[править | править код]

Для измерений плотности используются:

• Пикнометр — прибор для измерения истинной плотности
• Различные виды ареометров — измерители плотности жидкостей.
• Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
• Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
• Метод гидростатического взвешивания.

Остеоденситометрия — процедура измерения плотности костной ткани человека.

См. также[править | править код]

• Список химических элементов с указанием их плотности
• Удельный вес
• Удельная плотность
• Относительная плотность
• Объёмная плотность
• Конденсация
• Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
• Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
• Концентрация частиц
• Концентрация растворов
• Плотность заряда
• Уравнение неразрывности

Примечания[править | править код]

Литература[править | править код]

• Плотность — статья из Большой советской энциклопедии.  — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
• Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
• Krebs R. E. . The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.

Ссылки[править | править код]

• Онлайн интерактивная таблица плотности веществ Архивная копия от 29 апреля 2011 на Wayback Machine (рус.)
• Подробная таблица значений плотности распространенных жидкостей Архивная копия от 5 октября 2016 на Wayback Machine (рус.)
• Урок по теме “Плотность вещества” Архивная копия от 30 января 2022 на Wayback Machine

2010-03-24 22:34

Для определения плотности

 однородного тела неправильной формы, объем которого трудно найти при помощи измерения размеров тела, можно поступить следующим образом.

Тело дважды взвешивают на весах: один раз обычным способом, другой раз — погружая тело в жидкость, плотность

 которой известна. Первое взвешивание дает вес тела

, который равен

 (

— плотность тела,

 — его объем). Результат второго взвешивания

 дает разность между весом тела

 и выталкивающей силой

:

. (161.1)

Согласно закону Архимеда

. Заменив в этом равенстве

 на

, получим

. Подставив это выражение в формулу (161.1), придем к соотношению

,

откуда

. (161.2)

В случае неоднородного тела определяемая этой формулой величина

 даст среднюю плотность тела.

161.1.
Определите плотность камня, если вес его в воздухе равен 3,2 Н, а вес в воде равен 1,8 Н.

161.2.
Как определить плотность жидкости

, зная вес какого-нибудь тела в воздухе

, в воде

 и в исследуемой жидкости

?

161.3.
Кусок меди весит в воздухе 4,00 Н, а при погружении в некоторую жидкость весит 3,59 Н. Найдите плотность жидкости, если плотность меди равна

.

161.4.
Кусок пробки весит в воздухе 0,15 Н, кусок свинца весит 1,14 Н. Если, связав их вместе, подвесить оба куска к чашке весов и опустить в керосин, то показание весов будет 0,70 Н. Найдите плотность пробки, полагая плотность свинца равной

, а плотность керосина равной

.

Как найти плотность тела

При решении некоторых физических задач требуется найти плотность тела. Иногда плотность физического тела необходимо определить и на практике, например, для того чтобы узнать, утонет оно или нет. Кстати, тело человека также можно отнести к физическим телам. Причем понятие «плотности» человеческого тела давно уже вошло в обиход. Так «крепко сбитого» человека обычно называют «плотным», а того, кто имеет противоположную конституцию тела – «рыхлым».

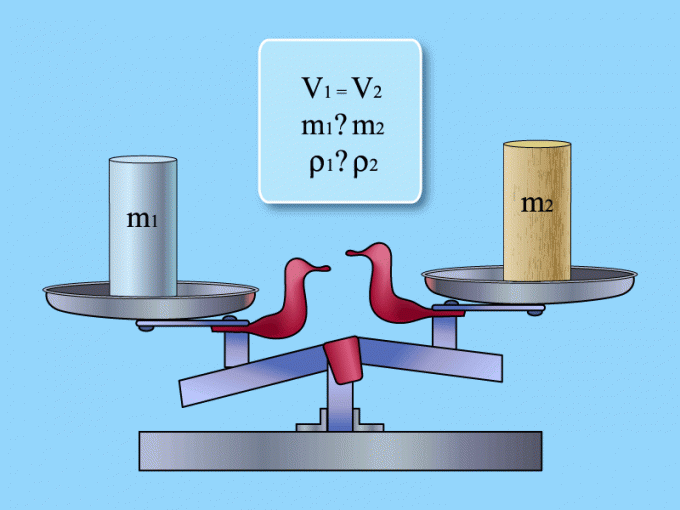
Вам понадобится

• калькулятор, весы, линейка, мерная кружка, таблица плотности веществ.

Инструкция

Чтобы найти плотность физического тела, определите из какого вещества или материала оно состоит. Затем возьмите таблицу плотности веществ и найдите в ней соответствующее вещество. Так, например, если предмет изготовлен из алюминия, его плотность будет равна 2,7 г/см³.

Если тело состоит из нескольких веществ, то найдите в соответствующих таблицах плотность каждого из них. Чтобы найти плотность тела в целом, определите вклад каждого вещества в формирование плотности предмета. Для этого определите объем или массу каждой однородной части, а затем посчитайте массу и объем всего тела.

Пусть, например, тело состоит из двух частей массой m1 и m2, соответственно. Плотность каждой части – ρ1 и ρ2. Чтобы найти среднюю плотность тела, найдите общий объем: V = V1 + V2 = m1 * ρ1 + m2 * ρ2, а затем разделите на общую массу тела (m = m1 + m2): ρ = V / m = (m1 * ρ1 + m2 * ρ2) / (m1 + m2), где:V – общий объем тела;
V1 и V2 – объем первой и второй части тела соответственно;
m – общая масса тела;
m1 и m2 – масса первой и второй части тела соответственно;
ρ – средняя плотность тела;
ρ1 и ρ2 – плотность первой и второй части тела соответственно.

Если известны объемы (V1 и V2) каждой части тела, а также их плотности, для вычисления плотности тела воспользуйтесь аналогичной формулой:ρ = V / m = (V1 + V2) / (m1 + m2) = (V1 + V2) / (V1 / ρ1 + V2 / ρ2). Обозначения параметров те же, что и в предыдущей формуле.

Если материал (вещество), из которого состоит тело, неизвестен или имеет непостоянную плотность (например, дерево, плотность которого зависит от влажности), чтобы найти его плотность, определите его объем и разделите на массу. То есть воспользуйтесь формулой:ρ = V / m.Для этого, конечно, придется посчитать или измерить объем и массу тела, зато такой метод даст самый точный результат. Если тело имеет форму простой геометрической фигуры, посчитайте его объем, воспользовавшись соответствующими формулами стереометрии. Объем сложных тел определите через объем вытесненной ими жидкости. Массу тела найдите с помощью взвешивания.

Источники:

• как определить плотность тела

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?