Как найти плотность теоретическая

Расчет теоретической плотности кристаллических веществ

Теоретическую
плотность кристаллических веществ
нередко и наиболее точно определяют с
помощью рентгенографического метода
(рассчитанная таким образом плотность
носит название рентгенографической).
При определении плотности по данным
рентгенографического анализа используется
связь значений плотности вещества с
атомными массами составляющих его
элементов и объемом, занимаемым ими.

Для
определения рентгенографической
плотности необходимо знать объем
элементарной ячейки (V₀),
число атомов (Z)
в ней и суммарную массу этих атомов.
Тогда масса атомов в элементарной ячейке
равна

(A/N₀)
Z,
[г], где

A/N₀
– масса одного атома в граммах; N₀
= 6,0224102 (число Авогадро),

А – грамм–атом.

Таким образом,
плотность равна:

ρ
= (A·Z
/ N₀)·(1/
V₀),
[г/см³],

При
переводе значений объема элементарной
ячейки из кубических ангстремов в
кубические сантиметры в знаменателе
формулы появляется V₀·10^–24,
тогда

ρ=1,6602
(A·Z/V₀),
[г/см³].

Объем
элементарной ячейки определяется исходя
из сингонии и формально–геометрических
соображений (Приложение 3).

Значение
рассчитанной таким образом плотности
кристаллического вещества характеризует
идеализированную кристаллическую
решетку с реальными параметрами.
Справочные значения плотности, как
правило, будут отличаться от
рентгенографической в меньшую или
большую сторону. Эта разница может быть
вызвана наличием в реальных кристаллах
примесей, дефектов кристаллической
решетки, внутренних напряжений

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте
   определение кристаллического тела.

2. Что
   понимают под атомно–кристаллической
   структурой?

3. Что
   такое кристаллическая решетка?

4. Назовите
   основные типы кристаллических решеток
   для металлов.

5. Сколько
   атомов приходится на элементарную
   ячейку ОЦК, ГЦК и ГПУ решеток?

6. В
   каких единицах измеряется период
   решетки?

7. Что
   понимают под индексом Миллера?

8. Что
   характеризует координационное число?

9. Дайте
   понятие плотности поликристаллических
   веществ.

ПОРЯДОК ВЫПОЛНЕНИЯ
РАБОТЫ

1.
Изучить предложенную теоретическую
часть и дидактическое обеспечение.

2. Выбрать вариант в соответствии с
порядковым номером в учебном журнале
и выполнить следующие задания:

Задание
1. Из таблицы 1 взять предложенные
исходные данные в соответствии с номером
выбранного варианта.

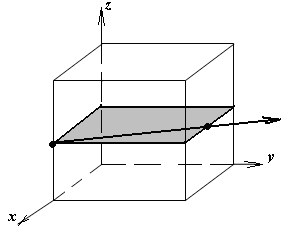
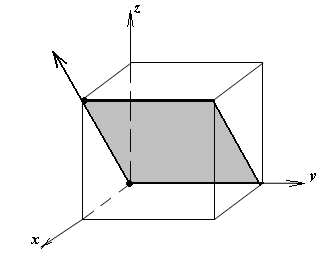
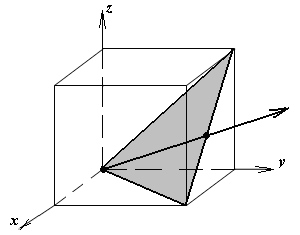
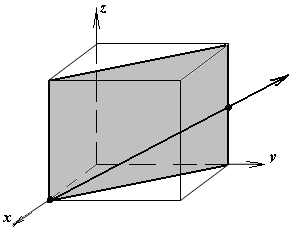
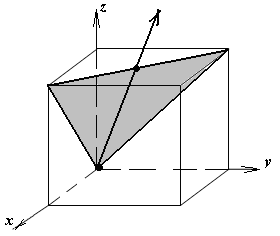
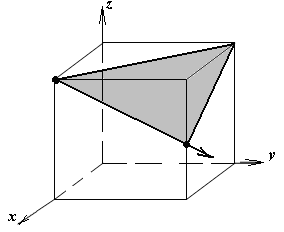
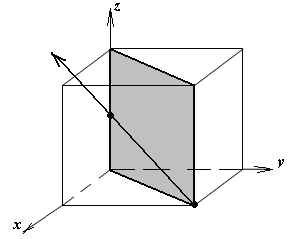
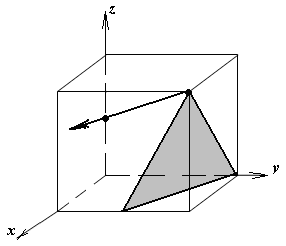
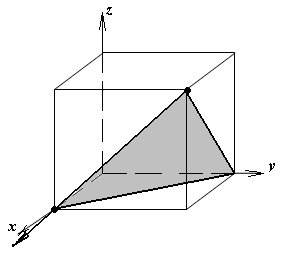
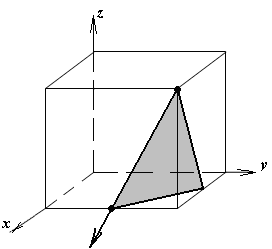
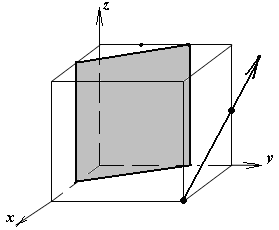
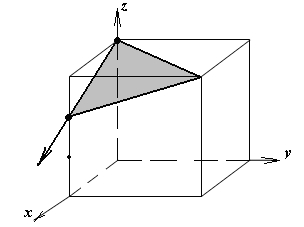
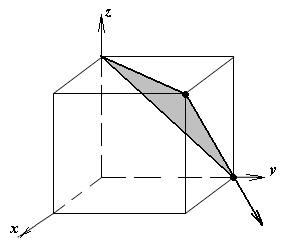
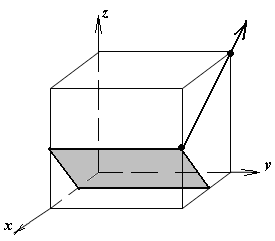
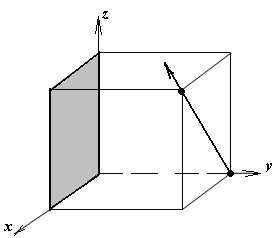
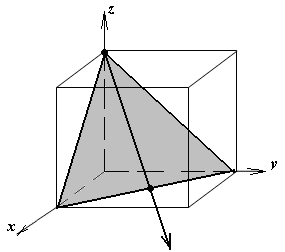
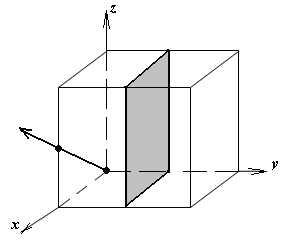
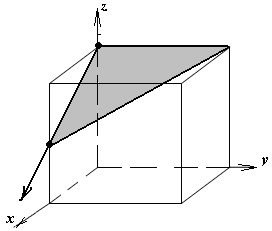
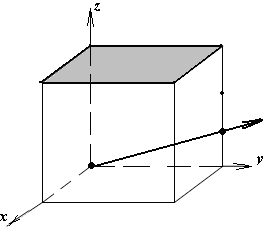
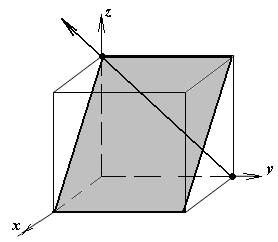
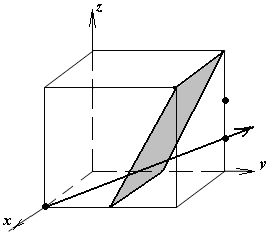
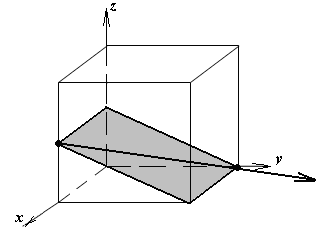
1.а
определить индексы плоскости и
направления, изображенных на рисунке;

1.б изобразить в элементарной ячейке
кубической решетки плоскость и
направление, индексы которых даны в
задании.

Задание 2. Рассчитать плотность
металла, используя данные о его
кристаллической решетке в соответствии
с номером варианта (таблица 2).

Формулы для расчета объема элементарной
ячейки приведены в приложении 2.

Сравнить полученные результаты расчета
со справочными данными (Таблица 3).

3. Сделать вывод по результатам работы.

4. Оформить отчет.

СОДЕРЖАНИЕ ОТЧЕТА

1. Тема
   работы, номер варианта.

2. Рисунок
   элементарной ячейки кубической решетки,
   приведенный в задании с указанием
   найденных индексов Миллера; рисунок
   элементарной ячейки с изображением
   плоскости и направления, приведенных
   в задании.

3. Расчет
   плотности металла.

4. Вывод
   по работе.

Таблица 1

Варианты
задания 1

Таблица 2

Варианты задания 2

Таблица
3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Enter the number of atoms per unit cell, the atomic weight, and the volume of a unit cell into the calculator to determine the theoretical density. This calculator can also evaluate any of the variables in the formula below when given the other variables.

• All Density Calculators
• Density to Mass Calculator
• Linear Density Calculator
• Density Calculator
• Cell Density Calculator

Theoretical Density Formula

The formula for calculating the theoretical density is as follows:

• Where ρ is the density (g/cm^3)
• n is the number of atoms per unit cell
• A is the atomic weight (g/mol)
• V is the volume per unit cell (cm^3/cell)
• N is Avogadro’s number (6.023*10^23)

To calculate a theoretical density, multiply the number of atoms per unit cell by the atomic weight, then divide by the result of the product of the volume per unit cell multiplied by Avogadro’s number.

Theoretical Density Definition

A theoretical density is defined as the maximum density of a material or element that could be achieved assuming there are no voids or contaminants in the overall material.

What is the theoretical maximum density?

The theoretical maximum density of an element or material can be calculated using the formula p = (n*A)/(V*N). This represents the true or maximum density the material can reach in a given sample.

How to calculate a theoretical density?

1. First, determine the number of atoms per cell of material or element.
2. Next, determine the atomic weight. Calculate the average weight of all of the elements in the material.
3. Next, determine the volume per unit cell. Typically this is 1 cm^3 per cell.
4. Finally, calculate the theoretical density. Using the formula along with Avogadro’s number, you can calculate the theoretical density.

Рассмотрим в статье, как найти плотность, и что это такое. При проектировании многих конструкций и транспортных средств учитывается ряд физических характеристик, которыми должен обладать конкретный материал. Одной из них является плотность.

Масса и объем

Расшифруем значение двух физических величин, которые к ней имеют непосредственное отношение – это масса и объем. Прежде, чем мы ответим на вопрос, как найти плотность.

Массой называется такая характеристика, которая описывает инерционные свойства тел и их способность проявлять гравитационное притяжение друг к другу. Масса измеряется в килограммах в системе СИ.

Вам будет интересно:Общая характеристика неметаллов главных подгрупп

Понятия инерционной и гравитационной масс были впервые введены в физику Исааком Ньютоном при формулировке законов механики и Всемирного тяготения.

Объем – это исключительно геометрическая характеристика тела, которая отражает количественно часть занимаемого им пространства. Измеряется объем в кубических единицах длины, например, в СИ это метры в кубе.

Для тел известной формы (параллелепипед, шар, пирамида) эту величину можно определить по специальным формулам, для объектов же неправильной геометрической формы объем определяют с помощью погружения их в жидкость.

Физическая величина плотность

Теперь можно переходить непосредственно к ответу на вопрос, как найти плотность. Эта характеристика определяется отношением массы тела к объему, который оно занимает, что математически записывается так:

ρ = m/V.

Это равенство показывает единицы измерения величины ρ (кг/м3). Таким образом, плотность масса и объем связаны единым равенством, причем величина ρ для любого материала показывает объемную концентрацию его массы.

Приведем простой пример: если взять в руку пластмассовый и железный шарики одинакового размера, то второй будет иметь гораздо больший вес, чем первый. Этот факт связан с большой плотностью железа по сравнению с таковой для пластмассы.

Одним из основных проявлений соотношения плотностей в природе будет плавучесть тел. Если тело имеет меньшую плотность, чем жидкость, то оно в ней никогда не утонет.

Плотность материалов

Когда речь ведут о плотности определенных материалов, то имеют в виду твердые вещества. Газы и жидкости тоже имеют определенную плотность, но здесь мы о них говорить не будем.

Твердые материалы могут иметь кристаллическое или аморфное строение. Величина ρ зависит от строения, межатомных расстояний и атомных и молекулярных масс материалов. Например, все металлы – это кристаллы, а стекло или дерево имеют аморфное строение. Ниже приведем таблицу плотности разных сортов дерева.

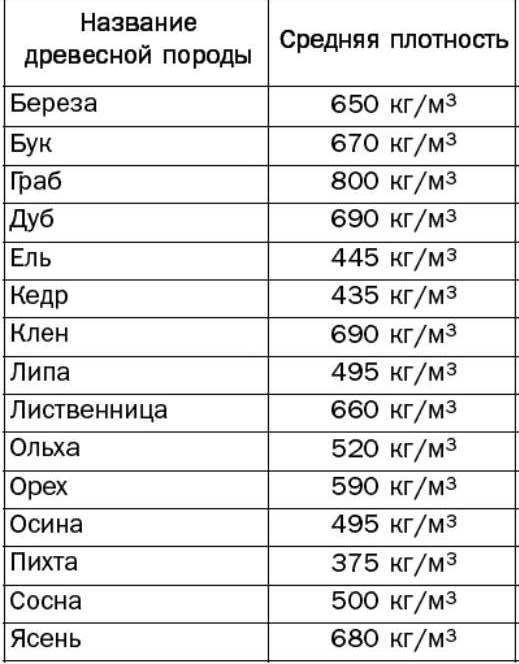
Обращаем внимание, что в данном случае приводится средняя плотность. В реальных условиях каждое дерево обладает уникальными особенностями, включая пустоты, поры и наличие некоторого процента влаги в древесине.

Ниже приведена еще одна таблица. В ней в г/см3 даны плотности всех чистых химических элементов, которые находятся при комнатной температуре.

Видно из таблицы, что все элементы имеют плотность больше, чем у воды. Исключение составляют всего три металла – литий, калий и натрий, которые не тонут, а плавают на поверхности воды.

Как измеряют плотность экспериментально?

По сути, существуют две техники определения изучаемой характеристики. Первая заключается в непосредственном взвешивании тела и измерении его линейных размеров.

Если же геометрическая форма тела сложная, тогда используют так называемый гидростатический метод.

Его суть заключается в следующем: сначала взвешивают тело на воздухе. Предположим, что полученный вес составил P1. После этого тело взвешивают в жидкости с известной плотностью ρl. Пусть вес тела в жидкости равен P2. Тогда значение плотности ρ исследуемого материала составит:

ρ = ρl*P1/(P1-P2).

Эту формулу может получить каждый школьник самостоятельно, если рассмотрит закон Архимеда для описанного случая.

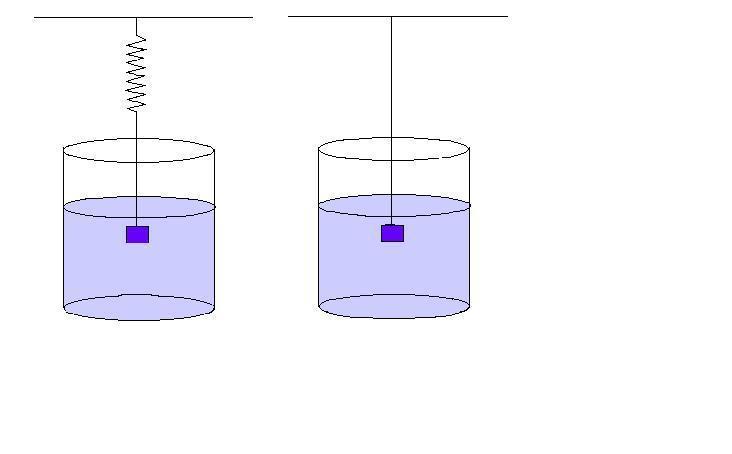
Исторически считается, что впервые гидростатическое взвешивание использовал греческий философ Архимед для определения подделки золотой короны. Первые же гидростатические весы были изобретены Галилео Галилеем в конце XVI века. В настоящее время для экспериментального определения величины ρ жидкостей, твердых тел и газов широко используются электронные пикнометры и плотномеры.

Теоретическое определение плотности

Выше был рассмотрен вопрос, как найти плотность экспериментально. Тем не менее, эту найти ρ неизвестного материала можно теоретическим путем. Для этого необходимо знать тип кристаллической решетки, параметры этой решетки, а также массу образующих ее атомов. Поскольку любая элементарная кристаллическая решетка имеет определенную геометрическую форму, то несложно найти формулу для определения ее объема.

Если кристаллический материал состоит из нескольких химических элементов, например, металлические сплавы, то его среднюю плотность можно определить по следующей простой формуле:

ρ = ∑mi/∑(mi/ρi).

Где mi, ρi – масса и плотность i-го компонента, соответственно.

Если материал имеет аморфную структуру, то теоретически определить точно его плотность не получится, и необходимо использовать экспериментальные техники.

Теоретическая плотность Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Общий объем элементарной ячейки: 90 Кубический метр –> 90 Кубический метр Конверсия не требуется
Масса атома: 42 грамм –> 0.042 Килограмм (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

2142.85714285714 Килограмм на кубический метр –> Конверсия не требуется