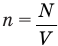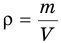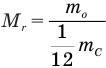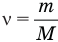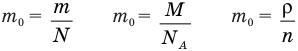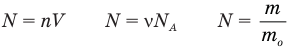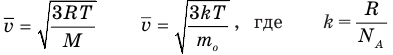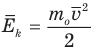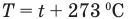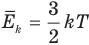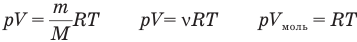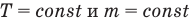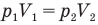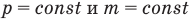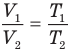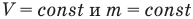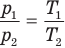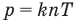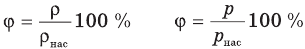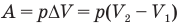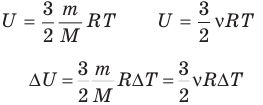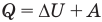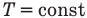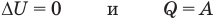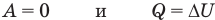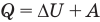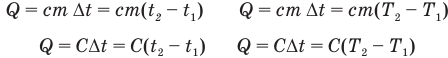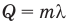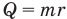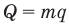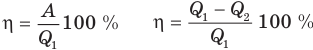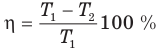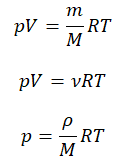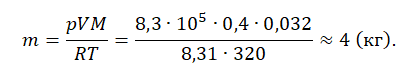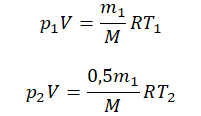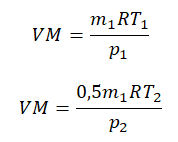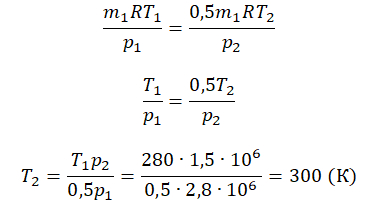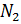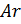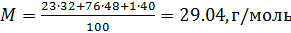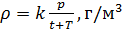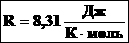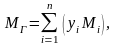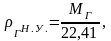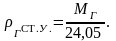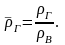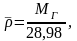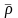Как найти плотность в молекулярной физике

Формулы молекулярной физики

Формула концентрации молекул

Здесь n — концентрация , N — количество молекул (безразмерное), V — объем .

Формула плотности

Здесь — плотность вещества , m — масса вещества (кг), V — объем .

Формула относительной молекулярной массы

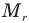
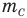
Здесь — относительная молекулярная масса (безразмерная), — масса одной молекулы (кг), — масса атома углерода (кг).

Формула количества вещества (количества молей)

Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).

Формулы массы одной молекулы

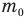
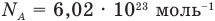
Здесь — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), — число Авогадро, — плотность вещества , n — концентрация молекул .

Формулы количества молекул

Здесь A — количество молекул (безразмерное), п — концентрация молекул , V— объем , v — количество вещества (количество молей) (моль), — число Авогадро , m — масса вещества (кг), — масса одной молекулы.

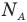
Формулы средней квадратичной скорости молекул

Здесь — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), Дж/К — постоянная Больцмана, — масса одной молекулы (кг).

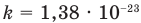
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па), — масса одной молекулы (кг), n — концентрация молекул , — средняя квадратичная скорость молекул (м/с), — средняя кинетическая энергия молекул (Дж).

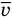
Формула средней кинетической энергии молекул

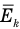
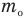
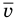
Здесь — средняя кинетическая энергия молекул (Дж), — масса одной молекулы (кг), — средняя квадратичная скорость молекул (м/с).

Связь шкал Цельсия и Кельвина

Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.

Связь средней кинетической энергии молекул идеального газа с абсолютной температурой

Здесь — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).

У равнение состояния идеального газа — уравнение Клапейрона — Менделеева

Здесь р — давление газа (Па), V — объем , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), — объем моля .

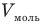
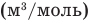
Объединенный газовый закон — уравнение Клапейрона

при

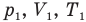
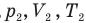
Здесь — давление (Па), объем и абсолютная температура (К) газа в первом состоянии, — давление (Па), объем и абсолютная температура (К) газа во втором состоянии.

Закон Бойля — Мариотта (изотермический процесс)

при

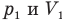
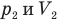
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), — давление (Па) и объем газа в первом состоянии, — давление (Па) и объем газа во втором состоянии.

Закон Гей-Люссака (изобарный процесс)

при

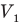
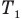
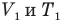
Здесь р — давление газа (Па), m — масса газа (кг), и — объем и абсолютная температура (К) газа в первом состоянии, — объем и абсолютная температура (К) газа во втором состоянии.

Закон Шарля

при

Здесь V — объем газа , m — масса газа (кг), — давление (Па) и абсолютная температура (К) газа в первом состоянии, — давление (Па) и абсолютная температура (К) газа во втором состоянии.

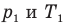
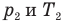
Связь давления идеального газа с концентрацией его молекул и температурой

Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа , абсолютная температура Т (К).

Формулы относительной влажности

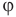
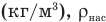
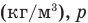
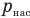
Здесь — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре — плотность насыщенного водяного пара при той же температуре — давление водяного пара в воздухе при данной температуре (Па), — давление насыщенного водяного пара в воздухе при той же температуре (Па).

Работа при изобарном изменении объема газа

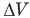
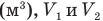
Здесь А — работа (Дж), р — давление газа (Па), — изменение объема газа — соответственно начальный и конечный объемы газа .

Внутренняя энергия идеального одноатомного газа

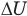
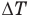
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), — изменение внутренней энергии (Дж), — изменение температуры (К).

Первый закон термодинамики

Здесь Q — количество теплоты, переданное термодинамической системе (Дж), — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)

Применение первого закона термодинамики к термодинамическим процессам

к изотермическому: при

к изохорному: при V = const

к изобарному: при р = const

к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К), — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем , р — давление (Па).

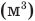
Формулы количества теплоты при нагревании или охлаждении тел

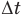
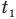
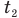
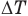
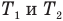
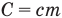
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), — изменение температуры тела по шкале Цельсия, и — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, — изменение абсолютной температуры тела (К), — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), — теплоемкость тела (Дж/К).

Формула количества теплоты при плавлении или кристаллизации

Здесь Q — количество теплоты (Дж), т — масса тела (кг), 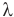— удельная теплота плавления вещества (Дж/кг).

Формула количества теплоты при парообразовании или конденсации

Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).

Формула количества теплоты при сгорании топлива

Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).

Коэффициент полезного действия теплового двигателя

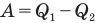
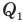
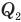
Здесь — коэффициент полезного действия (безразмерный или в %), — работа, совершенная двигателем (Дж), — количество теплоты, полученное рабочим веществом от нагревателя (Дж), — количество теплоты, отданное рабочим веществом холодильнику (Дж).

Коэффициент полезного действия идеального теплового двигателя

Здесь — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), — абсолютная температура нагревателя (К), — абсолютная температура холодильника(К).

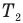
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза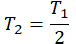
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул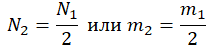
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы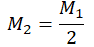
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

2,8 МПа = 2,8∙10 6 Па

1,5 МПа = 1,5∙10 6 Па

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

Преобразим уравнения и получим:

Приравняем правые части и выразим искомую величину:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Как найти плотность зная температуру и давление

Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.

Идеальный газ

Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:

• пренебрежение размерами молекул;
• силы молекулярного взаимодействия не учитываются;
• соударение атомов и молекул абсолютно упруго;
• газ находится в термодинамическом равновесии.

Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.

Газовые законы

Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:

• при постоянном давлении уменьшить температуру;
• при постоянной температуре увеличить давление.

Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.

В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.

Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.

Комбинированный закон

Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:

где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.

Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.

Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.

Пример использования калькулятора

Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.

Заключение

Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?

Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Теперь немного формул.

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.

Введение

Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].

Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.

К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.

В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.

Математическая модель определения плотности газа

Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:

1. Уравнение Менделеева-Клапейрона:

(1),

— давление газа;

— молярный объём;

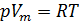
R — универсальная газовая постоянная,

;

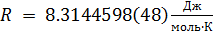
T — абсолютная температура, T=273.16 К.

2. Два измеряемых параметра:

p – давление газа, Па
t – температура газа, °С.

Известно, что молярный объём зависит от объёма газа V и количества молей газа в этом объёме:

(2)

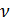
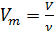
Также известно, что

(3),

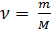
где: m – масса газа, M – молярная масса газа.

Учитывая (2) и (3) перепишем (1) в виде:

(4).

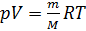
Как известно, плотность вещества

равна:

(5).

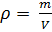
Из (4) и (5) выведем уравнение для плотности газа

:

(6)

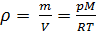
и введём обозначение параметра

, который зависит от молярной массы газовой смеси:

(7).

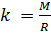
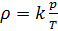
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.

Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.

Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:

• 23 % по весу из молекул кислорода
• 76 % по весу из молекул азота
• 1 % по весу из атомов аргона

Молярные массы этих веществ воздуха будут соответственно равны:

, г/моль.

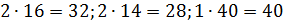
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:

Теперь, зная значение константы

, мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений

и t:

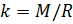
Приведение плотности газа к нормальным, стандартным условиям

Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].

Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.

Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.

Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.

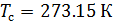
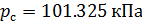
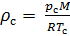
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура и абсолютное давление :

(9).

Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для :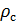

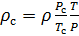
(10).

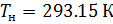
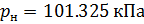
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура и абсолютное давление

:

(11).

В уравнениях (10) и (11) используем значения параметров воздуха , T и P из уравнения (8), полученные в рабочих условиях.

Реализация измерительного канала давления и температуры

Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.

Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).

Для этого, на аппаратном уровне, нам понадобятся компоненты:

1. Arduino (Uno, …) – используем как программатор;
2. микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
3. кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
4. тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
5. BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
6. преобразователь интерфейсов TTL/USB;
7. расходные материалы – провода, припой, монтажная плата, и др.

Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.

Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры

Теперь рассмотрим этапы осуществления нашей задачи.

1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.

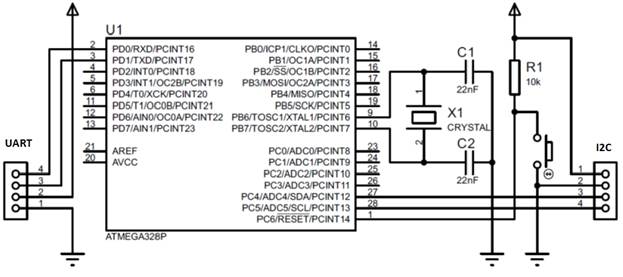
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.

Рис. 2 – Схема подключения микроконтроллера к программатору

3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры

Программа Python для фильтрации по каналам температуры и давления, и получение результатов

Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.

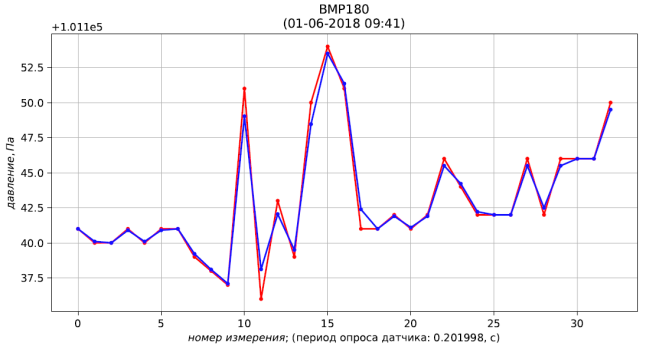
Результаты расчёта представлены листингом и рис. 4, 5, 6.

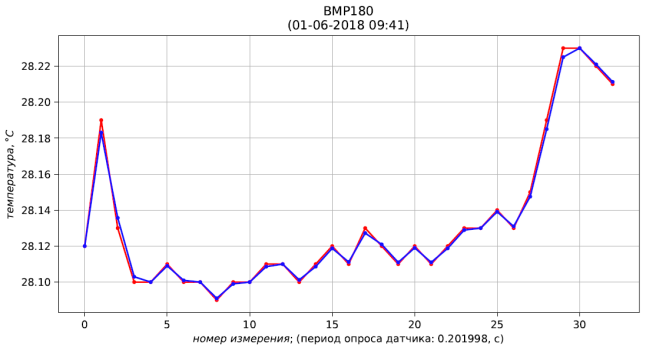
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления

Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры


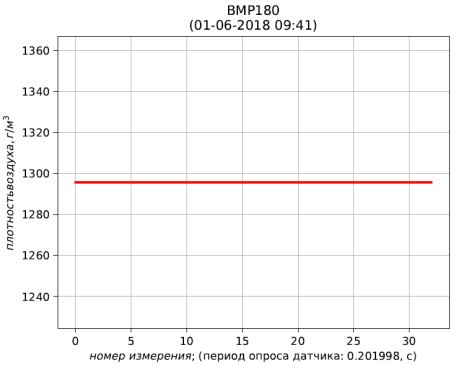
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)

Выводы

Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.

Уравнение состояния идеального газа. Газовые законы.

Уравнение состояния идеального газа

(уравнение Менделеева – Клапейрона).

Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние.

В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеаль­ного газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.

В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.

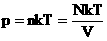
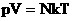
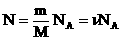
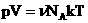
Мы знаем, что . Следовательно, . Учитывая, что , получим: .

Произведение постоянных величин есть величина постоянная, следовательно: 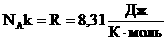– универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).

Таким образом, имеем:

– уравнение состояния (уравнение Менделеева – Клапейрона).

Другие формы записи уравнения состояния идеального газа.

1.Уравнение для 1 моля вещества.

Если n=1 моль, то, обозначив объем одного моля V_м, получим: .

Для нормальных условий получим:

2. Запись уравнения через плотность: – плотность зависит от температуры и давления!

3. Уравнение Клапейрона.

Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда:

Эта запись означает, что для данной массы данного газа справедливо равенство:

Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: .

Газовые законы.

1. Закон Авогадро.

В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов).

Доказательство:

Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.

2. Закон Дальтона.

Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.

Доказательство:

3. Закон Паскаля.

Давление, производимое на жидкость или газ, передается во все стороны без изменения.

[spoiler title=”источники:”]

http://planshet-info.ru/kompjutery/kak-najti-plotnost-znaja-temperaturu-i-davlenie

http://www.eduspb.com/node/1742

[/spoiler]

Основные формулы молекулярной физики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

— масса вещества, — объём вещества, — плотность вещества (масса единицы объёма). Отсюда

— число частиц вещества (атомов или молекул).
— масса частицы вещества. Тогда

— концентрация вещества (число частиц в единице объёма), . Отсюда

Что получится, если умножить на ? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т. е. плотность. Формально:

Итак,

Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка г, размер атома порядка см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно.

Оперировать столь грандиозными числами, как число частиц, неудобно. Поэтому для измерения количества вещества используют специальную единицу — моль.

Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в граммах углерода. А в граммах углерода содержится примерно атомов. Стало быть, в одном моле вещества содержится частиц. Это число называется постоянной Авогадро: моль.

Количество вещества обозначается . Это число молей данного вещества.

Что получится, если умножить на ? Число молей, умноженное на число частиц в моле, даст общее число частиц:

Масса одного моля вещества называется молярной массой этого вещества и обозначается ( = кг/моль). Ясно, что

Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Например, для алюминия , поэтому молярная масса алюминия равна г/моль или кг/моль.

Почему так получается? Очень просто. Молярная масса углерода равна г/моль по определению. В то же время ядро атома углерода содержит нуклонов. Выходит, что каждый нуклон вносит в молярную массу г/моль. Поэтому молярная масса химического элемента с атомной массой оказывается равной г/моль.

Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа равна г/моль кг/моль.

Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна г/моль, поскольку его молекула состоит из двух атомов . То же касается часто встречающихся в задачах азота и кислорода Вместе с тем, наиболее частый персонаж задач — гелий — является одноатомным газом и имеет молярную массу г/моль, предписанную таблицей Менделеева.

Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку 🙂

Что получится, если умножить на ? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. е. молярную массу:

You probably learned early on in science classes that density is mass divided by volume, or the “amount” of a substance in a certain space. For solids, this is a pretty straightforward measure. If you fill a jar full of pennies, it would have a lot more “oomph” than if you filled it with marshmallows. There’s a lot more substance packed into the jar when you fill it with pennies, whereas marshmallows are very puffy and light.

How about molecular weight? Molecular weight and density ​seem​ extremely similar, but there’s an important difference. Molecular weight is a substance’s mass per mole. It’s not about how much space the substance takes up, but the “amount,” the “oomph” or the “heft” of a certain amount of a substance.

So, to recap: ​Density​ is mass divided by volume. The mathematical formula looks like this:

rho = frac{m}{V}

The SI unit for mass is kilograms (although you may occasionally see it expressed in grams), and for volume it’s typically m³. So density in SI units is measured in kg/m³.

Molecular weight is mass per mole, which is written:

text{molecular weight}=frac{m}{n}

Again, units matter: Mass, m, will probably be in kilograms, and n is a measurement of the number moles. So the units for molecular weight will be kilograms/mole.

The Ideal Gas Law

So how do you convert back and forth between these measures? To convert a gas’ molecular weight to density (or vice versa), use the ​Ideal Gas Law​. The Ideal Gas Law defines the relationship between the pressure, volume, temperature and moles of a gas. It’s written:

PV=nRT

where P stands for pressure, V stands for volume, n is the number of moles, R is a constant that depends on the gas (and is usually given to you), and T is the temperature.

Use the Ideal Gas Law to Convert Molecular Weight to Density

But the Ideal Gas Law doesn’t mention molecular weight! However, if you rewrite n, the number of moles, in slightly different terms, you can set yourself up for success.

​Moles​ is the same as mass divided by molecular weight.

n=frac{m}{text{molecular weight}}

With that knowledge, you can rewrite the Ideal Gas Law like this:

PV=frac{m}{M}RT

where M stands for molecular weight.

Once you have that, solving for density becomes simple. Density equals mass over volume, so you want to get mass over volume on one side of the equals sign and everything else on the other side.

So, the previous equation becomes:

frac{PV}{RT}=frac{m}{M}

when you divide both sides by RT.

Then multipling both sides by M and dividing by volume gives:

frac{PM}{RT}=frac{m}{V}

m÷V equals density, so

rho=frac{PM}{RT}

Try an Example

Find the density of carbon dioxide (CO2) gas when the gas is at 300 Kelvin and 200,000 pascals of pressure. The molecular weight of CO2 gas is 0.044 kg/mole, and its gas constant is 8.3145 J/mole Kelvin.

You can start with the Ideal Gas Law, PV=nRT, and derive for density from there like you saw above (the advantage of that is that you only have to memorize one equation). Or, you can start with the derived equation and write:

rho=frac{PM}{RT}=frac{200000times 0.044}{8.3145times 300}=3.53text{ kg/m}^3

Phew! Well done.

Одним из важных
параметров газа является его молекулярная
масса,
которая определяется путем суммирования
масс атомов, входящих в молекулу.

Молекулярная масса
углеводородного газа, представляющего
собою смесь компонентов, при известном
объёмном составе, рассчитывается по
формуле:

(2.6)

где y_i
– объёмная
доля i–
го компонента в газовой смеси;

M_i
– молекулярная
масса i–
го компонента;

n
– число компонентов в смеси газов.

Под плотностью
углеводородного газа понимают его
массу, заключенную в 1 м³
при определенных условиях (нормальных
или стандартных), в системе СИ измеряется
в кг/м³.

_г
= m/V.

(2.7)

Под нормальными
условиями понимают условия, при которых
давление Р = 0,1 МПа, а температура Т = 273
К (0С);
под стандартными условиями – Р = 0,1 МПа,
Т = 293 К (20С).

Для всех газов
объем 1 киломоля постоянен и равен при
нормальных условиях – 22,41 м³,
при стандартных условиях – 24,05 м³.
Зная молекулярную массу газа, плотность
газа при нормальных условиях можно
вычислить по формуле:

(2.8)

при стандартных
условиях – по формуле:

(2.9)

На практике часто
пользуются относительной
плотностью газа,
равной отношению плотности газа к
плотности воздуха при определенных
условиях:

(2.10)

При расчетах
следует помнить, что плотность воздуха
при нормальных условиях
составляет
_в^н.у.
= 1,293
кг/м³,
при стандартных
_в^ст.у.
= 1,205
кг/м³.

Зная молекулярную
массу газа М_Г,
относительную плотность газа можно
также рассчитать по формуле:

(2.11)

где 28,98 –
молекулярная масса воздуха.

Задача 2.2. Даны
составы газов типичных газовых,
газоконденсатных и нефтяных месторождений.
Рассчитать молекулярную массу М_i
каждого компонента, входящего в состав
газа, молекулярную массу газа М_г,
плотность газа при нормальных (_г^н.у.)
и стандартных
условиях (_г^ст.у.),
а также относительную плотность по
воздуху

_г
(при нормальных
и стандартных условиях). Определить тип
газа (природный, попутный или газ
газоконденсатного месторождения).
Исходные данные для расчетов приведены
в таблицах 2.2 и 2.3.

Таблица 2.2 –
Компонентный состав газа

Вариант	Месторождение	Компонентный состав газа, % объёмные
СН4	С2Н6	С3Н8	С4Н10	С5Н12 и выше	СО2	N2	H2S
1	2	3	4	5	6	7	8	9	10
1	Самотлорское	53,40	7,20	15,1	8,30	6,30	0,10	9,60	–
2	Уренгойское (сеноман)	98,84	0,10	0,03	0,02	0,01	0,30	1,70	–
3	Оренбургское	84,00	5,00	1,60	0,70	1,80	1,10	4,20	1,60
4	Шатлыкское	95,60	2,00	0,34	0,10	0,05	1,15	0,76	–
5	Астраханское	58,80	1,88	0,60	0,23	0,12	11,0	1,37	26,0
6	Ромашкинское	37,30	20,70	18,9	9,50	4,80	–	8,80	–
7	Туймазинское	39,47	16,83	6,58	2,80	1,10	–	31,62	1,60
8	Южно-Первомайское	55,18	13,67	8,09	1,02	20,20	0,30	1,54	–
9	Бавлинское	35,00	20,70	19,9	9,80	5,80	0,40	8,40	–
10	ПО Пермьнефть	38,70	22,60	10,7	2,70	0,70	0,50	23,8	0,30
11	Коробковское	81,50	8,00	4,00	2,30	0,50	0,50	3,20	–
12	ПО Самаранефть	58,00	17,20	7,40	2,10	0,50	0,80	13,50	0,50
13	Ямбургское	89,67	4,39	1,64	0,74	2,36	0,94	0,26	–
14	ПО Грознефть	76,70	13,20	5,40	2,50	2,20	–	–	–
15	Медвежье	98,78	0,10	0,02	–	–	0,10	1,00	–
16	Вуктыльское	74,80	8,70	3,90	1,80	6,4	0,10	4,30	–
17	Тенгизское	42,23	8,47	5,21	3,34	21,18	2,60	0,77	16,2
18	Карачаганакское	72,99	6,22	2,59	1,50	7,55	5,35	0,57	3,23
19	Калужское	88,18	2,94	2,31	2,48	3,59	0,50	–	–
20	Узеньское	50,10	20,10	16,8	7,70	3,00	–	2,30	–
21	Талинское	44,88	7,38	3,85	1,39	42,50	–	–	–
22	Марковское	45,46	11,23	5,55	4,13	33,12	–	0,51	–
23	Уренгойское (валанжин)	82,27	6,56	3,24	1,49	5,62	0,50	0,32	–
24	Северо-Соленинское	89,52	4,15	1,82	0,48	2,58	0,49	0,96	–
25	Совхозное ПХГ	84,85	5,77	2,33	0,75	0,35	0,95	5,00	–
26	Дмитриевское	35,88	2,82	1,69	2,17	56,12	0,33	0,99	–
27	Северо-Ставропольское	92,80	2,80	0,90	0,40	0,10	0,50	2,50	–
28	Александровское	85,10	1,93	6,74	3,38	0,28	2,57	–	–
29	Радаевское	32,70	13,40	15,2	4,90	2,60	27,8	3,20	–
30	Ново-Дмитриевское	64,76	9,68	10,8	7,02	6,01	0,81	0,91	–

Таблица 2.3 – Атомные
массы компонентов

Компонент	Водород	Углерод	Кислород	Сера	Азот
Атомная масса	1,008	12,011	15,999	32,064	14,007

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #