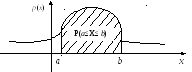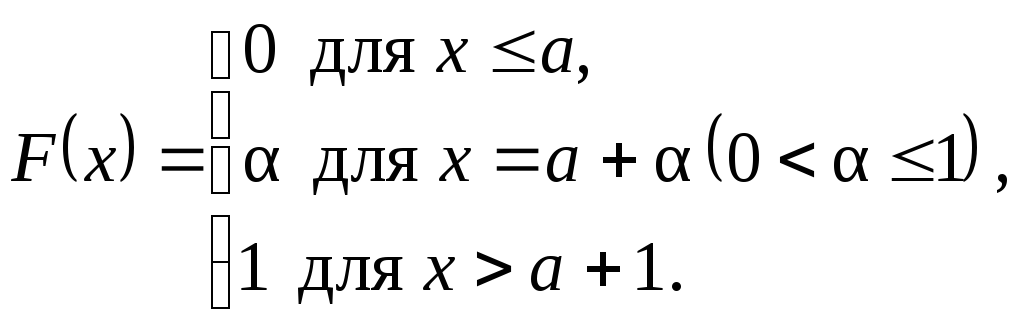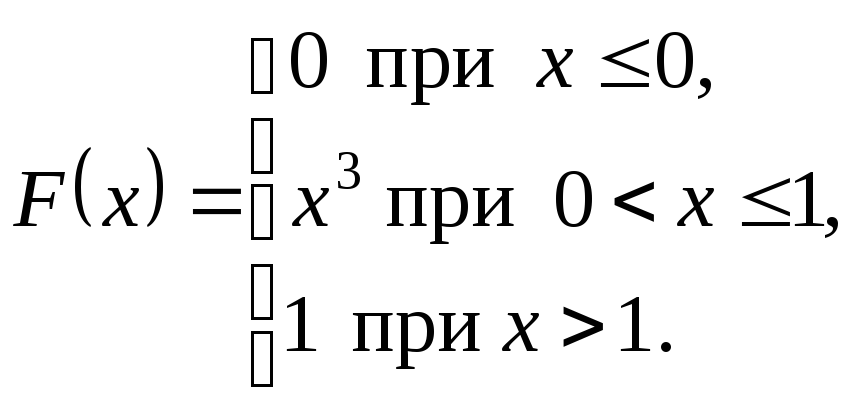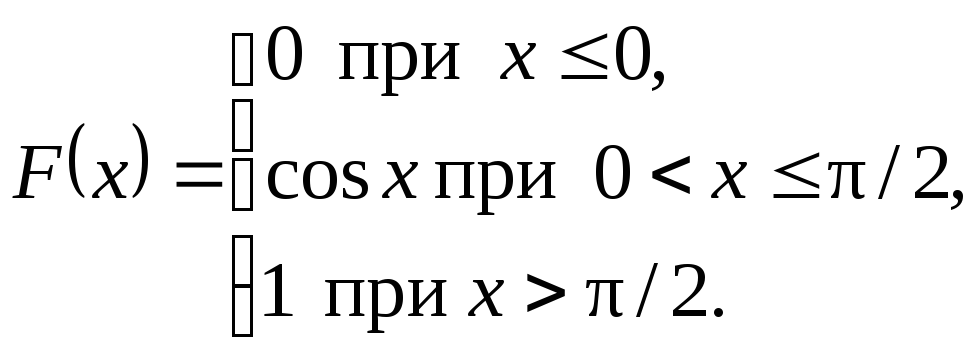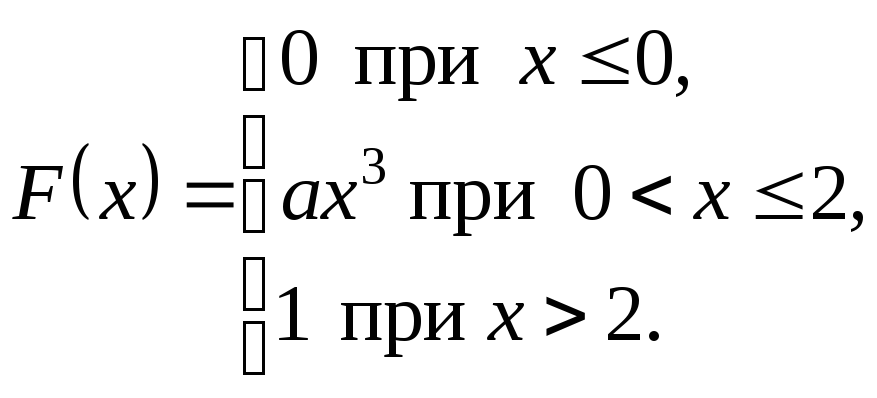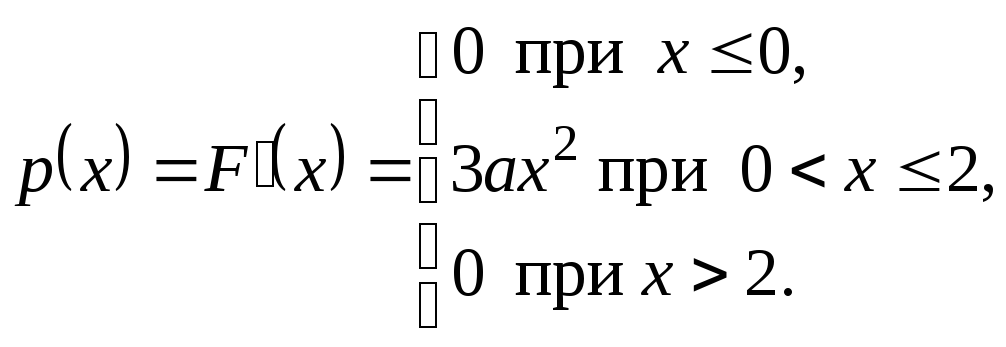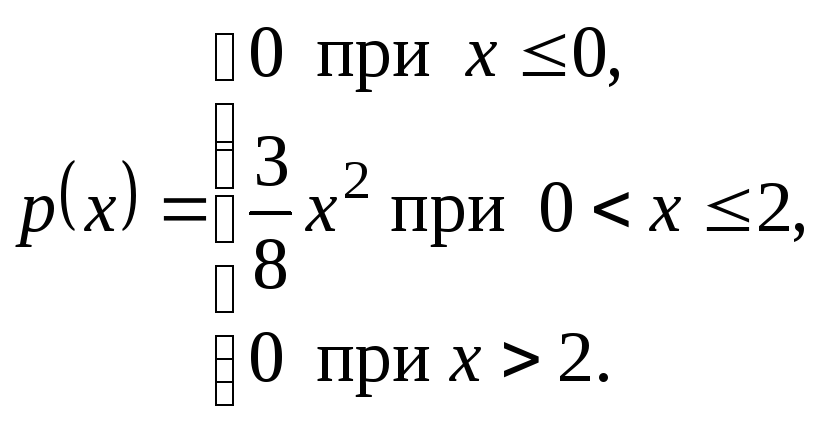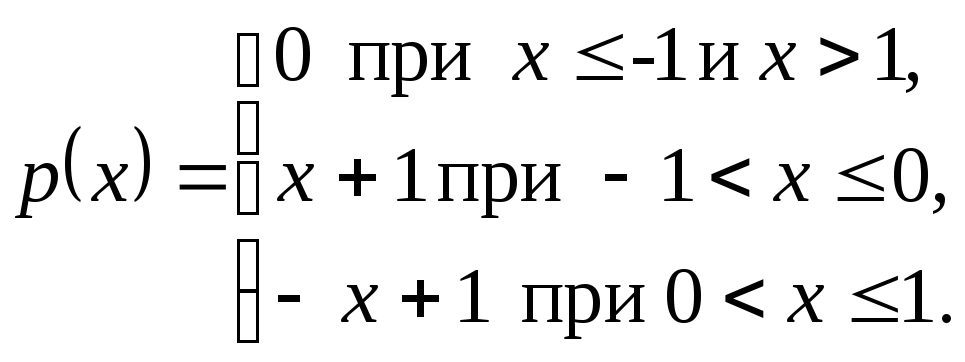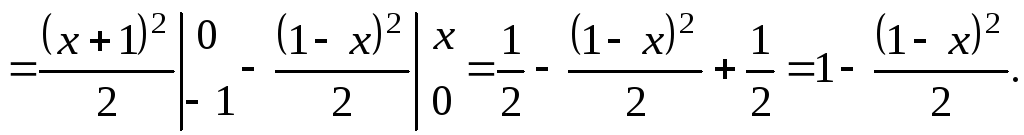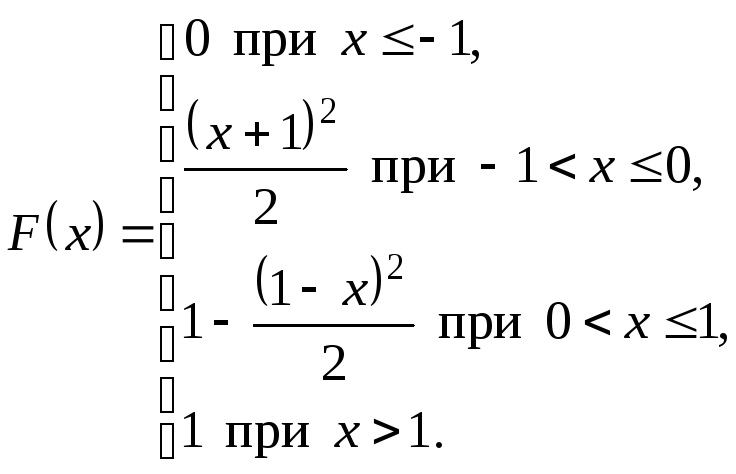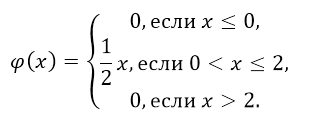Как найти плотность вероятности непрерывной случайной величины

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2021 года; проверки требуют 7 правок.

Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются^{[источник не указан 1058 дней]} и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Прикладное описание понятия[править | править код]

Плотность распределения одномерной непрерывной случайной величины — это числовая функция f(x) , отношение ${displaystyle f(x_{1})/f(x_{2})}$ значений которой в точках $x_{1}$ и $x_{2}$ задаёт отношение вероятностей попаданий величины в узкие интервалы равной ширины ${displaystyle [x_{1},x_{1}+Delta x]}$ и ${displaystyle [x_{2},x_{2}+Delta x]}$ вблизи данных точек.

Плотность распределения неотрицательна при любом и нормирована, то есть

${displaystyle int _{-infty }^{+infty }f(x),{mbox{d}}x=1}$

При стремлении к функция f(x) стремится к нулю. Размерность плотности распределения всегда обратная к размерности случайной величины — если исчисляется в метрах, то размерностью будет м^-1.

Если в конкретной ситуации известно выражение для f(x) , с его помощью можно вычислить вероятность попадания величины в интервал [a,b] как

${displaystyle P(xi in [a,b])=int _{a}^{b}f(x),{mbox{d}}x}$

Зная плотность вероятности, можно также определить наиболее вероятное значение (моду) случайной величины как максимум f(x) .
Также с помощью плотности вероятности находится среднее значение случайной величины:

${displaystyle Exi =int _{-infty }^{+infty }xf(x),{mbox{d}}x}$

и среднее значение измеримой функции случайной величины:

${displaystyle langle g(xi )rangle =int _{-infty }^{+infty }g(x)f(x),{mbox{d}}x}$

Чтобы перейти к плотности распределения ${displaystyle {f}_{chi }(y)}$ другой случайной величины , нужно взять

${displaystyle {f}_{chi }(y)=f(z^{-1}(y))cdot left|{frac {{mbox{d}}z^{-1}(y)}{{mbox{d}}y}}right|}$

где ${displaystyle z^{-1}(y)}$ — обратная функция по отношению к (предполагается, что z — взаимно однозначное отображение).

Значение плотности распределения $f(x_{1})$ не является вероятностью принять случайной величиной значение $x_{1}$ . Так, вероятность принятия непрерывной случайной величиной значения $x_{1}$ равна нулю. При непрерывном распределении случайной величины вопрос может ставиться о вероятности её попадания в некий диапазон, а не о вероятности реализации её конкретного значения.

Интеграл

${displaystyle int _{-infty }^{x}f(t),{mbox{d}}t=F(x)}$

называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция является неубывающей и изменяется от 0 при до 1 при .

Самым простым распределением является равномерное распределение на отрезке [a,b] . Для него плотность вероятности равна:

${displaystyle f(x)=left{{begin{matrix}{1 over b-a},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}$

Широко известным распределением является «нормальное», оно же гауссово, плотность которого записывается как

${displaystyle f(x)={frac {1}{{sqrt {2pi }}sigma }}exp left[-{frac {(x-mu )^{2}}{2sigma ^{2}}}right]}$

где и sigma — параметры: математическое ожидание и среднеквадратичное отклонение. Другие примеры плотностей распределения — одностороннее лапласовское ():

{displaystyle f(x)=Aexp left[-lambda ,xright],,(xgeq 0)}

и максвелловское ():

${displaystyle f(x)=Ax^{2}exp left[-alpha x^{2}right],,(xgeq 0)}$

В двух последних примерах множитель подбирается в зависимости от параметра lambda или alpha так, чтобы обеспечить нормировку интеграла от плотности вероятности. В случае распределения Лапласа оказывается, что .

Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе. При этом для аргумента функции нередко используют тот же символ, что и для рассматриваемой в физической задаче случайной величины (как если бы выше на месте всюду стояло ). Так, в выражении максвелловской плотности распределения пишут не формальную переменную , а символ скорости . В простейших ситуациях такая вольность с обозначениями не приводит к недоразумениям.

Спадающий при стремлении аргумента к +infty или -infty участок графика плотности вероятности f(x) в областях, где ${displaystyle fll f_{max}}$ , называется хвостом. Из упомянутых распределений, нормальное и лапласовское имеют по два хвоста (слева и справа), а максвелловское в выписанном виде — один (справа).

Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность нередко является функцией нескольких величин, в рассуждениях неявно предполагались не всегда гарантируемые непрерывность и дифференцируемость функций и так далее.

Определение плотности вероятности в теории меры[править | править код]

Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве $mathbb {R} ^{n}$ .
Пусть является вероятностной мерой на $mathbb {R} ^{n}$ , то есть определено вероятностное пространство $left(mathbb{R}^n,mathcal{B}(mathbb{R}^n),mathbb{P}right)$ , где $mathcal{B}(mathbb{R}^n)$ обозначает борелевскую σ-алгебру на $mathbb {R} ^{n}$ . Пусть обозначает меру Лебега на $mathbb {R} ^{n}$ .
Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

$forall B in mathcal{B}(mathbb{R}^n),; ( m(B) = 0 ) Rightarrow ( mathbb{P}(B) = 0 ) .$

Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция $fcolonmathbb{R}^n to [0,infty)$ такая, что

$mathbb{P}(B) = intlimits_{B} f(x), dx$

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде

то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают

$f=frac{dnu}{dmu}$

Плотность случайной величины[править | править код]

Пусть определено произвольное вероятностное пространство , и $Xcolon Omega to mathbb {R} ^{n}$ случайная величина (или случайный вектор). индуцирует вероятностную меру $mathbb {P} ^{X}$ на $left(mathbb{R}^n,mathcal{B}(mathbb{R}^n)right)$ , называемую распределением случайной величины .

Если распределение $mathbb {P} ^{X}$ абсолютно непрерывно относительно меры Лебега, то его плотность $f_X = frac{dmathbb{P}^X}{dx}$ называется плотностью случайной величины . Сама случайная величина называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

$mathbb{P}(X in B) = intlimits_{B} f_X(x), dx$

Замечания[править | править код]

Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

Функция распределения абсолютно непрерывной случайной величины непрерывна и может быть выражена через плотность следующим образом:

$F_X(x_1,ldots, x_n) = mathbb{P}left(X in prodlimits_{i=1}^n (-infty,x_i]right) = intlimits_{-infty}^{x_n} !! ldots !! intlimits_{-infty}^{x_1} f_X(x'_1,ldots, x'_n), dx'_1ldots dx'_n$

В одномерном случае:

$F_X(x) = intlimits_{-infty}^x f_X(x'), dx'$

Если $f_X in C(mathbb{R}^n)$ , то $F_X in mathcal{D}(mathbb{R}^n)$ , и

$frac{partial^n}{partial x_1 ldots partial x_n} F_X(x_1,ldots, x_n) = f_X(x_1,ldots, x_n)$

В одномерном случае:

$frac{d}{dx} F_X(x) = f_X(x)$

Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:

$mathbb{E}[g(X)] = intlimits_{mathbb{R}^n} g(x) , mathbb{P}^X(dx) = intlimits_{mathbb{R}^n} g(x), f_X(x), dx$

где $gcolon mathbb{R}^n to mathbb{R}$ — борелевская функция, так что определено и конечно.

Плотность преобразования случайной величины[править | править код]

Пусть $Xcolon Omega to mathbb {R} ^{n}$ — абсолютно непрерывная случайная величина, и $gcolonmathbb{R}^n to mathbb{R}^n$ — инъективная непрерывно дифференцируемая функция такая, что $J_g(x) not=0,; forall xin mathbb{R}^n$ , где J_g(x) — якобиан функции в точке . Тогда случайная величина также абсолютно непрерывна, и её плотность имеет вид:

$f_Y(y) = f_Xleft(g^{-1}(y)right) vert J_{g^{-1}}(y) vert$

В одномерном случае:

$f_Y(y) = f_Xleft(g^{-1}(y)right) leftvert frac{dg^{-1}}{dy}(y)rightvert$

Свойства плотности вероятности[править | править код]

Интеграл от плотности по всему пространству равен единице:

$mathbb{P}left(mathbb{R}^nright) = intlimits_{mathbb{R}^n} f(x), dx = 1$

Обратно, если f(x) — неотрицательная почти всюду функция, такая что $intlimits_{mathbb{R}^n}f(x), dx = 1$ , то существует абсолютно непрерывная вероятностная мера на $mathbb {R} ^{n}$ такая, что f(x) является её плотностью.

Замена меры в интеграле Лебега:

$intlimits_{mathbb{R}^n} varphi(x), mathbb{P}(dx) = intlimits_{mathbb{R}^n}varphi(x), f(x), dx$

где ${displaystyle varphi ::mathbb {R} ^{n}to mathbb {R} }$ любая борелевская функция, интегрируемая относительно вероятностной меры .

Примеры абсолютно непрерывных распределений[править | править код]

Бета-распределение
Гамма-распределение
Гиперэкспоненциальное распределение
Двумерное нормальное распределение
Логнормальное распределение
Многомерное нормальное распределение
Непрерывное равномерное распределение
Нормальное распределение
Обобщённое гиперболическое распределение
Полукруговой закон Вигнера
Распределение variance-gamma
Распределение Вейбулла
Распределение Гомпертца
Распределение Колмогорова
Распределение копулы
Распределение Коши
Распределение Лапласа
Распределение Накагами
Распределение Парето
Распределение Пирсона
Распределение Райса
Распределение Рэлея
Распределение Стьюдента
Распределение Трейси — Видома
Распределение Фишера
Распределение хи-квадрат
Частотное распределение
Экспоненциальное распределение

См. также[править | править код]

Распределение вероятностей
Сингулярное распределение
Функция вероятности

Литература[править | править код]

Плотность вероятности // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Источник

Функцией распределенияслучайной
величиныХназывается функцияF(х),
выражающая для каждогохвероятность
того, что случайная величинаХпримет
значение, меньшеех:.

Функцию
F(х)
иногда называют интегральной
функцией распределения,
или интегральным
законом распределения.

Случайная
величина Х
называется непрерывной,
если ее функция распределения непрерывна
в любой точке и дифференцируема всюду,
кроме, быть может, отдельных точек.

Примеры
непрерывных случайных величин: диаметр
детали, которую токарь обтачивает до
заданного размера, рост человека,
дальность полета снаряда и др.

Теорема.
Вероятность любого отдельно взятого
значения непрерывной случайной величины
равна нулю

Следствие.
Если Х —
непрерывная случайная величина, то
вероятность попадания случайной величины
в интервал
не зависит от того, является этот интервал
открытым или закрытым, т.е.

Если
непрерывная случайная величина Х
может принимать только значения в
границах от а
до b
(где а
и b —
некоторые постоянные), то функция
распределения ее равна нулю для всех
значений
и единице для значений .

Для непрерывной случайной величины

Все свойства функций распределения
дискретных случайных величин выполняются
и для функций распределения непрерывных
случайных величин.

Задание
непрерывной случайной величины с помощью
функции распределения не является
единственным.

Плотностью
вероятности
(плотностью
распределения
или плотностью)
р(х)
непрерывной случайной величины Х
называется производная ее функции
распределения

Плотность
вероятности р(х), как и функция
распределенияF(х), является
одной из форм закона распределения, но
в отличие от функции распределения она
существует только длянепрерывныхслучайных величин.

Плотность
вероятности иногда называют дифференциальной
функцией, или дифференциальным законом
распределения.

График плотности
вероятности называется кривой
распределения.

Свойства
плотности вероятности непрерывной
случайной величины:

.
(рис. 8.1).

Рис. 8.1

(рис. 8.2).

Рис. 8.2

4.
.

Геометрически
свойства плотности вероятности означают,
что ее график — кривая распределения —
лежит не ниже оси абсцисс, и полная
площадь фигуры, ограниченной кривой
распределения и осью абсцисс, равна
единице.

Пример
8.1. Минутная
стрелка электрических часов передвигается
скачками поминутно. Вы бросили взгляд
на часы. Они показывают а
минут. Тогда для вас истинное время в
данный момент будет случайной величиной.
Найти ее функцию распределения.

Решение.
Очевидно, что функция распределения
истинного времени равна 0 для всех

и единице для
.
Время течет равномерно. Поэтому
вероятность того, что истинное время
меньше а
+
0,5 мин, равна 0,5, так как одинаково
вероятно, прошло ли после а
менее или более полминуты. Вероятность
того, что истинное время меньше а
+ 0,25 мин, равна 0,25 (вероятность этого
времени втрое меньше вероятности того,
что истинное время больше а
+ 0,25 мин, а сумма их равна единице, как
сумма вероятностей противоположных
событий). Аналогично рассуждая, найдем,
что вероятность того, что истинное время
меньше а
+ 0,6 мин, равна 0,6. В общем случае вероятность
того, что истинное время меньше а
+ + α мин

,
равна α.
Следовательно, функция распределения
истинного времени имеет следующее
выражение:

Она
непрерывна всюду, а производная ее
непрерывна во всех точках, за исключением
двух:х = аих = а+ 1.
График этой функции имеет вид
(рис. 8.3):

Рис. 8.3

Пример
8.2. Является
ли функцией распределения некоторой
случайной величины функция

Решение.

Рис. 8.4

Все
значения этой функции принадлежат
отрезку
,
т.е.
.
Функция F(х)
является неубывающей: в промежутке

она постоянна, равна нулю, в промежутке

возрастает, в промежутке

также постоянна, равна единице (см.
рис. 8.4). Функция непрерывна в каждой
точке х₀
области ее определения — промежутка

,
поэтому непрерывна слева, т.е. выполняется
равенство

Выполняются и
равенства:

Следовательно,
функция
удовлетворяет всем свойствам, характерным
для функции распределения. Значит данная
функцияявляется функцией распределения
некоторой случайной величиныХ.

Пример
8.3.
Является
ли функцией распределения некоторой
случайной величины функция

Решение.Данная функция не является функцией
распределения случайной величины, так
как напромежутке

она убывает и не является непрерывной.
График функции изображен на рис. 8.5.

Рис. 8.5

Пример
8.4.
Случайная величина Х
задана функцией распределения

Найти
коэффициент а
и плотность вероятности случайной
величины Х.
Определить вероятность неравенства .

Решение.
Плотность распределения равна первой
производной от функции распределения

Коэффициент
а
определяем с помощью равенства

отсюда

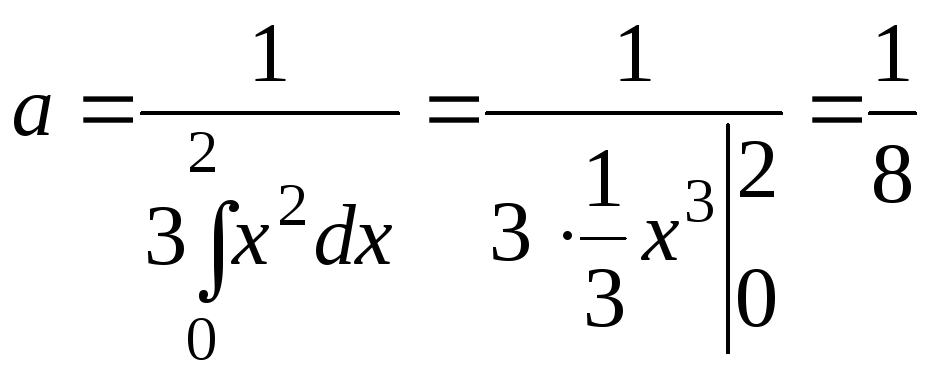
Тот
же результат можно было получить,
используя непрерывность функции
в точке

Следовательно,
.

Поэтому плотность
вероятности имеет вид

Вероятность
попадания
случайной величины Х
в заданный промежуток вычисляется по
формуле

Пример
8.5.
Случайная величина Х
имеет плотность вероятности (закон
Коши)

Найти
коэффициент а
и вероятность того, что случайная
величина Х
примет какое-нибудь значение из интервала

.
Найти функцию распределения этой
случайной величины.

Решение.
Найдем коэффициент а
из равенства

но

Следовательно,
.

Итак,
.

Вероятность того, что случайная величина
Хпримет какое-нибудь значение из
интервала
,
равна

Найдем функцию распределения данной
случайной величины

Пример
8.6.График плотности вероятности
случайной величиныХизображен на
рис. 8.6 (закон Симпсона). Написать
выражение плотности вероятности ифункцию
распределения этой случайной величины.

Рис. 8.6

Решение.
Пользуясь графиком, записываем
аналитическое выражение плотности
распределения вероятностей данной
случайной величины

Найдем
функцию распределения.

Если

,
то
.

Если

,
то
.

Если

,
то

Если

,
то

Следовательно, функция распределения
имеет вид

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Александр Мельник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Понятие плотности распределения вероятностей непрерывной случайной величины

Пусть $X$ — непрерывная случайная величина с функцией распределения вероятностей $F(x)$. Напомним определение функции распределения:

Определение 1

Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F(x) = P(X⩽x)$.

Так как случайная величина является непрерывной, то, как нам уже известно, что функция распределения вероятностей F(x) будет непрерывной функцией. Пусть F(x) также дифференцируема на всей области определения.

Рассмотрим интервал (x,x+△x) (где △x – приращение величины x на нем).

Теперь устремляя значения приращения △x к нулю, получим:

Рисунок 1.

Таким образом, получаем:

Определение 2

Плотность распределения (плотность вероятности) φ(x) — это производная функции распределения непрерывной случайной величины.

Плотность распределения, как и функция распределения, – это одна из форм закона распределения случайной величины. Однако закон распределения может быть записан через плотность распределения только для непрерывных случайных величин.

Геометрический смысл плотности распределения вероятностей непрерывной случайной величины

Кривая распределения — это график функции φ(x) плотность распределения случайной величины (рис.2).

Рисунок 2. График плотности распределения. Автор24 — интернет-биржа студенческих работ

«Плотность распределения вероятностей непрерывной случайной величины» 👇

Геометрический смысл 1: Вероятность попадания непрерывной случайной величины в интервал (α,β) равна площади криволинейной трапеции, ограниченной графиком функции распределения φ(x) и прямыми x=α, x=β и y=0 (рис. 3).

Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал (α, β). Автор24 — интернет-биржа студенческих работ

Геометрический смысл 2: Площадь бесконечной криволинейной трапеции, ограниченной графиком функции распределения φ(x), прямой y=0 и переменной прямой x есть ни что иное как функция распределения F(x) (рис. 4).

Рисунок 4. Геометрическое изображение функции вероятности F(x) через плотность распределения φ(x). Автор24 — интернет-биржа студенческих работ

Пример 1

Пусть функция распределения F(x) случайной величины X имеет следующий вид:

Рисунок 5.

а) Найти значение α.
б) Найти плотность распределения φ(x).
в) Построить кривую распределения.

Решение:

а) Так как необходимо найти плотность распределения, то случайная величина X является непрерывной. Тогда, при x=2, получим, что $αx^2=1$, то есть 4α=1, α=1/4.

То есть:

Рисунок 6.

б) Так как:

Рисунок 7.

то получим:

Рисунок 8.

в) Построим график функции φ(x).

Рисунок 9.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Прикладное описание понятия[править | править код]

Определение плотности вероятности в теории меры[править | править код]

Плотность случайной величины[править | править код]

Замечания[править | править код]

Плотность преобразования случайной величины[править | править код]

Свойства плотности вероятности[править | править код]

Примеры абсолютно непрерывных распределений[править | править код]

См. также[править | править код]

Литература[править | править код]

Для непрерывной случайной величины

Понятие плотности распределения вероятностей непрерывной случайной величины

Геометрический смысл плотности распределения вероятностей непрерывной случайной величины

Вам также может понравиться

Как найти сектор круга зная угол

Как найти сумму двузначных чисел в питоне

Формула оксида цинка как найти

Добавить комментарий Отменить ответ