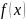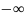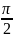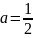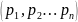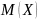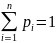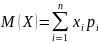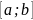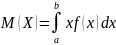Как найти плотность вероятности распределение случайной величины

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2021 года; проверки требуют 7 правок.

Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются^{[источник не указан 1062 дня]} и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Прикладное описание понятия[править | править код]

Плотность распределения одномерной непрерывной случайной величины — это числовая функция f(x) , отношение ${displaystyle f(x_{1})/f(x_{2})}$ значений которой в точках $x_{1}$ и $x_{2}$ задаёт отношение вероятностей попаданий величины в узкие интервалы равной ширины ${displaystyle [x_{1},x_{1}+Delta x]}$ и ${displaystyle [x_{2},x_{2}+Delta x]}$ вблизи данных точек.

Плотность распределения неотрицательна при любом и нормирована, то есть

${displaystyle int _{-infty }^{+infty }f(x),{mbox{d}}x=1}$

При стремлении к функция f(x) стремится к нулю. Размерность плотности распределения всегда обратная к размерности случайной величины — если исчисляется в метрах, то размерностью будет м^-1.

Если в конкретной ситуации известно выражение для f(x) , с его помощью можно вычислить вероятность попадания величины в интервал [a,b] как

${displaystyle P(xi in [a,b])=int _{a}^{b}f(x),{mbox{d}}x}$

Зная плотность вероятности, можно также определить наиболее вероятное значение (моду) случайной величины как максимум f(x) .
Также с помощью плотности вероятности находится среднее значение случайной величины:

${displaystyle Exi =int _{-infty }^{+infty }xf(x),{mbox{d}}x}$

и среднее значение измеримой функции случайной величины:

${displaystyle langle g(xi )rangle =int _{-infty }^{+infty }g(x)f(x),{mbox{d}}x}$

Чтобы перейти к плотности распределения ${displaystyle {f}_{chi }(y)}$ другой случайной величины , нужно взять

${displaystyle {f}_{chi }(y)=f(z^{-1}(y))cdot left|{frac {{mbox{d}}z^{-1}(y)}{{mbox{d}}y}}right|}$

где ${displaystyle z^{-1}(y)}$ — обратная функция по отношению к (предполагается, что z — взаимно однозначное отображение).

Значение плотности распределения $f(x_{1})$ не является вероятностью принять случайной величиной значение $x_{1}$ . Так, вероятность принятия непрерывной случайной величиной значения $x_{1}$ равна нулю. При непрерывном распределении случайной величины вопрос может ставиться о вероятности её попадания в некий диапазон, а не о вероятности реализации её конкретного значения.

Интеграл

${displaystyle int _{-infty }^{x}f(t),{mbox{d}}t=F(x)}$

называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция является неубывающей и изменяется от 0 при до 1 при .

Самым простым распределением является равномерное распределение на отрезке [a,b] . Для него плотность вероятности равна:

${displaystyle f(x)=left{{begin{matrix}{1 over b-a},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}$

Широко известным распределением является «нормальное», оно же гауссово, плотность которого записывается как

${displaystyle f(x)={frac {1}{{sqrt {2pi }}sigma }}exp left[-{frac {(x-mu )^{2}}{2sigma ^{2}}}right]}$

где и sigma — параметры: математическое ожидание и среднеквадратичное отклонение. Другие примеры плотностей распределения — одностороннее лапласовское ():

{displaystyle f(x)=Aexp left[-lambda ,xright],,(xgeq 0)}

и максвелловское ():

${displaystyle f(x)=Ax^{2}exp left[-alpha x^{2}right],,(xgeq 0)}$

В двух последних примерах множитель подбирается в зависимости от параметра lambda или alpha так, чтобы обеспечить нормировку интеграла от плотности вероятности. В случае распределения Лапласа оказывается, что .

Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе. При этом для аргумента функции нередко используют тот же символ, что и для рассматриваемой в физической задаче случайной величины (как если бы выше на месте всюду стояло ). Так, в выражении максвелловской плотности распределения пишут не формальную переменную , а символ скорости . В простейших ситуациях такая вольность с обозначениями не приводит к недоразумениям.

Спадающий при стремлении аргумента к +infty или -infty участок графика плотности вероятности f(x) в областях, где ${displaystyle fll f_{max}}$ , называется хвостом. Из упомянутых распределений, нормальное и лапласовское имеют по два хвоста (слева и справа), а максвелловское в выписанном виде — один (справа).

Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность нередко является функцией нескольких величин, в рассуждениях неявно предполагались не всегда гарантируемые непрерывность и дифференцируемость функций и так далее.

Определение плотности вероятности в теории меры[править | править код]

Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве $mathbb {R} ^{n}$ .
Пусть является вероятностной мерой на $mathbb {R} ^{n}$ , то есть определено вероятностное пространство $left(mathbb{R}^n,mathcal{B}(mathbb{R}^n),mathbb{P}right)$ , где $mathcal{B}(mathbb{R}^n)$ обозначает борелевскую σ-алгебру на $mathbb {R} ^{n}$ . Пусть обозначает меру Лебега на $mathbb {R} ^{n}$ .
Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

$forall B in mathcal{B}(mathbb{R}^n),; ( m(B) = 0 ) Rightarrow ( mathbb{P}(B) = 0 ) .$

Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция $fcolonmathbb{R}^n to [0,infty)$ такая, что

$mathbb{P}(B) = intlimits_{B} f(x), dx$

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде

то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают

$f=frac{dnu}{dmu}$

Плотность случайной величины[править | править код]

Пусть определено произвольное вероятностное пространство , и $Xcolon Omega to mathbb {R} ^{n}$ случайная величина (или случайный вектор). индуцирует вероятностную меру $mathbb {P} ^{X}$ на $left(mathbb{R}^n,mathcal{B}(mathbb{R}^n)right)$ , называемую распределением случайной величины .

Если распределение $mathbb {P} ^{X}$ абсолютно непрерывно относительно меры Лебега, то его плотность $f_X = frac{dmathbb{P}^X}{dx}$ называется плотностью случайной величины . Сама случайная величина называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

$mathbb{P}(X in B) = intlimits_{B} f_X(x), dx$

Замечания[править | править код]

Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

Функция распределения абсолютно непрерывной случайной величины непрерывна и может быть выражена через плотность следующим образом:

$F_X(x_1,ldots, x_n) = mathbb{P}left(X in prodlimits_{i=1}^n (-infty,x_i]right) = intlimits_{-infty}^{x_n} !! ldots !! intlimits_{-infty}^{x_1} f_X(x'_1,ldots, x'_n), dx'_1ldots dx'_n$

В одномерном случае:

$F_X(x) = intlimits_{-infty}^x f_X(x'), dx'$

Если $f_X in C(mathbb{R}^n)$ , то $F_X in mathcal{D}(mathbb{R}^n)$ , и

$frac{partial^n}{partial x_1 ldots partial x_n} F_X(x_1,ldots, x_n) = f_X(x_1,ldots, x_n)$

В одномерном случае:

$frac{d}{dx} F_X(x) = f_X(x)$

Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:

$mathbb{E}[g(X)] = intlimits_{mathbb{R}^n} g(x) , mathbb{P}^X(dx) = intlimits_{mathbb{R}^n} g(x), f_X(x), dx$

где $gcolon mathbb{R}^n to mathbb{R}$ — борелевская функция, так что определено и конечно.

Плотность преобразования случайной величины[править | править код]

Пусть $Xcolon Omega to mathbb {R} ^{n}$ — абсолютно непрерывная случайная величина, и $gcolonmathbb{R}^n to mathbb{R}^n$ — инъективная непрерывно дифференцируемая функция такая, что $J_g(x) not=0,; forall xin mathbb{R}^n$ , где J_g(x) — якобиан функции в точке . Тогда случайная величина также абсолютно непрерывна, и её плотность имеет вид:

$f_Y(y) = f_Xleft(g^{-1}(y)right) vert J_{g^{-1}}(y) vert$

В одномерном случае:

$f_Y(y) = f_Xleft(g^{-1}(y)right) leftvert frac{dg^{-1}}{dy}(y)rightvert$

Свойства плотности вероятности[править | править код]

Интеграл от плотности по всему пространству равен единице:

$mathbb{P}left(mathbb{R}^nright) = intlimits_{mathbb{R}^n} f(x), dx = 1$

Обратно, если f(x) — неотрицательная почти всюду функция, такая что $intlimits_{mathbb{R}^n}f(x), dx = 1$ , то существует абсолютно непрерывная вероятностная мера на $mathbb {R} ^{n}$ такая, что f(x) является её плотностью.

Замена меры в интеграле Лебега:

$intlimits_{mathbb{R}^n} varphi(x), mathbb{P}(dx) = intlimits_{mathbb{R}^n}varphi(x), f(x), dx$

где ${displaystyle varphi ::mathbb {R} ^{n}to mathbb {R} }$ любая борелевская функция, интегрируемая относительно вероятностной меры .

Примеры абсолютно непрерывных распределений[править | править код]

Бета-распределение
Гамма-распределение
Гиперэкспоненциальное распределение
Двумерное нормальное распределение
Логнормальное распределение
Многомерное нормальное распределение
Непрерывное равномерное распределение
Нормальное распределение
Обобщённое гиперболическое распределение
Полукруговой закон Вигнера
Распределение variance-gamma
Распределение Вейбулла
Распределение Гомпертца
Распределение Колмогорова
Распределение копулы
Распределение Коши
Распределение Лапласа
Распределение Накагами
Распределение Парето
Распределение Пирсона
Распределение Райса
Распределение Рэлея
Распределение Стьюдента
Распределение Трейси — Видома
Распределение Фишера
Распределение хи-квадрат
Частотное распределение
Экспоненциальное распределение

См. также[править | править код]

Распределение вероятностей
Сингулярное распределение
Функция вероятности

Литература[править | править код]

Плотность вероятности // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Источник

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

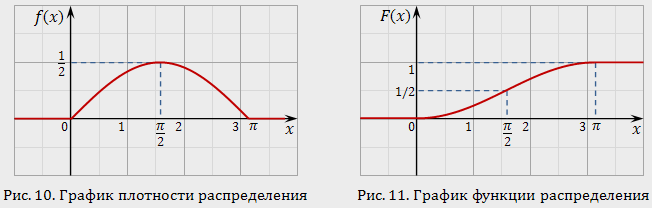
График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

– функцию
распределения вероятностей;

–
математическое ожидание;

–
дисперсию;

– среднее
квадратическое отклонение;

– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

–
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

–
составить функцию плотности распределения и построить ее график;

– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Плотность распределения вероятности и ее свойства

Функция
распределения непрерывной случайной
величины является ее вероятностной
характеристикой. Но она имеет недостаток,
заключающийся в том, что по ней трудно
судить о характере распределения
случайной величины в небольшой окрестности
той или другой точки числовой оси. Более
наглядное представление о характере
распределения непрерывной случайной
величины дает функция, которая называется
плотностью распределения вероятности,
или дифференциальной функцией
распределения случайной величины.

Плотность
распределения

равна производной от функции распределения

,
т. е.

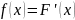
Смысл
плотности распределения

состоит в том, что она указывает на то,
как часто случайная величина

появляется в некоторой окрестности
точки

при повторении опытов. Кривая, изображающая
плотность распределения

случайной величины, называется кривой
распределения.

Рассмотрим
свойства
плотности распределения.

Свойство
1.
Плотность распределения неотрицательна,
т. е.

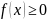
Свойство
2.
Функция распределения случайной величины
равна интегралу от плотности в интервале
от

до

,
т. е.

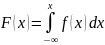
Свойство
3.
Вероятность попадания непрерывной
случайной величины

на участок

равна интегралу от плотности распределения,
взятому по этому участку, т. е.

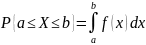
Свойство
4.
Интеграл в бесконечных пределах от
плотности распределения равен единице:

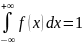
Пример
2.
Случайная величина

подчинена закону распределения с
плотностью

Определить
коэффициент а; построить график плотности
распределения; найти вероятность
попадания случайной величины на участок
от 0 до

.
Определить функцию распределения и
построить ее график.

Решение.
Площадь, ограниченная кривой распределения,
численно равна

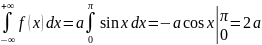
Учитывая
свойство 4 плотности распределения,
находим

.
Следовательно, плотность распределения
можно выразить так:

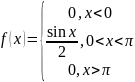
График
плотности распределения на рис. 10. По
свойству 3, имеем

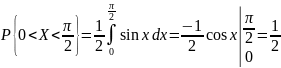
Для
определения функции распределения
воспользуемся свойством 2:

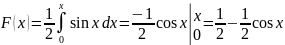
Таким
образом, имеем

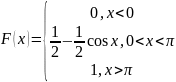
График
функции распределения изображен на
рис. 11

Числовые характеристики случайных величин

Закон
распределения полностью характеризует
случайную величину с вероятностной
точки зрения. Но при решении ряда
практических задач нет необходимости
знать все возможные значения случайной
величины и соответствующие им вероятности,
а удобнее пользоваться некоторыми
количественными показателями. Такие
показатели называются числовыми
характеристиками
случайной величины.
Основными из них являются математическое
ожидание и дисперсия.

Математическое
ожидание иногда называют средним
значением случайной величины. Рассмотрим
дискретную случайную величину

,
принимающую значения

с вероятностями соответственно

.
Определим среднюю арифметическую
значений случайной величины, взвешенных
по вероятностям их появлений. Таким
образом, вычислим среднее значение
случайной величины, или ее математическое
ожидание

:

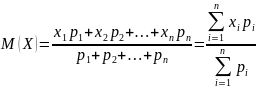
Учитывая,
что

получаем

(4.1)

Итак,
математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений на соответствующие вероятности.

Для
непрерывной случайной величины
математическое ожидание

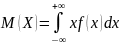
Математическое
ожидание непрерывной случайной величины

,
возможные значения которой принадлежат
отрезку

,

(4.2)

Используя
функцию распределения вероятностей

,
математическое ожидание случайной
величины можно выразить так:

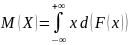
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Что такое плотность вероятности

Плотность вероятности — это производная от функции F(x), описывающей распределение случайной величины.

Двумерная, трехмерная, N-мерная плотность, иначе называемая совместной, определяет одновременное выполнение двух и более условий. Чтобы проанализировать взаимосвязь между характеристиками одного процесса, сдвинутыми на определенный интервал времени, или результаты одновременного броска двух игральных костей, нужно рассматривать двумерную плотность вероятности. Функция в таком случае должна определять одновременное выполнение двух условий: случайные величины (X) и (Y) одновременно принимают значения из интервалов (x_{1;}leq Xleq x_2\) и (y_{1;}leq Yleq y_2\).

Практические задачи, где требуется вычислить случайные величины, часто приходится решать в квантовой механике, например, рассчитывая коэффициенты отражения и прохождения квантовых частиц, движущихся в потенциальном поле. Также непрерывные случайные величины широко используют в генетике, ядерной физике.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Плотность (f(x)) аналогична таким понятиям, как плотность тока в теории электричества или плотность распределения масс на оси абсцисс.

Свойства плотности распределения

Плотность распределения обладает следующими свойствами:

Интеграл от плотности равен единице по всему пространству: (int_{-infty}^infty f(x)dx=1). Выражение (f(x)dx) называют элементом вероятности.
Плотность распределения выполняется почти всюду, множество, на котором функция не будет выполнена, имеет меру ноль. Отрицательной плотность быть не может.
Вероятность попадания непрерывной случайной величины в промежуток ([a,b]) равна определенному интегралу от ее плотности в пределах этого промежутка.

Функция распределения непрерывной случайной величины

Функцию распределения непрерывной случайной величины можно представить в виде формулы (F(x);=;P(X)).

Любое дискретное распределение не является абсолютно непрерывным относительно меры Лебега, поэтому дискретные случайные величины не имеют плотности.

Согласно центральной предельной теореме теории вероятностей, чаще всего сумма множества случайных и слабо связанных друг с другом величин стремится к нормальному распределению. Если распределить группу людей на подгруппы по росту, большинство окажется среднего роста, то же самое будет с весом, коэффициентом интеллекта и многими другими параметрами.

Также встречаются следующие абсолютно непрерывные распределения:

равномерное на отрезке ([a,b]);
хи-квадрат;
логнормальное;
многомерное нормальное;
экспоненциальное;
Вейбулла;
Коши;
Парето;
Стьюдента;
Фишера.

График плотности распределения

Площадь, заштрихованная на иллюстрации, соответствует вероятности события ({aleq Xleq b}.)

Графики

Нормальное распределение задается функцией плотности вероятности, совпадающей с функцией Гаусса.

(mu) — математическое ожидание, (sigma) — среднеквадратическое отклонение, (а sigma^2) — дисперсия распределения.

Примеры задач

Задача 1

Распределение непрерывной случайной величины (X) задано функцией

(F(x);=;left{begin{array}{lc}0,&x<-1\frac15(x+1),&cleq xleq d\1,&x>4end{array}right.)

Нужно найти значения (с) и (d), плотность распределения вероятностей (f(x)), построить графики функций (F(x)) и (f(x)).

Решение:

функция распределения непрерывна, следовательно:

(F(c);=;frac15(c+1);=;0;Rightarrow;c;=;-1)

(F(d);=;frac15(d+1);=;1;Rightarrow;d;=;4)

Таким образом:

(F(x);=;left{begin{array}{lc}0,&x<-1\frac15(x+1),&-1leq xleq4\1,&x>4end{array}right.)

(f(x);=;F'(x);=;left{begin{array}{lc}0,&x<-1\frac15,&-1leq xleq4\1,&x>4end{array}right.)

Задача 1

Задача 2

Написать функцию плотности нормального распределения случайной величины (X), если известно, что (M(X) = 2) и (D(x) = 5.)

Решение:

при распределении по нормальному закону функция имеет вид: (f(x);=;frac1{sigmasqrt{2pi}}e^frac{{(x-a)}^2}{10}), где (a) — математическое ожидание, (sigma) — среднее квадратическое отклонение.

Подставим значения из условий задачи:

(а = М(Х) = 2, sigma;=;sqrt{D(X)};=;sqrt5)

Таким образом:

(f(x);=;frac1{sqrt{10pi}}e^frac{{(x-2)}^2}{10})

Источник

Прикладное описание понятия[править | править код]

Определение плотности вероятности в теории меры[править | править код]

Плотность случайной величины[править | править код]

Замечания[править | править код]

Плотность преобразования случайной величины[править | править код]

Свойства плотности вероятности[править | править код]

Примеры абсолютно непрерывных распределений[править | править код]

См. также[править | править код]

Литература[править | править код]

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория

Свойства плотности распределения

Примеры решения задач

Пример 1

Пример 2

Пример 3

Задачи контрольных и самостоятельных работ

Плотность распределения вероятности и ее свойства

Числовые характеристики случайных величин

Что такое плотность вероятности

Свойства плотности распределения

Функция распределения непрерывной случайной величины

График плотности распределения

Примеры задач

Вам также может понравиться

Как найти долготу на карте видео

Как найти уравнение перемещения по графику

Как найти партнеров на ночь

Добавить комментарий Отменить ответ