Масса
Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.
До недавнего времени в Международном бюро мер и весов в Париже хранился цилиндр массой один килограмм. Цилиндр был изготовлен из сплава иридия и платины и служил для всего мира эталоном килограмма. Правда, со временем его масса изменилась, и пришлось придумать новый эталон — электромагнитные весы.
Высота этого цилиндра была приблизительно равна 4 см, но чтобы его поднять, нужно было приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.
Второй закон Ньютона
F = ma
F — сила [Н]
m — масса [кг]
a — ускорение [м/с2]
В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне. 🙃
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Откуда берется масса
Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.
Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.
Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.

Источник: Википедия
Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.
Объем тела
Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.
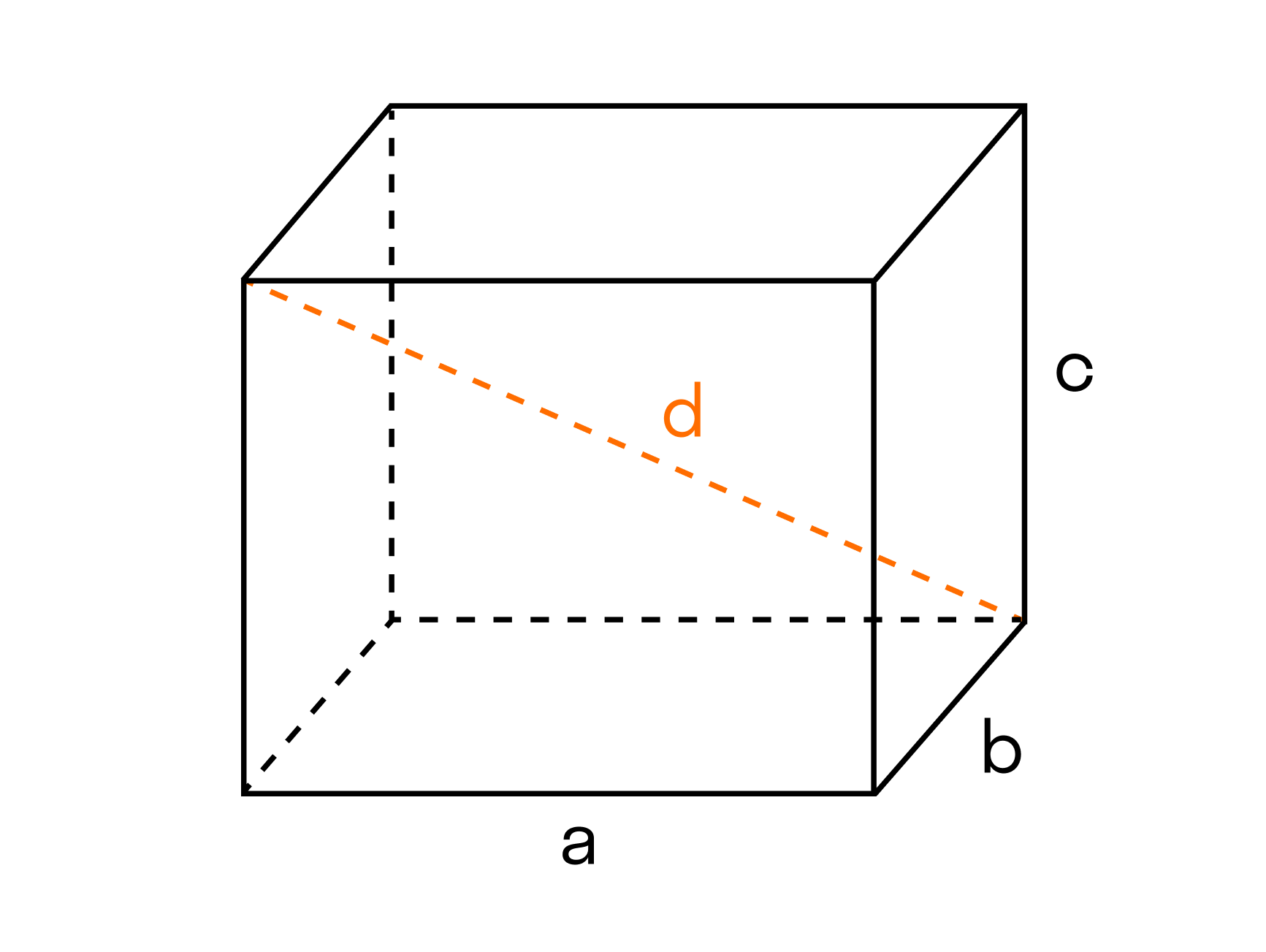
Скажем, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.
Формула объема параллелепипеда
V = abc
V — объем [м3]
a — длина [м]
b — ширина [м]
c — высота [м]
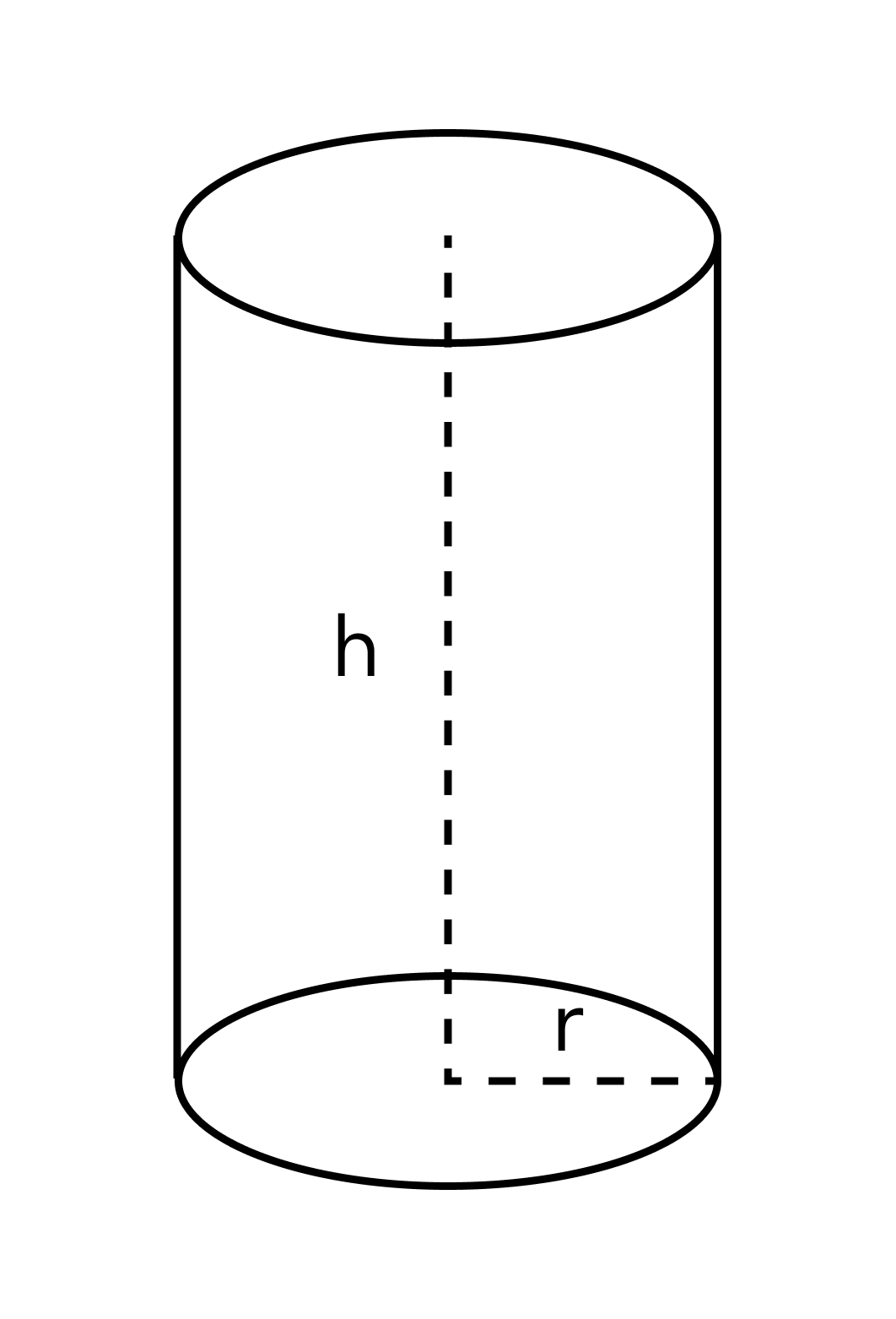
А для цилиндра будет справедлива такая формула:
Формула объема цилиндра
V = Sh
V — объем [м3]
S — площадь основания [м2]
h — высота [м]
Плотность вещества
Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объему.
Формула плотности вещества
р = m/V
р — плотность вещества [кг/м3]
m — масса вещества [кг]
V — объем вещества [м3]
Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.
Маленькое исключение
Исключение составляет вода. Так, плотность воды меньше плотности льда. Объяснение кроется в молекулярной структуре льда. Когда вода переходит из жидкого состояния в твердое, она изменяет молекулярную структуру так, что расстояние между молекулами увеличивается. Соответственно, плотность льда меньше плотности воды.
Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.
|
Твердое вещество |
кг/м3 |
г/см3 |
|
Платина |
21500 |
21,5 |
|
Золото |
19300 |
19,3 |
|
Вольфрам |
19000 |
19,0 |
|
Свинец |
11400 |
11,4 |
|
Серебро |
10500 |
10,5 |
|
Медь |
8900 |
8,9 |
|
Никель |
8800 |
8,8 |
|
Латунь |
8500 |
8,5 |
|
Сталь, железо |
7900 |
7,9 |
|
Олово |
7300 |
7,3 |
|
Цинк |
7100 |
7,1 |
|
Чугун |
7000 |
7,0 |
|
Алмаз |
3500 |
3,5 |
|
Алюминий |
2700 |
2,7 |
|
Мрамор |
2700 |
2,7 |
|
Гранит |
2600 |
2,6 |
|
Стекло |
2600 |
2,6 |
|
Бетон |
2200 |
2,2 |
|
Графит |
2200 |
2,2 |
|
Лёд |
900 |
0,9 |
|
Парафин |
900 |
0,9 |
|
Дуб (сухой) |
700 |
0,7 |
|
Берёза (сухая) |
650 |
0,65 |
|
Пробка |
200 |
0,2 |
|
Платиноиридиевый сплав |
21500 |
21,5 |
|
Жидкость |
кг/м3 |
г/см3 |
|
Ртуть |
13600 |
13,6 |
|
Мёд |
1300 |
1,3 |
|
Глицерин |
1260 |
1,26 |
|
Молоко |
1036 |
1,036 |
|
Морская вода |
1030 |
1,03 |
|
Вода |
1000 |
1 |
|
Подсолнечное масло |
920 |
0,92 |
|
Нефть |
820 |
0,82 |
|
Спирт |
800 |
0,8 |
|
Бензин |
700 |
0,7 |
|
Газ |
кг/м3 |
|
Хлор |
3,22 |
|
Озон |
2,14 |
|
Пропан |
2,02 |
|
Диоксид углерода |
1,98 |
|
Кислород |
1,43 |
|
Воздух |
1,29 |
|
Азот |
1,25 |
|
Гелий |
0,18 |
|
Водород |
0,09 |
Где самая большая плотность?
Самая большая плотность во Вселенной — в черной дыре. Плотность черной дыры составляет около 1014 кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Средняя плотность
В школьном курсе чаще всего говорят о средней плотности тела. Дело в том, что если мы рассмотрим какое-нибудь неоднородное тело, то в одной его части будет, например, большая плотность, а в другой — меньшая.
Если вы когда-то делали ремонт, то знакомы с такой вещью, как цемент. Он состоит из двух веществ: клинкера и гипса. Значит нам нужно отдельно найти плотность гипса, плотность клинкера по формуле, указанной выше, а потом найти среднее арифметическое двух плотностей. Можно сделать так.
А можно просто массу цемента разделить на объем цемента и мы получим ровно то же самое. Просто в данном случае мы берем не массу и объем вещества, а массу и объем тела.
Формула плотности тела
р = m/V
р — плотность тела [кг/м3]
m — масса тела [кг]
V — объем тела [м3]
Решение задач: плотность вещества
А теперь давайте тренироваться!
Задача 1
Цилиндр 1 поочерёдно взвешивают с цилиндром 2 такого же объёма, а затем с цилиндром 3, объем которого меньше (как показано на рисунке).
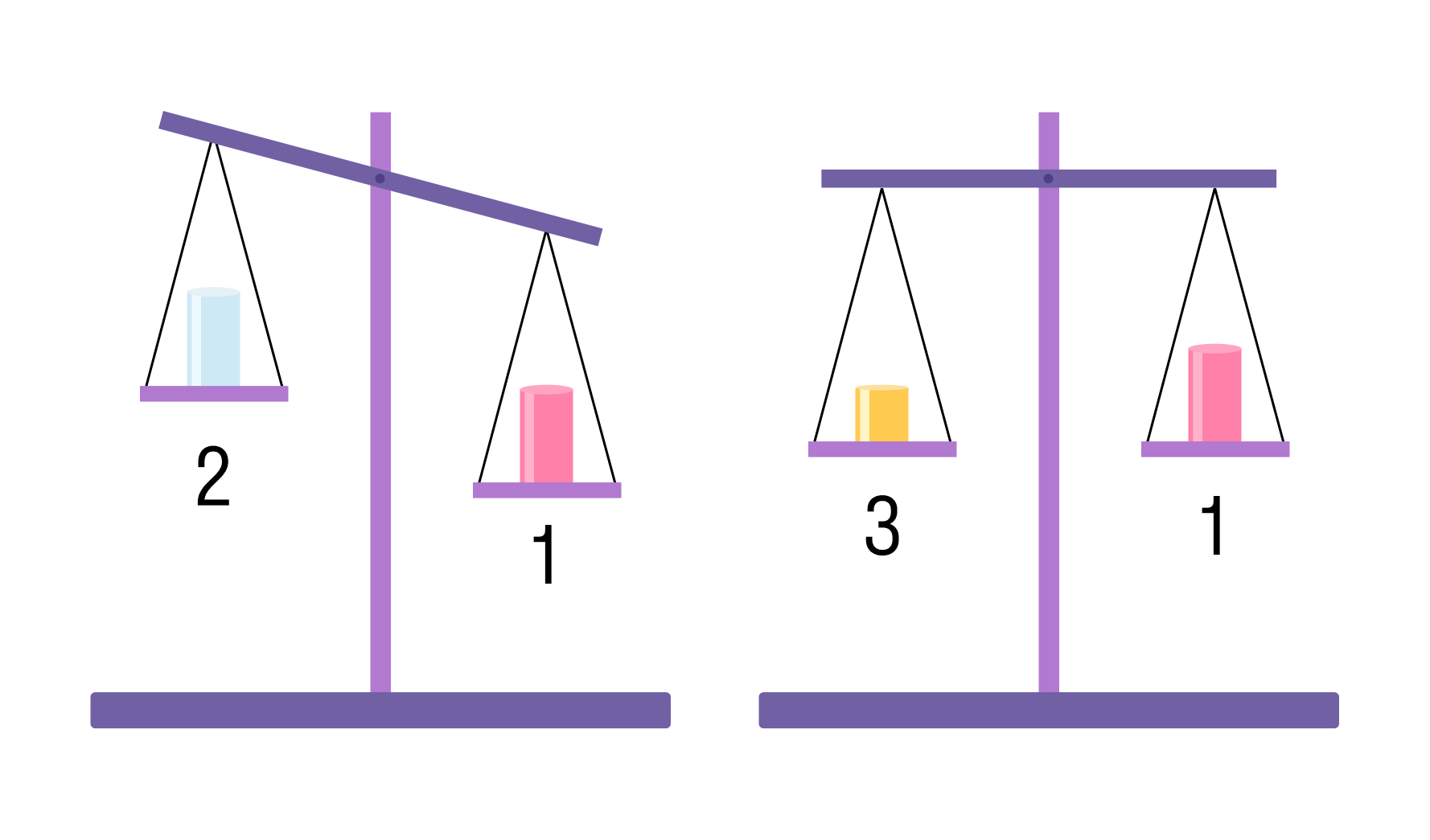
Какой цилиндр имеет максимальную среднюю плотность?
Решение:
Плотность тел прямо пропорциональна массе и обратно пропорциональна объему:
р = m/V
Исходя из проведенных опытов можно сделать следующие выводы:
1) масса первого цилиндра больше массы второго цилиндра при одинаковом объеме. Значит плотность первого цилиндра выше плотности второго.
2) масса первого цилиндра равна массе третьего цилиндра, объем которого меньше. Следовательно, плотность третьего цилиндра больше плотности первого цилиндра.
Таким образом, средние плотности цилиндров:
р2 < р1 < р3
Ответ: 3.
Задача 2
Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (как показано на рисунке). Для объёмов шаров справедливо соотношение V1 = V3 < V2.
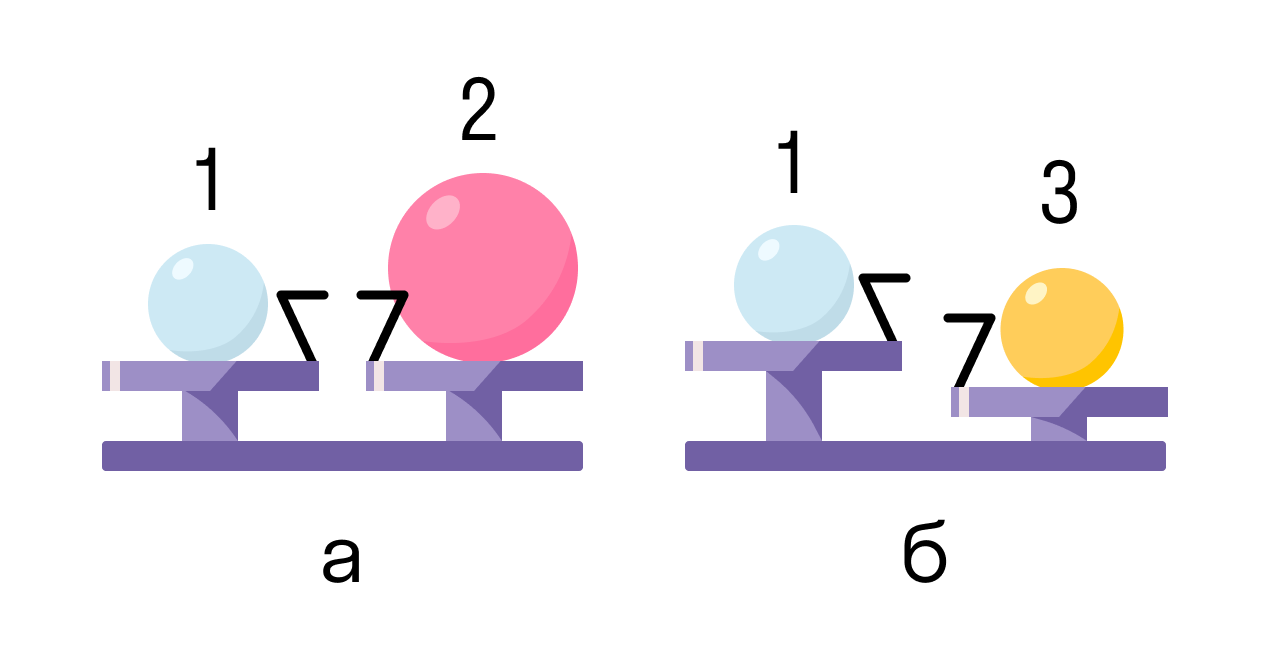
Какой шар имеет максимальную среднюю плотность?
Решение:
Из рисунка ясно, что масса шаров 1 и 2 равна — следовательно, плотность второго шара меньше, чем первого. Третий шар тяжелее, чем первый при одинаковом объёме, поэтому плотность третьего шара больше плотности первого. Таким образом, максимальную среднюю плотность имеет шар 3.
Ответ: 3
Задача 3
Найти плотность шара объемом 0,5 м3 и массой 1,5 кг.
Решение:
Возьмем формулу плотности и подставим в нее данные нам значения.
р = m/V
р = 1,5/0,5 = 3 кг/м3
Ответ: р = 3 кг/м3
Плавание тел
Почему шарик с гелием взлетает? Или мяч при игре в водное поло не тонет?
Жидкости и газы действуют на погруженные тела с выталкивающей силой. Подробно это явление рассматривают в теме «Сила Архимеда». Если говорить простым языком: если плотность тела, погруженного в жидкость, больше плотности жидкости — тело пойдет ко дну. Если меньше – оно всплывет на поверхность.
Задача 1
Стальной шарик в воде падает медленнее, чем в воздухе. Чем это объясняется?
Решение:
Плотность воды значительно выше, чем воздуха, поэтому стальной шарик в воде падает медленнее
Задача 2
В таблице даны плотности некоторых твердых веществ. Если вырезать из этих веществ кубики, то какие кубики смогут плавать в воде? Плотность воды — 1000 кг/м3.
|
Название вещества |
Плотность вещества, кг/м3 |
|
Алюминий |
2700 |
|
Парафин |
900 |
|
Плексиглас |
1200 |
|
Фарфор |
2300 |
|
Сосна |
400 |
Решение:
Плавать будут кубики, плотность которых меньше плотности воды, то есть сделанные из парафина или сосны.
Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.
Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.
Сегодня мы познакомимся с такой характеристикой как плотность. Она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.
Связь массы, объема и вещества, из которого состоит тело
Рассмотрим опыт, представленный на рисунке 1.
Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.
Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.
В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.
Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.
На рисунке изображены 2 тела массой $100 space г$: лед, железо и золото.
Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.
Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.
Определение плотности вещества
Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.
Рассмотрим два тела объемом $1 space м^3$ каждое. Если они будут состоять из разных веществ, то их массы тоже будут разными.
Итак, алюминий такого объема будет иметь массу 2700 кг, а свинец такого же объема ( $1 space м^3$) будет имеет массу 11 300 кг.
На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.
Плотность показывает, чему равна масса вещества, взятого в объеме $1 space м^3$ (или $1 space см^3$). Чтобы найти плотность вещества, нужно массу тела разделить на его объем.
По какой формуле можно рассчитать плотность вещества? Дадим определение.
Плотность — это физическая величина, которая равна отношению массы тела к его объему:
$плотность = frac{масса}{объем}$
или
$rho = frac{m}{V}$,
где $rho$ (“ро”) — плотность вещества, $m$ — масса тела, $V$ — объем тела.
Единицы измерения плотности
Какова единица плотности в СИ?
В СИ плотность вещества измеряется в килограммах на кубический метр ($1 frac{кг}{м^3}$).
Какие еще единицы плотности вам известны?
Часто используется другая единица измерения — граммы на кубический сантиметр ($1 frac{г}{см^3}$) (рисунок 4).
Иногда нам потребуется переводить плотность веществ, выраженную в $frac{кг}{м^3}$ в $ frac{г}{см^3}$.
Давайте выразим плотность мрамора ($2700 frac{кг}{м^3}$) в $frac{г}{см^3}$:
$$rho = 2700 cdot frac{1 space кг}{1 space м^3} = 2700 cdot frac{1000 space г}{1 space 000 space 000 space см^3} = frac{2700}{1000} cdot frac{г}{см^3} = 2.7 frac{г}{см^3}$$
Таблицы плотности некоторых тел и веществ
Плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна.
Например, плотность воды составляет $1000 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, водяного пара — $0.590 frac{кг}{м^3}$ (рисунок 5).
Плотности различных твердых тел
| Твердое тело | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Твердое тело | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Осмий | 22 600 | 22,6 | Мрамор | 2700 | 2,7 |
| Иридий | 22 400 | 22,4 | Стекло | 2500 | 2,5 |
| Платина | 21 500 | 21,5 | Фарфор | 2300 | 2,3 |
| Золото | 19 300 | 19,3 | Бетон | 2300 | 2,3 |
| Свинец | 11 300 | 11,3 | Кирпич | 1800 | 1,8 |
| Серебро | 10 500 | 10,5 | Сахар | 1600 | 1,6 |
| Медь | 8900 | 8,9 | Оргстекло | 1200 | 1,2 |
| Латунь | 8500 | 8,5 | Капрон | 1100 | 1,1 |
| Сталь, железо | 7800 | 7,8 | Полиэтилен | 920 | 0,92 |
| Олово | 7300 | 7,3 | Парафин | 900 | 0,90 |
| Цинк | 7100 | 7,1 | Лед | 900 | 0,90 |
| Чугун | 7000 | 7,0 | Дуб сухой | 700 | 0,70 |
| Корунд | 4000 | 4,0 | Сосна сухая | 400 | 0,40 |
| Алюминий | 2700 | 2,7 | Пробка | 240 | 0,24 |
Плотности различных жидкостей
| Жидкость | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Жидкость | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Ртуть | 13 600 | 13,60 | Керосин | 800 | 0,80 |
| Серная кислота | 1800 | 1,80 | Спирт | 800 | 0,80 |
| Мед | 1350 | 1,35 | Нефть | 800 | 0,80 |
| Вода морская | 1030 | 1,03 | Ацетон | 790 | 0,79 |
| Молоко цельное | 1030 | 1,03 | Эфир | 710 | 0,41 |
| Вода чистая | 1000 | 1,00 | Бензин | 710 | 0,71 |
| Масло подсолнечное | 930 | 0,93 | Жидкое олово (при $400^{circ}$) | 6800 | 6,80 |
| Масло машинное | 900 | 0,90 | Жидкий воздух (при $-194^{circ}$) | 860 | 0,86 |
Плотности различных газов
| Газ | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ | Газ | $rho, frac{кг}{м^3}$ | $rho, frac{г}{см^3}$ |
|---|---|---|---|---|---|
| Хлор | 3,210 | 0,00321 | Угарный газ | 1,250 | 0,00125 |
| Углекислый газ | 1,980 | 0,00198 | Природный газ | 0,800 | 0,0008 |
| Кислород | 1,430 | 0,00143 | Водяной пар (при $100^{circ}$) | 0,590 | 0,00059 |
| Воздух (при $0^{circ}C$ | 1,290 | 0,00129 | Гелий | 0,180 | 0,00018 |
| Азот | 1,250 | 0,00125 | Водород | 0,090 | 0,00009 |
Примеры задач на расчет плотности вещества
Задача №1
В таблице 1 указана плотность сахара — $1600 frac{кг}{м^3}$. Что это значит? Какой здесь физический смысл?
Посмотреть ответ
Скрыть
Ответ:
Значение плотности показывает нам, какое количество вещества (его масса) будет находиться в объеме $1 space м^3$. Итак, это означает, что масса сахара объемом $1 space м^3$ будет равна $1600 space кг$.
Задача №2
Канистра объемом 30 л наполнена бензином. Масса полной канистры составляет 21,3 кг. Рассчитайте плотность бензина.
Переведем литры в кубические метры ($1 space л = 0.001 space м^3$):
$30 cdot 0.001 = 0.03 space м^3$.
Дано:
$V = 30 space л$
$m = 21.3 space кг$
$rho -?$
Показать решение и ответ
Скрыть
Решение:
По определению плотности:
$rho = frac{m}{V}$.
$rho = frac{21.3 space кг}{0.03 space м^3} = 710 frac{кг}{м^3}$.
Если мы сравним полученное значение с табличным, то получим подтверждение, что задача решена верно.
Ответ: $rho = 710 frac{кг}{м^3}$.
Задача №3
Деревянный брусок из березы имеет следующие размеры: длину 3 м, высоту 10 см, и ширину 50 см. Масса бруска составляет 75 кг. Найдите плотность березы.
Дано:
$а = 3 space м$
$b = 10 space см$
$c = 50 space см$
$m = 75 space кг$
$rho -?$
Показать решение и ответ
Скрыть
Решение:
Найдем объем бруска:
$V = a cdot b cdot c$,
$V = 3 space м cdot 0.1 space м cdot 0.5 space м = 0.15 space м^3$.
По определению плотности:
$rho = frac{m}{V}$.
$rho = frac{75 space кг}{0.15 space м^3} = 500 frac{кг}{м^3}$.
Ответ: $rho = 500 frac{кг}{м^3}$.
Больше задач с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Плотность редкого металла осмия равна $22 space 600 frac{кг}{м^3}$. Что это означает?
Посмотреть ответ
Скрыть
Ответ:
Значение плотности показывает нам, какое количество вещества (его масса) будет находиться в объеме $1 space м^3$. Итак, это означает, что масса осмия объемом $1 space м^3$ будет равна $22 space 600 space кг$ или $22.6 space т$.
Упражнение №2
Пользуясь таблицами плотностей (таблицы 1, 2), определите, плотность какого вещества больше: цинка или серебра; бетона или мрамора; бензина или спирта.
Показать ответ
Скрыть
Плотность цинка составляет $7100 frac{кг}{м^3}$, а серебра — $10 space 500 frac{кг}{м^3}$. Получается, что плотность серебра больше плотности цинка.
Плотность бетона составляет $2300 frac{кг}{м^3}$, а мрамора — $2700 frac{кг}{м^3}$. Получается, что плотность мрамора больше плотности бетона.
Плотность бензина составляет $710 frac{кг}{м^3}$, а спирта — $800 frac{кг}{м^3}$. Получается, что плотность спирта больше плотности бензина.
Упражнение №3
Три кубика — из мрамора, льда и латуни — имеют одинаковый объем. Какой из них имеет большую массу, а какой — меньшую?
Показать ответ
Скрыть
Выразим массу из формулы плотности:
$rho = frac{m}{V}$,
$m = rho V$.
Объем кубиков у нас одинаковый. Значит, чем больше плотность вещества, из которого изготовлен кубик, тем больше его масса.
Плотность мрамора составляет $2700 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, а латуни — $8500 frac{кг}{м^3}$. У латуни наибольшая плотность, а у льда — наименьшая. Значит, кубик из латуни будет иметь наибольшую массу, а из льда — наименьшую.
Упражнение №4
Самое легкое дерево — бальза. Масса древесины этого дерева равна $12 space г$ при объеме в $100 space см^3$. Определите плотность древесины в $frac{г}{см^3}$ и $frac{кг}{м^3}$.
Дано:
$m = 12 space г$
$V = 100 space см^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Мы не стали переводить единицы измерения в СИ. Сначала мы рассчитаем плотность этой древесины в $frac{г}{см^3}$, а затем переведем в $frac{кг}{м^3}$.
Рассчитаем плотность по известной нам формуле:
$rho = frac{m}{V}$,
$rho = frac{12 space г}{100 space см^3} = 0.12 frac{г}{см^3}$.
Теперь переведем полученное значение в $frac{кг}{м^3}$:
$rho = 0.12 frac{г}{см^3} = 0.12 frac{0.001 space кг}{0.01^3 space м^3} = 0.12 frac{10^{-3} space кг}{10^{-6} space м^3} = 0.12 cdot 10^3 frac{кг}{м^3} = 120 frac{кг}{м^3}$.
Ответ: $rho = 0.12 frac{г}{см^3} = 120 frac{кг}{м^3}$.
Упражнение №5
Кусочек сахара имеет размеры: $а = 2.5 space см$, $b = 1 space см$, $с = 0.7 space см$ (рис. 53). Его масса равна $0.32 space г$. Определите плотность сахара. Проверьте полученный результат по таблице 1.
Дано:
$а = 2.5 space см$
$b = 1 space см$
$с = 0.7 space см$
$m = 0.32 space г$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Чтобы рассчитать плотность сахара, нужно знать его объем. Его мы можем вычислить перемножив друг на друга известные высоту, ширину и длину:
$V = a cdot b cdot c$.
Подставим в формулу плотности и рассчитаем ее:
$rho = frac{m}{V} = frac{m}{a cdot cdot b cdot c}$,
$rho = frac{0.32 space г}{2.5 space см cdot 1 space см cdot 0.7 space см} = frac{0.32 space г}{1.75 space см^3} approx 0.18 frac{г}{см^3}$.
Полученный результат не совпадает с табличным ($rho = 1.6 frac{г}{см^3}$). Расчеты произведены верно, значит ошибка или в условии задачи, или мы наблюдаем очень необычный сахар.
Ответ: $rho approx 0.18 frac{г}{см^3}$.
Задание
В вашем распоряжении имеются весы с разновесами, измерительный цилиндр с водой и металлический шарик на нити. Предложите, как определить плотность шарика.
Взвесим шарик, мы узнаем его массу. Чтобы определить его объем, мы можем использовать измерительный цилиндр с водой. Для этого нужно опустить шарик в воду, и посмотреть, до какого уровня теперь поднялась воды. Разность этого объема и первоначального объема жидкости будет равна объему шарику.
Зная его массу и объем, мы сможем рассчитать его плотность по формуле: $rho = frac{m}{V}$.
Плотностью вещества называется величина, численно равная массе единицы объёма этого вещества.
Каждое вещество занимает некоторый объём. И может оказаться, что объёмы двух тел равны, а их массы различны. В этом случае говорят, что плотности этих веществ различны.
Рис. (1). Тела равных объёмов на весах
Рассмотрим кусок железа, масса которого равна 1 кг, и кусок дерева, масса которого равна 1 кг. Объём дерева больше, чем объём куска железа. Плотность дерева меньше, чем плотность железа (молекулы прилегают не так плотно друг к другу).

Рис. (2). Железо и дерево
Плотность равна отношению массы тела к его объёму.
В физике плотность обозначают греческой буквой (ρ) (ро).
, где (m) — масса, (V) — объём.
Основной единицей плотности вещества является
кгм3
. Иногда используют единицу плотности
г/см3
.
Пример:
плотность железа равна 7900
кгм3
, это означает, что масса 1
м3
железа равна 7900 кг.
Плотность воды равна 1000
кгм3
, значит, масса 1
м3
воды равна 1000 кг.
Выражая по-другому, плотность воды равна 1
г/см3
, значит, масса 1
см3
воды равна 1 г.
В различных состояниях плотность вещества различна.
Например, плотность расплавленного железа меньше плотности твёрдого железа.
Плотности веществ могут быть очень различны. Самое плотное вещество находится не на Земле.
Например, в космосе плотность белого карлика Сириуса Б (звезда) так велика, что масса спичечного коробка из этого вещества была бы равна 127 тоннам.
Пример:
10 вёдер вместимостью 1 литр до краёв наполнены мёдом, масса всего мёда равна 14 кг. Найди плотность мёда.
|
(V )(= )(10) л (=) 0,01 м3 ; |
ρ=mV | ρ (= )14 кг0,01м3=1400кгм3 |
Обрати внимание!
Плотность вещества зависит от температуры: при повышении температуры обычно плотность снижается. Это связано с термическим расширением, когда при неизменной массе увеличивается объём.
Источники:
Рис. 1. Тела равных объёмов на весах. © ЯКласс.
Плотность вещества


4.4
Средняя оценка: 4.4
Всего получено оценок: 118.
Обновлено 16 Июля, 2021
4.4
Средняя оценка: 4.4
Всего получено оценок: 118.
Обновлено 16 Июля, 2021
Как известно из курса физики 7 класса, одной из важнейших характеристик любого тела является его масса. Большие тела, как правило, тяжелы, мелкие — легки. Однако, если тела имеют одинаковые размеры, они вовсе не обязательно будут иметь одну и ту же массу. И это обязательно отразится на физических явлениях с этими телами. Как в физике учитывается различная масса одинаковых по размеру тел?
Масса и плотность вещества
Шарик для настольного тенниса весит 2,7 г.
Но такой же по размеру шарик из дерева будет весить 15–20 г, а из железа — 260 г. Если же шарик изготовить из свинца, его масса достигнет 380 г.
Столь большая разница в массе одинаковых по размеру тел объясняется тем, что элементарные частицы внутри различных веществ имеют различное пространственное расположение, и в одном и том же объёме помещается разное их количество. Например, в ядрах атомов свинца в среднем 208 нуклонов, составляющих основную массу. А в ядрах железа — только 56 нуклонов. В ядрах элементов, из которых состоят молекулы дерева и воздуха, нуклонов ещё меньше.
Мало того, в составе молекул и кристаллических решёток атомы могут находиться на разных расстояниях, и в одном и том же объёме будет помещаться их различное количество. Наконец, в газах молекулы находятся друг от друга на относительно больших расстояниях, это и объясняет лёгкость газов (и малую массу шарика от пинг-понга, на 99 % заполненного воздухом).
Возникает вопрос: как учесть эту разницу?
В физике для этого используется специальная величина — плотность, которая показывает, насколько сильно «упаковано» вещество в данном объёме.
В приведённом примере наивысшая плотность будет у свинцового шарика, наименьшая — у шарика для пинг-понга.
Формула плотности вещества
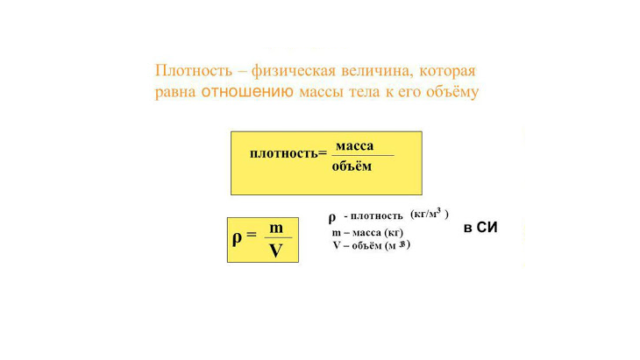
Плотность вещества равна отношению массы вещества к объёму, который эта масса занимает. Плотность обозначается греческой буквой $rho$ (ро).
То есть, если объём тела обозначить буквой $V$, а массу — $m$, то формула плотности вещества примет вид:
$$rho = {m over V}$$
Из данной формулы можно получить единицу плотности. Поскольку масса измеряется в килограммах, а объём — в кубических метрах, то единицей измерения плотности будет килограмм на кубический метр:
$$[rho] = {кг over м^3}$$
Физический смысл плотности — это масса одного кубического метра данного вещества.
Использование плотности в расчётах
Плотность вещества — это табличная величина, и она позволяет по известной массе вычислить объём тела, или наоборот, получить массу тела известного объёма.
Например, в приведённом примере с шариками из различных веществ не требуется изготавливать шарики, чтобы знать их массу. Достаточно измерить диаметр шарика (для настольного тенниса он составляет 0,04 м) и по геометрическим формулам вычислить его объём (он составит 0,0000335 куб. м). Умножая полученный объём на плотность вещества, взятую из таблицы, можно получить вес шарика, не изготавливая и не взвешивая его. Например, стеклянный шарик такого размера будет весить около 85 г, а золотой шарик — 647 г.
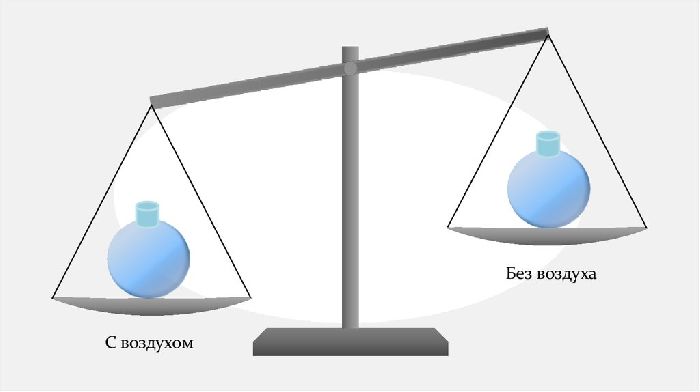
Плотность можно измерить не только для твёрдых, но и для жидких и газообразных тел. Например, плотность воздуха составляет 1,29 кг на кубический метр. А значит, воздух, находящийся в комнате средних размеров (например, $6 times 3.5 times 3$м) весит около 80 кг! Вполне заметная масса, хотя обычно кажется, что воздух ничего не весит. Масса и плотность воздуха впервые была определена Г. Галилеем путём взвешивания сосуда до и после откачивания из него воздуха.

Что мы узнали?
Плотность — это физическая величина, показывающая, насколько сильно «упаковано» вещество в данном объёме. Она равна отношению массы вещества к объёму, занимаемому этой массой, и измеряется в килограммах на кубический метр.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 118.
А какая ваша оценка?
§ 1 Плотность вещества
На этом уроке мы введем новую характеристику вещества – плотность, рассмотрим зависимость свойства вещества от его плотности.
Известно, что окружающие нас тела состоят из разных веществ, они могут иметь разный объем, могут отличаться по массе.

Поставим несколько опытов.
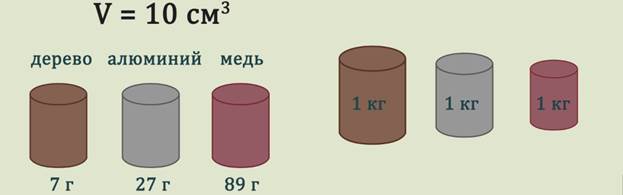
Возьмем два цилиндра равного объема – металлический и деревянный.
Измерим их массу при помощи рычажных весов . Мы видим, что масса металлического цилиндра больше.
Возьмем цилиндры разного объема и снова взвесим . Видим, что массы цилиндров равны.
Опыты показывают, что тела одинакового объема, но изготовленные из разных веществ, могут иметь разные массы (См. рис.). Тела, имеющие разный объем, могут иметь одинаковую массу (См. рис.). Причина в том, что разные вещества имеют разную плотность.
Плотность – это скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3 (или 1 см3).
Как можно определить плотность тела? Рассмотрим пример.
На стройке используют бетонные плиты объемом 2 м3, масса которых равна 4600 кг. Найти плотность бетона.

Известно, что плотность показывает массу тела в объеме 1 м3. Если масса 2 м3 бетона 4600 кг, то масса 1 м3 в 2 раза меньше. Поделив 4600 на 2, получим 2300 кг, то есть плотность бетонной плиты равна 2300 кг/м3.
Итак, чтобы найти плотность вещества, нужно массу тела разделить на его объем:
![]()
Физические величины имеют обозначение, единицу измерения и числовое значение. Масса обозначается буквой m, объем – буквой V. Плотность принято обозначать греческой буквой «ро» – ρ.
Тогда формула плотности запишется так:
![]()
По этой формуле определим единицу измерения плотности в Международной системе единиц: масса измеряется в килограммах, объем – в кубических метрах. Тогда единица плотности – кг/м3. Внесистемная единица плотности – г/см3.
Установим связь между ними:

Зная молекулярное строение вещества, можно объяснить, почему разные вещества имеют разную плотность.

Молекулы разных веществ различны, между ними разные межмолекулярные расстояния, значит, в единице объема будет находиться разное число молекул, и сами молекулы разных веществ имеют разную массу, то есть плотность различна для разных веществ. Плотность алюминия больше плотности дерева, плотность меди больше плотности алюминия (См. рис.).
Известно, что одно и то же вещество в разных агрегатных состояниях имеет разные свойства, что связано с разными расстояниями между молекулами. В газах промежутки между молекулами большие, в жидкостях и в твердых телах – сравнимы с размерами самих молекул (рис.5). Следовательно, одно и то же вещество имеет разную плотность в разных агрегатных состояниях. Например, плотность льда 900 кг/м3, то есть 1 м3 льда имеет массу 900 кг; плотность воды – 1000 кг/м3, то есть 1 м3 воды имеет массу 1000 кг, а плотность водяного пара 0,59 кг/м3, то есть 1 м3 пара имеет массу всего 59 кг (рис.6).
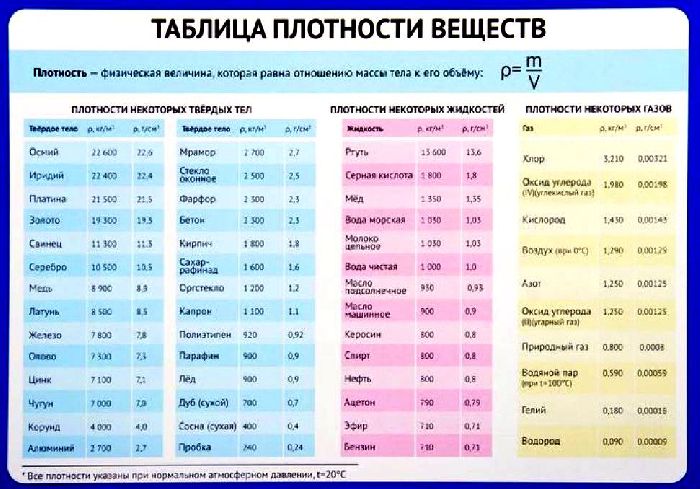
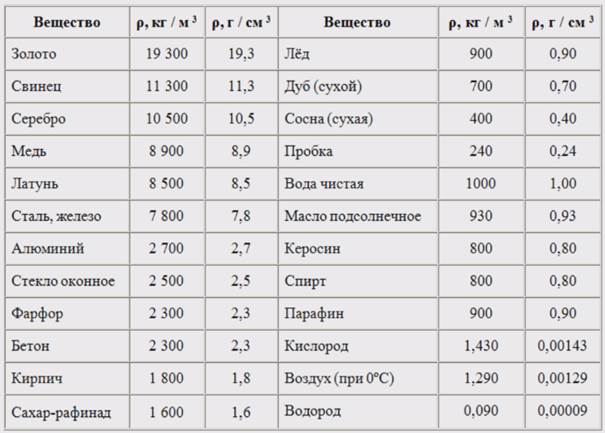
Плотности веществ экспериментально измерены, значения некоторых из них приведены в таблице.
Для измерения плотности жидких и сыпучих тел применяют специальный
прибор – ареометр – прибор в виде стеклянного поплавка с измерительной шкалой и грузом в нижней части.

Для измерения плотности жидкости сухой и чистый ареометр помещают в сосуд с этой жидкостью так, чтобы он свободно плавал в нём. Значения плотности считывают по шкале ареометра (рис.7).
Знание плотности вещества важно для решения практических задач.
Например, инженер, зная плотности используемых веществ, может заранее рассчитать массу отдельной детали или всего изделия, строитель может рассчитать массу здания и его давление на фундамент, водитель может определить грузоподъемность автомобиля.
§ 2 Краткий итог урока
Плотность – это скалярная физическая величина, равная отношению массы тела к его объему.
Чтобы найти плотность вещества, нужно массу тела разделить на его объем:
![]()
Формула плотности:
![]()
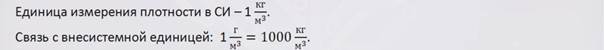
Плотность показывает, какую массу имеет вещество, взятое в объеме 1 м3 или 1 см3.
