По какой формуле вычисляется плотность вещества через массу молекулы и концентрацию?
Денис Дущенко
Знаток
(269),
на голосовании
7 лет назад
По какой формуле вычисляется плотность вещества через массу молекулы и концентрацию
Голосование за лучший ответ
Shiko-1
Ученик
(170)
7 лет назад
Плотность вещества (р) равна массе вещества (m) поделить на объём (V):
p=m/V
Масса (m) в свою очередь равна массе частицы вещества (m0) умноженное на число частиц вещества (N):
p=mV=m0*N/V
Концентрация вещества (n) равна числу частиц (N) в единице объёма (V), откуда следует, что N=nV.
Отсюда получаем:
p=mV=m0*N/V= m0*nV/V=m0*n
Таким образом плотность вещества (р) равна произведению массы частицы вещества на ее концентрацию.
Формулы молекулярной физики
Формула концентрации молекул
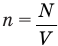
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
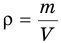
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
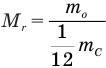
Здесь 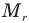 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 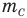 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
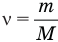
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
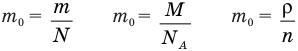
Здесь 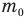 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 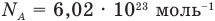 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
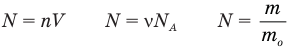
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 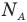 — число Авогадро
— число Авогадро 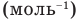 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
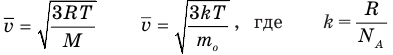
Здесь 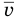 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 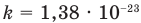 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 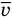 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
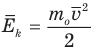
Здесь 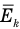 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 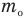 — масса одной молекулы (кг),
— масса одной молекулы (кг), 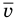 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
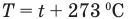
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
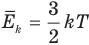
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
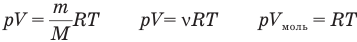
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 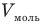 — объем моля
— объем моля 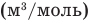 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 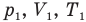 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 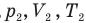 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 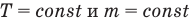
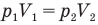
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 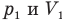 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 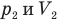 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 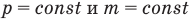
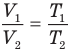
Здесь р — давление газа (Па), m — масса газа (кг), 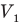 и
и 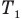 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 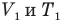 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 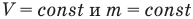
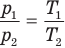
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 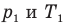 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 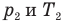 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
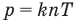
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
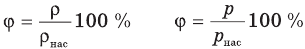
Здесь 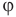 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 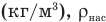 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 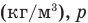 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 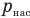 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
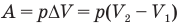
Здесь А — работа (Дж), р — давление газа (Па), 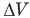 — изменение объема газа
— изменение объема газа 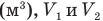 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
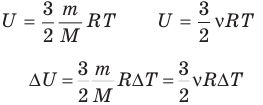
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 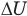 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 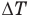 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
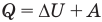
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 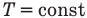
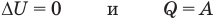
к изохорному: при V = const
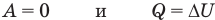
к изобарному: при р = const
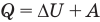
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 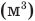 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
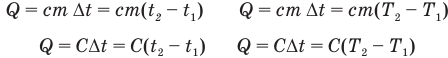
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 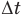 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 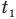 и
и 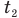 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 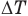 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 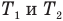 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 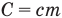 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
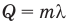
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 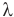 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
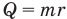
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
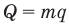
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
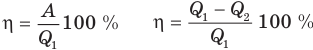
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 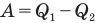 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 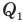 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 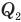 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
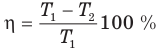
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 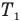 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 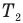 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

Содержание:
- Определение и формула плотности вещества
- Виды плотности вещества
- Единицы измерения плотности вещества
- Примеры решения задач
Определение и формула плотности вещества
Определение
Плотностью вещества (плотностью вещества тела) называют скалярную физическую величину, которая равна отношению массы
(dm) малого элемента тела к его единичному объему (dV). Чаще всего плотность вещества обозначают греческой буквой
$rho$. И так:
$$rho=frac{d m}{d V}$$
Виды плотности вещества
Применяя выражение (1) для определения плотности, говорят о плотности тела в точке.
Плотность тела зависит от материала тела и его термодинамического состояния.
В том случае, если тело можно считать однородным (плотность вещества во всем теле одинакова (
$rho = const$), то $rho$ определяют следующей формулой:
$$rho=frac{m}{V}$$
где m – масса тела, V – объем тела.
Если тело является неоднородным, то иногда пользуются понятием средней плотности
$langlerhorangle$, которая рассчитывается как:
$$langlerhorangle=frac{m}{V}(3)$$
где m – масса тела, V – объем тела. В технике для неоднородных (например, сыпучих) тел используют понятие объемной плотности.
Объемную плотность рассчитывают так же как $langlerhorangle=frac{m}{V}(3)$ (3). Объем определяют,
включая промежутки в сыпучих и рыхлых материалах (таких как: песок, гравий, зерно и т.д.).
При рассмотрении газов, находящихся в нормальных условиях для вычисления плотности применяют формулу:
$$rho=frac{mu}{V_{mu}}(4)$$
где $mu$ – молярная масса газа,
$V_{mu}$ – молярный объем газа, который при нормальных условиях составляет 22,4 л/моль.
Единицы измерения плотности вещества
В соответствии с определением, можно записать, что
единицами измерения плотности в системе СИ служит: [$rho$]=кг/м3
в СГС: [$rho$]=г/(см)3
При этом: 1 кг/м3 = (10)-3 г/(см)3 .
Примеры решения задач
Пример
Задание. Какова плотность воды, если объем, который занимает одна молекула H2O,
примерно равен $Delta V approx 3 cdot 10^{-29}$ м3? Считайте, что молекулы в воде плотно упакованы.
Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как:
$$rho=frac{m_{0}}{Delta V}$$
где m0 – масса молекулы воды. Найдем m0, используя известное соотношение:
$$frac{m}{mu}=frac{N}{N_{A}}$$
где N=1 – количество молекул (в нашем случае одна молекула), m – масса рассматриваемого количества молекул
(в нашем случае m=m0), NА=6,02• 1023 моль-1 – постоянная Авогадро,
$mu$=18•10-3
кг/моль (так как относительная молекулярная масса воды равна Mr=18). Следовательно, применяя выражение (2)
для нахождения массы одной молекулы имеем:
$$m_{0}=frac{mu}{N_{A}}(3)$$
Подставим m0 в выражение (1), получаем:
$$rho=frac{mu}{Delta V N_{A}}(4)$$
Проведем расчет искомой величины:
$rho=frac{18 cdot 10^{-3}}{3 cdot 10^{-29} cdot 6,02 cdot 10^{23}}=10^{3} mathrm{kr} / mathrm{m}^{3}$ кг/м3
Ответ. Плотность воды равна 103 кг/м3 .

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
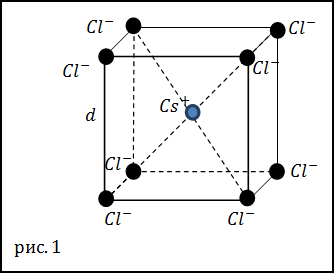
Задание. Какова плотность кристаллов хлорида цезия (CsCl), если кристаллы имеют кубическую кристаллическую
решетку (рис.1) в вершинах которой находятся ионы хлора (Cl–), а в центре расположен ион цезия
(Cs+). Ребро кристаллической решетки считайте равным d=0, 41 нм.
Решение. За основу решения задачи примем выражение:
$$frac{m}{mu}=frac{N}{N_{A}}(2.1)$$
где m – масса вещества (в нашем случае это масса одной молекулы
$left.operatorname{CsCl}left(m_{0}right)right), N=1, N_{A}=6,02 cdot 10^{23}$ – постоянная Авогадро,
$mu=168 cdot 10^{-3}$ кг/моль молярная масса хлорида Цезия
(так как относительная молекулярная хлорида цезия равна $M_r = 168$).
Выражение (2.1) для одной молекулы примет вид:
$$frac{m_{0}}{mu}=frac{1}{N_{A}}$$
В выражении (2.2) массу молекулы можно выразить через ее плотность как:
$$m_{0}=rho V_{m}(2.3)$$
где Vm – объем исследуемой молекулы. Так как кристаллы имеют кубическую кристаллическую решетку, ребро которой нам известно
(и равно d), то вместо объема Vm можно использовать выражение:
$$V_{m}=d^{3}(2.4)$$
Подставим выражения (2.3) и (2.4) в формулу (2.2), получим:
$$frac{rho V_{m}}{mu}=frac{1}{N_{A}}(2.5)$$
Тогда выражение для плотности примет вид:
$$rho=frac{mu}{d^{3} N_{A}}$$
Переведем размер стороны кристаллической решетки в единицы системы СИ, получим d=0,41нм=0, 41•10-9) м. Проведем вычисления:
$rho=frac{168 cdot 10^{-3}}{left(0,41 cdot 10^{-9}right)^{3} cdot 6,02 cdot 10^{23}}=4047,6$ кг/м3
Ответ. $rho=4047,6$ кг/м3
Читать дальше: Формула потенциальной энергии.
Молярная масса — что это? Как рассчитать? Формулы и примеры
Поможем понять и полюбить химию
Начать учиться
163.1K
Для решения многих задач по химии нужно знать количество молекул или других частиц, необходимое для реакции. Однако оперировать столь малыми числами неудобно, поэтому ученые ввели новые величины. В этой статье вы познакомитесь с такими понятиями, как моль, количество вещества, молярная масса в химии.
Что такое моль
Прежде чем говорить о том, как найти молярную массу вещества, определимся с понятием «моль». Его ввели как искусственную величину для упрощения расчетов. Это количество вещества, в котором содержится столько же мельчайших частиц, сколько в 12 г одного из изотопов углерода — C12.
Для всех химических веществ это количество одинаково и представляет собой число Авогадро 6,02 · 1023. Постоянная Авогадро обозначается NA, а измеряется в моль-1.
Число Авогадро — это количество молекул, ионов или других мельчайших частиц в 1 моле вещества.
NA = 6,02 · 1023 моль-1.
Историческая справка
В 1811 году химик Амедео Авогадро предположил, что если взять два равных объема газов в равных значимых условиях (при одинаковой температуре и давлении), то количество молекул в этих объемах тоже будет одинаковым. Опираясь на свою гипотезу, он определил атомные и молекулярные массы многих веществ, а также рассчитал количество атомов в молекулах воды, оксидов азота и т. д. Однако в научных кругах гипотеза Авогадро долго не находила понимания. Общепринятой она стала только в 1860 году.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Что такое молярная масса
Молярная масса — это масса одного моля вещества, она измеряется в граммах деленных на моль (г/моль). Данная величина представляет собой отношение массы вещества к его количеству, которое измеряется в молях.
Данная величина представляет собой отношение массы вещества к его количеству, которое измеряется в молях.
Как обозначается молярная масса: М.
, где — это масса вещества, а — количество вещества.
Единица измерения молярной массы: г/моль.
Запоминаем!
Правильно говорить именно молярная, а не мольная масса.
Несмотря на то, что в 1 моле любого химического вещества содержится одинаковое количество молекул (и оно равно числу Авогадро), молярные массы разных веществ отличаются. Все потому, что отличаются атомы, которые входят в состав этих молекул. В частности, разница между ними заключается в относительной атомной массе (Ar) — например, Ar(Mg) = 24, а Ar(Hg) = 200. Сейчас станет ясно, какое это имеет значение.
Как определить молярную массу
Данная величина тесно связана с такими понятиями, как относительные атомная и молекулярная массы. Именно относительные, потому что абсолютную массу молекулы или атома вещества в химии не используют для решения задач — это слишком малые величины.
Именно относительные, потому что абсолютную массу молекулы или атома вещества в химии не используют для решения задач — это слишком малые величины.
Относительная атомная масса вещества (Ar) показывает, во сколько раз его атом больше 1/12 атома углерода. Это значение для каждого химического элемента можно увидеть в таблице Менделеева.
Относительная молекулярная масса (Mr) складывается из Ar каждого атома в молекуле вещества с учетом индексов. Она показывает, на сколько масса молекулы больше 1/12 атома углерода.
, где — это количество атомов.
Разберемся на примерах.
В молекуле хлорида натрия NaCl есть 1 атом натрия и 1 атом хлора, при этом Ar(Na) = 23, Ar (Cl) = 35,5.
Mr(NaCl) = 23 + 35,5 = 58,5.
В молекуле NaNO2 есть 1 атом натрия, 1 атом азота и 2 атома кислорода.
Ar(Na) = 23, Ar(N) = 14, Ar(O) = 16.
Mr(NaNO2) = 23 + 14 + 16 · 2 = 69.
Собственно, для вычисления молярной массы больше ничего и не требуется.
Важно
Молярная масса вещества численно равна относительной молекулярной массе. Но путать эти два понятия не стоит — у них разный физический смысл. Молярная масса характеризует 1 моль, а относительная молекулярная — 1 молекулу.
Количество вещества
Из предыдущих формул понятно, что молярная масса и количество вещества тесно связаны. Рассмотрим эту связь подробнее. Начнем с того, что количество вещества может обозначаться как латинской буквой , так и греческой буквой (ню). Международное обозначение — , но не стоит удивляться, встретив в формулах любую из этих букв.
В формуле нахождения молярной массы мы обозначили количество вещества через :
, следовательно .
Пользуясь этим, можно найти количество вещества (в молях), если нам известны его абсолютная и молярная масса.
Пример 1
Как определить, какое количество вещества включают 350 г сульфата бария BaSO4?
Воспользуемся формулой .
Мы помним, что M = Mr (значение молярной массы равно значению относительной молекулярной).
Mr(BaSO4) = Ar(Ba) + A
r(S) + Ar(O) · 4 = 137 + 32 + 16 · 4 = 233.
М(BaSO4) = Mr(BaSO4) = 233 г/моль.
Подставим значение молярной массы в формулу:
моль.
Есть и еще одна формула количества вещества, которая позволяет найти его, если известно число молекул или других структурных единиц.
, где — число структурных единиц, — число Авогадро.
Пример 2
Допустим, некий объем CaCO3 содержит 3,01 · 1023 молекул. Как найти количество вещества, соответствующее данному объему?
Воспользуемся формулой моль.
Молярный объем
Выше мы находили количество вещества через молярную массу, но для газов это можно сделать и через молярный объем. Согласно закону Авогадро количество любого газа, равное 1 моль, будет занимать один и тот же объем, если газы рассматриваются при одинаковой температуре и давлении.
При стандартных физических условиях — температуре 0°С и давлении 1 атм или 760 мм ртутного столба, 1 моль газа занимает объем 22,4 л.
Молярный объем — это объем газа, взятого в количестве 1 моль. Он обозначается Vm.
При нормальных условиях Vm = 22,4 л/моль.
Значения молярного и фактического объема газа помогают найти количество вещества.
, где — фактический объем газа, а — молярный объем.
Пример 1
Сколько молей содержится в 120 литрах газа при нормальных условиях?
Рассчитаем по формуле моль.
Ответ: 120 литров любого газа при стандартных условиях содержат 5,36 моль.
Относительная плотность одного газа по другому
Иногда для решения задачи нужно знать, как найти молярную массу газа, о котором сообщается лишь его плотность по воздуху или по другому газу. Это возможно, если знать формулу относительной плотности, которая обозначается буквой D.
, где и — некие газы.
Пример 1
Как определить, во сколько раз угарный газ плотнее водорода?
Для начала найдем молярную массу CO и H2:
М(CO) = Mr(CO) = Ar(C) + Ar(O) = 12 + 16 = 28.
М(H) = Mr(H2) = 2 · Ar(H) = 2 · 1 = 2.
.
Ответ: угарный газ в 14 раз плотнее водорода.
Пример 2
Как посчитать молярную массу газа х, о котором известно, что он в 10 раз плотнее углекислого газа CO2?
Подсчитаем для начала молярную массу углекислого газа:
M(CO2) = Mr(CO2) = 12 + 2 · 16 = 44.
Ориентируясь на формулу относительной плотности, произведем расчет молярной массы искомого газа х.
М(х) = D(х/CO2) · M(CO2) = 10 · 44 = 440 г/моль.
Ответ: у данного газа молярная масса 440 г/моль.
Примеры задач
Итак, мы разобрались, как находить молярную массу жидкости, газа или твердого тела и как это понятие связано с количеством вещества, а также с относительной плотностью одного газа по другому.
Чтобы закрепить знания, посмотрите, как эти сведения применяются в решении задач.
Задача 1
Известно, что 300 г неустановленного вещества содержат 12,04 · 1023 молекул. Чему равна молярная масса данного вещества?
Дано:
N(х) = 12,04 · 1023.
m(х) = 300 г.
M(х) = ?
Решение:
Найдем количество вещества моль.
Подставим количество вещества в формулу :
г/моль.
Ответ: молярная масса данного вещества 150 г/моль.
Задача 2
Какой объем займет водород в количестве 0,7 моль?
Дано:
моль.
Решение:
По формуле мы можем найти объем .
Зная, что молярный объем при обычных условиях составляет 22,4 л/моль, вычислим фактический объем водорода:
л.
Ответ: объем водорода составляет 15,68 литров.
Задача 3
В порции оксида серы SO3 содержится 8,356 · 1023 атомов кислорода. Какова масса этой порции?
Дано:
N(O) = 8,356 · 1023.
m(SO3) = ?
Решение:
Для решения задачи нам подходит формула , т. е. . Но для начала нужно найти количество вещества.
Мы знаем, что в одной молекуле SO3 есть 3 атома кислорода, исходя из этого можно вычислить количество молекул в порции оксида:
, следовательно .
Зная количество молекул, рассчитаем количество вещества:
моль.
Теперь можно узнать молярную массу SO3:
M(SO3) = 32 + 16 · 3 = 80 г/моль.
Рассчитаем фактическую массу через молярную массу:
г.
Ответ: абсолютная масса порции оксида серы 36,8 грамм.
Задача 4
Как рассчитать молярную массу простого вещества, о котором известно, что в порции 100 г содержится 15,05 · 1023 молекул? Назовите это вещество.
Дано:
m(x) = 100 г.
N(x) = 15,05 · 1023.
М(х) = ?
Решение:
В данном случае поможет вычислить молярную массу NA, с помощью которого мы сначала узнаем количество вещества:
моль.
Исходя из этого, рассчитаем молярную массу:
г/моль.
Ответ: согласно таблице Менделеева можно предположить, что это кальций Ca.
Задача 5
Определите, насколько сероводород H2S плотнее водорода H2?
Решение:
Нам требуется вычислить относительную плотность сероводорода по водороду:
.
Для этого вычислим молярные массы H2S и H2:
М(H2S) = 1 · 2 + 32 = 34 г/моль.
М(H2) = 1 · 2 = 2 г/моль.
Подставим значения в формулу:
.
Ответ: сероводород в 17 раз плотнее водорода.
Вопросы для самопроверки
-
Что такое число Авогадро и чему оно равно?
-
В чем измеряется молярная масса?
-
Напишите формулу молярной массы вещества.
-
Какая формула связывает количество вещества и его объем?
-
Как узнать количество вещества, если известно число молекул в порции?
Яна Кононенко
К предыдущей статье
Сложные эфиры
К следующей статье
138. 9K
9K
Окислительно-восстановительные реакции
Получите план обучения, который поможет понять и полюбить химию
На вводном уроке с методистом
-
Выявим пробелы в знаниях и дадим советы по обучению
-
Расскажем, как проходят занятия
-
Подберём курс
Плотность вещества — как определить и чему равна?
Покажем, как применять знание физики в жизни
Начать учиться
Есть такая детская загадка: что тяжелее килограмм ваты или килограмм гвоздей? Кажется, что гвозди тяжелее, а потом понимаешь, что килограмм — он и в Африке килограмм. Но почему же создается такая иллюзия?
Масса
Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.
На самом деле, все сложнее.
До недавнего времени в Международном бюро мер и весов в Париже хранился цилиндр массой один килограмм. Цилиндр был изготовлен из сплава иридия и платины и служил для всего мира эталоном килограмма. Правда, со временем его масса изменилась, и пришлось придумать новый эталон — электромагнитные весы.
Высота этого цилиндра была приблизительно равна 4 см, но чтобы его поднять, нужно было приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.
Второй закон Ньютона
F = ma
F — сила [Н]
m — масса [кг]
a — ускорение [м/с2]
В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.
Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне. 🙃
Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне. 🙃
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Откуда берется масса
Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.
Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.
Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.
Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.
Источник: Википедия
Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.
Объем тела
Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.
Скажем, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.
Формула объема параллелепипеда
V = abc
V — объем [м3]
a — длина [м]
b — ширина [м]
c — высота [м]
А для цилиндра будет справедлива такая формула:
Формула объема цилиндра
V = Sh
V — объем [м3]
S — площадь основания [м2]
h — высота [м]
Плотность вещества
Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объему.
Определяется как отношение массы тела к занимаемому этим телом объему.
Формула плотности вещества
р = m/V
р — плотность вещества [кг/м3]
m — масса вещества [кг]
V — объем вещества [м3]
Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.
Маленькое исключение
Исключение составляет вода. Так, плотность воды меньше плотности льда. Объяснение кроется в молекулярной структуре льда. Когда вода переходит из жидкого состояния в твердое, она изменяет молекулярную структуру так, что расстояние между молекулами увеличивается. Соответственно, плотность льда меньше плотности воды.
Так, плотность воды меньше плотности льда. Объяснение кроется в молекулярной структуре льда. Когда вода переходит из жидкого состояния в твердое, она изменяет молекулярную структуру так, что расстояние между молекулами увеличивается. Соответственно, плотность льда меньше плотности воды.
Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.
|
Твердое вещество |
кг/м3 |
г/см3 |
|
Платина |
21500 |
21,5 |
|
Золото |
19300 |
19,3 |
|
Вольфрам |
19000 |
19,0 |
|
Свинец |
11400 |
11,4 |
|
Серебро |
10500 |
10,5 |
|
Медь |
8900 |
8,9 |
|
Никель |
8800 |
8,8 |
|
Латунь |
8500 |
8,5 |
|
Сталь, железо |
7900 |
7,9 |
|
Олово |
7300 |
7,3 |
|
Цинк |
7100 |
7,1 |
|
Чугун |
7000 |
7,0 |
|
Алмаз |
3500 |
3,5 |
|
Алюминий |
2700 |
2,7 |
|
Мрамор |
2700 |
2,7 |
|
Гранит |
2600 |
2,6 |
|
Стекло |
2600 |
2,6 |
|
Бетон |
2200 |
2,2 |
|
Графит |
2200 |
2,2 |
|
Лёд |
900 |
0,9 |
|
Парафин |
900 |
0,9 |
|
Дуб (сухой) |
700 |
0,7 |
|
Берёза (сухая) |
650 |
0,65 |
|
Пробка |
200 |
0,2 |
|
Платиноиридиевый сплав |
21500 |
21,5 |
|
Жидкость |
кг/м3 |
г/см3 |
|
Ртуть |
13600 |
13,6 |
|
Мёд |
1300 |
1,3 |
|
Глицерин |
1260 |
1,26 |
|
Молоко |
1036 |
1,036 |
|
Морская вода |
1030 |
1,03 |
|
Вода |
1000 |
1 |
|
Подсолнечное масло |
920 |
0,92 |
|
Нефть |
820 |
0,82 |
|
Спирт |
800 |
0,8 |
|
Бензин |
700 |
0,7 |
|
Газ |
кг/м3 |
|
Хлор |
3,22 |
|
Озон |
2,14 |
|
Пропан |
2,02 |
|
Диоксид углерода |
1,98 |
|
Кислород |
1,43 |
|
Воздух |
1,29 |
|
Азот |
1,25 |
|
Гелий |
0,18 |
|
Водород |
0,09 |
Где самая большая плотность?
Самая большая плотность во Вселенной — в черной дыре. Плотность черной дыры составляет около 1014 кг/м3.
Плотность черной дыры составляет около 1014 кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Средняя плотность
В школьном курсе чаще всего говорят о средней плотности тела. Дело в том, что если мы рассмотрим какое-нибудь неоднородное тело, то в одной его части будет, например, большая плотность, а в другой — меньшая.
Если вы когда-то делали ремонт, то знакомы с такой вещью, как цемент. Он состоит из двух веществ: клинкера и гипса. Значит нам нужно отдельно найти плотность гипса, плотность клинкера по формуле, указанной выше, а потом найти среднее арифметическое двух плотностей. Можно сделать так.
А можно просто массу цемента разделить на объем цемента и мы получим ровно то же самое. Просто в данном случае мы берем не массу и объем вещества, а массу и объем тела.
Формула плотности тела
р = m/V
р — плотность тела [кг/м3]
m — масса тела [кг]
V — объем тела [м3]
Решение задач: плотность вещества
А теперь давайте тренироваться!
Задача 1
Цилиндр 1 поочерёдно взвешивают с цилиндром 2 такого же объёма, а затем с цилиндром 3, объем которого меньше (как показано на рисунке).
Какой цилиндр имеет максимальную среднюю плотность?
Решение:
Плотность тел прямо пропорциональна массе и обратно пропорциональна объему:
р = m/V
Исходя из проведенных опытов можно сделать следующие выводы:
1) масса первого цилиндра больше массы второго цилиндра при одинаковом объеме. Значит плотность первого цилиндра выше плотности второго.
2) масса первого цилиндра равна массе третьего цилиндра, объем которого меньше. Следовательно, плотность третьего цилиндра больше плотности первого цилиндра.
Таким образом, средние плотности цилиндров:
р2 < р1 < р3
Ответ: 3.
Задача 2
Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (как показано на рисунке). Для объёмов шаров справедливо соотношение V1 = V3 < V2.
Для объёмов шаров справедливо соотношение V1 = V3 < V2.
Какой шар имеет максимальную среднюю плотность?
Решение:
Из рисунка ясно, что масса шаров 1 и 2 равна — следовательно, плотность второго шара меньше, чем первого. Третий шар тяжелее, чем первый при одинаковом объёме, поэтому плотность третьего шара больше плотности первого. Таким образом, максимальную среднюю плотность имеет шар 3.
Ответ: 3
Задача 3
Найти плотность шара объемом 0,5 м3 и массой 1,5 кг.
Решение:
Возьмем формулу плотности и подставим в нее данные нам значения.
р = m/V
р = 1,5/0,5 = 3 кг/м3
Ответ: р = 3 кг/м3
Плавание тел
Почему шарик с гелием взлетает? Или мяч при игре в водное поло не тонет?
Жидкости и газы действуют на погруженные тела с выталкивающей силой. Подробно это явление рассматривают в теме «Сила Архимеда». Если говорить простым языком: если плотность тела, погруженного в жидкость, больше плотности жидкости — тело пойдет ко дну. Если меньше – оно всплывет на поверхность.
Подробно это явление рассматривают в теме «Сила Архимеда». Если говорить простым языком: если плотность тела, погруженного в жидкость, больше плотности жидкости — тело пойдет ко дну. Если меньше – оно всплывет на поверхность.
Задача 1
Стальной шарик в воде падает медленнее, чем в воздухе. Чем это объясняется?
Решение:
Плотность воды значительно выше, чем воздуха, поэтому стальной шарик в воде падает медленнее
Задача 2
В таблице даны плотности некоторых твердых веществ. Если вырезать из этих веществ кубики, то какие кубики смогут плавать в воде? Плотность воды — 1000 кг/м3.
|
Название вещества |
Плотность вещества, кг/м3 |
|
Алюминий |
2700 |
|
Парафин |
900 |
|
Плексиглас |
1200 |
|
Фарфор |
2300 |
|
Сосна |
400 |
Решение:
Плавать будут кубики, плотность которых меньше плотности воды, то есть сделанные из парафина или сосны.
Карина Хачатурян
К предыдущей статье
Сила тяжести
К следующей статье
140.9K
Основные агрегатные состояния вещества
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
-
Выявим пробелы в знаниях и дадим советы по обучению
-
Расскажем, как проходят занятия
-
Подберём курс
10.8: Плотность газа — Химия LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 53772
Рисунок (PageIndex{1}) (Источник: Фонд CK-12; Источник: Фонд CK-12; Лицензия: Лицензия на учебные материалы CK-12)
Почему углекислый газ тонет в воздухе?
Когда мы запускаем реакцию для получения газа, мы ожидаем, что он поднимется в воздух. Многие студенты проводили эксперименты с образованием таких газов, как водород. Газ можно уловить в пробирке, которую держат вверх дном над реакцией. Углекислый газ, с другой стороны, тонет, когда он выделяется. Углекислый газ имеет большую плотность, чем воздух, поэтому он не будет подниматься, как газообразный водород.
Многие студенты проводили эксперименты с образованием таких газов, как водород. Газ можно уловить в пробирке, которую держат вверх дном над реакцией. Углекислый газ, с другой стороны, тонет, когда он выделяется. Углекислый газ имеет большую плотность, чем воздух, поэтому он не будет подниматься, как газообразный водород.
Плотность газа
Как известно, плотность определяется как масса на единицу объема вещества. Поскольку все газы занимают один и тот же объем в пересчете на моль, плотность конкретного газа зависит от его молярной массы. Газ с малой молярной массой будет иметь меньшую плотность, чем газ с большой молярной массой. Плотность газа обычно указывается в (text{г/л}). Плотность газа можно рассчитать по молярной массе и молярному объему.
Рисунок (PageIndex{2}): Воздушные шары, наполненные газообразным гелием, плавают в воздухе, потому что плотность гелия меньше плотности воздуха. (Источник: Фотограф: Уоррен Деннинг, любезно предоставлено компанией Pioneer Balloon Company; Источник: http://commons. wikimedia.org/wiki/File:Congrats_bqt.jpg(открывается в новом окне); Лицензия: Общественное достояние)
wikimedia.org/wiki/File:Congrats_bqt.jpg(открывается в новом окне); Лицензия: Общественное достояние)
Пример ( PageIndex{1}): Плотность газа
Какова плотность газообразного азота на STP ?
Раствор
Шаг 1: Перечислите известные количества и спланируйте проблему.
Известно
- (ce{N_2} = 28,02 : text{г/моль})
- (1 : text{моль} = 22,4 : text{L})
Неизвестно
- плотность = ? г/л
Молярная масса, деленная на молярный объем, дает плотность газа при нормальных условиях.
Шаг 2: Расчет.
[frac{28,02 : text{g}}{1 : text{mol}} times frac{1 : text{mol}}{22,4 : text{L} } = 1,25 : text{г/л}номер]
При установке с коэффициентом преобразования единица (text{моль}) отменяется, оставляя (text{г/л}) в качестве единицы измерения в результате.
Шаг 3: Подумайте о своем результате.
Молярная масса азота немного больше молярного объема, поэтому плотность немного больше (1 : text{г/л}).
В качестве альтернативы можно определить молярную массу газа, если известна плотность газа при нормальных условиях.
Пример (PageIndex{2}): Молярная масса из плотности газа
Какова молярная масса газа, плотность которого равна (0,761 : text{г/л}) при нормальных условиях?
Решение
Шаг 1: Перечислите известные количества и спланируйте задачу .
Известно
- (ce{N_2} = 28,02 : text{г/моль})
- (1 : text{моль} = 22,4 : text{L})
Неизвестно
- молярная масса = ? г/моль
Молярная масса равна плотности, умноженной на молярный объем.
Шаг 2: Расчет.
[frac{0,761 : text{g}}{1 : text{L}} times frac{22,4 : text{L}}{1 : text{mol} } = 17,0 : text{г/моль}номер ]
Шаг 3: Подумайте о своем результате.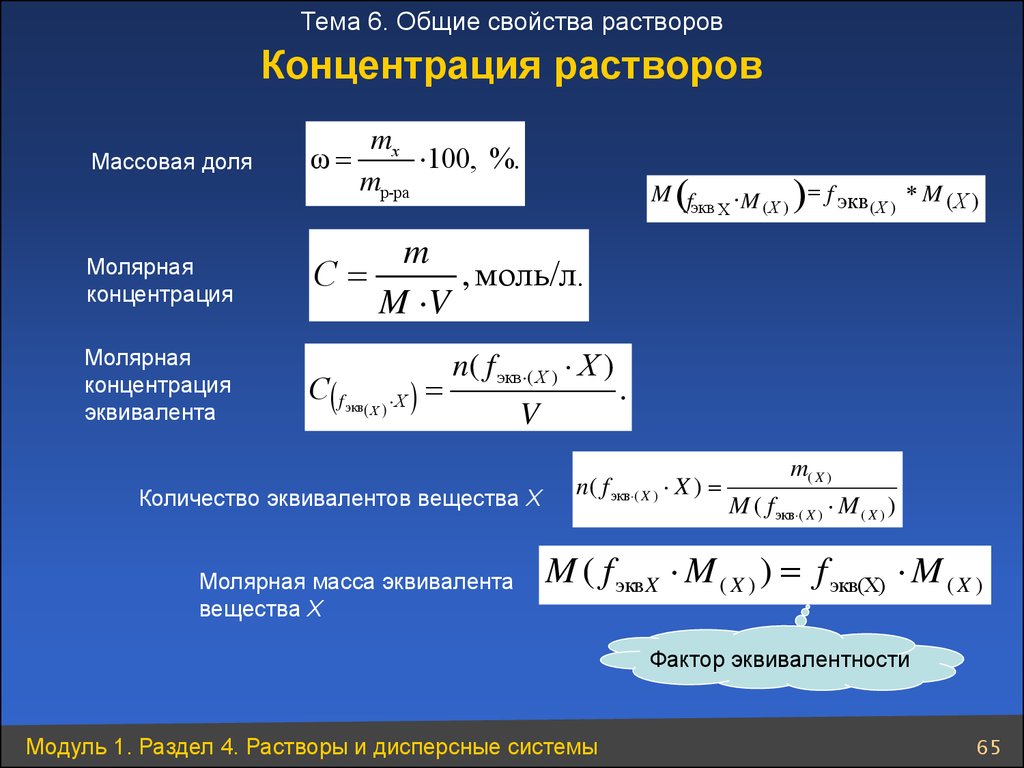
Поскольку плотность газа меньше (1 : text{г/л}), молярная масса меньше 22,4.
Резюме
- Описаны расчеты, показывающие преобразование молярной массы в плотность для газов.
Обзор
- Как рассчитывается плотность?
- Как рассчитывается молярная масса?
- Каков будет объем 3,5 молей газа?
Эта страница под названием 10.8: Плотность газа распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ЛИЦЕНЗИЯ ПОД
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Фонд CK-12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать страницу TOC
- № на стр.

-
- Теги
-
- Плотность газа
- источник@https://flexbooks.ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
Как преобразовать молекулярный вес в плотность
Обновлено 14 декабря 2020 г.
Автор: Элиза Хансен
Вы, вероятно, рано узнали на уроках естествознания, что плотность — это масса, деленная на объем, или «количество» вещества в определенном пространстве. Для твердых тел это довольно простая мера. Если вы наполните банку монетами, она будет иметь гораздо больше «привлекательности», чем если бы вы наполнили ее зефиром. Когда вы наполняете ее монетами, в банку набивается гораздо больше вещества, тогда как зефир очень пухлый и легкий.
Как насчет молекулярной массы? Молекулярный вес и плотность кажутся очень похожими, но есть важное различие. Молекулярная масса – это масса вещества на моль. Дело не в том, сколько места занимает вещество, а в «количестве», «силе» или «весе» определенного количества вещества.
Молекулярная масса – это масса вещества на моль. Дело не в том, сколько места занимает вещество, а в «количестве», «силе» или «весе» определенного количества вещества.
Итак, резюмируем: Плотность это масса, деленная на объем. Математическая формула выглядит следующим образом:
rho = frac{m}{V}
Единицей СИ для массы являются килограммы (хотя вы можете иногда видеть, что она выражается в граммах), а для объема обычно используется m 3 . Итак, плотность в единицах СИ измеряется в кг/м 3 .
Молекулярная масса — это масса на моль, которая записывается:
text{молекулярная масса}=frac{m}{n}
Опять же, единицы измерения имеют значение: масса, m, вероятно, будет в килограммах, а n равно измерение числа молей. Таким образом, единицами измерения молекулярной массы будут килограммы на моль.
Закон об идеальном газе
Итак, как вы выполняете преобразование между этими мерами? Чтобы преобразовать молекулярную массу газа в плотность (или наоборот), используйте Закон идеального газа . Закон идеального газа определяет взаимосвязь между давлением, объемом, температурой и количеством молей газа. Написано:
Закон идеального газа определяет взаимосвязь между давлением, объемом, температурой и количеством молей газа. Написано:
PV=nRT
где P обозначает давление, V обозначает объем, n — количество молей, R — постоянная, зависящая от газа (и обычно дается тебе), а T — температура.
Использование закона идеального газа для преобразования молекулярного веса в плотность
Но в законе идеального газа молекулярный вес не упоминается! Однако, если вы перепишете n, число родинок, в несколько иных терминах, вы можете настроить себя на успех.
Моль равно массе, деленной на молекулярную массу.
n=frac{m}{text{молекулярная масса}}
Зная это, вы можете переписать закон идеального газа следующим образом:
PV=frac{m}{M}RT
где M обозначает молекулярную массу.
Как только вы это сделаете, вычисление плотности станет простым.
Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
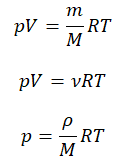
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
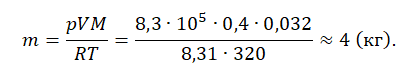
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
Важна только та масса, что осталась в сосуде. Поэтому:
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 о С | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 о С) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | 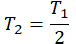 |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы | |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы: |
| Газ потерял половину молекул | 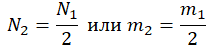 |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | 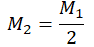 |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К Давление p0 = 10 5 Па |
| Единицы измерения давления | 1 атм = 10 5 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙10 6 Па
1,5 МПа = 1,5∙10 6 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
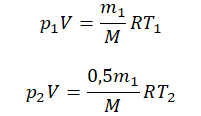
Преобразим уравнения и получим:
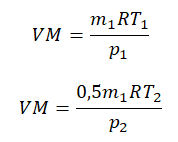
Приравняем правые части и выразим искомую величину:
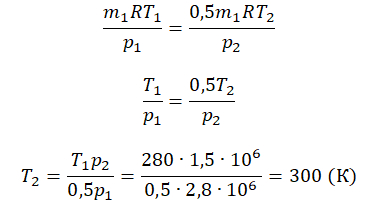
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Как найти плотность зная температуру и давление
Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.
Идеальный газ
Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:
- пренебрежение размерами молекул;
- силы молекулярного взаимодействия не учитываются;
- соударение атомов и молекул абсолютно упруго;
- газ находится в термодинамическом равновесии.
Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.
Газовые законы
Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:
- при постоянном давлении уменьшить температуру;
- при постоянной температуре увеличить давление.
Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.
В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.
Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.
Комбинированный закон
Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:
где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.
Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.
Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.
Пример использования калькулятора
Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.
Заключение
Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?
Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Теперь немного формул.
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
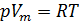 (1),
(1),
 — давление газа;
— давление газа;
 — молярный объём;
— молярный объём;
R — универсальная газовая постоянная,
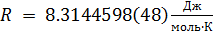 ;
;
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па
t – температура газа, °С.
Известно, что молярный объём  зависит от объёма газа V и количества молей газа
зависит от объёма газа V и количества молей газа 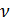 в этом объёме:
в этом объёме:
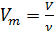 (2)
(2)
Также известно, что
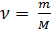 (3),
(3),
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
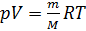 (4).
(4).
Как известно, плотность вещества
 равна:
равна:
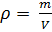 (5).
(5).
Из (4) и (5) выведем уравнение для плотности газа
 :
:
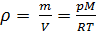 (6)
(6)
и введём обозначение параметра
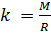 , который зависит от молярной массы газовой смеси:
, который зависит от молярной массы газовой смеси:
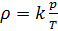 (7).
(7).
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
- 23 % по весу из молекул кислорода

- 76 % по весу из молекул азота
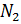
- 1 % по весу из атомов аргона
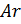
Молярные массы этих веществ воздуха будут соответственно равны:
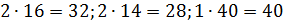 , г/моль.
, г/моль.
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
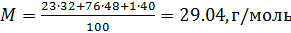
Теперь, зная значение константы
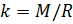 , мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений
, мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений
 и t:
и t:
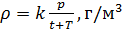
Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 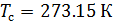 и абсолютное давление
и абсолютное давление 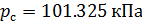 :
:
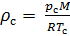 (9).
(9).
Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для 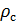 :
:
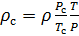 (10).
(10).
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 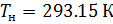 и абсолютное давление
и абсолютное давление
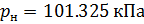 :
:
 (11).
(11).
В уравнениях (10) и (11) используем значения параметров воздуха  , T и P из уравнения (8), полученные в рабочих условиях.
, T и P из уравнения (8), полученные в рабочих условиях.
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
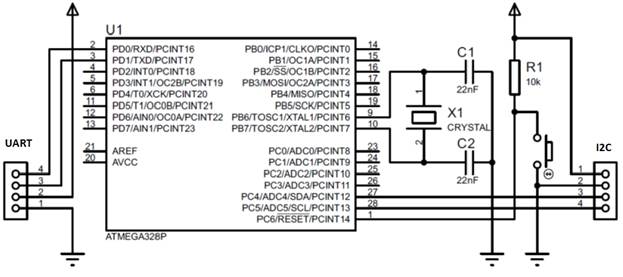
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.
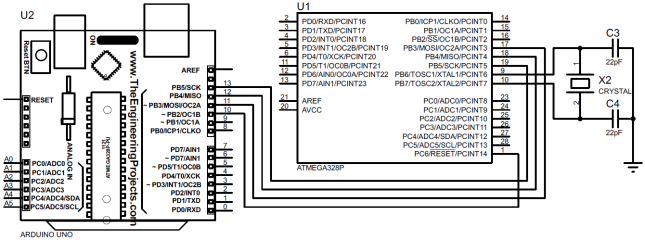
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры
Программа Python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Результаты расчёта представлены листингом и рис. 4, 5, 6.
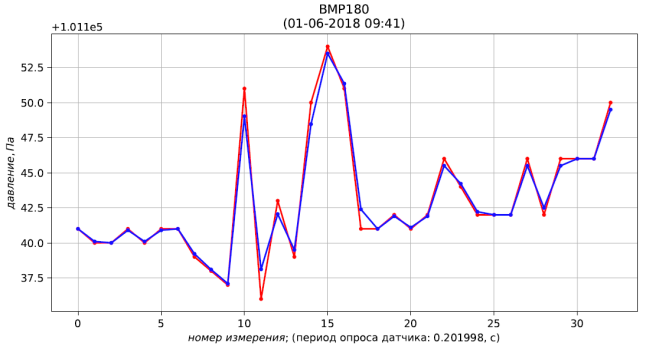
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления
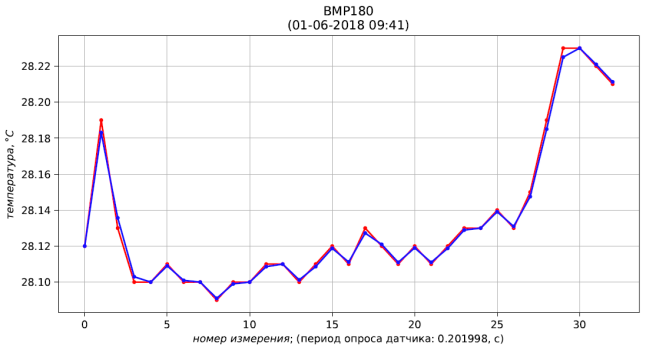
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры
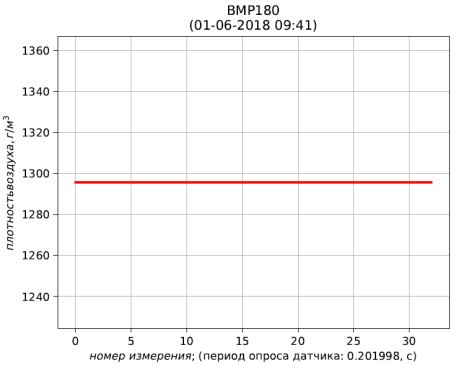
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.
Уравнение состояния идеального газа. Газовые законы.
Уравнение состояния идеального газа
(уравнение Менделеева – Клапейрона).
Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние.
В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.
Мы знаем, что 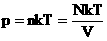 . Следовательно,
. Следовательно, 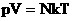 . Учитывая, что
. Учитывая, что 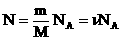 , получим:
, получим: 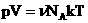 .
.
Произведение постоянных величин есть величина постоянная, следовательно: 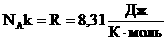 – универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
– универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
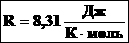
Таким образом, имеем:
– уравнение состояния (уравнение Менделеева – Клапейрона).
Другие формы записи уравнения состояния идеального газа.
1.Уравнение для 1 моля вещества.
Если n=1 моль, то, обозначив объем одного моля Vм, получим: .
Для нормальных условий получим:
2. Запись уравнения через плотность: – плотность зависит от температуры и давления!
3. Уравнение Клапейрона.
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда:
Эта запись означает, что для данной массы данного газа справедливо равенство:
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: .
Газовые законы.
1. Закон Авогадро.
В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов).
Доказательство:
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
2. Закон Дальтона.
Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.
Доказательство:
3. Закон Паскаля.
Давление, производимое на жидкость или газ, передается во все стороны без изменения.
[spoiler title=”источники:”]
http://planshet-info.ru/kompjutery/kak-najti-plotnost-znaja-temperaturu-i-davlenie
http://www.eduspb.com/node/1742
[/spoiler]
