| Плотность воздуха | |
|---|---|
 |
|
| Размерность | L−3 M |
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
| скалярная величина |
Пло́тность во́здуха — масса газа атмосферы Земли на единицу объема или удельная масса воздуха при естественных условиях. Плотность воздуха является функцией от давления, температуры и влажности. Обычно стандартной величиной плотности воздуха на уровне моря в соответствии с Международной стандартной атмосферой принимается значение 1,2255 кг/м³, которая соответствует плотности сухого воздуха при 15 °С и давлении 101 330 Па.
Взаимосвязи в пределах модели идеального газа[править | править код]
| Влияние температуры на свойства воздуха на уровне моря | |||
|---|---|---|---|
| Температура | Скорость звука |
Плотность воздуха из уравнения Клапейрона |
Акустическое сопротивление |
 , °С , °С |
c , м/с | ρ , кг/м³ | Z , Н·с/м³ |
| +35 | 351,96 | 1,1455 | 403,2 |
| +30 | 349,08 | 1,1644 | 406,5 |
| +25 | 346,18 | 1,1839 | 409,4 |
| +20 | 343,26 | 1,2041 | 413,3 |
| +15 | 340,31 | 1,2250 | 416,9 |
| +10 | 337,33 | 1,2466 | 420,5 |
| +5 | 334,33 | 1,2690 | 424,3 |
| 0 | 331,30 | 1,2920 | 428,0 |
| −5 | 328,24 | 1,3163 | 432,1 |
| −10 | 325,16 | 1,3413 | 436,1 |
| −15 | 322,04 | 1,3673 | 440,3 |
| −20 | 318,89 | 1,3943 | 444,6 |
| −25 | 315,72 | 1,4224 | 449,1 |
Температура, давление и плотность[править | править код]
Плотность сухого воздуха может быть вычислена с использованием уравнения Менделеева — Клапейрона для идеального газа при заданных температуре и давлении:
Здесь 




- при стандартной атмосфере Международного союза теоретической и прикладной химии (температуре 0 °С, давлении 100 кПа, нулевой влажности) плотность воздуха 1,2754 кг/м³;
- при 20 °C, 101,325 кПа и сухом воздухе плотность атмосферы составляет 1,2041 кг/м³.
В приведенной таблице даны различные параметры воздуха, вычисленные на основании соответствующих элементарных формул, в зависимости от температуры (давление взято равным 101,325 кПа).
Влияние влажности воздуха[править | править код]
Под влажностью понимается наличие в воздухе газообразного водяного пара, парциальное давление которого не превосходит давления насыщенного пара для данных атмосферных условий. Добавление водяного пара в воздух приводит к уменьшению его плотности, что объясняется более низкой молярной массой воды (18 г/моль) по сравнению с молярной массой сухого воздуха (~29 г/моль)[1]. Влажный воздух может рассматриваться как смесь идеальных газов, комбинация плотностей каждого из которых позволяет получить требуемое значение для их смеси[2]. Подобная интерпретация позволяет определять значение плотности с относительной погрешностью менее 0,2 % в диапазоне температур от −10 до +50 °C и может быть выражена следующим образом[2]:
- где
— плотность влажного воздуха (кг/м³);
— парциальное давление сухого воздуха (Па);
— газовая постоянная для сухого воздуха (287,058 Дж/кг·К);
— температура (K);
— давление водяного пара (Па) и
— постоянная для пара (461,495 Дж/кг·К).
Давление водяного пара может быть определено исходя из относительной влажности:
- где
— давление водяного пара;
— относительная влажность;
— парциальное давление насыщенного пара.
Парциальное давление насыщенного пара может быть представлено в виде следующего упрощенного выражения[2]:
которое дает результат в миллибарах.
Давление сухого воздуха 
- где
обозначает абсолютное давление рассматриваемой системы.
Влияние высоты над уровнем моря в тропосфере[править | править код]
Зависимость давления, температуры и плотности воздуха от высоты по отношению к значениям этих величин на уровне моря (


Для вычисления плотности воздуха на определённой высоте в тропосфере (формула справедлива для высот менее 20 км) могут использоваться следующие параметры (в параметрах атмосферы указано значение для стандартной атмосферы):
Для тропосферы (то есть области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте 
Давление на высоте 
Тогда плотность может быть вычислена подстановкой соответствующих данной высоте 


Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа.
Графики нормализованы — показывают общий вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (термометра и барометра) на данный момент на уровне моря.
См. также[править | править код]
Видеоурок: плотность воздуха
- Стандартная атмосфера
- Модели атмосферы (англ.) (рус.
Примечания[править | править код]
- ↑ Для любого газа в соответствии с законом Авогадро при постоянных температуре, давлении и объёме количество молекул остается неизменным, поэтому добавление молекул воды приводит к снижению плотности воздуха.
- ↑ 1 2 3 Equations — Air Density and Density Altitude Архивная копия от 30 ноября 2010 на Wayback Machine (англ.)
Ссылки[править | править код]
- Conversions of density units ρ Архивная копия от 29 ноября 2010 на Wayback Machine (англ.)
- Air density and density altitude calculations Архивная копия от 30 ноября 2010 на Wayback Machine (англ.)
- Reference manual for air density, density altitude, and grains of water Архивная копия от 23 октября 2014 на Wayback Machine (англ.)
- Air density, density altitude, grains of water calculator by region Архивная копия от 3 марта 2022 на Wayback Machine (англ.)
Движение молекул связано с тепловым состоянием тела. Чем более нагрето тело, тем оживленнее беспорядочное движение молекул. Термин «беспорядочное движение молекул» с полным правом может быть заменен термином «тепловое движение молекул».
Вследствие хаотического движения молекулы, разлетаясь во все стороны, должны бы равномерно распределиться в предоставленном им объеме. Почему же воздух, окружающий Землю, не разлетается по всему мировому пространству? Его удерживает притяжение к Земле. Это притяжение нарушает равномерное распределение молекул в мировом пространстве. С другой стороны, если бы не тепловое движение, то все молекулы упали бы на Землю. В результате борьбы этих двух тенденций — падения вниз и стремления равномерно рассеяться в окружающем пространстве — в атмосфере наблюдается некоторое распределение плотности воздуха по высоте. Молекулы сосредоточены гуще в нижних слоях и реже в верхних. Математическое выражение этой закономерности дается формулой, называемой барометрической:
Здесь ρ – плотность воздуха на высоте h, ρ0 – плотность воздуха при h = 0, m – масса молекулы, T — абсолютная температура воздуха, k — так называемая постоянная Больцмана (k = 1,38 * 10-23 Дж/К). Описываемая барометрической формулой функция ρ есть показательная функция; ее основание выражается числом e = 2,71828… Такие показательные функции называют экспоненциальными. Заметим, что приведенная формула является упрощенной. Во-первых, как известно, воздух состоит из нескольких различных газов – азота, кислорода, водорода и др. Молекулы разных газов имеют разные массы. Чем легче газ, тем медленнее уменьшается с высотой его плотность. Во-вторых, в барометрической формуле предполагается, что температура воздуха одинакова на всех рассматриваемых высотах. Известно, однако, что температура воздуха с высотой понижается. В-третьих, надо учитывать также, что ускорение g зависит от высоты. Наконец, приведенная выше формула не учитывает ветра и конвекционных потоков воздуха, которые могут весьма заметно влиять на плотность воздуха.
Тем не менее барометрической формулой можно пользоваться как приближенной формулой, которая правильно передает основную закономерность в уменьшении плотности воздуха с высотой. Эту формулу применяют по отношению к определенному типу газа и при этом рассматривают относительно небольшие высоты.
Подчеркнем, что описываемое барометрической формулой распределение плотности по высоте оказывается неизменным, сколько бы времени мы ни наблюдали (ветер не принимается во внимание). Молекулы воздуха находятся все время в движении, сталкиваются, перемещаются из одних точек пространства в другие; тем не менее в среднем их число в единице объема на данной высоте остается неизменным.
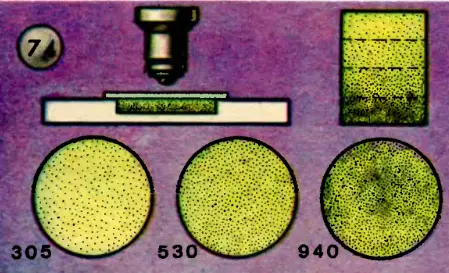
Рассмотренный закон распределения оказывается применимым не только к нижним слоям атмосферы Земли, но и к растворам, содержащим множество мелких частичек во взвешенном состоянии. Французский физик Перрен, изучавший броуновское движение, производил опыты с эмульсией спиртового раствора смолы гуммигута или мастики в воде. Предварительно жидкость подвергалась многократному центрифугированию для получения эмульсии, состоящей из очень мелких зернышек одинакового размера. Капля эмульсии помещалась в стеклянную кюветку и рассматривалась в микроскоп через маленькую диафрагму. Тогда в поле зрения можно было пересчитать видимые частицы. Изменяя высоту подвижной части микроскопа, можно получать четкие изображения частиц в разных слоях эмульсии, расположенных на разных глубинах кюветки (рис. 74). В каждом из этих слоев и подсчитывались зерна эмульсии. Чтобы исключить случайность, брали для каждого слоя среднее значение из нескольких тысяч измерений. Применяя к этому распределению барометрическую формулу, Перрен смог определить число молекул в 1 моль любого газа.
Полученное значение очень мало отличается от значения, определенного при помощи других способов. В настоящее время число молекул в 1 моль любого газа считают равным 6,02 * 1023. Это число называют числом Авогадро. Известно, что 1 моль газа при нормальных условиях занимает объем 22,4 л. Отсюда легко определить и число молекул в 1 см3 газа при нормальных условиях:
Нет, конечно, необходимости объяснять, что найденное число передает только порядок количества молекул, т. е. оно приведено так же округленно, как, скажем, число, характеризующее плотность населения какого-нибудь города.
| Плотность воздуха | |
 |
|
| Размерность | L−3 M |
|---|---|
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
| скалярная величина |
Пло́тность во́здуха — масса газа атмосферы Земли на единицу объема или удельная масса воздуха при естественных условиях. Плотность воздуха является функцией от давления, температуры и влажности. Обычно, стандартной величиной плотности воздуха на уровне моря в соответствии с Международной стандартной атмосферой принимается значение 1,2250 кг/м³, которая соответствует плотности сухого воздуха при 15 °С и давлении 101330 Па.
Содержание
- 1 Взаимосвязи в пределах модели идеального газа
- 1.1 Температура, давление и плотность
- 1.2 Влияние влажности воздуха
- 1.3 Влияние высоты над уровнем моря в тропосфере
- 2 См. также
- 3 Примечания
- 4 Ссылки
Взаимосвязи в пределах модели идеального газа
| Влияние температуры на свойства воздуха на уровне моря | |||
|---|---|---|---|
| Температура | Скорость звука | Плотность воздуха из уравнения Клапейрона |
Акустическое сопротивление |
 , °С , °С |
c , м/с | ρ , кг/м³ | Z , Н·с/м³ |
| +35 | 351,96 | 1,1455 | 403,2 |
| +30 | 349,08 | 1,1644 | 406,5 |
| +25 | 346,18 | 1,1839 | 409,4 |
| +20 | 343,26 | 1,2041 | 413,3 |
| +15 | 340,31 | 1,2250 | 416,9 |
| +10 | 337,33 | 1,2466 | 420,5 |
| +5 | 334,33 | 1,2690 | 424,3 |
| 0 | 331,30 | 1,2920 | 428,0 |
| −5 | 328,24 | 1,3163 | 432,1 |
| −10 | 325,16 | 1,3413 | 436,1 |
| −15 | 322,04 | 1,3673 | 440,3 |
| −20 | 318,89 | 1,3943 | 444,6 |
| −25 | 315,72 | 1,4224 | 449,1 |
Температура, давление и плотность
Плотность сухого воздуха может быть вычислена с использованием уравнения Менделеева-Клапейрона для идеального газа при заданных температуре и давлении:
Здесь 




- при стандартной атмосфере Международного союза теоретической и прикладной химии (температуре 0 °С, давлении 100 кПа, нулевой влажности) плотность воздуха 1,2754 кг/м³;
- при 20 °C, 101,325 кПа и сухом воздухе плотность атмосферы составляет 1,2041 кг/м³.
В приведенной таблице даны различные параметры воздуха, вычисленные на основании соответствующих элементарных формул, в зависимости от температуры (давление взято равным 101,325 кПа).
Влияние влажности воздуха
Под влажностью понимается наличие в воздухе газообразного водяного пара, парциальное давление которого не превосходит давления насыщенного пара для данных атмосферных условий. Добавление водяного пара в воздух приводит к уменьшению его плотности, что объясняется более низкой молярной массой воды (18 г/моль) по сравнению с молярной массой сухого воздуха (~29 г/моль).[1] Влажный воздух может рассматриваться как смесь идеальных газов, комбинация плотностей каждого из которых позволяет получить требуемое значение для их смеси.[2] Подобная интерпретация позволяет определение значения плотности с уровнем ошибки менее 0,2 % в диапазоне температур от −10 до +50 °C и может быть выражена следующим образом:[2]
где 





Давление водяного пара может быть определено исходя из относительной влажности:
где 


которое дает результат в миллибарах.
Давление сухого воздуха 
где 
Влияние высоты над уровнем моря в тропосфере
Зависимость давления, температуры и плотности воздуха от высоты по отношению к значениям этих величин на уровне моря (


Для вычисления плотности воздуха на определенной высоте в тропосфере (формула справедлива для высот менее 20 км) могут использоваться следующие параметры (в параметрах атмосферы указано значение для стандартной атмосферы):
Для тропосферы (то есть области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте 
Давление на высоте 
Тогда плотность может быть вычислена подстановкой соответствующих данной высоте 


Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа.
Графики нормализованы — показывают общий вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (термометра и барометра) на данный момент на уровне моря.
См. также
Видеоурок: плотность воздуха
- Стандартная атмосфера
- Модели атмосферы (англ.)русск.
Примечания
- ↑ Для любого газа в соответствии с законом Авогадро при постоянных температуре, давлении и объеме количество молекул остается неизменным, поэтому добавление молекул воды приводит к снижению плотности воздуха.
- ↑ 1 2 3 Equations — Air Density and Density Altitude (англ.)
Ссылки
- Conversions of density units ρ (англ.)
- Air density and density altitude calculations (англ.)
- Reference manual for air density, density altitude, and grains of water (англ.)
- Air density, density altitude, grains of water calculator by region (англ.)
Барометрические формулы
Основное
уравнение статики является одним из
важнейших уравнений метеорологии, на
основе которого устанавливаются
закономерности распределения давления,
плотности и массы воздуха по высоте. В
своем дифференциальном виде основное
уравнение статики позволяет выполнить
расчет изменения давления лишь для
малых приращении высоты dz.
На
практике всегда необходимо иметь данные
о распределении давления в слоях
атмосферы конечной толщины или определить
толщину таких слоев по измеренным
значениям давления. Для этой цели
основное уравнение статики записывают
в конечном (интегральном) виде, т.е.
находят его интегралы. Интегралы
основного уравнения статики атмосферы,
полученные при разных предположениях
относительно изменения температуры и
плотности воздуха с высотой, называются
барометрическими
формулами.
На основе этих формул решаются такие
важные практические задачи, как расчет
распределения давления и плотности по
высоте, определение высот различных
летательных аппаратов по измеренному
давлению, приведение давления к уровню
моря и др.
Для
получения интегральной формы основного
уравнения статики проинтегрируем левую
и правую части уравнения
– dp
= ρgdz
в
пределах от уровня моря z
= 0 (или земной
поверхности), где давление p0
,
до произвольной
высоты z,
где давление p.
Получим интегральную форму для сухого
воздух:

Здесь
ρ = ρ(z)
– функция высоты.
Вторую
интегральную форму основному уравнению
статики можно придать, если воспользоваться
уравнением состояния влажного воздуха
p
= RcρTv
,
где
Rc
–
удельная
газовая постоянная; Tv
–
виртуальная температура. Найдем из
этого уравнения значение ρ
и перепишем
уравнение статики в следующем виде:
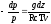
Интегрируя
в пределах от 0
до z
и от p0
до p,
получаем интегральную форму для влажного
воздуха

Полученные
интегральные формы для сухого и влажного
воздуха широко используются для получения
различных барометрических формул.
Причем давление p0
может
обозначать как давление на уровне моря,
так и на поверхности Земли. Различие
будет состоять лишь в начале отсчета
высоты z.
В общем случае температура, а вместе с
ней и плотность воздух являются достаточно
сложными функциями высоты, установить
аналитический вид которых далеко не
всегда представляется возможным.
Поэтому, прежде чем перейти к общему
случаю, рассмотрим несколько частных
с заданным распределением температуры
по высоте. При этом обычно считают состав
воздуха неизменным (μ
= const)
и пренебрегают изменением g
с высотой, принимая g
(z)
= const,
что, конечно, вносит некоторую неточность
и допустимо до высот около 80 – 100 км.
Обычно
в метеорологии рассматривают следующие
частные случаи:
однородная
атмосфера
– плотность атмосферы ρ
с высотой
не изменяется;
изотермическая
атмосфера
– температура в атмосфере с высотой
остается неизменной (T
= const);
политропная
атмосфера –
температура воздуха в атмосфере убывает
с высотой по линейному закону


Выделение
таких случаев имеет смысл, потому, что
хотя в целом для атмосферы они и
неприменимы, но атмосфера до изучаемой
высоты может быть разбит на ряд отдельных
слоев, каждый из которых более или менее
близко соответствует одному из указанных
условий. Рассмотрим изменение давления
при этих условиях.
Однородная
атмосфера.
Предположим, что плотность воздуха в
пределах всей атмосферы не изменяется
с высотой (однородная
атмосфера),
т.е. ρ = ρ0
= const.
Здесь ρ0
– плотность воздуха при z=0.
Пренебрежем зависимостью ускорения
свободного падения от высоты. Тогда на
основании
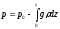
формулу однородной атмосферы
Согласно
этой формуле, давление в однородной
атмосфере убывает с высотой по линейному
закону. В
приложении к атмосфере эта формула дает
далекое от реальных условий распределение
давления. Однако для гидросферы, плотность
которой изменяется в узких пределах
(плотность воды близка к 1г/см3)
она дает удовлетворительные результаты.
Поэтому её можно назвать барометрической
формулой гидросферы
(высота в этом случае отсчитывается от
дна моря или океана).
Высота
однородной атмосферы (высота
на которой давление обращается в нуль).
Высота однородной атмосферы обозначается
через H.
Согласно
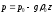

Так
как

то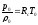
– температура воздуха при z
= 0) получаем
Отсюда
следует, что высота однородной атмосферы
конечна и зависит только от температуры
воздуха на поверхности Земли. При t0
= 0ºC она
составляет
Так
как плотность в однородной атмосфере
постоянна, а давление быстро убывает с
высотой, температура её, равная по
уравнению состояния

высоте от левой и правой части, получаем
Привлекая

находим следующее выражение для
вертикального градиента температуры
γА
в однородной
атмосфере:

γА
=
3,42ºС/100 м.
Таким
образом, в однородной атмосфере
температура убывает с высотой по
линейному закону:

при
этом скорость понижения (градиент)
значительно больше среднего значения
γ в пределах тропосферы.
Изменение
плотности воздуха с высотой в общем
случае.
Возьмем логарифмическую производную
по высоте от левой и правой части
уравнения состояния p
= RcρT
:

Заменив
dp/dz
по

по уравнению
p
= RcρT
найдем


Эта
формула справедлива для любого
распределения температуры воздуха по
высоте. На основе её можно сделать выводы
относительно изменения плотности
воздуха о высоте. Возможны три различных
случая.
-
Если
γ >
γА
=
3,42ºС/100м, то dρ
/dz
> 0, т.е.
плотность воздуха возрастает с высотой.
Вертикальные градиенты температуры
γ,
больше 3,42ºС/100м, в реальных условиях
атмосферы могут наблюдаться лишь в
дневные часы летом в приземном слое
атмосферы. При таких условиях плотность
в этом слое растет с высотой. -
Если
γ =
γА,
то dρ
/dz
= 0 т.е.
плотность воздуха не изменяется с
высотой: ρ
= ρ0 =
const.
Это случай однородной атмосферы. -
Если
γ <
γА
, то dρ
/dz
< 0, т.е.
плотность воздуха убывает с высотой.
Этот случай является абсолютно
преобладающим в условиях атмосферы.
Прежде всего выше приземного слоя γ
<
γА
при любых состояниях атмосферы. В
приземном слое случаи когда γ
<
γА,
наблюдаются также значительно чаще,
чем случаи γ
>
γА.
Таким образом, наиболее характерным
состоянием атмосферы является такое,
когда плотность воздуха убывает с
высотой.
Изотермическая
атмосфера. Такая
атмосфера наблюдается при условии когда
температура с высотой не изменяется,
т.е. Т = Т0
=const,
здесь Т0
– температура на уровне моря или
поверхности Земли. Изотермическая
атмосфера по своим свойствам противоположна
однородной атмосфере. Считая атмосферу
сухой и пренебрегая зависимостью
ускорения свободного падения от высоты,
на основании

формулу изотермической атмосферы:


т.е.
давление в изотермической атмосфере
убывает с высотой по экспоненциальному
закону.
Отсюда
видно, что изотермическая атмосфера не
имела бы верхней границы и простиралась
бы до бесконечности, а на высоте z
= H
давление в ней уменьшилось бы только в
exp
раз, в то
время как в однородной атмосфере на
этой высоте оно было бы равно нулю.
Высоту
z,
на которой в изотермической атмосфере
давление равно pz,
можно выразить формулой

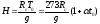
получим
ПринимаяH0
= 8000 м,
последнее уравнение перепишем в виде
Главные
выводы изотермической атмосферы
1.Если
высота растет в прогрессии арифметической,
то давление убывает в прогрессии
геометрической.
2.При
более высокой Т давление в изотермич.
атм. убывает с высотой медленнее, чем
при более низкой Т
3.Чем
выше расположен слой атмосферы
определенной толщины, тем меньше давление
в этом слое.
Можно
отметить, что в изотермической атмосфере
давление уменьшилось бы (при t=0º)
в 10 раз на высоте 18,4 км и в 100 раз на высоте
около 37 км. В действительности эта высота
несколько меньше, так как средняя
температура такого слоя меньше нуля.
Политропная
атмосфера.
Политропной называют такую атмосферу,
которая характеризуется линейным
изменением температуры воздуха с высотой
(или постоянным значением вертикального
градиента температуры):

Считая
атмосферу сухой (Tv=T)
и подставляя Т в формулу


Выполнив
интегрирование (в предположении g
= const),
приходим к барометрической
формуле политропной атмосферы:

Графически
зависимость p
от z
изображена на рисунке. Кривые соответствуют
одним и тем же значениям p
и T0,
но разным значениям вертикального
градиента температуры: γ1
> γ2.
Давление при большем значении вертикального
градиента температуры (γ1)
убывает с высотой быстрее, чем при
меньшем (γ2).
Рисунок.
Распределение давления по высоте в
политропной атмосфере [Матвеев].
Для
сравнения приведены кривые изменения
давления в однородной и изотермической
атмосферах (штриховые кривые). Высота
политропной атмосферы конечна. Т.е.
согласно

давление обращается в нуль на такой
высотеz
= Hγ,
на которой
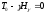
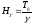
Формула
для плотности воздуха в политропной
атмосфере имеет вид

Полная
барометрическая формула (формула
Лапласа). Общий
случай: температура распределяется
произвольно по высоте, реальный воздух
влажный, ускорение свободного падения
– функция широты и высоты. С полным
выводом уравнения можно ознакомиться
на с.87 [Матвеев].
Полная
барометрическая формула (Формула
Лапласа)
окончательно имеет вид:

Величина
В = 2,30×
м называетсябарометрической
постоянной,
а средние значения


(температуры и удельной влажности
соответственно).
В
таком полном виде барометрическая
формула на практике используется лишь
при барометрическом нивелировании. При
решении подавляющего большинства
метеорологических задач такой высокой
точности не требуется. Поэтому, если
считать воздух сухим и пренебречь
зависимостью ускорения свободного
падения от широты и высоты, получим
барометрическую
формулу реальной атмосферы:
Возвращаясь
к натуральным логарифмам и абсолютной
температуре эту формулу можно записать
в виде:

где
(1+
–средняя
барометрическая температура слоя
воздуха, заключенного между уровнями


Средняя барометрическая температура
– это такая постоянная в пределах слоя
температура, которая обеспечивает
значения давления на границах его,
наблюдаемые при реальном распределении
температуры по высоте. Практически
арифметической температурой, т.е.
полагают

где


температуры воздуха на нижней и верхней
границах слоя. Если уровень



то формула


Решение
задач с помощью барометрических формул:
-
Вычисление
распределения давления по высоте.
Задача состоит в определении величины
давления
на некотором уровне
по заданному значению
на
уровнеи среднему значению
в слое
–
.
Обычно при этих расчетах применяются
формулы для изотермической атмосферы. -
Барометрическое
нивелирование.
Оно применяется, когда ставится задача
определить разность высот двух точек
–
по значениям давления в них
,
и виртуальной температуры
и
.
При необходимости получения большой
точности расчету следует вести по
формуле Лапласа. Обычно на практике
проводят вычисления по формуле для
изотермической атмосферы, используя
её последовательно для небольших слоев
(1-2км). Также используются гипсометрические
таблицы и номограммы. -
Приведение
давления к уровню моря.
Известны
,
,
,
и
.
Требуется найти.
Эта задача имеет широкое применение в
метеорологии, когда давление,
наблюденное на некоторой станции на
высоте,
приводится к давлениюна
уровне моря. Практически это осуществляется
при помощи готовых таблиц. -
Определение
средней температуры слоя
.
В этом случае известны
и
на
высотахи
и требуется найти
,
что осуществляется с помощью приведенных
выше формул.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
01.05.20157.16 Mб23Менеджмент учебник.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
Random converter
- Калькуляторы
- Термодинамика — теплота
Калькулятор зависимости температуры, давления и плотности воздуха от высоты в стандартной атмосфере
Калькулятор Международной стандартной атмосферы (МСА) и Стандартной атмосферы США 1976 г.
Этот калькулятор определяет атмосферное давление, плотность воздуха, температуру и скорость звука для заданных высоты и отклонения температуры от стандартного значения с использованием методики, принятой в Международной стандартной атмосфере (International Standard Atmosphere, МСА, англ. ISA) и Стандартной атмосфере США 1976 г. (1976 U.S. Standard Atmosphere, USSA). В диапазоне высот 0–86 км, на который рассчитан этот калькулятор, обе модели дают одинаковые результаты. Отклонение температуры, которое вводится в калькулятор — это отклонение от стандартной температуры атмосферы 15 °C. Например, если реальная температура воздуха над поверхностью земли равна 28 °C, то нужно ввести отклонение температуры 10 °C. Калькулятор позволяет выбрать различные величины радиуса Земли, используемые в расчетах.
Пример: рассчитать давление атмосферы, плотность воздуха, температуру и скорость звука на обычной крейсерской высоте полета 35 000 футов (10 600 м) при отклонении температуры от нормальной 10 °С.
Входные данные
Высота (геометрическая)
h
Отклонение температуры
to
Радиус Земли, R⊕
Поделиться ссылкой на этот калькулятор, включая входные параметры
Выходные данные
Давление
p Па
p psi ат
Плотность воздуха
ρ кг/м³ (г/л)
Температура
t К °C
Скорость звука
c м/с км/ч
Ускорение силы тяжести
ge м/с²
Геопотенциальная высота
h км
Для расчета введите значения в соответствующие поля, выберите метрические или традиционные единицы измерения и нажмите кнопку Рассчитать.
Международная стандартная атмосфера (ISA)
Стандартная атмосфера США
Определения, константны и формулы, используемые в расчетах
Высота и эшелон полета
Селектор радиуса Земли R⊕
Удельная газовая постоянная для сухого воздуха Rsp
Стаднартное ускорение свободного падения
Геопотенциальная высота
Скорость звука
Зависимость силы тяжести от высоты
Зависимость температуры от высоты
Зависимость давления от высоты
Плотность воздуха
Земная атмосфера находится в непрерывном движении. Поэтому были разработаны гипотетические модели, которые приблизительно показывают поведение атмосферы, если воздух не содержит пыли и влаги, а также нет ветра и возмущений. Эти модели известны под названием «стандартная атмосфера». Они необходимы для расчетов и проектирования воздушных судов, для изучения их характеристик, для сравнения результатов испытаний воздушных судов и для решения многих других задач в авиации и других отраслях науки и техники.
Концепция стандартной атмосферы была разработана для стандартизации и унификации калибровки высотомеров, для изучения характеристик авиационных двигателей, при разработке которых очень важно точно знать величины плотности и давления воздуха, температуры атмосферы на среднем уровне моря, а также их распределение по высоте. Международная стандартная атмосфера (ISA) является одной из таких моделей. Международная организация по стандартизации (ISO) опубликовала эту модель в качестве международного стандарта ISO 2533:1975. Организации по стандартизации разных стран публикуют собственные атмосферные модели, основанные на стандарте ISA. Широко известным стандартом атмосферы является Стандартная атмосфера США 1976 г., в которой используется модель атмосферы, основанная на стандарте ISA. Различие между этими двумя моделями имеются на высотах более 86 км, которые в данном калькуляторе не рассматриваются. В России используется ГОСТ 4401-81 «Атмосфера стандартная. Параметры», также основанный на стандарте ISA.
Земная атмосфера находится в постоянном движении
Международная стандартная атмосфера (ISA)
Международная стандартная атмосфера «предназначена для использования в расчетах летательных аппаратов, для приведения результатов испытаний летательных аппаратов и их компонентов к одинаковым условиям и для унификации разработки и калибровки приборов». Использование этой атмосферной модели также рекомендуется при обработке данных геофизических и метеорологических наблюдений. Модель атмосферы используется в качестве стандарта, с которым можно сравнить реальную атмосферу. Значения температуры, давления и плотности воздуха уменьшаются с ростом высоты. На уровне моря они имеют следующие значения:
- Давление 101,325 кПа.
- Температура +15 °C.
- Плотность 1,225 кг/м³.
Стандартная атмосфера США
«Стандартная атмосфера США, 1976 г. является идеализированным представлением земной атмосферы в статическом состоянии от поверхности до высоты 1000 км». Модель основана на существующих международных стандартах и, в основном, использует методологию, принятую в Международной стандартной атмосфере (ISA). Уравнения модели были приняты Комитетом по расширению стандартной атмосферы США (United States Committee on Extension to the Standard Atmosphere, COESA), который представлял 29 научных, правительственных, военных и инженерных организаций США. В модели атмосфера разделяется на семь слоев до максимальной высоты 86 км. Главным отличием Стандартной атмосферы США от Международной стандартной атмосферы является предложенное распределение температур на больших высотах, которое данный в данном калькуляторе не рассматривается.
Определения, константны и формулы, используемые в расчетах
Высота и эшелон полета
Современный высотомер с барабанным цифровым счетчиком, установленный на самолете Fokker 100. В двух окнах показано значение давления в гектопаскалях и дюймах ртутного столба, которое вводится путем вращения ручки кремальеры (слева внизу)
Несмотря на то, что эшелон и высота полета измеряются в одних и тех же единицах длины (метрах, километрах, футах и милях), они являются разными физическими величинами:
- Высота полета — вертикальное расстояние объекта от среднего уровня моря, измеренное с помощью прибора для измерения длины или расстояния, например, лазерного дальномера или радиовысотомера.
- Эшелон — условная вертикальная стандартная высота, рассчитанная по давлению, обозначаемая в сотнях футов с добавлением букв FL (англ. Flight Level — эшелон). Например, эшелон 34 000 футов обозначается как FL340. Эшелон измеряется с помощью прибора для измерения давления (например, барометрического высотомера, который фактически является точным барометром, откалиброванным в единицах высоты). При подготовке к взлету высотомер устанавливается на нулевую высоту. Когда самолет поднялся достаточно высоко (на высоту перехода), летчик устанавливает на высотомере стандартное давление 29,921 дюйма ртутного столба или 1013,25 гектопаскалей. При подготовке к посадке самолета, летчик должен на небольшой высоте (в разных юрисдикциях она может быть от 3000 до 18000 футов над уровнем моря установить на высотомере давление в аэропорту назначения, чтобы высотомер показывал при приземлении реальную высоту над уровнем моря.
Механический высотомер с ручкой установки барометрического давления измеряет атмосферное давление на приемнике статического давления, расположенном на обшивке борта самолета. Он откалиброван так, чтобы показывать давление в единицах высоты над уровнем моря. Перед взлетом и посадкой летчик получает от диспетчера величины давления на взлетно-посадочной полосе и устанавливает их в окошке, поворачивая ручку кремальеры.
Селектор радиуса Земли R⊕
В селекторе используется четыре константы радиуса Земли:
Средний радиус Земли, определенный Всемирной геодезической системой координат WGS-84: R₁ = 6371,0088 км.
Средний радиус Земли, определенный в Стандартной атмосфере США: R₀ = 6356,766 км.
Экваториальный радиус Земли (большая полуось), определенный Всемирной геодезической системой координат WGS-84: a = 6378,1370 км.
Полярный радиус Земли (малая полуось), определенный Всемирной геодезической системой координат WGS-84: b = 6356,7523142 км.
А — экваториальный, В — полярный и С — средний радиус Земли; С = (2А + В)/3
Удельная газовая постоянная для сухого воздуха Rsp
Удельная газовая постоянная для сухого воздуха Rsp определяется как универсальная газовая постоянная, отнесенная к молярной массе сухого воздуха. В Стандартной атмосфере США 1976 г. и в ГОСТ 4401-81 «Стандартная атмосфера. Параметры» универсальная газовая постоянная определена как R* = 8314,32 Н м кмоль⁻¹ K⁻¹. Следовательно, удельная газовая постоянная для сухого воздуха в Дж K⁻¹ кг⁻¹ рассчитывается как
Стаднартное ускорение свободного падения
Стандартное ускорение свободного падения определяется международным стандартом ISO 80000-3 «Величины и единицы. Часть 3. Пространство и время»: g₀ = 9,80665 м/с² или 32,17405 фут/с². Несмотря на то, что ускорение свободного падения в разных местах Земли различное, для измерений всегда используется указанная выше стандартная величина.
Геопотенциальная высота
Сила тяготения зависит от высоты и широты места. Переход от геометрической высоты к геопотенциальной устраняет переменную — ускорение свободного падения. Геопотенциальная высота — это вертикальная координата относительно среднего уровня моря, вычисленная из геометрической высоты (измеренной с помощью прибора для измерения длины) с учетом изменения ускорения свободного падения в зависимости от высоты и широты. Иными словами, геопотенциальная высота — это высота, учитывающая силу тяжести. При этом изменение силы тяжести от широты места малó и не учитывается. Геопотенциальная высота является мерой удельной потенциальной энергии на данной геометрической высоте относительно поверхности Земли. Она используется в метеорологии и авиации. Соотношение между геометрической H и геопотенциальной высотой Z определяется следующей формулой (формула 18 в 1976 USSA), которая используется в этом калькуляторе
Например, для максимальной геометрической высоты, которую позволяет рассчитать этот калькулятор (Z = 86 км), соответствующая геопотенциальная высота будет H = 84,852 км. В калькуляторе геопотенциальная высота рассчитывается до определения температуры и давления.
Скорость звука
Скорость звука в воздухе около 343 м/с, или 1,235 км/час, или 767 миль в час. Это означает, что звук может проходить в воздухе один километр за 3 секунды или милю за 5 секунд. Скорость звука в воздухе зависит главным образом от его температуры; зависимость от частоты звуковых колебаний и давления воздуха пренебрежимо мала.
Конденсация влаги при околозвуковой скорости
Если предположить, что воздух сухой и что он является идеальным газом при относительно низком давлении и плотности, что имеет место в стандартных условиях на уровне моря, а также предположить, что температура ниже или равна комнатной, то скорость звука определяется по следующей формуле, которая используется в этом калькуляторе:
Здесь γ — рассматриваемый ниже показатель адиабаты, R = 287,052 Дж·кг⁻¹·K⁻¹ — удельная газовая постоянная и T — абсолютная температура воздуха в кельвинах.
Показатель адиабаты газа, называемый также коэффициентом Пуассона и фактором изоэнтропийного расширения, обозначается греческой буквой γ (гамма) и является отношением теплоемкости при постоянном давлении Cp к теплоемкости при постоянном объеме Cv
Для сухого воздуха при 20 °C, γ=1,40.
Зависимость силы тяжести от высоты
Зависимость гравитационного ускорения Gh от высоты h приблизительно определяется следующей формулой, которая используется в этом калькуляторе:
Здесь
g0 — стандартное ускорение свободного падения. Например, ускорение свободного падения на максимальной для этого калькулятора геометрической высоте 86 км равно Gh = 0,9874·g0, то есть разница очень мала.
Зависимость температуры от высоты
В тропосфере температура воздуха уменьшается с увеличением высоты. В Международной стандартной атмосфере, Стандартной атмосфере США 1976 г. и ГОСТ 4401-81 скорость уменьшения температуры (вертикальный температурный градиент) равна 6,5 К/км от уровня моря до 11 км или 36089 футов. В тропопаузе (слое атмосферы от 11 до 20 км или 65617 футов) температура постоянная и равна to –56.5 °C (–69.7 °F или 216.7 K). В ионосфере, от 20 до 32 км или 104987 футов скорость уменьшения температуры (вертикальный градиент) равна 1,0 K/км. Температурные градиенты приведены ниже в таблице до высоты 86 км (геопотенциальной высоты 84,85 км). Таблица приводится по документу USSA 1796.
Таблица 1
| Слой атмосферы | Диапазон геопотенциальных высот (км) | Номер диапазона, b | Базовая геопотенциальная высота над средним уровнем моря, Hb (км) | Базовое статическое давление, Pb (Па) | Базовая температура, Tb (K) | Базовый вертикальный температурный градиент на километр геопотенциальной высоты Lb (K/км) |
|---|---|---|---|---|---|---|
| Тропосфера | 0–11 | 0 | 0 | 101325 | 288,15 | -6,5 |
| Тропопауза (стратосфера I) | 11–20 | 1 | 11 | 22632,06 | 216,65 | 0 |
| Стратосфера II | 20–32 | 2 | 20 | 5474,889 | 216,65 | +1,0 |
| Стратосфера III | 32–47 | 3 | 32 | 868,0187 | 228,65 | +2,8 |
| Стратопауза (мезосфера I) | 47–51 | 4 | 47 | 110,9063 | 270,65 | 0 |
| Мезосфера II | 51–71 | 5 | 51 | 66,93887 | 270,65 | -2,8 |
| Мезосфера III | 71–84,9 | 6 | 71 | 3,95642 | 214,65 | -2,0 |
| 7 | 84,852 | 0,3734 | 186,87 | — |
«Базовый» в этой таблице означает величину на нижней границе диапазона высот. Отрицательный градиент означает уменьшение температуры с высотой, а положительный — ее увеличение. Большее значение градиента означает, что при увеличении высоты воздух охлаждается (нагревается) сильнее.
Для определения зависимости температуры от высоты:
- определите геопотенциальную высоту по геометрической высоте;
- определите номер интервала, b;
- определите температуру TM на геопотенциальной высоте H от поверхности до 84,85 км с помощью семи последовательных линейных уравнений в различных интервалах высоты. Для этого вставьте в формулу ниже значения из таблицы 1
Здесь
Hb — базовая геопотенциальная высота (Табл. 1),
Tb — базовая температура,
Lb базовый вертикальный температурный градиент
Температура TM называется молекулярной температурой, определяемой как
Здесь T — кинетическая температура, то есть температура воздуха, которую обычно измеряют термометром. Она является функцией скорости движения молекул газа в земной атмосфере. M0 — молекулярная масса воздуха на уровне моря и MH — молекулярная масса воздуха на высоте H. На высотах до 100 км молекулярная масса воздуха остается постоянной, поэтому молекулярная температура равна кинетической температуре.
Отклонение температуры от стандартного значения. Конечно, реальная атмосфера никогда не соответствует стандартной. Изменения температуры влияют на плотность воздуха и, следовательно, на его давление и вес. В холодном воздухе давление уменьшается с высотой быстрее, чем в горячем. В жаркий день вся атмосфера и график зависимости температуры от высоты будут смещены (см. график ниже), так как отклонение температуры будет прибавлено к кривой температуры и летчики, которые используют барометрические приборы для измерения высоты полета должны помнить, что в жаркий день геометрическая высота их самолета будет больше, чем показанная на высотомере. И, наоборот, в холодный день реальная высота будет меньше, чем показанная на высотомере.
Зависимость температуры, плотности и давления воздуха от геопотенциальной высоты. Синий график — давление, фиолетовый — плотность при отклонении температуры от стандартной +20 °C, оранжевый — плотность при отклонении 0 °C, зеленый — температура, отклонение +20 °C, красный — температура, отклонение 0 °C.
Если самолет входит в зону, где температура значительно ниже, чем стандартная по ISA (+15 °C на уровне моря), высотомер покажет завышенную высоту, что опасно. Чтобы учесть отклонение от стандартной атмосферы, в калькуляторе имеется поле Отклонение температуры от стандартного значения, которое можно использовать, например, для анализа или прогноза летно-технических характеристик воздушного судна в жаркий день. Следует помнить, что отклонение температуры — это температурный интервал и при преобразовании градусов Цельсия или кельвинов в градусы Фаренгейта или Ранкина нужно использовать только масштабирующий коэффициент 1 К = 1 °C = 9/5 °F = 1.8 °F = 1.8 °R. Для преобразования можно также воспользоваться нашим калькулятором температурных интервалов.
Зависимость давления от высоты
В ISA, USSA и ГОСТ 4401-81 для моделирования зависимости давления и плотности воздуха от высоты используется барометрическая формула и данные таблицы 1. Для определения зависимости давления от высоты в различных слоях атмосферы используются два выражения.
Если базовый вертикальный градиент температуры Lb нулевой, то используется формула
Если же базовый вертикальный градиент температуры Lb отличен от нуля, то используется формула
или
В этих уравнениях все величины с индексом b берутся из таблицы 1:
Pb — базовое статическое давление в слое b в паскалях
Tb — базовая температура в слове b в кельвинах
Lb — базовый вертикальный градиент температуры в слое b в К/м
Hb — базовая геопотенциальная высота слоя b в метрах
H — геопотенциальная высота над уровнем моря в метрах
R* = 8,31432·10³ Н м кмоль⁻¹ K⁻¹ — универсальная газовая постоянная
g0 = 9,80665 м/с² — гравитационное ускорение
M = 0.0289644 кг/моль — молярная масса земной атмосферы
TM — молекулярная температура на высоте H, определенная выше:
Плотность воздуха
Плотность воздуха — это масса воздуха на единицу объема. Она обозначает греческой буквой ρ и измеряется в in кг/м³ в СИ или фунт/фут³ в традиционных единицах. В ISA и USSA плотность воздуха при стандартном давлении 1013,25 гПа и температуре 15 °С равна 1,225 кг/м³ или 0,0765 фунт/фут³. На плотность воздуха влияет не только температура и давление, но также и количество воды в воздухе. Чем больше водяного пара содержится в воздухе тем ниже его плотность.
Плотность воздуха зависит от температуры и давления. При «стандартных» температуре и давлении значение плотности воздуха зависит от используемого стандарта. В Международной стандартной атмосфере (ISA) плотность сухого воздуха определяется как 1,225 кг/м³ или 0,0765 фунт/фут³. Международный союз теоретической и прикладной химии (ИЮПАК) определяет стандартную плотность сухого воздуха иначе: она равна 1,2754 кг/м³ or 0,0796 фунт/фут³ при 1000 гПа и 0 °C.
В этом калькуляторе мы рассматриваем только сухой воздух. Плотность сухого воздуха ρ рассчитывается с использованием идеального газа с учетом давления, определенного для данной высоты по следующей формуле:
Здесь:
p — абсолютное давление в паскалях (Па),
T — абсолютная температура воздуха в кельвинах (K) и
R = 287,052 Дж·кг⁻¹·K⁻¹ — удельная газовая постоянная.
Отметим, что поскольку мы рассматриваем воздух как идеальный газ, не содержащий влаги, результат наших расчетов является теоретическим приближением. Наиболее точные результаты получается при низких температурах и давлениях (то есть на больших высотах).








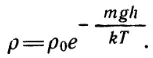
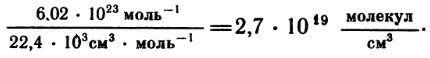










 на некотором уровне
на некотором уровне по заданному значению
по заданному значению на
на и среднему значению
и среднему значению в слое
в слое –
– .
. –
– по значениям давления в них
по значениям давления в них ,
, и виртуальной температуры
и виртуальной температуры и
и .
. ,
, ,
, ,
, и
и .
. .
. ,
, ,
, на
на .
. и
и на
на и
и и требуется найти
и требуется найти ,
,












