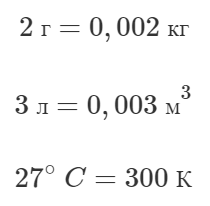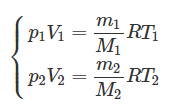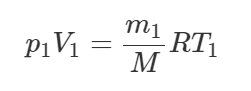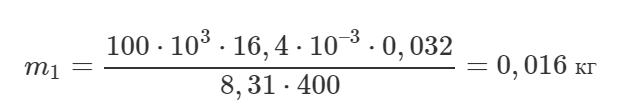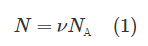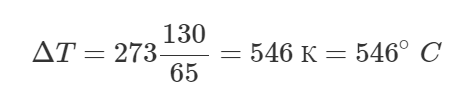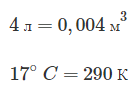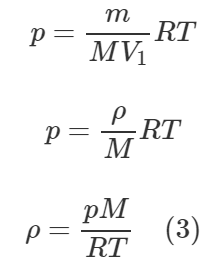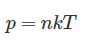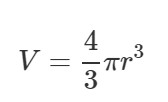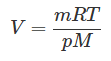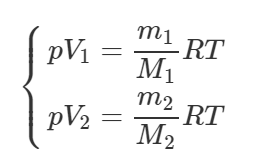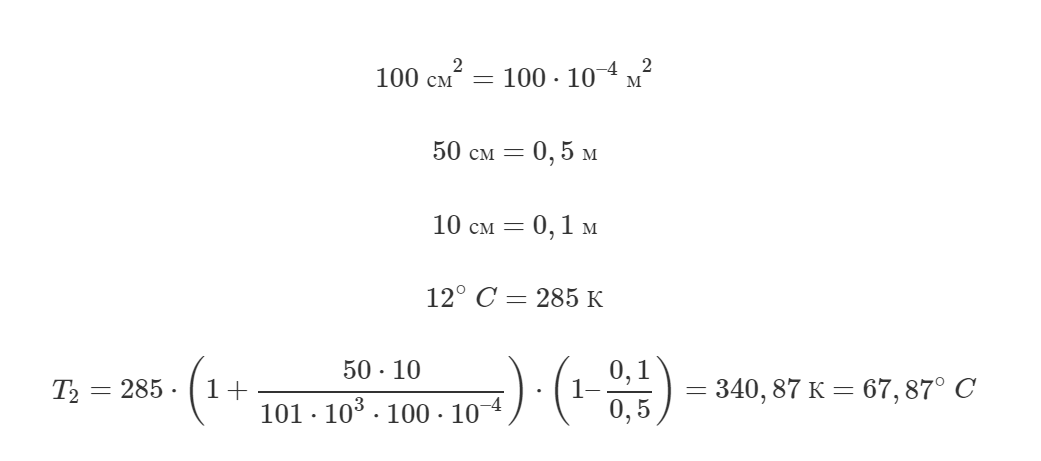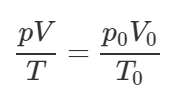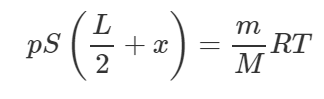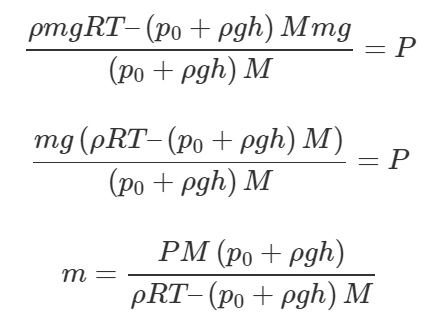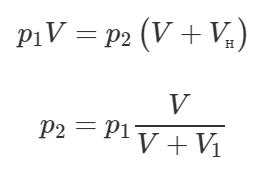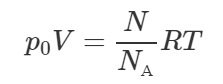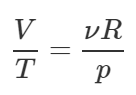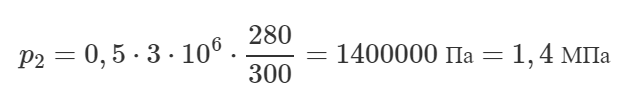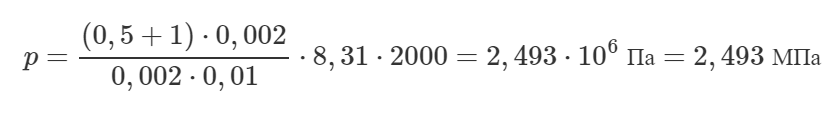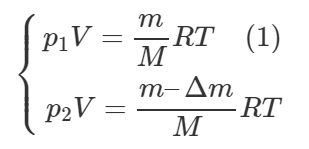Условие задачи:
Определить плотность воздуха при 27° C и давлении 0,1 МПа.
Задача №4.1.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(t=27^circ) C, (p=0,1) МПа, (rho-?)
Решение задачи:
Запишем уравнение Клапейрона-Менделеева:
[pV = frac{m}{M}RT]
Плотность (rho) – это масса единицы объема вещества, её находят как отношение массы вещества (m) к объему (V):
[rho = frac{m}{V};;;;(1)]
Давайте разделим обе части уравнения Клапейрона-Менделеева на объем (V):
[p = frac{m}{{MV}}RT]
Учитывая (1), имеем:
[p = frac{rho }{M}RT]
Из полученной формулы выразим плотность (rho):
[rho = frac{{pM}}{{RT}}]
Молярная масса воздуха (M) равна 0,029 кг/моль, универсальная газовая постоянная (R) – 8,31 Дж/(моль·К). Перед тем, как считать ответ, переведем температуру в шкалу абсолютных температур:
[27^circ;C = 300;К]
[rho = frac{{0,1 cdot {{10}^6} cdot 0,029}}{{8,31 cdot 300}} = 1,16;кг/м^3 = 1,16;мг/см^3]
Ответ: 1,16 мг/см3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.1.29 Сколько молекул кислорода находится в сосуде объемом 1 л, если температура
4.1.31 Какое давление на стенки сосуда производят молекулы газа, если масса газа 3 г, объем
4.1.32 Какое давление производит углекислый газ при температуре 330 К, если его плотность
Выбрать другой вопрос
Смотреть ответ
Перейти к выбору ответа
Вопрос от пользователя
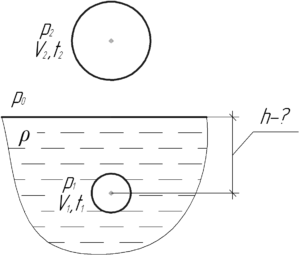
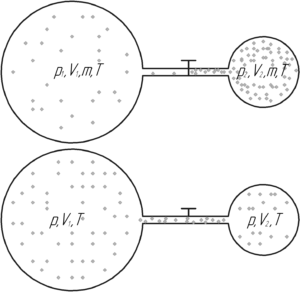
Сосуд с воздухом откачан до давления p=1,33·10-4 Па. Найти плотность ρ воздуха в сосуде, число молекул n в единице объема сосуда и среднюю длину свободного пробега λ молекул. Диаметр молекул воздуха σ=0,3 нм. Молярная масса воздуха μ=0,029 кг/моль. Температура воздуха t=17° C.
Ответ от эксперта
Решение к задаче представлено в виде картинки и приложено к ответу


Пример 1:
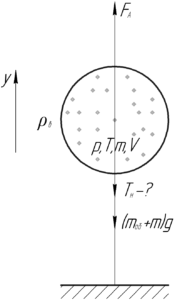
Надувной шарик, заполненный гелием, удерживают на нити. Найдите натяжение нити, если масса оболочки шарика 2 г, объем 3 л, давление гелия 104 кПа, температура 27°C. Плотность воздуха 1,3 кг/м3.
Решение от преподавателя:
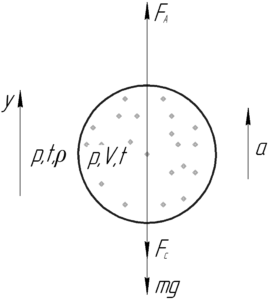
На шарик действуют три силы: сила Архимеда FА, сила тяжести шарика и гелия (mоб+m)g и сила натяжения нити Tн. Надувной шарик находится в равновесии, запишем первый закон Ньютона в проекции на ось y:
Выразим силу натяжения нити Tн, которую нужно найти по условию задачи:
Силу Архимеда FА (её ещё называют выталкивающей силой) можно определить по формуле:
Чтобы определить массу гелия mm, содержащуюся в шарике, запишем уравнение Клапейрона-Менделеева для гелия в шарике:
В этом уравнении M – молярная масса гелия, равная 0,004 кг/моль. Выразим массу гелия:
Формула (1) после подстановки в неё выражений (2) и (3) примет такой вид:
Переведем массу оболочки mоб, объем шарика V и температуру гелия t в систему СИ:
Посчитаем численный ответ к задаче:
Пример 2:
Какой объем занимает 1 кг кислорода при 0° C и давлении 800 кПа?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева:
Молярная масса кислорода M равна 0,032 кг/моль. Поскольку все входящие в уравнение величины, кроме объема, известны, то можем сразу выразить искомый объем V:
Переведем температуру t в шкалу абсолютных температур:
Посчитаем ответ:
Ответ: 88,6 л.
Пример 3:
Два баллона с объемами 20 и 10 л соединены длинной тонкой трубкой и содержат 6 моль водорода. Первый баллон находится при температуре 20°C. Какую температуру имеет второй баллон, если известно, что в нем содержится 9 г водорода?
Решение от преподавателя:
Пример 4:
Найти массу углекислого газа в баллоне вместимостью 40 л при температуре 288 К и давлении 5,07 МПа.
Решение от преподавателя:
Применим уравнение Клапейрона-Менделеева:
В этом уравнении R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К), M – молярная масса углекислого газа, равная 0,044 кг/моль. Все величины, входящие в уравнение, кроме искомой массы, известны. Выразим массу m, тогда получим такую формулу:
Переведем объем баллона в систему СИ:
Произведем вычисления:
Ответ: 3,73 кг.
Пример 5:
В некотором процессе давление и объем идеального газа связаны соотношением pV1/2=const. При температуре 27°C давление 100 кПа. Найти давление при температуре 127°C.
Решение от преподавателя:
Пример 6:
В баллоне емкостью 25,6 л находится 1,04 кг азота при давлении 3,55 МПа. Определите температуру газа.
Решение от преподавателя:
Уравнение Клапейрона-Менделеева выглядит так:
Молярная масса азота N2 M равна 0,028 кг/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Выразим из уравнения температуру T:
Переведем объем баллона в кубические метры (то есть в единицы системы СИ):
Температура равна:
Пример 7:
Какой радиус должен иметь наполненный гелием воздушный шар, чтобы он мог подняться в воздух, если масса 1 м2 оболочки шара 50 г? Температура воздуха 27° C, давление 100 кПа.
Решение от преподавателя:
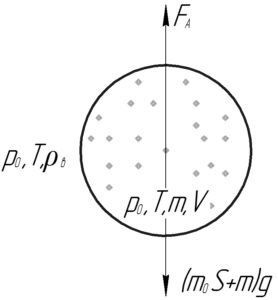
Шар поднимется в воздух, если сила Архимеда станет равной силе тяжести, то есть выполнится условие плавания тел:
В этой формуле S – площадь поверхности воздушного шара, m – масса гелия, заключённого в шаре. Выталкивающую силу (силу Архимеда) найдём по следующей формуле:
Здесь ρв – плотность окружающего воздуха, а V – объем воздушного шара. Тогда:
Чтобы определить плотность воздуха ρвρв и массу гелия m, запишем дважды уравнение Клапейрона-Менделеева для воздуха произвольного объема V1 и гелия. Отметим, что давления окружающего воздуха и гелия внутри шара равны друг другу:
Молярная масса воздуха Mв равна 0,029 кг/моль, гелия M – 0,004 кг/моль. Поделим обе части верхнего уравнения системы на V1. Отношение массы воздуха m1 к объему V1, который занимает эта масса воздуха, есть плотность воздуха ρвρв, поэтому:
Из первого уравнения выразим плотность воздуха ρвρв, а из второго – массу гелия m:
С учётом полученных выражений формула (1) примет вид:
Площадь поверхности шара S и объем шара V определяют по формулам:
Тогда:
Решение задачи в общем виде получилось таким:
Переведём некоторые величины в систему СИ:
Посчитаем численное значение радиуса шара r:
Ответ: 0,15 м.
Пример 8:
Баллон содержит 28 кг кислорода при давлении 770 кПа. Какова масса гелия, занимающего такой же объем при давлении 825 кПа? Температура газов одинакова.
Решение от преподавателя:
Запишем дважды уравнение Клапейрона-Менделеева для кислорода и гелия:
Молярная масса кислорода M1 равна 0,032 кг/моль, а молярная масса гелия M2 – 0,004 кг/моль. Поделим нижнее равенство на верхнее, тогда получим следующее:
Поскольку согласно условию их объемы и температуры равны (V1=V2 и T1=T2), то:
Выразим искомую массу гелия m2:
Посчитаем ответ:
Ответ: 3,75 кг.
Пример 9:
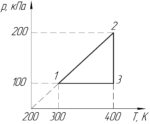
На PT-диаграмме изображен замкнутый процесс, который совершает кислород некоторой массы. Известно, что максимальный объем, который занимал газ в этом процессе, 16,4 дм3. Определите массу газа в точке 1. Значения T1, T2, p1, p2 указаны на рисунке.
Решение от преподавателя:
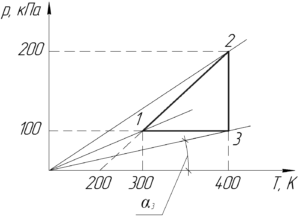
Во-первых, разберемся в какой точке графика процесса газ занимает наибольший объем. Для этого запишем уравнение Клапейрона-Менделеева:
Выразим из уравнения отношение pT, поскольку для любой прямой, проведённой через начало координат, оно равно тангенсу угла наклона прямой к положительному направлению оси T:
Отсюда видно, что чем больше угол αα, тем меньше объем газа V, и наоборот. Обязательно покажем на графике начало координат (на схеме к условию оно не показано). Проведём прямые через начало координат и точки 1,2 и 3. Угол α3 наименьший, поэтому газ занимает наибольший объем в точке 3, то есть:
Запишем уравнение Клапейрона-Менделеева для газа в точке 1:
Здесь M – молярная масса кислорода, равная 0,032 кг/моль. Выразим массу газа m1:
Чтобы определить объем V1 заметим, что процесс 3-1 является изобарным, поэтому можно применить закон Гей-Люссака:
Полученное выражение подставим в формулу (2), тогда:
Учитывая (1), получим следующую конечную формулу:
Переведем объем Vmax в систему СИ:
Численно масса газа в точке 1 m1 равна:
Ответ: 0,016 кг.
Пример 10:
В изотермическом процессе объем газа уменьшился вдвое. Во сколько раз изменилось давление?
Решение от преподавателя:
Изотермический процесс – это процесс, протекающий при постоянной температуре (T=const). Такой процесс подчиняется закону Бойля-Мариотта:
Из этого закона следует, что если объем газа уменьшится, то давление увеличится, то есть конечное давление p2 больше начального давления p1. Узнаем, во сколько раз увеличится давление из такого выражения:
По условию объем уменьшится в два раза, то есть V2=V1/2, поэтому:
Ответ: увеличилось в 2 раза.
Пример 11:
Если нагреть 1 моль идеального газа на 1 К при постоянном объеме, то давление возрастет на 10 Па. Если из того же исходного состояния нагреть газ на 1 К при постоянном давлении, то объем увеличивается на 0,001 м3. Вычислите температуру газа в исходном состоянии.
Решение от преподавателя:
Три раза запишем уравнение Клапейрона-Менделеева: для исходного состояния газа, а также для конечного состояния газа после изохорного и изобарного нагревания.
Искомую начальную температуру газа T выразим из уравнения (1):
Если вычесть из уравнения (2) уравнение (1), то получим такое равенство:
Откуда начальный объем газа V равен:
Также, если вычесть из уравнения (3) уравнение (1), получим:
Откуда начальное давление газа p равно:
Осталось только подставить в формулу (4) полученные выражения для начального давления и объема:
Задача решена в общем виде, теперь произведём вычисления:
Ответ: 558°C.
Пример 12:
Некоторая масса газа при давлении 126 кПа и температуре 295 К занимает объем 500 л. Найти объем газа при нормальных условиях.
Решение от преподавателя:
Дважды запишем уравнение Клапейрона-Менделеева – один раз для данных в задаче условий, а второй раз – для нормальных условий. Нормальным условиям соответствует давление p0, равное 100 кПа, и температура T0, равная 0 °C или 273 К.
Поделим нижнее равенство на верхнее, получим:
Из полученного равенства выразим объем при нормальных условиях V0:
Выразим объем V в кубических метрах:
Произведем вычисление ответа:
Ответ: 0,583 м3.
Пример 13:
Имеется два сосуда с одним и тем же газом при одинаковой температуре. Плотность газа в первом сосуде 30 кг/м3, во втором – 20 кг/м3. Объем первого сосуда в 3 раза меньше объема второго. Какая плотность газа установится, если сосуды соединить?
Решение от преподавателя:
Применим уравнение Клапейрона-Менделеева для начального состояния газов в различных сосудах и конечного состояния после соединения сосудов:
Сложим уравнения (1) и (2), тогда получим следующее равенство:
У полученного равенства и уравнения (3) равны правые части, значит равны и левые, то есть:
По условию объем первого сосуда в 3 раза меньше объема второго (V2=3V1), поэтому:
Вернёмся к системе уравнений. Если поделить обе части каждого уравнения на соответствующую массу, то получим такую систему (так как плотность газа – это отношение массы газа к объему):
С учётом этого формула (4) примет вид:
Посчитаем ответ:
Ответ: 0,023 г/см3.
Пример 14:
Сколько молекул хлора содержится при нормальных условиях в колбе емкостью 0,5 л?
Решение от преподавателя:
Напомним, что нормальные условия – это давление p0, равное 100 кПа, и температура T, равная 0 °C или 273 К. Вообще число молекул N можно определить, если знать количество вещества ν, по формуле:
В этой формуле NА – число Авогадро, равное 6,023·1023 моль-1. Запишем теперь уравнение Клапейрона-Менделеева:
Откуда количество вещества ν равно:
Полученное выражение подставим в (1), в итоге имеем:
Переведем объем колбы в систему СИ (в кубические метры):
Считаем ответ:
Ответ: 1,327·1022.
Пример 15:
При увеличении температуры газа на 60 К его объем возрос на 1 л. На сколько литров увеличится объем по сравнению с первоначальным, если температуру увеличить ещё на 30 К?
Решение от преподавателя:
Подразумевается, что процессы с газом происходили при постоянном давлении (p=constt). Запишем закон Гей-Люссака для первого изобарного нагревания газа:
Перемножим “крест-накрест” и сразу раскроем скобки, тогда:
Аналогично запишем закон Гей-Люссака для второго изобарного нагревания газа, при этом обратите внимание, что увеличение объема нужно найти относительно начального объема V0, а изменение температуры задают относительной конечной температуры предыдущего нагревания:
Также перемножаем “крест-накрест” и раскрываем скобки:
Выразим искомую величину ΔV2:
Учитывая ранее полученное равенство (1), имеем:
Переведём изменение объема ΔV1 в систему СИ:
Посчитаем ответ:
Ответ: 1,5 л.
Пример 16:
До какой температуры нужно нагреть запаянный шар, содержащий 9 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление не более 4,053 МПа, а его объем 1,2 л?
Решение от преподавателя:
Если нагревать запаянный шар с водой, то вода рано или поздно превратится в водяной пар, который оказывает давление на стенки шара. Когда давление водяного пара станет равным максимальному давлению p, которое может выдержать шар, он разорвётся.
Давайте запишем уравнение Клапейрона-Менделеева, чтобы определить до какой температуры нужно нагреть водяной пар, чтобы он оказывал давление p:
Откуда температура равна:
Молярная масса водяного пара M равна 0,018 кг/моль. Переведем массу воды (или водяного пара) и объем шара в систему СИ:
Посчитаем ответ:
Пример 17:
Насос захватывает при каждом качании 1 л воздуха при нормальных условиях и нагнетает его в автомобильный баллон объемом 0,5 м3 при 290 К. Сколько качаний необходимо, чтобы площадь соприкосновения баллона с дорогой уменьшилась на 100 см2, если до этого она была 450 см2 и на колесо приходится нагрузка 4,9 кН?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния воздуха в автомобильном баллоне, а также для той части воздуха, которая закачивается в баллон при каждом качании насоса.
Нормальные условия (для части воздуха, которая закачивается при каждом качании) – это давление p0, равное 100 кПа, и температура T0, равная 273 К (0° C). Из уравнения (2) выразим искомое число качаний насоса N:
Начальное количество вещества в баллоне ν, а также количество вещества ν0, которое нагнетается в баллон при каждом качании, выразим из уравнений (1) и (3):
С учётом этого формула (4) примет вид:
Чем меньше давление в баллоне, тем больше площадь его соприкосновения с землей, поэтому справедливы следующие равенства:
Подставим эти выражения в формулу (5), тогда:
Переведём в систему СИ некоторые величины:
Посчитаем ответ к задаче:
Полученное число необходимо округлить в большую сторону:
N=147
Пример 18:
Сколько молекул воздуха содержится в комнате объемом 60 м3 при нормальных условиях?
Решение от преподавателя:
Отметим, что воздух – это смесь газов (азота, кислорода, углекислого газа), поэтому говорить “молекула воздуха” можно лишь в случае, если рассматривать воздух как однородный газ (т.е. состоящий из одинаковых молекул) с молярной массой M, равной 0,029 кг/моль.
Известно, что в 1 моль вещества содержится молекул, число которых равно числу Авогадро NА (равное 6,023·1023 моль-1). Поэтому чтобы решить эту задачу, нужно определить количество вещества ν, тогда число молекул N можно будет определить по формуле:
Запишем уравнение Клапейрона-Менделеева:
Выразим количество вещества ν:
Подставим полученное выражение в формулу (1), тогда:
Напомним, что нормальным условиям соответствует давление p0, равное 100 кПа, и температура T0, равная 0°C и 273 К. Произведем вычисления:
Ответ: 1,59·1027.
Пример 19:
Воздушный шар имеет легкорастяжимую теплоизолированную оболочку массой 130 кг, которая была заполнена 65 кг воздуха при атмосферных давлении и температуре. На сколько градусов нужно нагреть воздух внутри шара, чтобы он взлетел? Температура окружающей среды 0° C.
Решение от преподавателя:
Шар взлетит, когда сила Архимеда станет равной силе тяжести, т.е выполнится условие плавания тел:
Выталкивающая сила FА равна произведению плотности окружающего воздуха ρ, ускорения свободного падения g и объема воздушного шара V.
Поэтому:
Теперь запишем уравнение Клапейрона-Менделеева для окружающего воздуха и воздуха внутри шара. Давление воздуха внутри шара равно давлению окружающего воздуха, т.е. атмосферному давлению p0, так как оболочка шара является легкорастяжимой.
Обе части уравнения (2) разделим на некоторый объем V1. Учитывая, что отношение массы m1 к объему V1 равно плотности окружающего воздуха ρ, получим:
Выразим плотность окружающего воздуха ρ:
Из уравнения (3) выразим объем шара V:
Полученные выражения для плотности ρ и объема шара V подставим в формулу (1):
Переведем температуру в систему СИ:
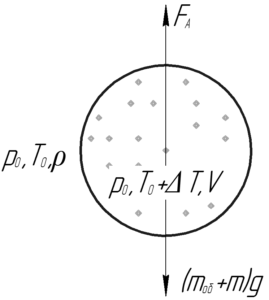
Посчитаем ответ:
Помните, что изменение температуры выражается одним и тем же числом, что в шкале Кельвина, что в шкале Цельсия! Ответ: 546° C.
Пример 20:
Сколько весит воздух, занимающий объем 150 л при температуре 15°C и давлении 150 кПа?
Решение от преподавателя:
Вес воздуха P легко определить по формуле:
Чтобы определить массу воздуха mm, запишем уравнение Клапейрона-Менделеева:
Выразим массу m:
Полученное выражение подставим в формулу (1):
Молярная масса воздуха M равна 0,029 кг/моль. Переведем температуру t в шкалу Кельвина и объем V в кубические метры, далее посчитаем численный ответ к задаче:
Пример 21:
Воздушный шар объемом 20 м3, наполненный гелием, поднялся на высоту 180 м за 0,5 минуты. Масса шара с оборудованием и корзиной 12 кг. Найти массу груза, поднятого шаром. Плотности воздуха и гелия при этих высотах считать постоянными и равными 1,29 и 0,18 кг/м3, соответственно.
Решение от преподавателя:
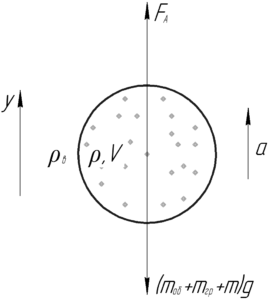
Воздушный шар будет двигаться равноускоренно вверх под действием следующих сил: силы Архимеда и силы тяжести шара с оборудованием, грузом и гелием. Запишем второй закон Ньютона в проекции на ось y:
Силу Архимеда FА определяет по следующей формуле:
Тогда равенство (1) станет таким:
Выразим отсюда искомую массу груза mгр:
Уравнение движения шара вдоль оси y выглядит так:
Тогда ускорение шара aa найдем по формуле:
Массу гелия в шаре mm найдём через его плотность ρ и объем шара V:
Формула (2) с учетом выражений (3) и (4) примет вид:
Переведём время подъема в систему СИ:
Произведём вычисления:
Ответ: 9,21 кг.
Пример 22:
В баллоне емкостью 4 л создано давление 0,1 мкПа. Сколько молекул газа содержится в баллоне, если его температура 17°C?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева, чтобы определить количество вещества ν:
Здесь R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К). Выразим из уравнения количество вещества ν:
Число молекул N можно определить по формуле:
В этой формуле NА – число Авогадро, равное 6,023·1023 моль-1. Учитывая (1), в итоге получим такую формулу:
Переведем объем в кубические метры, а температуру – в шкалу абсолютных температур:
Произведем вычисления:
Ответ: 9,997·1010.
Пример 23:
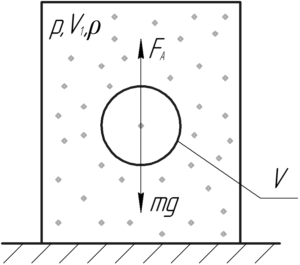
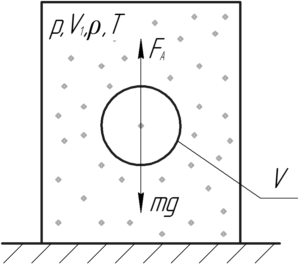
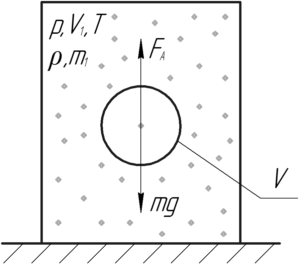
Внутри замкнутого цилиндра, наполненного воздухом, находится шарик радиусом 3 см и массой 3 г. Какое давление необходимо создать внутри цилиндра, чтобы шарик находился во взвешенном состоянии, если поддерживается температура 17° C?
Решение от преподавателя:
На шарик действует сила Архимеда FА и сила тяжести mgmg. Выталкивающую силу (так ещё называют силу Архимеда) FАFА находят по следующей формуле:
Изначально шарик будет находиться на дне цилиндра. Затем при повышении давления повысится и плотность воздуха (смотри формулу (3)) в цилиндре, вследствие чего увеличится и сила Архимеда FА (это видно по формуле (1)). Когда выполнится следующее условие, шарик всплывёт:
Тогда:
Запишем уравнение Клапейрона-Менделеева для находящегося в цилиндре воздуха:
Молярная масса воздуха M равна 29 г/моль или 0,029 кг/моль. Поделим обе части уравнения на объем цилиндра V1, тогда можем отношение массы воздуха m к объему цилиндра V1 в правой части заменить плотностью воздуха ρ.
Объем шарика определяют по такой формуле:
Равенство (2) с учётом выражений (3) и (4) примет вид:
Откуда давление воздуха p, при котором всплывёт шарик, равно:
Переведём величины в систему СИ:
Посчитаем ответ:
Ответ: 2,21 МПа.
Пример 24:
Баллон емкостью 40 л содержит 2,6 кг кислорода. При какой температуре возникает опасность взрыва, если допустимое давление не более 5 МПа?
Решение от преподавателя:
Чтобы решить эту задачу, достаточно записать уравнение Клапейрона-Менделеева:
Молярная масса кислорода (химическая формула O2) M равна 0,032 кг/моль. Выразим искомую температуру T:
Переведем объем баллона в систему СИ:
Численное значение температуры T, при которой возникает опасность взрыва, равно:
Ответ: 296,2 К.
Пример 25:
На дне цилиндра, наполненного воздухом, плотность которого 1,29 кг/м3, лежит полый металлический шарик радиусом 1 см. До какого давления нужно сжать воздух в цилиндре, чтобы шарик всплыл? Опыт проводят при температуре 290 К, масса шарика 5 г.
Решение от преподавателя:
Шарик всплывёт, если сила Архимеда FА станет равной силе тяжести mg:
При этом силу Архимеда определяют по формуле:
Тогда равенство (1) примет вид:
Когда это произойдёт? При увеличении давления в цилиндре повысится плотность воздуха, а значит увеличится и выталкивающая сила FА (смотрите формулу (2)). Когда выполнится условие (1), изначально лежащий на дне цилиндра шарик всплывёт. Объем шарика V определяют по формуле:
Плотность воздуха ρ равна отношению массы воздуха в цилиндре m к объему цилиндра V1. Запишем уравнение Клапейрона-Менделеева и поделим обе части уравнения на объем V1, тогда:
Откуда плотность воздуха ρ равна:
С учётом выражений (4) и (5) равенство (3) примет вид:
В итоге получим:
Здесь M – молярная масса воздуха, равная 0,029 кг/моль. Переведём радиус шарика и его массу в систему СИ:
Произведём вычисления:
Ответ: 0,1 ГПа.
Пример 26:
Найти концентрацию молекул газа, если в баллоне емкостью 4 л создано давление 0,5 мкПа при температуре 27° C?
Решение от преподавателя:
Самый быстрый способ решить эту задачу – это записать формулу связи давления газа p с концентрацией молекул n и абсолютной температурой T. Решить эту задачу через уравнение Клапейрона-Менделеева также возможно, но так вы потратите больше времени, хотя придёте к той же конечной формуле.
В этой формуле k – постоянная Больцмана, равная 1,38·10-23 Дж/К. Откуда концентрация n равна:
Переведем температуру из градусов Цельсия в Кельвины:
Посчитаем ответ:
Интересно, но при расчёте ответа нам не понадобился данный в условии объем V.
Ответ: 1,207·105 мм-3.
Пример 27:
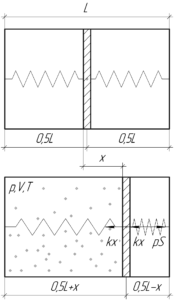
В замкнутом сосуде к верхней стенке на пружине жесткостью 4 Н/м подвешена сфера объемом 2 л. На какую высоту поднимется сфера, если при постоянной температуре 17° C давление воздуха в сосуде повысить от 100 до 500 кПа?
Решение от преподавателя:
На сферу действуют три силы: сила тяжести mg, сила Архимеда FА и сила упругости пружины kx. При разном давлении воздуха в цилиндре плотность воздуха в цилиндре будет разной, а значит разной будет и величина силы Архимеда. Поэтому будет меняться и деформация пружины x.
Неизвестно, была ли пружина изначально растянутой или сжатой. Если она была растянутой, то после увеличения давления она может оставаться растянутой или же сжаться. Также она может быть изначально сжатой, тогда после увеличения давления она сожмётся ещё сильнее. На решение задачи это никак не влияет, мы рассмотрим тот случай, когда пружина всегда растянута. Так как сфера в обоих случаях находится в равновесии, запишем первый закон Ньютона в проекции на ось y для этих случаев (смотрите схему):
Вычтем из первого равенства второе:
В этом случае высота подъема сферы определяется по формуле (смотрите схему):
Тогда:
Силу Архимеда FА определяют по формуле:
Плотность воздуха в сосуде можно найти из уравнения Клапейрона-Менделеева:
Тогда:
Формула (1) примет вид:
Переведём объем сферы и температуру в цилиндре в систему СИ:
Посчитаем ответ:
Ответ: 0,024 м.
Пример 28:
Сколько молекул ртути содержится в 1 м3 воздуха в помещении, зараженном ртутью, при температуре 293 К, если давление насыщенного пара ртути при этой температуре 133 мПа?
Решение от преподавателя:
Для начала нужно определить количество вещества ν. Сделать это можно с помощью уравнения Клапейрона-Менделеева:
Откуда количества вещества νν можно определить по формуле:
Количество молекул N определяет так:
В итоге получим такую формулу:
Число Авогадро NА равно 6,023·1023 1/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Посчитаем ответ:
Ответ: 3,29·1019.
Пример 29:
Во сколько раз изменится температура идеального газа, если уменьшить его объем в два раза при осуществлении процесса, в котором давление и объем связаны соотношением pV2=const.
Решение от преподавателя:
Запишем уравнение Клапейрона:
pVT=const
Домножим и числитель, и знаменатель левой части на объем V, тогда:
Поскольку в условии сказано, что pV2=const (смотрите числитель), значит и знаменатель постоянен, то есть:
TV=const
Откуда:
Объем уменьшится в два раза (V2=V12), значит:
Ответ: увеличится в 2 раза.
Пример 30:
В баллоне емкостью 40 л содержится 1,98 кг углекислого газа при 0° С. При повышении температуры на 48 К баллон с газом взорвался. При каком давлении произошел взрыв?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для момента, когда произошёл взрыв:
Откуда давление углекислого газа pp, при котором произошёл взрыв баллона, равно:
Молярная масса углекислого газа M равна 0,044 кг/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Переведем температуру t из градусов Цельсия в Кельвины, а объём – в кубические метры:
Численное значение искомого давления p равно:
Ответ: 3 МПа.
Пример 31:
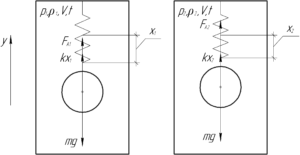
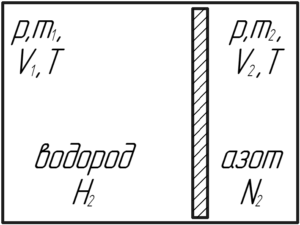
Внутри закрытого с обоих концов горизонтального цилиндра есть поршень, который скользит без трения. С одной стороны поршня находится водород массой 3 г, а с другой – азот массой 17 г. Какую часть объема цилиндра занимает водород?
Решение от преподавателя:
Давление водорода и азота будет одинаковым, поскольку в противном случае поршень бы двигался. Так как не сказано, что поршень теплоизолированный, то температуры двух газов также равны. Запишем уравнение Клапейрона-Менделеева для этих газов:
Молярная масса водорода M1 равна 0,002 кг/моль, а азота M2 – 0,028 кг/моль. Поделим нижнее уравнение на верхнее, тогда:
Сумма объемов, занимаемых водородом и азотом, равна объему сосуда:
V1+V2=V
Учитывая (1), получим:
Приведем в левой части под общий знаменатель:
Переведём массы газов в систему СИ:
Посчитаем ответ:
Ответ: 0,71.
Пример 32:
Баллон содержится 50 л кислорода, температура 27°C, давление 2 МПа. Найти массу кислорода.
Решение от преподавателя:
Это элементарная задача на применение уравнения Клапейрона-Менделеева:
В этой формуле p – давление кислорода, V – объем баллона, m – масса кислорода, M – молярная масса кислорода, равная 0,032 кг/моль, R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К), T – абсолютная температура кислорода (то есть выраженная в шкале Кельвина). Откуда масса кислорода m равна:
Переведем давление и объем баллона в систему СИ (в Паскали и в кубические метры), а температуру – в шкалу абсолютных температур, поскольку именно в таком виде она фигурирует в уравнении (1):
Посчитаем ответ:
Ответ: 1,28 кг.
Пример 33:
Тонкий резиновый шар радиусом 2 см наполнен воздухом при температуре 20° C и давлении 100 кПа. Каким будет радиус шара, если его опустить в воду с температурой 4° C на глубину 20 м?
Решение от преподавателя:
Запишем объединённый газовый закон (уравнение Клапейрона) для воздуха, находящегося в шаре:
p0V0T0=p1V1T1(1) p0V0T0=p1V1T1(1)
Поскольку резиновый шар легко деформируется, то давление воздуха внутри него всегда равно внешнему давлению. Поэтому изначально воздух в шаре оказывал давление, равное атмосферному p0. Затем, после погружения на глубину hh, давление воздуха в шаре станет равным давлению воды, которое определяется законом Паскаля:
Здесь ρ – плотность воды, равная 1000 кг/м3. Объем шара в общем случае можно найти через его радиус r по формуле:
Тогда уравнение (1) примет вид:
Выразим из этого равенства искомый радиус r1:
Переведем величины в систему СИ:
Посчитаем ответ:
Ответ: 0,014 м.
Пример 34:
Сколько молекул газа заключено в объеме 0,5 м3, если он при температуре 300 К находится под давлением 748 кПа?
Решение от преподавателя:
Число молекул N находят через количество вещества ν по формуле:
Число Авогадро равно 6,023·1023 1/моль. Запишем уравнение Клапейрона-Менделеева, чтобы определить количество вещества ν:
Формула (1) в итоге примет вид:
Произведем вычисления:
Ответ: 9,04·1025.
Пример 35:
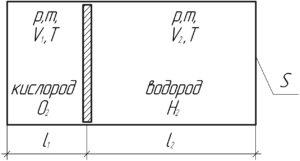
Цилиндрический сосуд делится невесомым поршнем на две части. В одну часть сосуда поместили кислород, а в другую – такую же массу водорода. Общая длина сосуда 85 см. Какую часть длины цилиндра будет занимать кислород?
Решение от преподавателя:
Так как поршень невесомый, то ориентация сосуда (горизонтально или вертикально) роли не играет. Давления газов будут одинаковы, поскольку в противном случае поршень будет двигаться, причём до тех пор, пока давление не станет одинаковым в обеих частях сосуда. Температуры газов также одинаковы, поскольку не сказано, что поршень теплоизолированный. Запишем уравнение Клапейрона-Менделеева для кислорода и водорода. Объем, занимаемый газами, запишем в виде произведения площади сечения сосуда на длину части сосуда, который занимает каждый газ.
Молярная масса кислорода M1 равна 0,032 кг/моль, водорода M2 – 0,002 кг/моль. Поделим нижнее уравнение на верхнее:
Сумма длин частей сосуда (l1 и l2), который занимает каждый газ, равна общей длине сосуда L.
l1+l2=L
Принимая во внимание выражение (1), получим:
В левой части приведём под общий знаменатель:
В итоге имеем такую конечную формулу:
Произведём вычисления:
Ответ: 0,06.
Пример 36:
В баллоне для сжиженных газов находится 4,2 кг метана (CH4) при давлении 1 МПа и температуре 300 К. Определить объем баллона.
Решение от преподавателя:
Применим уравнение Клапейрона-Менделеева:
Молярная масса метана M равна 0,016 кг/моль. Все величины, входящие в уравнение, кроме искомого объема V, известны. Выразим объем V:
Посчитаем ответ к задаче:
Ответ: 654,4 л.
Пример 37:
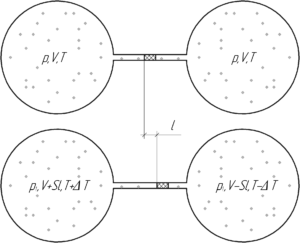
Два одинаковых шара соединены тонкой трубкой, в которой находится капелька ртути, разделяющая шары. При 0° C капелька находится посередине трубки. Объем воздуха в каждом шаре и части трубки до капельки ртути равен 0,2 л. Площадь сечения трубки 200 мм2. На какое расстояние передвинется капелька, если один шар нагреть на 2°C, а другой на столько же охладить?
Решение от преподавателя:
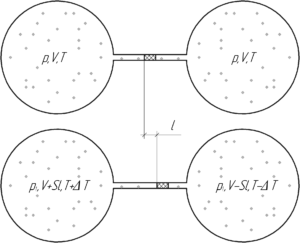
Так как в начале воздух в обоих шарах занимает одинаковый объем, имеет одинаковую температуру и давление (поскольку капелька ртути не движется), значит в шарах находится одинаковое количество вещества воздуха ν. Пусть после нагревания левого шара на величину ΔT и охлаждения правого (на столько же) капелька ртути сместиться вправо на величину l. Тогда объем, занимаемый воздухом в левом сосуде увеличится на величину Sl, а в правом – уменьшится на эту величину. Давление воздуха в каждом сосуде будет одинаковым (иначе капелька бы двигалась), но возможно отличным от начального (нам это не интересно). Запишем уравнение Клапейрона-Менделеева для конечного состояния воздуха в двух шарах:
Поделим верхнее уравнение на нижнее, тогда:
Перемножим крест-накрест:
Раскроем скобки и выразим искомое перемещение l:
Переведём исходные данные задачи в систему СИ:
Посчитаем численный ответ к задаче:
Ответ: 7,33 мм.
Пример 38:
В 1 м3 газа при давлении 120 кПа содержится 2·1025 молекул, средняя квадратичная скорость которых 600 м/с. Определить массу молекулы этого газа.
Решение от преподавателя:
Запишем основное уравнение молекулярно-кинетической теории идеального газа:
В этой формуле n – концентрация молекул, m0 – масса одной молекулы, υкв – средняя квадратичная скорость молекул. Концентрацию молекул n находят как отношение числа молекул N к объему V:
Тогда формула (1) примет следующий вид:
Выразим искомую массу одной молекулы m0:
Все величины, входящие в эту формулу, известны и даны в единицах системы СИ. Произведем вычисления:
Ответ: 5·10-23 г.
Пример 39:
Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень, который может скользить в цилиндре без трения. С одной стороны поршня находится водород массой 3 г, с другой – азот массой 23 г. Какую часть объема цилиндра занимает водород?
Решение от преподавателя:
Давления водорода и азота будут одинаковыми, поскольку в противном случае поршень пришёл бы в движение и двигался до тех пор, пока давление в обеих частях цилиндра не станет одинаковым. Температура газов также одинакова, так как в условии не сказано, что поршень теплоизолированный. Запишем уравнение Клапейрона-Менделеева для водорода и азота:
Здесь M1 – молярная масса водорода, равная 0,002 кг/моль, а M2 – молярная масса азота, равная 0,028 кг/моль. Поделим нижнее уравнение на верхнее, тогда получим:
Сумма объемов частей цилиндра, занимаемых газами (V1 и V2), равна общему объему цилиндра, то есть:
V1+V2=V
Учитывая выражение (1), получим:
Приведём в левой части равенства под общий знаменатель:
Тогда искомое отношение равно:
Переведём массы газов в систему СИ и произведём вычисления:
Ответ: 0,65.
Пример 40:
Найти массу водорода, находящегося в баллоне объемом 20 л под давлением 830 кПа при 17°C.
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева:
В этом уравнении p – давление водорода, V – объем баллона, m – искомая масса водорода, M – молярная масса водорода (она равна 0,002 кг/моль), R – универсальная газовая постоянная (R=8,31 Дж/(моль·К)), T – абсолютная температура. Выразим из уравнения (1) массу водорода m:
Переведем объем в единицы системы СИ, а температуру – в Кельвины:
Посчитаем ответ:
Ответ: 0,0138 кг.
Пример 41:
Два одинаковых сосуда, содержащих газ при 300 К, соединили горизонтальной трубкой сечением 0,4 см2, посередине которой находится столбик ртути. Объемы сосудов (до столбика ртути) равны 80 см3 каждый. На какое расстояние сместится столбик ртути, если один сосуд нагреть, а другой охладить на 3 К? Расширением сосудов пренебречь.
Решение от преподавателя:
Так как в начале оба одинаковых по объему сосуда находились под одинаковым давлением (так как столбик ртути покоился) и температурой, значит в них содержалось одинаковое количество вещества νν. После нагревания газа в одном сосуде и охлаждения в другом давление газов давления газов также будут одинаковыми, но не факт, что они равны начальному. При этом объем, занимаемый газом в левом сосуде (который нагревают), увеличится на Sl, а объем, занимаемый газом в правом сосуде – уменьшится на ту же величину. Запишем уравнение Клапейрона-Менделеева для конечного состояния газов в двух сосудах:
Поделим верхнее уравнение на нижнее, тогда получим следующее:
Перемножим крест-накрест:
Раскроем скобки в обеих частях равенства:
После сокращения имеем:
Откуда перемещение столбика ртути l равно:
Переведём данные величины в систему СИ:
Численное значение перемещения столбика ртути равно:
Ответ: 0,02 м.
Пример 42:
Газ массой 16 г при давлении 1 МПа и температуре 112° C занимает объем 1600 см3. Определить, какой это газ.
Решение от преподавателя:
Определить, какой это газ – это значит найти его молярную массу M. Это можно сделать, если применить уравнение Клапейрона-Менделеева:
Выразим из этого уравнения молярную массу M:
Перед тем, как производить расчёты, нужно перевести массу и объем в систему СИ, а температуру – в шкалу абсолютных температур:
Считаем ответ:
Такую молярную массу имеет кислород O2.
Ответ: 0,032 кг/моль (кислород).
Пример 43:
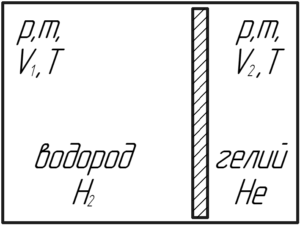
Горизонтально расположенный цилиндр разделен скользящей без трения перегородкой на две части. С одной стороны от перегородки находится водород, с другой – гелий. Массы и температуры газов одинаковы. Во сколько раз объем, занимаемый водородом, больше объема, занимаемого гелием?
Решение от преподавателя:
Если внутри цилиндра находится скользящая без трения перегородка, то давления газов по обе стороны от перегородки равны. В противном случае перегородка пришла бы в движение и двигалась бы до тех пор, пока давления газов не стали бы одинаковыми. Запишем уравнение Клапейрона-Менделеева для двух газов:
Поделим верхнее уравнение на нижнее, чтобы найти искомое отношение объемов V1V2:
Молярная масса водорода M1 равна 0,002 кг/моль, а гелия M2 – 0,004 кг/моль. Посчитаем численное значение искомого отношения:
Ответ: 2.
Пример 44:
Найти число молекул воздуха в комнате, имеющей объем 8x5x4 м3, при температуре 10° C и давлении 100 кПа.
Решение от преподавателя:
Сразу отметим, что молекул воздуха не существует, так как воздух – это смесь газов (азота, кислорода, углекислого газа и других). В этой задаче воздух рассматривается как однородный газ (то есть состоящий из одинаковых молекул), что верно лишь в качестве модели, но в действительности это не так.
Запишем формулу связи давления идеального газа p с концентрацией молекул n и температурой T (она выводится в молекулярно-кинетической теории):
Здесь k – постоянная Больцмана, равная 1,38·10-23 Дж/К. Концентрацию молекул n можно найти по следующей формуле:
В этой формуле N – число молекул, V – объем газа. Полученное выражение для нахождения концентрации подставим в формулу (1), тогда получим:
Откуда число молекул N равно:
Объем комнаты легко найти по следующей формуле:
В итоге получим:
Переведем температуру в Кельвины и посчитаем ответ к задаче:
Число молекул в физике является безразмерной величиной.
Ответ: 4,097·1027.
Пример 45:
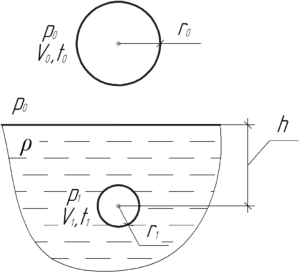
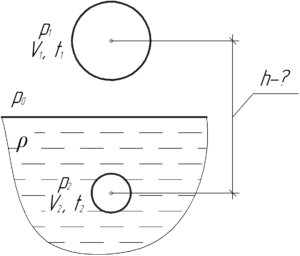
Объем пузырька, всплывающего на поверхность со дна озера, увеличился в два раза. Определить глубину озера. Температура воздуха на поверхности озера 27° C, а на его дне – 17° C. Атмосферное давление нормальное.
Решение от преподавателя:
Давление воздуха внутри пузырька всегда равно внешнему давлению. Поэтому при нахождении пузырька на поверхности давление воздуха в нём p2 равно атмосферному давлению p0 (оно равно 100 кПа). Когда же пузырёк находился на дне озера, то давление воздуха в нём p1 больше атмосферного на величину гидростатического давлению воды высотой h (согласно закону Паскаля).
Здесь ρ – плотность воды, равная 1000 кг/м3. Применим объединённый газовый закон для воздуха, находящегося в пузырьке:
Учитывая равенства, приведённые выше в системе, получим:
Тогда:
Согласно условию задачи объем всплывающего пузырька увеличился в два раза, то есть V2=2V1, поэтому:
Переведём данные температуры в систему СИ:
Произведем вычисления:
Пример 46:
Вычислить молярную массу бутана, 2 л которого при температуре 15°C и давлении 87 кПа имеют массу 4,2 г.
Решение от преподавателя:
Чтобы найти молярную массу бутана M, применим уравнение Клапейрона-Менделеева:
Поскольку все величины, кроме искомой молярной массы M, известны, то можно её сразу выразить из уравнения:
Переведем некоторые величины:
Произведем вычисления:
Если производить определение молярной массы бутана (химическая формула C4H10) с помощью таблицы Менделеева, то получим тот же ответ.
Ответ: 0,058 кг/моль.
Пример 47:
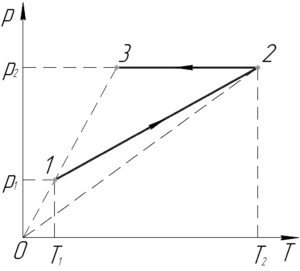
Состояние одного киломоля идеального газа менялось по графику 1-2-3. Определить конечный объем газа, если p1= 150 кПа, T1= 300 К, p2= 370 кПа, T2= 450 К.
Решение от преподавателя:
Обратите внимание, что точки 1 и 3 лежат на одной прямой, проходящей через начало координат, при этом перед нами график зависимости давления газа от температуры (график p-T). Если бы через эти точки были соединены на графике, то на этом участке над газом производился бы изохорный процесс. Но так как они не соединены, мы можем только утверждать, что объемы газа в этих точках одинаковы, то есть V1=V3. Исходя из этого равенства, нам достаточно найти объем газа V1, который легко определить из уравнения Клапейрона-Менделеева, записанного для газа в состоянии 1.
Здесь R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К).
Ранее было доказано, что V1=V3, поэтому:
Посчитаем ответ:
Ответ: 16,62 м3.
Пример 48:
Какая часть газа осталась в баллоне, давление в котором было 12,2 МПа, а температура 300 К, если давление упало до 1,013 МПа? Баллон при этом охладился до температуры 250 К.
Решение от преподавателя:
Пусть N – начальное число молекул в баллоне, а ΔN – число молекул, которое покинуло баллон. Значит (N–ΔN) – это число молекул, которое осталось в баллоне. Тогда искомую часть газа αα, которая осталась в баллоне, можно найти по формуле:
Для начала запишем уравнение Клапейрона-Менделеева:
Количество вещества νν находят как отношение числа молекул (в этой задаче оно разное в начале и конце) к числу Авогадро NА. Уравнение (2) для начального и конечного момента запишется в виде:
Поделим нижнее равенство на верхнее, получим:
Учитывая (1), имеем:
Откуда искомая величина α равна:
Посчитаем ответ:
Ответ: 0,1.
Пример 49:
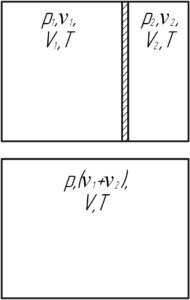
Сосуд объемом 5 л разделен перегородкой на две части, заполненные одним газом под давлением 80 и 30 кПа. После удаления перегородки в сосуде установилось давление 70 кПа. Определить, какой объем имела часть сосуда с большим давлением.
Решение от преподавателя:
Запишем три раза уравнение Клапейрона-Менделеева: для частей газа по обе стороны от перегородки до её удаления и для всего газа после удаления перегородки. Будем считать, что температура газа всегда оставалась неизменной.
Сложим уравнения (1) и (2), тогда получим:
Правые части полученного равенства и уравнения (3) равны, поэтому:
Очевидно, что сумма объемов V1 и V2 равна объему сосуда V:
Тогда имеем:
Осталось только из этого равенства выразить объем V1, для чего раскроем скобки в левой части:
Переведём объем сосуда в систему СИ (из литров в кубические метры):
Посчитаем ответ:
Ответ: 0,004 м3.
Пример 50:
Идеальный газ при давлении 1,33 кПа и температуре 15°C занимает объем 2 л. Каким будет его давление, если температура увеличится в два раза, а объем уменьшится на 0,25 от первоначального?
Решение от преподавателя:
Приведём небольшое разъяснение насчёт условия задачи: во фразе “температура увеличится в два раза” речь ведётся об абсолютной температуре газа (которая выражается в Кельвинах)!
Неверно думать, что конечная температура газа равна 30°C. Поскольку масса газа не изменяется, то запишем объединённый газовый закон (уравнение Клапейрона):
По условию задачи
поэтому:
Посчитаем ответ:
Ответ: 3547 Па.
Пример 51:
При некотором процессе идеального газа связь между давлением и объемом газа pV3=const. Во сколько раз изменится температура газа, если увеличить его объем в два раза?
Решение от преподавателя:
Пример 52:
Из баллона емкостью 5 л из-за неисправности вентиля произошла утечка газа, в результате чего давление понизилось на 2,9 кПа. Температура не менялась и была равна 17°C. Сколько молекул ушло из баллона?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева:
Пусть изначально в баллоне было N молекул, а ΔN молекул ушло из баллона. Тогда начальное и конечное количества вещества можно найти по формулам:
Здесь NА – число Авогадро, показывающее сколько молекул содержится в 1 моль любого вещества.
С учётом этого уравнение (1) для начального и конечного состояний запишется так:
Поскольку в начале давление было выше (p1>p2), то вычтем из первого равенства второе:
Очевидно, что Δp=p1–p2, поэтому:
Осталось только выразить искомую величину ΔN:
Переведем объем в кубические метры, а температуру – в шкалу абсолютных температур:
Произведем вычисления:
Ответ: 3,62·1021.
Пример 53:
Воздушный шар объемом 1000 м3 наполнен гелием при температуре окружающего воздуха 27° C и давлении 100 кПа. Общая масса шара 500 кг. Определите силу сопротивления воздуха, если шар поднимается вверх с ускорением 2,2 м/с2.
Решение от преподавателя:
Шар движется с ускорением вверх, запишем для него второй закон Ньютона в проекции на ось y:
Здесь FА – сила Архимеда (выталкивающая сила), действующая на шар, mg – сила тяжести шара (вместе с гелием), Fс – сила сопротивления воздуха. Выразим искомую силу сопротивления Fс:
Силу Архимеда находят по следующей формуле:
В этой формуле ρ – плотность окружающего воздуха. Чтобы определить её, запишем уравнение Клапейрона-Менделеева для воздуха произвольного объема V1, поделим обе части уравнения на этот объем, тогда в правой части появится плотность ρ.
Таким образом, силу Архимеда можно найти по такой формуле:
Тогда формула (1) примет вид:
Молярная масса воздуха M равна 0,029 кг/моль. Переведём температуру в шкалу абсолютных температур:
Посчитаем ответ:
Ответ: 5532,6 Н.
Пример 54:
Газ, объем которого 0,8 м3 при температуре 300 К производит давление 280 кПа. На сколько надо повысить его температуру, чтобы при давлении 160 кПа он занял объем 1,4 м3?
Решение от преподавателя:
Так как масса газа не меняется, то можно применить объединённый газовый закон, который также называют уравнением Клапейрона:
Очевидно, что верно следующее соотношение: T2=T1+ΔT
Тогда получим:
Задача решена в общем виде, давайте подставим численные значения величин и посчитаем ответ.
Удивительно, но температуру газа изменять не нужно!
Ответ: 0 К.
Пример 55:
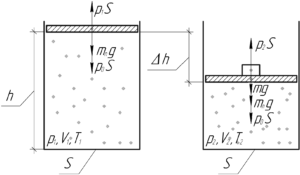
В цилиндре с площадью основания 100 см2 находится воздух. Поршень расположен на высоте 50 см от дна цилиндра. На поршень кладут груз массой 50 кг, при этом он опускается на 10 см. Найти температуру воздуха после опускания поршня, если первоначальное давление было равно 101 кПа, а температура 12°C.
Решение от преподавателя:
Для начала запишем уравнение Клапейрона (объединённый газовый закон) для начального и конечного состояния воздуха в сосуде:
Выразим из уравнения конечную температуру T2:
Объем, занимаемый газом в каждом состоянии, можно найти как произведение площади основания S на высоту, на которой находится поршень, поэтому:
Теперь разберемся с давлением. Запишем условие равновесия поршня (первый закон Ньютона) при начальном и конечном состоянии газа:
Здесь mп – масса поршня, p0 – атмосферное давление. Видно, что имеет место равенство:
Можно сделать вывод, что конечное давление p2 больше начального p1 на величину давления, которое создаёт груз, то есть:
В итоге формула (1) примет такой вид:
Мы решили задачу в общем виде. Выполним перевод некоторых единиц в систему СИ и посчитаем ответ:
Ответ: 67,87°C.
Пример 56:
В баллоне объемом 200 л при температуре 20°C и давлении 10 МПа находится кислород. Найти объем, который газ занимал бы в нормальных условиях.
Решение от преподавателя:
Нормальные условия – это:
давление p0, равное нормальному атмосферному давлению, то есть 100 кПа;
температура T0, равная 0° C или 273 К.
Масса кислорода не меняется (m=const), поэтому запишем объединённый газовый закон:
Выразим из этого равенства объем V0:
Переведем объем из литров в кубические метры, а температуру – из градусов Цельсия в Кельвины:
Объем V0 численно равен:
Ответ: 18635 л.
Пример 57:
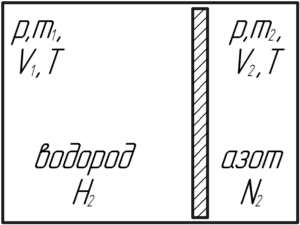
В сосуд, на дне которого лежит твердый шар, нагнетают воздух при температуре 27° C. Когда давление в сосуде стало равно 2 МПа, шар поднялся вверх. Чему равна масса шара, если его радиус 5 см?
Решение от преподавателя:
Шар поднимется, когда выполнится условие плавания тел, т.е. сила Архимеда, действующая на шар, станет равной силе тяжести шара:
Выталкивающую силу FА определяют по формуле:
Здесь ρ – плотность среды, в которую погружен шар, то есть плотность воздуха, V – объем твёрдого шара. Тогда:
Зная радиус шара, легко определить его объем из следующего выражения:
Чтобы найти плотность воздуха, запишем уравнение Клапейрона-Менделеева для воздуха в объеме сосуда V1 (пусть в этом объеме содержится воздух массой m1):
Разделим обе части уравнения на объем V1:
Молярная масса воздуха M равна 29 г/моль или 0,029 кг/моль. Отношение массы воздуха m1 к объему V1 есть плотность воздуха:
Подставим выражения (2) и (3) в формулу (1), в итоге получим:
Выполним перевод величин в систему СИ:
Численно масса шара равна:
Ответ: 0,0122 кг.
Пример 58:
Некоторый газ массой 7 г, находящийся в баллоне при температуре 27°C, создает давление 50 кПа. Водород массой 4 г в этом же баллоне при температуре 60°C создает давление 444 кПа. Какова молярная масса неизвестного газа?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для каждого из газов:
Поделим нижнее равенство системы на верхнее, тогда получим:
Выразим отсюда молярную массу неизвестного газа M1:
Молярная масса водорода M2 равна 0,002 кг/моль. Перед тем, как приступать к расчёту численного ответа, переведем массы газов в килограммы, а температуры – в Кельвины:
Считаем ответ:
Такую молярную массу имеет азот N2.
Ответ: 0,028 кг/моль.
Пример 59:
В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами одинаковой жесткости 1500 Н/м. Вначале цилиндр откачан, пружины находятся в ненапряженном состоянии, а поршень – в середине цилиндра. На какое расстояние переместится поршень, если в одну из частей цилиндра ввести 28 г азота при 273 К?
Решение от преподавателя:
Поскольку изначально пружины были не напряжены, то по сути нам необходимо найти деформацию пружин x, ведь именно на такую же величину переместится поршень. Обе пружины деформируются на одну и ту же величину, разве что одна растягивается (если в тот объем цилиндра, где находилась эта пружина, был введён азот), а другая – сжимается. Обратите внимание на схеме, куда направлены силы упругости у каждой пружины. Запишем условие равновесия поршня (первый закон Ньютона) после введения азота (смотрите схему):
Азот в конце займёт следующий объем:
Применим уравнение Клапейрона-Менделеева для азота:
Молярная масса азота M равна 0,028 кг/моль. Учитывая выражение (2), получим:
Выразим отсюда произведение pS:
Тогда равенство (1) примет вид:
Запишем это равенство в виде квадратного уравнения относительно x:
Определим дискриминант:
Тогда искомая величина x равна:
Очевидно, что решение, где перед квадратным корнем стоит знак “минус”, будет отрицательным, поэтому его можно отбросить.
Переведём массу в систему СИ и посчитаем ответ:
Ответ: 0,5 м.
Пример 60:
Сколько молекул воздуха выходит из комнаты объемом 80 м3 при повышении температуры от 15 до 27°C? Атмосферное давление 100 кПа.
Решение от преподавателя:
Хочется сразу отметить, что воздух – это смесь газов (азота, кислорода, углекислого газа и других), поэтому фактически молекулы воздуха не существует. Так можно лишь говорить, если воспринимать воздух в виде модели как однородный газ (то есть состоящий из одинаковых молекул) с молярной массой M, равной 0,029 кг/моль. Пусть изначально в комнате содержалось N молекул, а ΔN молекул вышло из комнаты вследствие повышения температуры. Давление в комнате будет постоянным и равным атмосферному pp, так как комната не может быть герметичной (если бы она была герметичной, то куда вышли молекулы?). Запишем уравнение Клапейрона-Менделеева для начального и конечного моментов времени, при этом распишем количество вещества νν как отношение числа молекул к числу Авогадро NА:
Левые части уравнений, входящих в систему, равны, поэтому можем приравнять их правые части:
Выразим из полученного равенства ΔN:
В полученной формуле нам неизвестно начальное количество молекул N, которое можно выразить из уравнения (1):
В конце концов мы должны получить такую формулу:
Переведем температуры в шкалу абсолютных температур, поскольку именно в таком виде они фигурируют в уравнении Клапейрона-Менделеева:
Произведем вычисления:
Ответ: 8,05·1025.
Пример 61:
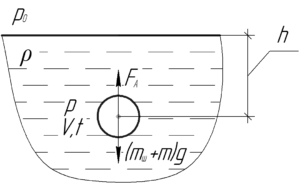
Тонкостенный резиновый шар собственным весом 0,6 Н наполнен неоном и погружен в озеро на глубину 120 м. Найти массу неона, если шар находится в положении равновесия. Температура воды 4° C. Натяжением резины пренебречь.
Решение от преподавателя:
На резиновый шар действуют такие силы: сила Архимеда FА и суммарная сила тяжести (mшg+mg), действующая на шар с неоном. Так как шар находится в равновесии, то эти силы компенсируют друг друга, то есть справедливо равенство:
Собственный вес резинового шара P равен силе тяжести mшg, действующей на этот шар, поэтому:
Выталкивающую силу воды FА определяют по такой формуле:
Здесь ρρ – плотность воды, равная 1000 кг/м3. Чтобы определить объем шара V на глубине h, запишем уравнение Клапейрона-Менделеева для неона:
Молярная масса неона M равна 0,020 кг/моль. Выразим объем шара:
Поскольку стенка шара является тонкой, то давление неона внутри резинового шара равно внешнему давлению воды. Последнее определяется по закону Паскаля:
В этой формуле p0 – атмосферное давление, равное 100 кПа.
Формула (3) для определения выталкивающей силы станет такой:
Подставим выражения (2) и (4) в формулу (1), тогда:
Осталось только выразить из полученного равенства массу неона m:
Переведём температуру в систему СИ:
Произведём вычисления:
Ответ: 685 мг.
Пример 62:
В цилиндре дизеля воздух сжимается от 80 до 3000 кПа, а объем уменьшается от 7,5 до 0,5 л. Определить температуру воздуха в конце такта сжатия, если его начальная температура 47°C.
Решение от преподавателя:
Масса воздуха в цилиндре не меняется, поэтому можем применить объединённый газовый закон (уравнение Клапейрона-Менделеева):
Откуда температура воздуха в конце такта сжатия T2 равна:
Давайте переведем начальную температуру в шкалу абсолютных температур, а объемы – в кубические метры:
Численно конечная температура T2 равна:
Ответ: 800 К.
Пример 63:
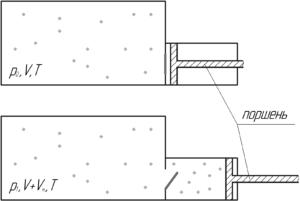
Давление воздуха в сосуде равно 102,4 кПа. Вместимость цилиндра разрежающего насоса в три раза меньше внутреннего объема сосуда. Какое давление установится в сосуде после трех ходов поршня? Изменением температуры пренебречь.
Решение от преподавателя:
Если изменением температуры можно пренебречь, значит над воздухом совершается изотермический процесс (T=const). Изначально воздух занимает объем сосуда V. После того, как откроется клапан, воздух займет объем, равный (V+Vн). Очевидно, что давление воздуха упадёт. Запишем закон Бойля-Мариотта:
Откуда давление воздуха p1 после одного хода поршня равно:
Теперь давление воздуха в сосуде равно p1. Опять произойдёт открытие клапана, и объем, занимаемый воздухом, увеличится, значит давление опять уменьшится. Также запишем закон Бойля-Мариотта:
Подставим в последнюю формулу выражение (1), тогда:
Из этой формулы видно, что давление воздуха в сосуде после N ходов поршня можно определять по формуле:
Таким образом, после трёх ходов поршня (N=3) давление в сосуде можно находить по формуле:
Так как в условии говорится, что объем цилиндра разрежающего насоса Vн в три раза меньше внутреннего объема сосуда V (Vн=V3), то имеем:
Численный ответ равен:
Ответ: 43,2 кПа.
Пример 64:
В открытом сосуде газ нагрели так, что его температура увеличилась в 3 раза. Сколько газа было в сосуде, если в конце нагревания в сосуде осталось 0,24 кг газа?
Решение от преподавателя:
При нагревании газа в открытом сосуде давление будет оставаться постоянным, но количество газа (а значит и масса) в объеме этого открытого сосуда будет уменьшаться. Запишем уравнение Клапейрона-Менделеева для начального и конечного моментов:
Левые части уравнений, входящих в систему, равны, значит равны и правые, поэтому:
По условию T2=3T1, значит в начале нагревания в сосуде была следующая масса газа m1:
Ответ: 720 г.
Пример 65:
Компрессор всасывает в 1 мин 3 м3 сухого воздуха при температуре 290 К и давлении 100 кПа и нагнетает его в резервуар, объем которого 8,5 м3. За какое время компрессор накачает воздух в резервуар до давления 700 кПа? Температура в резервуаре 300 К, перед накачиванием он был заполнен воздухом при давлении 200 кПа.
Решение от преподавателя:
Если компрессор равномерно закачивает за время ττ количество вещества воздуха, равное ν0, то за искомое время t он закачает количество вещества, равное
Запишем три раза уравнение Клапейрона-Менделеева: для воздуха, который закачивается за время τ, а также для начального и конечного состояния воздуха в резервуаре.
Из уравнения (3) выразим нужное время t:
Неизвестные количества вещества ν0 и ν1 выразим из уравнений (1) и (2):
Тогда формула (4) примет такой вид:
Домножим и числитель, и знаменатель на RTT0.
Мы решили задачу в общем виде. Переведём время ττ в систему СИ:
1мин=60с
Посчитаем ответ:
Ответ: 821,67 с.
Пример 66:
Температура воздуха в комнате была 10°C. После того как печь протопили, температура поднялась до 27°C. Объем комнаты 50 м3, давление в ней 97 кПа. На сколько изменилась масса воздуха, находящегося в комнате?
Решение от преподавателя:
Давление воздуха в комнате будет оставаться постоянным, так как комната негерметична. В противном случае, если бы комната не пропускала воздух, то масса воздуха в комнате оставалась бы постоянной. Пусть изначально в комнате содержалась масса воздуха, равная m, и Δm – это масса воздуха, которая вышла из комнаты. Запишем уравнения Клапейрона-Менделеева для двух моментов:
Левые части уравнений равны, значит равны и правые, поэтому:
Выразим искомую величину Δm:
Начальную массу газа m выразим из уравнения (1):
Подставим полученное выражение в формулу (2), тогда:
Молярная масса воздуха M равна 0,029 кг/моль. Переведем температуры в Кельвины и посчитаем ответ:
Ответ: 3389 г.
Пример 67:
Перед проведением газосварочных работ манометр баллона с кислородом показывал давление 10 МПа, а после сварки 4 МПа. Сколько кислорода было израсходовано? Температуру считать постоянной.
Решение от преподавателя:
Пусть m – начальная масса кислорода в баллоне, а Δm – масса израсходованного кислорода. Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния кислорода в баллоне:
Из уравнений видно, что определить массу израсходованного кислорода Δm мы не сможем, так как неизвестных больше чем уравнений. Поэтому определим какую часть кислорода αα израсходовали:
Для этого поделим уравнения системы друг на друга:
Учитывая (1), имеем:
Посчитаем ответ:
Ответ: 60%.
Пример 68:
Газ массой 1,2 г занимает объем 400 см3 при температуре 280 К. После нагревания газа при постоянном давлении его плотность стала равна 0,6 кг/м3. До какой температуры был нагрет газ?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния газа:
Обе части первого уравнения поделим на V1, а второго – на V2, тогда получим:
Если равны левые части этих уравнений, то равны и правые, поэтому:
Сократим обе части полученного равенства на молярную массу M и универсальную газовую постоянную R. Отношение массы газа mm к объему газа V2 равно плотности газа после нагревания ρ2. Тогда:
Переведем массу газа и объем в систему СИ:
Посчитаем ответ:
Ответ: 1127°C.
Пример 69:
В сосуде находится 1 литр воды при температуре 27° C. Чему стало бы равным давление внутри сосуда, если бы силы взаимодействия между молекулами воды внезапно исчезли?
Решение от преподавателя:
Пример 70:
Из баллона со сжатым водородом объемом 0,01 м3 вытекает газ, при температуре 280 К и начальном давлении газа 5 МПа. Через некоторое время при температуре 290 К давление оказывается тем же. Найти массу вытекшего газа.
Решение от преподавателя:
Пусть m – масса водорода, изначально находившаяся в баллоне, а Δm – масса вытекшего газа. Тогда в конце в баллоне осталась масса водорода, равная (m–Δm). Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния газа:
Так как по условию p2=p1, тогда левые части уравнений равны, а значит равны и правые. Поэтому:
Неизвестную массу m выразим из уравнения (1):
В итоге:
Молярная масса водорода M равна 0,002 кг/моль. Подставим значения величин в формулу и посчитаем ответ:
Ответ: 1482 мг.
Пример 71:
В двух сосудах находится одинаковое количество одного и того же газа. В первом сосуде давление равно 400 кПа, температура T, во втором – давление 600 кПа, температура 3T. Чему равно отношение объемов сосудов.
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для газов, содержащихся в двух сосудах:
Поделим нижнее уравнение на верхнее, и выразим искомое отношение V2V1:
По условию ν1=ν2, T1=T и T2=3T, поэтому:
Посчитаем ответ:
Ответ: 2.
Пример 72:
Откачанная лампа накаливания объемом 10 см3 имеет трещину, в которую проникает 1018 частиц газа за 1 секунду. Сколько времени нужно, чтобы в лампе установилось нормальное давление при температуре 27°C?
Решение от преподавателя:
За время τ0 в лампу проникает N0 молекул, а за искомое время τ – N молекул. Если считать, что количество молекул, проникающих в лампу за секунду, всегда постоянно, то справедливо отношение:
Заметим, что в начале в лампе совсем не было газа (так как она откачанная). Запишем уравнение Клапейрона-Менделеева для момента, когда в лампе установится нормальное давление p0 (оно равно 100 кПа). При этом количество вещества νν представим как отношение числа молекул N к числу Авогадро NА:
Учитывая (1), уравнение примет вид:
Откуда искомое время τ равно:
Число Авогадро NА равно 6,023·1023 моль-1, универсальная газовая постоянная R равна 8,31 Дж/(моль·К). Переведем некоторые величины:
Произведем вычисления:
Ответ: 241,6 с.
Пример 73:
Резиновая камера содержит воздух при температуре 27° C и нормальном атмосферном давлении. На какую глубину нужно опустить камеру в воду, чтобы её объем уменьшился вдвое? Температура воды 4° C.
Решение от преподавателя:
Давление воздуха в резиновой камере всегда равно внешнему давлению. Поэтому, когда резиновая камера находится в воздухе, то воздух внутри неё оказывает атмосферное давление, а если она находится в воде на глубине h – давление воздуха внутри камеры будет равно давлению воды на этой искомой глубине h.
Здесь ρ – плотность воды, равная 1000 кг/м3. Если опустить резиновую камеру на некоторую глубину в воду, то её объем уменьшится (об этом сказано в условии), а температура воздуха в камере станет равной температуре воды. Запишем объединенный газовый закон (уравнение Клапейрона):
Из этого равенства выразим p2:
Подставим в это равенство выражения (1) и (2) и учтём, что по условию V2=V12, тогда:
Осталось только выразить искомую глубину h:
Переведём данные в условии температуры в систему СИ:
Пример 74:
Когда из сосуда выпустили некоторое количество газа, давление в нем упало на 40%, а абсолютная температура – на 10%. Какую часть газа выпустили?
Решение от преподавателя:
Если m – масса газа, содержавшаяся в сосуде в начале, а Δm – это масса газа, которую выпустили из сосуда, то искомую величину αα найдем по формуле:
Запишем уравнение Клапейрона-Менделеева для начального и конечного состояний газа:
Поделим нижнее уравнение на верхнее, тогда:
Поделим почленно числитель на знаменатель в скобках в правой части равенства:
Учитывая равенство (1) и то, что по условию
получим:
Ответ: 1/3.
Пример 75:
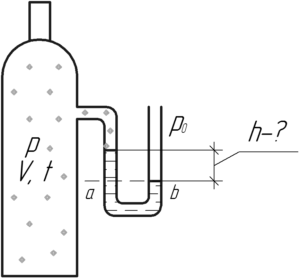
В баллоне объемом 10 л находится кислород, масса которого 12,8 г. Давление в баллоне измеряется U-образным манометром, заполненным водой. Какова разность уровней воды в трубках манометра при температуре газа 27° C? Атмосферное давление нормальное.
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева, чтобы определить давление кислорода в баллоне p:
В этой формуле M – молярная масса кислорода, равная 0,032 кг/моль, R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К). Все величины, входящие в эту формулу известны, значит мы можем узнать давление кислорода (перевод величин в систему СИ указан ниже):
Давление кислорода pp меньше нормального атмосферного давления p0, значит уровень воды в левом колене U-образного манометра будет выше, чем в правом (смотрите схему). Выделим горизонтальный уровень (на схеме ab), ниже которого находится только вода. Применим закон сообщающихся сосудов, согласно которому в сообщающихся сосудах при равновесии давление жидкости на любом горизонтальном уровне одинаково. Значит будет верно записать, что:
Здесь ρ – плотность воды, равная 1000 кг/м3, а p0 – нормальное атмосферное давление, равное 100 кПа. Подставим в формулу выражение (1), тогда:
Переведем массу газа, объем баллона и температуру в систему СИ:
Посчитаем ответ:
Ответ: 0,028 м.
Пример 76:
При температуре 727°C газ занимает объем 8 л и производит давление 200 кПа на стенки сосуда. При каком давлении этот газ при температуре -23°C будет занимать объем 160 л.
Решение от преподавателя:
Масса газа не меняется, поэтому можем применить уравнение Клапейрона (объединенный газовый закон):
Выразим отсюда искомое давление p2:
Температуры переведем в шкалу абсолютных температур, а объемы – в кубические метры:
Посчитаем ответ:
Ответ: 2500 Па.
Пример 77:
Баллон содержит 0,3 кг гелия. Абсолютная температура в баллоне уменьшилась на 10%, масса газа тоже уменьшилась. В результате давление упало на 20%. Сколько молекул гелия ушло из баллона?
Решение от преподавателя:
Пусть N – начальное число атомов гелия в баллоне, а ΔN – число ушедших из баллона атомов гелия. Запишем дважды уравнение Клапейрона-Менделеева для двух состояний гелия, о которых говорится в условии. При этом количество вещества гелия представим как отношение числа молекул к числу Авогадро NА.
Поделим нижнее уравнение на верхнее, тогда:
По условию температура гелия уменьшилась на 10% (T2=0,9T1), а давление упало на 20% (p2=0,8p1), поэтому:
Начальное число атомов гелия N можно найти так:
Число Авогадро NА равно 6,023·1023 моль-1. Количество вещества ν определим как отношение начальной массы гелия m к молярной массе гелия M (она равна 0,004 кг/моль):
Решение задачи в общем виде такое:
Посчитаем ответ:
Пример 78:
Воздух в открытом сосуде нагревают от 10 до 600°C и затем, герметически закрыв сосуд, охлаждают до первоначальной температуры. Найти плотность воздуха в сосуде после охлаждения, если атмосферное давление 100 кПа.
Решение от преподавателя:
В процессе охлаждения масса m и объем газа V не будут меняться (так как сосуд закроют), поэтому искомая плотность газа после охлаждения ρ равна плотности газа при температуре t2. Запишем уравнение Клапейрона-Менделеева для воздуха при температуре t2:
Поделим обе части уравнения на объем V:
Отношение массы газа m к объему V равно плотности газа ρ, поэтому:
В итоге получим:
Молярная масса воздуха M равна 0,029 кг/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Переведем температуру из шкалы Цельсия в шкалу Кельвина:
Посчитаем ответ:
Ответ: 0,4 кг/м3.
Пример 79:
В откачанной ампуле объемом 3 см3 содержится радий массой 5 г в течение одного года. В результате радиоактивного распада из радия массой 1 г в одну секунду вылетает 3,7·1010 альфа-частиц, представляющих собой ядра гелия. Какое давление будет производить гелий при температуре 300 К?
Решение от преподавателя:
Если скорость распада радия, то есть количество вылетающих альфа-частиц (ядер гелия) в одну секунду постоянно, то справедливо равенство:
Здесь N1 – число альфа-частиц, образующихся в результате распада радия массой 1 г (m0) за 1 год (τ). Вполне очевидно, что из 5 г радия (m) образуется в 5 раз больше гелия, то есть верна такая формула:
Учитывая (1), имеем:
Запишем уравнение Клапейрона-Менделеева, при этом количество вещества νν запишем в виде отношения количества частиц N к числу Авогадро NА:
В это уравнение подставим выражение (2), далее выразим искомое давление p:
Переведем некоторые величины в систему СИ:
Посчитаем ответ:
Пример 80:
До какой температуры нагрели колбу, содержащую воздух, если давление воздуха в ней увеличилось в два раза? Начальная температура колбы равна 20° C, а её объем за счёт теплового расширения увеличился на 10%.
Решение от преподавателя:
Колба с воздухом была закрытой, поскольку в противном случае давление не могло бы увеличиваться. Значит масса воздуха в колбе оставалась постоянной, что даёт возможность применить объединённый газовый закон (уравнение Клапейрона):
Выразим из равенства температуру T2:
В условии сказано, что p2=2p1 и V2=1,1V1, поэтому:
Переведем начальную температуру в шкалу абсолютных температур:
Численно конечная температура T2 равна:
Ответ: 644,6 К.
Пример 81:
Два сосуда, содержащих одинаковую массу одного и того же газа, соединены трубкой с краном. В первом давлении 100 кПа, во втором – 300 кПа. Температура одинакова. Какое давление установится после открытия крана?
Решение от преподавателя:
Запишем три раза уравнение Клапейрона-Менделеева: для газов в сосудах до открытия крана и после:
Из уравнений (1) и (2) следует, что:
Также сложим уравнения (1) и (2), тогда получим:
Так как равны правые части получившегося равенства и уравнения (3), то равны и левые, то есть:
Выразим давление p:
Поделим числитель и знаменатель дроби справа на V2, тогда:
Учитывая (4), получим:
Задача решена в общем виде, давайте посчитаем ответ:
Ответ: 150 кПа.
Пример 82:
Баллон, содержащий 1 кг азота, при испытании взорвался при температуре 630 К. Какое количество водорода можно хранить в таком баллоне при температуре 270 К, имея десятикратный запас прочности?
Решение от преподавателя:
Пусть давление азота, при котором произошёл взрыв баллона, равно p. Вы должны понимать, что баллону безразличен хранимый газ, и его прочность (то есть давление, которое он может выдержать) зависит от материала баллона, его геометрических параметров и т.д. Поэтому если водород будет оказывать давление p, то баллон также взорвётся. Но если применить запас прочности n, то водород можно хранить только при давлении в n раз меньшем, чем максимальное давление p. Запишем уравнение Клапейрона-Менделеева для этих газов (для азота – при взрыве, для водорода – с учетом запаса прочности):
Поделим уравнения друг на друга:
Откуда масса водорода m2 равна:
Молярная масса азота M1 равна 0,028 кг/моль, водорода M2 – 0,002 кг/моль. Произведем вычисления:
Ответ: 16,7 г.
Пример 83:
Сколько молей газа следует добавить к одному молю данного газа, чтобы его давление увеличилось в 9,1 раза при постоянном объеме и в два раза большей температуре?
Решение от преподавателя:
Пример 84:
При какой температуре давление 240 л водорода равно 126,6 кПа, если при нормальных условиях тот же газ занимает объем 364 л?
Решение от преподавателя:
Нормальные условия – это давление p0, равное 100 кПа, и температура T0, равная 0° C или 273 К. Запишем уравнение Клапейрона для двух состояний газа, описанных в условии:
Тогда температуру T можно найти по формуле:
Поскольку в формуле фигурирует отношение давлений и объемов, то смысла переводить их в систему СИ нет. Считаем ответ:
Ответ: -45,1° C.
Пример 85:
В открытом цилиндре находится 90 г газа. Температуру газа увеличили от 300 до 450 К при постоянном давлении 166 кПа. Сколько молей газа выйдет из цилиндра, если его плотность в начале процесса равна 1 кг/м3?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для двух состояний газа:
Поскольку равны левые части представленных уравнений, то равны и правые, поэтому:
Начальное количество вещества ν выразим из уравнения (1):
Неизвестный объем газа V найдем через начальную массу газа m и начальную плотность ρ1:
Тогда:
Полученное выражение подставим в формулу (1), таким образом мы получим решение задачи в общем виде:
Переведем массу газа mm в систему СИ и произведем вычисления:
Ответ: 2 моль.
Пример 86:
В баллоне находилось 5 кг газа при давлении 1 МПа. Какое количество газа взяли из баллона, если давление стало равным 100 кПа? Температуру считать постоянной.
Решение от преподавателя:
Пусть m – начальная масса газа, а Δm – масса газа, которую взяли из баллона. Запишем уравнение Клапейрона-Менделеева для начального и конечного состояний газа:
Поделим нижнее уравнение на верхнее, тогда получим:
Разделим почленно числитель дроби в правой части:
Посчитаем ответ:
Ответ: 4,5 кг.
Пример 87:
Из баллона объемом 200 дм3, содержащего гелий при давлении 2 МПа и температуре 273 К, израсходовали часть газа, занявшего при нормальных условиях объем 1 м3. При повторном измерении давления в баллоне получено значение 1,4 МПа. При какой температуре проведено это измерение?
Решение от преподавателя:
Запишем три раза уравнение Клапейрона-Менделеев – два раза для двух состояний газа в баллоне и для выпущенного газа при нормальных условиях:
Из уравнения (2) выразим искомую температуру газа T2:
Начальное количество вещества νν выразим из уравнения (1):
Количество вещества Δν, выпущенное из баллона, выразим из уравнения (3):
Тогда формула (4) примет вид:
Напомним, что нормальные условия – это давление p0p0, равное 100 кПа, и температура T0T0, равная 0° C или 273 К. Переведем объем баллона V в систему СИ:
Произведём вычисления:
Ответ: -18,2° C.
Пример 88:
Во сколько раз изменится объем кислорода массой 0,32 кг, если его давление увеличится в 3 раза, а температура уменьшится в 3 раза?
Решение от преподавателя:
Масса газа не будет изменяться, что даёт нам возможность применить объединённый газовый закон:
Выразим из этого равенства отношение конечного объема к начальному V2V1:
Согласно условию давление увеличится в 3 раза (p2=3p1), а температура упадёт в 3 раза (T2=T13), поэтому:
Так как мы получили дробь, которая меньше 1, значит объем уменьшился, то есть V1>V2. В данном случае он уменьшился в 9 раз.
Ответ: 1/9.
Пример 89:
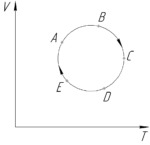
На рисунке показан график процесса, происходящего с идеальным газом. Укажите точки, соответствующие минимальному и максимальному давлению. Ответ обоснуйте.
Решение от преподавателя:
Для начала запишем уравнение Клапейрона-Менделеева:
Выразим из уравнения следующее отношение:
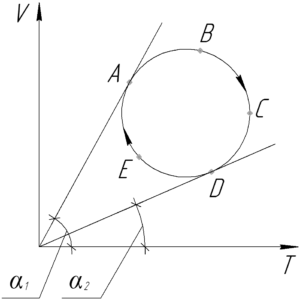
Для любой прямой на графике V-T, проведённой через начало координат, данное отношение равно тангенсу угла наклона прямой к положительному направлению оси T, то есть:
Значит точки, лежащие на одной такой прямой имеют одинаковое давление. При этом обратите внимание, что чем больше угол αα, тем меньше имеют давление точки, лежащие на этой прямой, и наоборот. Чтобы определить, где имеет место минимальное и максимальное давление, проведем касательные прямые к графику процесса через начало координат (смотрите схему).
Так как угол α1 – наибольший, то минимальное давление газ имеет в точке A. Поскольку угол α2 – наименьший, то максимальное давление газ оказывает в точке D.
Ответ: pmin – точка A, pmax – точка D.
Пример 90:
Баллон содержит газ при температуре 7° C и давлении 91,2 МПа. Каким будет давление, если из баллона выйдет 0,25 массы газа и при этом температура повысится до 27°C?
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для момента, когда в баллоне находилась масса газа m1m1, и для момента, когда из него выпустят некоторую массу газа, и она станет равной m2:
Подели нижнее уравнение на верхнее:
По условию из баллона выпустят 0,25 начальной массы, то есть справедливо отношение m2=0,75m1, поэтому:
В итоге получим такую формулу:
В условии задачи температуры даны в градусах Цельсия, их обязательно нужно перевести в Кельвины, поскольку именно в таком виде они фигурируют в уравнении Клапейрона-Менделеева:
Посчитаем ответ:
Ответ: 73,29 МПа.
Пример 91:
В баллоне находится газ при температуре 15° C. Во сколько раз изменится его давление, если 40% газа выйдет из баллона, а температура понизится на 8° C?
Решение от преподавателя:
Запишем дважды уравнение Клапейрона-Менделеева:
Так как 40% газа вышло из баллона, то справедливо равенство m2=0,6m1. Поскольку температура понизилась, значит
Поделим нижнее уравнение на верхнее, тогда получим:
Теперь обратите внимание на следующие факты: изменение температуры что в шкале Цельсия, что в шкале Кельвина выражается одинаковой величиной, поскольку цены деления обеих шкал равны, поэтому:
А вот начальную температуру нужно перевести в шкалу абсолютных температур:
Так как получившаяся дробь меньше единицы, значит давление уменьшилось (p2
Ответ: уменьшится в 1,72 раза.
Пример 92:
Сколько электронов заключается в 1 л кислорода при давлении 1 МПа и температуре 473 К?
Решение от преподавателя:
Кислород O – это 8-ой элемент периодической таблицы Д.И. Менделеева, то есть его зарядовое число Z равно 8. Это говорит о том, что атом кислорода O содержит 8 электронов на электронных оболочках (и 8 протонов в ядре). Но газ состоит не из атомов кислорода O, а молекул O2, образованных из двух атомов. Значит можно утверждать, что одна молекул кислорода содержит 16 электронов, и поэтому число электронов связано с числом молекул кислорода следующим соотношением:
Запишем уравнение Клапейрона-Менделеева, при этом количество вещества νν запишем как отношение числа молекул N к числу Авогадро NА:
Тогда учитывая равенство (1), число электронов Ne можно будет найти по формуле:
Переведем объем V в кубические метры и посчитаем ответ:
Ответ: 2,45·1024.
Пример 93:
Плотность пара некоторого соединения углерода с водородом равна 3 г/л при 43° C и 820 мм. рт. ст. Какова молекулярная формула этого соединения?
Решение от преподавателя:
Для начала запишем уравнение Клапейрона-Менделеева:
Если поделить обе части на объем газа V, то в правой части появится плотность газа ρ:
Давление газа в условии выражено длиной ртутного столба. Чтобы перевести её в единицы измерения СИ (Па), нужно воспользоваться формулой:
Плотность ртути ρрт равна 13600 кг/м3. Подставив выражение (2) в формулу (1), тогда получим:
Переведем плотность газа, длину ртутного столба и температуру в систему СИ:
Численно молярная масса газа M равна:
Такую молярную массу имеет углеводород пентан C5H12 .
Ответ: C5H12.
Пример 94:
В комнате объемом в 30 м3 температура с 15° C поднялась до 25° C. На сколько при этом изменилась масса воздуха в комнате, если атмосферное давление 100 кПа?
Решение от преподавателя:
Пример 95:
Баллон содержит сжатый газ при 27°C и давлении 3 МПа. Каково будет давление, если из баллона будет выпущена половина массы газа, а температура понизится до 7°C?
Решение от преподавателя:
Запишем два раза уравнение Клапейрона-Менделеева для начального и конечного состояния газа в баллоне:
Поделим нижнее уравнение на верхнее, тогда получим следующее равенство:
По условию из баллона была выпущена половина массы газа, т.е. m2=0,5m1, поэтому:
В конце концов получим такое решение задачи в общем виде:
Данные в условии задачи температуры переведём в систему СИ:
Произведём вычисления:
Ответ: 1,4 МПа.
Пример 96:
На сколько уменьшится масса воздуха в открытом сосуде, если его нагреть от 0 до 100° C? Начальная масса воздуха 373 г.
Решение от преподавателя:
В открытом сосуде давление всегда постоянно, при этом при повышении температуры масса воздуха в открытом сосуде будет уменьшаться. Пусть m – начальная масса воздуха, а Δm – масса части воздуха, которая покинула открытый сосуд в процессе нагревания. Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния воздуха:
Левые части уравнений равны, значит можно приравнять правые:
Переведем начальную массу в килограммы, а температуры – из градусов Цельсия в Кельвины:
Посчитаем ответ:
Ответ: 0,1 кг.
Пример 97:
Баллон содержит сжатый газ при 27°C и давлении 2000 кПа. Каково будет давление, если из баллона будет выпущено 0,3 массы газа, а температура понизится до 12°C?
Решение от преподавателя:
Для начального и конечного состояния газа в баллоне запишем уравнение Клапейрона-Менделеева:
Поделим нижнее уравнение на верхнее, тогда получим такое равенство:
В условии сказано, что из баллона выпущено 0,3 массы газа, значит справедливо равенство m2=0,7m1, поэтому:
В итоге мы получили следующее решение задачи в общем виде:
Переведём температуры в систему СИ:
Конечное давление p2 равно:
Ответ: 1330 кПа.
Пример 98:
Перед проведением газосварочных работ манометр баллона с кислородом показывал давление 10 МПа, а после сварки – 8 МПа. Какая часть кислорода была израсходована? Температура в баллоне не изменялась.
Решение от преподавателя:
Пусть m – начальная масса газа, а Δm – израсходованная масса газа. Тогда искомую величину αα можно найти по формуле:
Для начального и конечного состояния кислорода в баллоне запишем уравнение Клапейрона-Менделеева:
Как обычно, поделим нижнее уравнение на верхнее, тогда:
В правой части полученного равенства разделим числитель почленно на знаменатель:
Учитывая равенство (1), имеем:
В итоге:
Посчитаем ответ:
Ответ: 0,2.
Пример 99:
Газ при давлении 126,6 кПа и температуре 300 К занимает объем 0,6 м3. Найти объем газа при нормальных условиях.
Решение от преподавателя:
Применим объединённый газовый закон (уравнение Клапейрона):
Выразим из равенства объем газа при нормальных условиях V0:
Напомним, что нормальным условиям соответствует давление p0, равное 100 кПа, и температура T0, равная 0° C или 273 К. Посчитаем численное значение объема V0:
Ответ: 691 л.
Пример 100:
Газ при давлении 0,2 МПа и температуре 15° C имеет объем 5 л. Чему равен объем этой массы газа при нормальных условиях?
Решение от преподавателя:
Нормальные условия – это:
давление, равное 100 кПа, то есть нормальному атмосферному давлению;
температура, равная 0° C или 273 К (температура тройной точки воды).
Запишем уравнение Клапейрона (объединённый газовый закон):
Выразим отсюда искомый объем V0:
Переведем температуру t и объем V в систему СИ:
Посчитаем ответ:
Ответ: 9479 см3.
Пример 101:
Сосуд вместимостью 0,6 м3, содержащий гелий массой 2 кг, разорвался при температуре 400°C. Определите, какое максимальное количество азота можно хранить в таком сосуде при 30°C с учётом пятикратного запаса прочности.
Решение от преподавателя:
Запишем уравнение Клапейрона-Менделеева для гелия и азота:
Поделим верхнее уравнение системы на нижнее:
Запас прочности n – это отношение максимального давления к допустимому. Так как при давлении гелия p1 баллон разорвался, то максимальное давление равно p1. Допустимое давление в данном случае – это давление, при котором хранится азот p2.
Тогда равенство (1) примет вид:
Выразим искомую массу азота m2:
Молярная масса гелия M1 равна 0,004 кг/моль, азота M2 – 0,028 кг/моль. Переведём температуры в систему СИ:
Произведём вычисления:
Ответ: 6219 г.
Пример 102:
В сосуде объемом 10 литров находится 2 г водорода при температуре 2000 К. Определить давление газа, если при такой температуре половина молекул диссоциирована на атомы.
Решение от преподавателя:
При высокой температуре молекулярный водород H2 начинает диссоциировать (распадаться) на атомы. При этом отношение количества распавшихся молекул к начальному числу молекул водорода H2 называется степенью диссоциации α. В этой задаче степень диссоциации равна 0,5 согласно условию. Давление газа в сосуде будет равно сумме парциальных давлений атомарного (H) p1 и молекулярного (H2) p2 водорода согласно закону Дальтона.
Пусть до начала диссоциации в сосуде содержалось N молекул H2. Если степень диссоциации равна α, то число атомов водорода будет равно 2αN, так как из одной молекулы образуется два атома, а число молекул водорода – (1–α)N. Запишем уравнение Клапейрона-Менделеева для обоих газов, представив количество вещества как отношение числа частиц к числу Авогадро NА:
Поделим обе части представленных уравнений на объем V, тогда:
Оба выражения для давлений подставим в формулу (1):
Отношение числа молекул N к числу Авогадро NА равно количеству вещества νν, которое также можно найти по формуле:
Здесь M – молярная масса водорода, равная 0,002 кг/моль. В итоге получим такую окончательную формулу:
Переведём массу m и объем V в систему СИ:
Искомое давление p будет равно:
Ответ: 2,493 МПа.
Пример 103:
Воздух в сосуде объемом 5 л находится при температуре 27° C под давлением 2 МПа. Какую массу воздуха надо выпустить из сосуда, чтобы давление в нём упало до 1 МПа?
Решение от преподавателя:
Пусть m – начальная масса воздуха в сосуде, а Δm – масса выпущенной из сосуда части воздуха. Температуру газа в процессе будет считать постоянной. Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния воздуха:
Поделим нижнее уравнение на верхнее, тогда получим такое равенство:
Неизвестную начальную массу воздуха в сосуде mm найдём из уравнения (1):
Полученное выражение подставим в формулу (2) – так мы получим решение задачи в общем виде:
Перед подстановкой численных значений величин в формулу некоторые из них (объем V и температуру t) нужно перевести в систему СИ:
Произведём вычисления:
Ответ: 58 г.
Пример 104:
Некоторая масса водорода находится при температуре 200 К и давлении 0,4 кПа. Газ нагревают до температуры 10000 К, при которой молекулы водорода практически полностью распадаются на атомы. Найти давление после нагрева, если объем и масса газа не меняются.
Решение от преподавателя:
Пусть при температуре T1 в сосуде находилось N молекул водорода H2. Тогда при температуре T2, когда все молекулы водорода H2 распадутся на атомы H, в сосуде будет содержаться 2N атомов водорода (так как из одной молекулы образуется два атома). Значит, если изначально в сосуде содержалось количество вещества νν, то в конце оно будет равно 2ν.
Запишем уравнение Клапейрона-Менделеева для двух состояний газа, о которых говорится в условии:
Поделим нижнее уравнение на верхнее, тогда:
Посчитаем ответ:
Ответ: 40 кПа.
Пример 105:
Какова минимальная разница в массе воздуха зимой и летом при нормальном атмосферном давлении для комнаты объемом 100 м3, если летом температура в помещении повышается до 30° C, а зимой падает до 5° C?
Решение от преподавателя:
Давление в комнате в любое время года равно нормальному атмосферному давлению p (оно равно 100 кПа). При этом чем выше температура в комнате, тем меньше воздуха в ней содержится (это видно из нижеприведённых уравнений). Значит зимой воздуха в комнате больше, чем летом. Пусть m – масса воздуха в комнате летом, а Δm – разница в массе воздуха летом и зимой. Запишем уравнение Клапейрона-Менделеева для воздуха комнаты летом и зимой:
Из уравнения (1) выразим массу воздуха в комнате летом m:
Также, поскольку левые части уравнения равны, значит равны и правые:
Учитывая формулу (2), в итоге получим:
Молярная масса воздуха M равна 0,029 кг/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Переведём температуры в систему СИ:
Посчитаем численный ответ к задаче:
Ответ: 10,36 кг.
Калькулятор определяет плотность воздуха в зависимости от:
-
- давления воздуха;
- температуры воздуха;
- относительной влажности воздуха.
Определение плотности воздуха.
Примечание.
Расчеты №1 и №2 составлены на основании уравнения идеального газа. Формулы не учитывают влажность воздуха и коэффициент сжимаемости воздуха. В связи с этим в реальных условиях эти формулы применимы для воздуха низкого давления близкого к атмосферному (атмосферный воздух, воздух в системах вентиляции и кондиционирования). Учитывая, что количество водяных паров в воздухе относительно невелико, уменьшением плотности в практических расчетах система вентиляции и кондиционирования можно смело пренебречь. При проведении метрологических расчетов данные формулы не используются.
Расчет №3 составлен на основании формулы Е.3-1 из ГОСТ OIML R 111-1-2009 . Формула позволяет учесть влажность воздуха. При области применения формулы 900 мбар≤P≤1100 мбар, 15ºC≤t≤25ºC и ≤80% относительная неопределенность определения плотности воздуха, вычисленная по формуле (Е.3-1), не превышает 2·10%.
Расчеты №1, №2, №3 не предназначен для определения плотности сжатого воздуха.
В комментарии приветствуются пожелания, замечания и рекомендации по улучшению программы.
Поделиться ссылкой: