Тема: Определить поверхностную плотность зарядов (Прочитано 7408 раз)
0 Пользователей и 1 Гость просматривают эту тему.
1. 34. Определить поверхностную плотность зарядов на пластинах плоского слюдяного (ε = 7) конденсатора, заряженного до разности потенциалов U = 200 B, если расстояние между его пластинами равно d = 0,5 мм. Ответ: 3,54 мкКл/м2. Сделать рисунок.
Записан
Решение.
Разность потенциалов между обкладками конденсатора определим по формуле:
[ U=Ecdot d (1). ]
Напряженность поля между двумя пластинами конденсатора определяется по формуле:
[ E=frac{sigma }{varepsilon cdot {{varepsilon }_{0}}}(2). ]
Где: ε = 7 – диэлектрическая проницаемость слюды, ε0 = 8,854∙10-12 Ф/м – электрическая постоянная.
(2) подставим в (1) определим поверхностную плотность зарядов на пластинах плоского слюдяного конденсатора.
[ U=frac{sigma }{varepsilon cdot {{varepsilon }_{0}}}cdot d,sigma =frac{Ucdot varepsilon cdot {{varepsilon }_{0}}}{d}.sigma =frac{200cdot 7cdot 8,85cdot {{10}^{-12}}}{0,5cdot {{10}^{-3}}}=24,78cdot {{10}^{-6}}.
]
Оитвет: 24,78 мкКл/м2.
« Последнее редактирование: 16 Августа 2016, 16:26 от alsak »
Записан
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Будем искать не распределение плотности зарядов, а сами эти заряды, так как их легко можно получить умножением плотности на S.
Введем следующие обозначения
– заряд на внешней части верхней пластины, 
– заряд на внутренней части верхней пластины, 
– ее общий заряд
– заряд на внешней части нижней пластины, 
– заряд на внутренней части нижней пластины, 
– ее общий заряд
Мы имеем 4 неизвестные величины. Выпишем СЛУ для их нахождения:
Заряды на внеш. и внутр. частях пластины в сумме должны давать известную из условия величину q:
Рассмотрим поле внутри верхней пластины. Поле внутри проводника равно нулю. Таким образом, поле, создаваемое зарядом компенсируется полем, созданным зарядом , из чего можно заключить, что:
, аналогично
Решая данную СЛУ находим:
Верно ли?
В статье поле плоской пластины была выведена формула напряжённости электрического поля бесконечной плоской пластины. Если эту пластину рассмотреть в разрезе и ввести понятие поверхностной плотности заряда σ, то согласно указанной статьи в любой точке пространства напряжённость электрического поля направлена перпендикулярно плоскости пластины и по величине равно:
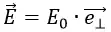
E0 здесь жёстко определяется поверхностной плотностью заряда σ:
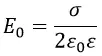
где σ – поверхностная плотность заряда;
ε0 – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.
Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.
Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.
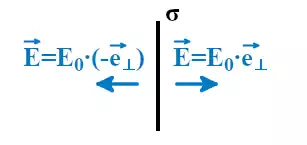
Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.
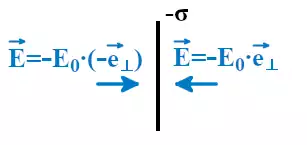
Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.
Расчёт и вывод формулы ёмкости плоского конденсатора
Напряжённость электрического поля конденсатора
Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.
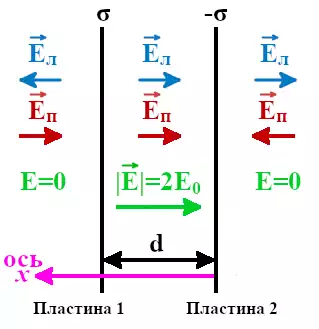
Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как Eл, при этом положительные заряды будут отталкиваться от пластины.
Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как Eп, при этом поле пластины будет притягивать к себе положительные заряды.
При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.
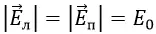
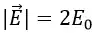
где E0 – напряжённость поля при положительной σ.
Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.
Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.
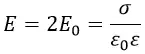
Работа по перемещению заряда
Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:
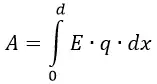
При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:
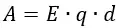
В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ1-ϕ2.
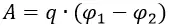
Напряжение между пластинами плоского конденсатора
Разность электрических потенциалов между двумя точками называют напряжением и обозначают U12:
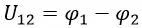
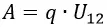
Таким образом, сравнивая две формулы для работы мы получим:
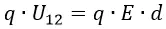
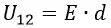
В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:
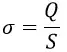
где Q – заряд пластины;
S – площадь пластины.
Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.
В таком случае имеем следующее выражение:
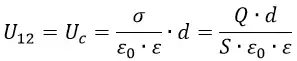
Напряжение между пластинами пропорционально полному заряду этих пластин:
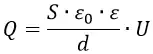
Электрическая ёмкость плоского конденсатора
Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:
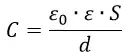
Подробности венецианская штукатурка для внутренней отделки цена на сайте.
