Идея представления функции в виде многочлена с остаточным слагаемым основана на разложении функции в степенной ряд.
Ряды Тейлора и Маклорена
Бесконечно дифференцируемую в точке x0x_0 функцию действительной переменной f(x)f(x) можно разложить в ряд по степеням двучлена (x−x0)(x-x_0):
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{”}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =
=∑k=0∞f(k)(x0)k!(x−x0)k=sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд называют рядом Тейлора.
В случае x0=0x_0=0, полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=f(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{”}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =
=∑k=0∞f(k)(x0)k!(x−x0)k=sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Запишем разложения основных элементарных функций в ряд Маклорена, укажем соответствующие интервалы сходимости и приведем примеры их определения.
- Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+…=∑k=1∞xnn!,∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+ldots=sumlimits_{k=1}^{infty} dfrac{x^n}{n!},quad |x|<infty
- Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+…=∑k=1∞(−1)k+1x2k−1(2k−1)!,∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{2 k -1}}{(2 k -1)!},quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+…=∑k=0∞(−1)kx2k(2k)!,∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{k}x^{2 k }}{(2 k)!},quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+…=∑k=0∞(−1)kx2k+12k+1,∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{ k }x^{2 k +1}}{2 k +1},quad |x|le{1}
- Логарифмическая функции:
ln(1+x)=x1!−x22!+x33!−x44!+…+(−1)n+1xnn!+…=∑k=1∞(−1)k+1xkk!,x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -dfrac{x^4}{4!} +ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{ k }}{ k!},quad xin (-1;1]
- Степенная функции:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+…=(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ldots=
=∑k=0∞α(α−1)…(α−k+1)k!xk=sumlimits_{ k =0}^{infty} dfrac{alpha (alpha -1) ldots ( alpha-k+1)}{ k!} {x^ k }
11−x=1+x+x2+…+xn+…=∑k=0∞xk,∣x∣<1dfrac{1}{1-x}=1+x+x^2+ldots+x^n+ldots =sumlimits_{ k =0}^{infty}x^{ k },quad |x|<1
Пример 1
Найдем для функции:
f(x)=sinxf(x)=sin x
интервал сходимости ряда:
f(x)=sinx==∑n=1∞(−1)n+1x2n−1(2n−1)!f(x)=sin x==sumlimits_{n=1}^{infty} dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}
Воспользуемся признаком Даламбера:
limn→∞∣an+1an∣=limn→∞∣x2n+1/(2n+1)!x2n−1/(2n−1)!∣=x2limn→∞12n(2n+1)=0limlimits_{n to infty } left | dfrac {a_{n+1}}{a_n} right | = limlimits_{n to infty } left | dfrac {x^{2n+1}/{(2n+1)!}}{ x^{2n-1}/{(2n-1)!}} right | =x^2 limlimits_{n to infty } dfrac {1} {2n(2n+1)}=0
Полученный результат говорит о том, что предел равен нулю для любого xx, и, следовательно, интервалом сходимости ряда является вся числовая ось.
Пример 2
Найдем интервал сходимости ряда для функции
f(x)=arctgx=∑n=0∞(−1)nx2n+12n+1,∣x∣≤1f(x)=arctg x= sumlimits_{n=0}^{infty} dfrac{(-1)^{n}x^{2n+1}}{2n+1}, quad |x|le{1}
Воспользовавшись признаком Даламбера применительно к степенному ряду, получаем:
limn→∞∣an+1an∣=limn→∞∣x2n+1/(2n+1)x2n−1/(2n−1)∣=x2limn→∞2n−12n+1=x2limn→∞2−1n2+1n=x2limlimits_{n to infty } left | dfrac {a_{n+1}}{a_n} right | = limlimits_{n to infty } left | dfrac {x^{2n+1}/(2n+1)}{ x^{2n-1}/(2n-1)} right | =x^2 limlimits_{n to infty } dfrac {2n-1} {2n+1}=x^2 limlimits_{n to infty } dfrac {2-dfrac{1}{n}}{2+dfrac{1}{n}}= x^2
Условие сходимости по этому признаку имеет вид:
x2<1x^2<1
В граничных точках x=±1x=pm1 получаем знакопеременный ряд вида:
∑n=0∞anx2n+1sumlimits_{n=0}^{infty} a_n x^{2n+1},
где ∣an∣=1n+1|a_n|=dfrac {1}{n+1}
Заметим, что
limn→∞∣an∣=0limlimits_{n to infty } |a_n|=0
и, согласно признаку Лейбница, знакопеременный ряд сходится. Таким образом, интервалом сходимости исходного ряда является: ∣x∣≤1|x| le 1.
Применение формулы и рядов Маклорена
Вычисление значений функций
Идея использования рядов для приближенного вычисления примечательна тем, что можно добиться требуемой точности, т.е. фактически найти требуемое значение со сколь угодно высокой точностью.
Пример
Вычислим значение числа ee с точностью до второго знака после запятой. Воспользуемся разложением в ряд Маклорена функции f(x)=exf(x)=e^x при x=1x=1, вычислив сумму до шестого члена в разложении и с остаточным членом в форме Лагранжа:
e1=1+11!+12!+13!+14!+15!+ec6!,0≤c≤1e^1=1+dfrac {1}{1!} +dfrac {1}{2!} +dfrac {1}{3!} +dfrac {1}{4!} +dfrac {1}{5!} +dfrac {e^c}{6!},quad 0le c le 1
Далее:
e1=16360!+ec6!≈2.716+ec6!,0≤c≤1e^1=dfrac {163}{60!} +dfrac {e^c}{6!}approx 2.716+dfrac {e^c}{6!},quad 0le c le 1
Учитывая, что ec6!<0.0014dfrac {e^c}{6!}<0.0014 получаем результат e≈2.72e approx 2.72
Вычисление пределов функций
На практике часто встречаются такие пределы, которые нельзя найти, используя первый и второй замечательные пределы, правило Лопиталя или другие способы вычислений. В этих случаях можно воспользоваться разложением элементарных функций в степенной ряд Маклорена и уже затем найти сам предел.
Пример
Вычислим:
limx→0e2x−1−2x−2x2x−sinxlimlimits_{x to 0 } dfrac {e^{2x}-1-2x-2x^2}{x-sin {x}}
Заменим exe^x и sinxsin{x} их разложениями в степенные ряды, находим:
limx→0e2x−1−2x−2x2x−sinx=limx→0(1+2x+4×22!+8×33!+…)−1−2x−2x2x−(x−x33!+x55!−…)=limlimits_{x to 0 } dfrac {e^{2x}-1-2x-2x^2}{x-sin {x}}=limlimits_{x to 0 } dfrac {left( 1+2x+dfrac{4x^2}{2!}+dfrac{8x^3}{3!}+ldots right)-1-2x-2x^2}{x-left( x-dfrac{x^3}{3!}+dfrac{x^5}{5!}-ldots right)}=
=limx→08×33!+16×44!+…x33!−x55!+…=limx→083!+16×4!+…13!−x25!+…=8=limlimits_{x to 0 } dfrac {dfrac{8x^3}{3!}+dfrac{16x^4}{4!}+ldots} {dfrac{x^3}{3!} -dfrac{x^5}{5!}+ldots} = limlimits_{x to 0 } dfrac {dfrac{8}{3!}+dfrac {16x}{4!} +ldots} {dfrac{1}{3!} -dfrac{x^2}{5!}+ldots}=8
Вычисление определенных интегралов
Конечно, на практике лучше всего вычислять точное значение определенного интеграла. Но очень часто соответствующие неопределенные интегралы является «неберущимися». Поэтому для приближенного вычисления определенного интеграла используется разложение подынтегральной функции в ряд Маклорена.
Пример
Вычислим с точностью до третьего знака после запятой:
∫01x3e−xdxdisplaystyle intlimits_0^1 sqrt[3] x e^{-x} dx
Для приближенного вычисления этого определенного интеграла используется разложение функции f(x)=sqrt[3]xe−xf(x)= sqrt[3] x e^{-x} в ряд Маклорена:
f(x)=sqrt[3]xe−x=x1/3−x4/3+12×7/3−16×10/3+…f(x)= sqrt[3] x e^{-x}=x^{1/3}-x^{4/3}+dfrac{1}{2}x^{7/3}-dfrac{1}{6}x^{10/3}+ldots
Интервал, заданный пределами интегрирования: 0≤x≤10 le x le 1 входит в радиус сходимости полученного ряда (−∞;+∞)(-infty;+infty).
Интегрируя почленно, получаем:
∫01f(x)=∫01×1/3dx−∫01×4/3dx+12∫01×7/3dx−16∫01×10/3dx+…=displaystyleintlimits_0^1 f(x)= intlimits_0^1 x^{1/3}dx-intlimits_0^1 x^{4/3}dx+dfrac{1}{2}intlimits_0^1 x^{7/3}dx-dfrac{1}{6}intlimits_0^1 x^{10/3}dx+ldots=
=34×4/3∣01−37×7/3∣01+32⋅10×10/3∣01−36⋅13×13/3∣01+…= dfrac{3}{4} Biggl. x^{4/3}Biggr |_0^1-dfrac{3}{7} Biggl. x^{7/3}Biggr |_0^1+dfrac{3}{2 cdot 10} Biggl. x^{10/3}Biggr |_0^1-dfrac{3}{6 cdot 13} Biggl. x^{13/3}Biggr|_0^1+ldots
и с учетом требуемой точности:
∫01x3e−xdx≈34−37+32⋅10−36⋅13≈928+29260≈197455≈0,433displaystyleintlimits_0^1 sqrt[3] x e^{-x} dx approx dfrac{3}{4}-dfrac{3}{7}+dfrac{3}{2 cdot 10}-dfrac{3}{6 cdot 13}approx dfrac{9}{28}+dfrac{29}{260} approx dfrac{197}{455} approx 0,433
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена.
Ряд Тейлора был известен задолго до публикаций Брука Тейлора[1] — его использовали ещё в XIV веке в Индии[2], а также в XVII веке Грегори и Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами.
В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье.
Определение[править | править код]
1. Многочленом Тейлора функции 



,
используемая в приближённых вычислениях, как обобщение следствия теоремы Лагранжа о среднем значении дифференцируемой функции:
- при
верно
.
При записи суммы использованы обозначение 


2. Рядом Тейлора в точке 



с общим членом
, зависящим от параметра
.
Другими словами, рядом Тейлора функции 


.[3]
Как указано ниже в примерах, наличия бесконечной дифференцируемости функции 


3. Рядом Тейлора в точке 


удовлетворяющей в некоторой окрестности 

называется степенной ряд
.
В отличие от вещественного случая, из условий следует, что найдётся такое значение радиуса 


4. В случае 
называется рядом Маклорена.
Аналитическая функция[править | править код]
1. Функция 








то есть 


Функция называется аналитической на промежутке (на множестве), если она является аналитической в каждой точке этого промежутка (множества).
2. Степенной ряд 


Если в 



Таким образом, для аналитической в точке 




Следствие. Функция 




3. Вопрос: будет ли для произвольной бесконечно дифференцируемой в точке 






Ответ: нет.
Существуют бесконечно дифференцируемые функции вещественной переменной, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности

Примеры. Функции вещественной переменной 

являются бесконечно дифференцируемыми в точке 
Следовательно, ряды Тейлора всех этих функций с параметром 
Однако, для любого 


в которых функции отличны от 
Таким образом, эти функции не являются в точке 
Доказательство
Доказательство проведём для функции 
Функция 
для всех 
Для 

Функция 



дополненная пределами слева
и справа 

Найдём производную функции 

По определению:

Поскольку для 

то
докажем, что для произвольного 

Применение правила Лопиталя непосредственно к частям
не приводит к результату.
Выполним замену переменной: 

Пусть 
Применяя правило Лопиталя 




.
Таким образом,
.
Найдём (для 
производных функции 
И так далее. Во всех случаях, очевидно,
получается произведение
на сумму целых отрицательных степеней

Конечная сумма
бесконечно малых является бесконечно малой.
Таким образом,

Вычисляя последовательно по определению (как выше) производные 

обнаруживаем, что все производные в
точке 
Область сходимости ряда Тейлора[править | править код]
Ряд Тейлора, являясь степенным рядом, имеет в качестве области сходимости круг (с центром в точке 
и интервал (с центром в точке 
1. Например, функция 





2. Радиус сходимости ряда Тейлора можно определить, например, по формуле Даламбера:
.
3. Рассмотрим для примера экспоненциальную функцию 



4. От параметра — точки разложения 
Например, разложим в общем случае (для произвольного 


Можно доказать с помощью формулы суммы геометрической прогрессии, что данный ряд, как функция аргумента 


Действительно,
.
Область сходимости ряда может быть задана неравенством 





Формула Тейлора[править | править код]
Предположим, что функция 









Достаточно легко доказать, что такой многочлен имеет вид 








Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена[править | править код]
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- В асимптотической форме (форме Пеано, локальной форме):
Критерий аналитичности функции[править | править код]
Основной источник: [5]
Предположим, что некоторую функцию 



Во-первых, необходимым условием аналитичности функции является сходимость ряда Тейлора в некоторой непрерывной области. Действительно, если ряд Тейлора сходится всего в одной точке, то это точка 

Во-вторых, по формуле Тейлора в ряд Тейлора с остаточным членом может быть разложена любая (а не только аналитическая) функция, бесконечно дифференцируемая в окрестности, содержащей точку 





Очевидно, что функция 






В качестве примера рассмотрим экспоненциальную функцию 



Остаточный член разложения этой функции в форме Лагранжа имеет вид 



Здесь используется, что на фиксированном промежутке экспонента ограничена некоторым числом 
Причем, как видно, предел остаточного члена равен нулю для любых 

Ряды Маклорена некоторых функций[править | править код]
- Гиперболические функции[6][10]:
- Обратные гиперболические функции[6][11]:
Формула Тейлора для функции двух переменных[править | править код]
Пусть функция 


Введём дифференциальный оператор
.
Тогда разложение (формула Тейлора) функции 



где 
Следует иметь в виду, что операторы 
в 



Аналогичным образом формула строится для функций любого числа переменных, меняется только число слагаемых в операторе 
В случае функции одной переменной 
Формула Тейлора многих переменных[править | править код]
Для получения формулы Тейлора функции 



Тогда разложение (формула Тейлора) функции по степеням 

где 

Для функции 


В другой форме ряд Тейлора можно записать таким образом:

Пример разложения в ряд Маклорена функции трёх переменных[править | править код]
Найдём выражение для разложения в ряд Тейлора функции трёх переменных 




Разложение в ряд Тейлора запишется в виде
Учитывая, что
получим
Например, при 
Примечания[править | править код]
- ↑ Taylor, Brook, Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (London, 1715), pages 21-23 (Proposition VII, Theorem 3, Corollary 2). Translated into English in D. J. Struik, A Source Book in Mathematics 1200—1800 (Cambridge, Massachusetts: Harvard University Press, 1969), pages 329—332.
- ↑ Gupta R. C. The Madhava-Gregory series, Math. Education 7 (1973), B67-B70.
- ↑ Запорожец Г. И. «Руководство к решению задач по математическому анализу» — С. 371
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления. — Мифрил, 1996. — С. Том 1, глава 4, параграф 6.
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления для втузов. — тринадцатое. — МОСКВА “НАУКА”, 1985. — С. Том 2, глава 16, параграф 16.
- ↑ 1 2 3 4 5 6 Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — 4-е изд. — М.: Наука, 1963.
- ↑ Цукер Р. Тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 37—43. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 44—47. — 832 с. — 50 000 экз.
- ↑ При значении x, близком к 1, эта расчётная формула сходится медленно, т.е. даёт большую погрешность при приближении функции суммой первых нескольких членов ряда. Поэтому можно воспользоваться формулой
где
- ↑ Цукер Р. Гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 48—49. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 50—53. — 832 с. — 50 000 экз.
Литература[править | править код]
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Камынин Л. И. Математический анализ. Т. 1, 2. — 2001.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Маркушевич А. И. Теория аналитических функций. В 2 т. — Изд. 2-е. — М.: Наука, 1967. — Т. 1: Начала теории. — 486 с.
- Нарасимхан Р. Анализ на действительных и комплексных многообразиях. — пер. с англ. Е. М. Чирки. — М.: Мир, 1971. — 232 с.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10—24.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 1. — 432 с.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 2. — 560 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3 т. — Изд. 8-е. — М.: ФИЗМАТЛИТ, 2003. — Т. I. — 680 с. — ISBN ISBN 5-9221-0156-0.
Формула Маклорена.
Колин Маклорен
(1698-1746) шотландский математик.
Формулой Маклорена
называется формула Тейлора при а
= 0:
![]()
![]()
Мы
получили так называемую формулу Маклорена
с остаточным членом в форме Лагранжа.
Следует отметить,
что при разложении функции в ряд
применение формулы Маклорена
предпочтительнее, чем применение
непосредственно формулы Тейлора, т.к.
вычисление значений производных в нуле
проще, чем в какой- либо другой точке,
естественно, при условии, что эти
производные существуют.
Однако, выбор числа
аочень важен для практического
использования. Дело в том, что при
вычислении значения функции в точке,
расположенной относительно близко к
точкеа, значение, полученное по
формуле Тейлора, даже при ограничении
тремя – четырьмя первыми слагаемыми,
совпадает с точным значением функции
практически абсолютно. При удалении же
рассматриваемой точки от точкиадля получения точного значения надо
брать все большее количество слагаемых
формулы Тейлора, что неудобно.
Т.е. чем больше по
модулю значение разности (х – а) тем
более точное значение функции отличается
от найденного по формуле Тейлора.
Кроме того, можно
показать, что остаточный член Rn+1(x)
является бесконечно малой функцией при
ха, причем долее
высокого порядка, чем (х – а)m,
т.е.
![]() .
.
Таким образом, ряд
Маклорена можно считать частным случаем
ряда Тейлора.
Представление некоторых элементарных функций по формуле Тейлора.
Применение формулы
Тейлора для разложения функций в
степенной ряд широко используется и
имеет огромное значение при проведении
различных математических расчетов.
Непосредственное вычисление интегралов
некоторых функций может быть сопряжено
со значительными трудностями, а замена
функции степенным рядом позволяет
значительно упростить задачу. Нахождение
значений тригонометрических, обратных
тригонометрических, логарифмических
функций также может быть сведено к
нахождению значений соответствующих
многочленов.
Если при разложении
в ряд взять достаточное количество
слагаемых, то значение функции может
быть найдено с любой наперед заданной
точностью. Практически можно сказать,
что для нахождения значения любой
функции с разумной степенью точности
(предполагается, что точность, превышающая
10 – 20 знаков после десятичной точки,
необходима очень редко) достаточно 4-10
членов разложения в ряд.
Применение принципа
разложения в ряд позволяет производить
вычисления на ЭВМ в режиме реального
времени, что немаловажно при решении
конкретных технических задач.
Функция f(x)
= ex.
Находим: f(x)
=ex,f(0) = 1
f(x)
= ex,
f(0)
= 1
……………………
f(n)(x)
= ex, f(n)(0)
= 1
[an error occurred while processing
this directive]
Тогда: ![]()
Пример:Найдем
значение числа е.
В полученной выше
формуле положим х = 1.
![]()
Для 8 членов разложения:
e= 2,71827876984127003
Для 10 членов разложения:
e= 2,71828180114638451
Для 100 членов разложения:
e = 2,71828182845904553
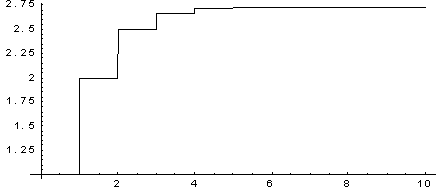
На графике показаны
значения числа е с точностью в зависимости
от числа членов разложения в ряд Тейлора.
Как
видно, для достижения точности, достаточной
для решения большинства практических
задач, можно ограничиться 6-7 – ю членами
ряда.
Функция f(x)
= sinx.
Получаем f(x)
=sinx;f(0)
= 0
f(x)
=cosx=sin(x+/2); f(0)
= 1;
f(x)
= -sinx = sin(x + 2/2);
f(0)
= 0;
f(x)
= -cosx = sin(x + 3/2);
f(0)=-1;
…………………………………………
f(n)(x)
= sin(x + n/2);
f(n)(0)
= sin(n/2);
f(n+1)(x)
= sin(x + (n + 1)/2); f(n+1)()
= sin(
+ (n + 1)/2);
Итого: 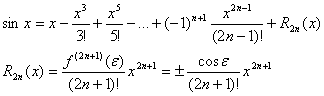
Функция f(x)
= cosx.
Для функции cosx,
применив аналогичные преобразования,
получим:
![]()
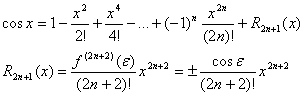
Функция
f(x) = (1 + x).
[an error occurred while
processing this directive]
(- действительное число)
![]()
![]()
…………………………………………………..
![]()
Тогда:
![]()
![]()
Если в
полученной формуле принять =n, гдеn-
натуральное число иf(n+1)(x)=0,
тоRn+1= 0, тогда
![]()
Получилась
формула, известная как бином Ньютона.
Пример:Применить
полученную формулу для нахождения
синуса любого угла с любой степенью
точности.
На приведенных
ниже графиках представлено сравнение
точного значения функции и значения
разложения в ряд Тейлора при различном
количестве членов разложения.
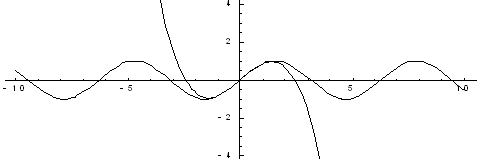
Рис. 1. Два члена разложения
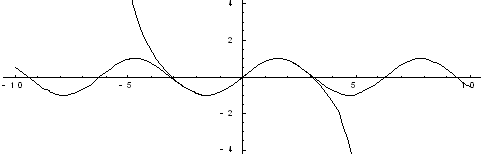
Рис. 2. Четыре члена разложения
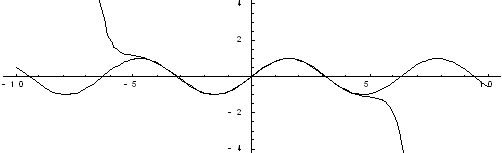
Рис. 3. Шесть членов разложения
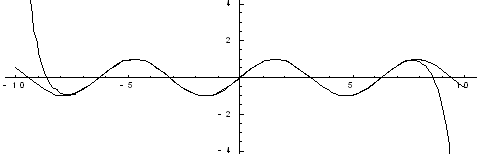
Рис. 4. Десять
членов разложения
Чтобы получить
наиболее точное значение функции при
наименьшем количестве членов разложения
надо в формуле Тейлора в качестве
параметра авыбрать такое число,
которое достаточно близко к значениюх, и значение функции от этого числа
легко вычисляется.
Для
примера вычислим значение sin200.
Предварительно
переведем угол 200в радианы: 200=/9.
Применим
разложение в ряд Тейлора, ограничившись
тремя первыми членами разложения:
![]()
В четырехзначных
таблицах Брадиса для синуса этого угла
указано значение 0,3420.
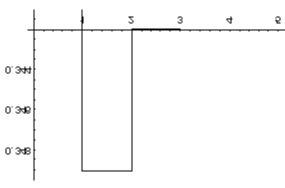
На графике показано
изменение значений разложения в ряд
Тейлора в зависимости от количества
членов разложения. Как видно, если
ограничиться тремя членами разложения,
то достигается точность до 0,0002.
Выше говорилось,
что при х0 функцияsinxявляется бесконечно
малой и может при вычислении быть
заменена на эквивалентную ей бесконечно
малую функцию х. Теперь видно, что при
х, близких к нулю, можно практически
без потери в точности ограничиться
первым членом разложения, т.е.sinxx.
Пример:
Вычислить sin2801315.
[an error occurred while processing this
directive]
Для
того, чтобы представить заданный угол
в радианах, воспользуемся соотношениями:
10=
![]() ;
;
280![]() ;
;
1![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() рад
рад
Если при разложении
по формуле Тейлора ограничиться тремя
первыми членами, получим: sinx=
![]() .
.
Сравнивая полученный
результат с точным значением синуса
этого угла,
sin![]() =
=
0,472869017612759812,
видим, что даже при
ограничении всего тремя членами
разложения, точность составила 0,000002,
что более чем достаточно для большинства
практических технических задач.
Функция f(x)
= ln(1 + x).
Получаем: f(x)
= ln(1 + x); f(0)
= 0;
f(x)
=
![]() ;
; ![]()
![]()
![]()
![]()
![]()
………………………………………
![]()
![]()
Итого:
![]()
![]()
![]()
Полученная формула
позволяет находить значения любых
логарифмов (не только натуральных) с
любой степенью точности. Ниже представлен
пример вычисления натурального логарифма
ln1,5. Сначала получено
точное значение, затем – расчет по
полученной выше формуле, ограничившись
пятью членами разложения. Точность
достигает 0,0003.
ln1,5 = 0,405465108108164381
![]()
Разложение
различных функций по формулам Тейлора
и Маклорена приводится в специальных
таблицах, однако, формула Тейлора
настолько удобна, что для подавляющего
большинства функций разложение может
быть легко найдено непосредственно.
Ниже будут рассмотрены
различные применения формулы Тейлора
не только к приближенным представлениям
функций, но и к решению дифференциальных
уравнений и к вычислению интегралов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Формула Тейлора и ее применение
Формула Тейлора
Теорема: Если функция 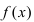
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора 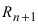 называется остаточным членом, вид которого установил Лагранж:
называется остаточным членом, вид которого установил Лагранж: 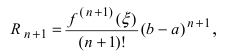 величина
величина 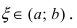
В этой формуле неизвестной является только величина 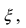 причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид:
причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид: 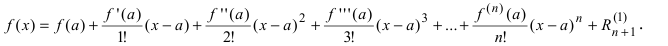
При a = 0 формула Тейлора переходит в формулу Маклoрена:
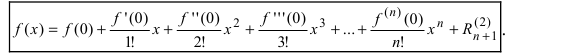
Пример:
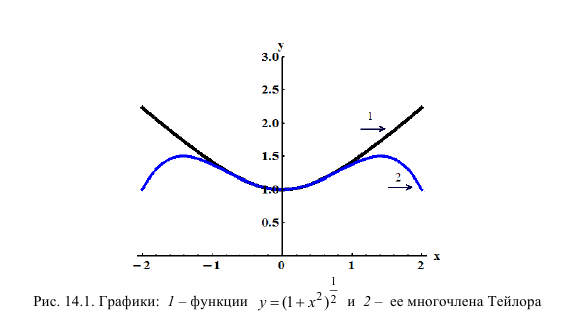
Представить по формуле Маклорена функцию 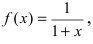 ограничившись n=2.
ограничившись n=2.
Решение:
Вычислим три первых производных заданной функции:
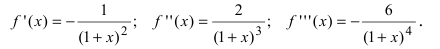 При х = 0 получим
При х = 0 получим 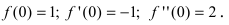 Остаточный член имеет вид
Остаточный член имеет вид 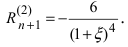 Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид:
Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид: 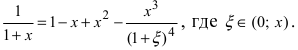 Отметим, что полученное выражение справедливо при
Отметим, что полученное выражение справедливо при 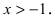 Решим найденное равенство относительно величины
Решим найденное равенство относительно величины 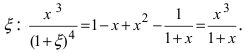 Отсюда получаем
Отсюда получаем 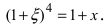 Следовательно,
Следовательно, 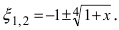 Так как выражение под радикалом 4-ой степени должно быть неотрицательным и
Так как выражение под радикалом 4-ой степени должно быть неотрицательным и 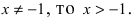 Таким образом, из двух корней теореме Тейлора удовлетворяет только корень
Таким образом, из двух корней теореме Тейлора удовлетворяет только корень 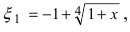 который действительно лежит между нулем и х.
который действительно лежит между нулем и х.
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
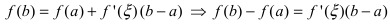 (см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем
(см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем 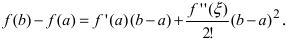 Если положить
Если положить 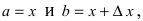 то получим формулу
то получим формулу
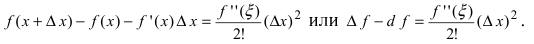
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 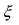 в остаточном члене в форме Лагранжа лежит в пределах от а до х.
в остаточном члене в форме Лагранжа лежит в пределах от а до х.
Пример:
Представить функцию 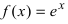 по формуле Маклорена.
по формуле Маклорена.
Решение:
Так как 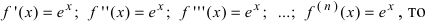
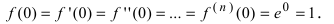 Следовательно,
Следовательно, 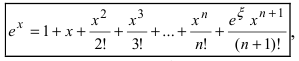 где
где 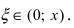 Отсюда следует,
Отсюда следует, 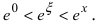
Пример:
Вычислить 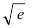 с точностью
с точностью 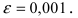
Решение:
Так как основание 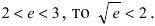 Следовательно, при х = 1/2 остаточный член равен
Следовательно, при х = 1/2 остаточный член равен 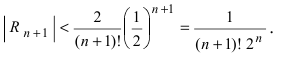 При n = 3: остаточный член
При n = 3: остаточный член 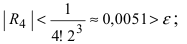
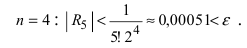 Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что
Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что 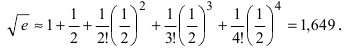
Пример:
Вычислить число е с точностью 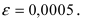
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа 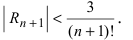
При n = 6 имеем 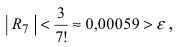
при n = 7 получаем 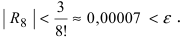
Итак, 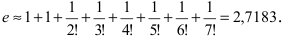
Если вычислять значение числа е с точностью 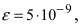 то потребуется взять 13 первых слагаемых, при этом
то потребуется взять 13 первых слагаемых, при этом 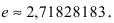 Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций. Например, для вычисления натуральных логарифмов используется формула:
Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций. Например, для вычисления натуральных логарифмов используется формула: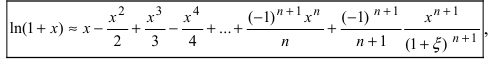 причем
причем 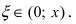
Пример:
Вычислить 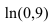 с точностью
с точностью 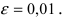
Решение:
В данном примере х = -0,1. Так как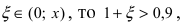 следовательно, остаточный член
следовательно, остаточный член 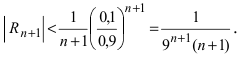 При n = 1 получаем
При n = 1 получаем 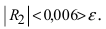 Следовательно, достаточно взять первый член в формуле Маклорена-Тейлора
Следовательно, достаточно взять первый член в формуле Маклорена-Тейлора 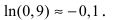
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке 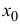 . Тогда (см. формулу (9.5)) ее приращение
. Тогда (см. формулу (9.5)) ее приращение 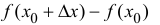
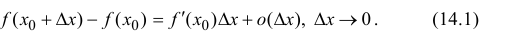
Пусть 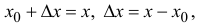 тогда (14.1) перепишется в виде
тогда (14.1) перепишется в виде 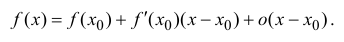
Рассмотрим многочлен 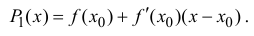
Многочлен 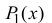 обладает следующими свойствами:
обладает следующими свойствами:
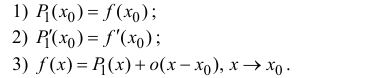
Пусть функция y=f(x) n раз дифференцируема в точке 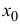 . Найдем многочлен
. Найдем многочлен
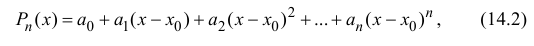
обладающий аналогичными свойствами:
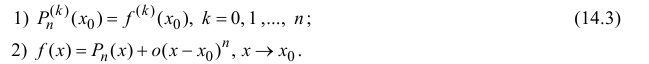
Из (14.2), (14.3) следует, что
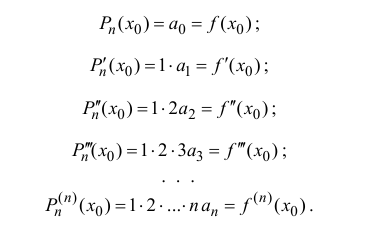
Поэтому коэффициенты 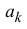 многочлена (14.2) задаются формулой
многочлена (14.2) задаются формулой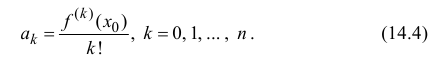
Далее

Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 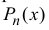 задаются формулами (14.4)). Тем самым теорема доказана.
задаются формулами (14.4)). Тем самым теорема доказана.
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке 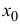 , тогда
, тогда
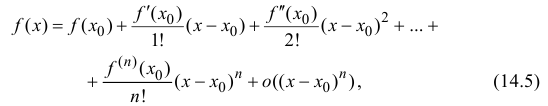
где 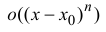 – бесконечно малая функция более высокого порядка
– бесконечно малая функция более высокого порядка
малости, чем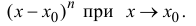
Формула (14.5) называется формулой Тейлора, многочлен
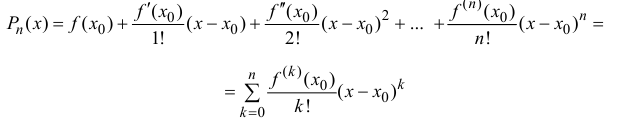
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности 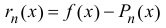 в виде
в виде 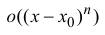 – остаточным членом в форме Пеано.
– остаточным членом в форме Пеано.
Если функция 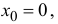 то (14.5) перепишется в виде
то (14.5) перепишется в виде
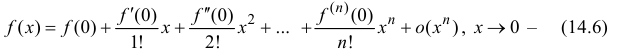
формула Маклорена.
Если функция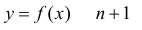 раз дифференцируема в некоторой окрестности
раз дифференцируема в некоторой окрестности
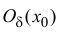 точки
точки 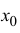 , то остаточный член
, то остаточный член 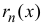 можно представить в виде
можно представить в виде
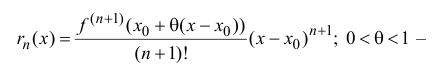 остаточный член в форме Лагранжа и формула
остаточный член в форме Лагранжа и формула
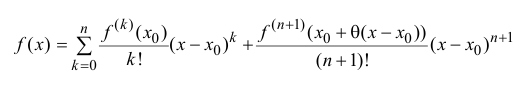
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений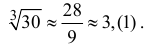
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа:
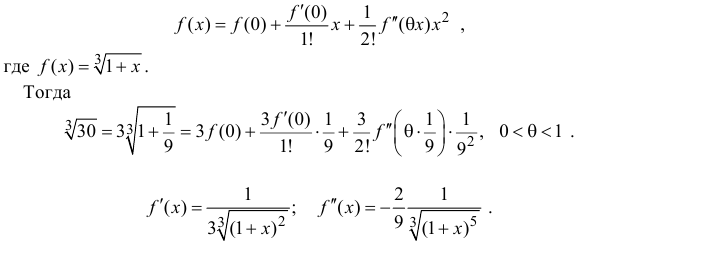
Поэтому
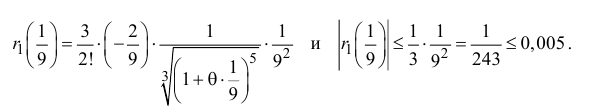
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
- Заказать решение задач по высшей математике
Пример 14.3
Разложить 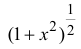 по формуле Маклорена до члена
по формуле Маклорена до члена 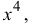 используя основные разложения. Оценить погрешность при
используя основные разложения. Оценить погрешность при 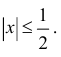
Решение
Пусть 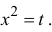 Тогда (см. формулу (14.10))
Тогда (см. формулу (14.10))
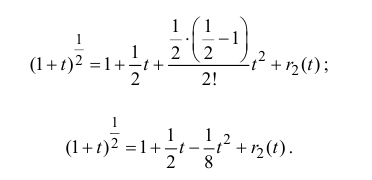
Остаточный член запишем в форме Лагранжа:
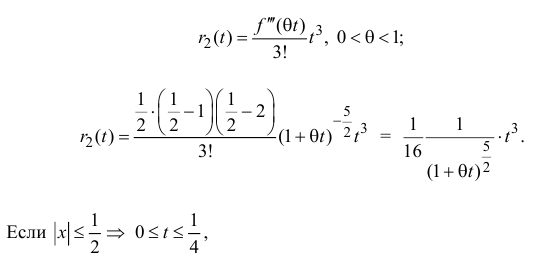
поэтому 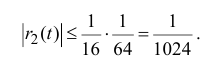
Таким образом, 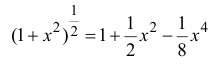 и погрешность при
и погрешность при 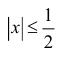 меньше чем
меньше чем
Пример 14.4
Найти 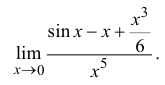
Решение
Воспользуемся разложением (14.7):
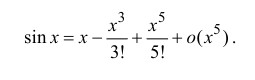
Тогда
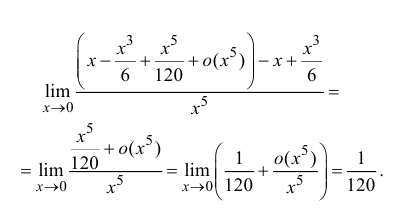
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
Разложение по формуле Маклорена некоторых элементарных функций
Содержание:
- Использование формулы Маклорена
- Правило Лопиталя





По этой ссылке вы найдёте полный курс лекций по математике:
Представим формулой Маклорена некоторые элементарные функции. Имеем По формуле (1) будем иметь Поскольку сумма дает приближенное значение числа е с недостатком и погрешностью, меньшей Имеем Следовательно, в многочлене Тейлора для sin х обращаются в нуль коэффициенты при четных степенях х,так что (2п + 1)-й многочлен и (2п + 2)-й многочлен тождественны между собой.
По формуле Маклорена (1), беря n = 2fc + 1, получим 0, если m = 2k, если m = 2k + 1, Очевидно, Имеем если Поэтому в силу формулы (1) (если взять Очевидно, Формулами (4) и (5) можно пользоваться для вычисления приближенных значений sin х и cos х с любой степенью точности. На рис. 6 и 7 показано приближение функций sin х и cos х в окрестности точки х = 0 многочленами Тейлора этих функций. Эта функция определена и дифференцируема любое число раз для х > -1.
Имеем В силу формулы Маклорсна (I) где 1 Имеем Разложение по формуле Маклорена некоторых элементарных функций.
Использование формулы Маклорена
Использование формулы Маклорена для получения асимптотических оценок элементарных функций и вычисления пределов где Если a — m — натуральномучислу,товсечленыформулы (1) начинаяс (m + 1 )-ro исчезают, и формула Маклорена превращается в известную формулу бинома Ньютона §5.
Использование формулы Маклорена для получения асимптотических оценок элементарных функций и вычисления пределов.
В свое время мы установили асимптотические формулы для элементарных функций (глава VIII, §17). Формулы (1) дают представление элементарных функций при малых значениях )х|. Мы пользовались ими при вычислении простейших пределов. Для вычисления более тонких пределов, когда определяющую роль играют члены высокого порядка относительно х при х —♦ 0, формулы (1) оказываются недостаточными.
Возможно вам будут полезны данные страницы:
Поэтому возникает необходимость получить более точные асимптотические оценки для элементарных функций. Такие оценки легко получаем из формулы Маклорена, если в этой формуле взять остаточный член в форме Пеано. Приведем эти оценки: Пример. Найти предел * При помощи формул (1) предел этот найти невозможно, поскольку по виду знаменателя можно заключить, что определяющую роль играют члены 3-го порядка относительно х (х -* 0).
Поэтому воспользуемся оценками (2).
Правило Лопиталя
Получим Упражнения Применяя правило Лопиталя, найдите пределы 10. Разложите многочлен по степеням двучлена 11. Разложите м ногочлен х3 – 2х2 + Зх + 5 по степеням двучлена х – 2. 12. Разложите по формуле Тейлора функцию /(х) = -я в окрестности точки хо = -1. 13. Разложите по формуле Тейлора функцию /(х) = хе’ в окрестности точки х0 = О (формула Маклорена). 14. Разложите по формуле Маклорена до о(х”) функцию /(х) = е>+2. 15. Тяжелая нить под действием собственного веса провисает по цепной линии у – ci ch J (a – const). Покажите, что для малых |х| форма нити приближенно выражается параболой. Используя формулу Маклорена. найдите пределы:
Лекции:
- Некоторые простые уравнения. Уравнения координатных плоскостей
- Ряды Фурье. Тригонометрические ряды. Ортогональность тригонометрической системы
- Тела вращения
- Дифференцируемость функции. Дифференциал функции
- Биномиальный закон распределения
- Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- Признаки равенства треугольников
- Понятие обратной функции. Производная обратной функции
- Преобразование Фурье. Интеграл Фурье. Комплексная форма интеграла
- Функциональные ряды






![{displaystyle R_{n}(x)={(x-a)^{n+1} over (n+1)!}f^{(n+1)}[a+theta (x-a)]qquad p=n+1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9581ea19ed64de9723d6f3725f0470e9a0f23c)
![{displaystyle R_{n}(x)={(x-a)^{n+1}(1-theta )^{n} over n!}f^{(n+1)}[a+theta (x-a)]qquad p=1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616cdc3cb043af06990a174a073b35ea0e3fbee1)

![{displaystyle R_{n}(x)=o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eca3be3644e41dedb8f25e26357ddb9a08386d)


![R_n(x,y)=dfrac {mathrm{T}^{(n+1)} f(xi,zeta)} {(n+1)!}, xi in [x_0,x], zeta in [y_0,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/144e134c30b8d4c579305c2bbaf6591647deb6c9)











