Как найти по какой прямой пересекаются плоскости

Данная глава рассказывает о том, как найти координаты точки пересечения прямой с плоскостью при заданных уравнениях, определяющих эту плоскость. Будет рассмотрено понятие точки пересечения прямой с плоскостью, два способа нахождения координат точки пересечения прямой с плоскостью.

Точка пересечения прямой  и плоскости – определение

Для углубленного изучения теории необходимо начать рассмотрение с  понятия точки, прямой, плоскости. Понятие о точке, прямой линии рассматривается как  на плоскости, так и в пространстве. Для детального рассмотрения необходимо обратиться к теме о прямой  и плоскости в пространстве.

Существует несколько вариаций расположения прямой относительно плоскости и пространства:

• прямая лежит в плоскости;
• прямая параллельна плоскости;
• прямая пересекает плоскость.

Если рассмотреть третий случай, то отчетливо видно, что прямая с плоскостью при пересечении образуют общую точку, которую  называют точкой пересечения прямой  и плоскости. рассмотрим данный случай на примере.

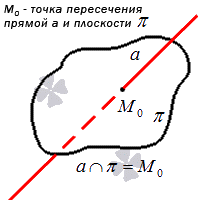
Нахождение координат точки пересечения прямой и плоскости

Была введена прямоугольная система координат Охуz трехмерного пространства.  Каждая прямая имеет свое собственное уравнение, а каждая плоскость соответствует своему заданному уравнению, каждая точка имеет определенное количество действительных чисел – координат.

Чтобы подробно разобраться в теме координат пересечения, необходимо знать все виды уравнения прямой в пространстве и уравнений плоскости. в данном случае пригодятся знания о переходе от одного вида уравнения к другому.

Рассмотрим задачу, которая основывается на заданном пересечении прямой и плоскости. она сводится к нахождению координат пересечений.

Если координаты точки пересечения являются решением обоих уравнений, то они пересекаются.

Первый способ нахождения координат пересечения прямой и плоскости.

Когда задается прямая a  с плоскостью α прямоугольной системы координат, известно, что они пересекаются в точке М0. Для начала займемся поиском координат заданной точки пересечения при заданном уравнении плоскости, имеющего вид Ax+By+Cz+D=0 с прямой линией a, являющейся пересечением плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Данный способ задания прямой в пространстве рассматривается в статье уравнения прямой и уравнения двух пересекающихся плоскостей.

Необходимые нам координаты прямой a и плоскости α должны удовлетворять обоим уравнениям. Таким образом задается система линейных уравнений, имеющая вид

Ax+By+Cz+D=0A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0

Решение системы подразумевает обращение каждого тождества в верное равенство. Следует отметить, что при таком решении мы определяем координаты пересечения 3 плоскостей вида Ax+By+Cz+D=0, A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Для закрепления материала рассмотрим решение данных задач.

Система уравнений вида Ax+By+Cz+D=0A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 имеет одно единственное решение. Когда прямая a определена такими уравнениями, как A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, а плоскость α задается уравнением Ax+By+Cz+D=0, то они пересекаются. Когда прямая лежит в плоскости, система выдает бесконечное множество решений. При их параллельности уравнение решений не имеет, так как нет общих точек пересечения.

Когда прямая имеет задана параметрическим или каноническим уравнением, то отсюда можно найти уравнение пересекающихся плоскостей, которые определяют прямую a, после чего искать необходимые координаты точки пересечений. Имеется еще один метод, который применяется для  нахождения координат точки пересечения прямой и плоскости.

Второй способ нахождения точки начинается с  задания прямой a, пересекающей плоскость α в точке М0. Необходимо найти координаты заданной точки пересечения при заданном уравнении плоскости Ax+By+Cz+D=0. Прямую а определяем параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λz=z1+az·λ , λ∈R.

Когда в уравнение Ax+By+Cz+D=0 производится подстановка x=x1+ax·λ, y=y1+ay·λ, z=z1+az·λ,  выражение примет вид уравнения с неизвестной λ. Необходимо разрешить его относительноλ, тогда получим λ=λ0, которое соответствует координатам точки, в которой они пересекаются. Вычисление координат точки производится  из x=x1+ax·λ0y=y1+ay·λ0z=z1+az·λ0.

Подробнее этот способ будет рассмотрен на примерах, приведенных ниже.

Когда прямая вида x=x1+ax·λy=y1+ay·λz=z1+az·λ, λ∈R принадлежит плоскости Ax+By+Cz+D=0, тогда необходимо подставить туда уравнение плоскости выражения x=x1+ax·λ, y=y1+ay·λ, z=z1+az·λ, тогда получим тождество такого вида 0≡0. При параллельности плоскости и прямой получаем неверное равенство, так как нет точек пересечения.

Если прямая задана каноническим уравнением, имеющим вид x-x1ax=y-y1ay=z-z1az, тогда необходимо переходить от канонических к параметрическим при поиске координат точки пересечения прямой с плоскостью Ax+By+Cz+D=0, то есть получим x-x1ax=y-y1ay=z-z1az⇔x=x1+ax·λy=y1+ay·λz=z1+az·λ и применим необходимы способ для нахождения координат точки пересечения заданной прямой и плоскости в пространстве.

Линия
пересечения двух плоскостей – прямая
линия. Рассмотрим сначала частный случай
(рис. 3.9), когда одна из пересекающихся
плоскостей параллельна горизонтальной
плоскости проекций (α ׀׀
π₁,
f⁰_α
׀׀Х).
В этом случае линия пересечения а,
принадлежащая плоскости α,
будет также параллельна плоскости π₁,
(рис. 3.9. а) т.
е. будет совпадать с горизонталью
пересекающихся плоскостей (а ≡ h).

Если одна из
плоскостей параллельна фронтальной
плоскости проекций (рис. 3.9. б), то линия
пересечения а, принадлежащая этой
плоскости, будет параллельна плоскости
π₂
и будет совпадать с фронталью
пересекающихся
плоскостей (а ≡ f).

а)
б)

Рис. 3.9. Частный
случай пересечения плоскости общего
положения с плоскостями: а) горизонтального
уровня; б) фронтального уровня

Пример построения
точки пересечения (К) прямой а (АВ) с
плоскостью α (DEF)
показан на рис. 3.10. Для этого прямая а
заключена в произвольную плоскость β
и определена линия пересечения плоскостей
α и β.

В рассматриваемом
примере прямые АВ и MN
принадлежат одной плоскости β и
пересекаются в точке К, а т. к. прямая MN
принадлежит заданной плоскости α (DEF),
то точка К является и точкой пересечения
прямой а (АВ) с плоскостью α. (рис. 11).

Рис. 3.10. Построение
точки пересечения прямой с плоскостью

Для решения подобной
задачи на комплексном чертеже необходимо
уметь находить точку пересечения прямой
общего положения с плоскостью общего
положения.

Рассмотрим пример
нахождения точки пересечения прямой
АВ c
плоскостью треугольника DEF
представленный на рис. 3.11.

Для нахождения
точки пересечения через фронтальную
проекцию прямой А₂В₂
проведена фронтально-проецирующая
плоскость β которая пересекла треугольник
в точках M
и N.
На фронтальной плоскости проекций (π₂)
эти точки представлены проекциями M₂,
N₂.
Из условия принадлежности прямой
плоскости на горизонтальной плоскости
проекций (π₁)
находятся горизонтальные проекции
полученных точек M₁
N₁.
В пересечении горизонтальных проекций
прямых А₁В₁
и M₁N₁
образуется горизонтальная проекция
точки их пересечения (К₁).
По линии связи и условиям принадлежности
на фронтальной плоскости проекций
находится фронтальная проекция точки
пересечения (К₂).

В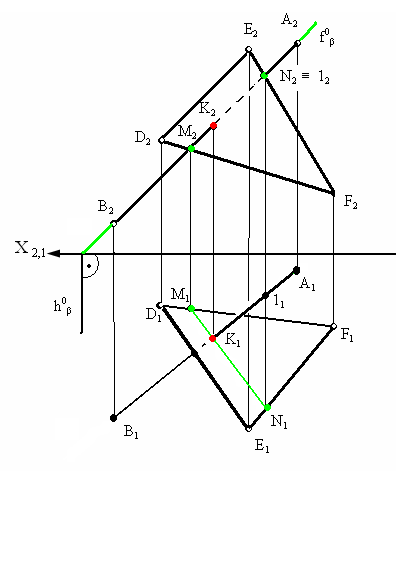идимость
отрезка АВ относительно треугольника
DEF
определена методом конкурирующих
точек.

На плоскости π₂
рассмо- трены две точки NEF
и

Рис. 3.11. Пример
определения точки

пересечения прямой
и плоскости

1АВ.
По горизонтальным проекциям этих
точек можно установить, что точка N
рас- положена ближе к наблюда-
телю (Y_N>Y₁
), чем точка 1 (направление луча
зрения параллельно S).
Следовательно, прямая АВ, т. е. часть
прямой АВ (К₁)
закрыта плоскостью DEF
на плоскости π₂
(ее проекция К₂1₂
показана штриховой линией). Аналогично
установлена видимость на плоскости
π₁.

Вопросы для
самоконтроля

1. В чем заключается
   сущность метода конкурирующих точек
   ?

2. Свойства прямой.

3. Каков алгоритм
   определения точки пересечения прямой
   и плоскости ?

4. Каков алгоритм
   определения линии пересечения плоскостей
   ?

5. Какие задачи
   называются позиционными ?

6. Сформулируйте
   условия принадлежности прямой плоскости.

Соседние файлы в папке Лекции нг

• #
• #
• #
• #
• #
• #
• #
• #



5.3.4. Взаимное расположение двух плоскостей

С параллельными плоскостями мы только что столкнулись и сейчас разовьём тему. Рассмотрим две плоскости пространства, заданные общими уравнениями:

Они могут:

1) совпадать;

2) быть параллельными: ;

3) пересекаться по некоторой прямой «эль»: .

По пунктам:

1) Совпадающие плоскости

Две плоскости совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства

Рассмотрим плоскости  и составим систему:

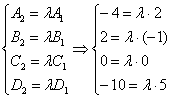
Из каждого уравнения системы следует, что . Таким образом, система совместна и плоскости  совпадают.

2) Параллельные плоскости

Две плоскости параллельны тогда и только тогда, когда их коэффициенты при переменных  пропорциональны: , но

На практике первые три коэффициента часто банально попарно совпадают :
 (Задача 139),  но могут и не совпадать, как, например, в следующей Задаче 140:

.

Убедимся, что эти прямые действительно параллельны. Составим пропорцию из соответствующих коэффициентов , но , что и требовалось проверить. Теперь способ академический, составим соответствующую систему:

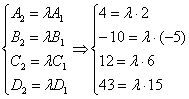
Из первых трёх уравнений следует, что , а из четвёртого уравнения следует, что , значит, система несовместна, но коэффициенты при переменных  пропорциональны, следовательно, плоскости параллельны.

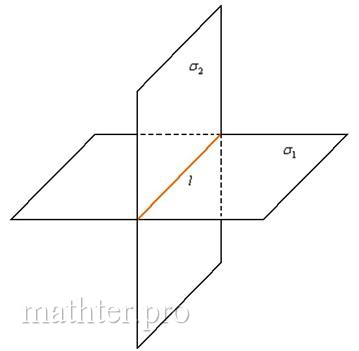
3) Пересекающиеся плоскости

И третий, самый распространённый случай, когда две плоскости пересекаются по некоторой прямой :
Две плоскости пересекаются тогда и только тогда, когда их коэффициенты при переменных  НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Попутно заметим важный факт: если плоскости  пересекаются, то система линейных уравнений  задаёт уравнение прямой в пространстве.

Но о пространственной прямой позже.

В качестве примера рассмотрим плоскости . Составим систему для соответствующих коэффициентов:

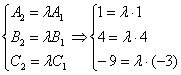
Из первых двух уравнений следует, что , но из третьего уравнения следует, что , значит, система несовместна и плоскости пересекаются.
Проверку можно выполнить и «по пижонски», одной строкой: .
И из этого случая логично вытекает следующий параграф:

5.3.5. Как найти угол между плоскостями?

5.3.3. Как найти расстояние между плоскостями?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Линия пересечения плоскостей онлайн

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

α1:  A1x+B1y+C1z+D1=0,

(1)

α2:  A2x+B2y+C2z+D2=0,

(2)

где n₁={A₁, B₁, C₁} и n₂={A₂, B₂, C₂} − нормальные векторы плоскостей α₁ и α₂, соответственно.

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

1. Нормальные векторы n₁ и n₂ плоскостей α₁ и α₂ коллинеарны (Рис.1).

Поскольку векторы n₁ и n₂ коллинеарны, то существует такое число λ≠0, что выполнено равенство n₁=λn₂, т.е. A₁=λA₂, B₁=λB₂, C₁=λC₂.

Умножив уравнение (2) на λ, получим:

α2:  A1x+B1y+C1z+λD2=0,

(3)

Если выполненио равенство D₁=λD₂, то плоскости α₁ и α₂ совпадают, если же D₁≠λD₂то плоскости α₁ и α₂ параллельны, то есть не пересекаются.

2. Нормальные векторы n₁ и n₂ плоскостей α₁ и α₂ не коллинеарны (Рис.2).

Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁={A₁, B₁, C₁} и n₂={A₂, B₂, C₂} не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

где x₀, y₀, z₀, m, p, l действительные числа, а t − переменная.

Равенство (5) можно записать в следующем виде:

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α₁ имеет нормальный вектор n₁={A₁, B₁, C₁}={1, 2, 1}. Плоскость α₂ имеет нормальный вектор n₂={A₂, B₂, C₂}={2, 9, −5}.

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Получим решение:

где t− произвольное действительное число.

Запишем (11) в следующем виде:

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α₁ имеет нормальный вектор n₁={A₁, B₁, C₁}={1, 2, 7}. Плоскость α₂ имеет нормальный вектор n₂={A₂, B₂, C₂}={2, 4, 14}.

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α₁ имеет нормальный вектор n₁={A₁, B₁, C₁}={5, −2, 3}. Плоскость α₂ имеет нормальный вектор n₂={A₂, B₂, C₂}={15, −6, 9}.

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

Плоскость — это одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Линия пересечения двух плоскостей — это прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Содержание:

1. Понятие пересекающихся плоскостей
2. Двугранные углы

Понятие пересекающихся плоскостей

Определение. Плоскости, которые имеют хотя бы одну общую точку, называют пересекающимися.

Аксиома 5. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой . Плоскости и в этом случае являются пересекающимися по прямой (рис. 2.379).

Пример: 

Дана плоскость . Доказать, что существует другая плоскость (3, пересекающая .

Решение: 

Из условия задачи имеем:

1.    Плоскость (дано) (рис. 2.380).

2.    Нужно доказать, что существует другая плоскость , пересекающая .

Мы знаем, что на основании аксиомы 3 (аксиомы плоскости) три точки определяют единственную плоскость.

3.    Возьмем точки А и В, принадлежащие плоскости , и точку С, не лежащую на прямой АВ и не принадлежащую (построение) (рис. 2.381).

4.    Точки А, В и С не лежат на одной прямой. Через них можно провести плоскость , и притом только одну (3, аксиома 3).

5.    Плоскости и имеют общую точку (1, 3, 4).

6.    Плоскости и  пересекаются по прямой АВ (5, аксиома 5) (рис. 2.382).

7.    Мы доказали, что существует плоскость Р, пересекающая . (6)

Замечание. Если допустить, что точка С лежит на прямой АВ, то она будет лежать и в плоскости , что противоречит выбору точки С.

Двугранные углы

При пересечении плоскостей образуются двугранные углы.

Определение. Фигуру, образованную двумя полуплоскостями, исходящими из одной прямой, называют двугранным углом. Прямую называют ребром, а полуплоскости — сторонами или гранями двугранного угла.

На рисунке 2.383 изображен двугранный угол с ребром АВ.

Этот угол можно обозначать двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежит несколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, одна крайняя — у одной грани, другая — у другой (рис. 2.384).

Определение. Если через произвольную точку ребра двугранного угла провести плоскость, перпендикулярную ребру, то в пересечении этой плоскости с двугранным углом образуется угол, который называют линейным углом двугранного угла.

На рисунке 2.385 изображен линейный угол АОВ двугранного угла АОСВ. Вершиной линейного угла служит точка О, лежащая на ребре ос двугранного угла, а сторонами — лучи граней, исходящие из точки о и перпендикулярные ребру двугранного угла.

Двугранный угол имеет бесконечное множество линейных углов (рис. 2.386).

Определение. Градусной мерой двугранного угла называют градусную меру любого из его линейных углов.

Определение. Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).

Можно доказать следующее утверждение.

Теорема 1. Все линейные углы двугранного угла равны друг другу.

Для двугранных углов так же, как и для плоских, вводится понятие его градусной меры — величины.

Определение. Два двугранных угла называют равными, если они имеют одну и ту же градусную меру.

Если градусная мера одного из двугранных углов больше градусной меры другого, то говорят, что первый двугранный угол больше второго, а второй меньше первого. На рисунке 2.387 изображены три двугранных угла с общим ребром АВ. Двугранные углы CABD и DABE равны, так как их градусные меры равны 30°. Двугранный угол САВЕ больше двугранного угла CABD.

Подобно плоским углам, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

Все сказанное можно сформулировать в виде теорем.

Теорема 2. 1. Равным двугранным углам соответствуют равные линейные углы.

2. Большему двугранному углу соответствует больший линейный угол.

Верна и обратная теорема.

Теорема 3. 1. Равным линейным углам соответствуют равные двугранные углы.

2. Большему линейному углу соответствует больший двугранный угол.

Из теорем 2 и 3 легко получить три следствия.

Следствие 1. Прямому двугранному углу соответствует прямой линейный угол, и обратно.

Следствие 2. Все прямые двугранные углы равны, потому что у них равны линейные углы.

Следствие 3. Вертикальные двугранные углы равны.

Пример: 

Докажем теорему 3.

Из условия теоремы имеем:

1.    PABQ и — два данных двугранных угла (рис. 2.388).

2.    Вложим угол  в угол АВ так, чтобы ребро совпало с ребром АВ, а грань  — с гранью Р (построение) (рис. 2.389).

3.    Если эти двугранные углы равны, то грань совпадает с Q; если же двугранные углы не равны, то грань займет некоторое положение, не совпадающее с Q, например положение (1, 2).

4.    Возьмем на общем ребре какую-нибудь точку В и проведем через нее плоскость , перпендикулярную ребру АВ (построение) (рис. 2.390).

5.    От пересечения этой плоскости с гранями двугранных углов получатся линейные углы.

Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол cbd; если же двугранные углы не совпадут (если, например, грань займет положение  то у большего двугранного угла окажется больший линейный угол (именно ) (3, 4).

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету “Математика”: