Арксинус(y = arcsin(x)) – это обратная тригонометрическая функция к синусу x = sin(y). Область определения -1 ≤ x ≤ 1 и множество значений -π/2 ≤ y ≤ +π/2.
График пересекает оси в начале координат.
| arcsin(0) = 0° | arcsin(0.8660254038) = 120° | arcsin(-0.8660254038) = 240° |
| arcsin(0.01745240644) = 1° | arcsin(0.8571673007) = 121° | arcsin(-0.8746197071) = 241° |
| arcsin(0.0348994967) = 2° | arcsin(0.8480480962) = 122° | arcsin(-0.8829475929) = 242° |
| arcsin(0.05233595624) = 3° | arcsin(0.8386705679) = 123° | arcsin(-0.8910065242) = 243° |
| arcsin(0.06975647374) = 4° | arcsin(0.8290375726) = 124° | arcsin(-0.8987940463) = 244° |
| arcsin(0.08715574275) = 5° | arcsin(0.8191520443) = 125° | arcsin(-0.906307787) = 245° |
| arcsin(0.1045284633) = 6° | arcsin(0.8090169944) = 126° | arcsin(-0.9135454576) = 246° |
| arcsin(0.1218693434) = 7° | arcsin(0.79863551) = 127° | arcsin(-0.9205048535) = 247° |
| arcsin(0.139173101) = 8° | arcsin(0.7880107536) = 128° | arcsin(-0.9271838546) = 248° |
| arcsin(0.156434465) = 9° | arcsin(0.7771459615) = 129° | arcsin(-0.9335804265) = 249° |
| arcsin(0.1736481777) = 10° | arcsin(0.7660444431) = 130° | arcsin(-0.9396926208) = 250° |
| arcsin(0.1908089954) = 11° | arcsin(0.7547095802) = 131° | arcsin(-0.9455185756) = 251° |
| arcsin(0.2079116908) = 12° | arcsin(0.7431448255) = 132° | arcsin(-0.9510565163) = 252° |
| arcsin(0.2249510543) = 13° | arcsin(0.7313537016) = 133° | arcsin(-0.956304756) = 253° |
| arcsin(0.2419218956) = 14° | arcsin(0.7193398003) = 134° | arcsin(-0.9612616959) = 254° |
| arcsin(0.2588190451) = 15° | arcsin(0.7071067812) = 135° | arcsin(-0.9659258263) = 255° |
| arcsin(0.2756373558) = 16° | arcsin(0.6946583705) = 136° | arcsin(-0.9702957263) = 256° |
| arcsin(0.2923717047) = 17° | arcsin(0.6819983601) = 137° | arcsin(-0.9743700648) = 257° |
| arcsin(0.3090169944) = 18° | arcsin(0.6691306064) = 138° | arcsin(-0.9781476007) = 258° |
| arcsin(0.3255681545) = 19° | arcsin(0.656059029) = 139° | arcsin(-0.9816271834) = 259° |
| arcsin(0.3420201433) = 20° | arcsin(0.6427876097) = 140° | arcsin(-0.984807753) = 260° |
| arcsin(0.3583679495) = 21° | arcsin(0.629320391) = 141° | arcsin(-0.9876883406) = 261° |
| arcsin(0.3746065934) = 22° | arcsin(0.6156614753) = 142° | arcsin(-0.9902680687) = 262° |
| arcsin(0.3907311285) = 23° | arcsin(0.6018150232) = 143° | arcsin(-0.9925461516) = 263° |
| arcsin(0.4067366431) = 24° | arcsin(0.5877852523) = 144° | arcsin(-0.9945218954) = 264° |
| arcsin(0.4226182617) = 25° | arcsin(0.5735764364) = 145° | arcsin(-0.9961946981) = 265° |
| arcsin(0.4383711468) = 26° | arcsin(0.5591929035) = 146° | arcsin(-0.9975640503) = 266° |
| arcsin(0.4539904997) = 27° | arcsin(0.544639035) = 147° | arcsin(-0.9986295348) = 267° |
| arcsin(0.4694715628) = 28° | arcsin(0.5299192642) = 148° | arcsin(-0.999390827) = 268° |
| arcsin(0.4848096202) = 29° | arcsin(0.5150380749) = 149° | arcsin(-0.9998476952) = 269° |
| arcsin(0.5) = 30° | arcsin(0.5) = 150° | arcsin(-1) = 270° |
| arcsin(0.5150380749) = 31° | arcsin(0.4848096202) = 151° | arcsin(-0.9998476952) = 271° |
| arcsin(0.5299192642) = 32° | arcsin(0.4694715628) = 152° | arcsin(-0.999390827) = 272° |
| arcsin(0.544639035) = 33° | arcsin(0.4539904997) = 153° | arcsin(-0.9986295348) = 273° |
| arcsin(0.5591929035) = 34° | arcsin(0.4383711468) = 154° | arcsin(-0.9975640503) = 274° |
| arcsin(0.5735764364) = 35° | arcsin(0.4226182617) = 155° | arcsin(-0.9961946981) = 275° |
| arcsin(0.5877852523) = 36° | arcsin(0.4067366431) = 156° | arcsin(-0.9945218954) = 276° |
| arcsin(0.6018150232) = 37° | arcsin(0.3907311285) = 157° | arcsin(-0.9925461516) = 277° |
| arcsin(0.6156614753) = 38° | arcsin(0.3746065934) = 158° | arcsin(-0.9902680687) = 278° |
| arcsin(0.629320391) = 39° | arcsin(0.3583679495) = 159° | arcsin(-0.9876883406) = 279° |
| arcsin(0.6427876097) = 40° | arcsin(0.3420201433) = 160° | arcsin(-0.984807753) = 280° |
| arcsin(0.656059029) = 41° | arcsin(0.3255681545) = 161° | arcsin(-0.9816271834) = 281° |
| arcsin(0.6691306064) = 42° | arcsin(0.3090169944) = 162° | arcsin(-0.9781476007) = 282° |
| arcsin(0.6819983601) = 43° | arcsin(0.2923717047) = 163° | arcsin(-0.9743700648) = 283° |
| arcsin(0.6946583705) = 44° | arcsin(0.2756373558) = 164° | arcsin(-0.9702957263) = 284° |
| arcsin(0.7071067812) = 45° | arcsin(0.2588190451) = 165° | arcsin(-0.9659258263) = 285° |
| arcsin(0.7193398003) = 46° | arcsin(0.2419218956) = 166° | arcsin(-0.9612616959) = 286° |
| arcsin(0.7313537016) = 47° | arcsin(0.2249510543) = 167° | arcsin(-0.956304756) = 287° |
| arcsin(0.7431448255) = 48° | arcsin(0.2079116908) = 168° | arcsin(-0.9510565163) = 288° |
| arcsin(0.7547095802) = 49° | arcsin(0.1908089954) = 169° | arcsin(-0.9455185756) = 289° |
| arcsin(0.7660444431) = 50° | arcsin(0.1736481777) = 170° | arcsin(-0.9396926208) = 290° |
| arcsin(0.7771459615) = 51° | arcsin(0.156434465) = 171° | arcsin(-0.9335804265) = 291° |
| arcsin(0.7880107536) = 52° | arcsin(0.139173101) = 172° | arcsin(-0.9271838546) = 292° |
| arcsin(0.79863551) = 53° | arcsin(0.1218693434) = 173° | arcsin(-0.9205048535) = 293° |
| arcsin(0.8090169944) = 54° | arcsin(0.1045284633) = 174° | arcsin(-0.9135454576) = 294° |
| arcsin(0.8191520443) = 55° | arcsin(0.08715574275) = 175° | arcsin(-0.906307787) = 295° |
| arcsin(0.8290375726) = 56° | arcsin(0.06975647374) = 176° | arcsin(-0.8987940463) = 296° |
| arcsin(0.8386705679) = 57° | arcsin(0.05233595624) = 177° | arcsin(-0.8910065242) = 297° |
| arcsin(0.8480480962) = 58° | arcsin(0.0348994967) = 178° | arcsin(-0.8829475929) = 298° |
| arcsin(0.8571673007) = 59° | arcsin(0.01745240644) = 179° | arcsin(-0.8746197071) = 299° |
| arcsin(0.8660254038) = 60° | arcsin(0) = 180° | arcsin(-0.8660254038) = 300° |
| arcsin(0.8746197071) = 61° | arcsin(-0.01745240644) = 181° | arcsin(-0.8571673007) = 301° |
| arcsin(0.8829475929) = 62° | arcsin(-0.0348994967) = 182° | arcsin(-0.8480480962) = 302° |
| arcsin(0.8910065242) = 63° | arcsin(-0.05233595624) = 183° | arcsin(-0.8386705679) = 303° |
| arcsin(0.8987940463) = 64° | arcsin(-0.06975647374) = 184° | arcsin(-0.8290375726) = 304° |
| arcsin(0.906307787) = 65° | arcsin(-0.08715574275) = 185° | arcsin(-0.8191520443) = 305° |
| arcsin(0.9135454576) = 66° | arcsin(-0.1045284633) = 186° | arcsin(-0.8090169944) = 306° |
| arcsin(0.9205048535) = 67° | arcsin(-0.1218693434) = 187° | arcsin(-0.79863551) = 307° |
| arcsin(0.9271838546) = 68° | arcsin(-0.139173101) = 188° | arcsin(-0.7880107536) = 308° |
| arcsin(0.9335804265) = 69° | arcsin(-0.156434465) = 189° | arcsin(-0.7771459615) = 309° |
| arcsin(0.9396926208) = 70° | arcsin(-0.1736481777) = 190° | arcsin(-0.7660444431) = 310° |
| arcsin(0.9455185756) = 71° | arcsin(-0.1908089954) = 191° | arcsin(-0.7547095802) = 311° |
| arcsin(0.9510565163) = 72° | arcsin(-0.2079116908) = 192° | arcsin(-0.7431448255) = 312° |
| arcsin(0.956304756) = 73° | arcsin(-0.2249510543) = 193° | arcsin(-0.7313537016) = 313° |
| arcsin(0.9612616959) = 74° | arcsin(-0.2419218956) = 194° | arcsin(-0.7193398003) = 314° |
| arcsin(0.9659258263) = 75° | arcsin(-0.2588190451) = 195° | arcsin(-0.7071067812) = 315° |
| arcsin(0.9702957263) = 76° | arcsin(-0.2756373558) = 196° | arcsin(-0.6946583705) = 316° |
| arcsin(0.9743700648) = 77° | arcsin(-0.2923717047) = 197° | arcsin(-0.6819983601) = 317° |
| arcsin(0.9781476007) = 78° | arcsin(-0.3090169944) = 198° | arcsin(-0.6691306064) = 318° |
| arcsin(0.9816271834) = 79° | arcsin(-0.3255681545) = 199° | arcsin(-0.656059029) = 319° |
| arcsin(0.984807753) = 80° | arcsin(-0.3420201433) = 200° | arcsin(-0.6427876097) = 320° |
| arcsin(0.9876883406) = 81° | arcsin(-0.3583679495) = 201° | arcsin(-0.629320391) = 321° |
| arcsin(0.9902680687) = 82° | arcsin(-0.3746065934) = 202° | arcsin(-0.6156614753) = 322° |
| arcsin(0.9925461516) = 83° | arcsin(-0.3907311285) = 203° | arcsin(-0.6018150232) = 323° |
| arcsin(0.9945218954) = 84° | arcsin(-0.4067366431) = 204° | arcsin(-0.5877852523) = 324° |
| arcsin(0.9961946981) = 85° | arcsin(-0.4226182617) = 205° | arcsin(-0.5735764364) = 325° |
| arcsin(0.9975640503) = 86° | arcsin(-0.4383711468) = 206° | arcsin(-0.5591929035) = 326° |
| arcsin(0.9986295348) = 87° | arcsin(-0.4539904997) = 207° | arcsin(-0.544639035) = 327° |
| arcsin(0.999390827) = 88° | arcsin(-0.4694715628) = 208° | arcsin(-0.5299192642) = 328° |
| arcsin(0.9998476952) = 89° | arcsin(-0.4848096202) = 209° | arcsin(-0.5150380749) = 329° |
| arcsin(1) = 90° | arcsin(-0.5) = 210° | arcsin(-0.5) = 330° |
| arcsin(0.9998476952) = 91° | arcsin(-0.5150380749) = 211° | arcsin(-0.4848096202) = 331° |
| arcsin(0.999390827) = 92° | arcsin(-0.5299192642) = 212° | arcsin(-0.4694715628) = 332° |
| arcsin(0.9986295348) = 93° | arcsin(-0.544639035) = 213° | arcsin(-0.4539904997) = 333° |
| arcsin(0.9975640503) = 94° | arcsin(-0.5591929035) = 214° | arcsin(-0.4383711468) = 334° |
| arcsin(0.9961946981) = 95° | arcsin(-0.5735764364) = 215° | arcsin(-0.4226182617) = 335° |
| arcsin(0.9945218954) = 96° | arcsin(-0.5877852523) = 216° | arcsin(-0.4067366431) = 336° |
| arcsin(0.9925461516) = 97° | arcsin(-0.6018150232) = 217° | arcsin(-0.3907311285) = 337° |
| arcsin(0.9902680687) = 98° | arcsin(-0.6156614753) = 218° | arcsin(-0.3746065934) = 338° |
| arcsin(0.9876883406) = 99° | arcsin(-0.629320391) = 219° | arcsin(-0.3583679495) = 339° |
| arcsin(0.984807753) = 100° | arcsin(-0.6427876097) = 220° | arcsin(-0.3420201433) = 340° |
| arcsin(0.9816271834) = 101° | arcsin(-0.656059029) = 221° | arcsin(-0.3255681545) = 341° |
| arcsin(0.9781476007) = 102° | arcsin(-0.6691306064) = 222° | arcsin(-0.3090169944) = 342° |
| arcsin(0.9743700648) = 103° | arcsin(-0.6819983601) = 223° | arcsin(-0.2923717047) = 343° |
| arcsin(0.9702957263) = 104° | arcsin(-0.6946583705) = 224° | arcsin(-0.2756373558) = 344° |
| arcsin(0.9659258263) = 105° | arcsin(-0.7071067812) = 225° | arcsin(-0.2588190451) = 345° |
| arcsin(0.9612616959) = 106° | arcsin(-0.7193398003) = 226° | arcsin(-0.2419218956) = 346° |
| arcsin(0.956304756) = 107° | arcsin(-0.7313537016) = 227° | arcsin(-0.2249510543) = 347° |
| arcsin(0.9510565163) = 108° | arcsin(-0.7431448255) = 228° | arcsin(-0.2079116908) = 348° |
| arcsin(0.9455185756) = 109° | arcsin(-0.7547095802) = 229° | arcsin(-0.1908089954) = 349° |
| arcsin(0.9396926208) = 110° | arcsin(-0.7660444431) = 230° | arcsin(-0.1736481777) = 350° |
| arcsin(0.9335804265) = 111° | arcsin(-0.7771459615) = 231° | arcsin(-0.156434465) = 351° |
| arcsin(0.9271838546) = 112° | arcsin(-0.7880107536) = 232° | arcsin(-0.139173101) = 352° |
| arcsin(0.9205048535) = 113° | arcsin(-0.79863551) = 233° | arcsin(-0.1218693434) = 353° |
| arcsin(0.9135454576) = 114° | arcsin(-0.8090169944) = 234° | arcsin(-0.1045284633) = 354° |
| arcsin(0.906307787) = 115° | arcsin(-0.8191520443) = 235° | arcsin(-0.08715574275) = 355° |
| arcsin(0.8987940463) = 116° | arcsin(-0.8290375726) = 236° | arcsin(-0.06975647374) = 356° |
| arcsin(0.8910065242) = 117° | arcsin(-0.8386705679) = 237° | arcsin(-0.05233595624) = 357° |
| arcsin(0.8829475929) = 118° | arcsin(-0.8480480962) = 238° | arcsin(-0.0348994967) = 358° |
| arcsin(0.8746197071) = 119° | arcsin(-0.8571673007) = 239° | arcsin(-0.01745240644) = 359° |
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция – arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
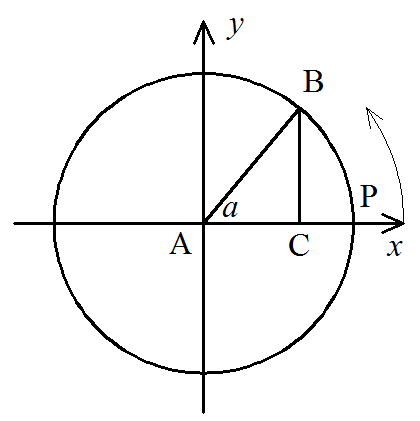
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы
Таблица синусов, найти угол синуса
Тригонометрические функции: синус угла
Зачем надо знать значение синуса? Представим ситуацию: известен один из углов (А=60⁰), вписанный в прямоугольный треугольник, и длина гипотенузы. Больше нет никакой информации. Надо узнать вычислить дальний к углу (А) катет. Как поступить?

Ситуация очень простая: смотрим таблицы Брадиса, находим значение sin(60⁰)=0,866, подставляем данные в формулу тригонометрической функции и решаем линейное уравнение. Из школьного курса известно, что sin угла – это отношение дальнего к углу, в данном случае А=60⁰, катета к гипотенузе.
Произвести все расчеты проще, если воспользоваться онлайн калькулятором на сайте. Таким образом можно вычислить длину любой из сторон прямоугольного треугольника. Знаем угол – значит, знаем sin этого угла. И наоборот, знаем sin – найти угол не составит проблемы.
Таблица синусов 0°- 360°
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

|
Как найти угол имея цифровое значение синуса, косинуса, тангенса,котангенса? например есть значение sin a=0,3452 какой угол этому соответствует?
Функции: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), называются тригонометрическими. Они выражают зависимости длин сторон от углов треугольника при гипотенузе. Определяются отношением какой-либо из сторон треугольника к другой. То есть, показывают, насколько одна сторона больше другой. Это отношение может быть характерно только для строго определенного угла. Выражаются тригонометрические функции в безразмерных единицах. Если известно значение какой-либо тригонометрической функции (в данном случае, синуса – sin), а требуется найти соответствующий ему угол в градусах, то нужно:
Определение значения arcsin угла (в радианах) и значения в градусах – с помощью функций Excel Итак, ответ получен: Синусу угла альфа со значением 0,3452 соответствует угол 20,194 градуса. автор вопроса выбрал этот ответ лучшим
RIOLIt 6 лет назад Данному значению синуса соответствует угол- немногим более 20 градусов, это- по таблице, а если есть значение гипотенузы, то- по отношению- можно найти катет и другие элементы треугольника и- возможно- все улы, здесь- главное- зацепка- кончик ниточки, чтобы размотать весь клубочек,( а имея в хозяйстве инженерный калькулятор, можно сразу- по функции найти угол с точностью до н- ого знака после запятой…) Можно без компьютера, без калькулятора, без таблиц Брадиса найти этот угол. Для этого нужен такой инструмент, как транспортир. Можно воспользоваться угломером. Если есть чертежный прибор, который еще называют кульман, то и им. Но сначала высисляют катет и гипотенузу. Чем больше длина, тем точгее. Допустим, гипотенуза 100 мм, тогда противолежащий катет будет равен 100*0,3452=34,52мм. Берем клетчатую бумагу, по вертикали откладываем 35 мм от горизонтальной линии вверх. Из верхней точки циркулем с разведенными ножками на 100 мм делаем засечку на глризонтальной линии. Соединяем три точки линиями и измеряем угол. Если честно, то в повседневной жизни не припомню, чтобы приходилось определять углы по синусу или тагенсу. Вот строить углы приходится постоянно. Например, нужно обрезать плинтуса под углом 45 градусов. Никакой транспортир или угломер не нужен. На заводе плинтус обрезан под прямым углом, тогда просто отмеряешь два одинаковых катета и проводишь гипотенузу, угол получантся сам собой. Так же легко строить углы 30 и 60 градусов, так как гипотенуза равна двум противолежащим катетам. Еще углы можно измерять смартфоном илитпланшетом, если в нем установлено приложение по измерению углов, очень удобная штука, не надо покупать строительный уровень. bezdelnik 6 лет назад Найти угол имея цифровое значение синуса, косинуса, тангенса можно по таблицам Брадиса, на логарифмической линейке или на калькуляторе. Если sin a=0,3452, то a=20,194… градуса. Можно найти приближенное значение тригонометрических функций по их графикам, для синуса и косинуса это графики синусоиды и косинусоиды. Найдя значения синуса и косинуса значения тангенса и котангенса можно вычислить по формулам tg a = Sin a /Cos a, ctg a = Cos a/Sin a
DartFallen 6 лет назад Я открою Вам одну старую и великую тайну! Все эти величины давно вычислены и сведены в таблицу. Носит она название таблицы Браддиса. Когда я учился в старших классах у каждого ученика была желтенькая такая брошюрка, в которой и представлены многие данные и не только для градусной меры углов. Величины эти постоянные и периодического пересчета не требуют. Вот как-то так…
Blockphild 8 месяцев назад Зачем так все сложно и это в век компьютеров? Иди сюда -> https://allcalc.ru/node/1039 вставляй величины катетов и гипотенуз –> жми на кнопку -> ВЫЧИСЛИТЬ и вот тебе результат в градусах и радианах. Недостаток: нужно иметь интернет Не надо никаких там EXCEL, таблиц Брадисов и прочей ерунды, мы в 21 веке живем, все делается очень быстро. Успехов! bezdelnik 5 лет назад Для некоторых значений тригонометрических функций соответствующие углы общеизвестны из учебников по математике. Например,для углов 0°, 30°, 45°, 60°, 90° синус равен 0, 1/2, √2/2, √3/2, 1 ,соответственно, а косинус такие же значения в обратном порядке. Это должны знать все получившие среднее школьное образование. Знаете ответ? |
Смотрите также: В треугольнике АВС угол С равен 90°, АВ=10, АС=√51. Как найти sin A? Как вычислить площадь параллелограма по формуле S=a·b·sin A с след.данными? В треугольнике ABC угол C = 90°, sin A = 4/5, AC=9. Найти AB. Как решить? Как доказать теорему о равенстве синусов острых углов? Как построить угол, если известен синус? Если синус X равен 1, чему равен косинус X(см)? Как найти котангенс, тангенс, синус, косинус? Как выучить таблицу значений синуса, косинуса, тангенса разных углов? Перечислите все формулы, объединяющие синус, косинус, тангенс и котангенс? Как записать две различные функции для синуса и косинуса? |
Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).
Из основного тригонометрического тождества:
выразим косинус в квадрате угла а:

Значит косинус угла равен либо корню квадратному из этого выражения, либо ему же, только со знаком -.
Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.
Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0< a< 90) значение косинуса будет положительным. Здесь выбираем знак плюс. Во второй четверти (90< a< 180) значение косинуса будет отрицательным. Тогда перед корнем выбираем знак минус.
Если значение синуса отрицательное, то угол расположен в 3-й или 4-й четверти. В 3 четверти (180< a< 270) косинус угла будет меньше нуля.
В 4 четверти (270< a< 360) косинус угла будет больше нуля.
Примеры.
Пример 1. Найти косинус угла, если sina = -0,6. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).
-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:
1-0,36=0,64
Получили квадрат значения косинуса. Для нахождения значения самого косинуса, извлечем корень квадратный из 0,64 и возьмем его со знаком + или со знаком – . Получим 0,8 или -0,8.
Так как по условию угол находится в 3 четверти, то искомое значение косинуса будет также меньше нуля. Значит выбираем -0,8.
Ответ: cos a =-0,8.
Рассмотрим пример для случая, когда угол находится в 4 четверти:
Пример 2. Найти косинус угла, если sina = -0,6. 270<a<360 (в градусах)
Решение такое же (см. пример 1).
Перед выбором ответа рассуждаем так:
Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.
Ответ: cos a =0,8.


