Как найти по точкам интерполяция

Интерполяция данных: соединяем точки так, чтобы было красиво

Время на прочтение
7 мин

Количество просмотров 150K

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

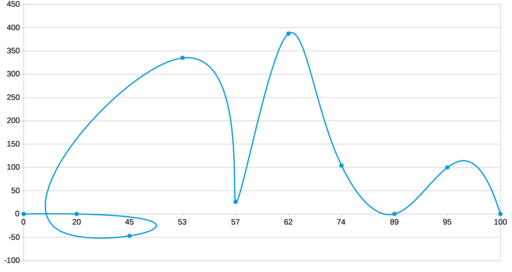
Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P₁ … P_n, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:

Функции f_i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P_i) называется сплайном.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Ставим опыты

Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):

Результат линейной интерполяции этих точек выглядит так:

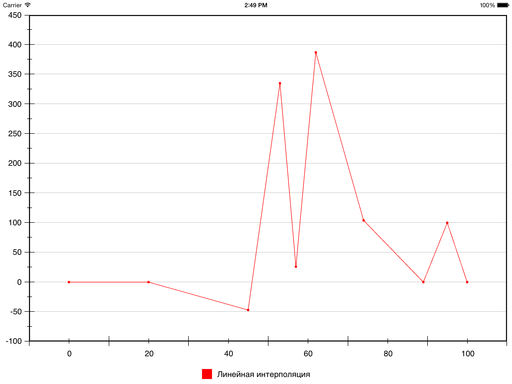
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P_i, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:

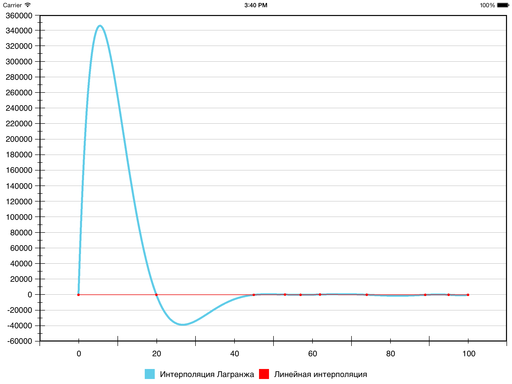
Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P_i), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:

В качестве прямых, на которых лежат точки C_i – 1⁽²⁾, P_i и C_i⁽¹⁾, целесообразно взять касательные к графику интерполируемой функции в точках P_i. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Эвристика 1

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C₁⁽¹⁾ и C_n – 1⁽²⁾ совпадают с точками P₁ и P_n соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки P_i до точек C_i – 1⁽²⁾ и C_i⁽¹⁾, но при этом сохраняем их все лежащими на одной прямой:

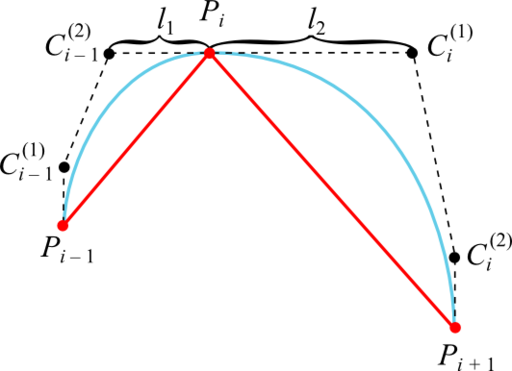
Эвристика для вычисления расстояний будет такой:

Эвристика 2

Расчёт l₁ и l₂ такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки P_i и P_i + 1 по ординате, и, если совпали, полагать l₁ = l₂ = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

Результат получается такой:

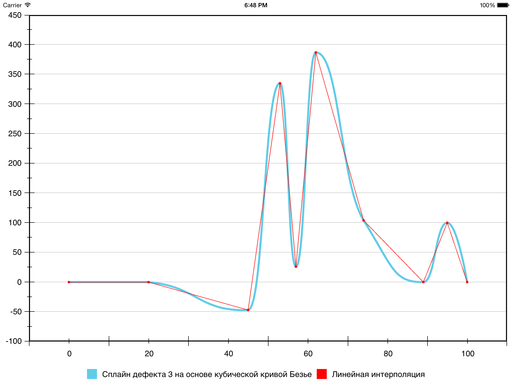
В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Эвристика 3

Если абсцисса точки пересечения касательных в точках P_i(x_i, y_i) и P_i + 1(x_i + 1, y_i + 1) лежит в отрезке [x_i; x_i + 1], то l₁ либо l₂ полагаем равным нулю. В том случае, если касательная в точке P_i направлена вверх, нулю полагаем максимальное из l₁ и l₂, если вниз — минимальное.

Результат следующий:

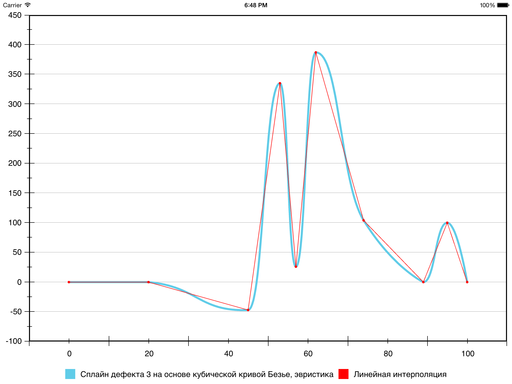
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.

А как люди-то делают?

Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

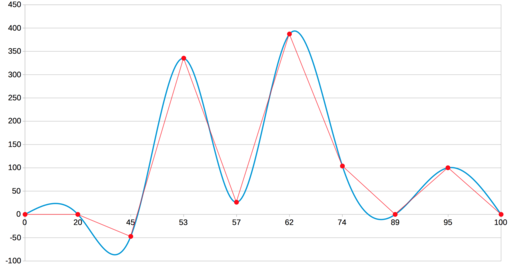
В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Вместо заключения

В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.

Источник

Как найти число методом интерполяции???

Ученик

(240),
закрыт

8 лет назад

Дополнен 12 лет назад

допустим дано
7 – 2400
8,87 – ?
10 – 2600

как найти ???

Дополнен 12 лет назад

Желательно какая нибудь формула, по которой можно будет найти подобные выражения

Дополнен 12 лет назад

Ответ я знаю, мне нужна формула как вы его получили. Благодарю за ранее

Велон

Просветленный

(36271)

12 лет назад

число 2524,67 – ответ
как делается – на разницу 10-7 = 3 приходится 2600-2400 = 200
на одну единицу – 200/3 = 66,67
8.87 – 7 =1,87 Х 66,67 = 124,67
2400 +124,67 = 2524,67

Jurijus Zaksas

Искусственный Интеллект

(393138)

12 лет назад

Зависит от того, что за интерполяция.
В общем случае на основе неких известных точек строится некая стандартная непрерывная функция и из этой функции вычисляется нужная промежуточная точка.
Если известны только 2 точки, используется линейная интерполяция.
Уравнение прямой y=kx+b
Коеэфф. k=dy/dx
b вычисляется подстановкой в уравнение k и любой из известных точек.
Когда коэфф. посчитаны и уравнение известно, остается только подставить в него известную координату искомой точки.

Источник

5Л. Методы пространстве

1НЯ

207

подробно в курсе математики, а анализ пространственных моделей входит в задачи курса «Математико-картографическое моделирование» [Тикунов, 1997]. В ГИС-пакетах и других специализированных графических пакетах программ обычно предлагается несколько способов интерполяции, из которых пользователь выбирает наиболее подходящий для моделируемой поверхности и существующего набора точек (обычно экспериментально). Рассмотрим некоторые особенности разных методов интерполяции, знание которых необходимо для выбора лучшего для поставленной задачи способа.

Общая задача интерполяции по точкам формулируется так: дан ряд точек (узлов интерполяции), положение и значения характеристик в которых известны, необходимо определить значения характеристик для других точек, для которых известно только положение. При этом различают методы глобальной и локальной интерполяции, и среди них точные и аппроксимирующие.

При глобальной интерполяции для всей территории одновременно используется единая функция вычисления z = F(x, у). В этом случае изменение одного значения (х, у) на входе сказывается на всей результирующей ЦМР. При локальной интерполяции многократно применяют алгоритм вычисления для некоторых выборок из общего набора точек, как правило, близко расположенных. Тогда изменение выбора точек сказывается лишь на результатах обработки небольшого участка территории. Алгоритмы глобальной интерполяции создают сглаженные поверхности с небольшим числом резких перепадов; они применяются в случаях, если предположительно известна форма поверхности, например, тренд. При включении в процесс локальной интерполяции большой доли общего набора данных она, по сути, становится глобальной.

Точные методы интерполяции воспроизводят данные в точках (узлах), на которых базируется интерполяция, и поверхность проходит через все точки с известными значениями.

При точной интерполяции необходимо решить два вопроса: как выбирать точки из сети и как представлять поверхность между ними. Проще всего они решаются для регулярной сети точек, и вместе с тем применяются для построения такой сети и ее сгущения. Наиболее часто используемые методы основаны на линейной интерполяции,

208	Глава 5. Географический анализ и пространственное моделирование

выполняемой от точки к точке: каждая пара точек сети соединяется отрезками прямых линий.

Локальная кусочно-линейная интерполяция поверхности.

В этом методе аппроксимируемая поверхность представляется совокупностью плоских треугольников с вершинами в трех соседних точках (х, уг г.). Эта плоскость, уравнение которой, очевидно, есть

х-	i	У- У	z- zt
–	X 1	У2- У	z = 0
*3″–	X“i	Уз- У	21	(5.9)
или
У2 ~1/1*2-21		Х2~ xl Z2~ zl
Уъ~У гз~			х 23″ zi
х2~ Х У2 ~Ух	хх ) +Х•2~ Х1 У2~У	(У~У)>
х3~ хУз~	У		х3 ~ хУз~ У	(5.10)

проходит через высоты г. всех трех выбранных точек. Таким образом, получается мозаичная поверхность, состоящая из треугольников, прилегающих друг к другу смежными сторонами (рис. 5.5).

Рис. 5.5. Кусочно-линейная интерполяция поверхности

Таким способом представляют поверхность в TIN-моделях Поскольку для каждого треугольника она задается высотами трех его вершин, то в общей мозаичной поверхности треугольники для смежных участков точно прилегают по сторонам; образуемая поверх-

$ J. Методы пространственного моделирования

209

ность непрерывна. Однако если на поверхности проведены горизонтали, то в этом случае они будут прямолинейны и параллельны

впределах треугольников, а на границах будет происходить резкое изменение их направления. Поэтому для некоторых приложений TIN

впределах каждого треугольника строится математическая поверхность, характеризующаяся плавным изменением углов наклона на границах треугольников.

Другой метод — анализ соседства, в котором все значения моделируемых характеристик принимаются равными значениям в ближайшей известной точке. В результате образуются полигоны Тиссена с резкой сменой значений на границах. Такой метод применяется в экологических исследованиях, при оценке зон воздействия, и больше подходит для номинальных данных.

Аппроксимационные методы интерполяции применяются в тех случаях, когда существует некоторая неопределенность в отношении имеющихся данных о поверхности; в их основе лежит соображение о том, что во многих наборах данных отображается медленно изменяющийся тренд поверхности, на который накладываются местные, быстро меняющиеся отклонения, приводящие к неточностям или ошибкам в данных. В таких случаях сглаживание за счет аппроксимации поверхности позволяет уменьшить влияние ошибочных данных на характер результирующей поверхности.

В аппроксимационных методах интерполяции осуществляется подбор некоторой функции, такой что z ~ F(x, у). Обычно функция отыскивается в виде полиномов заданной степени т вида

где z — моделируемый показатель, а.. — коэффициенты полинома, х, у — координаты точек сети. Коэффициенты обычно определяют методом минимизации среднеквадратических отклоненийJ поверхности z(x, у) от заданных высот zs:

		2
Z5	-XXatJX^S	mm,
5 = 1	1=0>=0	(5.12)

для чего необходимо, чтобы число точек было больше величины (т + 1 )(т + 2)/2. Для определения неизвестных коэффициентов

210	Глава 5. Географический анализ и пространственное моделирование

аппроксимации а., необходимо решить систему линейных уравнений

Множество аналитических средств географического анализа и моделирования, наиболее востребованных в ГИС и доступных в той или иной форме в современных ГИС-пакетах, представляют методы:

•построения и анализа статистических поверхностей;

•определения местоположения и оптимального размещения;

•моделирования пространственных распределений.

5.2.4. Построение статистических поверхностей

Поверхности, представляемые математическим соотношением 2 = F(x,y), принято считать «статистическими», поскольку в общем случае2 представляет статистическое распределение характеристик рассматриваемых явлений [Robinson et al, 1995]. Значения z могут быть либо непрерывны в области исследования, либо считаться непрерывными в целях моделирования и картографирования. Пространственное моделирование на основе информации о реальных и так называемых расчетных объектах и процессах, в том числе социально-экономических, базируется на методах пространственной интерполяции.

Получаемые поверхности могут быть непрерывными или дискретными. Непрерывные поверхности представляются матрицами значений, TIN-моделями или изолиниями. Дискретные поверхности создают по данным о дискретных по своей природе объектах, а методы их изображения и анализа основаны на построении карт плотности точек или картограмм, которые, как правило, отражают области сбора данных.

Наиболее развиты методы представления географических полей — непрерывных поверхностей, определяемых набором пространственных координат и скалярными значениями характеристик в точках с этими координатами, например, создание карт рельефа на основе его цифровых моделей (ЦМР). Подобные процедуры имеются во многих растровых пакетах программ (ERDAS. Idrisi, Ilwis), векторных (Arclnfo, Spatial Analyst), в пакете программ

$J.Методы пространственного моделирования	211
моделирования поверхностей Surfer и др. Для	моделирования

и анализа географической информации на кафедре картографии и геоинформатики МГУ создан пакет программ МАГ, хорошо зарекомендовавший себя во многих прикладных исследованиях, но не имеющий статуса коммерческого ГИС-пакета.

Непрерывные статистические поверхности, создаваемые на основе отдельных точек с известными значениями моделируемого показателя (высот, концентраций, загрязнений и т. п.), представля- ются в растровом формате. Задача выбранного метода моделиро- вания — присвоить каждой ячейке растра (прямоугольной сетки или GRID’a) рассчитанное в результате интерполяции значение.

Используются четыре основные класса методов моделирования статистических поверхностей, отличающиеся разными математическими подходами.

1.Методы обратных взвешенных расстояний, основанные на предположении, что каждая измеренная точка имеет влияние, убывающее с расстоянием.

2.Методы сплайнов, исходящие из условия минимальной кривизны поверхности, проведенной через исходные точки.

3.Методы кригинга, в основе которых лежит предположение, что расстояние и направление изменений между точками указы- вает на пространственную корреляцию, помогающую описанию поверхности.

4.Методы выявления тренда, базирующиеся на вычислении полиномиальной математической функции для всех исходных точек методом наименьших квадратов, тем самым минимизируется откло- нение от исходных точек.

Большая часть других разработок представляет различные модификации этих методов, использующие математические либо полуэмпирические приемы для их усовершенствования и улучшения компьютерной реализации.

Выбор одного из методов, эффективного для конкретного практического применения — довольно сложная экспертная процедура. Она, как правило, осуществляется экспериментальным путем, в результате чего может быть сделан вывод о необходимости использования разных способов для разных участков территории и «склейки» результирующих моделей. Часто достаточно хорошего знания методов и используемых данных.

212 Глава 5. Географический анализ и пространственное моделирование

Метод обратно взвешенных расстояний (ОВР) используется наиболее широко, особенно для моделирования плавно меняющихся поверхностей. Он основан на главном принципе географии — чем ближе расположены объекты, тем более они похожи. Для ячейки сетки, значение которой не измерено, в пределах заданной окрестности (или расстояния) ведется поиск измеренных значений. Поскольку более близкие значения должны быть более похожи, на расчет значения ячейки они окажут больше влияния, чем дальние значения. Отсюда название «вес, обратно пропорциональный расстоянию» — чем больше расстояние до известной точки, тем меньше вес (вклад) ее измеренного значения в интерполированном. Процедура поиска выполняется для каждой ячейки сетки, построенной для исследуемой территории.

Интерполированные значения представляют собой среднюю величину значений для п известных точек, либо среднее, полученное по интерполируемым точкам, и в общем случае представляются формулой

пп

М	;=i	(5.14)
где w— некоторая функция	расстояния	d, например: w = 1 /d~
или w = e~fl. Можно использовать почти	неограниченное число

алгоритмов, влияющих на характеристики интерполируемой поверхности, различающихся по характеру функции расстояния, количеству исходных точек, способу их отбора. Обычно выбирают либо заданное число ближайших точек, либо точки, лежащие в окрестности заданного радиуса. При задании необходимого для интерполяции числа ближайших точек радиус поиска будет переменным, зависящим от разброса измеренных точек. Фиксированный радиус задает одинаковые круговые окрестности для всех интерполируемых ячеек, и если измеренные точки расположены неравномерно, то интерполяция будет выполнена с использованием разного количества точек. Может возникнуть ситуация, когда в заданной окрестности число точек будет недостаточным для выполнения интерполяции.

Рассмотрим способ, основанный на вычислении расстояний между точками, получивший название мультиквадриковой интерполяции, который описывается уравнением

$ J. Методы пространственного моделирования	213
Z(x, у)= i c j ( ( X j – х)2+ (у J-	у)2)2.
	(5.15)

Коэффициенты с. играют роль весовых коэффициентов и вычисляются через значения, измеренные в точках, как произведение обратной матрицы расстояний между известными п точками (хгу), 1=1,…, п на вектор измеренных значений z в этих точках:

(5.16)

элементы матрицы определяются как

((*,- Xj)2+ (у,- y j f f 2 .

Подставляя с. в уравнение (5.15), определяют z в произвольной

точке (х, у).

Точки для этого способа находят следующим образом. Сначала строят прямоугольник, содержащий все опорные точки. Затем он разбивается линиями, параллельными сторонам, на более мелкие квадраты (или прямоугольники) таким образом, чтобы в них входило число точек, достаточное для обеспечения точности аппроксимации поверхности в пределах каждого квадрата. Точки, лежащие на границах двух смежных квадратов, участвуют в обработке дважды, а четырех — четырежды. Таким образом, связующие точки (известные и построенные узловые) «склеивают» поверхности соприкасающихся квадратов в единую непрерывную поверхность.

Преимуществом метода ОВР является его локальность: на значения моделируемой функции в любой точке практически не оказывают влияния опорные точки, далеко отстоящие от нее. Этот метод дает хорошие результаты в случае плотно расположенных известных точек.

Метод Кригинга, известный как кригинг, получил широкое распространение для интерполяции физических и абстрактных поверхностей, особенно при редких или разбросанных данных. Применение

1 Разработан Дж. Матероном как «метод регионализированных переменных» и Д. С. Кригом как способ интерполяции данных в горной индустрии.

214 Глава 5. Географический анализ и пространственное моделирование

метода базируется на том факте, что географические данные пространственно коррелированны. Метод схож с методом ОВР, поскольку также учитывает вес измеренных значений в окружающих точках при расчете значения для ячейки, в которой нет измерений. Но метод ОВР относится к детерминистическим методам интерполяции, поскольку он опирается только на окружающие измеренные значения, а кригинг относится к методам геостатистической интерполяции, учитывающим также статистическую взаимосвязь между точками измерений. Основа кригинга — определение закономерностей изменения разброса значений моделируемого показателя (дисперсии) между точками в пространстве и подчеркивание существенных различий в значениях данных, используя весовые коэффициенты. Это статистический метол вычисления корреляции точек измерений с помощью вариографии — структурного анализа путем построения экспериментальной кривой, называемой вариограммой. При расчете неизвестного значения ячейки ближайшим точкам измерений присваивается вес, зависящий от их распределения вокруг рассчитываемой ячейки. Метод позволяет оптимизировать интерполяцию путем подразделения пространственных вариаций на три компоненты: 1) детерминированную вариацию (тренд); 2) пространственно автокоррелированную, зависящую от соседних значений данных, но физически трудно объяснимую вариацию; 3) некоррелированный шум.

Рассмотрим метод на примере одномерной	функции z(x)
Значения г в точке х может быть представлено как
z{x) = т(х) + ех) + в”,	(5.17)

где т(х), ех), е” — три описанные компоненты.

Различают ординарный и универсальный кригинг. В ординарном кригинге тренд т(х) предполагается постоянным, но неизвестным и рассматривается как константа, эквивалентная среднему значению данных. При универсальном кригинге предполагается, что в данных имеется тенденция к доминированию определенных значений, и т(х) можно смоделировать с помощью полиномиальной функции; обычно используют полиномы первой или второй степени.

В обоих случаях необходимо определить компоненту ех) которая отражает закономерность возрастания дисперсии значений: (полудисперсии), представленных неупорядоченной выборкой точек, в зависимости от расстояния. Определяют ее экспериментально.

$J. Методы пространственного моделирования

215

представляя результаты в виде графика — вариограммы (рис. 5.6). Вариограмма имеет три характерные составляющие, позволяющие оценить параметры модели: верхний предел роста вариограммы — асимптота d(h) или «пласт» (sill); расстояние, на котором этот предел достигается, — предельный радиус корреляции или диапазон (range); отрезок от начала координат до пересечения с осью d(h) — эффект самородка или остаточная дисперсия (nugget variance).

Рис. 5.6. Вариограмма

Вариограмма показывает, насколько в каждом случае верно предположение (соответствующее определению пространственной автокорреляции), что пары точек, расположенные ближе, должны иметь меньшую разницу в измеренных значениях.

Для ускорения построения вариограммы при вычислении расстояний между всеми парами точек их объединяют в интервальные группы (лаги). Один из способов может быть таким. Сначала весь диапазон расстояний разбивается на ряд равных интервалов, например, на 10, от 0 до максимального значения расстояния между точками на изучаемой территории; тем самым задается размер интер- вала А. Для каждой пары точек вычисляется расстояние и квадрат разности значений г. Эта пара точек включается в соответствующий интервал расстояний, а для каждого из них накапливается общая дисперсия. После обработки всех пар точек (или выборки пар при большом массиве данных) для каждого интервала расстояний подсчитывается средняя дисперсия

216 Глава 5. Географический анализ и пространственное моделирование

представляющая среднее различие между значениями в двух любых точках, находящихся на расстоянии h друг от друга. Эта величина отмечается на графике в средней точке соответствующего интервала (см. рис. 5.6).

Положительное значение d(h) при h—>0 или «эффект самородка* служит оценкой е”. Если «эффект самородка» отличен от нуля, это означает, что повторные измерения в одной и той же точке дали разные результаты. Нужно помнить, что кривая является оценочной, поэтому разница между нулевой дисперсией при нулевом шаге и предсказываемым положительным значением является пространственно некоррелированной шумовой дисперсией. Как указывает П. А. Бэрроу [Burrough, 1998], остаточная дисперсия «объединяет дисперсию ошибок измерения с дисперсией, которая имеет место на расстояниях, меньших, чем интервалы снятия отсчетов, и которые не могут быть устранены».

Эмпирическая вариограмма предоставляет информацию о пространственной автокорреляции наборов измеренных данных, но не дает информацию для всех возможных направлений и расстояний. Поэтому необходимо подобрать модель автокорреляции к точкам вариограммы — непрерывную кривую (аналогично регрессивному анализу). Для построения кривой используют метод наименьших квадратов и разные функции: круговую, сферическую, экспоненциальную, линейную. Выбор модели влияет на вычисление неизвестных значений точек. Чем круче кривая вблизи точки начала отсчета, тем больше влияние ближайших точек измерений на вычисление. В результате полученная поверхность будет менее гладкой.

Модель вариограммы и пространственное распределение ближайших точек используют для расчета весовых коэффициентов при интерполяции и построения поверхности. Интерполированное значение — это сумма взвешенных значений некоторого числа известных точек, причем веса зависят от расстояний между ними и точкой, для которой производится интерполяция. Весовые коэффициенты выбираются таким образом, чтобы минимизировать вариации оцениваемых показателей.

Метод кригинга гибок и эффективен для многих произвольных наборов данных, даже если не делаются предположения, что вариограмма имеет асимптоту (вариограмма линейна); он позволяет не только получить расчетную поверхность, но также определить

$J.Методы пространственного моделирования

217

значение точности или достоверности расчета. Кроме ГИС-пакетов, процедуры кригинга имеются, например, в пакете Surfer (Golden

Software).

Метод кригинга применяют для оценки статистических свойств самих исходных данных, таких как изменчивость пространственных данных, их распределение, репрезентативность, зависимость (взаимосвязи) и глобальные тренды. При решении подобных задач, которые называют «исследовательский анализ данных», в ArcGIS используют модуль Geostatistical Analyst.

Для интерполяции и аппроксимации различных поверхностей используют также полиномы Фурье, анализ автокорреляции, кусочно-полиномиальную интерполяцию с заданием степени полинома и прямоугольника, включающего все точки сети. Этот прямоугольник разбивают на сеть более мелких, для каждого из которых и строится свой полином известной степени.

Метод полиномиального тренда строит поверхность, аппрок-

симируемую многочленом, и структура выходных данных имеет вид алгебраической функции, которую можно использовать для расчета значений в точках растра или в любой точке поверхности. Функция подбирается так, чтобы наилучшим образом пройти через все точки, т. е. минимизировать отклонение от точек измерений. Для нахождения коэффициентов полинома применяют метод наименьших квадратов. Полином позволяет рассчитать глобальный тренд поверхности, а локальные вариации показывают отклонения

от тренда.

Линейное уравнение, например, z = a + bx+cy описывает наклонную плоскую поверхность, а квадратичное z = а + Ьх +су + (be1 + еху + fу1— простой холм или долину. Вообще говоря, любое сечение поверхности ш-го порядка имеет не более ( т – 1) чередующихся максимумов и минимумов. Например, кубическая поверхность может иметь в любом сечении один максимум и один минимум. Возможны значительные краевые эффекты, поскольку полиномиальная модель дает выпуклую поверхность. Для сложных поверхностей создают множества локальных полиномов.

Метод целесообразно применять в случаях, когда интерес представляют общие тенденции изменения поверхности, а не точное моделирование ее мелких деталей. Он полезен в тех случаях, когда есть некоторая неопределенность в отношении имеющихся данных

Источник

Интерполяция, интерполирование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Проще говоря: способ приближенного вычисления значения величины, находящегося между двумя известными значениями.

Примечание! Для удобства можно воспользоваться другими удобными формами для рассчета:

– Линейная интерполяция по графику

– Двойная интерполяция

Источник

From Wikipedia, the free encyclopedia

Given the two red points, the blue line is the linear interpolant between the points, and the value y at x may be found by linear interpolation.

In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.

Linear interpolation between two known points[edit]

In this geometric visualisation, the value at the green circle multiplied by the horizontal distance between the red and blue circles is equal to the sum of the value at the red circle multiplied by the horizontal distance between the green and blue circles, and the value at the blue circle multiplied by the horizontal distance between the green and red circles.

If the two known points are given by the coordinates $(x_{0},y_{0})$ and $(x_{1},y_{1})$ , the linear interpolant is the straight line between these points. For a value x in the interval $(x_{0},x_{1})$ , the value y along the straight line is given from the equation of slopes

${displaystyle {frac {y-y_{0}}{x-x_{0}}}={frac {y_{1}-y_{0}}{x_{1}-x_{0}}},}$

which can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with n = 1.

Solving this equation for y, which is the unknown value at x, gives

${displaystyle {begin{aligned}y&=y_{0}+(x-x_{0}){frac {y_{1}-y_{0}}{x_{1}-x_{0}}}\&={frac {y_{0}(x_{1}-x_{0})}{x_{1}-x_{0}}}+{frac {y_{1}(x-x_{0})-y_{0}(x-x_{0})}{x_{1}-x_{0}}}\&={frac {y_{1}x-y_{1}x_{0}-y_{0}x+y_{0}x_{0}+y_{0}x_{1}-y_{0}x_{0}}{x_{1}-x_{0}}}\&={frac {y_{0}(x_{1}-x)+y_{1}(x-x_{0})}{x_{1}-x_{0}}},end{aligned}}}$

which is the formula for linear interpolation in the interval $(x_{0},x_{1})$ . Outside this interval, the formula is identical to linear extrapolation.

This formula can also be understood as a weighted average. The weights are inversely related to the distance from the end points to the unknown point; the closer point has more influence than the farther point. Thus, the weights are ${textstyle 1-{frac {x-x_{0}}{x_{1}-x_{0}}}}$ and ${textstyle 1-{frac {x_{1}-x}{x_{1}-x_{0}}}}$ , which are normalized distances between the unknown point and each of the end points. Because these sum to 1,

${displaystyle {begin{aligned}y&=y_{0}left(1-{frac {x-x_{0}}{x_{1}-x_{0}}}right)+y_{1}left(1-{frac {x_{1}-x}{x_{1}-x_{0}}}right)\&=y_{0}left(1-{frac {x-x_{0}}{x_{1}-x_{0}}}right)+y_{1}left({frac {x-x_{0}}{x_{1}-x_{0}}}right)\&=y_{0}left({frac {x_{1}-x}{x_{1}-x_{0}}}right)+y_{1}left({frac {x-x_{0}}{x_{1}-x_{0}}}right)end{aligned}}}$

yielding the formula for linear interpolation given above.

Interpolation of a data set[edit]

Linear interpolation on a data set (red points) consists of pieces of linear interpolants (blue lines).

Linear interpolation on a set of data points (x₀, y₀), (x₁, y₁), …, (x_n, y_n) is defined as the concatenation of linear interpolants between each pair of data points. This results in a continuous curve, with a discontinuous derivative (in general), thus of differentiability class C^0 .

Linear interpolation as approximation[edit]

Linear interpolation is often used to approximate a value of some function f using two known values of that function at other points. The error of this approximation is defined as

${displaystyle R_{T}=f(x)-p(x),}$

where p denotes the linear interpolation polynomial defined above:

${displaystyle p(x)=f(x_{0})+{frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}$

It can be proven using Rolle’s theorem that if f has a continuous second derivative, then the error is bounded by

${displaystyle |R_{T}|leq {frac {(x_{1}-x_{0})^{2}}{8}}max _{x_{0}leq xleq x_{1}}left|f''(x)right|.}$

That is, the approximation between two points on a given function gets worse with the second derivative of the function that is approximated. This is intuitively correct as well: the “curvier” the function is, the worse the approximations made with simple linear interpolation become.

History and applications[edit]

Linear interpolation has been used since antiquity for filling the gaps in tables. Suppose that one has a table listing the population of some country in 1970, 1980, 1990 and 2000, and that one wanted to estimate the population in 1994. Linear interpolation is an easy way to do this. It is believed that it was used in the Seleucid Empire (last three centuries BC) and by the Greek astronomer and mathematician Hipparchus (second century BC). A description of linear interpolation can be found in the ancient Chinese mathematical text called The Nine Chapters on the Mathematical Art (九章算術),^[1] dated from 200 BC to AD 100 and the Almagest (2nd century AD) by Ptolemy.

The basic operation of linear interpolation between two values is commonly used in computer graphics. In that field’s jargon it is sometimes called a lerp (from linear interpolation). The term can be used as a verb or noun for the operation. e.g. “Bresenham’s algorithm lerps incrementally between the two endpoints of the line.”

Lerp operations are built into the hardware of all modern computer graphics processors. They are often used as building blocks for more complex operations: for example, a bilinear interpolation can be accomplished in three lerps. Because this operation is cheap, it’s also a good way to implement accurate lookup tables with quick lookup for smooth functions without having too many table entries.

Extensions[edit]

Comparison of linear and bilinear interpolation some 1- and 2-dimensional interpolations.
Black and red/yellow/green/blue dots correspond to the interpolated point and neighbouring samples, respectively.
Their heights above the ground correspond to their values.

Accuracy[edit]

If a C⁰ function is insufficient, for example if the process that has produced the data points is known to be smoother than C⁰, it is common to replace linear interpolation with spline interpolation or, in some cases, polynomial interpolation.

Multivariate[edit]

Linear interpolation as described here is for data points in one spatial dimension. For two spatial dimensions, the extension of linear interpolation is called bilinear interpolation, and in three dimensions, trilinear interpolation. Notice, though, that these interpolants are no longer linear functions of the spatial coordinates, rather products of linear functions; this is illustrated by the clearly non-linear example of bilinear interpolation in the figure below. Other extensions of linear interpolation can be applied to other kinds of mesh such as triangular and tetrahedral meshes, including Bézier surfaces. These may be defined as indeed higher-dimensional piecewise linear function (see second figure below).

Example of bilinear interpolation on the unit square with the z values 0, 1, 1 and 0.5 as indicated. Interpolated values in between represented by colour.

A piecewise linear function in two dimensions (top) and the convex polytopes on which it is linear (bottom)

Programming language support[edit]

Many libraries and shading languages have a “lerp” helper-function (in GLSL known instead as mix), returning an interpolation between two inputs (v0, v1) for a parameter (t) in the closed unit interval [0, 1]. Signatures between lerp functions are variously implemented in both the forms (v0, v1, t) and (t, v0, v1).

// Imprecise method, which does not guarantee v = v1 when t = 1, due to floating-point arithmetic error.
// This method is monotonic. This form may be used when the hardware has a native fused multiply-add instruction.
float lerp(float v0, float v1, float t) {
  return v0 + t * (v1 - v0);
}

// Precise method, which guarantees v = v1 when t = 1. This method is monotonic only when v0 * v1 < 0.
// Lerping between same values might not produce the same value
float lerp(float v0, float v1, float t) {
  return (1 - t) * v0 + t * v1;
}

This lerp function is commonly used for alpha blending (the parameter “t” is the “alpha value”), and the formula may be extended to blend multiple components of a vector (such as spatial x, y, z axes or r, g, b colour components) in parallel.

References[edit]

^ Joseph Needham (1 January 1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 147–. ISBN 978-0-521-05801-8.

Meijering, Erik (2002), “A chronology of interpolation: from ancient astronomy to modern signal and image processing”, Proceedings of the IEEE, 90 (3): 319–342, doi:10.1109/5.993400.

External links[edit]

Equations of the Straight Line at cut-the-knot
Well-behaved interpolation for numbers and pointers
“Linear interpolation”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
“Finite-increments formula”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Источник

Интерполяция данных: соединяем точки так, чтобы было красиво

Немного матчасти

Ставим опыты

Думаем и экспериментируем

А как люди-то делают?

MS Excel

LibreOffice Calc

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

amCharts, ещё одна популярная JS-библиотека

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Вместо заключения

Как найти число методом интерполяции???

5.2.4. Построение статистических поверхностей

Linear interpolation between two known points[edit]

Interpolation of a data set[edit]

Linear interpolation as approximation[edit]

History and applications[edit]

Extensions[edit]

Accuracy[edit]

Multivariate[edit]

Programming language support[edit]

See also[edit]

References[edit]

External links[edit]

Добавить комментарий Отменить ответ

Интерполяция данных: соединяем точки так, чтобы было красиво

Немного матчасти

Ставим опыты

Думаем и экспериментируем

А как люди-то делают?

MS Excel

LibreOffice Calc

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

amCharts, ещё одна популярная JS-библиотека

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Вместо заключения

Как найти число методом интерполяции???

5.2.4. Построение статистических поверхностей

Linear interpolation between two known points[edit]

Interpolation of a data set[edit]

Linear interpolation as approximation[edit]

History and applications[edit]

Extensions[edit]

Accuracy[edit]

Multivariate[edit]

Programming language support[edit]

See also[edit]

References[edit]

External links[edit]

Вам также может понравиться

Как найти поставщика спортивного питания для продажи

Как найти ту свою пони

Как найти предков поляков

Добавить комментарий Отменить ответ