|
Определение имени победителя по наибольшему баллу |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
|
Обычно помогает сортировка данных по убыванию-возрастанию. Но часто использование сортировки не целесообразно. Например спортсмены в таблице расположены по алфавиту, и менять их местами недопустимо, а требуется периодически определять их места в процессе, допустим, соревнования. В этом случае может помочь функция “РАНГ”. Формат функции РАНГ(число;ссылка;порядок) Число — число, для которого определяется ранг. Ссылка — массив или ссылка на список чисел. Нечисловые значения в ссылке игнорируются. Следует помнить, что если два показателя равны, и принадлежат например первому месту (два победителя), следующий за ними получит ранг 3. Иногда это не удобно, но логика в этом есть. модератор выбрал этот ответ лучшим
Sagavaha более года назад Есть несколько способов. К примеру, можно создать специальный столбик, который будет высчитывать среднее время, оценки или баллы каждого спортсмена в зависимости от того, что принято как критерий и какой вид спорта. Потом в этой колонке использовать любой из стандартного набора функций – сортирование, выделение МИНимального или МАКСимального числа чтоб определить первое место. Но зачастую это не совсем удобно, так как итоговая таблица может перевернуться с ног на голову. В этом случае поможет формула РАНГ.РВ, которая не будет менять местами строки, но в дополнительном столбце укажет место каждого из участников соревнований. Более подробно как воспользоваться функцие – внизу в кратком трёхминутном видео будет наглядно
88SkyWalker88 более года назад В таблице Эксель с помощью разных команд можно менять информацию и получать необходимые данные. Например, если Вам нужно узнать места по конкретным результатам, то в тот столбик, где внесены результаты, например, метры или секунды, нужно задать команду “сортировка данных по значению”. Данные распределятся от большего к меньшему. Если нужно просто указать места, то для этого воспользуйтесь командой, которая называется РАНГ. В скобках можно указать число (номер ячейки, место которой необходимо определить), ссылку на диапазон ячеек, 0 или 1 (где 0 означает сортировку по убыванию, а 1 – сортировку по возрастанию).
Y7 более года назад Надо смотреть конкретные данные и отсюда уже вести расчеты. Так будет, конечно, правильней. Так, например, если имеется в виду кто на первом месте по сумме, то достаточно просто сделать сортировку поля. А если у нас таблица с фамилиями и результатами и надо определить по ним места без сортировки, то здесь уже упоминалась формула РАНГ. Можно использовать ее. А еще можно применить промежуточные функции. Например, функцию ВПР. Берем данные и копируем их в отдельную таблицу, эту таблицу сортируем по возрастанию. Создаем дополнительный столбик с указанием места, а затем с помощью ВПР подставляем это значение в первую таблицу. Если с функцией ВПР хорошо знакомы, то много времени это не займет.
Марина Вологда более года назад Чем и хорош Эксель, это как раз тем, что там надо знать команды, а все остальное он сам высчитает. Если у вас есть результаты, занесенные в таблицы, и вам необходимо определить места этих участников, то можно воспользоваться функцией “Сортировка данных по значению”. Она подойдет, если вы уже знаете точно результаты и они подсчитаны. Столбик выделяем полностью и нажимаем на “сортировку”, фамилии и результаты встанут по порядку, в соответствии с средним значением. Так же можно воспользоваться функцией: РАНГ и РАНГ,РВ. Но тут уже учитывайте то, что одинаковые значения имеют одинаковый ранг, а значит следующий ранг будет на один больше.
Ронни Салливан более года назад Это можно сделать двумя способами:
Спасибо за интересный вопрос!
-Irinka- более года назад Чаще при сортировке данных в таблице Эксель, если сортировка будет происходить не по алфавиту – по каким-либо числовым данным (достижениям, результатам) используется функция “РАНГ”. Формат функции РАНГ (число;ссылка;порядок). Пример расчёта приведён ниже.
Krustall 5 месяцев назад Таблица Excel с различными командами очень удобна в этом плане, там вы можете изменить информацию и получить необходимые данные. Например, если вы хотите найти места по конкретным результатам, то в столбце, где заносятся результаты, например, метры или секунды, нужно установить команду «сортировать данные по значению». Данные будут отсортированы от большего к меньшему, или наоборот. Если вам просто нужно указать места, используйте для этого команду Ранг. В скобках можно ввести число (номер ячейки, место которой вы хотите указать), ссылку на диапазон ячеек, 0 или 1 (где 0 означает сортировку по убыванию, а 1 — сортировку по возрастанию ).
tsivat 5 лет назад Надо применить функции Для решения этой задачи: МИН, МАКС, НАИМЕНЬШИЙ или НАИБОЛЬШИЙ для столбца, по которому выбор делается. Это сложнеее. Проще отсортировать данные по этому столбцу от большего (или меньшего) значения для чисел, удалив все начальные пробелы. Подробнее могу описать, если задание вышлите. Или смотрите здесь с функциями. А тут сортировка для чисел описана.
Долинн 4 месяца назад Даже в Ворде можно включить сортировку через меню “Макет”, а уж в Экселе тем более.
Прямо на главной странице есть кнопка Сортировка и фильтр, которая позволяет отсортировать данные от меньших к большим, и наоборот, или вообще выбрать данные, соответствующие какому-то признаку. Знаете ответ? |
Даже если в вашей организации вопросами проведения тендеров и заключения договоров занимается отдел закупок, выбор поставщиков — это ваша прерогатива. В конце концов ведь именно вам придется иметь с ними дело, контролировать их действия и выяснять, соответствуют ли вашим требованиям поставляемые ими продукты или услуги.
Существует немало способов отбора поставщиков. Возможно, ваша организация располагает списком поставщиков, из которого вы можете выбрать того, кто наиболее подходит для вашего проекта. Если у вас нет опыта работы с каким-то определенным поставщиком, необходимо навести о нем справки. Выясните, работал ли этот поставщик с проектами аналогичного масштаба и тематики и располагает ли он квалификацией, требуемой для выполнения вашего проекта. Важно также узнать, приходилось ли представителям этого поставщика взаимодействовать с работниками вашей организации (как в дружественной, так и профессиональной атмосфере) и насколько плодотворным оказалось такое сотрудничество. При рассмотрении предложений, поступивших в ответ на ваше объявление о проведении тендера, вы можете воспользоваться специальными методами выбора, такими как система отсеивания или модель взвешенных оценок. Сейчас мы рассмотрим эти два метода.
Системы отсеивания
Для оценки ответов, поступивших после объявления о проведении тендера, в системах отсеивания используются специальные, заранее установленные критерии. Если ответ не отвечает этим критериям, он отбрасывается. Например, один из критериев отсеивания, который мы могли бы использовать для выбора подрядчика на прокладку кабеля в новом здании по проекту Grant St. Move заключается в том, что у такого подрядчика должен быть опыт работы с волоконно-оптическим кабелем. Если в предложении потенциального поставщика о наличии такого опыта ничего не говорится, этот поставщик немедленно исключается из дальнейшего рассмотрения.
Критерии отсеивания определяются во время подготовки RFP. Руководитель проекта и другие члены комитета но отбору поставщиков работают совместно над определением надлежащих критериев отбора. Закупочные процессы могут предусматривать несколько этапов для мелких закупок и несколько этапов для более крупных. Типичными этапами закупочного процесса являются публикация RFP и получение ответов, презентации поставщиков и собеседования, период постановки вопросов и возможность внесения поправок в RFP, выбор поставщика и заключение договора.
Системы отсеивания нередко используются в сочетании с моделью взвешенных оценок, которую нам предстоит рассмотреть ниже.
Модель взвешенных оценок
Модели взвешенных оценок представляют собой объективный способ оценивания ответов поставщиков на RFP. При этом мы исходим из того, что для оценивания ответов все члены комитета по отбору поставщиков используют одни и те же критерии. Как и в случае систем отсеивания, критерии для модели взвешенных оценок определяются примерно в то же время, когда составляется RFP. Иногда модель взвешенных оценок может включаться в RFP. В таком случае поставщикам заранее становится известно, по каким критериям они будут оцениваться.
Для модели взвешенных оценок вырабатывается несколько критериев, причем каждому из них приписывается определенный вес в зависимости от важности соответствующего критерия: чем больше важность, тем выше вес. Типичным вариантом является приписывание весов от единицы до пяти (пять соответствует самому важному критерию). Все члены комитета по отбору поставщиков получают по экземпляру ответа на RFP, после чего оценивают каждый из критериев модели взвешенных оценок согласно тому, в какой степени поставщик способен удовлетворить данное требование. Выставляемая оценка базируется на индивидуальном суждении и интерпретации. При наличии значительного количества экспертов (по нашему мнению, их должно быть не менее трех-пяти человек) окончательная оценка достаточно точно отражает способность того или иного поставщика (в случае одного эксперта точность его оценок может вызывать большое сомнение). После того как все эксперты оценят ответы на RFP, путем усреднения взвешенных оценок всех экспертов определяется окончательная, суммарная оценка.
Если бы мы назначали весовые коэффициенты критериям для оценки компаний-перевозчиков, участвующих в тендере по проекту Grant St. Move, то они бы выглядели примерно так, как показано на рис. 1 (здесь представлена лишь часть критериев, которые нам следовало бы использовать).

Рис. 1. Модель взвешенных оценок
Как видно из этого примера, самыми важными для нас критериями в данном случае являются опыт корпоративных перевозок (Experience with corporate move) и наличие сертификата на перевозку компьютерного оборудования (Certified to move computer equipment). Весовой коэффициент для каждого фактора (Weight) умножается на рейтинг, присвоенный экспертом (Vendor score), а затем все баллы суммируются для определения окончательной, итоговой оценки. Нетрудно заметить, что самую высокую оценку получил перевозчик В.
В программе Excel легко создать электронную таблицу подобную той, которая была создана нами (см. рис. 1). Чтобы определить взвешенную оценку компании-перевозчика (Vendor Weighted Score), нужно умножить оценку каждого перевозчика (Vendor Score) на соответствующий весовой коэффициент. Сложив суммы, указанные в этом столбце, вы получите окончательную, итоговую оценку (Total Weighted Score).
Лотерея – это не охота за удачей,
это охота за неудачниками.
С завидной регулярностью (а в последнее время – всё чаще) мне пишут люди с просьбами помочь в различных вычислениях, связанных с лотереями. Кто-то хочет реализовать в Excel свой секретный алгоритм подбора выигрышных чисел, кто-то – найти закономерности в выпавших номерах прошедших тиражей, кто-то – подловить организаторов лотереи на нечестной игре.
В этой статье мне хотелось бы ответить на часть этих вопросов. Благо, в Excel для решения таких задач достаточно инструментов, многие из которых, кстати, могут пригодиться и в более прозаических рабочих ситуациях.
Задача 1. Вероятность выигрыша
Возьмем для примера классическую лотерею “Столото 6 из 45”. По правилам суперприз (10 млн. рублей или больше, если накопился остаток призового фонда с прошлых тиражей) получают только те, кто угадал все 6 чисел из 45. Если вы угадали 5, то получите 150 тыс. рублей, если 4 – 1500 р., если 3 числа из 6, то 150 р., если 2 числа – вернете 50 р., потраченных на билет. Угадаете только одно или ни одного – получите только эндорфины от процесса игры.
Математическую вероятность выигрыша можно легко рассчитать с помощью стандартной функции ЧИСЛКОМБ (COMBIN), которая имеется в Microsoft Excel на такой случай. Эта функция вычисляет количество комбинаций N чисел из M. Так для нашей лотереи “6 из 45” это будет:
=ЧИСЛКОМБ(45;6)
… что равно 8 145 060 – общее число всех возможных комбинаций в этой лотерее.
Если же хочется рассчитать вероятность для частичного выигрыша (2-5 чисел из 6), то придётся сначала вычислить количество таких вариантов, которое равно произведению числа комбинаций угаданных чисел из 6 на количество не угаданных чисел из оставшихся (45-6)=39 чисел. Затем общее количество всех возможных комбинаций (8 145 060) мы делим на полученное количество выигрышей по каждому варианту – и получим вероятности выигрыша для каждого случая:
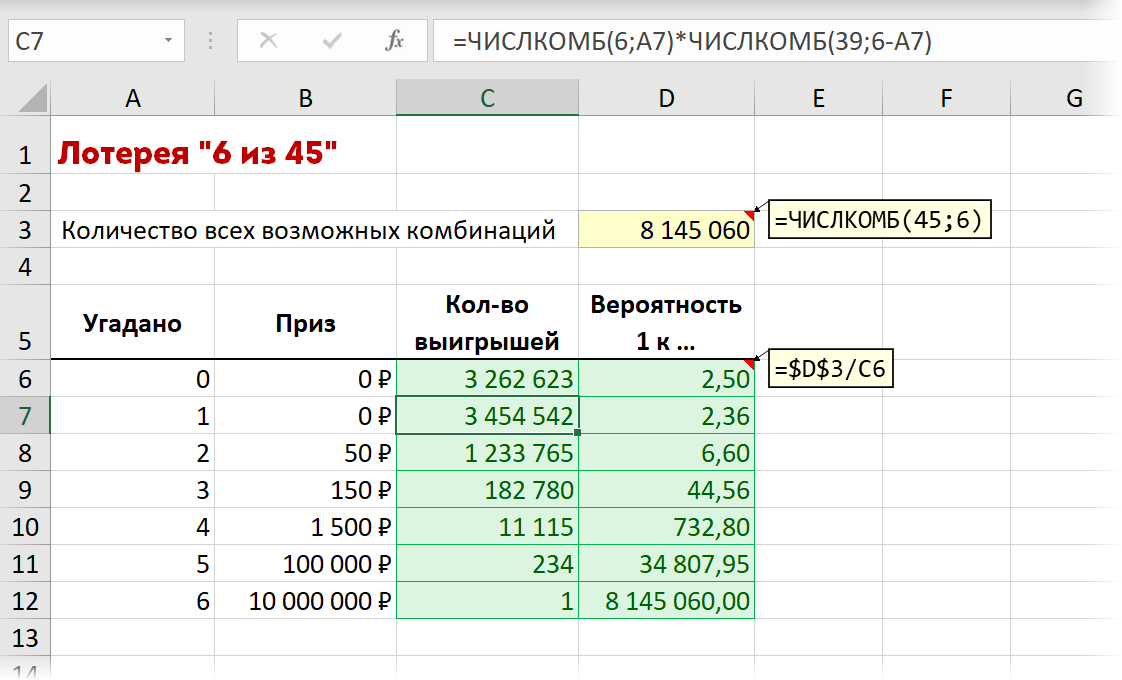
К слову, вероятность, например, погибнуть в авиакатастрофе в России оценивается примерно как 1 к миллиону. А вероятность выиграть в казино в рулетку, поставив всё на один номер – 1 к 37.
Если всё вышеперечисленное вас не остановило и вы по-прежнему готовы играть дальше – продолжаем.
Задача 2. Частота выпадения каждого числа
Для начала давайте определим с какой частотой выпадают те или иные числа. В идеальной лотерее, если брать для анализа достаточно большой временной интервал, у всех шаров должна быть одинаковая вероятность попадания в победную выборку. В реальности же особенности конструкции лототрона и вес-форма шаров могут вносить искажения в эту картину и для каких-то шаров вероятность выпадения вполне может оказаться выше/ниже, чем для других. Давайте проверим эту гипотезу на практике.
Возьмём для примера данные по всем прошедшим в 2020-21 году тиражам лотереи 6 из 45 с сайта их организатора Столото, оформленные в виде вот такой удобной для анализа “умной” таблицы с именем таблАрхивТиражей. Розыгрыши проходят два раза в день (в 11 утра и в 11 вечера), т.е. в этой таблице у нас полторы тысячи тиражей-строк – вполне достаточная для начала выборка для анализа:
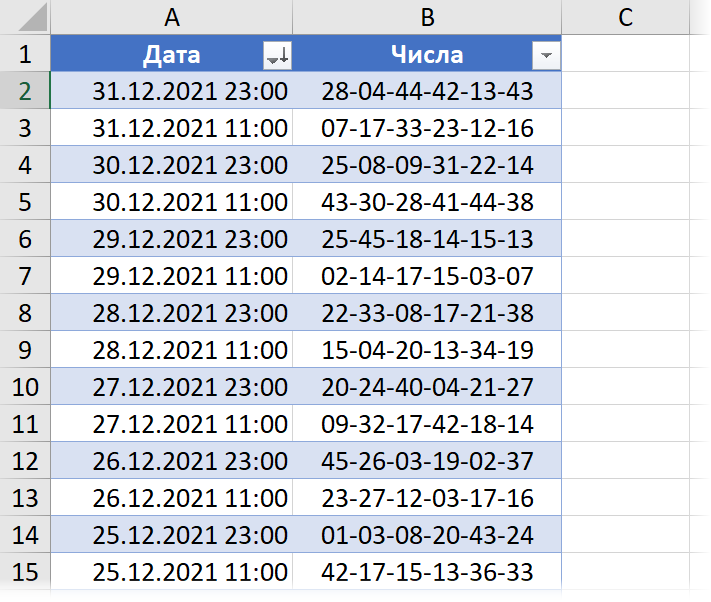
Для подсчёта частоты выпадения каждого числа используем функцию СЧЁТЕСЛИ (COUNTIF) и дополнительно вложим в неё функцию ТЕКСТ (TEXT), чтобы добавить к одноразрядным числам начальные нули и звёздочки перед и после, чтобы СЧЁТЕСЛИ искала вхождение числа в любом месте комбинации в столбце В. Также для пущей наглядности построим диаграмму по результатам и отсортируем частоты по убыванию:
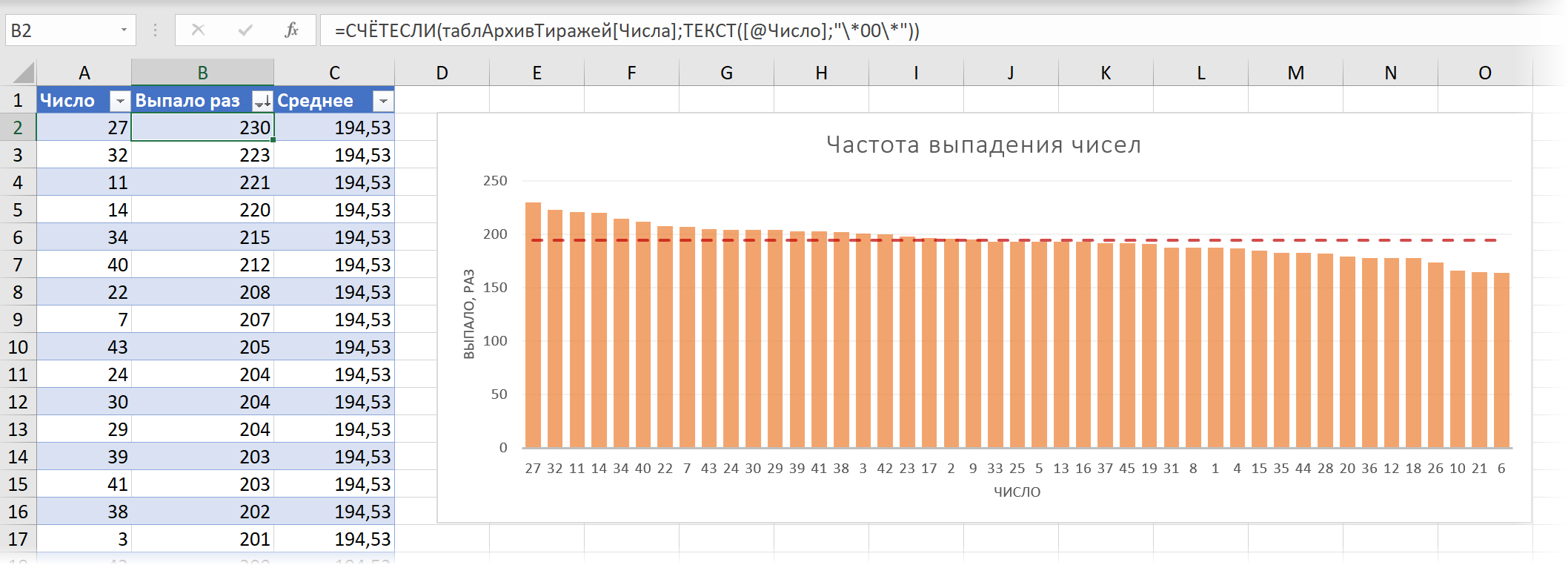
В среднем любой шар должен выпадать 1459 тиражей * 6 шаров / 45 номеров = 194,53 раз (это как раз то, что называется в статистике математическим ожиданием), но хорошо видно, что некоторые числа (27, 32, 11…) выпадали заметно чаще (+18%), а некоторые (10, 21, 6…) наоборот заметно реже (-15%), чем основная масса. Соответственно, можно попробовать использовать эту информацию для стратегии выигрыша, т.е. либо ставить на те шары, что выпадают чаще, либо наоборот – делать ставку на редко выпадающие шары в надежде, что они должны нагнать отставание.
Задача 3. Какие числа давно не выпадали?
Ещё одна стратегия базируется на идее, что при достаточно большом количестве тиражей рано или поздно должно выпасть каждое число из всех имеющихся от 1 до 45. Так что если какие-то числа давно не появлялись среди выигравших (“холодные шары”), то логично попробовать сделать на них ставку в будущем.
Можно легко найти все давно не выпадавшие номера, если отсортировать наш архив тиражей за 2020-21 год по убыванию даты и использовать функцию ПОИСКПОЗ (MATCH). Она будет сверху-вниз (т.е. от новых к старым тиражам) искать каждое число и выдавать порядковый номер тиража (считая от конца года к началу), где последний раз это число выпало:
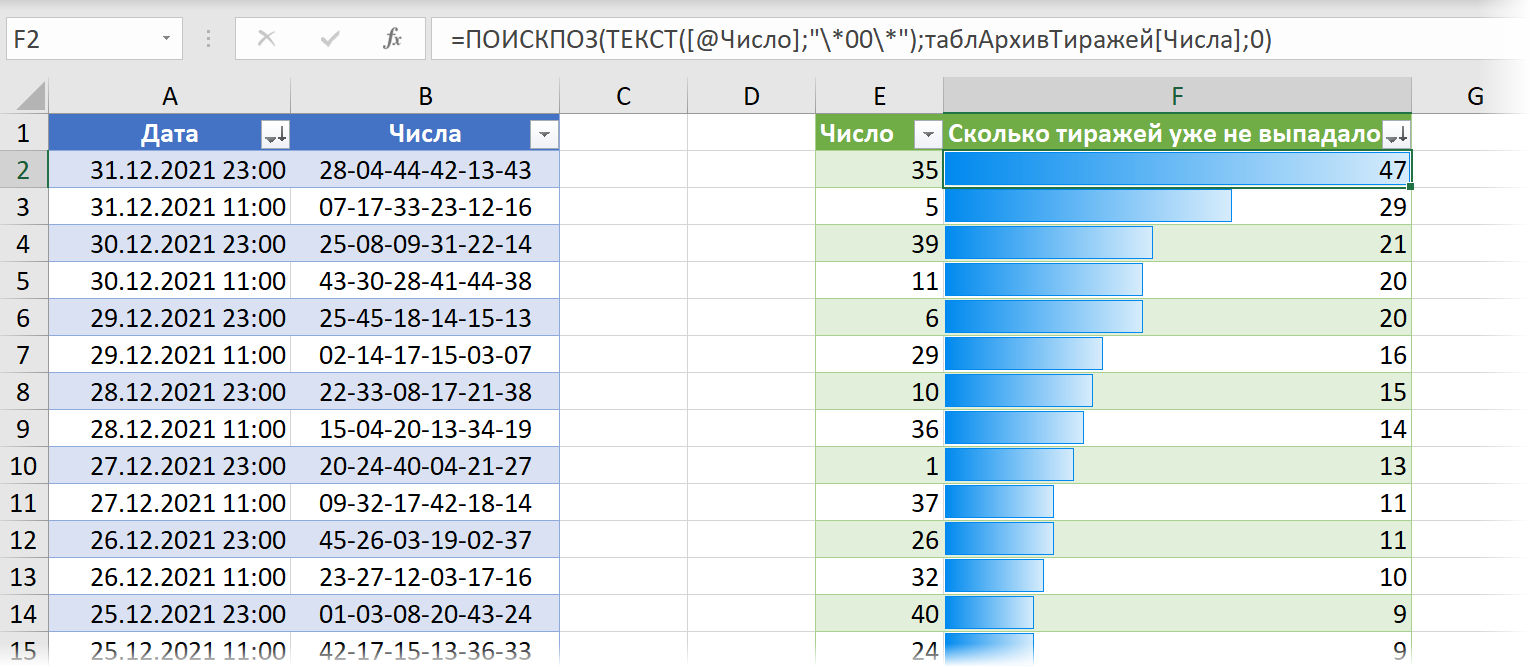
Задача 4. Генератор случайных чисел
Ещё одна стратегия игры основана на том, чтобы исключить психологический фактор при угадывании номеров. Когда игрок выбирает числа, делая свою ставку, то подсознательно делает это не совсем рационально. По статистике, например, числа от 1 до 31 выбирают на 70 % чаще, чем остальные (любимые даты), реже выбирают 13 (чертова дюжина), чаще выбирают числа содержащие “счастливую” семерку и т.д. Но играем мы против машины (лототрона), для которой все числа одинаковы, так что имеет смысл выбирать их с такой же математической беспристрастностью, чтобы уравнять наши шансы. Для этого нам потребуется создать в Excel генератор случайных и – что особенно важно – неповторяющихся чисел:
Для этого:
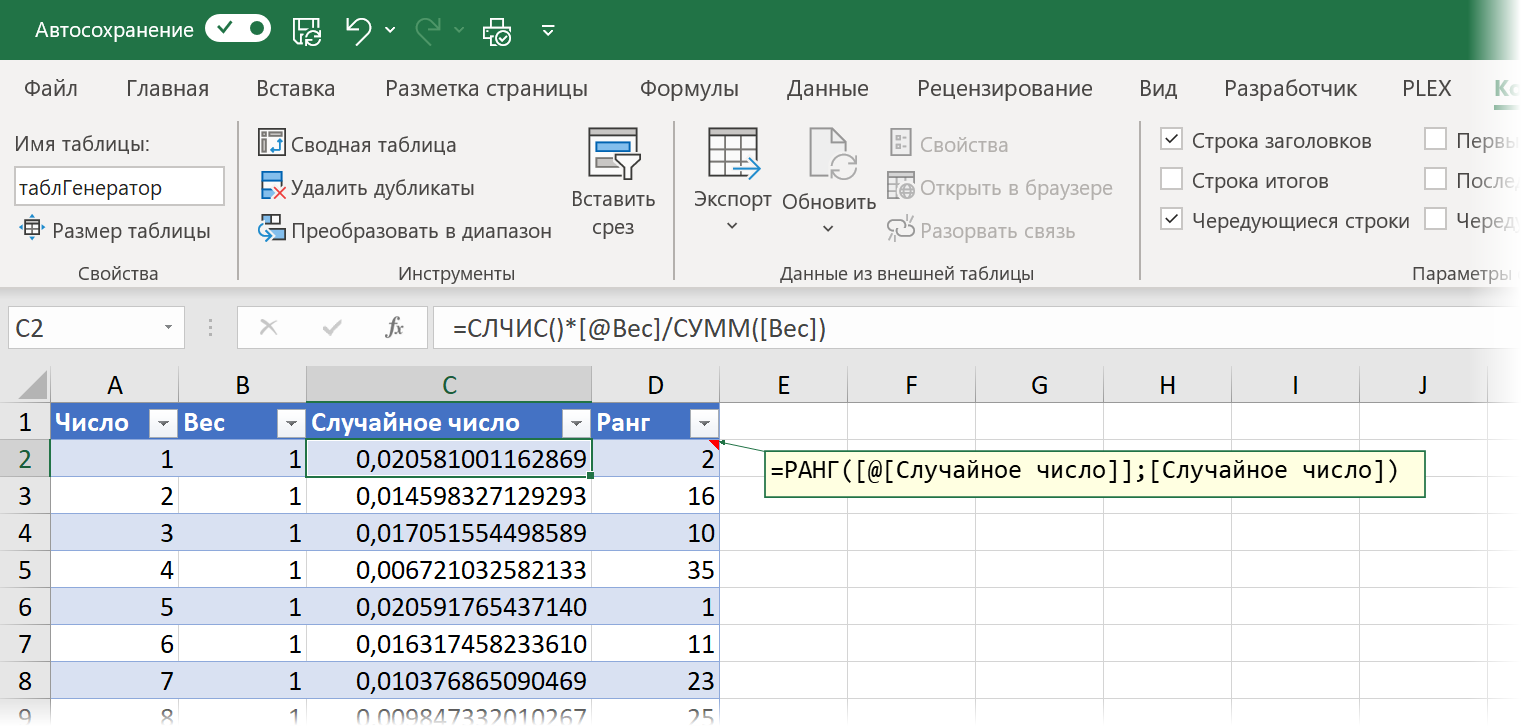
- Создадим “умную” таблицу с именем таблГенератор, где в первом столбце будут наши числа от 1 до 45.
- Во втором столбце введём вес для каждого числа (он потребуется нам чуть позднее). Если все числа для нас одинаково ценны и мы хотим выбирать их с равной вероятностью, то вес везде можно поставить равным 1.
- В третьем столбце используем функцию СЛЧИС (RAND), которая в Excel генерирует случайное дробное число от 0 до 1, добавив к нему вес из предыдущего столбца. Таким образом каждый раз при пересчёте листа (нажатии на клавишу F9) будет генерироваться новый набор из 45 случайных чисел с учётом веса для каждого из них.
- Добавим четвертый столбец, где с помощью функции РАНГ (RANK) вычислим ранг (позицию в топе) для каждого из чисел.
Теперь останется сделать выборку первых шести по рангу 6 чисел с помощью функции ПОИСКПОЗ (MATCH):
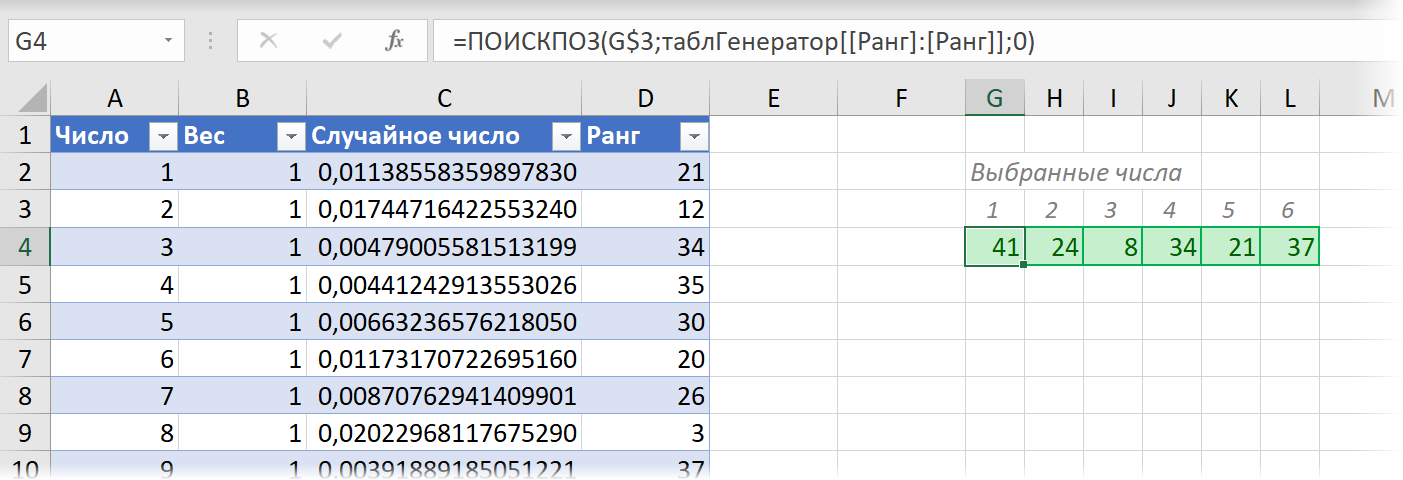
При нажатии на клавишу F9 формулы на листе Excel будут пересчитываться и мы будем каждый раз получать новый набор из 6 чисел в зеленых ячейках. Причём числа, для которых был задан в столбце B больший вес, будут получать пропорционально больший ранг и, таким образом, чаще оказываться в результатах нашей случайной выборки. Если же вес для всех чисел задать одинаковым, то все они будут выбираться с одинаковой вероятностью. Таким образом мы получаем справедливый и беспристрастный генератор случайных чисел 6 из 45, но с возможностью внести корректировки в случайность распределения при необходимости.
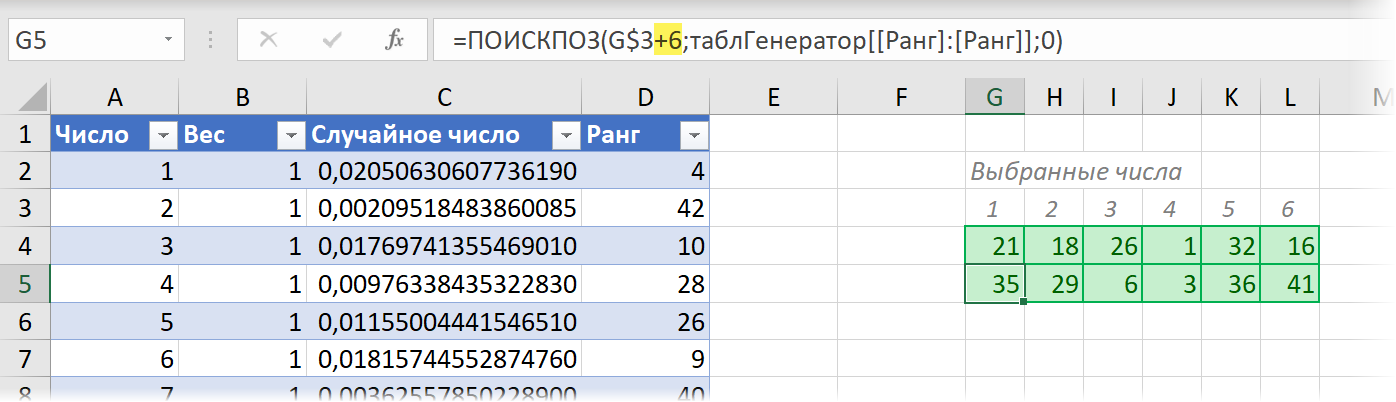
Если же мы решим играть в каждом тираже не одним, а, например, двумя билетами сразу, в каждом из которых будем выбирать неповторяющиеся числа, то можно просто добавить к зелёному диапазону дополнительные строки снизу, прибавив к рангу 6, 12, 18 и т.д. соответственно:
Задача 5. Симулятор лотереи в Excel
В качестве апофеоза всей этой темы давайте создадим в Excel полноценный симулятор лотереи, на котором можно будет опробовать любые стратегии и сравнить результаты (в теории оптимизации что-то похожее ещё называют методом Монте-Карло, но у нас будет попроще).
Чтобы все было максимально приближено к реальности, представим на минуту, что сейчас 1 января 2022 года и впереди у нас тиражи этого года, в которых мы планируем играть. Реальные выпавшие числа я занёс в таблицу таблТиражи2022, отделив дополнительно выпавшие числа друг от друга в отдельные столбцы для удобства последующих вычислений:
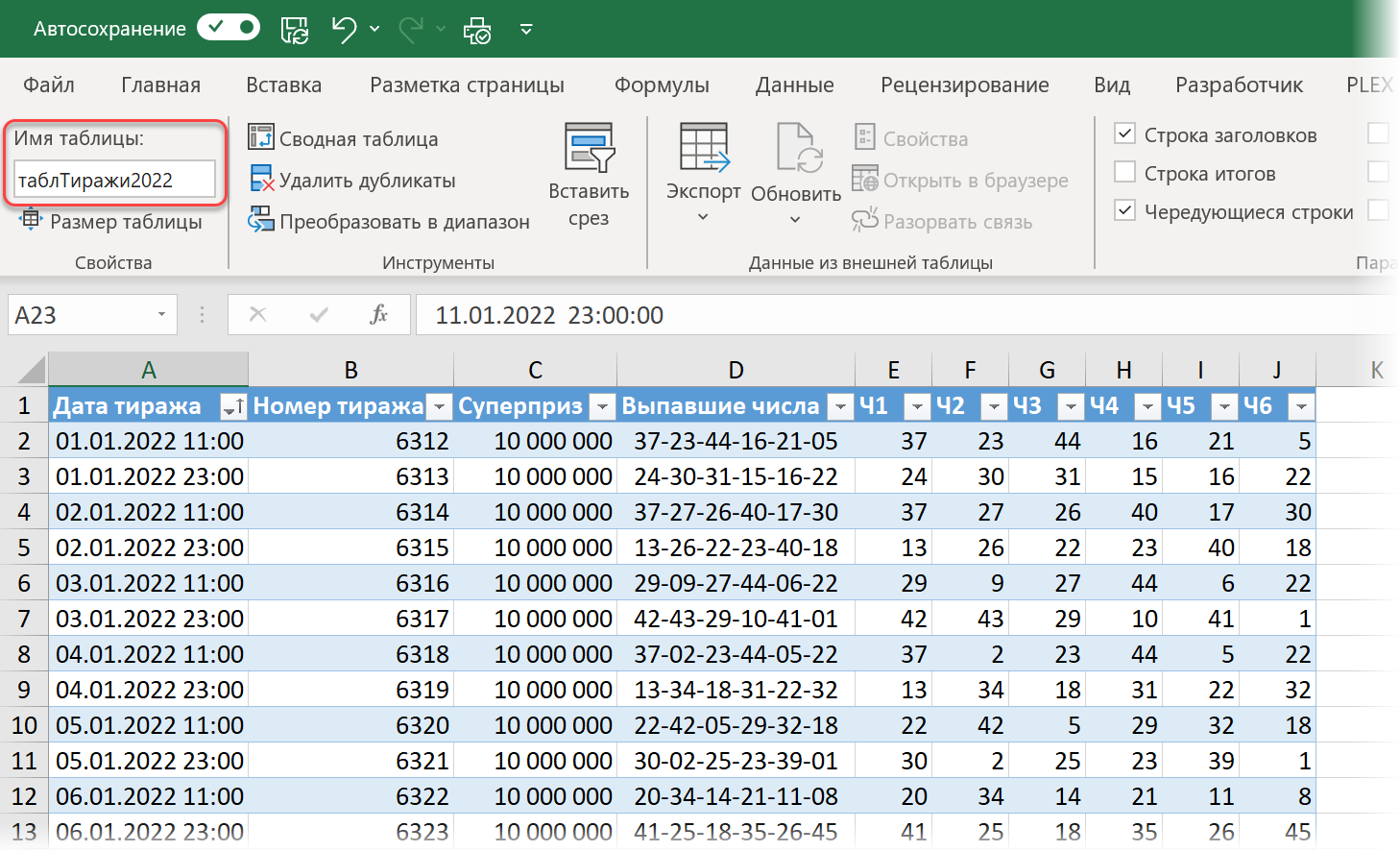
На отдельном листе Игра создадим заготовку для моделирования в виде “умной” таблицы с именем таблИгра следующего вида:
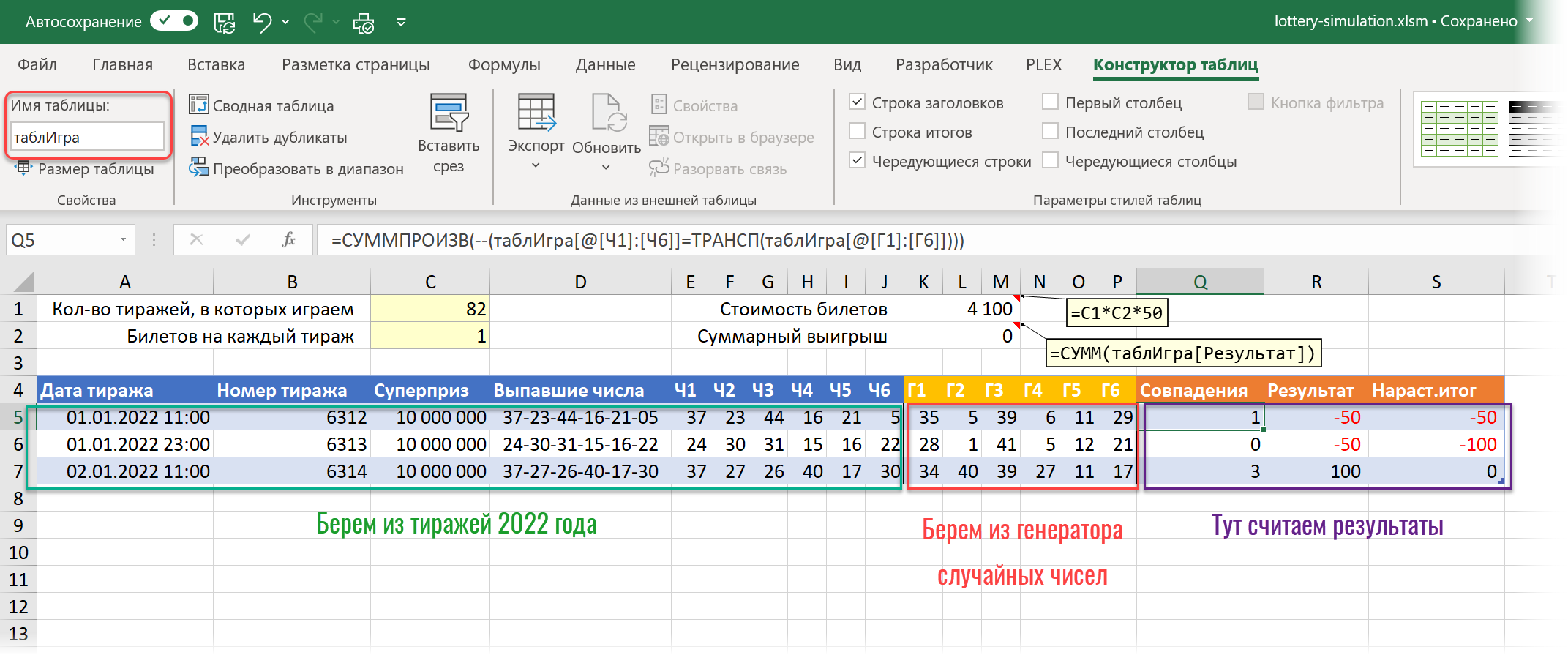
Здесь:
- В желтых ячейках сверху будем задавать для макроса количество тиражей 2022 года, в которых мы хотим участвовать (1-82) и количество билетов, которыми мы играем в каждом тираже.
- Данные для первых 11 столбцов (A-J) макрос будет копировать с листа тиражей 2022 года.
- Данные для следующих шести столбцов (K-P) макрос будет брать с листа Генератор, где мы реализовали генератор случайных чисел (см. задачу 4 выше).
- В столбце Q мы считаем количество совпадений выпавших чисел и сгенерированных с помощью функции СУММПРОИЗВ (SUMPRODUCT).
- В столбце R вычисляем финансовый результат (если не выиграли, то минус 50 рублей за билет, если выиграли, то приз – 50 р. за билет)
- В последнем столбце S считаем общий результат всей игры нарастающим итогом, чтобы видеть динамику в процессе.
И чтобы оживить всю эту конструкцию нам потребуется небольшой макрос. На вкладке Разработчик (Developer) выберем команду Visual Basic или воспользуемся сочетанием клавиш Alt+F11. Затем добавим новый пустой модуль через меню Insert – Module и введем туда следующий код:
Sub Lottery()
Dim iGames As Integer, iTickets As Integer, i As Long, t As Integer, b As Integer
'объявляем переменные для ссылки на листы
Set wsGame = Worksheets("Игра")
Set wsNumbers = Worksheets("Генератор")
Set wsArchive = Worksheets("Тиражи 2022")
iGames = wsGame.Range("C1") 'количество тиражей
iTickets = wsGame.Range("C2") 'количество билетов в каждом тираже
i = 5 'первая строка в таблице таблИгра
wsGame.Rows("6:1048576").Delete 'очищаем старые данные
For t = 1 To iGames
For b = 1 To iTickets
'копируем выигравшие номера с листа Тиражи 2022 и вставляем на лист Игра
wsArchive.Cells(t + 1, 1).Resize(1, 10).Copy Destination:=wsGame.Cells(i, 1)
'копируем и вставляем специальной вставкой значений сгенерированные номера с листа Генератор
wsNumbers.Range("G4:L4").Copy
wsGame.Cells(i, 11).PasteSpecial Paste:=xlPasteValues
i = i + 1
Next b
Next t
End Sub
Останется ввести желаемые исходные параметры в жёлтые ячейки и запустить макрос через Разработчик – Макросы (Developer – Macros) или сочетанием клавиш Alt+F8.
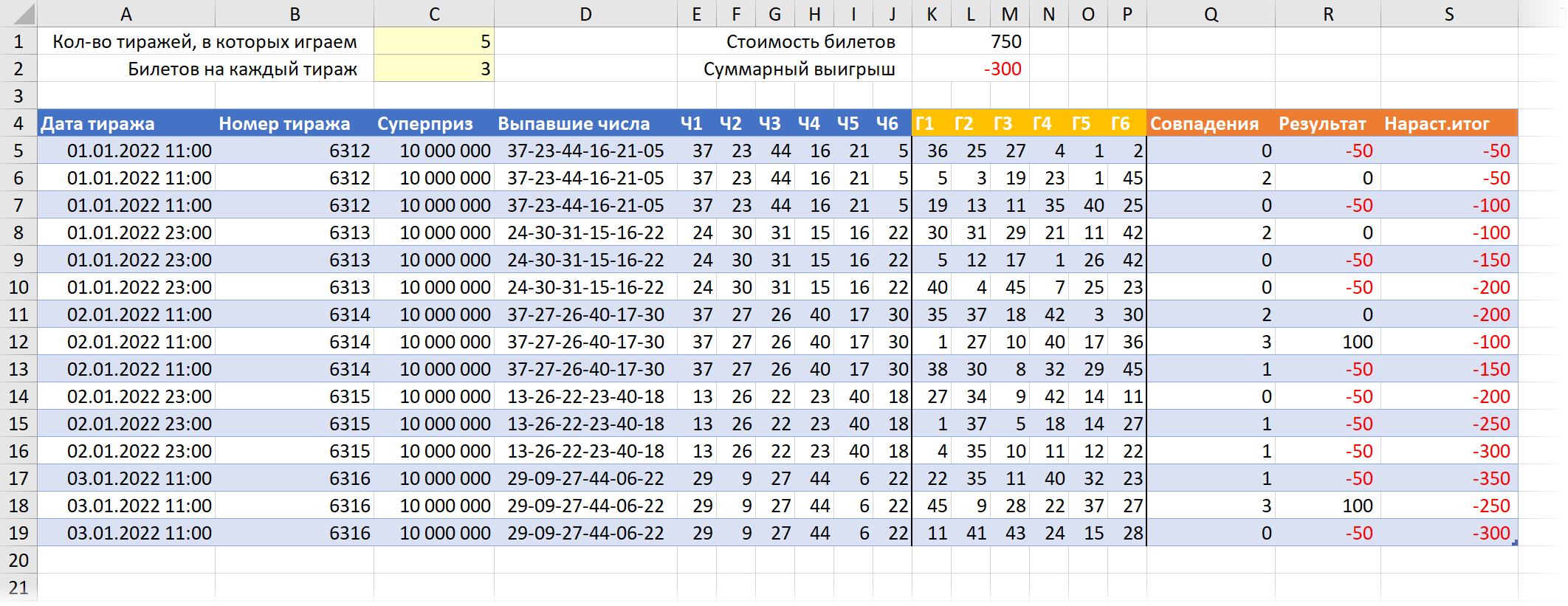
Для наглядности можно ещё построить диаграмму по последнему столбцу с нарастающим итогом, отражающую изменение денежного баланса в процессе игры:
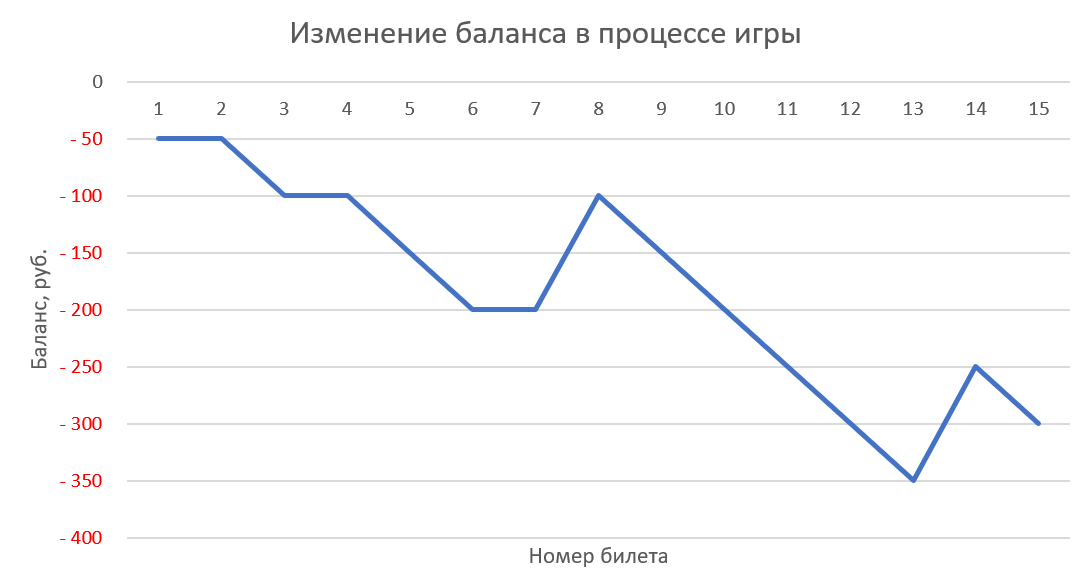
Сравнение разных стратегий
Теперь, используя созданный симулятор, можно протестировать на реальных тиражах 2022 года любую стратегию игры и посмотреть на результаты, которые бы она принесла. Если играть 1 билетом в каждом тираже, то общая картина “слива” выглядит примерно так:
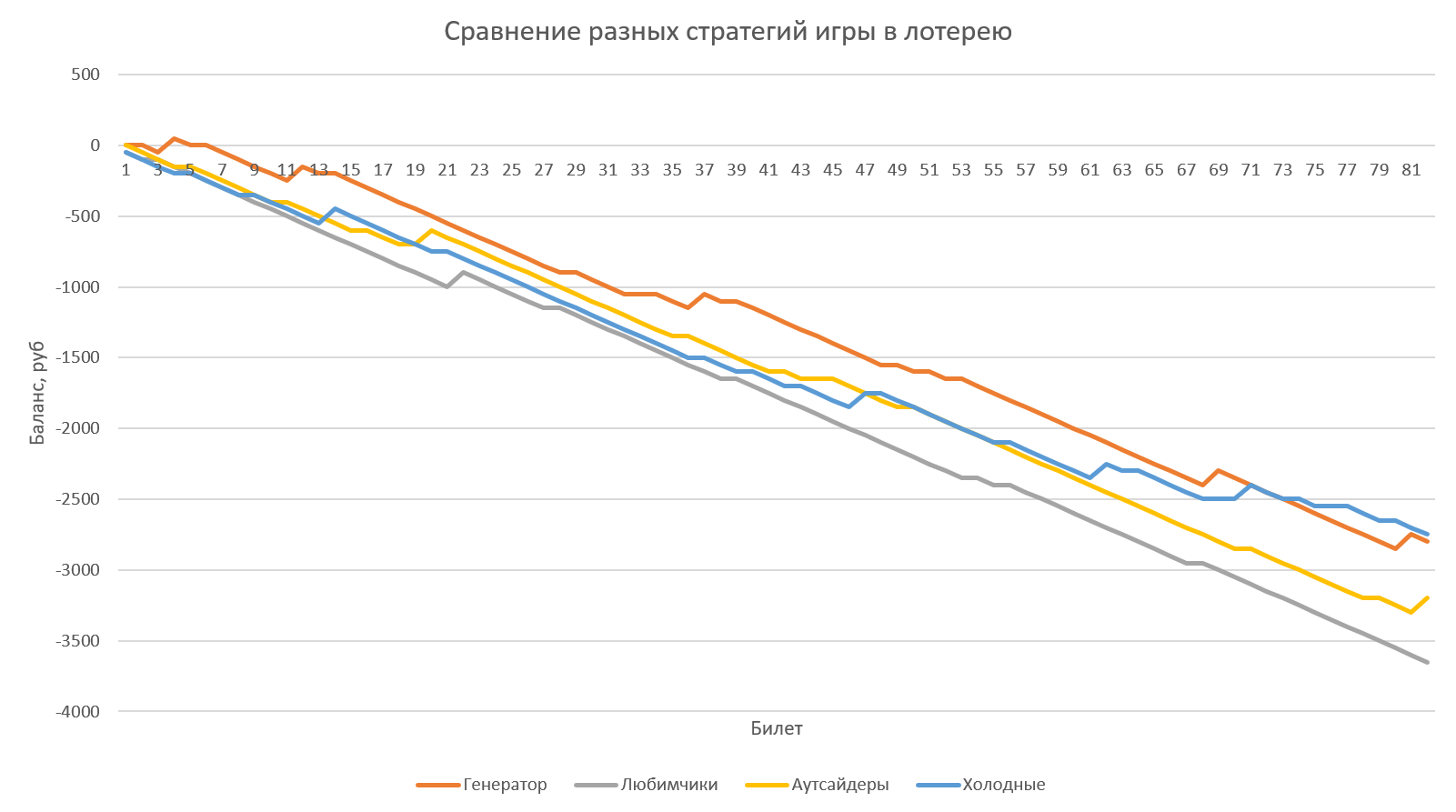
Здесь:
- Генератор – игра, где в каждом тираже мы выбираем случайные числа, созданные нашим генератором (с одинаковым весом).
- Любимчики – игра, где в каждом тираже мы используем одни и те же числа – те, что чаще всего выпадали в тиражах за последние два года (27, 32, 11, 14, 34, 40).
- Аутсайдеры – то же самое, но используем самые редко выпадающие числа (12, 18, 26, 10, 21, 6).
- Холодные – в всех тиражах используем числа, которые давно не выпадали (35, 5, 39, 11, 6, 29).
Как видите, разницы большой нет, но генератор случайных чисел ведёт себя чуть лучше остальных “стратегий”.
Можно также попробовать играть большим количеством билетов в каждом тираже, чтобы перекрыть большее количество вариантов (иногда для этого несколько игроков объединяются в группу).
Игра в каждом тираже одним билетом со случайно сгенерированными числами (с одинаковым весом):
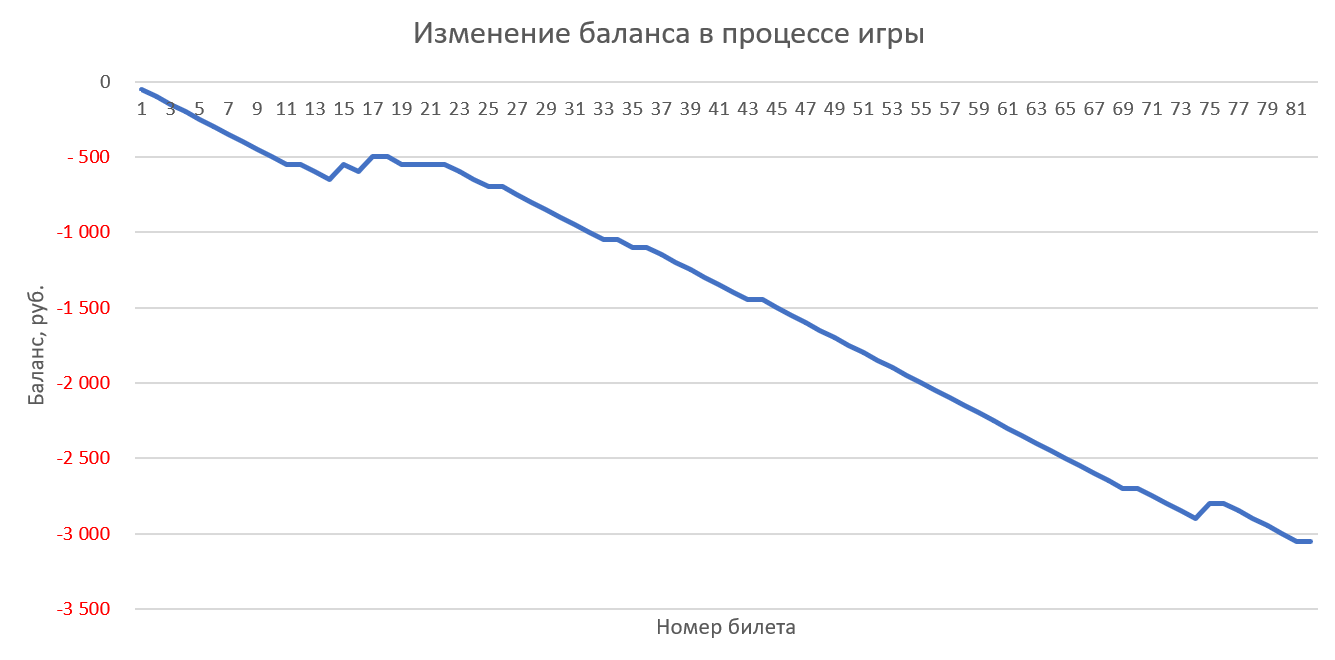
Игра 10 билетами в каждом тираже со случайно сгенерированными числами (с одинаковым весом):
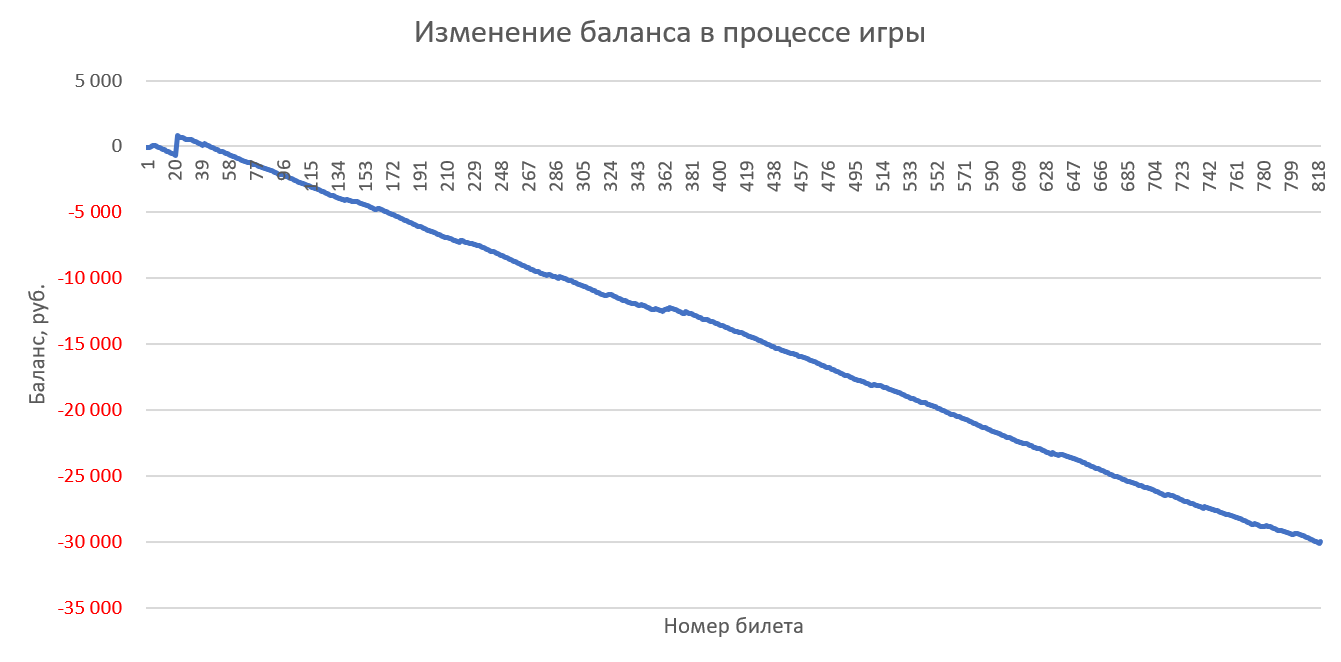
Игра 100 билетами в каждом тираже со случайными числами (с одинаковым весом):
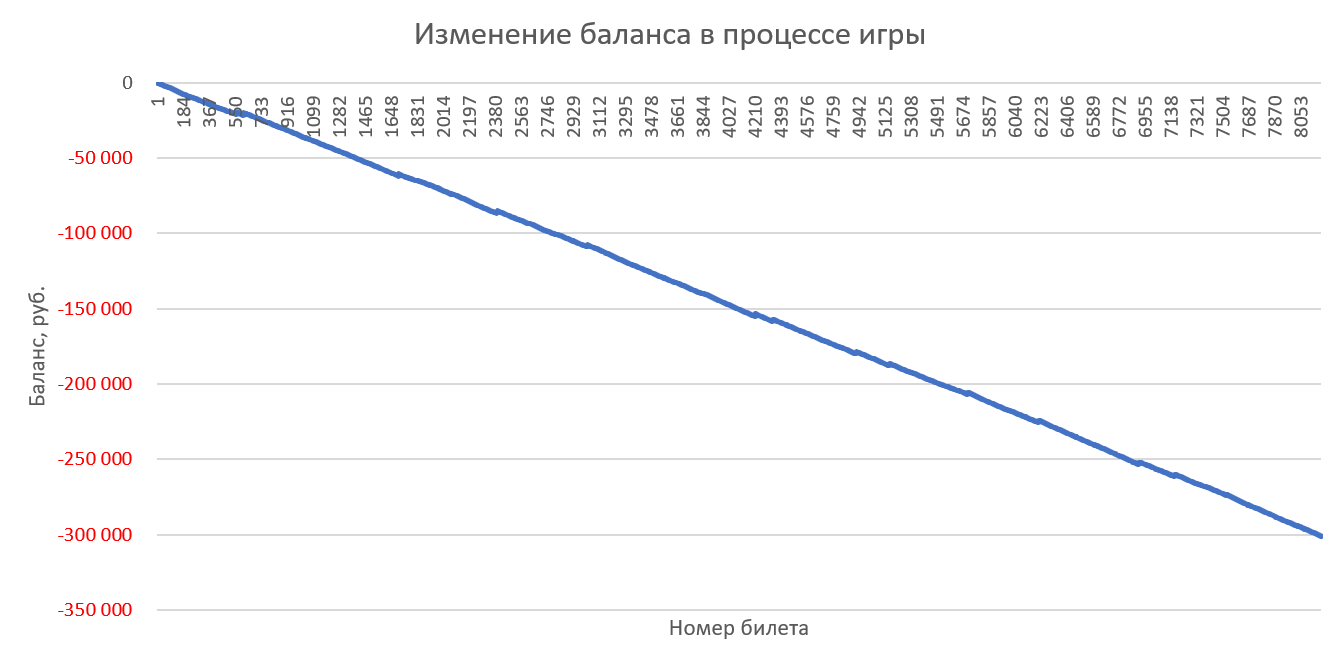
Комментарии, как говорится, излишни – слив депозита неизбежен во всех случаях 🙂
Время на прочтение
6 мин
Количество просмотров 13K
Каждый раз, когда мы используем сложные математические алгоритмы и современные методы машинного обучения, мы ставим задачу получить тренд, понять внутренние зависимости, и в конечном счете произвести предсказания. Более точные результаты можно получить, если алгоритм может быть адаптирован под имеющиеся знания, под имеющуюся модель процесса. Одним из направлений в машинном обучении, которое позволяет создавать и обучать модели для получения предсказаний, является «порождающее (или Байесовское) моделирование» (в отличие от «дискриминативного» моделирования, например, нейронных сетей). Для создания вероятностных моделей и работы с ними существуют платформы, которые в последнее время относятся к направлению «вероятностным программированием». Более подробно о вероятностном программировании можно почитать в других статьях на Хабрахабре: «Вероятностное программирование», «Вероятностное программирование – ключ к искусственному интеллекту?» и «Вероятностное программирование».
Совсем недавно появился стартап Invrea, который в качестве вероятностного языка программирования предлагает использовать Excel: вероятностная модель может быть создана в Экселе и предсказания могут быть получены там же. Ниже находится перевод одной из статьи с сайта стартапа (перевод выполнен исключительно в образовательных целях). В статье авторы рассматривают пример «бытовой» ситуации. Им интересно понять, кто победит в теннисном турнире на Олимпийских играх 2016. Они производят предсказания о том, кто наиболее вероятный кандидат на победу. Статья была написана 7 августа, во время игр, после завершения всех игр первого тура.
***
Описание задачи
«На наш взгляд, очень важно сделать машинное обучение простым в использовании и доступным каждому. Нужно максимально устранить необходимость подгонять имеющийся вопрос или задачу под необходимые рамки для возможных вычислений. Авторы представляют плагин «Сценарии Invrea» (для Excel), который может быть использован для принятия решений о текущих и регулярных событиях. Чтобы продемонстрировать это, авторы воспроизвели ход турнира в мужском одиночном турнире в электронной таблице Excel. Используя плагин, были определены вероятности победы для каждого из игроков, входящих в Ассоциацию теннисистов-профессионалов (АТП), основываясь на их рейтинге в этой организации.
Видео-демонстрация (на английском) использования Эксель-плагина для предсказания победителя мужского турнира по теннису на Рио 2016:
Предсказания относительно обладателя золотой медали после первого тура. Рассчитано с использованием плагина Invrea:
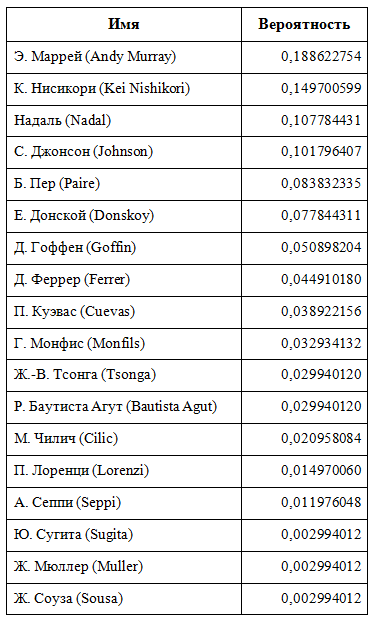
В мужском одиночном турнире участвуют 64 человека, каждый из которых сталкивается лицом к лицу один на один с другим игроком. Победитель проходит в следующий тур, проигравший выходит из соревнования. Это продолжается до финала, где победителю вручают золотую медаль. Вопрос в том, кто вероятнее всего получит золото? Было бы неплохо получить вероятности победы каждого игрока в турнире. Теннис имеет большую долю неопределенности. Тот факт, что Маррей имеет рейтинг выше, чем у Нисикори, не гарантирует, что Маррей пройдет дальше. Как и в любом спортивном состязании разочарования и сюрпризы могут произойти в любой момент.
К счастью, машинное обучение создано с целью найти возможность справиться с этой проблемой. С его использованием мы можем учесть определенную долю случайности при принятии решения, выиграет ли Маррей или Нисикори. Маррей имеет немного большую вероятность согласно рейтингу, но справедлива и возможность, что победит Нисикори.
Представляем вероятностную модель в электронной таблице
Далее представлена электронная таблица Excel, которую авторы создали с целью определить шансы на победу в Рио каждого игрока. Файл имеет два листа: первый содержит список всех игроков, его рейтинг и логарифм от этого рейтинга. К каждой из оценок была добавлена случайная величина, потому что количество очков не всегда имеет решающее значение в описании игрока (см. рис. 1). Например, Дель Потро имеет всего лишь 140 очков в рейтинге АТП, но в основном это так из-за небольшого игрового периода. Его последние результаты приводят нас к мысли, что он более хороший игрок, чем показывает его рейтинг. Случайность помогает учесть эти небольшие несоответствия.
Вспомогательная электронная таблица с априорными «силами» каждого из игроков, основанная на рейтинге Ассоциации теннисистов-профессионалов:
Рис. 1.
Второй лист содержит турнирную таблицу. Столбец C отражает первый раунд, который вы можете найти на любой странице, описывающей данный турнир. Но вы также можете видеть, что также заполнено и все дальнейшее состояние турнира, включая победителя (см. рис. 2). Как это получилось? Если обновить электронную таблицу (нажатием клавиши F9) вы можете заметить, что все игроки во втором раунде и после него поменяются. Другими словами, ячейки, которые отражают, кто пройдет в следующий раунд, содержат значения, рассчитанные на основе вероятности.
Основная электронная таблица для моделирования результатов матчей:
Рис. 2.
Но их случайный характер основан на правиле: представьте, что вы выбираете случайную величину, близкую к рейтингу игрока A и выбираете другую случайную величину, близкую к рейтингу игрока B. Иногда эти величины будут ниже, чем реальный рейтинг…иногда выше. В таком случае, правило: тот, у кого более высокая случайная величина, выигрывает. Таким образом, обладание более высоким рейтингом АТП означает, что у вас более высокий шанс победить вашего соперника, но у вас может быть неудачный день / вы можете страдать от травмы и условно приобрести низкое значение случайной величины. Отсюда, вещи повторяются. Третий раунд отображает такое же равенство для игроков, которые прошли во втором раунде. И так далее. Вот почему, если вы будете обновлять электронную таблицу много раз, различные люди будут объявляться победителями турнира.
Что «Сценарии» Invrea позволяют вам делать – так это определять эти случайные ячейки, используя такие функции, как GAUSSIAN, и этот плагин позволяет вам генерировать тысячи сценариев автоматически и отображать их. Можно увидеть, что из себя представляет распределение в каждой случайной ячейке: кто победит в первом туре? Во втором туре? В полуфинале? В финале? Вы можете взглянуть на вероятности в любой ячейке, которая вам интересна.
Генерируем и производим анализ апостериорного распределения
Гистограмма, которую вы видите ниже (см. рис. 3) – это апостериорные вероятности, рассчитанные на победу каждого игрока, не зная, что произошло по окончании первого раунда. Чем выше столбик, тем более вероятна победа соответствующего игрока. Лишь бросив взгляд на нее, мы видим, что Джокович имеет довольно хороший шанс. Единственные, кто потенциально может остановить его – это Маррей, Надаль и Нисикори (Федерер не участвует в соревновании). Благодаря этой информации вы можете быть иметь больше оснований сказать о своих ожиданиях на победу Джоковича.
Рис. 3.
В действительности, можно поступить еще интереснее. Как только будут получены результаты по завершении раунда, вы можете учесть это в таблице, используя ACTUAL (специальную функцию Invrea). С учетом этого, мы можем увидеть сценарии, кто же победит в финале, ориентируясь на уже полученные результаты предыдущих раундов. Например, авторы использовали результаты всех матчей после первого раунда.
В их числе содержалось несколько непредвиденных ситуаций, в числе которых тот факт, что Джокович проиграл Дель Потро (см. рис. 4).
Рис. 4.
После запуска плагина с учетом новых данных можно увидеть (см. рис. 5) изменение распределения вероятностей того, кто победит в финале: теперь игроков меньше, и вероятность победы Джоковича теперь равна нулю, в то время, как результаты Маррея, Надаля и Нисикори повысились после первого раунда.
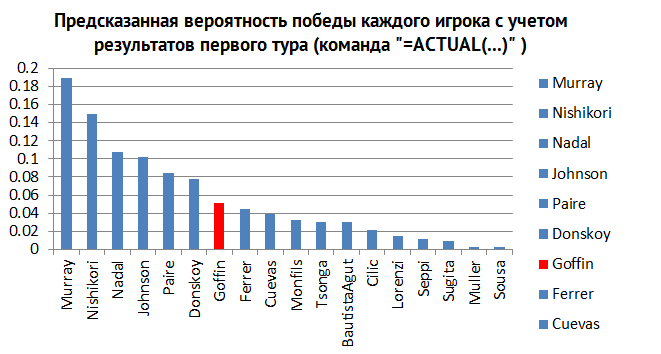
Рис. 5.
В действительности, распределение каждой случайной ячейки изменилось, потому что информация о результатах первого круга помогал плагина лучше рассчитать, кто будет наиболее вероятным победителем. Делая выводы по этим результатам, можно предположить победителя в лице Маррея или Нисикори. Можно следовать и далее, по ходу турнира добавляя информацию о происходящих событиях. Как только появятся результаты второго раунда, можно добавить их, используя ACTUALS, и предсказания станут еще лучше.
Также, существует большое количество информации, которое можно спрогнозировать по ходу турнира. Кто является наиболее вероятным победителем в 4-м четвертьфинале (рис. 6)? Втором полуфинале (рис. 7)? Глядя на гистограммы выше, мы можем получить ответы на каждый из этих вопросов.
Рис. 6.
Рис. 7.
„Сценарии“ Invrea помогают с получением предсказаний такого рода, но это не все. Плагин может смоделировать неопределенность и предсказать что-либо, основываясь на допущениях, новой информации и новых данных для бизнес-решений, страхованию, графику выплат. Если возможно смоделировать свое решение как отношение между клетками в электронной таблице Excel, тогда есть достаточно вероятности, что Invrea сможет помочь. Далее, мы продолжим цикл статей, связанных с прогнозированием тех или иных событий, используя ситуации и задачи из других сфер нашей жизни».
***
Послесловие
Как мы упомянули ранее, статья была написана 7 августа, после окончания только первого тура мужского турнира. Как мы уже знаем, победителем на Рио 2016 стал Энди Маррей, победа которого была предсказана в статье с наибольшей вероятностью (см. рис. 5 в переводе).
Если вам интересно это направление и понравился перевод, есть планы по переводы других статей, связанных с машинным обучением в целом и с вероятностным программированием в частности. Также есть идеи рассказать о современных приложениях машинного обучения в образовательных и коммерческих проектах.



