Как найти подгруппу циклической группы порядка - Сайт, где вы сможете решить свои вопросы

В общем случае задача о нахождении числа всех подгрупп циклической группы порядка $%n$% решается следующим образом.

Как сказано в комментарии @falcao, подгрупп у циклической группы столько, сколько натуральных делителей числа $%n$%. Чтобы найти число делителей, разложим $%n$% в произведение простых сомножителей: $$n=p_1^{k_1}p_2^{k_2}ldots p_m^{k_m}.$$ Тогда число делителей равно $%(k_1+1)(k_2+1)cdotldotscdot(k_m+1)$%, а сам делитель имеет вид $$d=p_1^{l_1}p_2^{l_2}ldots p_m^{l_m}, где 0leqslant l_1leqslant k_1,0leqslant l_2leqslant k_2,ldots, 0leqslant l_mleqslant k_m.$$

Чтобы найти собственные подгруппы, надо число всех подгрупп уменьшить на 2.

В случае данной задачи: $%48=2^4cdot 3$%, поэтому делителей будет $%(4+1)cdot(1+1)=10$%.

Источник

Циклические подгруппы

Если подгруппа группы может быть сгенерирована, используя возведение в степень элемента, то такая подгруппа называется циклической подгруппой. Термин возведение в степень здесь означает многократное применение к элементу групповой операции:

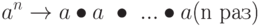
${a^n} to a bullet a{text{ }} bullet {text{ }}... bullet a {text{(n раз)}}$

Множество, полученное в результате этого процесса, обозначается в тексте как <a>. Обратите внимание также, что a⁰ = e.

Пример 5.7

Из группы G = < Z₆, +> могут быть получены четыре циклических подгруппы. Это H₁ = <{0},+>, H₂ =<{0, 2, 4}, +>, H₃ = <{0, 3}, +> и H₄ = G. Заметим, что когда операция — сложение, то aⁿ означает умножение n на a. Заметим также, что во всех этих группах операция — это сложение по модулю 6. Ниже показано, как мы находим элементы этих циклических подгрупп.

a. Циклическая подгруппа, сгенерированная из 0, — это H₁, имеет только один элемент (нейтральный элемент).

0⁰ mod 6 = 0 (остановка, далее процесс повторяется).

б. Циклическая подгруппа, сгенерированная на основе 1, — это H₄, которая есть сама группа G.

1⁰ mod 6 = 0
1¹ mod 6 = 1
1² mod 6 = (1 + 1) mod 6 = 2
1³ mod 6 = (1 + 1 + 1) mod 6 = 3
1⁴ mod 6 = (1 + 1 + 1 + 1) mod 6 = 4
1⁵ mod 6 = (1 + 1 + 1 + 1 + 1) mod 6 = 5(остановка, далее процесс повторяется)

в. Циклическая подгруппа, сгенерированная на основе 2, — это H₂, которая имеет три элемента: 0, 2, и 4.

2⁰ mod 6 = 0
2¹ mod 6 = 2
2² mod 6 = (2 + 2) mod 6 = 4 (остановка, далее процесс повторяется)

г. Циклическая подгруппа, сгенерированная на основе 3, — это H₃, которая имеет два элемента: 0 и 3.

3⁰ mod 6 = 0 
3¹ mod 6 = 3 (остановка, далее процесс повторяется)

д. Циклическая подгруппа, сгенерированная на основе 4, — H₂ ; это — не новая подгруппа.

4⁰ mod 6 = 0
4¹ mod 6 = 4
4² mod 6 = (4 + 4) mod 6 = 2 (остановка, далее процесс повторяется)

е. Циклическая подгруппа, сгенерированная на основе 5, — это H₄, она есть сама группа G.

5⁰ mod 6 = 0
5¹ mod 6 = 5
5² mod 6 = 4
5³ mod 6 = 3
5⁴ mod 6 = 2
5⁵ mod 6 = 1  (остановка, далее процесс повторяется)

Пример 5.8

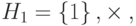
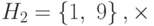Из группы ${text{G}} = < {{text{Z}}_{{text{1}}0*}}, times >$ можно получить три циклических подгруппы. G имеет только четыре элемента: 1, 3, 7 и 9. Циклические подгруппы — ${H_1} = <left{ 1 right}, times >,$ ${H_2} = <left{ {1,{text{ }}9} right}, times >$ и ${H_3} = G$ . Ниже показано, как мы находим элементы этих подгрупп.

a. Циклическая подгруппа, сгенерированная на основе 1, — это H₁. Подгруппа имеет только один элемент, а именно — нейтральный.

1⁰ mod 10 = 1 (остановка, далее процесс повторяется)

б. Циклическая подгруппа, сгенерированная на основе 3, — это H₃, которая есть группа G.

3⁰ mod 10 = 1
3¹ mod 10 = 3
3² mod 10 = 9
3³ mod 10 = 7 (остановка, далее процесс повторяется)

в. Циклическая подгруппа, сгенерированная на основе 7, — это H₃, которая есть группа G.

7⁰ mod 10  = 1
7¹ mod 10  = 7
7² mod 10  = 9
7³ mod 10  = 3 (остановка, далее процесс повторяется)

г. Циклическая подгруппа, сгенерированная на основе 9, — это H₂. Подгруппа имеет только два элемента.

9⁰ mod 10 = 1
9¹ mod 10 = 9 (остановка, далее процесс повторяется)

Циклические группы

Циклическая группа — группа, которая является собственной циклической подгруппой. В примере 5.7 группа G имеет циклическую подгруппу H₅ = G. Это означает, что группа G — циклическая группа. В этом случае элемент, который генерирует циклическую подгруппу, может также генерировать саму группу. Этот элемент далее именуется “генератор”. Если g — генератор, элементы в конечной циклической группе могут быть записаны как

{e,g,g²,….., g^n-1}, где gⁿ = e.

Заметим, что циклическая группа может иметь много генераторов.

Пример 5.9

а. Группа G = <Z₆, +> — циклическая группа с двумя генераторами, g = 1 и g = 5.

б. Группа ${text{G}} = < {{text{Z}}_{{text{1}}0*}}, times >$ — циклическая группа с двумя генераторами, g = 3 и g = 7.

Теорема Лагранжа

Теорема Лагранжа показывает отношение между порядком группы к порядку ее подгруппы. Предположим, что G — группа и H — подгруппа G. Если порядок G и H — |G| и |H|, соответственно, то согласно этой теореме |H| делит |G|. В примере 5.7 |G| = 6. Порядок подгруппы — |H1| = 1, | H2| = 3, |H3| = 2 и |H4| = 6. Очевидно, все эти порядки есть делители 6.

Теорема Лагранжа имеет очень интересное приложение. Когда дана группа G и ее порядок |G|, могут быть легко определены порядки потенциальных подгрупп, если могут быть найдены делители. Например, порядок группы G = <Z₁₇, +> — это |17|. Делители 17 есть 1 и 17. Это означает, что эта группа может иметь только две подгруппы — нейтральный элемент и H₂ = G.

Порядок элемента

Порядок элемента в группе ord (a) (порядок (a)) является наименьшим целым числом n, таким, что aⁿ = e. Иными словами: порядок элемента — порядок группы, которую он генерирует.

Пример 5.10

a. В группе G = <Z₆, +>, порядки элементов: порядок ord(0) = 1, порядок ord (1) = 6, порядок ord (2) = 3, порядок ord (3) = 2, порядок ord (4) = 3, порядок ord (5) = 6.

b. В группе G = <Z₁₀, * >, порядки элементов: порядок ord (1) = 1, порядок ord (3) = 4, порядок ord (7) =4, порядок (9) = 2.

Кольцо

Кольцо, обозначенное как 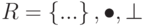, является алгебраической структурой с двумя операциями. Первая операция должна удовлетворять всем пяти свойствам, требуемым для абелевой группы. Вторая операция должна удовлетворять только первым двум свойствам абелевой группы. Кроме того, вторая операция должна быть распределена с помощью первой. Дистрибутивность означает, что для всех a, b и c элементов из R мы имеем 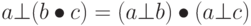и . 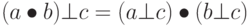Коммутативное кольцо — кольцо, в котором коммутативное свойство удовлетворено и для второй операции. Рисунок 5.4 показывает кольцо и коммутативное кольцо.

Дополнительное замечание

Кольцо включает две операции. Однако вторая операция может не соответствовать третьему и четвертому свойствам. Другими словами, первая операция — фактически операция пары операций, таких как сложение и вычитание; вторая операция может содержать единственную операцию, например умножение, но может не содержать деление.

Пример 5.11

Множество Z с двумя операциями — сложением и умножением — является коммутативным кольцом, которое обозначается 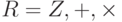. Сложение удовлетворяет всем пяти свойствам; умножение удовлетворяет только трем свойствам.

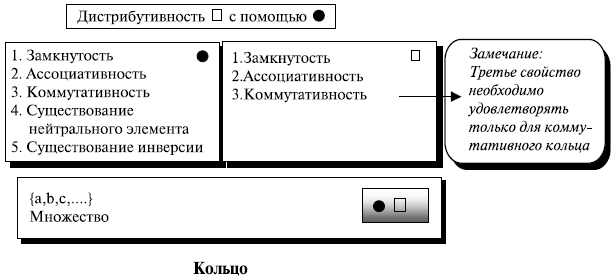
Рис.
5.4.
Кольцо

Умножение дистрибутивно с помощью сложения. Например, 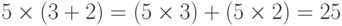. Хотя, мы можем выполнить на этом множестве сложение и вычитание и умножение, но не деление. Деление не может применяться в этой структуре, потому что оно приводит к элементу из другого множества. Результат деления 12 на 5 есть 2,4, и он не находится в заданном множестве.

Источник

The conjecture above is true. To prove it we need the following result:

Lemma: Let $G$ be a group and $x in G$. If $o(x) = n$ and $operatorname{gcd}(m, n) = d$, then $o(x^m) = frac{n}{d}$

Here now is a proof of the conjecture.

Proof: Let $G = langle x rangle$ be a finite cyclic group of order $n$, then we have $o(x) = n$.

Choose a subgroup $H leq G$, by theorem $(1)$ mentioned in the question above, $|H| = m$ where $m$ is some divisor of $n$. Since $m | n$ (and both $m$ and $n$ are positive integers), there exists a $d in mathbb{N}$ such that $md = n iff frac{n}{d}=m$. Note also that $d$ is a divisor of $n$.

By the above lemma and the fact that $operatorname{gcd}(d, n) = d$ (since $d$ is a divisor of $n$) it follows that $o(x^d) = frac{n}{d} = m$. Hence the subgroup $langle x^d rangle$ has order $m$. But since by theorem $(1)$ there is only one subgroup of order $m$ in $G$ we must have $H = langle x^d rangle$. Thus any subgroup of $G$ is of the form $langle x^d rangle$ where $d$ is a positive divisor of $n$. $ square$

The above conjecture and its subsequent proof allows us to find all the subgroups of a cyclic group once we know the generator of the cyclic group and the order of the cyclic group.

Источник

Множество
элементов из группы G
называется порождающим, если G
получается замыканием этого множества
относительно групповой операции.

Группа,
порожденная одним элементом, называется
циклической.

Следствие 2.10.
Любая группа содержит циклическую
подгруппу.

Доказательство.
Пусть a
–элемент группы G.
Множество

является циклической подгруппой.

Порядок
циклической подгруппы, порожденной
элементом a,
называется порядком элемента.

Свойство 2.14.
Если элемент
a имеет порядок n,
то aⁿ=e.

Доказательство.
Рассмотрим последовательность

.
Поскольку число членов в последовательности
бесконечно, а для степеней элемента a
существует конечное число возможностей,
то в последовательности встретятся
одинаковые члены. Пусть

,
где k<j
и k
первый повторяющийся член. Тогда

,
и значит, член k–j+1
повторяется. Следовательно, j=1
(иначе

).
Таким образом, последовательность
состоит из повторяющихся наборов вида

и в ней k–1
различных элементов. Следовательно,
k=n+1.
Так как

,
то

.

Порядок
любого элемента является делителем
порядка группы, следовательно, a^|^G^|=e
для любого элемента группы.

Следствие 2.11.
Порядок группы делится без остатка на
порядок любого элемента группы.

Доказательство
очевидно.

Теорема 2.10
(о циклических группах)

Для любого
натурального n
существует циклическая группа порядка
n.
Циклические группы одинаковых порядков изоморфны между собой.
Циклическая группа бесконечного порядка изоморфна группе целых чисел.
Любая подгруппа циклической группы циклическая.
Для каждого
делителя m
числа n
(и только для них) в циклической группе
n-го
порядка существует единственная
подгруппа порядка m.

Доказательство.
Множество комплексных корней степени
n
из 1 относительно операции умножения
образует циклическую группу порядка
n.
Тем самым первое утверждение доказано.

Пусть
циклическая группа G
порядка n
порождена элементом a,
а циклическая группа H,
того же порядка, порождена элементом
b.
Соответствие

взаимно однозначное и сохраняет операцию.
Второе утверждение доказано

Циклическая
группа бесконечного порядка, порожденная
элементом a,
состоит из элементов

.
Соответствие

является взаимно однозначным и сохраняет
операцию. Таким образом, третье утверждение
доказано.

Пусть
H
– подгруппа циклической группы G,
порожденной элементом a.
Элементы H
являются степенью a.
Выберем в H
элемент, который является наименьшей
по абсолютной величине ненулевой
степенью a.
Пусть это элемент

.
Покажем, что этот элемент является
порождающим в подгруппе H.
Возьмем произвольный элемент

из H.
Произведение

содержится в H
при любом r.
Выберем r
равным частному от деления k
на j,
тогда k–rj
есть остаток от деления k
на j
и, значит, меньше j.
Поскольку в H
нет элементов, которые являются не
нулевой степенью a,
меньше чем j,
то k–rj=0,
и

.
Четвертое утверждение доказано.

Пусть
циклическая группа G
порядка n
порождена элементом a.
Подгруппа, порожденная элементом

,
имеет порядок m.
Рассмотрим подгруппу H
порядка m.
Выберем в H
элемент, который является наименьшей
по абсолютной величине ненулевой
степенью a.
Пусть это элемент

.
Покажем, что j=n/m.
Элемент

принадлежит H.
Следовательно, отличное от нуля число
вида rj–nv
по абсолютной величине не меньше j,
что возможно только если n
делится на j
без остатка. Подгруппа, порожденная

,
имеет порядок n/j=m,
следовательно, j=n/m.
Поскольку порождающий элемент подгруппы
определяется однозначно по ее порядку,
то пятое утверждение доказано.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте

его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву

, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения

и указать конкретные затруднения.

Обязательно просмотрите тему

Правила данного раздела, иначе Ваша тема может быть удалена

или перемещена в Карантин, а Вы так и не узнаете, почему.

	Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 16:38
09/11/11 21	Помогите с подробным алгоритмом. С чего начать и что в итоге должно получиться? Перелопатила кучу литературы. Абстрактная теория не помогает(

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 16:53

Заслуженный участник

08/04/08
8549

Это $mathbb{Z}_{10}$ что-ли? Это просто. Для начала: какие у нее есть подгруппы? Если затрудняетесь назвать подгруппы, вспомните теорему Лагранжа о порядке подгрупп и то, что подгруппа циклической группы – тоже циклическая (это понятно почему?).

Lil	Re: Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 17:05
09/11/11 21	Я правильно понимаю, что по Лагранжа порядки подгрупп будут 1,2,5,10?

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 17:09

Заслуженный участник

08/04/08
8549

Я правильно понимаю, что по Лагранжа порядки подгрупп будут 1,2,5,10?

Точнее говорить, что если подгруппа существует, то ее порядок может быть лишь таким, каким Вы написали (в общем случае не факт, что подгруппа существует).
Дальше, выпишите саму группу, используя тот факт, что она циклическая и имеет порядок 10. Если сможете это сделать, дальше выпишите явно все нетривиальные подгруппы, используя тот факт, что они циклические.

Lil	Re: Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 17:30
09/11/11 21	не понимаю, как выписать группу((

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 17:36

Заслуженный участник

08/04/08
8549

Lil	Re: Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 17:58
09/11/11 21	Второй способ мне не знаком. $G={a^0, a^1, a^2, a^3, a^4, a^5, a^6, a^7, a^8, a^9}$ – это мне понятно. Просто я все время ждала, что будут конкретные числа. Что значит, упростить эту запись – не знаю. Дальше полагаю так: подгруппы будут состоять из 1, 2, 5, 10 элементов. Подгруппы тоже будут цикличны, а значит их элементы будут степенями одного элемента. Вот что это будут за элементы – снова тупик.

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 18:06

Заслуженный участник

08/04/08
8549

(формулы)

чтобы набрать фигурную скобку, нужно ставить перед ней слэш: { и } . Подробнее здесь:

topic183.html

Просто я все время ждала, что будут конкретные числа.

Можно конкретные числа, это 2-й способ! Например $mathbb{Z}_{10} = < { 0;1;2;3;4;5;6;7;8;9};+>$ – тут почти числа (классы вычетов по модулю $10$ ).

Что значит, упростить эту запись – не знаю.

Вы это уже сделали – выписали ровно $10$ элементов.

Подгруппы тоже будут цикличны, а значит их элементы будут степенями одного элемента. Вот что это будут за элементы – снова тупик.

Ну если $H$ – подгруппа $G$ , то группа $H$ это какое-то подмножество элементов из множества ${ e, a^1, a^2, a^3, a^4, a^5, a^6, a^7, a^8, a^9}$ . Для начала нужно отбросить тривиальные подгруппы. Далее попробуйте найти подгруппу порядка $2$ – ее найти проще всего. Один ее элемент – это обязательно $e$ . Какой второй?

Lil	Re: Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 18:24
09/11/11 21	Не понимаю, по каким критериям отбираются элементы в подгруппу. Соответственно, не знаю, какой второй элемент((

arseniiv

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 18:29

Заслуженный участник

27/04/09
28128

А чем плохо перебирать группы, порождаемые каждым из $a^n$ ?

Не понимаю, по каким критериям отбираются элементы в подгруппу.

Ну как же это. Подгруппа должна быть не просто подмножеством элементов группы, а и сама быть группой по той же операции.

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 18:33

Заслуженный участник

08/04/08
8549

Lil	Re: Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 18:59
09/11/11 21	Операция может быть применена к любым двум элементам группы, в результате чего получается третий элемент группы. А у меня до сих пор проблемы со вторым( Если исходить из свойств подгруппы, то должен быть еще обратный элемент, значит второй тоже единица?

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 19:06

Заслуженный участник

08/04/08
8549

Lil	Re: Как разложить циклическую группу порядка 10 по подгруппам? 09.11.2011, 19:47
09/11/11 21

Sonic86

Re: Как разложить циклическую группу порядка 10 по подгруппам?

09.11.2011, 19:59

Заслуженный участник

08/04/08
8549

Я сейчас ищу то самое a^j и не понимаю, откуда его вычислить ни абстрактно, ни в классе вычетов.

Ну Вы можете попробовать это сделать хоть перебором всех значений $j$ , т.е. вычислить – нужно найти всего $9$ произведений.

почему из следует, что $a^j$ нужно умножать на $a^j$ ?

$a^j cdot a^j in H = { e ; a^j}$ , т.е. либо , либо . Однако второе неверно, поскольку в группе мы можем сокращать,и тогда , что неверно, а значит верно лишь первое Так что $H$ – подгруппа $G Leftrightarrow H = { e ; a^j }$ , где .

Если совсем трудно, давайте попробуем заново: докажите по критерию подгруппы, что все множества ${ a^{ik} }$ для некоторого $k|n$ и всех $i=1,...,frac{n}{k}$ дают подгруппу циклической группы $G = { a^i}$ . И просто примените этот критерий к Вашей группе, а то мы так далеко не уедем.