Подпространства линейного пространства
Определение линейного подпространства
Непустое подмножество линейного пространства
называется линейным подпространством пространства
, если
1) (подпространство замкнуто по отношению к операции сложения);
2) и любого числа
(подпространство замкнуто по отношению к операции умножения вектора на число).
Для указания линейного подпространства будем использовать обозначение , а слово “линейное” опускать для краткости.
Замечания 8.7
1. Условия 1, 2 в определении можно заменить одним условием: и любых чисел
и
. Разумеется, что здесь и в определении речь идет о произвольных числах из того числового поля, над которым определено пространство
.
2. В любом линейном пространстве имеются два линейных подпространства:
а) само пространство , т.е.
;
б) нулевое подпространство , состоящее из одного нулевого вектора пространства
, т.е.
. Эти подпространства называются несобственными, а все остальные — собственными.
3. Любое подпространство линейного пространства
является его подмножеством:
, но не всякое подмножество
является линейным подпространством, так как оно может оказаться незамкнутым по отношению к линейным операциям.
4. Подпространство линейного пространства
само является линейным пространством с теми же операциями сложения векторов и умножения вектора на число, что и в пространстве
, поскольку для них выполняются аксиомы 1-8. Поэтому можно говорить о размерности подпространства, его базисе и т.п.
5. Размерность любого подпространства линейного пространства
не превосходит размерности пространства
. Если же размерность подпространства
равна размерности конечномерного пространства
, то подпространство совпадает с самим пространством:
.
Это следует из теоремы 8.2 (о дополнении системы векторов до базиса). Действительно, взяв базис подпространства , будем дополнять его до базиса пространства
. Если это возможно, то
. Если нельзя дополнить, т.е. базис подпространства
является базисом пространства
, то
. Учитывая, что пространство есть линейная оболочка базиса (см. следствие 1 теоремы 8.1), получаем
.
6. Для любого подмножества линейного пространства
линейная оболочка
является подпространством
и
.
В самом деле, если (пустое множество), то по определению
, т.е. является нулевым подпространством и
. Пусть
. Нужно доказать, что множество
замкнуто по отношению к операциям сложения его элементов и умножения его элементов на число. Напомним, что элементами линейной оболочки
служат линейные комбинации векторов из
. Так как линейная комбинация линейных комбинаций векторов является их линейной комбинацией, то, учитывая пункт 1, делаем вывод, что
является подпространством
, т.е.
. Включение
— очевидное, так как любой вектор
можно представить как линейную комбинацию
, т.е. как элемент множества
.
7. Линейная оболочка подпространства
совпадает с подпространством
, т.е.
.
Действительно, так как линейное подпространство содержит все возможные линейные комбинации своих векторов, то
. Противоположное включение
следует из пункта 6. Значит,
.
Примеры линейных подпространств
Укажем некоторые подпространства линейных пространств, примеры которых рассматривались ранее. Перечислить все подпространства линейного пространства невозможно, за исключением тривиальных случаев.
1. Пространство , состоящее из одного нулевого вектора пространства
, является подпространством, т.е.
.
2. Пусть, как и ранее, — множества векторов (направленных отрезков) на прямой, на плоскости, в пространстве соответственно. Если прямая принадлежит плоскости, то
. Напротив, множество единичных векторов не является линейным подпространством, так как при умножении вектора на число, не равное единице, получаем вектор, не принадлежащий множеству.
3. В n-мерном арифметическом пространстве рассмотрим множество
“полунулевых” столбцов вида
с последними
элементами, равными нулю. Сумма “полунулевых” столбцов является столбцом того же вида, т.е. операция сложения замкнута в
. Умножение “полунулевого” столбца на число дает “полунулевой” столбец, т.е. операция умножения на число замкнута в
. Поэтому
, причем
. Напротив, подмножество ненулевых столбцов
не является линейным подпространством, так как при умножении на нуль получается нулевой столбец, который не принадлежит рассматриваемому множеству. Примеры других подпространств
приводятся в следующем пункте.
4. Пространство решений однородной системы уравнений с
неизвестными является подпространством n-мерного арифметического пространства
. Размерность этого подпространства определяется матрицей системы:
.
Множество решений неоднородной системы (при
) не является подпространством
, так как сумма двух решений неоднородной ; системы не будет решением той же системы.
5. В пространстве квадратных матриц порядка л рассмотрим два подмножества: множество
симметрических матриц и множество
кососимметрических матриц. Сумма симметрических матриц является симметрической матрицей, т.е. операция сложения замкнута в
. Умножение симметрической матрицы на число также не нарушает симметричность, т.е. операция умножения матрицы на число замкнута в
. Следовательно, множество симметрических матриц является под пространством пространства квадратных матриц, т.е.
. Нетрудно найти размерность этого подпространства. Стандартный базис образуют : л матриц с единственным ненулевым (равным единице) элементом на глав ной диагонали:
, а также матрицы с двумя ненулевыми (равными единице) элементами, симметричными относительно главной диагонали:
. Всего в базисе будет
матриц. Следовательно,
. Аналогично получаем, что
и
.
Множество вырожденных квадратных матриц n-го порядка не является подпространством , так как сумма двух вырожденных матриц может оказаться невырожденной матрицей, например, в пространстве
6. В пространстве многочленов с действительными коэффициентами можно указать естественную цепочку подпространств
Множество четных многочленов является линейным подпространством
, так как сумма четных многочленов и произведение четно го многочлена на число будут четными многочленами. Множество нечетных многочленов
также является линейным пространством. Множество многочленов, имеющих действительные корни, не является линейным подпространством, так как при сложении таких двух многочленов может получиться многочлен, который не имеет действительных корней, например,
.
7. В пространстве можно указать естественную цепочку подпространств:
Многочлены из можно рассматривать как функции, определенные на
. Так как многочлен является непрерывной функцией вместе со своими производными любого порядка, можно записать:
и
. Пространство тригонометрических двучленов
является подпространством
, так как производные любого порядка функции
непрерывны, т.е.
. Множество непрерывных периодических функций не является подпространством
, так как сумма двух периодических функций может оказаться непериодической функцией, например,
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
2.1. Определение и примеры
В
любом линейном
пространстве
можно
выделить такое подмножество векторов,
которое
относительно операций из
само
является линейным пространством. Это
можно делать различными способами, и
структура таких подмножеств несет
важную информацию о самом линейном
пространстве

Определение
2.1. Подмножество
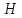
называют
линейным
подпространством, если
выполнены следующие два условия:
-
сумма
любых
двух векторов
из
принадлежит
:
;
-
произведение
любого
вектора
из
Н
на любое
действительное число
снова
принадлежит Н:
Определение
2.1 фактически говорит о том, что линейное
подпространство – это любое подмножество
данного
линейного пространства, замкнутое
относительно линейных операций, т.е.
применение линейных операций к векторам,
принадлежащим этому подмножеству, не
выводит результат за пределы подмножества.
Покажем, что линейное подпространство
Н
как
самостоятельный объект является линейным
пространством относительно операций,
заданных в объемлющем линейном
пространстве
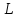
В
самом деле, эти операции определены для
любых элементов множества
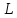
а значит, и для элементов подмножестваН.
Определение
2.1 фактически требует, чтобы для элементов
из Н
результат
выполнения операций также принадлежал
H.
Поэтому операции, заданные в

можно рассматривать как операции и на
более узком множествеH.
Для этих операций на множестве Н
аксиомы
линейного пространства а)-б) и д)-з)
выполнены в силу того, что они справедливы
в
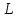
Кроме того, выполнены и две оставшиеся
аксиомы, поскольку, согласно определению
2.1, если

1)
и
0- нулевой
вектор в
Н;
2)

В
любом линейном пространстве
всегда
имеются два линейных подпространства:
само линейное пространство
и
нулевое
подпространство {0},
состоящее
из единственного элемента 0.
Эти
линейные подпространства называют
несобственными,
в
то время как все остальные линейные
подпространства называют собственными.
Приведем
примеры собственных линейных
подпространств.
Пример
2.1. В
линейном пространстве
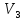
векторов трехмерного пространства
линейное подпространство образуют:
а)
все векторы, параллельные данной
плоскости;
б)
все векторы, параллельные данной прямой.
Это
вытекает из следующих соображений. Из
определения суммы свободных векторов
следует, что два вектора


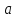
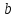
же плоскости будет параллельна и их
сумма. Тем самым установлено, что для
случая а) выполнено условие 1) определения
2.1. Если вектор умножить на число,
получится вектор, коллинеарный исходному
(рис. 2.1,6). Это доказывает выполнение
условия 2) определения 2.1. Случай б)
обосновывается аналогично.
Линейное
пространство
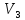
такое линейное подпространство.
Действительно, фиксируем некоторую
точку в пространстве. Тогда различным
плоскостям и различным прямым, проходящим
через эту точку, будут соответствовать
различные линейные подпространства из
Не
столь очевидно, что в
Если в линейном подпространствеН
в
–
нулевое
линейное подпространство, являющееся
несобственным. Если в Н
есть
ненулевой вектор, а любые два вектора
из Н
коллинеарны, то все векторы этого
линейного подпространства параллельны
некоторой прямой, проходящей через
фиксированную точку. Следовательно, Н
совпадает
с одним из линейных подпространств,
описанных в случае б). Если в Н
есть
два неколлинеарных вектора, а любые три
вектора компланарны, то все векторы
такого линейного подпространства
параллельны некоторой плоскости,
проходящей через фиксированную точку.
Это случай а). Пусть в линейном
подпространстве Н
существуют
три некомпланарных вектора. Тогда они
образуют базис
в

Любой
свободный вектор можно представить в
виде линейной
комбинации этих
векторов. Значит, все свободные векторы
попадают в линейное подпространство
Н,
и
поэтому оно совпадает с
В
этом случае мы получаем несобственное
линейное подпространство. Итак, в

представить в виде плоскостей или
прямых, проходящих через фиксированную
точку.
Пример
2.2. Любое
решение однородной системы линейных
алгебраических уравнений (СЛАУ) от п
переменных
можно рассматривать как вектор в линейном
арифметическом пространств

Множество
всех таких векторов является линейным
подпространством в
В
самом деле, решения однородной СЛАУ
можно покомпонентно складывать и
умножать на действительные числа, т.е.
по правилам сложения векторов из

Результат операции снова будет решением
однородной СЛАУ. Значит, оба условия
определения линейного подпространства
выполнены.
Уравнение

линейным подпространством в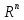
Но
это же уравнение можно рассматривать
как уравнение плоскости в некоторой
прямоугольной системе координат

Плоскость проходит через начало
координат, а радиус-векторы всех точек
плоскости образуют двумерное
подпространство в линейном пространстве
Множество
решений однородной СЛАУ
также
образует линейное подпространство в
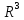
В
то же время эту систему можно рассматривать
как общие
уравнения прямой в
пространстве, заданные в некоторой
прямоугольной системе координат

Эта прямая проходит через начало
координат, а множество радиус-векторов
всех ее точек образует одномерное
подпространство в

Пример
2.3. В
линейном пространстве

линейное
подпространство образуют:
а)
все симметрические матрицы;
б)
все кососимметрические матрицы;
в)
все верхние (нижние) треугольные матрицы.
При
сложении таких матриц или умножении на
число мы получаем матрицу того же вида.
Напротив, подмножество вырожденных
матриц не является линейным подпространством,
так как сумма двух вырожденных матриц
может быть невырожденной матрицей:
Пример
2.4. В
линейном пространстве
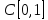
можно выделить следующие линейные
подпространства:
а)
множество функций, непрерывных на
отрезке [0,1] и непрерывно дифференцируемых
в интервале (0,1) (в основе этого утверждения
лежат свойства дифференцируемых функций:
сумма дифференцируемых функций есть
дифференцируемая функция, произведение
дифференцируемой функции на число есть
дифференцируемая функция);
б)
множество всех многочленов;
в)
множество
всех
многочленов степени не выше n.
Напротив,
множество всех монотонных функций,
непрерывных на отрезке [0,1], очевидно,
является подмножеством

но не является линейным подпространством,
так как сумма двух монотонных функций
может и не быть монотонной функцией.
Пусть
в линейном пространстве
задана
система
векторов

Рассмотрим
множество Н
всех
векторов в
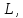
комбинацией этих векторов. Это множество
является линейным подпространством в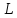
Действительно, пусть
Тогда
где

Описанное линейное подпространство
называют линейной
оболочкой системы
векторов
и
обозначают
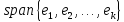
Примечательно
то, что любое собственное линейное
подпространство можно представить как
линейную оболочку некоторой системы
его векторов. В этом состоит универсальный
способ описания линейных подпространств.
Отметим, что само линейное пространство
является линейной оболочкой любого из
своих базисов.
Пример
2.5.
Рассмотрим
плоскость
проходящую через три произвольные точки
не
лежащие на одной прямой. Тогда линейное
подпространство векторов, компланарных
плоскости
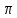
представляет собой линейную оболочку
двух свободных векторов, соответствующих
геометрическим векторам
(рис.
2.3). Действительно, любой вектор,
компланарный векторам
и

представляется в виде их линейной
комбинации.
Соседние файлы в папке re
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.
Линейное пространство
Определения
Пусть дано множество $ mathbb V_{}=left{ X,Y,Z,U,dots right} $
элементов произвольной природы. Пусть для элементов этого множества определены
две операции: сложения $ X+Y_{} $ и умножения на любое вещественное число $ alpha_{} $:
$ alpha cdot X_{} $, и множество $ mathbb V_{} $ замкнуто относительно этих операций:
$ X+Y in mathbb V , alpha cdot X in mathbb V_{} $. Пусть эти операции подчиняются
аксиомам:
1.
$ X+Y=Y+X_{} $ для $ { X,, Y} subset mathbb V_{} $;
2.
$ (X+Y)+Z_{}=X+(Y+Z) $ для $ { X,, Y,, Z } subset mathbb V_{} $;
3.
в $ mathbb V_{} $ cуществует нулевой вектор $ mathbb O_{} $ со свойством $ X+ mathbb O =X_{} $ для $ forall Xin mathbb V_{} $;
4.
для каждого $ Xin mathbb V_{} $ существует обратный вектор $ X^{prime}in mathbb V_{} $ со свойством $ X+X^{prime}=mathbb O_{} $;
5.
$ 1cdot X=X_{} $ для $ forall Xin mathbb V_{} $;
6.
$ lambda left(mu X right)_{}= left(lambda mu right)X $ для $ forall Xin mathbb V_{} $, $ {lambda ,, mu } subset mathbb R_{} $ ;
7.
$ (lambda + mu)X=lambda X + mu X_{} $ для $ forall Xin mathbb V_{} $, $ {lambda ,, mu }subset mathbb R_{} $ ;
8.
$ lambda (X + Y) =lambda X_{} + lambda Y $ для $ { X,, Y} subset mathbb V_{} ,
lambda in mathbb R $.
Тогда такое множество $ mathbb V_{} $ называется линейным (векторным) пространством,
его элементы называются векторами, и — чтобы подчеркнуть их отличие от
чисел из $ mathbb R_{} $ — последние называются скалярами1).
Пространство, состоящее из одного только нулевого вектора, называется тривиальным .
Если в аксиомах
6
–
8
допустить умножение и на комплексные скаляры, то такое линейное пространство называется комплексным. Для упрощения рассуждений в настоящем разделе будут рассматриваться только вещественные пространства.
Линейное пространство является группой относительно операции сложения, причем группой абелевой.
Элементарно доказывается единственность нулевого вектора, и единственность
вектора, обратного вектору $ Xin mathbb V_{} $: $ X^{prime}=-1cdot X_{} $, его привычно обозначают $ – X_{} $.
Подмножество $ mathbb V_{1} $ линейного пространства $ mathbb V_{} $, само являющееся линейным
пространством (т.е. $ mathbb V_{1} $ замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства $ mathbb V_{} $. Тривиальными подпространствами линейного пространства $ mathbb V_{} $
называются само $ mathbb V_{} $ и пространство, состоящее из одного нулевого вектора
$ mathbb O_{} $.
Примеры линейных пространств
П
Пример 1. Пространство $ mathbb R^{3} $ упорядоченных троек вещественных чисел $ (a_1,a_2,a_{3}) $ с операциями, определяемыми равенствами:
$$ (a_1,a_2,a_3)+(b_1,b_2,b_3)= (a_1+b_1,a_2+b_2,a_3+b_3),
alpha (a_1,a_2,a_3) = ( alpha a_1, alpha a_2, alpha a_3 ) .
$$
Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца $ (a_1,a_2,a_{3}) $. На рисунке показано и типичное подпространство пространства $ mathbb R^{3} $: плоскость, проходящая через начало координат.
Точнее говоря, элементами $ mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения2) очевидна.
Исходя из этой геометрической интерпретации, часто говорят о векторе $ X_{} $ произвольного линейного пространства $ mathbb V_{} $ как о точке пространства $ mathbb V_{} $. Иногда эту точку
называют «концом вектора $ X_{} $». Кроме удобства ассоциативного восприятия, этим словам не придается никакого формального смысла: понятие «конец вектора» отсутствует в аксиоматике линейного пространства.
П
Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства $ mathbb V_1 $ (заложенную, кстати, уже в самом происхождении слова «вектор»3))
— оно определяет набор «сдвигов» точек пространства $ mathbb R^{3} $. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости $ mathbb V_1 $.
Вообще говоря, с подобными интерпретациями понятия вектора все обстоит не так просто. Попытки аппелировать к его физическому смыслу — как к объекту, имеющему величину и направление — вызывают справедливую отповедь строгих математиков.
Определение же вектора как элемента векторного пространства очень напоминает эпизод с сепульками из знаменитого фантастического рассказа Станислава Лема (см.
☞
ЗДЕСЬ ). Не будем зацикливаться на формализме, а исследуем этот нечеткий объект в его частных проявлениях.
П
Пример 3. Естественным обобщением пространства $ mathbb R^{3} $ служит пространство $ mathbb R_{}^{n} $ —
векторное пространство строк $ (x_1,dots,x_{n}) $ или столбцов
$ (x_1,dots,x_n)^{^top} $. Один из способов задания подпространства
в $ mathbb R_{}^{n} $ — задание набора ограничений. Множество решений системы линейных однородных уравнений:
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&0,\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&0,\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&0
end{array}right.
iff
AX=mathbb O
$$
образует линейное подпространство пространства $ mathbb R_{}^{n} $. В самом деле, если
$$x_1=alpha_1,dots, x_n=alpha_n $$
— решение системы, то и
$$x_1=t alpha_1,dots, x_n= t alpha_n $$
— тоже решение при любом $ t in mathbb R $. Если
$$x_1=beta_1,dots, x_n=beta_n $$
— еще одно решение системы, то и
$$x_1=alpha_1+beta_1,dots,x_n=alpha_n+beta_n $$
— тоже будет ее решением.
?
Почему множество решений системы неоднородных уравнений не образует линейного подпространства?
П
Пример 4. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей
$$ (x_1,dots,x_n, dots ) , , $$
обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Подпространство этого пространства образуют, например, линейные рекуррентные последовательности $ {x_k}_{k=0,1,2,dots } $ удовлетворяющие — при произвольных числах $ {x_0,dots x_{n-1} } subset mathbb R $ — линейному однородному разностному уравнению $ n_{} $-го порядка,
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K npu K in {0,1,2,dots } ;
$$
здесь числа $ { a_1,dots,a_{n-1}, a_n ne 0 } subset mathbb R $ считаются фиксированными.
Можно рассматривать строки (последовательности) «бесконечные в обе стороны» $ { dots,x_{-2},x_{-1},x_0,x_1,x_2,dots } $ — они используются в ТЕОРИИ СИГНАЛОВ.
П
Пример 5. Множество $ mtimes n_{} $-матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство. Будем обозначать это пространство $ mathbb R^{mtimes n} $.
В пространстве квадратных матриц
фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство:
симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.
П
Пример 6. Множество полиномов одной переменной $ x_{} $ степени в точности равной $ n_{} $ с коэффициентами из $ mathbb A_{} $ (где $ mathbb A_{} $ — любое из множеств $ mathbb Z, mathbb Q, mathbb R_{} $ или $ mathbb C_{} $) с обычными операциями сложения полиномов и умножения на число из $ mathbb A_{} $
не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов
$$ f(x)=x^n -x+1 quad mbox{ и } quad g(x)=-x^n+x^{n-1}-2 $$
не является полиномом $ n_{} $-й степени. Но вот множество полиномов степени
не выше $ n_{} $ $$ mathbb P_n= left{ p(x) in mathbb A [x] big| deg p(x) le n right} $$
линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином4). Очевидными подпространствами $ mathbb P_{n} $ являются $ mathbb P_{0}, mathbb P_1,dots,mathbb P_{n-1} $. Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше $ n_{} $. Множество всевозможных полиномов
$$
mathbb P= bigcup_{n=0}^{infty} mathbb P_n
$$
(без ограничения на степени) тоже образует линейное пространство.
П
Пример 7. Обобщением предыдущего случая будет пространство полиномов нескольких переменных $ x_1,dots, x_{ell} $ степени не выше $ n_{} $ с коэффициентами из $ mathbb A_{} $. Например, множество линейных полиномов
$$ left{ a_1x_1+dots+a_{ell}x_{ell}+b big| (a_1,dots,a_{ell},b) in mathbb A^{ell+1} right} $$
образует линейное пространство. Множество однородных полиномов (форм) степени $ n_{} $ (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.
С точки зрения приведенного в предыдущем пункте определения, множество строк с целочисленными компонентами
$$ mathbb Z^n = left{ (x_1,dots,x_n) mid {x_j}_{j=1}^n subset mathbb Z right} , $$
рассматриваемое относительно операций покомпонентного сложения и умножения на целочисленные скаляры, не является линейным пространством. Тем не менее, все аксиомы
1
–
8
будут выполнены если мы допустим умножение только на целочисленные скаляры. В настоящем разделе мы не будем акцентировать внимание на этом объекте, но он довольно полезен в дискретной математике, например в
☞
ТЕОРИИ КОДИРОВАНИЯ. Линейные пространства над конечными полями рассматриваются
☞
ЗДЕСЬ.
Изоморфизм
Пусть имеются два линейных пространства разной природы: $ mathbb V_{} $ с операцией $ +_{} $ и $ mathbb W_{} $
с операцией $ boxplus_{} $. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.
Говорят, что пространства $ mathbb V_{} $ и $ mathbb W_{} $ изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если $ X_{} leftrightarrow X^{prime} $ и $ Y_{} leftrightarrow Y^{prime} $ то $ X+Y leftrightarrow X_{}^{prime} boxplus Y^{prime} $ и
$ lambda X_{} leftrightarrow lambda X^{prime} $.
=>
При изоморфизме пространств $ mathbb V_{} $ и $ mathbb W_{} $ нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.
П
Пример. Пространство $ mathbb R^{n}_{} $ изоморфно пространству $ mathbb P_{n-1}^{} $.
В самом деле, изоморфизм устанавливается соответствием
$$ [a_1,dots,a_n] leftrightarrow a_1+a_2x+dots + a_nx^{n-1} .$$
П
Пример. Пространство $ mathbb R^{mtimes n} $ вещественных матриц порядка $ m_{}times n $ изоморфно пространству
$ mathbb R_{}^{mn} $. Изоморфизм устанавливается с помощью операции векторизации матрицы
(матрица «вытягивается» в один столбец).
П
Пример. Пространство квадратичных форм от $ n_{} $ переменных изоморфно пространству симметричных матриц $ n_{} $-го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая $ n=3_{} $:
$$
a_{11}x_1^2+a_{12}x_1x_2+a_{13}x_1x_3+a_{22}x_2^2+a_{23}x_2x_3+a_{33}x_3^2 leftrightarrow
left(
begin{array}{ccc}
a_{11} & frac{1}{2}a_{12} & frac{1}{2}a_{13} \
frac{1}{2}a_{12} & a_{22} & frac{1}{2}a_{23} \
frac{1}{2}a_{13} & frac{1}{2}a_{23} & a_{33}
end{array}
right) .
$$
Понятие изоморфизма вводится для того, чтобы исследование объектов, возникающих в различных областях алгебры, но с «похожими» свойствами операций, вести на примере одного образца, отрабатывая на нем результаты, которые можно будет потом дешево тиражировать. Какое именно линейное пространство взять «за образец»? — См. концовку следующего пункта.
Линейная зависимость, базис, координаты
Линейной комбинацией системы векторов $ {X_1,dots,X_{m}} $ называется произвольный вектор
$$ alpha_1 X_1+dots+ alpha_m X_m $$
при каких-то фиксированных значениях скаляров $ alpha_{1}, dots, alpha_{m} $.
Множество всевозможных линейных комбинаций системы векторов $ {X_1,dots,X_{m}} $
$$
left{ alpha_1 X_1+dots+ alpha_m X_m bigg| {alpha_1,dots,alpha_m}subset mathbb R right}
$$
называется линейной оболочкой векторов $ X_1,dots,X_{m} $ и обозначается $ {mathcal L}(X_1,dots,X_{m}) $.
Т
Теорема 1. Линейная оболочка векторов $ X_1,dots,X_{m} $ образует линейное подпространство пространства $ mathbb V_{} $.
П
Пример. В пространстве $ mathbb P_{n} $ полиномов степеней $ le n_{} ge 3 $ линейной оболочкой полиномов $ x,x^2,x^3 $ будет множество полиномов вида
$ a_0x^3+a_1x^2+a_2x $, т.е. множество полиномов степеней $ le 3 $, имеющих корень $ lambda_{}=0 $.
♦
Система векторов $ { X_{1},dots,X_m } $
называется линейно зависимой (л.з.) если существуют числа $ alpha_{1},dots,alpha_m $, такие что хотя бы одно из них отлично от нуля и
$$
alpha_1X_1+dots+alpha_mX_m=mathbb O
$$
Если же это равенство возможно только при $ alpha_{1}=0,dots,alpha_m=0 $,
то система векторов называется линейно независимой (л.н.з.).
П
Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)
$$ f_1=(x_1+x_2+x_3)^2,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$
являются линейно зависимыми, поскольку
$$ f_1-2,f_2-f_3 equiv 0 . $$
Полиномы
$$ tilde f_1=x_1+x_2+x_3,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$
не являются линейно зависимыми, но являются функционально зависимыми, поскольку
$$ tilde f_1^2-2,f_2-f_3 equiv 0 . $$
♦
Т
Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.
б) Если система л.н.з., то и любая ее подсистема л.н.з.
в) При $ m>1 $ система $ {X_{1},dots,X_m} $ л.з. тогда и только тогда,
когда по меньшей мере один ее вектор линейно выражается через остальные,
т.е. существуют $ jin {1,dots,n } $ и константы $ gamma_{1},dots,gamma_{j-1},
gamma_{j+1},dots,gamma_{n} $ такие, что
$$ X_j=gamma_1X_1+dots+gamma_{j-1}X_{j-1}+ gamma_{j+1}X_{j+1}+dots + gamma_{m}X_{m} .$$
Т
Теорема 3. Если каждый из векторов системы $ { X_1,dots,X_{m} } $ линейно выражается через векторы другой системы $ { B_{1},dots,B_k } $ с меньшим числом векторов: $ k<m $, то система $ { X_{1},dots,X_m } $ будет л.з.
Доказательство аналогично приведенному
☞
ЗДЕСЬ.
Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.
Т
Теорема 4. Системы векторов
$$ { X_1,dots,X_{m} } quad mbox{ и } quad { Y_{1},dots,Y_k } $$
будут эквивалентными тогда и только тогда когда совпадают линейные оболочки этих систем:
$${mathcal L}(X_1,dots,X_m)={mathcal L}(Y_1,dots,Y_k) . $$
Т
Теорема 5. Если каждая из двух эквивалентных систем
$$ { X_1,dots,X_{m} } quad mbox{ и } quad { Y_{1},dots,Y_k } $$
является л.н.з., то эти системы состоят из одинакового числа векторов: $ m=k_{} $ .
Линейно независимая система векторов $ {X_{j}}subset mathbb V $ называется базисом этого пространства если каждый $ Xin mathbb V $
можно представить в виде линейной комбинации указанных векторов:
$$
X=sum_{j} alpha_j X_j .
$$
При этом не подразумевается конечность системы, т.е. суммирование может распространяться на бесконечное число слагаемых. Так, например, пространство бесконечных строк (или последовательностей) $ left[a_{1},a_2,dots, right] $ имеет бесконечный базис, состоящий из векторов
$$ [underbrace{0,dots,0,1}_j,0,dots , ] quad npu j in mathbb N . $$
В случае, когда базис пространства $ mathbb V_{} $ конечен,
пространство $ mathbb V_{} $ называется конечномерным, а число векторов
базиса тогда называется размерностью пространства $ mathbb V_{} $ и
обозначается5): $ dim mathbb V_{} $. Также полагают, что размерность тривиального пространства, состоящего из одного только нулевого вектора, равна нулю: $ dim {mathbb O_{} }= 0 $.
П
Пример. Линейное пространство $ mtimes n_{} $ матриц имеет размерность $ mn_{} $. Так, для случая $ m_{}=3 ,n=2 $ в качестве базиса можно выбрать следующий набор матриц
$$
left(
begin{array}{cc}
1 & 0 \
0 & 0 \
0 & 0
end{array}
right) ,
left(
begin{array}{cc}
0 & 1 \
0 & 0 \
0 & 0
end{array}
right) ,
left(
begin{array}{ccccc}
0 & 0 \
1 & 0 \
0 & 0 end{array}
right) ,
left(
begin{array}{cc}
0 & 0 \
0 & 1 \
0 & 0 end{array}
right) ,
left(
begin{array}{cc}
0 & 0 \
0 & 0 \
1 & 0
end{array}
right) ,
left(
begin{array}{cc}
0 & 0 \
0 & 0 \
0 & 1
end{array}
right) .
$$
♦
?
Найти размерности подпространства симметричных и подпространства кососимметричных матриц порядка $ n_{} $.
П
Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

под умножением цвета на положительное число $ k_{} $ — увеличение в $ k_{} $ раз яркости цвета
A
Анимация
☞
ЗДЕСЬ (1500 K, gif)
под умножением на $ (-1) $ — взятие дополнительного цвета. При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения.) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения.
♦
Если $ dim mathbb V=d_{} $ и вектора $ X_1,dots,X_{d} $ являются базисными для $ mathbb V_{} $, то разложение вектора $ X in mathbb V_{} $ в сумму:
$$ X=alpha_1 X_1+dots+ alpha_d X_d .$$
называется разложением вектора $ X_{} $ по базису $ X_1,dots,X_{d} $; при этом числа $ alpha_1,dots, alpha_{d} $ называются координатами вектора $ X_{} $
в данном базисе.
Т
Теорема 6. Если $ dim mathbb V=d>0 $, то любая система из $ d_{} $ линейно независимых векторов пространства образует базис этого пространства.
Доказательство. Пусть $ {Y_1,dots,Y_d} $ — л.н.з. система. Рассмотрим произвольный
$ Xin mathbb V_{} $. Если система $ {X,Y_1,dots,Y_d} $ л.н.з., то
$ dim mathbb V ge d+1 $, что противоречит условию теоремы. Следовательно, система линейно
зависима: $ alpha_0X+alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то из чисел
$ {alpha_j}_{j=0}^{d} $ не равном нулю. Если $ alpha_0=0 $, то $ alpha_1Y_1+dots+alpha_dY_d=mathbb O $
при каком-то ненулевом коэффициенте. Это означает, что система
$ {Y_1,dots,Y_d} $ линейно зависима, что противоречит предположению.
Следовательно $ alpha_0ne 0 $, но тогда вектор $ X_{} $ может быть представлен
в виде линейной комбинации векторов $ Y_1,dots,Y_d $:
$$X=- {alpha_1}/{alpha_0} Y_1-dots -{alpha_d}/{alpha_0}Y_d .$$
По определению, система $ {Y_1,dots,Y_d} $ является базисом $ mathbb V $.
♦
Т
Теорема 7. Любой вектор $ X in mathbb V_{} $ может быть разложен по фиксированному базису пространства единственным образом.
Очевидно, $ dim mathbb R^{n} = n $: строки из $ n_{} $ элементов
$$[1,0,0,dots,0], [0,1,0,dots,0], [0,0,1,dots,0], dots , [0,0,0,dots,1]
$$
образуют базис этого пространства.
Имеются два способа задания линейных подпространств в $ mathbb R^{n}_{} $. Пусть
$$ mathbb V_1 = {mathcal L}(A_1,dots,A_k) quad npu {A_1,dots,A_k }
subset mathbb R^n .$$
В разделе
☞
РАНГ установлено, что
$$ dim mathbb V_1 = operatorname{rank} { A_1,dots,A_k } = operatorname{rank} (A) ,$$
где $ A_{} $ — матрица, составленная из строк (столбцов) $ A_{1},dots,A_k $.
П
Пример. Найти базис подпространства
$$mathcal L left([1,2,1,1],, [-1,0,-1,0], , [-1,2,-1,1], , [0,1,0,1] right)
.$$
Решение. Ищем
$$
operatorname{rank}
left(
begin{array}{rrrr}
1 & 2 & 1 & 1 \
-1&0&-1&0 \
-1& 2 &-1 &1 \
0& 1& 0 & 1
end{array}
right)
$$
по методу окаймляющих миноров. Существует минор третьего порядка
$$
left|
begin{array}{rrrr}
1 & 2 & 1 \
-1&0&0 \
0& 1 & 1
end{array}
right|
$$
отличный от нуля, а определитель самой матрицы равен нулю. Замечаем,
что найденный отличный от нуля минор расположен в первой, второй и
четвертой строках матрицы. Именно эти строки и образуют базис.
Ответ. Базис составляют, например, первая, вторая и четвертая строки.
Другим способом задания линейного подпространства в $ mathbb R^{n} $ может служить
задание набора ограничений, которым должны удовлетворять векторы
подпространства. Таким набором ограничений может являться, например,
система уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&0,\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&0,\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&0
end{array}right. qquad iff qquad AX=mathbb O .
$$
Какова размерность подпространства решений этой системы?
На этот вопрос мы ответим сразу же,
если вспомним определение фундаментальной системы решений (ФСР).
Именно, ФСР — как набор линейно независимых
решений, через которые линейно выражается любое решение системы однородных уравнений — является базисом подпространства этих решений.
Т
Теорема 8. Множество решений системы однородных уравнений $ AX=mathbb O_{} $ образует линейное подпространство пространства $ mathbb R^{n} $. Размерность этого подпространства равна $ n-operatorname{rank} (A) $, а фундаментальная система решений образует его базис.
П
Пример. В пространстве $ mathbb P_{n} $ полиномов степеней $ le n_{} $ каноническим базисом можно взять систему мономов $ {1,x,x^2,dots, x^n } $, т.е. $ dim mathbb P_{n} =n+1 $. Координатами полинома
$$ f(x)=a_0+a_1x+a_2x^2+dots+a_nx^n $$ будут его коэффициенты. Можно выбрать и другой базис, например,
$ {1, x-c,(x-c)^2,dots,(x-c)^n } $ при произвольном числе $ c_{} $. Координатами полинома в этом базисе будут теперь коэффициенты формулы Тейлора:
$$
f(x) equiv f(c)+
frac{f^{prime}(c)}{1!} (x-c) + frac{f^{prime prime }(c)}{2!} (x-c)^2+
dots + frac{f^{(n)}(c)}{n!} (x-c)^{n} .
$$
?
Найти координаты полинома
$$ x^5-x^4+x^3-x^2-x+1 $$
в базисе $ {1,x+1,x^2+1,x^3+1,x^4+1,x^5+1} $.
Т
Теорема 9. Любое векторное пространство $ mathbb V_{} $ размерности $ d_{} $ изоморфно $ mathbb R^{d} $.
Доказательство. Изоморфизм можно установить следующим соответствием.
Если $ {X_1,dots , X_d } $ — какой-то базис $ mathbb V_{} $, то вектору
$ X in mathbb V $ поставим в соответствие набор его координат в этом базисе:
$$ X=x_1X_1+dots+x_d X_d Rightarrow
X mapsto [x_1,dots,x_d]in mathbb R^d .
$$
На основании теоремы $ 6 $, такое соответствие будет взаимно-однозначным,
а проверка двух свойств изоморфизма тривиальна.
♦
Последний результат позволяет свести исследование свойств произвольного линейного пространства $ mathbb V_{} $ к исследованию свойств пространства $ mathbb R^{d} $. Лишь бы только удалось нам найти базис пространства $ mathbb V_{} $, а также разложение произвольного вектора по этому базису.
Однако некоторые теоретические заключения можно сделать основываясь только лишь на фактах принципиального существования
базиса и возможности разложения по нему произвольного вектора.
Критерии линейной зависимости
Т
Теорема . Строки
$$
{(a_{11},dots,a_{1n}),dots, (a_{n1},dots,a_{nn})} subset mathbb C^n
$$
линейно зависимы тогда и только тогда, когда
$$
left|begin{array}{rrr}
a_{11}&dots & a_{1n} \
dots & & dots \
a_{n1}& dots & a_{nn}
end{array}
right|=0 , .
$$
Т
Теорема . Строки
$$
{(a_{11},dots,a_{1n}),dots, (a_{m1},dots,a_{mn})} subset mathbb C^n
$$
линейно зависимы тогда и только тогда, когда
$$
operatorname{rank} A <m , , npu A=left(begin{array}{rrr}
a_{11}&dots & a_{1n} \
dots & & dots \
a_{m1}& dots & a_{mn}
end{array}
right) , .
$$
=>
Строки
$$
{(a_{11},dots,a_{1n}),dots, (a_{m1},dots,a_{mn})} subset mathbb R^n
$$
линейно зависимы тогда и только тогда, когда
$$
det (A^{top} A) = 0 , .
$$
(Определитель в левой части можно интерпретировать как определитель Грама системы строк.)
Т
Теорема . Аналитические на интервале $ ]a,b[ $ функции $ u_1(x),dots,u_n(x) $ линейно зависимы на $ ]a,b[ $ тогда и только тогда, когда их вронскиан
$$
left|
begin{array}{llll}
u_1(x) & u_2(x) & dots & u_n(x) \
u_1^{prime}(x) & u_2^{prime}(x) & dots & u_n^{prime}(x) \
u_1^{prime prime}(x) & u_2^{prime prime}(x)&dots& u_n^{prime prime}(x)\
dots & & & dots \
u_1^{(n-1)}(x) &u_2^{(n-1)}(x) &dots & u_n^{(n-1)}(x)
end{array}
right|
$$
тождественно равен нулю на $ ]a,b[ $.
Относительный базис
В настоящем пункте $ mathbb V_1 $ обозначает линейное подпространство пространства $ mathbb V_{} $, отличное от тривиального; обозначаем $ d_1=dim mathbb V_1 $.
Т
Теорема. Произвольный базис подпространства $ mathbb V_1 $ можно дополнить до базиса пространства $ mathbb V_{} $.
Доказательство. Пусть $ {X_1,dots,X_{d_1} } $ — какой-то
базис $ mathbb V_1 $. В пространстве $ mathbb V_{} $ найдется вектор
$ X_{d_1+1} $ такой, что система $ {X_1,dots,X_{d_1}, X_{d_1+1 }} $ будет л.н.з. (В противном случае, $ dim mathbb V=d_1 $, что противоречит условию настоящего пункта.) Если
$ d_1+1=d = dim mathbb V $, то, на основании теоремы 5 предыдущего пункта, требуемый
базис построен. Если же $ d_1+1<d $, то в пространстве
$ mathbb V_{} $ найдется вектор
$ X_{d_1+2} $ такой, что система $ {X_1,dots,X_{d_1}, X_{d_1+1 },X_{d_1+2 } } $
будет л.н.з. И т.д. Процесс закончится за конечное число
шагов.
♦

Говорят, что система векторов $ {X_1,dots,X_k} $ линейно независима относительно подпространства $ mathbb V_1 $ пространства $ mathbb V_{} $ если
$${.}_{} mbox{ из условия } quad alpha_1X_1+dots+alpha_k X_k in mathbb V_1 quad mbox{ следует } quad
alpha_1=dots=alpha_k=0 .$$
Т
Теорема. Обозначим $ {Y_1,dots,Y_{d_1}} $ — произвольный базис $ mathbb V_1 $.
Система $ {X_{1},dots,X_k} $ л.н.з. относительно $ mathbb V_1 $ тогда и
только тогда, когда система $ {Y_1,dots,Y_{d_1},X_1,dots,X_k} $ линейно независима.
П
Пример. Найти все значения параметра $ {color{Red} alpha } $, при которых система
$${ X_1=[1,, 2,, {color{Red} alpha },, 1 ]^{^{top}}, X_2=[1,, {color{Red} alpha },, 2,, 1]^{^{top}} }
$$
л.н.з. относительно подпространства
$$mathbb V_1=left{X in mathbb R^4 bigg|
begin{array}{ll}
x_1+2,x_2-3,x_3+4, x_4 &=0, \
x_1+x_2-x_3 -x_4 &=0
end{array}
right} . $$
Решение. Базисом подпространства $ mathbb V_1 $ является произвольная
ФСР заданной системы однородных уравнений,
например $ {Y_1=[-1,2,1,0]^{^{top}}, Y_2=[6,-5,0,1]^{^{top}}} $. Теорема
утверждает, что система $ { X_1, X_2} $ л.н.з. относительно $ mathbb V_1 $
тогда и только тогда, когда система $ { X_1, X_2,Y_1,Y_2} $ л.н.з. (в обычном понимании). Последнее равносильно тому, что матрица, составленная
из этих векторов, должна иметь ранг равный $ 4_{} $.
$$operatorname{rank}
left(
begin{array}{rrrr}
1 & 1 &-1 & 6 \
2 & {color{Red} alpha } & 2 & -5 \
{color{Red} alpha } & 2 & 1 & 0 \
1 & 1 & 0 & 1
end{array}
right)=4 iff
left|
begin{array}{rrrr}
1 & 1 &-1 & 6 \
2 & {color{Red} alpha } & 2 & -5 \
{color{Red} alpha } & 2 & 1 & 0 \
1 & 1 & 0 & 1
end{array}
right|= {color{Red} alpha }^2-10, {color{Red} alpha } +16 ne 0 .
$$
Ответ. $ {color{Red} alpha }not in { 2,, 8} $.
Говорят, что система векторов $ {X_1,dots,X_k} $ образует базис пространства $ mathbb V_{} $ относительно (или над) $ mathbb V_1 $ если она л.н.з. относительно
$ mathbb V_1 $ и любой вектор $ Xin mathbb V_{} $ можно представить в виде
$$ X=c_1X_1+dots+c_kX_k+Y, quad mbox{ где } quad Yin mathbb V_1 . $$
Т
Теорема. Обозначим $ { Y_1,dots,Y_{d_1} } $ — произвольный базис подпространства $ mathbb V_1 $.
Система $ {X_1,dots,X_k} $ образует базис $ mathbb V_{} $ относительно $ mathbb V_1 $ тогда и
только тогда, когда система $ { X_1,dots,X_k,Y_1,dots,Y_{d_1} } $ образует
базис $ mathbb V_{} $.
Доказательство. Действительно, любой вектор $ Xin mathbb V_{} $ выражается через
векторы $ X_1,dots,X_k,Y_1,dots,Y_{d_1} $. По предыдущей теореме для линейной
независимости этих векторов необходимо и достаточно относительной линейной независимости
$ X_1,dots,X_k $.
♦
=>
Базис $ mathbb V_{} $ строится дополнением базиса $ mathbb V_1 $ векторами
$ X_1,dots,X_k $ линейно независимыми относительно $ mathbb V_1 $. Поэтому
$${.}_{} mbox{число векторов относительного базиса } = dim mathbb V – dim
mathbb V_1 .$$
Это число называется коразмерностью6) подпространства $ mathbb V_1 $ в пространстве $ mathbb V $.
Сумма и пересечение линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства
линейного пространства $ mathbb V_{} $. Множество
$$ mathbb V_1+ mathbb V_2 = left{X_1+X_2 big| X_1 in mathbb V_1, X_2 in mathbb V_2 right}$$
называется суммой, а множество
$$ mathbb V_1 cap mathbb V_2 = left{X big| X in mathbb V_1, X in mathbb V_2 right}$$
— пересечением подпространств $ mathbb V_1 $ и $ mathbb V_2 $. Аналогично
определяется сумма и пересечение произвольного количества подпространств.
Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.
Как правило, $ mathbb V_1+ mathbb V_2 ne mathbb V _1 cup mathbb V_2 $.

Т
Теорема. $ mathbb V_1+ mathbb V_2 $ и $ mathbb V_1 cap mathbb V_2 $ являются
подпространствами линейного пространства $ mathbb V_{} $.
?
Докажите, что $ mathbb V_1+ mathbb V_2 $ — это подпространство минимальной размерности, содержащее как $ mathbb V_1 $, так и $ mathbb V_2 $.
Понятие суммы линейных подпространств является частным случаем суммы Минковского двух произвольных подмножеств $ mathbb A_1 $ и $ mathbb A_2 $ линейного пространства:
$$ mathbb A_1 + mathbb A_2 = { X+Y mid X in mathbb A_1, Y in mathbb A_2 } . $$
Для подмножеств $ mathbb A_1={ [1,0], [0,1], [0,-1] } $ и $ mathbb A_2={ [0,0], [1,1] } $ пространства $ mathbb R^2 $ имеем:
$$ mathbb A_1 + mathbb A_2 = { [1,0], [0,1], [0,-1], [2,1], [1,2] } , . $$
Т
Теорема. Имеет место формула:
$$
dim , mathbb V_1 + dim , mathbb V_2=dim , (mathbb V_1 cap mathbb V_2) +
dim , (mathbb V_1 + mathbb V_2) . $$
Доказательство
☞
ЗДЕСЬ.
?
Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог
формулы включений-исключений в следующем виде:
$$dim , mathbb V_1 + dim , mathbb V_2 + dim , mathbb V_3 –
$$
$$
-left{dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 cap mathbb V_3) +
dim , (mathbb V_2 cap mathbb V_3) right} + $$
$$+ dim , (mathbb V_1 cap mathbb V_2 cap mathbb V_3) =dim , (mathbb V_1 + mathbb V_2 + mathbb V_3) ?$$
Т
Теорема. Имеет место формула:
$${mathcal L}(X_1,dots,X_m)+{mathcal L}(Y_1,dots,Y_{ell})=
{mathcal L}(X_1,dots,X_m,Y_1,dots,Y_{ell}) ;
$$
здесь $ {mathcal L} $ означает линейную оболочку.
П
Пример. Найти базис суммы и размерность пересечения
$$mathbb V_1={mathcal L}left(
left[ begin{array}{r} 0 \1 \ 1 \ 1
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 1 \ 2
end{array} right] ,
left[ begin{array}{r} -2 \0 \ 1 \ 1
end{array} right]
right)
quad mbox{ и } quad
mathbb V_2={mathcal L}left(
left[ begin{array}{r} -1 \3 \ 2 \ -1
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 0 \ -1
end{array} right]
right)
$$
Решение. Действуя согласно предыдущей теореме, составляем матрицу из всех векторов
$$
left( begin{array}{rrrrr}
0 & 1 & -2 & -1 & 1 \
1 & 1 & 0 & 3 & 1 \
1 & 1 & 1 & 2 & 0 \
1 & 2 & 1 & -1 & -1
end{array}
right)
$$
и ищем ее ранг методом окаймляющих миноров. Имеем: $ operatorname{rank} = 3 $ при ненулевом миноре матрицы расположенном в первых трех ее столбцах.
Ответ. Базис $ mathbb V_1 + mathbb V_2 $ составляют векторы $ X_1,X_2,X_3 $;
$ dim , (mathbb V_1 cap mathbb V_2) = 3+2 – 3 =2 $.
Алгоритм нахождения базиса
$ {mathcal L}(X_1,dots,X_m) cap {mathcal L}(Y_1,dots,Y_{ell}) $
проиллюстрируем на примере.
П
Пример. Найти базис $ mathbb V_1 cap mathbb V_2 $ при
$$
begin{array}{l}
mathbb V_1={mathcal L} left(
left[
begin{array}{r}
1 \ -1 \ 1 \ -1 \ 1
end{array}
right],,
left[
begin{array}{r}
1 \ 2 \ 1 \ 2 \ 1
end{array}
right],,
left[
begin{array}{r}
0 \ 1 \ 0 \ 1 \ 0
end{array}
right]
right) \
{}_{} qquad qquad quad X_1 quad quad X_2 quad quad X_3
end{array}
,
begin{array}{l}
mathbb V_2={mathcal L} left(
left[
begin{array}{r}
1 \ 0 \ 0 \ 0 \ 1
end{array}
right],,
left[
begin{array}{r}
1 \ 1 \ 0 \ 1 \ 1
end{array}
right],,
left[
begin{array}{r}
0 \ 1 \ 1 \ 1 \ 0
end{array}
right]
right) \
{}_{} quad qquad qquad Y_1 qquad Y_2 quad quad Y_3
end{array}
.
$$
Решение.
1.
Сначала найдем базисы каждого из подпространств:
$$dim mathbb V_1=2, mathbb V_1=mathcal L(X_1, X_2) ; dim mathbb V_2=3,
mathbb V_2=mathcal L(Y_1, Y_2, Y_3) . $$
2.
Произвольный вектор $ Zin mathbb R^5 $, принадлежащий
$ mathbb V_1 cap mathbb V_2 $, должен
раскладываться по базису каждого из подпространств:
$$Z=alpha_1 X_1 + alpha_2 X_2= beta_1 Y_1 + beta_2 Y_2 + beta_3 Y_3 .$$
Для определения неизвестных значений координат составляем систему уравнений
$$
begin{array}{l}
qquad X_1 X_2 \
qquad {color{RubineRed} downarrow} {color{RubineRed} downarrow} \
left( begin{array}{rrrrrrr}
1 & 1 & -1 & &-1 & & 0 \
-1 & 2 & 0 & & -1 & & -1 \
1 & 1 & 0 & & 0 & & -1 \
-1 & 2 & 0 & & -1 & & -1 \
1 & 1 & -1 & & -1 & & 0
end{array}
right) \
qquad qquad qquad {color{RubineRed} uparrow} qquad {color{RubineRed} uparrow} qquad quad {color{RubineRed} uparrow} \
quad qquad qquad -Y_1 quad – Y_2 quad -Y_3
end{array}
left(
begin{array}{r}
alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3
end{array}
right)= mathbb O_{5times 1}
$$
и решаем ее по методу Гаусса с нахождением фундаментальной системы решений:
$$
left( begin{array}{rrrrr}
1 & 1 & -1 & -1 & 0 \
0 & 3 & -1 & -2 & -1 \
0 & 0 & 1 & 1 & -1 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0
end{array}
right) left(
begin{array}{r}
alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3
end{array}
right)= mathbb O quad Rightarrow qquad mbox{ ФСР } qquad
begin{array}{rrr|rr}
alpha_1 & alpha_2 & beta_1 & beta_2 & beta_3 \ hline
-1/3 & 1/3 & -1 & 1 & 0 \
1/3 & 2/3 & 1 & 0 & 1
end{array}
$$
3.
Получившиеся значения координат позволяют выразить
базис пересечения — либо через базис подпространства $ mathbb V_1 $
(если использовать полученные значения для $ alpha_1,alpha_2 $), либо
через базис подпространства $ mathbb V_2 $
(если использовать $ beta_1,beta_2, beta_3 $). Например,
$$
Z_1=-1/3 X_1 + 1/3 X_2 = [0,1,0,1,0]^{^{top}},
$$
$$
Z_2=1/3 X_1 + 2/3 X_2 = [1,1,1,1,1]^{^{top}}
.
$$
Ответ.7) $ left{[0,1,0,1,0]^{^{top}},, [1,1,1,1,1]^{^{top}} right} $.
?
Найти базисы суммы и пересечения подпространств
$$
mathbb V_1=left{
Xin mathbb R^4 left|
begin{array}{rrrrl}
2,x_1&+x_2&+4,x_3&+x_4 &= 0, \
2,x_1&+x_2&+3,x_3& &=0
end{array}
right.
right}
$$
и
$$
mathbb V_2=
left{
Xin mathbb R^4 left|
begin{array}{rrrrl}
3,x_1&+2,x_2&-x_3&-6, x_4 &= 0, \
2,x_1&&+8,x_3 &+7, x_4 &=0
end{array}
right.
right} .
$$
Решение
☞
ЗДЕСЬ.
Прямая сумма линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_{} $.
Говорят, что $ mathbb V_{} $ раскладывается в прямую сумму подпространств
$ mathbb V_1 $ и $ mathbb V_2 $ если любой вектор $ Xin mathbb V_{} $ может быть представлен
в виде $ X=X_1+X_2 $, где $ X_1in mathbb V_1,X_2in mathbb V_2 $ и
такое представление единственно. Этот факт записывают: $ mathbb V= mathbb V_1 oplus mathbb V_2 $. Вектор $ X_{1} $ называется проекцией вектора $ X_{} $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_{2} $.

П
Пример. Линейное пространство квадратных матриц порядка $ n_{} $
раскладывается в прямую сумму подпространств: подпространства симметричных
матриц и подпространства кососимметричных матриц. В самом деле, для матрицы
$ A_{ntimes n} $ справедливо разложение
$$A=frac{1}{2} left(A+A^{^top} right) + frac{1}{2} left(A-A^{^top} right)
$$
и в правой части первая скобка дает симметричную матрицу, а
вторая — кососимметричную. Покажите, что не существует иного
разложения матрицы $ A_{} $ в сумму симметричной и кососимметричной.
Т
Теорема. Пусть $ mathbb V=mathbb V_1 + mathbb V_2 $.
Эта сумма будет прямой тогда и только тогда, когда подпространства $ mathbb V_1 $ и $ mathbb V_2 $ имеют тривиальное пересечение:
$$mathbb V_1 cap mathbb V_2={mathbb O } .$$
Доказательство. Необходимость. Пусть сумма $ mathbb V_1 + mathbb V_2 $ — прямая, но существует вектор $ Xne mathbb O $, принадлежащий $ mathbb V_1 cap mathbb V_2 $.
Но тогда и вектор $ (-X) $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Для нулевого вектора $ mathbb O $ получаем два представления в виде суммы проекций на подпространства:
$$ mathbb O = mathbb O + mathbb O = X+ (-X) , . $$
Это противоречит понятию прямой суммы.
Достаточность. Если $ mathbb V_1 cap mathbb V_2={mathbb O } $, но существует вектор $ X in mathbb V_1 + mathbb V_2 $, имеющий два различных разложения в сумму проекций
$$ X=X_1+X_2 =Y_1+ Y_2 quad npu quad {X_1,Y_1} subset mathbb V_1, {X_2,Y_2} subset mathbb V_2, $$
то
$$ (X_1-Y_1)+(X_2-Y_2) =mathbb O quad Rightarrow quad X_1-Y_1=Y_2-X_2 , , $$
т.е. вектор $ X_1-Y_1 $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Но, по предположению, $ mathbb V_1 cap mathbb V_2={mathbb O } $, следовательно, $ X_1-Y_1=mathbb O $, но тогда и $ Y_2-X_2=mathbb O $.
♦
=>
Сумма $ mathbb V=mathbb V_1 + mathbb V_2 $ будет прямой тогда и только тогда, когда
базис $ mathbb V_{} $ может быть получен объединением базисов $ mathbb V_{j} $.
Сформулированное таким образом утверждение содержится во многих учебниках по линейной алгебре. Тем не менее, с формальной точки зрения, оно неверно. В самом деле,
пусть $ mathbb V_1 = {mathcal L}(X_1,X_2),, mathbb V_2 = {mathcal L}(X_2,X_3) $ при
линейно независимых $ X_1,X_2,X_3 $. Очевидно базис
$ mathbb V_1 + mathbb V_2 ={mathcal L}(X_1,X_2,X_3) $ получается объединением базисов
$ mathbb V_1 $ и $ mathbb V_2 $. В то же время $ mathbb V_1 cap mathbb V_2ne {mathbb O } $.
Причина возникновения этой ошибки кроется в содержании термина
«объединение базисов». С точки зрения терминологии теории множеств,
во множестве не могут содержаться одинаковые элементы (во множестве
они неразличимы). Однако мы с самого начала изложения допустили,
что в систему векторов могут входить одинаковые, которые различаются
порядком своего расположения (хотя это особо и не подчеркивалось, векторы
в системе всегда пронумерованы). Исходя из этих соображений, объединение
базисов $ mathbb V_1 $ и $ mathbb V_2 $ будет пониматься8)
в настоящем пункте (и кое-где далее) как система векторов, в которую входят последовательно векторы базисов
$ mathbb V_1 $ и $ mathbb V_2 $ — с допуском дублей. В рамках такой договоренности,
для приведенного примера получим: объединение базисов линейных подпространств
$ {mathcal L}(X_1,X_2) $ и $ {mathcal L}(X_2,X_3) $ представляет систему
$ {X_1,X_2,X_2,X_3} $, которая, очевидно, не является базисом. Таким образом
сумма $ {mathcal L}(X_1,X_2)+{mathcal L}(X_2,X_3) $ не является прямой, и результат
следствия остается справедливым.
П
Пример [2]. Доказать, что сумма подпространств
$$mathbb V_1={mathcal L}left(
left[ begin{array}{r} 2 \3 \ 11 \ 5
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 5 \ 2
end{array} right] ,
left[ begin{array}{r} 0 \1 \ 1 \ 1
end{array} right]
right)
quad mbox{ и } quad
mathbb V_2={mathcal L}left(
left[ begin{array}{r} 2 \1 \ 3 \ 2
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 3 \ 4
end{array} right] ,
left[ begin{array}{r} 5 \2 \ 6 \ 2
end{array} right]
right)
$$
будет прямой и найти проекции вектора $ Z=[2,0,0,3]^{top} $ на эти подпространства.
Решение. Базисы $ mathbb V_1 $ и $ mathbb V_2 $ составляют соответственно системы
$ {X_2,X_3} $ и $ { Y_1,Y_2 } $, т.е. $ dim , mathbb V_1=dim , mathbb V_2 =2 $.
На основании следствия достаточно установить, что объединенная
система $ {X_2,X_3,Y_1,Y_2 } $ л.н.з. Для этого достаточно проверить, что определитель матрицы
$$
A=left(
begin{array}{rrrr}
1 & 0 & 2 & 1 \
1 & 1 & 1 & 1 \
5 & 1 & 3 & 3 \
2 & 1 & 2 & 4
end{array}
right)
$$
отличен от нуля. Поскольку это условие выполнено, то сумма $ mathbb V_1 + mathbb V_2 $ —
прямая и базис этой суммы состоит из взятых векторов.
Для нахождения разложения вектора $ X_{} $ по этому базису
решаем систему уравнений
$$A left[
begin{array}{c}
alpha_2 \ alpha_3 \ beta_1 \ beta_2
end{array}
right] = Z
$$
и получаем единственное решение:
$ alpha_2=-1,, alpha_3=-1,, beta_1 =1, , beta_2=1 $. Разложение
$ Z=Z_1+Z_2 $ составляют векторы $ Z_1=alpha_2 X_2+alpha_3 X_3 $ и
$ Z_2=beta_1 Y_1+beta_2 Y_2 $.
Ответ. $ Z=[-1,-2,-6,-3]^{top} + [3,2,6,6]^{top} $.
Линейные многообразия
Пусть $ mathbb V_1 $ — линейное подпространство пространства
$ mathbb V_{} $, а $ X_{0} $ — произвольный фиксированный вектор из $ mathbb V_{} $. Множество
$$ mathbb M = X_0+ mathbb V_1 = left{X_0+Y big| Y in mathbb V_1 right} $$
называется линейным многообразием (порожденным подпространством $ mathbb V_1 $). Размерностью этого
многообразия называется размерность порождающего его подпространства: $ dim mathbb M = dim mathbb V_1 $. В случае $ 1 < dim mathbb M = k < dim mathbb V $ о многообразии $ mathbb M $ говорят как о k-мерной плоскости (или гиперплоскости), а при $ k=1 $ — как о прямой.
Образно говоря, многообразие — это сдвиг порождающего его линейного подпространства.
П
Пример. Множество полиномов вида
$$ f(x)= a_0x^3+a_1x^2+a_2x+1 in mathbb R[x] , , $$
т.е. таких, что $ deg f le 3, f(0)=1 $ образует линейное многообразие, порожденное линейным подпространством полиномов $ { x(a_0x^2+a_1x+a_2) mid (a_0,a_1,a_2) in mathbb R^3 } $.
Пересечение многообразий определяется традиционным способом, а сумма многообразий не определяется. Будем называть многообразия, порожденные одним и тем же подпространством
$$ mathbb M = X_0+ mathbb V_1 quad u quad widetilde{mathbb M} = widetilde X_0+ mathbb V_1 , $$
параллельными многообразиями.
П
Пример. Множество столбцов пространства $ mathbb R^{n} $, удовлетворяющих системе уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1,\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2,\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&b_m
end{array}right.
iff
AX={mathcal B} ,
$$
образует линейное многообразие.
При $ {mathcal B}ne mathbb O_{mtimes 1} $ это многообразие не будет являться линейным пространством. Структуру этого множества описывала теорема из пункта
☞
ОБЩЕЕ РЕШЕНИЕ: если система совместна, то ее
общее решение можно представить как сумму какого-то одного ее решения и общего
решения соответствующей однородной системы $ AX= mathbb O $. Таким образом, многообразие решений неоднородной системы $ AX={mathcal B} $ допускает «параметрическое представление»:
$$mathbb M=X_0+ {mathcal L}(X_1,dots,X_{n-{mathfrak r}})=
$$
$$=left{X_0+t_1
X_1+dots+ t_{n-{mathfrak r}} X_{n-{mathfrak r}} mid (t_1,dots, t_{n-{mathfrak r}}) in mathbb R^{n-{mathfrak r}} right} ; $$
здесь $ X_{0} $ означает частное решение системы (т.е. $ AX_0={mathcal B} $),
$ {X_1,dots,X_{n-{mathfrak r}}} $ — ФСР для системы $ AX= mathbb O $,
а $ mathfrak r= operatorname{rank} A= operatorname{rank} [Amid mathcal B] $.
Получаем, следовательно, $ (n-{mathfrak r}) $-мерную плоскость в $ mathbb R^n $, a в случае $ (n-{mathfrak r})=1 $ — прямую
$$mathbb M=X_0+tX_1 quad npu t in mathbb R ; $$
в последнем случае вектор $ X_{1} $ называют направляющим вектором этой прямой.
§
Некоторые задачи на линейные многообразия
☞
ЗДЕСЬ.
Факторпространство
определяется
☞
ЗДЕСЬ.
Преобразование координат при замене базиса
Пусть $ mathbb V_{} $ — линейное пространство размерности $ n_{} $, пусть
$$ {X_1,dots,X_n} quad u quad {{mathfrak X}_1,dots,{mathfrak X}_n}$$
— два произвольных его базиса («старый» и «новый»).
Задача. Вывести соотношения, связывающие координаты произвольного
вектора $ Xin mathbb V_{} $ в старом и новом базисах:
$$X=x_1X_1+dots+x_nX_n={mathfrak x}_1{mathfrak X}_1+dots+{mathfrak x}_n{mathfrak X}_n
.$$
Предположим, что нам известны координаты векторов нового базиса в старом:
$$
left{
begin{array}{ccc}
{mathfrak X}_1&=&c_{11}X_1+c_{21}X_2+dots+c_{n1}X_n, \
{mathfrak X}_2&=&c_{12}X_1+c_{22}X_2+dots+c_{n2}X_n, \
dots& & dots \
{mathfrak X}_n&=&c_{1n}X_1+c_{2n}X_2+dots+c_{nn}X_n.
end{array}
right.
$$
Матрица
$$
C=left(
begin{array}{cccc}
c_{11} & c_{12} & dots & c_{1n} \
c_{21} & c_{22} & dots & c_{2n} \
dots & & & dots \
c_{n1} & c_{n2} & dots & c_{nn} \
end{array}
right),
$$
по столбцам которой стоят координаты новых базисных векторов в старом базисе называется матрицей перехода от старого базиса к новому, а также — ввиду одного из приведенных ниже результатов — матрицей преобразования координат.
Т
Теорема. Матрица $ C_{} $ неособенная.
Доказательство. Cначала покажем справедливость утверждения в частном случае $ mathbb V=mathbb R^n $. Вектора нового и старого базисов являются столбцами из $ n $ вещественных чисел, и равенства, задающие элементы матрицы $ C_{} $, можно переписать в матричном виде:
$$
left[{mathfrak X}_1|dots|{mathfrak X}_nright]=left[X_1|dots|X_nright]cdot C .
$$
Здесь $ | $ означает конкатенацию. Поскольку системы $ {X_1,dots,X_n} $ и $ {{mathfrak X}_1,dots,{mathfrak X}_n} $ — базисные, то
$$det left[X_1|dots |X_nright] ne 0, quad
det left[{mathfrak X}_1|dots |{mathfrak X}_nright] ne 0 .$$
Из последнего матричного равенства (и теоремы Бине-Коши ) тогда следует, что $ det Cne 0 $.
Теперь докажем теорему для случая произвольного пространства. Если $ det C= 0 $, то столбцы матрицы $ C_{} $ линейно зависимы (см.
☞
ЗДЕСЬ ), т.е. существует линейная комбинация
$$alpha_1 c_{j1}+ dots+alpha_n c_{jn}=0 quad npu quad forall jin {1,dots,n } $$
и при некотором $ alpha_kne 0 $. Но тогда из формул
$$
left{
begin{array}{ccc}
{mathfrak X}_1&=&c_{11}X_1+c_{21}X_2+dots+c_{n1}X_n, \
{mathfrak X}_2&=&c_{12}X_1+c_{22}X_2+dots+c_{n2}X_n, \
dots& & dots \
{mathfrak X}_n&=&c_{1n}X_1+c_{2n}X_2+dots+c_{nn}X_n.
end{array}
right.
$$
следует, что
$$alpha_1 {mathfrak X}_1+ dots+alpha_n {mathfrak X}_n=mathbb O ,$$
что противоречит линейной независимости системы $ {{mathfrak X}_1,dots,{mathfrak X}_n} $.
♦
П
Пример. Найти матрицу перехода
| от базиса | к базису | |
|---|---|---|
| $ left[1,1,0,0,0right] $ | $ left[1,1,1,1,1right] $ | |
| $ left[1,0,1,0,0right] $ | $ left[1,1,1,1,0right] $ | |
| $ left[1,0,0,1,0right] $ | $ left[1,1,1,0,0right] $ | |
| $ left[1,0,0,0,1right] $ | $ left[1,1,0,0,0right] $ | |
| $ left[1,1,1,1,1right] $ | $ left[1,0,0,0,0right] $ |
Решение. Можно попытаться найти элементы матрицы $ C_{} $ напрямую — устанавливая формулы связи между строками. В нашем конкретном примере это не очень трудно сделать — первый и четвертый
столбцы матрицы $ C_{} $ вообще очевидны поскольку $ {mathfrak X}_1 = X_5,, {mathfrak X}_4 = X_1 $. Но мы пойдем по формальному пути и воспользуемся определяющим матричным соотношением, которое мы получили при доказательстве предыдущей теоремы. Поставим координаты базисных векторов по столбцам соответствующих матриц:
$$
left[{mathfrak X}_1|dots|{mathfrak X}_nright]=left[X_1|dots|X_nright]cdot C quad Rightarrow
$$
$$
Rightarrow C= left[X_1|dots|X_nright]^{-1} cdot left[{mathfrak X}_1|dots|{mathfrak X}_nright] .
$$
В нашем примере имеем:
$$
C=
left(
begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 0 & 0 & 0 & 1 \
0 & 1 & 0 & 0 & 1 \
0 & 0 & 1 & 0 & 1 \
0 & 0 & 0 & 1 & 1
end{array}
right)^{-1}
left(
begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 1 & 1 & 1 & 0 \
1 & 1 & 1 & 0 & 0 \
1 & 1 & 0 & 0 & 0 \
1 & 0 & 0 & 0 & 0
end{array}
right)=
$$
$$
=frac{1}{3}
left(
begin{array}{rrrrr}
1 & 2 & -1 & -1 & -1 \
1 & -1 & 2 & -1 & -1 \
1 & -1 & -1 & 2 & -1 \
1 & -1 & -1 & -1 & 2 \
-1 & 1 & 1 & 1 & 1
end{array}
right)
left(
begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 1 & 1 & 1 & 0 \
1 & 1 & 1 & 0 & 0 \
1 & 1 & 0 & 0 & 0 \
1 & 0 & 0 & 0 & 0
end{array}
right) =
$$
$$
=left(
begin{array}{rrrrr}
0 & 1/3 & 2/3 & 1 & 1/3 \
0 & 1/3 & 2/3 & 0 & 1/3 \
0 & 1/3 & -1/3 & 0 & 1/3 \
0 & -2/3 & -1/3 & 0 & 1/3 \
1 & 2/3 & 1/3 & 0 & -1/3
end{array}
right) .
$$
♦
Т
Теорема. Координаты вектора в старом и новом базисах связаны посредством матрицы перехода $ C_{} $ соотношениями
$$
left{
begin{array}{ccc}
x_1&=&c_{11}{mathfrak x}_1+c_{12}{mathfrak x}_2+dots+c_{1n}{mathfrak x}_n, \
x_2&=&c_{21}{mathfrak x}_1+c_{22}{mathfrak x}_2+dots+c_{2n}{mathfrak x}_n, \
dots& & dots \
x_n&=&c_{n1}{mathfrak x}_1+c_{n2}{mathfrak x}_2+dots+c_{nn}{mathfrak x}_n
end{array}
right.
quad iff quad
left( begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array} right)
=C left( begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array} right) .
$$
Доказательство.
$$
begin{array}{lll}
X=x_1X_1+dots+x_nX_n&=&{mathfrak x}_1{mathfrak X}_1+dots+{mathfrak x}_n{mathfrak X}_n = \
&=&{mathfrak x}_1(c_{11}X_1+c_{21}X_2+dots+c_{n1}X_n)+\
&+&{mathfrak x}_2(c_{12}X_1+c_{22}X_2+dots+c_{n2}X_n)+\
&+& dots +\
&+&{mathfrak x}_n(c_{1n}X_1+c_{2n}X_2+dots+c_{nn}X_n)=\
=(c_{11}{mathfrak x}_1+c_{12}{mathfrak x}_2+dots+c_{1n}{mathfrak x}_n)X_1&+&dots+
(c_{n1}{mathfrak x}_1+c_{n2}{mathfrak x}_2+dots+c_{nn}{mathfrak x}_n)X_n
end{array}
$$
Поскольку при фиксированном базисе координаты вектора определяются однозначно (теорема $ 6 $
☞
ЗДЕСЬ ),
получаем равенства
$$
left{
begin{array}{ccc}
x_1&=&c_{11}{mathfrak x}_1+c_{12}{mathfrak x}_2+dots+c_{1n}{mathfrak x}_n, \
x_2&=&c_{21}{mathfrak x}_1+c_{22}{mathfrak x}_2+dots+c_{2n}{mathfrak x}_n, \
dots& & dots \
x_n&=&c_{n1}{mathfrak x}_1+c_{n2}{mathfrak x}_2+dots+c_{nn}{mathfrak x}_n
end{array}
right.
quad iff quad
left( begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array} right)
=C left( begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array} right)
$$
♦
Практическое значение последнего результата невелико, т.к. нас интересуют именно новые координаты.
=>
Новые координаты выражаются через старые по формуле
$$
left( begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array} right)
=C^{-1} left( begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array} right),
$$
при этом матрицу $ C^{-1} $ можно интерпретировать как матрицу перехода от нового базиса к старому.
?
Пусть в некотором «новейшем» базисе $ { {mathcal X}_1,dots,{mathcal X}_n } $
пространства $ mathbb V_{} $ вектор $ X_{} $ имеет координаты $ (varkappa_1,dots,varkappa_n) $.
Как они связаны с координатами $ (x_{1},dots,x_n) $ в старом базисе $ {X_1,dots,X_n} $, если известны матрица $ C_{} $ перехода от этого базиса к базису $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ и матрица $ D_{} $ перехода от базиса $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ к базису $ {{mathcal X}_1,dots,{mathcal X}_n } $ ?
Евклидовы пространства
— как линейные пространства, в которых вводится понятия угла и расстояния между векторами — рассматриваются
☞
ЗДЕСЬ.
Нормированные пространства
— как линейные пространства, в которых вводится понятие расстояния между векторами — рассматриваются
☞
ЗДЕСЬ.
Линейные отображения
пространств рассматриваются
☞
ЗДЕСЬ
Задачи
Источники
[1]. Лаврентьев М., Люстерник Л. Основы вариационного исчисления. Том 1. Часть I. М.-Л.ОНТИ. 1935, с. 22
[2]. Икрамов Х.Д. Задачник по линейной алгебре. М.1975
[3]. Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969
Способы описания подпространств линейного пространства
Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .
Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров ;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,
– столбцы матрицы , содержащие единичные элементы (в начале каждой “ступеньки”), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.
Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.
Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .
3. Из последних строк матрицы составить матрицу .
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы составляем матрицу искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы . Искомая размерность .
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;
– из последних столбцов матрицы составить фундаментальную матрицу .
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .
2. Столбцы являются искомым базисом, так как они линейно независимы и .
23. Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений
Пусть дано N-Мерное линейное пространство L и пусть в нём зафиксирован базис Е = (Е1, Е2, … , Еn ). Пусть М – линейное подпространство в L .
Определение 30. Будем говорить, что Система линейных уравнений задаёт подпространство М, если этой системе удовлетворяют координаты всех векторов из М и не удовлетворяют координаты никаких других векторов.
Из свойств решений однородной системы линейных уравнений следует, что любая однородная линейная система уравнений ранга R с n Переменными задаёт в любом N-Мерном пространстве Ln (если в нём зафиксирован базис) (N–r )-мерное линейное подпространство.
Справедливо и обратное утверждение. А именно, имеет место следующая теорема.
Теорема 30. Если в линейном N-Мерном пространстве Ln Зафиксирован базис, то любое его К-мерное линейное подпространство можно задать системой линейных однородных уравнений с N Неизвестными ранга (N – к).
Доказательство. Пусть в Ln зафиксирован базис Е = (Е1, Е2, … , Еn ). Пусть Lк – линейное К-мерное подпространство в Ln. Выберем в Lк Любой базис А = (А1, а2,… , ак). Пусть 

Так как А – базис, то ранг матрицы А Равен К.
Получили параметрические уравнения, определяющие Lк .
После исключения параметров получится система (N – к) линейных однородных уравнений. Векторы А1, а2, … , ак являются её линейно независимыми решениями. Все остальные решения являются их линейными комбинациями.
Следовательно, система векторов (А1, а2, … , ак) будет фундаментальной системой решений полученной системы уравнений и поэтому ранг этой системы уравнений равен (N – к).
Пример. В пространстве L5 зафиксирован базис Е = (Е1, Е2, е3, е4 , Е5 ). Найти систему линейных однородных уравнений, задающих L3 = , если А1 = (1, –2, 2, 0, 1), А2 = (0, 4, 7, 0, 1), А3 = (–2, 3, –1, 0, 0).
Решение. Найдём ранг системы векторов (А1, а2, а3 ). Для этого достаточно найти ранг матрицы 


D Î L3 Û D = с1А1 + С2А2 + С3А3 . Отсюда D Î L3 Û Х1 = с1 – 2с3 , х2 = –2с1 + 4с2 + 3с3 , х3 = 2с1 + 7с2 – с3 , х4 = 0, х5 = с1 + с2. Если из первого, второго и пятого уравнений выразить С1, с2 и С3 И подставить их в третье и четвёртое уравнения, то получим следующую систему
Замечание. Очевидно, система, задающая данное подпространство, определяется не единственным образом. К найденным уравнениям можно добавлять новые уравнения, являющиеся их линейными комбинациями.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.
Линейное пространство
Определения
Пусть дано множество $ mathbb V_<>=left < X,Y,Z,U,dots right>$ элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения $ X+Y_<> $ и умножения на любое вещественное число $ alpha_<> $: $ alpha cdot X_<> $, и множество $ mathbb V_<> $ замкнуто относительно этих операций: $ X+Y in mathbb V , alpha cdot X in mathbb V_<> $. Пусть эти операции подчиняются аксиомам:
1. $ X+Y=Y+X_<> $ для $ < X,, Y>subset mathbb V_<> $;
2. $ (X+Y)+Z_<>=X+(Y+Z) $ для $ < X,, Y,, Z >subset mathbb V_<> $;
3. в $ mathbb V_<> $ cуществует нулевой вектор $ mathbb O_<> $ со свойством $ X+ mathbb O =X_<> $ для $ forall Xin mathbb V_<> $;
4. для каждого $ Xin mathbb V_<> $ существует обратный вектор $ X^<prime>in mathbb V_<> $ со свойством $ X+X^<prime>=mathbb O_<> $;
5. $ 1cdot X=X_<> $ для $ forall Xin mathbb V_<> $;
6. $ lambda left(mu X right)_<>= left(lambda mu right)X $ для $ forall Xin mathbb V_<> $, $ <lambda ,, mu >subset mathbb R_<> $ ;
7. $ (lambda + mu)X=lambda X + mu X_<> $ для $ forall Xin mathbb V_<> $, $ <lambda ,, mu >subset mathbb R_<> $ ;
8. $ lambda (X + Y) =lambda X_<> + lambda Y $ для $ < X,, Y>subset mathbb V_<> , lambda in mathbb R $.
Тогда такое множество $ mathbb V_<> $ называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из $ mathbb R_<> $ — последние называются скалярами 1) . Пространство, состоящее из одного только нулевого вектора, называется тривиальным .
Элементарно доказывается единственность нулевого вектора, и единственность вектора, обратного вектору $ Xin mathbb V_<> $: $ X^<prime>=-1cdot X_<> $, его привычно обозначают $ – X_<> $.
Подмножество $ mathbb V_ <1>$ линейного пространства $ mathbb V_<> $, само являющееся линейным пространством (т.е. $ mathbb V_ <1>$ замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства $ mathbb V_<> $. Тривиальными подпространствами линейного пространства $ mathbb V_<> $ называются само $ mathbb V_<> $ и пространство, состоящее из одного нулевого вектора $ mathbb O_<> $.
Примеры линейных пространств
Пример 1. Пространство $ mathbb R^ <3>$ упорядоченных троек вещественных чисел $ (a_1,a_2,a_<3>) $ с операциями, определяемыми равенствами:
$$ (a_1,a_2,a_3)+(b_1,b_2,b_3)= (a_1+b_1,a_2+b_2,a_3+b_3), alpha (a_1,a_2,a_3) = ( alpha a_1, alpha a_2, alpha a_3 ) . $$ Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца $ (a_1,a_2,a_<3>) $. На рисунке показано и типичное подпространство пространства $ mathbb R^ <3>$: плоскость, проходящая через начало координат. Точнее говоря, элементами $ mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения 2) очевидна.
Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства $ mathbb V_1 $ (заложенную, кстати, уже в самом происхождении слова «вектор» 3) ) — оно определяет набор «сдвигов» точек пространства $ mathbb R^ <3>$. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости $ mathbb V_1 $.
Пример 3. Естественным обобщением $ mathbb R^ <3>$ служит пространство $ mathbb R_<>^ $: векторное пространство строк $ (a_1,dots,a_) $ или столбцов $ (a_1,dots,a_n)^ <^top>$. Один из способов задания подпространства в $ mathbb R_<>^ $ — задание набора ограничений. Множество решений системы линейных однородных уравнений:
$$ left<begin a_<11>x_1 +a_<12>x_2+ldots+a_<1n>x_n &=&0,\ a_<21>x_1 +a_<22>x_2+ldots+a_<2n>x_n &=&0,\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&0 endright. iff AX=mathbb O $$ образует линейное подпространство пространства $ mathbb R_<>^ $. В самом деле, если $$x_1=alpha_1,dots, x_n=alpha_n $$ — решение системы, то и $$x_1=t alpha_1,dots, x_n= t alpha_n $$ — тоже решение при любом $ t in mathbb R $. Если $$x_1=beta_1,dots, x_n=beta_n $$ — еще одно решение системы, то и $$x_1=alpha_1+beta_1,dots,x_n=alpha_n+beta_n $$ — тоже будет ее решением.
Почему множество решений системы неоднородных уравнений не образует линейного подпространства?
Пример 4. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей $ (a_1,dots,a_n, dots ) $, обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Подпространство этого пространства образуют, например, линейные рекуррентные последовательности $ _ $ удовлетворяющие — при произвольных числах $ > subset mathbb R $ — линейному однородному разностному уравнению $ n_<> $-го порядка, $$ x_=a_1 x_+ dots+ a_n x_K npu K in <0,1,2,dots > ; $$ здесь числа $ < a_1,dots,a_, a_n ne 0 > subset mathbb R $ считаются фиксированными.
Можно рассматривать строки (последовательности) «бесконечные в обе стороны» $ < dots,a_<-2>,a_<-1>,a_0,a_1,a_2,dots > $ — они используются в ТЕОРИИ СИГНАЛОВ.
Пример 5. Множество $ mtimes n_<> $-матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство. Будем обозначать это пространство $ mathbb R^ $.
В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.
Пример 6. Множество полиномов одной переменной $ x_<> $ степени в точности равной $ n_<> $ с коэффициентами из $ mathbb A_<> $ (где $ mathbb A_<> $ — любое из множеств $ mathbb Z, mathbb Q, mathbb R_<> $ или $ mathbb C_<> $) с обычными операциями сложения полиномов и умножения на число из $ mathbb A_<> $ не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов $ f(x)=x^n -x+1 $ и $ g(x)=-x^n+x^-2 $ не будет полиномом $ n_<> $-й степени. Но вот множество полиномов степени не выше $ n_<> $ $$ mathbb P_n= left < p(x) in mathbb A [x] big| deg p(x) le n right>$$ линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином 4) . Очевидными подпространствами $ mathbb P_ $ являются $ mathbb P_<0>, mathbb P_1,dots,mathbb P_ $. Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше $ n_<> $. Множество всевозможных полиномов $$ mathbb P= bigcup_^ <infty>mathbb P_n $$ (без ограничения на степени) тоже образует линейное пространство.
Пример 7. Обобщением предыдущего случая будет пространство полиномов нескольких переменных $ x_1,dots, x_ <ell>$ степени не выше $ n_<> $ с коэффициентами из $ mathbb A_<> $. Например, множество линейных полиномов $$ left< a_1x_1+dots+a_<ell>x_<ell>+b big| (a_1,dots,a_<ell>,b) in mathbb A^ <ell+1>right> $$ образует линейное пространство. Множество однородных полиномов (форм) степени $ n_<> $ (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.
Изоморфизм
Пусть имеются два линейных пространства разной природы: $ mathbb V_<> $ с операцией $ +_<> $ и $ mathbb W_<> $ с операцией $ boxplus_<> $. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.
Говорят, что пространства $ mathbb V_<> $ и $ mathbb W_<> $ изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если $ X_<> leftrightarrow X^ <prime>$ и $ Y_<> leftrightarrow Y^ <prime>$ то $ X+Y leftrightarrow X_<>^ <prime>boxplus Y^ <prime>$ и $ lambda X_<> leftrightarrow lambda X^ <prime>$.
При изоморфизме пространств $ mathbb V_<> $ и $ mathbb W_<> $ нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.
Пример. Пространство $ mathbb R^_<> $ изоморфно пространству $ mathbb P_^<> $. В самом деле, изоморфизм устанавливается соответствием $$ [a_1,dots,a_n] leftrightarrow a_1+a_2x+dots + a_nx^ .$$
Пример. Пространство $ mathbb R^ $ вещественных матриц порядка $ m_<>times n $ изоморфно пространству $ mathbb R_<>^ $. Изоморфизм устанавливается с помощью операции векторизации матрицы (матрица «вытягивается» в один столбец).
Пример. Пространство квадратичных форм от $ n_<> $ переменных изоморфно пространству симметричных матриц $ n_<> $-го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая $ n=3_<> $:
$$ a_<11>x_1^2+a_<12>x_1x_2+a_<13>x_1x_3+a_<22>x_2^2+a_<23>x_2x_3+a_<33>x_3^2 leftrightarrow left( begin a_ <11>& frac<1><2>a_ <12>& frac<1><2>a_ <13>\ frac<1><2>a_ <12>& a_ <22>& frac<1><2>a_ <23>\ frac<1><2>a_ <13>& frac<1><2>a_ <23>& a_ <33>end right) . $$
Линейная зависимость, базис, координаты
Линейной комбинацией системы векторов $ \> $ называется произвольный вектор $$ alpha_1 X_1+dots+ alpha_m X_m $$ при каких-то фиксированных значениях скаляров $ alpha_<1>, dots, alpha_ $.
Множество всевозможных линейных комбинаций системы векторов $ \> $ $$ left< alpha_1 X_1+dots+ alpha_m X_m bigg| <alpha_1,dots,alpha_m>subset mathbb R right> $$ называется линейной оболочкой векторов $ X_1,dots,X_ $ и обозначается $ <mathcal L>(X_1,dots,X_) $.
Теорема 1. Линейная оболочка векторов $ X_1,dots,X_ $ образует линейное подпространство пространства $ mathbb V_<> $.
Пример. В пространстве $ mathbb P_ $ полиномов степеней $ le n_<> ge 3 $ линейной оболочкой полиномов $ x,x^2,x^3 $ будет множество полиномов вида $ a_0x^3+a_1x^2+a_2x $, т.е. множество полиномов степеней $ le 3 $, имеющих корень $ lambda_<>=0 $. ♦
Система векторов $ < X_<1>,dots,X_m > $ называется линейно зависимой (л.з.) если существуют числа $ alpha_<1>,dots,alpha_m $, такие что хотя бы одно из них отлично от нуля и $$ alpha_1X_1+dots+alpha_mX_m=mathbb O $$ Если же это равенство возможно только при $ alpha_<1>=0,dots,alpha_m=0 $, то система векторов называется линейно независимой (л.н.з.).
Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)
$$ f_1=(x_1+x_2+x_3)^2,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$ являются линейно зависимыми, поскольку $$ f_1-2,f_2-f_3 equiv 0 . $$ Полиномы $$ tilde f_1=x_1+x_2+x_3,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$ не являются линейно зависимыми, но являются функционально зависимыми, поскольку $$ tilde f_1^2-2,f_2-f_3 equiv 0 . $$ ♦
Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.
б) Если система л.н.з., то и любая ее подсистема л.н.з.
в) При $ m>1 $ система $ ,dots,X_m> $ л.з. тогда и только тогда, когда по меньшей мере один ее вектор линейно выражается через остальные, т.е. существуют $ jin <1,dots,n >$ и константы $ gamma_<1>,dots,gamma_, gamma_,dots,gamma_ $ такие, что $$ X_j=gamma_1X_1+dots+gamma_X_+ gamma_X_+dots + gamma_X_ .$$
Теорема 3. Если каждый из векторов системы $ < X_1,dots,X_> $ линейно выражается через векторы другой системы $ < B_<1>,dots,B_k > $ с меньшим числом векторов: $ k ☞ ЗДЕСЬ.
Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.
Теорема 4. Системы векторов
$$ < X_1,dots,X_> quad mbox < и >quad < Y_<1>,dots,Y_k > $$ будут эквивалентными тогда и только тогда когда совпадают линейные оболочки этих систем: $$<mathcal L>(X_1,dots,X_m)=<mathcal L>(Y_1,dots,Y_k) . $$
Теорема 5. Если каждая из двух эквивалентных систем
$$ < X_1,dots,X_> quad mbox < и >quad < Y_<1>,dots,Y_k > $$ является л.н.з., то эти системы состоят из одинакового числа векторов: $ m=k_<> $ .
Линейно независимая система векторов $ \>subset mathbb V $ называется базисом этого пространства если каждый $ Xin mathbb V $ можно представить в виде линейной комбинации указанных векторов: $$ X=sum_ alpha_j X_j . $$
При этом не подразумевается конечность системы, т.е. суммирование может распространяться на бесконечное число слагаемых. Так, например, пространство бесконечных строк (или последовательностей) $ left[a_<1>,a_2,dots, right] $ имеет бесконечный базис, состоящий из векторов $$ [underbrace<0,dots,0,1>_j,0,dots , ] quad npu j in mathbb N . $$
В случае, когда базис пространства $ mathbb V_<> $ конечен, пространство $ mathbb V_<> $ называется конечномерным, а число векторов базиса тогда называется размерностью пространства $ mathbb V_<> $ и обозначается 5) : $ dim mathbb V_<> $. Также полагают, что размерность тривиального пространства, состоящего из одного только нулевого вектора, равна нулю: $ dim <mathbb O_<>>= 0 $.
Пример. Линейное пространство $ mtimes n_<> $ матриц имеет размерность $ mn_<> $. Так, для случая $ m_<>=3 ,n=2 $ в качестве базиса можно выбрать следующий набор матриц
$$ left( begin 1 & 0 \ 0 & 0 \ 0 & 0 end right) , left( begin 0 & 1 \ 0 & 0 \ 0 & 0 end right) , left( begin 0 & 0 \ 1 & 0 \ 0 & 0 end right) , left( begin 0 & 0 \ 0 & 1 \ 0 & 0 end right) , left( begin 0 & 0 \ 0 & 0 \ 1 & 0 end right) , left( begin 0 & 0 \ 0 & 0 \ 0 & 1 end right) . $$ ♦
Найти размерности подпространства симметричных и подпространства кососимметричных матриц порядка $ n_<> $.
Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением
под умножением цвета на положительное число $ k_<> $ — увеличение в $ k_<> $ раз яркости цвета
Анимация ☞ ЗДЕСЬ (1500 K, gif)
под умножением на $ (-1) $ — взятие дополнительного цвета. При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения.) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения. ♦
Если $ dim mathbb V=d_<> $ и вектора $ X_1,dots,X_ $ являются базисными для $ mathbb V_<> $, то разложение вектора $ X in mathbb V_<> $ в сумму: $$ X=alpha_1 X_1+dots+ alpha_d X_d .$$ называется разложением вектора $ X_<> $ по базису $ X_1,dots,X_ $; при этом числа $ alpha_1,dots, alpha_ $ называются координатами вектора $ X_<> $ в данном базисе.
Теорема 6. Если $ dim mathbb V=d>0 $, то любая система из $ d_<> $ линейно независимых векторов пространства образует базис этого пространства.
Доказательство. Пусть $ $ — л.н.з. система. Рассмотрим произвольный $ Xin mathbb V_<> $. Если система $ $ л.н.з., то $ dim mathbb V ge d+1 $, что противоречит условию теоремы. Следовательно, система линейно зависима: $ alpha_0X+alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то из чисел $ <alpha_j>_^ $ не равном нулю. Если $ alpha_0=0 $, то $ alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то ненулевом коэффициенте. Это означает, что система $ $ линейно зависима, что противоречит предположению. Следовательно $ alpha_0ne 0 $, но тогда вектор $ X_<> $ может быть представлен в виде линейной комбинации векторов $ Y_1,dots,Y_d $: $$X=- <alpha_1>/ <alpha_0>Y_1-dots -<alpha_d>/<alpha_0>Y_d .$$ По определению, система $ $ является базисом $ mathbb V $. ♦
Теорема 7. Любой вектор $ X in mathbb V_<> $ может быть разложен по фиксированному базису пространства единственным образом.
Очевидно, $ dim mathbb R^ = n $: строки из $ n_<> $ элементов $$[1,0,0,dots,0], [0,1,0,dots,0], [0,0,1,dots,0], dots , [0,0,0,dots,1] $$ образуют базис этого пространства.
Имеются два способа задания линейных подпространств в $ mathbb R^_<> $. Пусть $$ mathbb V_1 = <mathcal L>(A_1,dots,A_k) quad npu subset mathbb R^n .$$ В разделе ☞ РАНГ установлено, что $$ dim mathbb V_1 = operatorname < A_1,dots,A_k >= operatorname (A) ,$$ где $ A_<> $ — матрица, составленная из строк (столбцов) $ A_<1>,dots,A_k $.
Пример. Найти базис подпространства
Решение. Ищем $$ operatorname left( begin 1 & 2 & 1 & 1 \ -1&0&-1&0 \ -1& 2 &-1 &1 \ 0& 1& 0 & 1 end right) $$ по методу окаймляющих миноров. Существует минор третьего порядка $$ left| begin 1 & 2 & 1 \ -1&0&0 \ 0& 1 & 1 end right| $$ отличный от нуля, а определитель самой матрицы равен нулю. Замечаем, что найденный отличный от нуля минор расположен в первой, второй и четвертой строках матрицы. Именно эти строки и образуют базис.
Ответ. Базис составляют, например, первая, вторая и четвертая строки.
Другим способом задания линейного подпространства в $ mathbb R^ $ может служить задание набора ограничений, которым должны удовлетворять векторы подпространства. Таким набором ограничений может являться, например, система уравнений $$ left<begin a_<11>x_1 +a_<12>x_2+ldots+a_<1n>x_n &=&0,\ a_<21>x_1 +a_<22>x_2+ldots+a_<2n>x_n &=&0,\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&0 endright. qquad iff qquad AX=mathbb O . $$ Какова размерность подпространства решений этой системы? На этот вопрос мы ответим сразу же, если вспомним определение фундаментальной системы решений (ФСР). Именно, ФСР — как набор линейно независимых решений, через которые линейно выражается любое решение системы однородных уравнений — является базисом подпространства этих решений.
Теорема 8. Множество решений системы однородных уравнений $ AX=mathbb O_<> $ образует линейное подпространство пространства $ mathbb R^ $. Размерность этого подпространства равна $ n-operatorname (A) $, а фундаментальная система решений образует его базис.
Пример. В пространстве $ mathbb P_ $ полиномов степеней $ le n_<> $ каноническим базисом можно взять систему мономов $ <1,x,x^2,dots, x^n >$, т.е. $ dim mathbb P_ =n+1 $. Координатами полинома
$$ f(x)=a_0+a_1x+a_2x^2+dots+a_nx^n $$ будут его коэффициенты. Можно выбрать и другой базис, например, $ <1, x-c,(x-c)^2,dots,(x-c)^n >$ при произвольном числе $ c_<> $. Координатами полинома в этом базисе будут теперь коэффициенты формулы Тейлора: $$ f(x) equiv f(c)+ frac(c)> <1!>(x-c) + frac(c)> <2!>(x-c)^2+ dots + frac(c)> (x-c)^ . $$
Найти координаты полинома
Теорема 9. Любое векторное пространство $ mathbb V_<> $ размерности $ d_<> $ изоморфно $ mathbb R^ $.
Доказательство. Изоморфизм можно установить следующим соответствием. Если $ $ — какой-то базис $ mathbb V_<> $, то вектору $ X in mathbb V $ поставим в соответствие набор его координат в этом базисе: $$ X=x_1X_1+dots+x_d X_d Rightarrow X mapsto [x_1,dots,x_d]in mathbb R^d . $$ На основании теоремы $ 6 $, такое соответствие будет взаимно-однозначным, а проверка двух свойств изоморфизма тривиальна. ♦
Критерии линейной зависимости
Теорема . Строки
$$ <(a_<11>,dots,a_<1n>),dots, (a_,dots,a_)> subset mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ left|begin a_<11>&dots & a_ <1n>\ dots & & dots \ a_& dots & a_ end right|=0 , . $$
Теорема . Строки
$$ <(a_<11>,dots,a_<1n>),dots, (a_,dots,a_)> subset mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ operatorname A
$$ <(a_<11>,dots,a_<1n>),dots, (a_,dots,a_)> subset mathbb R^n $$ линейно зависимы тогда и только тогда, когда $$ det (A^ <top>A) = 0 , . $$ (Определитель в левой части можно интерпретировать как определитель Грама системы строк.)
Теорема . Аналитические на интервале $ ]a,b[ $ функции $ u_1(x),dots,u_n(x) $ линейно зависимы на $ ]a,b[ $ тогда и только тогда, когда их вронскиан
Относительный базис
В настоящем пункте $ mathbb V_1 $ обозначает линейное подпространство пространства $ mathbb V_<> $, отличное от тривиального; обозначаем $ d_1=dim mathbb V_1 $.
Теорема. Произвольный базис подпространства $ mathbb V_1 $ можно дополнить до базиса пространства $ mathbb V_<> $.
Доказательство. Пусть $ > $ — какой-то базис $ mathbb V_1 $. В пространстве $ mathbb V_<> $ найдется вектор $ X_ $ такой, что система $ , X_> $ будет л.н.з. (В противном случае, $ dim mathbb V=d_1 $, что противоречит условию настоящего пункта.) Если $ d_1+1=d = dim mathbb V $, то, на основании теоремы 5 предыдущего пункта, требуемый базис построен. Если же $ d_1+1 ♦
Говорят, что система векторов $ $ линейно независима относительно подпространства $ mathbb V_1 $ пространства $ mathbb V_<> $ если $$<.>_<> mbox < из условия >quad alpha_1X_1+dots+alpha_k X_k in mathbb V_1 quad mbox < следует >quad alpha_1=dots=alpha_k=0 .$$
Теорема. Обозначим $ \> $ — произвольный базис $ mathbb V_1 $. Система $ ,dots,X_k> $ л.н.з. относительно $ mathbb V_1 $ тогда и только тогда, когда система $ ,X_1,dots,X_k> $ линейно независима.
Пример. Найти все значения параметра $ <coloralpha > $, при которых система
Решение. Базисом подпространства $ mathbb V_1 $ является произвольная ФСР заданной системы однородных уравнений, например $ >, Y_2=[6,-5,0,1]^<^<top>>> $. Теорема утверждает, что система $ < X_1, X_2>$ л.н.з. относительно $ mathbb V_1 $ тогда и только тогда, когда система $ < X_1, X_2,Y_1,Y_2>$ л.н.з. (в обычном понимании). Последнее равносильно тому, что матрица, составленная из этих векторов, должна иметь ранг равный $ 4_<> $. $$operatorname left( begin 1 & 1 &-1 & 6 \ 2 & <coloralpha > & 2 & -5 \ <coloralpha > & 2 & 1 & 0 \ 1 & 1 & 0 & 1 end right)=4 iff left| begin 1 & 1 &-1 & 6 \ 2 & <coloralpha > & 2 & -5 \ <coloralpha > & 2 & 1 & 0 \ 1 & 1 & 0 & 1 end right|= <coloralpha >^2-10, <coloralpha > +16 ne 0 . $$
Ответ. $ <coloralpha >not in < 2,, 8>$.
Говорят, что система векторов $ $ образует базис пространства $ mathbb V_<> $ относительно (или над) $ mathbb V_1 $ если она л.н.з. относительно $ mathbb V_1 $ и любой вектор $ Xin mathbb V_<> $ можно представить в виде $$ X=c_1X_1+dots+c_kX_k+Y, quad mbox < где >quad Yin mathbb V_1 . $$
Теорема. Обозначим $ < Y_1,dots,Y_> $ — произвольный базис подпространства $ mathbb V_1 $. Система $ $ образует базис $ mathbb V_<> $ относительно $ mathbb V_1 $ тогда и только тогда, когда система $ < X_1,dots,X_k,Y_1,dots,Y_> $ образует базис $ mathbb V_<> $.
Доказательство. Действительно, любой вектор $ Xin mathbb V_<> $ выражается через векторы $ X_1,dots,X_k,Y_1,dots,Y_ $. По предыдущей теореме для линейной независимости этих векторов необходимо и достаточно относительной линейной независимости $ X_1,dots,X_k $. ♦
Базис $ mathbb V_<> $ строится дополнением базиса $ mathbb V_1 $ векторами $ X_1,dots,X_k $ линейно независимыми относительно $ mathbb V_1 $. Поэтому $$<.>_<> mbox <число векторов относительного базиса > = dim mathbb V – dim mathbb V_1 .$$
Это число называется коразмерностью 6) подпространства $ mathbb V_1 $ в пространстве $ mathbb V $.
Сумма и пересечение линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_<> $. Множество $$ mathbb V_1+ mathbb V_2 = left$$ называется суммой, а множество $$ mathbb V_1 cap mathbb V_2 = left$$ — пересечением подпространств $ mathbb V_1 $ и $ mathbb V_2 $. Аналогично определяется сумма и пересечение произвольного количества подпространств.
Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.
Теорема. $ mathbb V_1+ mathbb V_2 $ и $ mathbb V_1 cap mathbb V_2 $ являются подпространствами линейного пространства $ mathbb V_<> $.
Докажите, что $ mathbb V_1+ mathbb V_2 $ — это подпространство минимальной размерности, содержащее как $ mathbb V_1 $, так и $ mathbb V_2 $.
Теорема. Имеет место формула:
$$ dim , mathbb V_1 + dim , mathbb V_2=dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 + mathbb V_2) . $$
Доказательство ☞ ЗДЕСЬ.
Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:
$$dim , mathbb V_1 + dim , mathbb V_2 + dim , mathbb V_3 – $$ $$ -left <dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 cap mathbb V_3) + dim , (mathbb V_2 cap mathbb V_3) right>+ $$ $$+ dim , (mathbb V_1 cap mathbb V_2 cap mathbb V_3) =dim , (mathbb V_1 + mathbb V_2 + mathbb V_3) ?$$
Теорема. Имеет место формула:
Пример. Найти базис суммы и размерность пересечения
$$mathbb V_1=<mathcal L>left( left[ begin 0 \1 \ 1 \ 1 end right] , left[ begin 1 \1 \ 1 \ 2 end right] , left[ begin -2 \0 \ 1 \ 1 end right] right) quad mbox < и >quad mathbb V_2=<mathcal L>left( left[ begin -1 \3 \ 2 \ -1 end right] , left[ begin 1 \1 \ 0 \ -1 end right] right) $$
Решение. Действуя согласно предыдущей теореме, составляем матрицу из всех векторов $$ left( begin 0 & 1 & -2 & -1 & 1 \ 1 & 1 & 0 & 3 & 1 \ 1 & 1 & 1 & 2 & 0 \ 1 & 2 & 1 & -1 & -1 end right) $$ и ищем ее ранг методом окаймляющих миноров. Имеем: $ operatorname = 3 $ при ненулевом миноре матрицы расположенном в первых трех ее столбцах.
Ответ. Базис $ mathbb V_1 + mathbb V_2 $ составляют векторы $ X_1,X_2,X_3 $; $ dim , (mathbb V_1 cap mathbb V_2) = 3+2 – 3 =2 $.
Алгоритм нахождения базиса $ <mathcal L>(X_1,dots,X_m) cap <mathcal L>(Y_1,dots,Y_<ell>) $ проиллюстрируем на примере.
Пример. Найти базис $ mathbb V_1 cap mathbb V_2 $ при
$$ begin mathbb V_1= <mathcal L>left( left[ begin 1 \ -1 \ 1 \ -1 \ 1 end right],, left[ begin 1 \ 2 \ 1 \ 2 \ 1 end right],, left[ begin 0 \ 1 \ 0 \ 1 \ 0 end right] right) \ <>_<> qquad qquad quad X_1 quad quad X_2 quad quad X_3 end , begin mathbb V_2= <mathcal L>left( left[ begin 1 \ 0 \ 0 \ 0 \ 1 end right],, left[ begin 1 \ 1 \ 0 \ 1 \ 1 end right],, left[ begin 0 \ 1 \ 1 \ 1 \ 0 end right] right) \ <>_<> quad qquad qquad Y_1 qquad Y_2 quad quad Y_3 end . $$
Решение. 1. Сначала найдем базисы каждого из подпространств: $$dim mathbb V_1=2, mathbb V_1=mathcal L(X_1, X_2) ; dim mathbb V_2=3, mathbb V_2=mathcal L(Y_1, Y_2, Y_3) . $$
2. Произвольный вектор $ Zin mathbb R^5 $, принадлежащий $ mathbb V_1 cap mathbb V_2 $, должен раскладываться по базису каждого из подпространств: $$Z=alpha_1 X_1 + alpha_2 X_2= beta_1 Y_1 + beta_2 Y_2 + beta_3 Y_3 .$$ Для определения неизвестных значений координат составляем систему уравнений $$ begin qquad X_1 X_2 \ qquad <colordownarrow> <colordownarrow> \ left( begin 1 & 1 & -1 & &-1 & & 0 \ -1 & 2 & 0 & & -1 & & -1 \ 1 & 1 & 0 & & 0 & & -1 \ -1 & 2 & 0 & & -1 & & -1 \ 1 & 1 & -1 & & -1 & & 0 end right) \ qquad qquad qquad <coloruparrow> qquad <coloruparrow> qquad quad <coloruparrow> \ quad qquad qquad -Y_1 quad – Y_2 quad -Y_3 end left( begin alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3 end right)= mathbb O_ <5times 1>$$ и решаем ее по методу Гаусса с нахождением фундаментальной системы решений: $$ left( begin 1 & 1 & -1 & -1 & 0 \ 0 & 3 & -1 & -2 & -1 \ 0 & 0 & 1 & 1 & -1 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 end right) left( begin alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3 end right)= mathbb O quad Rightarrow qquad mbox < ФСР >qquad begin alpha_1 & alpha_2 & beta_1 & beta_2 & beta_3 \ hline -1/3 & 1/3 & -1 & 1 & 0 \ 1/3 & 2/3 & 1 & 0 & 1 end $$
3. Получившиеся значения координат позволяют выразить базис пересечения — либо через базис подпространства $ mathbb V_1 $ (если использовать полученные значения для $ alpha_1,alpha_2 $), либо через базис подпространства $ mathbb V_2 $ (если использовать $ beta_1,beta_2, beta_3 $). Например, $$ Z_1=-1/3 X_1 + 1/3 X_2 = [0,1,0,1,0]^<^<top>>, $$ $$ Z_2=1/3 X_1 + 2/3 X_2 = [1,1,1,1,1]^<^<top>> . $$
Найти базисы суммы и пересечения подпространств
Решение ☞ ЗДЕСЬ.
Прямая сумма линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_<> $. Говорят, что $ mathbb V_<> $ раскладывается в прямую сумму подпространств $ mathbb V_1 $ и $ mathbb V_2 $ если любой вектор $ Xin mathbb V_<> $ может быть представлен в виде $ X=X_1+X_2 $, где $ X_1in mathbb V_1,X_2in mathbb V_2 $ и такое представление единственно. Этот факт записывают: $ mathbb V= mathbb V_1 oplus mathbb V_2 $. Вектор $ X_ <1>$ называется проекцией вектора $ X_<> $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_ <2>$.
Пример. Линейное пространство квадратных матриц порядка $ n_<> $ раскладывается в прямую сумму подпространств: подпространства симметричных матриц и подпространства кососимметричных матриц. В самом деле, для матрицы $ A_ $ справедливо разложение
$$A=frac<1> <2>left(A+A^ <^top>right) + frac<1> <2>left(A-A^ <^top>right) $$ и в правой части первая скобка дает симметричную матрицу, а вторая — кососимметричную. Покажите, что не существует иного разложения матрицы $ A_<> $ в сумму симметричной и кососимметричной.
Теорема. Пусть $ mathbb V=mathbb V_1 + mathbb V_2 $. Эта сумма будет прямой тогда и только тогда, когда подпространства $ mathbb V_1 $ и $ mathbb V_2 $ имеют тривиальное пересечение:
$$mathbb V_1 cap mathbb V_2= <mathbb O > .$$
Доказательство. Необходимость. Пусть сумма $ mathbb V_1 + mathbb V_2 $ — прямая, но существует вектор $ Xne mathbb O $, принадлежащий $ mathbb V_1 cap mathbb V_2 $. Но тогда и вектор $ (-X) $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Для нулевого вектора $ mathbb O $ получаем два представления в виде суммы проекций на подпространства: $$ mathbb O = mathbb O + mathbb O = X+ (-X) , . $$ Это противоречит понятию прямой суммы.
Достаточность. Если $ mathbb V_1 cap mathbb V_2= <mathbb O >$, но существует вектор $ X in mathbb V_1 + mathbb V_2 $, имеющий два различных разложения в сумму проекций $$ X=X_1+X_2 =Y_1+ Y_2 quad npu quad subset mathbb V_1, subset mathbb V_2, $$ то $$ (X_1-Y_1)+(X_2-Y_2) =mathbb O quad Rightarrow quad X_1-Y_1=Y_2-X_2 , , $$ т.е. вектор $ X_1-Y_1 $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Но, по предположению, $ mathbb V_1 cap mathbb V_2= <mathbb O >$, следовательно, $ X_1-Y_1=mathbb O $, но тогда и $ Y_2-X_2=mathbb O $. ♦
Сумма $ mathbb V=mathbb V_1 + mathbb V_2 $ будет прямой тогда и только тогда, когда базис $ mathbb V_<> $ может быть получен объединением базисов $ mathbb V_ $.
Пример [2]. Доказать, что сумма подпространств
$$mathbb V_1=<mathcal L>left( left[ begin 2 \3 \ 11 \ 5 end right] , left[ begin 1 \1 \ 5 \ 2 end right] , left[ begin 0 \1 \ 1 \ 1 end right] right) quad mbox < и >quad mathbb V_2=<mathcal L>left( left[ begin 2 \1 \ 3 \ 2 end right] , left[ begin 1 \1 \ 3 \ 4 end right] , left[ begin 5 \2 \ 6 \ 2 end right] right) $$ будет прямой и найти проекции вектора $ Z=[2,0,0,3]^ <top>$ на эти подпространства.
Решение. Базисы $ mathbb V_1 $ и $ mathbb V_2 $ составляют соответственно системы $ $ и $ < Y_1,Y_2 >$, т.е. $ dim , mathbb V_1=dim , mathbb V_2 =2 $. На основании следствия достаточно установить, что объединенная система $ $ л.н.з. Для этого достаточно проверить, что определитель матрицы $$ A=left( begin 1 & 0 & 2 & 1 \ 1 & 1 & 1 & 1 \ 5 & 1 & 3 & 3 \ 2 & 1 & 2 & 4 end right) $$ отличен от нуля. Поскольку это условие выполнено, то сумма $ mathbb V_1 + mathbb V_2 $ — прямая и базис этой суммы состоит из взятых векторов. Для нахождения разложения вектора $ X_<> $ по этому базису решаем систему уравнений $$A left[ begin alpha_2 \ alpha_3 \ beta_1 \ beta_2 end right] = Z $$ и получаем единственное решение: $ alpha_2=-1,, alpha_3=-1,, beta_1 =1, , beta_2=1 $. Разложение $ Z=Z_1+Z_2 $ составляют векторы $ Z_1=alpha_2 X_2+alpha_3 X_3 $ и $ Z_2=beta_1 Y_1+beta_2 Y_2 $.
Линейные многообразия
Пусть $ mathbb V_1 $ — линейное подпространство пространства $ mathbb V_<> $, а $ X_ <0>$ — произвольный фиксированный вектор из $ mathbb V_<> $. Множество $$ mathbb M = X_0+ mathbb V_1 = left $$ называется линейным многообразием (порожденным подпространством $ mathbb V_1 $). Размерностью этого многообразия называется размерность порождающего его подпространства: $ dim mathbb M = dim mathbb V_1 $. В случае $ 1 ☞ ОБЩЕЕ РЕШЕНИЕ: если система совместна, то ее общее решение можно представить как сумму какого-то одного ее решения и общего решения соответствующей однородной системы $ AX= mathbb O $. Таким образом, многообразие решений неоднородной системы $ AX= <mathcal B>$ допускает «параметрическое представление»: $$mathbb M=X_0+ <mathcal L>(X_1,dots,X_>)= $$ $$=left> X_> mid (t_1,dots, t_>) in mathbb R^> right> ; $$ здесь $ X_ <0>$ означает частное решение системы (т.е. $ AX_0= <mathcal B>$),
$ >> $ — ФСР для системы $ AX= mathbb O $,
а $ mathfrak r= operatorname A= operatorname [Amid mathcal B] $.
Получаем, следовательно, $ (n-<mathfrak r>) $-мерную плоскость в $ mathbb R^n $, a в случае $ (n-<mathfrak r>)=1 $ — прямую $$mathbb M=X_0+tX_1 quad npu t in mathbb R ; $$ в последнем случае вектор $ X_ <1>$ называют направляющим вектором этой прямой.
Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.
[spoiler title=”источники:”]
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-uchebnoe-posobie-z-i-andreeva/23-zadanie-podprostranstv-konechnomernogo-lineinogo-prostranstva-s-pomoshchiu-sistem-lineinykh-uravnenii
http://vmath.ru/vf5/linear_space
[/spoiler]
In mathematics, and more specifically in linear algebra, a linear subspace or vector subspace[1][note 1] is a vector space that is a subset of some larger vector space. A linear subspace is usually simply called a subspace when the context serves to distinguish it from other types of subspaces.
Definition[edit]
If V is a vector space over a field K and if W is a subset of V, then W is a linear subspace of V if under the operations of V, W is a vector space over K. Equivalently, a nonempty subset W is a subspace of V if, whenever w1, w2 are elements of W and α, β are elements of K, it follows that αw1 + βw2 is in W.[2][3][4][5][6]
As a corollary, all vector spaces are equipped with at least two (possibly different) linear subspaces: the zero vector space consisting of the zero vector alone and the entire vector space itself. These are called the trivial subspaces of the vector space.[7]
Examples[edit]
Example I[edit]
In the vector space V = R3 (the real coordinate space over the field R of real numbers), take W to be the set of all vectors in V whose last component is 0.
Then W is a subspace of V.
Proof:
- Given u and v in W, then they can be expressed as u = (u1, u2, 0) and v = (v1, v2, 0). Then u + v = (u1+v1, u2+v2, 0+0) = (u1+v1, u2+v2, 0). Thus, u + v is an element of W, too.
- Given u in W and a scalar c in R, if u = (u1, u2, 0) again, then cu = (cu1, cu2, c0) = (cu1, cu2,0). Thus, cu is an element of W too.
Example II[edit]
Let the field be R again, but now let the vector space V be the Cartesian plane R2.
Take W to be the set of points (x, y) of R2 such that x = y.
Then W is a subspace of R2.
Proof:
- Let p = (p1, p2) and q = (q1, q2) be elements of W, that is, points in the plane such that p1 = p2 and q1 = q2. Then p + q = (p1+q1, p2+q2); since p1 = p2 and q1 = q2, then p1 + q1 = p2 + q2, so p + q is an element of W.
- Let p = (p1, p2) be an element of W, that is, a point in the plane such that p1 = p2, and let c be a scalar in R. Then cp = (cp1, cp2); since p1 = p2, then cp1 = cp2, so cp is an element of W.
In general, any subset of the real coordinate space Rn that is defined by a system of homogeneous linear equations will yield a subspace.
(The equation in example I was z = 0, and the equation in example II was x = y.)
Example III[edit]
Again take the field to be R, but now let the vector space V be the set RR of all functions from R to R.
Let C(R) be the subset consisting of continuous functions.
Then C(R) is a subspace of RR.
Proof:
- We know from calculus that 0 ∈ C(R) ⊂ RR.
- We know from calculus that the sum of continuous functions is continuous.
- Again, we know from calculus that the product of a continuous function and a number is continuous.
Example IV[edit]
Keep the same field and vector space as before, but now consider the set Diff(R) of all differentiable functions.
The same sort of argument as before shows that this is a subspace too.
Examples that extend these themes are common in functional analysis.
Properties of subspaces[edit]
From the definition of vector spaces, it follows that subspaces are nonempty, and are closed under sums and under scalar multiples.[8] Equivalently, subspaces can be characterized by the property of being closed under linear combinations. That is, a nonempty set W is a subspace if and only if every linear combination of finitely many elements of W also belongs to W.
The equivalent definition states that it is also equivalent to consider linear combinations of two elements at a time.
In a topological vector space X, a subspace W need not be topologically closed, but a finite-dimensional subspace is always closed.[9] The same is true for subspaces of finite codimension (i.e., subspaces determined by a finite number of continuous linear functionals).
Descriptions[edit]
Descriptions of subspaces include the solution set to a homogeneous system of linear equations, the subset of Euclidean space described by a system of homogeneous linear parametric equations, the span of a collection of vectors, and the null space, column space, and row space of a matrix. Geometrically (especially over the field of real numbers and its subfields), a subspace is a flat in an n-space that passes through the origin.
A natural description of a 1-subspace is the scalar multiplication of one non-zero vector v to all possible scalar values. 1-subspaces specified by two vectors are equal if and only if one vector can be obtained from another with scalar multiplication:
This idea is generalized for higher dimensions with linear span, but criteria for equality of k-spaces specified by sets of k vectors are not so simple.
A dual description is provided with linear functionals (usually implemented as linear equations). One non-zero linear functional F specifies its kernel subspace F = 0 of codimension 1. Subspaces of codimension 1 specified by two linear functionals are equal, if and only if one functional can be obtained from another with scalar multiplication (in the dual space):
It is generalized for higher codimensions with a system of equations. The following two subsections will present this latter description in details, and the remaining four subsections further describe the idea of linear span.
Systems of linear equations[edit]
The solution set to any homogeneous system of linear equations with n variables is a subspace in the coordinate space Kn:
For example, the set of all vectors (x, y, z) (over real or rational numbers) satisfying the equations
is a one-dimensional subspace. More generally, that is to say that given a set of n independent functions, the dimension of the subspace in Kk will be the dimension of the null set of A, the composite matrix of the n functions.
Null space of a matrix[edit]
In a finite-dimensional space, a homogeneous system of linear equations can be written as a single matrix equation:
The set of solutions to this equation is known as the null space of the matrix. For example, the subspace described above is the null space of the matrix
Every subspace of Kn can be described as the null space of some matrix (see § Algorithms below for more).
Linear parametric equations[edit]
The subset of Kn described by a system of homogeneous linear parametric equations is a subspace:
For example, the set of all vectors (x, y, z) parameterized by the equations
is a two-dimensional subspace of K3, if K is a number field (such as real or rational numbers).[note 2]
Span of vectors[edit]
In linear algebra, the system of parametric equations can be written as a single vector equation:
The expression on the right is called a linear combination of the vectors
(2, 5, −1) and (3, −4, 2). These two vectors are said to span the resulting subspace.
In general, a linear combination of vectors v1, v2, … , vk is any vector of the form
The set of all possible linear combinations is called the span:
If the vectors v1, … , vk have n components, then their span is a subspace of Kn. Geometrically, the span is the flat through the origin in n-dimensional space determined by the points v1, … , vk.
- Example
- The xz-plane in R3 can be parameterized by the equations
- As a subspace, the xz-plane is spanned by the vectors (1, 0, 0) and (0, 0, 1). Every vector in the xz-plane can be written as a linear combination of these two:
- Geometrically, this corresponds to the fact that every point on the xz-plane can be reached from the origin by first moving some distance in the direction of (1, 0, 0) and then moving some distance in the direction of (0, 0, 1).
Column space and row space[edit]
A system of linear parametric equations in a finite-dimensional space can also be written as a single matrix equation:
In this case, the subspace consists of all possible values of the vector x. In linear algebra, this subspace is known as the column space (or image) of the matrix A. It is precisely the subspace of Kn spanned by the column vectors of A.
The row space of a matrix is the subspace spanned by its row vectors. The row space is interesting because it is the orthogonal complement of the null space (see below).
Independence, basis, and dimension[edit]
The vectors u and v are a basis for this two-dimensional subspace of R3.
In general, a subspace of Kn determined by k parameters (or spanned by k vectors) has dimension k. However, there are exceptions to this rule. For example, the subspace of K3 spanned by the three vectors (1, 0, 0), (0, 0, 1), and (2, 0, 3) is just the xz-plane, with each point on the plane described by infinitely many different values of t1, t2, t3.
In general, vectors v1, … , vk are called linearly independent if
for
(t1, t2, … , tk) ≠ (u1, u2, … , uk).[note 3]
If v1, …, vk are linearly independent, then the coordinates t1, …, tk for a vector in the span are uniquely determined.
A basis for a subspace S is a set of linearly independent vectors whose span is S. The number of elements in a basis is always equal to the geometric dimension of the subspace. Any spanning set for a subspace can be changed into a basis by removing redundant vectors (see § Algorithms below for more).
- Example
- Let S be the subspace of R4 defined by the equations
- Then the vectors (2, 1, 0, 0) and (0, 0, 5, 1) are a basis for S. In particular, every vector that satisfies the above equations can be written uniquely as a linear combination of the two basis vectors:
- The subspace S is two-dimensional. Geometrically, it is the plane in R4 passing through the points (0, 0, 0, 0), (2, 1, 0, 0), and (0, 0, 5, 1).
Operations and relations on subspaces[edit]
Inclusion[edit]
The set-theoretical inclusion binary relation specifies a partial order on the set of all subspaces (of any dimension).
A subspace cannot lie in any subspace of lesser dimension. If dim U = k, a finite number, and U ⊂ W, then dim W = k if and only if U = W.
Intersection[edit]
In R3, the intersection of two distinct two-dimensional subspaces is one-dimensional
Given subspaces U and W of a vector space V, then their intersection U ∩ W := {v ∈ V : v is an element of both U and W} is also a subspace of V.[10]
Proof:
- Let v and w be elements of U ∩ W. Then v and w belong to both U and W. Because U is a subspace, then v + w belongs to U. Similarly, since W is a subspace, then v + w belongs to W. Thus, v + w belongs to U ∩ W.
- Let v belong to U ∩ W, and let c be a scalar. Then v belongs to both U and W. Since U and W are subspaces, cv belongs to both U and W.
- Since U and W are vector spaces, then 0 belongs to both sets. Thus, 0 belongs to U ∩ W.
For every vector space V, the set {0} and V itself are subspaces of V.[11][12]
Sum[edit]
If U and W are subspaces, their sum is the subspace[13][14]
For example, the sum of two lines is the plane that contains them both. The dimension of the sum satisfies the inequality
Here, the minimum only occurs if one subspace is contained in the other, while the maximum is the most general case. The dimension of the intersection and the sum are related by the following equation:[15]
A set of subspaces is independent when the only intersection between any pair of subspaces is the trivial subspace. The direct sum is the sum of independent subspaces, written as 
The dimension of a direct sum 
Lattice of subspaces[edit]
The operations intersection and sum make the set of all subspaces a bounded modular lattice, where the {0} subspace, the least element, is an identity element of the sum operation, and the identical subspace V, the greatest element, is an identity element of the intersection operation.
Orthogonal complements[edit]
If 















This operation, understood as negation (
In spaces with other bilinear forms, some but not all of these results still hold. In pseudo-Euclidean spaces and symplectic vector spaces, for example, orthogonal complements exist. However, these spaces may have null vectors that are orthogonal to themselves, and consequently there exist subspaces 

Algorithms[edit]
Most algorithms for dealing with subspaces involve row reduction. This is the process of applying elementary row operations to a matrix, until it reaches either row echelon form or reduced row echelon form. Row reduction has the following important properties:
- The reduced matrix has the same null space as the original.
- Row reduction does not change the span of the row vectors, i.e. the reduced matrix has the same row space as the original.
- Row reduction does not affect the linear dependence of the column vectors.
Basis for a row space[edit]
- Input An m × n matrix A.
- Output A basis for the row space of A.
- Use elementary row operations to put A into row echelon form.
- The nonzero rows of the echelon form are a basis for the row space of A.
See the article on row space for an example.
If we instead put the matrix A into reduced row echelon form, then the resulting basis for the row space is uniquely determined. This provides an algorithm for checking whether two row spaces are equal and, by extension, whether two subspaces of Kn are equal.
Subspace membership[edit]
- Input A basis {b1, b2, …, bk} for a subspace S of Kn, and a vector v with n components.
- Output Determines whether v is an element of S
- Create a (k + 1) × n matrix A whose rows are the vectors b1, … , bk and v.
- Use elementary row operations to put A into row echelon form.
- If the echelon form has a row of zeroes, then the vectors {b1, …, bk, v} are linearly dependent, and therefore v ∈ S.
Basis for a column space[edit]
- Input An m × n matrix A
- Output A basis for the column space of A
- Use elementary row operations to put A into row echelon form.
- Determine which columns of the echelon form have pivots. The corresponding columns of the original matrix are a basis for the column space.
See the article on column space for an example.
This produces a basis for the column space that is a subset of the original column vectors. It works because the columns with pivots are a basis for the column space of the echelon form, and row reduction does not change the linear dependence relationships between the columns.
Coordinates for a vector[edit]
- Input A basis {b1, b2, …, bk} for a subspace S of Kn, and a vector v ∈ S
- Output Numbers t1, t2, …, tk such that v = t1b1 + ··· + tkbk
- Create an augmented matrix A whose columns are b1,…,bk , with the last column being v.
- Use elementary row operations to put A into reduced row echelon form.
- Express the final column of the reduced echelon form as a linear combination of the first k columns. The coefficients used are the desired numbers t1, t2, …, tk. (These should be precisely the first k entries in the final column of the reduced echelon form.)
If the final column of the reduced row echelon form contains a pivot, then the input vector v does not lie in S.
Basis for a null space[edit]
- Input An m × n matrix A.
- Output A basis for the null space of A
- Use elementary row operations to put A in reduced row echelon form.
- Using the reduced row echelon form, determine which of the variables x1, x2, …, xn are free. Write equations for the dependent variables in terms of the free variables.
- For each free variable xi, choose a vector in the null space for which xi = 1 and the remaining free variables are zero. The resulting collection of vectors is a basis for the null space of A.
See the article on null space for an example.
Basis for the sum and intersection of two subspaces[edit]
Given two subspaces U and W of V, a basis of the sum 

Equations for a subspace[edit]
- Input A basis {b1, b2, …, bk} for a subspace S of Kn
- Output An (n − k) × n matrix whose null space is S.
- Create a matrix A whose rows are b1, b2, …, bk.
- Use elementary row operations to put A into reduced row echelon form.
- Let c1, c2, …, cn be the columns of the reduced row echelon form. For each column without a pivot, write an equation expressing the column as a linear combination of the columns with pivots.
- This results in a homogeneous system of n − k linear equations involving the variables c1,…,cn. The (n − k) × n matrix corresponding to this system is the desired matrix with nullspace S.
- Example
- If the reduced row echelon form of A is
- then the column vectors c1, …, c6 satisfy the equations
- It follows that the row vectors of A satisfy the equations
- In particular, the row vectors of A are a basis for the null space of the corresponding matrix.
See also[edit]
- Cyclic subspace
- Invariant subspace
- Multilinear subspace learning
- Quotient space (linear algebra)
- Signal subspace
- Subspace topology
Notes[edit]
- ^ The term linear subspace is sometimes used for referring to flats and affine subspaces. In the case of vector spaces over the reals, linear subspaces, flats, and affine subspaces are also called linear manifolds for emphasizing that there are also manifolds.
- ^ Generally, K can be any field of such characteristic that the given integer matrix has the appropriate rank in it. All fields include integers, but some integers may equal to zero in some fields.
- ^ This definition is often stated differently: vectors v1, …, vk are linearly independent if
t1v1 + ··· + tkvk ≠ 0 for (t1, t2, …, tk) ≠ (0, 0, …, 0). The two definitions are equivalent.
Citations[edit]
- ^ Halmos (1974) pp. 16-17, § 10
- ^ Anton (2005, p. 155)
- ^ Beauregard & Fraleigh (1973, p. 176)
- ^ Herstein (1964, p. 132)
- ^ Kreyszig (1972, p. 200)
- ^ Nering (1970, p. 20)
- ^ Hefferon (2020) p. 100, ch. 2, Definition 2.13
- ^ MathWorld (2021) Subspace.
- ^ DuChateau (2002) Basic facts about Hilbert Space — class notes from Colorado State University on Partial Differential Equations (M645).
- ^ Nering (1970, p. 21)
- ^ Hefferon (2020) p. 100, ch. 2, Definition 2.13
- ^ Nering (1970, p. 20)
- ^ Nering (1970, p. 21)
- ^ Vector space related operators.
- ^ Nering (1970, p. 22)
- ^ Hefferon (2020) p. 148, ch. 2, §4.10
- ^ Axler (2015) p. 21 § 1.40
- ^ Katznelson & Katznelson (2008) pp. 10-11, § 1.2.5
- ^ Halmos (1974) pp. 28-29, § 18
- ^ Halmos (1974) pp. 30-31, § 19
- ^ Axler (2015) p. 193, § 6.46
- ^ Axler (2015) p. 195, § 6.50
- ^ Axler (2015) p. 194, § 6.47
- ^ Axler (2015) p. 195, § 6.51
Sources[edit]
Textbook[edit]
- Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
- Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
- Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces (2nd ed.). Springer. ISBN 0-387-90093-4.
- Hefferon, Jim (2020). Linear Algebra (4th ed.). Orthogonal Publishing. ISBN 978-1-944325-11-4.
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
- Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8
- Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
- Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
- Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archived from the original on March 1, 2001
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
- Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
Web[edit]
- Weisstein, Eric Wolfgang. “Subspace”. MathWorld. Retrieved 16 Feb 2021.
{{cite web}}: CS1 maint: url-status (link) - DuChateau, Paul (5 Sep 2002). “Basic facts about Hilbert Space” (PDF). Colorado State University. Retrieved 17 Feb 2021.
{{cite web}}: CS1 maint: url-status (link)
External links[edit]
- Strang, Gilbert (7 May 2009). “The four fundamental subspaces”. Archived from the original on 2021-12-11. Retrieved 17 Feb 2021 – via YouTube.
- Strang, Gilbert (5 May 2020). “The big picture of linear algebra”. Archived from the original on 2021-12-11. Retrieved 17 Feb 2021 – via YouTube.
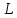

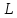
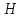 принадлежит
принадлежит :
: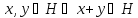 ;
;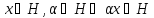


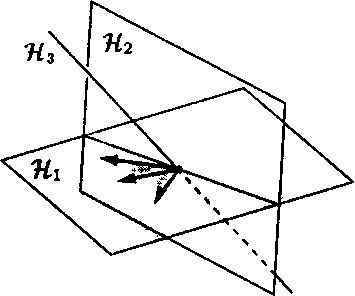

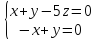
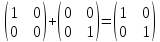


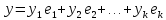


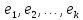








![{displaystyle left{left[!!{begin{array}{c}x_{1}\x_{2}\vdots \x_{n}end{array}}!!right]in K^{n}:{begin{alignedat}{6}a_{11}x_{1}&&;+;&&a_{12}x_{2}&&;+cdots +;&&a_{1n}x_{n}&&;=0&\a_{21}x_{1}&&;+;&&a_{22}x_{2}&&;+cdots +;&&a_{2n}x_{n}&&;=0&\&&&&&&&&&&vdots quad &\a_{m1}x_{1}&&;+;&&a_{m2}x_{2}&&;+cdots +;&&a_{mn}x_{n}&&;=0&end{alignedat}}right}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bd8572eebe4b09d3564daa060fae598d0b246bc)



![{displaystyle left{left[!!{begin{array}{c}x_{1}\x_{2}\vdots \x_{n}end{array}}!!right]in K^{n}:{begin{alignedat}{7}x_{1}&&;=;&&a_{11}t_{1}&&;+;&&a_{12}t_{2}&&;+cdots +;&&a_{1m}t_{m}&\x_{2}&&;=;&&a_{21}t_{1}&&;+;&&a_{22}t_{2}&&;+cdots +;&&a_{2m}t_{m}&\&&vdots ;;&&&&&&&&&&&\x_{n}&&;=;&&a_{n1}t_{1}&&;+;&&a_{n2}t_{2}&&;+cdots +;&&a_{nm}t_{m}&\end{alignedat}}{text{ for some }}t_{1},ldots ,t_{m}in Kright}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb71c80f35e28104a49c20580e8d8a1c8b6763b3)






![mathbf {x} =Amathbf {t} ;;;;{text{where}};;;;A=left[{begin{alignedat}{2}2&&3&\5&&;;-4&\-1&&2&end{alignedat}},right]{text{.}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bcfc4ef22388fd2887a19ddda5005d12d244bb3)









![left[{begin{alignedat}{6}1&&0&&-3&&0&&2&&0\0&&1&&5&&0&&-1&&4\0&&0&&0&&1&&7&&-9\0&&;;;;;0&&;;;;;0&&;;;;;0&&;;;;;0&&;;;;;0end{alignedat}},right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/750dec11df599c8b8d1c8953c8838a30ffc713aa)


