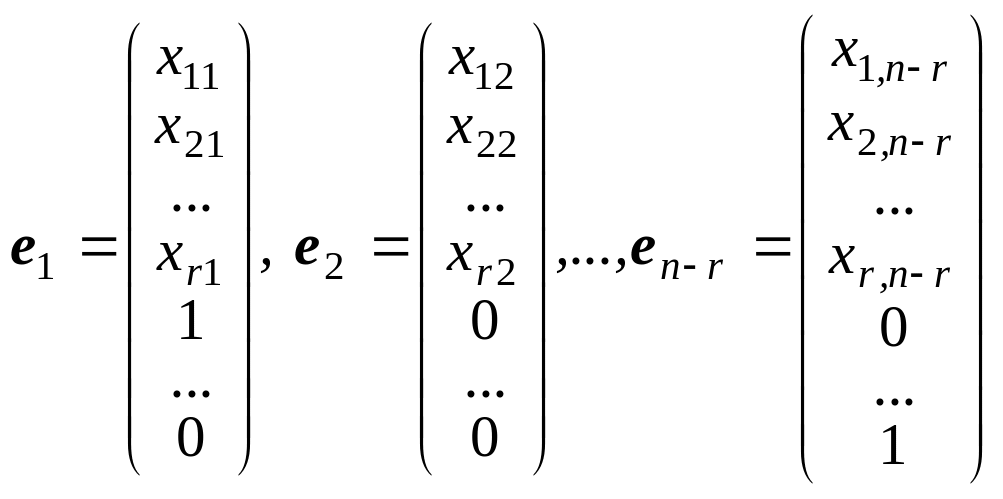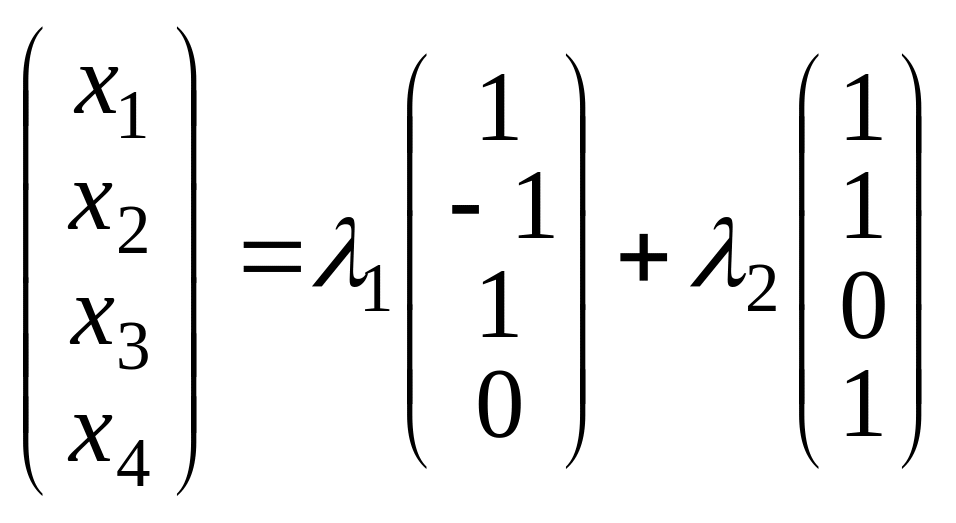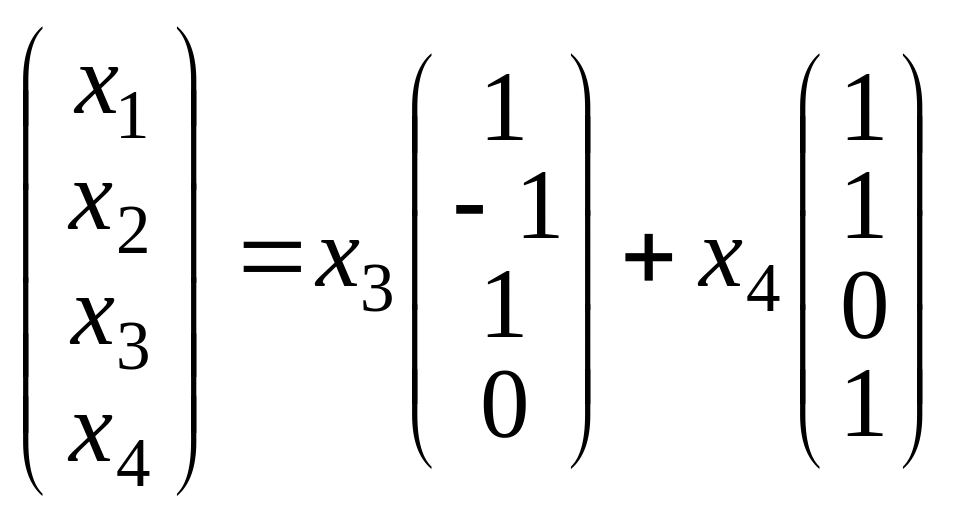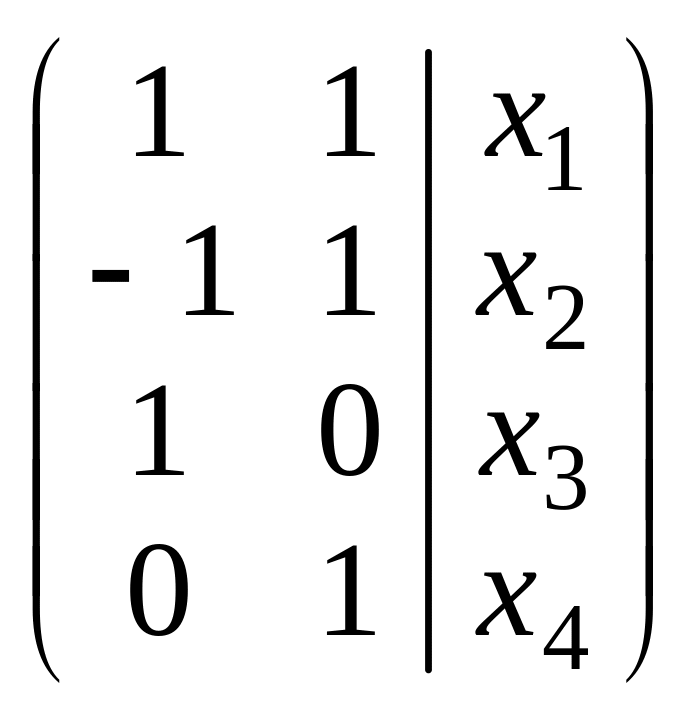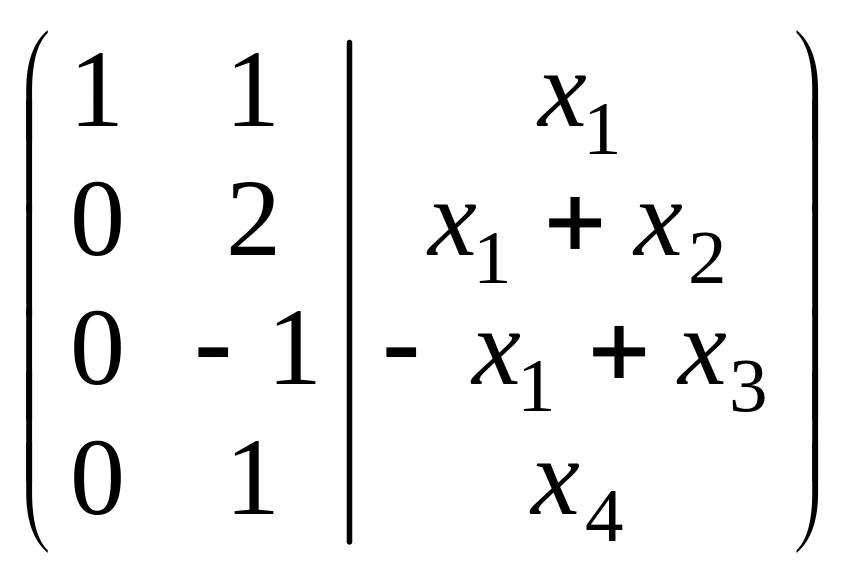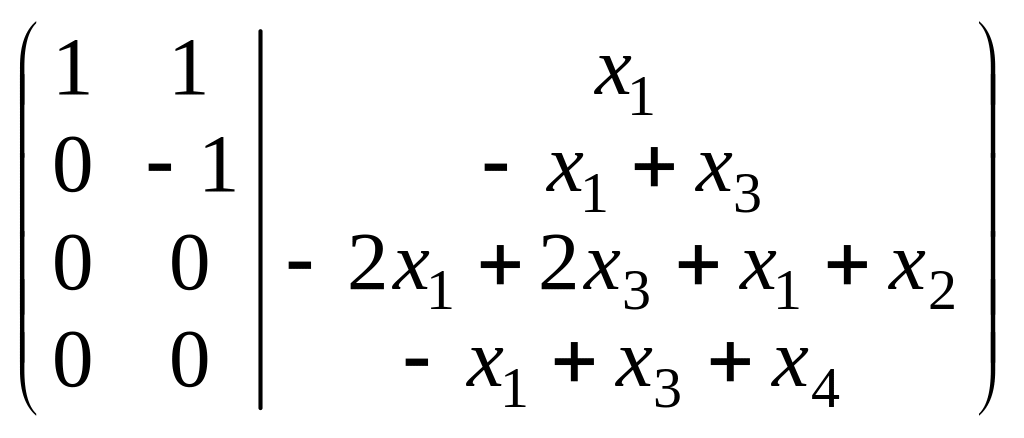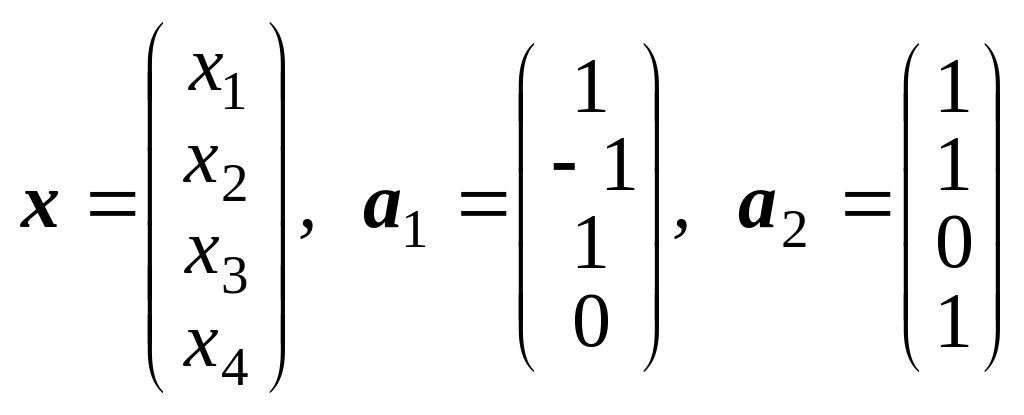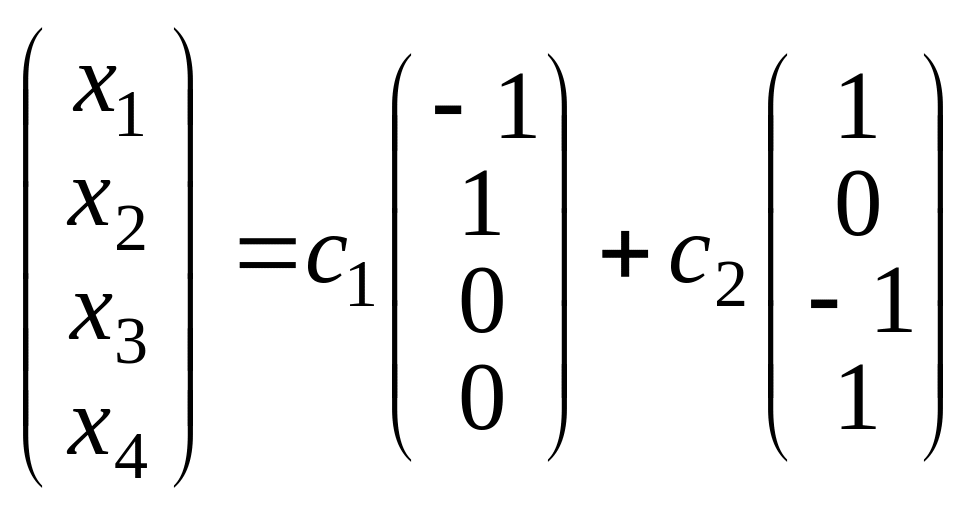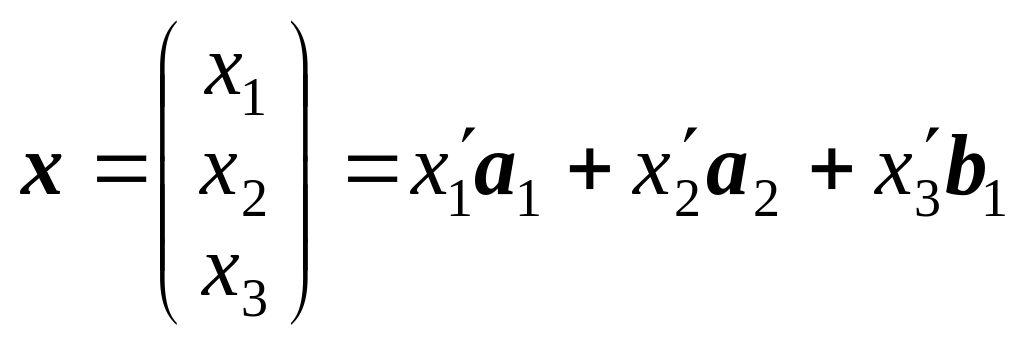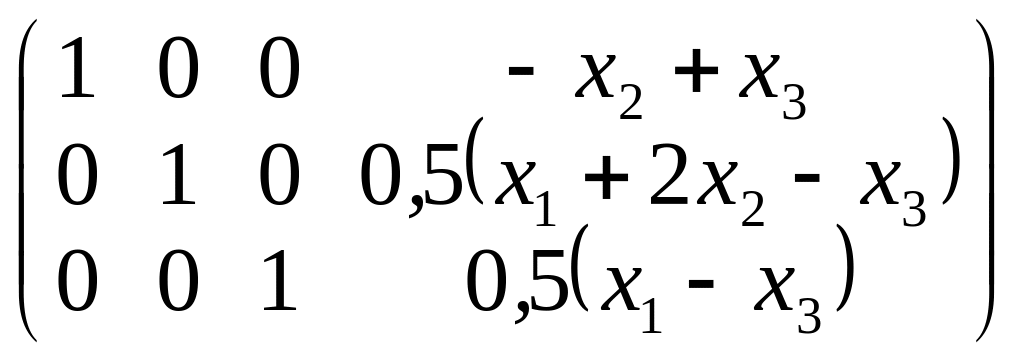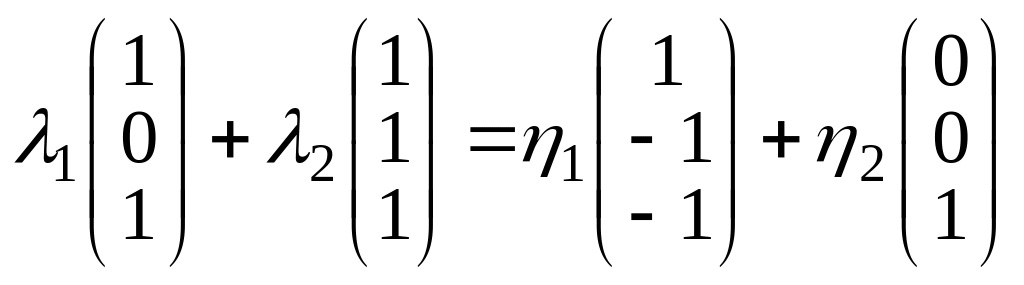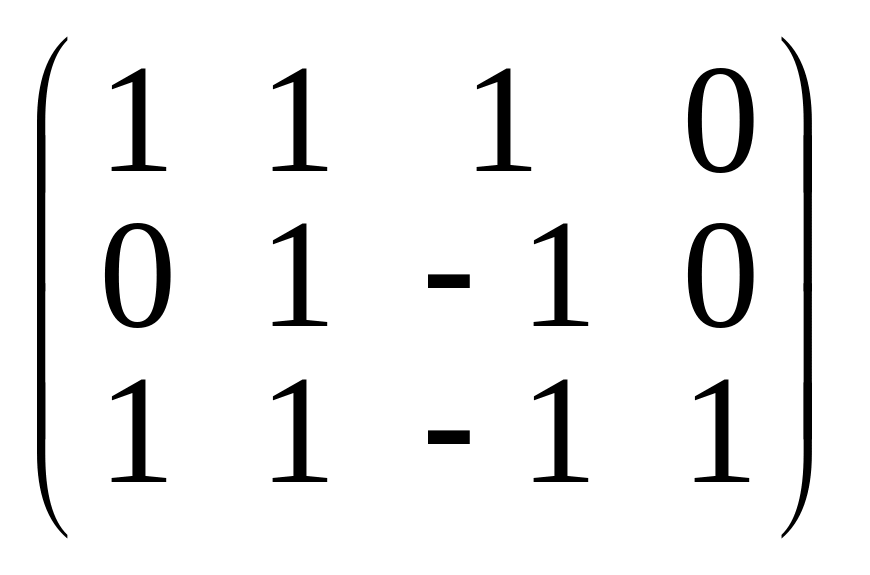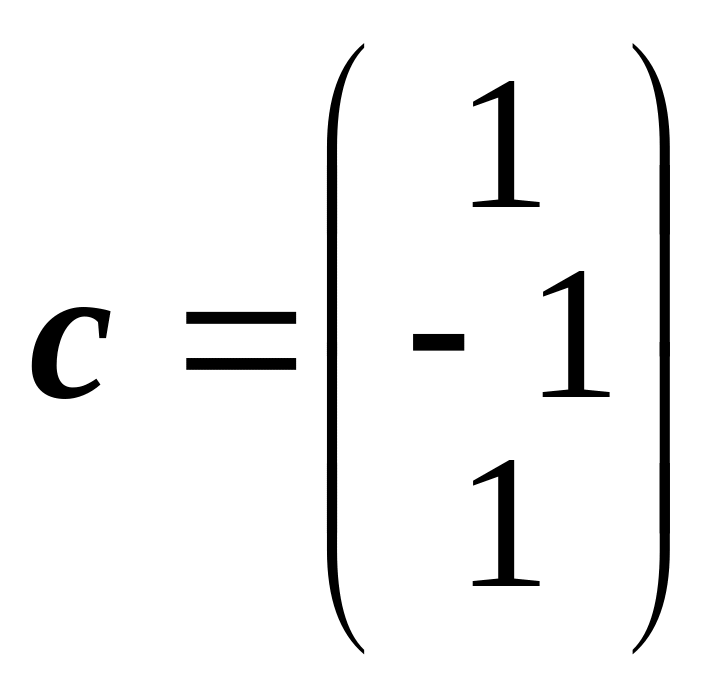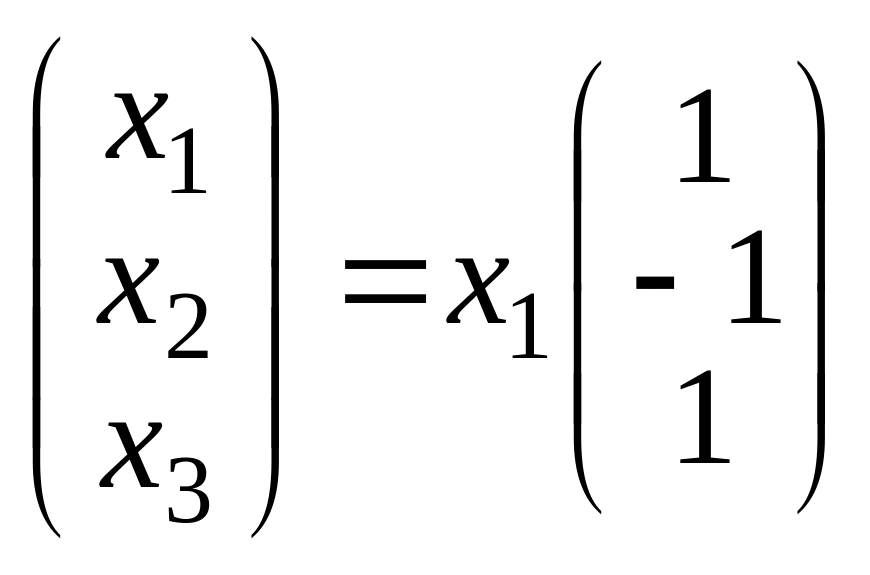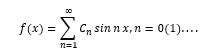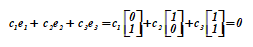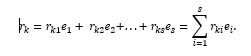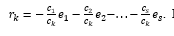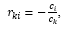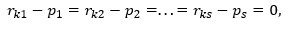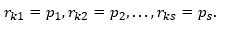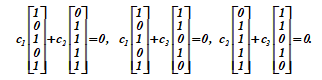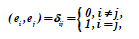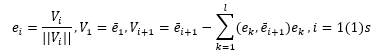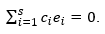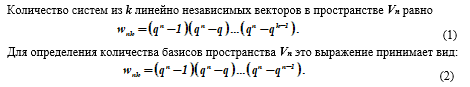Как найти подпространство трехмерного пространства

Линейные подпространства Способы задания линейных подпространств Операции с линейными подпространствами

Линейные
подпространства

Из

множества векторов линейного пространства

выберем некоторую совокупность векторов
и обозначим ее

.
Пусть для любых векторов

и

из

и любого числа

выполняются следующие условия:

1)

2)

.

Тогда
множество векторов

называется линейным
подпространством
пространства

.

Примеры
линейных подпространств:

1.
Каждое линейное пространство обладает
двумя подпространствами: нулевым
подпространством и самим пространством.
Эти подпространства называют
триви­аль­ными.

2.
Линейное пространство

векторов на прямой, проходящей через
начало координат, имеет два триви­альных
подпространства.

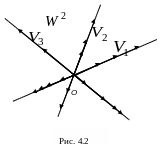
3.
Линейное пространство

векторов на плоскости (рис. 4.2) имеет
кроме двух тривиальных под­про­ст­ранств
бесконечное множество подпространств

.
Каждое из них состоит из векторов,
которые лежат на прямой, проходящей
через начало координат (предполагается,
что все векторы отложены от начала
координат).

4.
В геометрическом пространстве

векторов пространства каждая прямая и
каждая плоскость, проходящие через
начало координат, определяют линейное
подпространство.

Способы
задания линейных подпространств

Линейное
векторное подпространство задается
двумя возможными способами: набором
векторов или системами линейных
уравнений.

1-й
способ.
Набор линейно независимых векторов
(базис подпространства) тесно связан с
понятием линейной оболочки системы
векторов.

О
пределение.
Линейной
оболочкой



двух
векторов

и

,
принадлежащих линейному пространству

,
называется совокупность всех линейных
комбинаций этих векторов

,
где

.

Иначе
говоря, линейная оболочка состоит из
бесконечного множества векторов

,
предста­вимых в виде линейных комбинаций
векторов

и

.
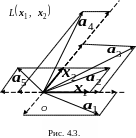
На рис. 4.3 построены векторы

и

,
а также приведено несколько их линейных
комби­наций

.

В
общем случае линейной оболочкой множества

векторов, принадлежащих линей­ному
пространству

,
называется совокупность всех линейных
комбинаций этих векторов

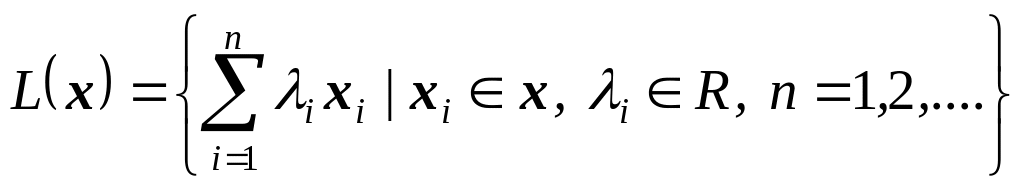
Свойства
линейной оболочки

1.
Линейная оболочка содержит само множество

векторов.

2.
Если линейное пространство

содержит множество

векторов,
то:

а)
пространство

содержит и его линейную оболочку

;

б)

–
линейное подпространство пространства

.

Замечание.
Из определения и свойств линейной
оболочки следует, что каждое векторное
пространство есть линейная оболочка
векторов своего базиса. Поэтому часто
в задачах в целях экономии места мы,
разыскивая базис подпространства, будем
ограничиваться перечислением векторов
базиса, не записывая конечным результатом
их произвольную линейную комбинацию.

2-й
способ.
Существует еще один способ задания
подпространства – в виде однородной
системы линейных уравнений. Рассмотрим
однородную линейную систему

уравнений с

переменными

имеющую
ненулевые решения. Пусть ранг системы
равен

.
Она обладает фундаментальным набором
решений (ФНР) (см. гл.2, §2,5
«Однородные системы уравнений»).

,

которые
линейно независимы. Эти независимые
решения, являющиеся совокупностями из

чисел, можно представить как

–
мерные линейно независимые векторы.
Любое решение сис­те­мы представляется
в виде линейной комбинации ФНР. Если
взять векторы

в ка­чес­тве базиса некоторого
линейного векторного подпространства,
то все множество решений одно­родной
системы и будет этим векторным
подпространством,
называемым пространством решений
однородной системы. Размерность
подпространства равна числу независимых
векторов, т.е.

.

Таким
образом, векторное подпространство
может быть задано как набором векторов,
составляющих базис векторного
подпространства, так и посредством
задания однородной системы линейных
уравнений, фундаментальный набор решений
которой есть базис линейного векторного
подпространства. Переход от задания
подпространства в виде набора векторов
к заданию в виде однородной системы
уравнений и обратно достаточно прост.

ПРИМЕР
1. Линейное подпространство

задано набором линейно независимых
векторов

,

.
Найти однородную систему линейных
уравнений, задающую подпространство

.

Решение.
Рассмотрим 2 способа решения задачи.
Введем произвольный вектор

,
принадлежащий подпространству

.
Разложим вектор

по векторам базиса

или в
координатном виде

(4)

1 способ.
Использование формы, в которой записывается
решение системы однородных уравнений
и представление в этой форме векторов
базиса как фундаментальных решений
некоторой системы. Запишем равенство
(4) в виде решения системы уравнений

.

Тогда
система имеет вид

Окончательно,

(5)

Замечание.
Переход к системе уравнений требует
наличия в каждом из векторов

нулевой координаты. Если ее нет, комбинируя
векторы

,
такие координаты легко получить.

2 способ
основан на использовании теоремы
Кронекера-Капелли. Составим расширенную
матрицу из коэффициентов и свободных
членов и преобразуем, используя метод
Гаусса

~
~
(6)

Система
должна иметь решения, поскольку вектор

принадлежит подпространству. Ранги
матрицы коэффициентов и расширенной
матрицы системы по теореме Кронекера-Капелли
должны быть равны. Это выполняется при
соблюдении условий:

(7)

Полученная
система однородных линейных уравнений
задает требуемое линейное подпространство.
Системы (5) и (7) несколько отличаются
друг от друга. От системы (7) можно перейти
к системе (5), взяв разность 1-го и 2-го
уравнений в системе (7).

Замечание.
Продолжив преобразование матрицы (6) по
методу Гаусса-Жордана, получим координаты

и

вектора

в базисе

линейного подпространства

.

,

т.е.

.

ПРИМЕР
2. Линейное подпространство

задано однородной системой линейных
уравнений

Найти
набор
линейно независимых векторов (базис),
задающий линейное подпространство

.

Решение.
Найдем фундаментальный набор решений
однородной системы. Ранг матрицы
коэффициентов уравнений равен 2. Поэтому
могут быть найдены две переменные,
выраженные через две другие. Положим
базисными переменными

.
Свободными переменными станут

.
Вычтем из первого уравнения второе.
Будем иметь

Запишем решения в
развернутой матричной форме

.

Обозначив
свободные переменные, стоящие в правой
части равенства:

,
получим

,

где

.

Любой
вектор

,
координаты которого являются переменными
в однородной системе уравнений,
представлен как линейная комбинация
двух линейно независимых векторов,
составляющих ФНР однородной системы.
Следовательно, все множество векторов

составляет линейное векторное
подпространство с базисом

.
Итак, базис линейного подпространства

:

,

.

ПРИМЕР. Найти линейную
оболочку множества решений системы
уравнений

Решение.
Ранг матрицы коэффициентов системы
уравнений равен 2. Выберем свободными
переменными

и

.
Тогда общее решение однородной системы
уравнений имеет вид

,
где

.

Векторы

и

образуют фундаментальный набор решений
однородной системы. Любое решение
системы является их линейной комбинацией.
Значит, линейная оболочка векторов

и

и есть множество решений однородной
системы уравнений, т.е.

,
где

.

Кратко оформим идеи перехода между
способами задания линейного подпространства
в виде таблицы

Подпространство задано своим базисом :		Подпространство задано системой уравнений :

Операции
с линейными под­пространствами

1
)
Сумма подпространств. Суммой

линейных подпространств

и

линейного пространства

называется совокупность всех векторов

,
которые можно представить в виде
(разложить)

,
где

,

.

2)
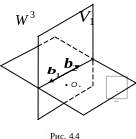
Пересечение подпространств. Пересечением

линейных подпространств

и

линейного про­странства

называется совокупность всех векторов

,
которые принадлежат одновременно
подпространствам

и

.
На рис. 4.4 пересечению под­пространств

и

геометричес­кого пространства

принадлежат векторы

и

.

3)
Умножение числа на подпространство.
Умножение числа

на линейное векторное подпространство

не изменяет его, т.е.

.

4)
Сумма подпространства и вектора.
Алгебраическая сумма векторного
подпространства

и отдельного вектора

,
принадлежащего подпространству

,
не изменяет последнего

,
если

.

Алгебраическая
сумма векторного подпространства

и отдельного вектора

,
не принадлежащего подпространству

,
порождает множество

векторов, которое не является векторным
подпространством

.

С
множеством

векторов, называемым линейным
многообразием,
мы познакомимся позже.

Свойства
суммы и пересечения линейных подпространств

1)
Сумма и пересечение линейных подпространств
являются линейными подпространствами.

2)Суммой
двух подпространств

и

является подпространство

,
т.е.

.

3)
Размерность суммы линейных подпространств
равна сумме размерностей подпространств
минус размерность их пересечения
(формула Грассмана)

.

Пусть линейные подпространства задаются
своими базисами или в виде систем
линейных уравнений. Тогда без труда
решается задача нахождения базиса или
системы уравнений, задающих сумму
подпространств или их пересечение. Идеи
решений таких задач оформим в виде
таблицы.

	Задание подпространств и
1 своими базисами : ; : .	2 системами линейных уравнений : ; : .
Идеи решения
	3 Находится ранг системы векторов , определяются все линейно независимые векторы, которые составляют базис суммы.	4 Находится объединение систем: .
	5 Используется равенство линейных комбинаций .	6 Находится пересечение систем .

ПРИМЕР.
Линейные подпространства

и

трехмерного векторного пространства

заданы
своими базисами векторов

:

;

:

.

Найти

1. системы
   линейных уравнений, задающие эти
   подпространства (переход
   
   );

2. базис

   (переход
   
   );

3. систему
   уравнений, задающую

   (переход
   

   или
   
   );

4. базис

   (переход
   

   или
   
   );

5. систему
   уравнений, задающую

   (переход
   

   или
   
   ).

Решение.
1) переход

нами был разобран в предыдущем примере.
Ответ:

:

;

:

.

2) Составим матрицу
из координат векторов и приведем ее к
треугольному виду

~

.

Очевидно,
ранг равен 3. Проводя элементарные
преобразования, мы не меняли положение
строк. Первые 3 вектора, написанные в
координатах по строкам матрицы, являются
линейно независимыми и могут составить
базис суммы подпространств. Итак, векторы

,

задают подпространство

.
Размерности пространств

и

совпадают. Следовательно, векторы

образуют базис всего пространства

.

3) Сумма
подпространств

имеет размерность векторного пространства

и системой уравнений описана быть не
может. Для обоснования утверждения
рассмотрим произвольный вектор

,
принадлежащий пространству

.
Вектор

раскладывается по базису

единственным образом.
.

Составим расширенную
матрицу и воспользуемся преобразованием
Гаусса-Жордана

.

Получим
выражение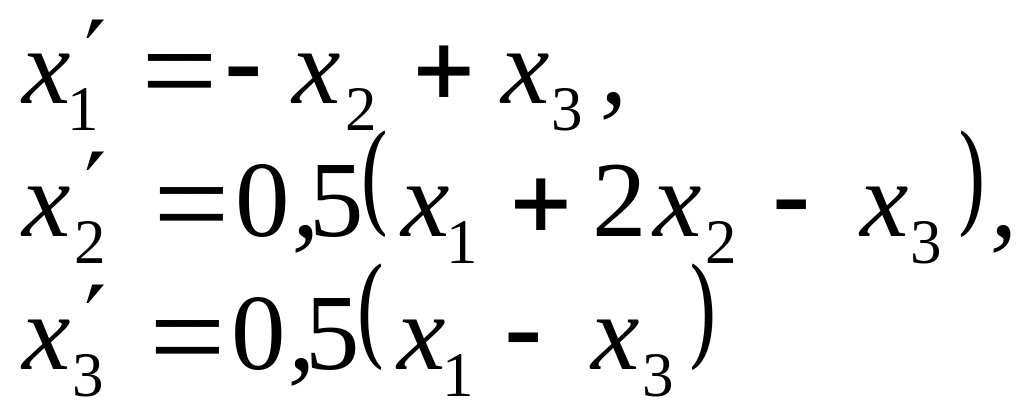

представляющее
собой связь координат произвольного
вектора

в новом и в старом базисах. Таким образом,
задача о нахождении системы линейных
уравнений, описывающей векторное
подпространство вырождается в задачу
нахождения связи координат произвольного
вектора в старом и новом базисах.

4) Базис
пересечения подпространств

.
Любой вектор

,
принадлежащий подпространствам

и

,
может быть разложен по базисам этих
подпространств.

(8)

Решение системы
уравнений по методу Гаусса-Жордана

~

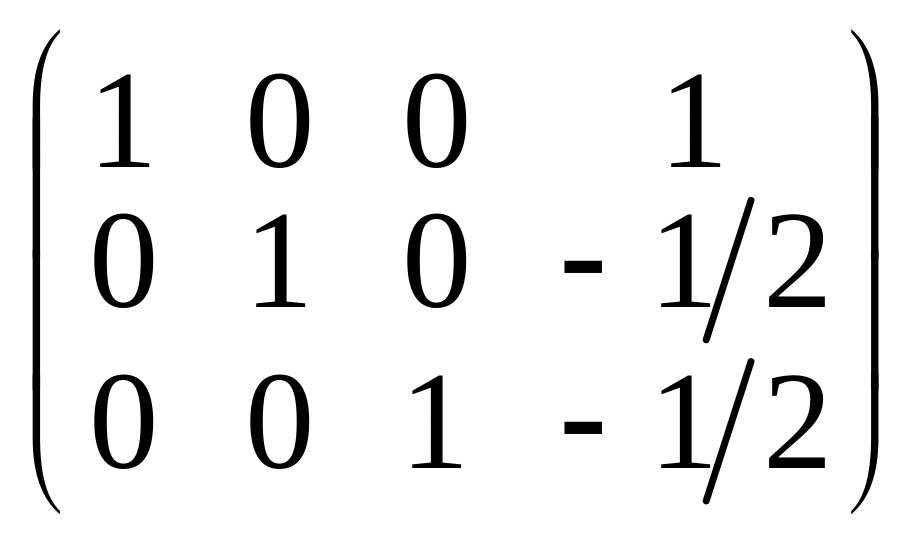
дает
следующие значения переменных

.

Вернемся
к системе (8)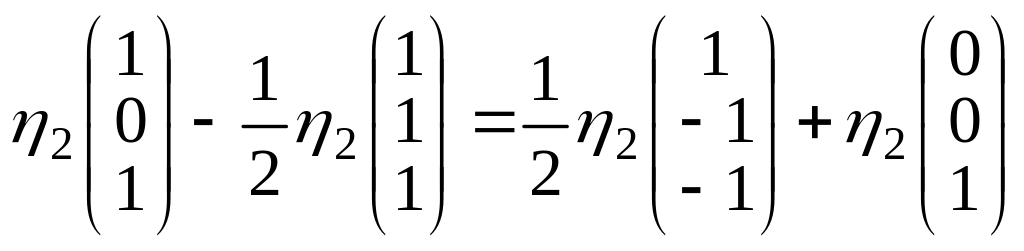

При

получим

или

.
Следовательно, вектор

является общим для подпространств

и

и может быть положен базисом их
пересечения. Ответ: базис пересечения

имеет вид

.

5) Найдем
систему уравнений, задающую пересечение
подпространств. Ее вид

.
Легко видеть, что фундаментальное
решение системы

совпадает с вектором

базиса пересечения подпространств.

Пусть
пересечение двух подпространств

и

является нулевым подпространством
.
Тогда сумма

называется прямой
суммой
и обозначается через
.
Если подпространство

совпадает со всем пространством
,
т.е
,
то подпрост­ранства

и

называются дополнениями
друг к другу в пространстве
.

Свойства
прямой суммы подпространств.

1. Прямая
   сумма подпространств есть подпространство.

2. Пересечение
   подпространств является нулевым
   подпространством.

3. Сумма
   базисов линейных подпространств линейно
   независима.

4. Сумма
   базисов линейных подпространств
   образует базис прямой суммы.

5. Размерность
   суммы подпространств равна размерности
   прямой суммы.

6. Любой
   вектор, принадлежащий прямой сумме,
   может быть разложен, причем единственным
   образом, по составляющим сумму
   подпространствам.

7. Совокупность
   любых двух векторов, взятых по одному
   от каждого подпространства, линейно
   независима.

8. Для
   любого подпространства существует
   дополнение.

9. Если
   подпространство не является нулевым,
   то дополнительное подпространство
   определено неоднозначно.

Пусть
задано подпространство

.
Любой вектор
,
принадлежащий подпрост­ранству
,
в соответствии со свойством 6 может быть
разложен на сумму векторов
,
где

и
.
Вектор

называется проекцией
вектора

на
подпространство

параллельно подпространству
,
вектор

называется проекцией вектора

на
подпространство

параллельно подпространству
.

ПРИМЕР.
В векторном пространстве

заданы подпространства

и
.
Найти проекцию вектора

на подпространство

параллельно подпространству
.

Решение.
Подпространства

и

составляют прямую сумму, поскольку их
пересечение, как легко определить,
является нулевым подпространством.
Подпространства

и

дополняют друг друга до всего векторного
пространства
,
так как размерность суммы подпространств
равна размерности всего пространства.
Разложим вектор

по
суммарному базису

и
перейдем к уравнению в координатах

.

Решив
уравнение, например, методом Гаусса,
получим

Вектор

,

разложенный
по базису подпространства
,
есть проекция

вектора

на
подпространство

параллельно подпространству
.

Замечание
1.
Для линейных векторных пространств и
подпространств мы не ввели расстояния
и углы. Это будет сделано при дальнейшем
изложении. Рисунки, содержащие декартову
систему координат, носят условный
характер.

Замечание
2.
Векторные пространства и подпространства
содержат нулевой вектор. Наглядная
геометрическая иллюстрация этого факта
приводит нас к необходимости рисовать
декартову систему координат и проводить
подпространства через начало координат,
хотя можно было бы ограничиться одной
точкой О – полюсом.

Определение 6. Подпространство векторного пространства — это множество его элементов, само являющееся векторным пространством относительно введенных в операций сложения и умножения на число.

Для того чтобы убедиться в том, что множество элементов векторного пространства является его подпространством, необходимо проверить, что для любых двух векторов х и у из их сумма тоже принадлежит и что для каждого вектора х из и произвольного произведение тоже принадлежит

Покажем, что этого и достаточно. Действительно, аксиомы 1, 2 и 5—8 векторного пространства, справедливые в будут выполняться, в частности, и для элементов из Далее, если какой-то вектор то и произведения 0-х тоже принадлежат Следовательно, нулевой вектор принадлежит и для каждого х из вектор — х тоже принадлежит

Размерность любого подпространства векторного пространства не превосходит размерности самого пространства: ведь линейно независимые векторы подпространства будут линейно независимыми и во всем пространстве, а значит, максимальное число линейно независимых векторов подпространства не превосходит размерности всего пространства.

Примеры. В обычном трехмерном пространстве (рассматриваемом как множество принадлежащих ему векторов) подпространствами будут все плоскости и все прямые, проходящие через начало координат. Подпространствами любого пространства будут само пространство и множество, состоящее из одного нуля. В пространстве многочленов степени не выше подпространствами будут, например, все при — ведь складывая и умножая на числа многочлены степени не выше мы будем получать снова такие же многочлены. С другой стороны, каждое из пространств содержится в качестве подпространства в пространстве Р всех многочленов с вещественными коэффициентами, а это последнее является подпространством пространства С не прерывных функций,

Рассмотрим систему линейных однородных уравнений, ранг матрицы коэффициентов которой равен

и пусть в векторном пространстве зафиксирован какой-то базис. Если каждое решение системы (3) рассматривать как вектор пространства то из результатов § 10 главы 1 вытекает, что совокупность всех решений системы (3) является -мерным подпространством (где базисом которого служит любая фундаментальная система решений.

Покажем, что и, обратно, каждое подпространство векторного пространства в любом базисе определяется некоторой системой линейных однородных уравнений.

Действительно, пусть -мерное подпространство в — базис Дополним эту линейно независимую систему векторов до базиса всего пространства Легко видеть, что если — координаты относительно этого («старого») базиса, то подпространство в этом базисе определяется системой уравнений:

Далее, если — координаты относительно любого другого («нового») базиса то, как показано в § 6, имеют место, в частности, равенства

где — некоторые числа, и значит, подпространство в базисе ей определяется системой линейных однородных уравнений

При проведении научных и прикладных исследование часто создаются модели, в которых рассматриваются точки и/или векторы определенных пространств. Например, в моделях шифров на эллиптических кривых используются аффинные и проективные пространства. К проективным прибегают тогда, когда необходимо ускорить вычисления, так как в формулах манипулирования с точками эллиптической кривой выводимых в рамках проективного пространства отсутствует операция деления на координату, которую в случае аффинного пространства обойти не удается.

Операция деления как раз одна из самых «дорогих» операций. Дело в том, что в алгебраических полях, а соответственно и в группах операция деления вообще отсутствует и выход из положения (когда не делить нельзя) состоит в том, что операцию деления заменяют умножением, но умножают не на саму координату, а на обращенное ее значение. Из этого следует, что предварительно надо привлекать расширенный алгоритм Евклида НОД и кое что еще. Одним словом, не все так просто как изображают авторы большинства публикаций о ЕСС. Почти все, что по этой теме опубликовано и не только в Интернете мне знакомо. Мало того, что авторы не компетентны и занимаются профанацией, оценщики этих публикаций плюсуют авторов в комментариях, т. е. не видят ни пробелов, ни явных ошибок. Про нормальную же статью пишут, что она уже 100500-я и от нее нулевой эффект. Так все пока на Хабре устроено, анализ публикаций делается огромный, но не качества содержания. Здесь возразить нечего — реклама двигатель бизнеса.

Линейное векторное пространство

Изучение и описание явлений окружающего мира с необходимостью приводит нас к введению и использованию ряда понятий таких как точки, числа, пространства, прямые линии, плоскости, системы координат, векторы, множества и др.

Пусть r_<3> = <r1, r2, r3> вектор трехмерного пространства, задает положение одной частицы (точки) относительно начала координат. Если рассматривать N элементов, то описание их положения требует задания 3∙N координат, которые можно рассматривать как координаты некоторого вектора в 3N-мерном пространстве. Если рассматривать непрерывные функции и их совокупности, то приходим к пространствам, размерность которых равна бесконечности. На практике часто ограничиваются использованием лишь подпространства такого бесконечномерного пространства функции координат, обладающего конечным числом измерений.

Пример 1. Ряд Фурье — пример использования пространства функций. Рассмотрим разложение произвольной функции в ряд Фурье

Его можно трактовать как разложение «вектора» f(x) по бесконечному набору «ортогональных» базисных векторов sinпх

Это пример абстрагирования и распространения понятия вектора на бесконечное число измерений. Действительно, известно, что при -π≤x≤π

Существо дальнейшего рассмотрения не пострадает, если мы отвлечемся от размерности абстрактного векторного пространства – будь — то 3, 3N или бесконечность, хотя для практических приложений больший интерес представляет конечномерные поля и векторные пространства.

Набор векторов r1, r2,… будем называть линейным векторным пространством L, если сумма любых двух его элементов тоже находится в этом наборе и если результат умножения элемента на число С также входит в этот набор. Оговоримся сразу, что значения числа С могут быть выбраны из вполне определенного числового множества Fр – поля вычетов по модулю простого числа р, которое считается присоединенным к L.

Пример 2. Набор из 8 векторов, составленных из n =5 -разрядных двоичных чисел
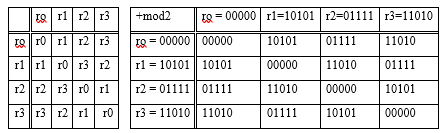
r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 образует векторное пространство L, если числа С є {0,1}. Этот небольшой пример позволяет убедиться в проявлении свойств векторного пространства, включенных в его определение.

Суммирование этих векторов выполняется поразрядно по модулю два, т. е. без переноса единиц в старший разряд. Отметим, что если все С действительные (в общем случае С принадлежат полю комплексных чисел), то векторное пространство называют действительным.

Формально аксиомы векторного пространства и записываются так:
r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L – коммутативность сложения и замкнутость;
(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 – ассоциативность сложения;
ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L–существование нейтрального элемента;
ri +(- ri) = r0, для ∀i существует противоположный вектор (-ri) є L;
1∙ ri = ri ∙1 = ri существование единицы для умножения;
α (β∙ri) = (α∙β)∙ri; α, β, 1, 0 – элементы числового поля F, ri є L; умножение на скаляры ассоциативно; результат умножения принадлежит L;
(α + β) ri = α∙ri + β∙ri; для ∀i, ri є L, α, β – скаляры;
а (ri + rj) = ari + arj для всех а, ri, rj є L;
a∙0 = 0, 0∙ri = 0; (-1) ∙ ri = – ri.

Размерность и базис векторного пространства

При изучении векторных пространств представляет интерес выяснение таких вопросов, как число векторов, образующих все пространство; какова размерность пространства; какой наименьший набор векторов путем применения к нему операции суммирования и умножения на число позволяет сформировать все векторы пространства? Эти вопросы основополагающие и их нельзя обойти стороной, так как без ответов на них утрачивается ясность восприятия всего остального, что составляет теорию векторных пространств.

Оказалось, что размерность пространства самым тесным образом связана с линейной зависимостью векторов, и с числом линейно независимых векторов, которые можно выбирать в изучаемом пространстве многими способами.

Линейная независимость векторов

Набор векторов r1, r2, r3 … rр из L называют линейно независимым, если для них соотношение

выполняется только при условии одновременного равенства

.
Все

, k = 1(1)p, принадлежат числовому полю вычетов по модулю два
F = {0, 1}.
Если в некотором векторном пространстве L можно подобрать набор из р векторов, для которых соотношение

выполняется, при условии, что не все

одновременно, т.е. в поле вычетов оказалось возможным выбрать набор

, k =1(1)р, среди которых есть ненулевые, то такие векторы

называются линейно зависимыми.

Пример 3. На плоскости два вектора

= <0, 1>^T и

= <1, 0>^T являются линейно независимыми, так как в соотношении (T-транспонирование)

невозможно подобрать никакой пары чисел

коэффициентов не равных нулю одновременно, чтобы соотношение было выполнено.
Три вектора

= <0, 1>^T,

= <1, 0>^T,

= <1, 1>^T образуют систему линейно зависимых векторов, так как в соотношении

равенство может быть обеспечено выбором коэффициентов

, не равных нулю одновременно. Более того, вектор

является функцией

и

(их суммой), что указывает на зависимость

от

и

. Доказательство общего случая состоит в следующем.

Пусть хотя бы одно из значений

, k = 1(1)р, например,

, а соотношение выполнено. Это означает, что векторы

, k = 1(1)р, линейно зависимы

Выделим явным образом из суммы вектор r_р

Говорят, что вектор r_р является л и н е й н о й комбинацией векторов

или r_р через остальные векторы выражается линейным образом, т.е. r_р линейно зависит от остальных. Он является их функцией.

На плоскости двух измерений любые три вектора линейно зависимы, но любые два неколлинеарных вектора являются независимыми. В трехмерном пространстве любые три некомпланарных вектора линейно независимы, но любые четыре вектора всегда линейно зависимы.

Зависимость/независимость совокупности {

} векторов часто определяют, вычисляя определитель матрицы Грама (ее строки скалярные произведения наших векторов). Если определитель равен нулю, среди векторов имеются зависимые, если определитель отличен от нуля — векторы в матрице независимы.

Определителем Грама (грамианом) системы векторов

в евклидовом пространстве называется определитель матрицы Грама этой системы:

где

— скалярное произведение векторов

и

.

Размерность и базис векторного пространства

Размерность s = d (L) пространства L определяется как наибольшее число векторов в L, образующих линейно независимый набор. Размерность – это не число векторов в L, которое может быть бесконечным и не число компонентов вектора.

Пространства, имеющие конечную размерность s ≠ ∞, называются конечномерными, если
s = ∞, – бесконечномерными.

Ответом на вопрос о минимальном числе и составе векторов, которые обеспечивают порождение всех векторов линейного векторного пространства является следующее утверждение.

Любой набор s линейно независимых векторов в пространстве L образует его б а з и с. Это следует из того, что любой вектор

линейного s-мерного векторного пространства L может быть представлен единственным способом в виде линейной комбинации векторов базиса.

Зафиксируем и обозначим символом

, i = 1(1)s, один из наборов, образующих базис пространства L. Тогда

Числа r_ki, i = 1(1)s называются координатами вектора

в базисе

, i = 1(1)s, причем r_ki = (

,

).
Покажем единственность представления

. Очевидно, что набор

,

является зависимым, так как

, i = 1(1)s – базис. Другими словами, существуют такие

не равные одновременно нулю, что

.
При этом пусть

, ибо если

, то хоть одно из

, было бы отлично от нуля и тогда векторы

, i = 1(1)s, были бы линейно зависимы, что невозможно, так как это базис. Следовательно,

Полагая

, будем иметь
Используя прием доказательства «от противного», допустим, что записанное представление

не единственное в этом базисе и существует другое

Тогда запишем отличие представлений, что, естественно, выражается как

Очевидно, что правая и левая части равны, но левая представляет разность вектора с самим собой, т. е. равна нулю. Следовательно, и правая часть равна нулю. Векторы

, i = 1(1)s линейно независимы, поэтому все коэффициенты при них могут быть только нулевыми. Отсюда получаем, что

а это возможно только при

Выбор базиса. Ортонормированность

Векторы называют нормированными, если длина каждого из них равна единице. Этого можно достичь, применяя к произвольным векторам процедуру нормировки.

Векторы называют ортогональными, если они перпендикулярны друг другу. Такие векторы могут быть получены применением к каждому из них процедуры ортогонализации. Если для совокупности векторов выполняются оба свойства, то векторы называются ортонормированными.

Необходимость рассмотрения ортонормированных базисов вызвана потребностями использования быстрых преобразований как одно –, так и многомерных функций. Задачи такой обработки возникают при исследовании кодов, кодирующих информационные сообщения в сетях связи различного назначения, при исследовании изображений, получаемых
посредством автоматических и автоматизированных устройств, в ряде других областей, использующих цифровые представления информации.

Определение. Совокупность n линейно независимых векторов n-мерного векторного
пространства V называется его базисом.

Теорема. Каждый вектор х линейного n-мерного векторного пространства V можно представить, притом единственным образом, в виде линейной комбинации векторов базиса. Векторное пространство V над полем F обладает следующими свойствами:
0·х = 0 (0 в левой части равенства – нейтральный элемент аддитивной группы поля F; 0 в правой части равенства – элемент пространства V, являющийся нейтральным единичным элементом аддитивной группы V, называемый нулевым вектором);
(– 1)·х = –х; –1є F; x є V; –x є V;
Если α·х = 0єV, то при х ≠ 0 всегда α = 0.
Пусть Vn(F) – множество всех последовательностей (х1, х2, …, хn) длины n с компонентами из поля F, т.е. Vn(F) ={x, таких, что х = (х1, х2, …, хn), хi є F;
i =1(1)n }.

Сложение и умножение на скаляр определяются следующим образом:
x + y =(x1 + y1, x2 + y2, …, xn + yn);
α·х = (α·х1, α·х2,…, α·хn), где у = (у1, у2,…, уn),
тогда Vn(F) является векторным пространством над полем F.

Пример 4. В векторном пространстве rо = 00000, r1 = 10101, r2 = 11010, r3 = 10101 над полем F2 = {0,1} определить его размерность и базис.
Решение. Сформируем таблицу сложения векторов линейного векторного пространства

В этом векторном пространстве V= {rо,r1,r2,r3} каждый вектор в качестве противоположного имеет самого себя. Любые два вектора, исключая rо, являются линейно независимыми, в чем легко убедиться
c1·r1 + c2·r2 = 0; c1·r1 + c3·r3 = 0; c2·r2 + c3·r3 = 0;

Каждое из трех соотношений справедливо только при одновременных нулевых значениях пар коэффициентов сi, сj є {0,1}.

При одновременном рассмотрении трех ненулевых векторов один из них всегда является суммой двух других или равен самому себе, а r1+r2+r3=rо.

Таким образом, размерность рассматриваемого линейного векторного пространства равна двум s = 2, d(L) = s = 2, хотя каждый из векторов имеет пять компонентов. Базисом пространства является набор (r1, r2). Можно в качестве базиса использовать пару (r1, r3).

Важным в теоретическом и практическом отношении является вопрос описания векторного пространства. Оказывается, любое множество базисных векторов можно рассматривать как строки некоторой матрицы G, называемой порождающей матрицей векторного пространства. Любой вектор этого пространства может быть представлен как линейная комбинация строк матрицы G ( как, например, здесь).

Если размерность векторного пространства равна k и равна числу строк матрицы G, рангу матрицы G, то очевидно, существует k коэффициентов с q различными значениями для порождения всех возможных линейных комбинаций строк матрицы. При этом векторное пространство L содержит q^k векторов.

Множество всех векторов из ℤpn с операциями сложения векторов и умножения вектора на скаляр из ℤp есть линейное векторное пространство.

Определение. Подмножество W векторного пространства V, удовлетворяющее условиям:
Если w1, w2 є W, то w1+ w2 є W,
Для любых α є F и w є W элемент αw є W,
само является векторным пространством над полем F и называется подпространством векторного пространства V.

Пусть V есть векторное пространство над полем F и множество W ⊆ V. Множество W есть подпространство пространства V, если W по отношению к линейным операциям, определенным в V, есть линейное векторное пространство.

Таблица. Характеристики векторных пространств

Компактность матричного представления векторного пространства очевидна. Например, задание L векторов двоичных 50-разрядных чисел, среди которых 30 векторов образуют базис векторного пространства, требует формирования матрицы G[30,50], а описываемое количество векторов превышает 10⁹, что в поэлементной записи представляется неразумным.

Все базисы любого пространства L разбиваются подгруппой Р невырожденных матриц с det G > 0 на два класса. Один из них (произвольно) называют классом с положительно ориентированными базисами (правыми), другой класс содержит левые базисы.

В этом случае говорят, что в пространстве задана ориентация. После этого любой базис представляет собой упорядоченный набор векторов.

Если нумерацию двух векторов изменить в правом базисе, то базис станет левым. Это связано с тем, что в матрице G поменяются местами две строки, следовательно, определитель detG изменит знак.

Норма и скалярное произведение векторов

После того как решены вопросы о нахождении базиса линейного векторного пространства, о порождении всех элементов этого пространства и о представлении любого элемента и самого векторного пространства через базисные векторы, можно поставить задачу об измерении в этом пространстве расстояний между элементами, углов между векторами, значений компонентов векторов, длины самих векторов.

Действительное или комплексное векторное пространство L называется нормированным векторным пространством, если каждый вектор r в нем может быть сопоставлен действительному числу || r || – модулю вектора, норме. Единичный вектор – это вектор, норма которого равна единице. Нулевой вектор имеет компонентами нули.

Определение. Векторное пространство называется унитарным, если в нем определена бинарная операция, ставящая каждой паре ri, rj векторов из L в соответствие скаляр. В круглых скобках (ri, rj) записывается (обозначается) скалярное или внутреннее произведение ri и rj, причем
1. (ri, rj) = ri ∙ rj;
2. (ri, rj) = (rj ∙ ri)*, где * указывает на комплексное сопряжение или эрмитову симметрию;
3. (сri, rj) = с(ri ∙ rj) – ассоциативный закон;
4. (ri + rj, rk) = (ri ∙ rk)+ (rj ∙ rk)– дистрибутивный закон;
5. (ri, rk) ≥ 0 и из (ri, rj ) = 0 следует ri = 0.

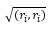
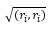
Определение. Положительное значение квадратного корня называют нормой (или длиной, модулем) вектора ri. Если = 1, то вектор ri называют нормированным.

Два вектора ri, rj унитарного векторного пространства L взаимно ортогональны, если их скалярное произведение равно нулю, т.е. (ri, rj) = 0.

При s = 3 в линейном векторном пространстве в качестве базиса удобно выбирать три взаимно перпендикулярных вектора. Такой выбор существенно упрощает ряд зависимостей и вычислений. Этот же принцип ортогональности используется при выборе базиса в пространствах и других размерностей s > 3. Использование введенной операции скалярного произведения векторов обеспечивает возможность такого выбора.

Еще большие преимущества достигаются при выборе в качестве базиса векторного пространства ортогональных нормированных векторов – ортонормированного базиса. Если не оговорено специально, то далее всегда будем считать, что базис еi, i = 1(1)s выбран именно таким образом, т.е.

, где ij — символ Кронекера (1823 — 1891).

В унитарных векторных пространствах такой выбор всегда реализуем. Покажем реализуемость такого выбора.

Определение. Пусть S = {v1, v2,…, vn} есть конечное подмножество векторного пространства V над полем F.
Линейная комбинация векторов из S есть выражение вида а1∙v1 + а2∙v2 +…+ аn∙vn, где каждое аi ∊ F.

Оболочка для множества S (обозначение {S}) есть множество всех линейных комбинаций векторов из S. Оболочка для S есть подпространство пространства V.

Если U есть пространство в V, то U натянуто на S (S стягивает U), если {S}=U.
Множество векторов S линейно зависимо над F, если в F существуют скаляры а1, а2,…, аn, не все нули, для которых а1∙v1+ а2∙v2 +…+ аn∙vn = 0. Если таких скаляров не существует, то множество векторов S линейно независимо над F.

Если векторное пространство V натянуто на линейно независимую систему векторов S (или система S стягивает пространство V), то система S называется базисом для V.

Приведение произвольного базиса к ортонормированному виду

Пусть в пространстве V имеется не ортонормированный базис ē _i, i = 1(1)s. Обозначим норму каждого вектора базиса символом

Известно следующее утверждение [11]. Если ē _i, i = 1(1)s – произвольная конечная или счетная система линейно независимых векторов в унитарном векторном пространстве, то существует ортонормированная система ē _i, i = 1(1)s, порождающая то же самое линейное пространство (многообразие).

В основу процедуры приведения базиса к ортонормированному виду положен процесс ортогонализации Грама — Шмидта, который в свою очередь, реализуется рекуррентными формулами

В развернутом виде алгоритм ортогонализации и нормирования базиса содержит следующие условия:

Делим вектор ē ₁, на его норму; получим нормированный вектор ē _i=ē ₁/(||ē ₁ ||);
Формируем V2 = ē ₂ — (ē ₁, ē ₂)e ₁ и нормируем его, получим е ₂. Ясно, что тогда
(е1, е2) ~ (е1, е2) – (е1, ē ₂)( е1, е1) = 0;
Построив V3 = ē ₃– (e1, ē ₃)e1 – (e2, ē ₃) e2 и нормируя его, получим е3.

Для него имеем сразу же (е1, е3) = (е2, е3) = 0.
Продолжая такой процесс, получим ортонормированный набор ē _i, i = 1(1)s. Этот набор содержит линейно независимые векторы, поскольку все они взаимно ортогональны.
Убедимся в этом. Пусть выполняется соотношение

Если набор ē _i, i = 1(1)s зависимый, то хотя бы один сj коэффициент не равен нулю сj ≠ 0.

Умножив обе части соотношения на еj, получаем
(ej, c1∙e1 ) + (ej, c2∙e2 )+ …+ ( ej, cj∙ej ) +…+ ( ej, cs∙rs ) = 0.
Каждое слагаемое в сумме равно нулю как скалярное произведение ортогональных векторов, кроме (ej ,cj∙ej), которое равно нулю по условию. Но в этом слагаемом
(ej, ej) = 1 ≠ 0, следовательно, нулем может быть только cj.
Таким образом, допущение о том, что cj ≠ 0 неверно и набор является линейно независимым.

Пример 5. Задан базис 3-х мерного векторного пространства:
{<-1, 2 ,3, 0>,<0, 1, 2, 1>,<2,-1,-1,1>}.
Скалярное произведение определено соотношением:
(<x1,x2,x3,x4>,<y1,y2,y3,y4>) = x1∙y1+x2∙y2+x3∙y3+x4∙y4.
Процедурой ортогонализации Грама — Шмидта получаем систему векторов:
а1 = <-1, 2, 3, 0>; a2 = <0, 1, 2, 1>-4<-1, 2, 3,0>/7=<4,-1, 2, 7>/7;
a3 =<2, -1, -1, 1>+½<-1, 2, 3, 0> — <4, -1, 2, 7>/5 =<7, 2, 1, -4>/10.
(a1,a2)= (1+4+9+0) = 14;
a1 ^E =a1/√14;
a2-(a1^E,a2)∙a1^E=a2-(8/√14)(a1/√14)=a2 — 4∙a1/7;
Третий вектор читателю предлагается обработать самостоятельно.

Нормированные векторы получают вид:
a1 ^E =a1/√14;
a2 ^E =<4, -1, 2, 7>/√70;
a3 ^E =<7, 2, 1,-4>/√70;

Ниже в примере 6 дается подробный развернутый процесс вычислений получения ортонормированного базиса из простого (взятого наугад).

Пример 6. Привести заданный базис линейного векторного пространства к ортонормированному виду.
Дано: векторы базиса

Подпространства векторных пространств

Структура векторного пространства

Представление объектов (тел) в многомерных пространствах весьма непростая задача. Так, четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы, и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени «образность» и наглядность объекта или его частей способствует более успешному его изучению.

Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что рассмотрение многомерных и тем более бесконечномерных пространств и объектов в них лишает нас наглядности представлений, что весьма затрудняет исследование объектов в таких
пространствах. Даже, казалось бы, такие простые вопросы, как количественные характеристики элементов многогранников (число вершин, ребер, граней, и т. п.) в этих пространствах решены далеко не полностью.

Конструктивный путь изучения подобных объектов состоит в выделении их элементов (например, ребер, граней) и описании их в пространствах меньшей размерности. Так четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени
«образность» и наглядность объекта или его частей способствует более успешному их изучению.

Если L – расширение поля К, то L можно рассматривать как векторное (или линейное) пространство над полем К. Элементы поля L (т. е. векторы) образуют по сложению абелеву группу. Кроме того, каждый «вектор» а є L может быть умножен на «скаляр» r є K, и при этом произведение ra снова принадлежит L (здесь ra – просто произведение в смысле операции поля L элементов r и а этого поля). Выполняются также законы
r∙(a+b) = r∙a+r∙b, (r+s)∙a = r∙a + r∙s, (r∙s)∙a = r∙(s∙a) и 1∙а = а, где r,s є K, a,b є L.

Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что основным результатом при таком подходе является сокращение размерности выделяемых подпространств. Пусть в векторном линейном пространстве L выделены подпространства L1 и L2. В качестве базиса L1 выбирается меньший набор еi, i = 1(1)s1, s1 < s, чем в исходном L.

Оставшиеся базисные векторы порождают другое подпространство L2, называемое «ортогональным дополнением» подпространства L1. Будем использовать запись L = L1 + L2. Она означает не то, что все векторы пространства L принадлежат либо L1, либо L2,, а то, что любой вектор из L можно представить в виде суммы вектора из L1 и ортогонального ему вектора из L2.
Разбивается не множество векторов векторного пространства L, а размерность d(L) и набор базисных векторов. Таким образом, подпространством L1 векторного пространства L называется множество L1, его элементов (меньшей размерности), само являющееся векторным пространством относительно введенных в L операций сложения и умножения на число.

Каждое линейное векторное подпространство Li – содержит нулевой вектор и вместе с любыми своими векторами содержит и все их линейные комбинации. Размерность любого линейного подпространства не превосходит размерности самого исходного пространства.

Пример 7. В обычном трехмерном пространстве подпространствами являются все прямые (размерность s =1) линии, плоскости (размерность s = 2), проходящие через начало координат. В пространстве Рn многочленов степени не выше n подпространствами будут, например, все Рk при k < n, так как складывая и умножая на числа многочлены степени, не выше k, снова будут получаться такие же многочлены.

Однако, каждое из пространств Рп содержится в качестве подпространств в пространстве Р всех многочленов с вещественными коэффициентами, а это последнее является подпространством пространства С непрерывных функций.

Матрицы одинакового типа над полем действительных чисел также образуют линейное векторное пространство, так как для них выполняются все аксиомы векторных пространств. Векторное пространство L2 наборов длины n, каждый из которых ортогонален подпространству L1 наборов длины п, образует подпространство L2, называемое нулевым пространством для L1. Другими словами, каждый вектор из L2 ортогонален каждому вектору из L1 и наоборот.

Оба подпространства L1 и L2 являются подпространствами векторного пространства L наборов длины п. В теории кодирования [4] каждое из подпространств L1 и L2 порождает линейный код, двойственный по отношению к коду, порожденному другими подпространства-ми. Если L1 есть (п, k)-код, то L2 — это (п, п – k)-код. Если код является векторным пространством строк некоторой матрицы, то двойственный к нему код — нулевое пространство этой матрицы и наоборот.

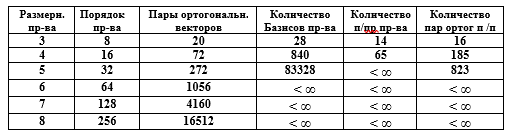
Важным вопросом при изучении векторных пространств Vn является установление их структуры (строения). Другими словами, интерес представляют элементы, их совокупности (подпространства размерности 1<k<п ), а также их отношения (упорядоченность, вложенность и т.п.). Будем считать заданным векторное пространство Vn над конечным полем GF(q), образованным q = р r элементами, где р — простое число, r — целое.
Известны следующие результаты.

Количества подпространств векторного пространства

Приведем следующее обоснование. Каждый вектор v1 ≠ 0 из системы k линейно независимых ( v1,v2,…,vk ) векторов может быть выбран qⁿ – 1 способами. Следующий вектор v2 ≠ 0 не может быть выражен линейно через v1, т.е. может быть выбран qⁿ – q способами и т.д.

Последний вектор vk ≠ 0 также линейно не выражается через предыдущие выбранные векторы v1,v2,…,vk и, следовательно, может быть выбран qⁿ – q^k – 1 способами. Общее число способов для выбора совокупности векторов v1,v2,…,vk, таким образом, определится как произведение числа выборов отдельных векторов, что и дает формулу (1). Для случая, когда k = п, имеем wп = wn, n и из формулы (I) получаем формулу (2).

Важные обобщающие результаты о размерностях подпространств.
Совокупность всех наборов длины n, ортогональных подпространству V1 наборов длины n, образует подпространство V2 наборов длины n. Это подпространство V2 называется нулевым пространством для V1.
Если вектор ортогонален каждому из векторов, порождающих подпространство V1, то этот вектор принадлежит нулевому пространству для V1.
Примером (V1) может служить множество 7-разрядных векторов порождающей матрицы (7,4)-кода Хемминга, с нулевым подпространством (V2) 7-разрядных векторов, образующих проверочную матрицу этого кода.

Если размерность подпространства (V1) наборов длины n равна k, то размерность нулевого подпространства (V2) равна n — k.

Если V2 — подпространство наборов длины n и V1 — нулевое пространство для V2, то (V2) — нулевое пространство для V1.

Пусть U∩V обозначает совокупность векторов, принадлежащих одновременно U и V, тогда U∩V является подпространством.

Пусть U⊕V обозначает подпространство, состоящее из совокупности всех линейных комбинаций вида au +bv, где u є U, v є V, a b — числа.

Сумма размерностей подпространств U∩V и U⊕V равна сумме размерностей подпространств U и V.

Пусть U2 — нулевое подпространство для U1, а V2 -нулевое пространство для V1. Тогда U2∩V2 является нулевым пространством для U1⊕V1.

Заключение

В работе рассмотрены основные понятия векторных пространств, которые часто используются при построении моделей анализа систем шифрования, кодирования и стеганографических, процессов, протекающих в них. Так в новом американском стандарте шифрования использованы пространства аффинные, а в цифровых подписях на эллиптических кривых и аффинные и
проективные (для ускорения обработки точек кривой).

Об этих пространствах в работе речь не идет (нельзя валить все в одну кучу, да и объем публикации я ограничиваю), но упоминания об этом сделаны не зря. Авторы, пишущие о средствах защиты, об алгоритмах шифров наивно полагают, что понимают детали описываемых явлений, но понимание евклидовых пространств и их свойств без всяких оговорок переносится в другие пространства, с другими свойствами и законами. Читающая аудитория вводится в заблуждение относительно простоты и доступности материала.

Создается ложная картина действительности в области информационной безопасности и специальной техники (технологий и математики).

В общем почин мною сделан, насколько удачно судить читателям.

Литература

1. Авдошин С.М., Набебин А.А. Дискретная математика. Модулярная алгебра, криптография, кодирование. — М.: ДМК Пресс, 2017. -352 с.
2. Акимов О.Е. Дискретная математика.Логика, группы, графы- М.: Лаб.Баз. Зн., 2001. -352 с.
3. Андерсон Д.А. Дискретная математика и комбинаторика.- М.: Вильямс, 2003. -960 с.
4. Берлекэмп Э. Алгебраическая теория кодирования. -М.: Мир,1971.- 478 с.
5. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 1- СПб.: ВКА им. А.Ф. Можайского, 2015. -219 с.
6. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 2- СПб.: ВКА им. А.Ф. Можайского, 2017. -151 с.
7. Горенстейн Д. Конечные простые группы. Введение в их классификацию.-М.: Мир,1985.- 352 с.
7. Грэхем Р., Кнут Д., Пташник О. Конкретная математика.Основание информатики.-М.: Мир,1998.-703 с.
9. Елизаров В.П. Конечные кольца.- М.: Гелиос АРВ,2006. — 304 с.
Иванов Б.Н. Дискретная математика: алгоритмы и программы-М.: Лаб.Баз. Знаний., 2001. -280 с.
10. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения-М.: Вузовская книга, 2000.-280 с.
11. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.-М.: Наука, 1973.-832 с.
12. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.1 -М.: Мир,1988. — 430 с.
13. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.2 -М.: Мир,1988. — 392 с.
14. Ляпин Е.С., АйзенштатА.Я., Лесохин М.М., Упражнения по теории групп.- М.: Наука,1967.-264 с.
15. Муттер В.М. Основы помехоустойчивой телепередачи информации. -Л. Энергоатомиздат,1990.- 288 с.
16. Набебин А.А.Дискретная математика.- М.: Лаб.Баз. Знаний., 2001. -280 с.
17. Новиков Ф.А. Дискретная математика для программистов.- СПб.: Питер, 2000. -304 с.
18. Розенфельд Б.А. Многомерные пространства.-М.: Наука,1966.-648 с.
18. Холл М. Теория групп.-М.: Изд. ИЛ, 1962.- 468 с.
19. Шиханович Ю.А. Группы, кольца, решётки. — СПб.: Кирцидели,2006. — 368 с.
20. Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях: В 2-х ч Ч.2.-Мн.: Выш. шк., 1987. -256 с.
21. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел.- Минск: Дизайн ПРО, 2000. -240 с.

линейная оболочка , где – коэффициенты, а – собственные векторы матриц

А что за коэффициенты ? Они подобраны так, чтобы достигалось равенство?
Эти две матрицы (обозначим их и ) симметричны, а значит, диагонализируемы, следовательно, существует базис в , состоящий из собственных векторов (или ). Какие-нибудь три собственных вектора , образующих базис, обозначим , а какие-нибудь три собственных вектора , образующих базис, обозначим . (Требование «образующих базис» необходимо, потому что три произвольных собственных вектора могут оказаться линейно зависимыми.) Но теперь произвольный вектор может быть разложен как по первому, так и по второму базису:

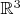
Иначе говоря, подпространство всех векторов вида (и аналогично ) совпадает со всем пространством.
Поэтому непонятно, что даёт это равенство.

Вы можете указать все одномерные инвариантные подпространства и все одномерные инвариантные подпространства (пока не заботясь, чтобы они были общими)?