10. Линейная зависимость и независимость векторов
Рассмотрим далее основополагающие в линейной алгебре понятие о линейной зависимости и независимости векторов, а также определение базиса системы векторов.
Любую конечную последовательность векторов 




Система векторов 

Линейная зависимость и независимость есть свойства системы векторов. Однако часто соответствующие прилагательные относят и к самим векторам. Поэтому вместо «линейно независимая система векторов» допустимо говорить «линейно независимые векторы».
Например, двумерные арифметические векторы 






Если взять векторы 



Из определения линейной зависимости (независимости) системы векторов вытекают следующие утверждения.
1) Если некоторая система векторов содержит нулевой вектор, то она является линейно зависимой.
Пусть для определенности первый вектор системы является нулевым, т. е.
Тогда линейная комбинация векторов вида 
2) Если среди векторов системы есть такие, которые сами образуют линейно зависимую подсистему, то вся система также линейно зависима.
Так как исходная подсистема линейно зависима, то среди коэффициентов линейной комбинации векторов подсистемы имеется хотя бы один отличный от нуля. Добавим к этой линейной комбинацию линейную комбинацию векторов, не вошедших в исходную подсистему, с числовыми коэффициентами, равными нулю. Мы получим линейную комбинацию из векторов полной системы, которая равна нулевому вектору, причем имеется хотя бы один коэффициент отличный от нуля. Таким образом, наше утверждение доказано.
3) Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Если предположить обратное, т. е. существование некоторой линейно зависимой подсистемы, то по предыдущему утверждению отсюда следует зависимость исходной системы, что противоречит условию доказываемой теоремы. Полученное противоречие доказывает сформулированное утверждение.
4) Для того чтобы система из 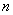
Необходимость. Пусть система векторов 

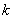

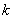


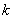




Достаточность. Пусть имеется некоторый вектор 


По аналогичной схеме доказывается следующее утверждение.
5) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы может быть представлен в виде линейной комбинации остальных векторов.
Как найти подсистему системы векторов
Определение 1. Система векторов 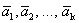
Определение 1´. Система векторов 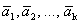
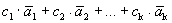
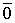
Покажем, что эти определения эквивалентны.
Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:
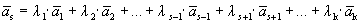
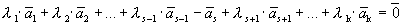
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна 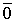
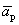
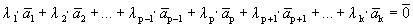
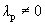
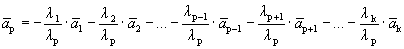
Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.
Определение 2. Единичным вектором, или ортом, 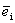
. 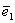
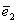
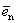
Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.
Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.
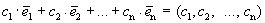
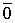
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.
Каждый вектор n -мерного пространства ā(а 1 , а 2 , . а n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора
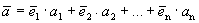
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.
Доказательство. Пусть дана система векторов 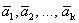
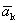
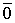
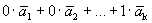
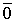
Следовательно, система линейно зависима.
Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.
Доказательство. Дана система векторов 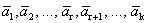
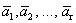
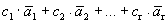
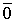
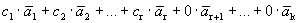
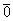
Получилось, что линейная комбинация векторов всей системы равна 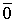
Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.
Теорема 4 (теорема Штейница). Если каждый из векторов 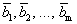
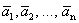
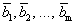
Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.
Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.
Как найти подсистему системы векторов
1.4. РАНГ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим систему векторов (1.1), где . Максимальной линейно независимой подсистемой системы векторов (1.1) называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы (1.1) линейно выражается через векторы этого набора. В общем, система векторов (1.1) может иметь несколько разных максимальных линейно независимых подсистем.
Теорема 1. 6. Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.
Число векторов в максимальной линейно независимой подсистеме системы векторов (1.1) называется рангом последней. Системы векторов (1.1) и (1.2) называются эквивалентными, если векторы системы (1.1) линейно выражаются через систему векторов (1.2) и наоборот.
Теорема 1. 7. Ранги эквивалентных систем векторов равны.
Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:
1) изменение нумерации векторов в системе;
2) удаление нулевого вектора;
3) удаление вектора, являющегося линейной комбинацией остальных векторов системы;
4) умножение произвольного вектора системы на любое, не равное нулю число;
5) прибавление к одному из векторов системы линейной комбинации остальных векторов системы.
[spoiler title=”источники:”]
http://lms2.sseu.ru/courses/eresmat/course1/razd8z1/par8_5z1.htm
http://www.math.mrsu.ru/text/courses/method/rang_sist_vect.htm
[/spoiler]
Пример 1. Доказать, что следующее
множество образует векторное пространство
над полем
относительно операций сложения матриц
и умножения матриц на число.
Найти его базис и размерность.
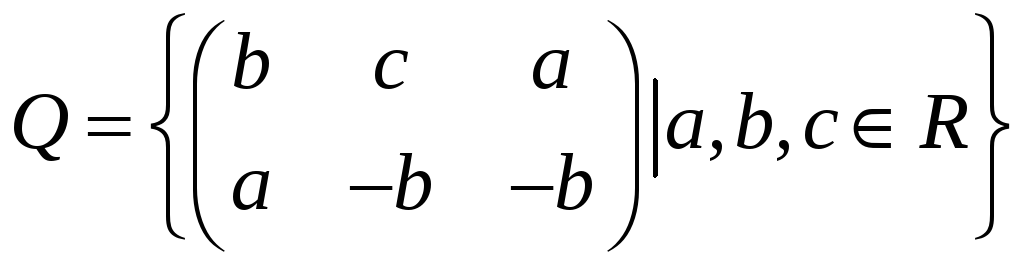
Решение.
является непустым подмножеством
пространства матриц размерности
.
Докажем, что
является подпространством в
,
пользуясь критерием подпространства.
Пусть
и
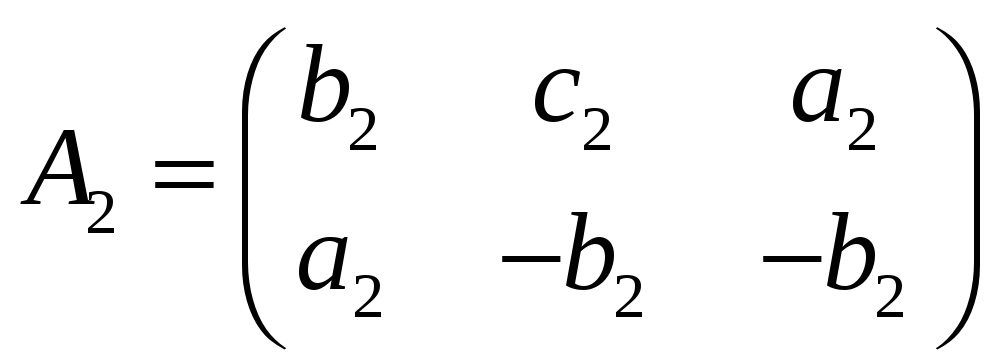
произвольные матрицы из
.
Рассмотрим их сумму
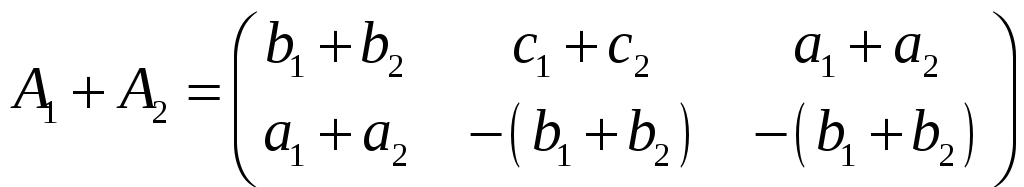
Очевидно
.
Произведение
на любое число
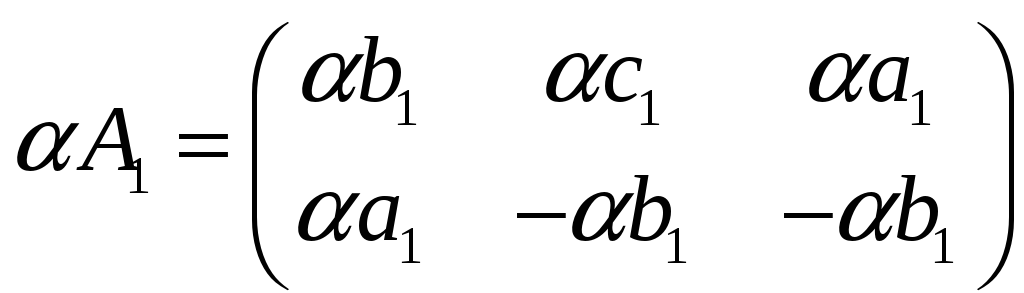
также принадлежит
.
Итак,
является подпространством пространства
,
а значит, само является пространством.
Найдем базис этого пространства.
Ясно, что в базис можно включить,
например,
, так как
.
Так как
, то
нельзя получить в виде
.
Поэтому в качестве второго базисного
вектора можно взять
.
Рассмотрим вектор
.
Его нельзя представить в виде линейной
комбинации
и
,
так как
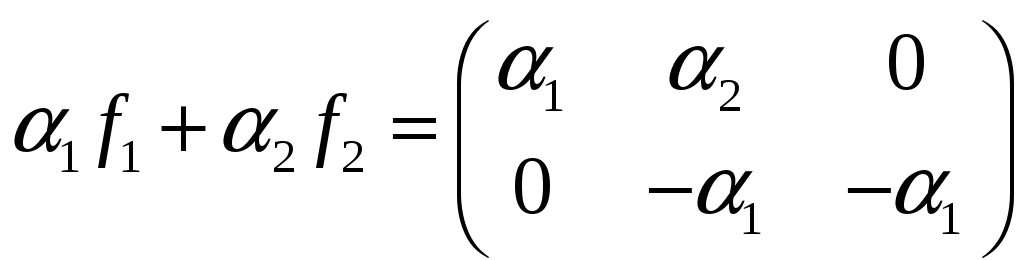
Поэтому в качестве третьего базисного
вектора возьмем
.
Всякий другой вектор
можно представить в виде линейной
комбинации
.
.
Следовательно, система векторов
является системой образующих пространства
.
По построению, эта система линейно
независима. Значит, она является базисом.
Пример2. Выяснить, является ли
система векторов
линейно зависимой. Найти коэффициенты
линейной зависимости.
Решение. Пусть
,
где
— некоторые числа. Подставляем в это
равенство векторы
.
.
После выполнения операции над векторами
получаем
,
откуда
Эту систему линейных уравнений решаем
методом Гаусса:
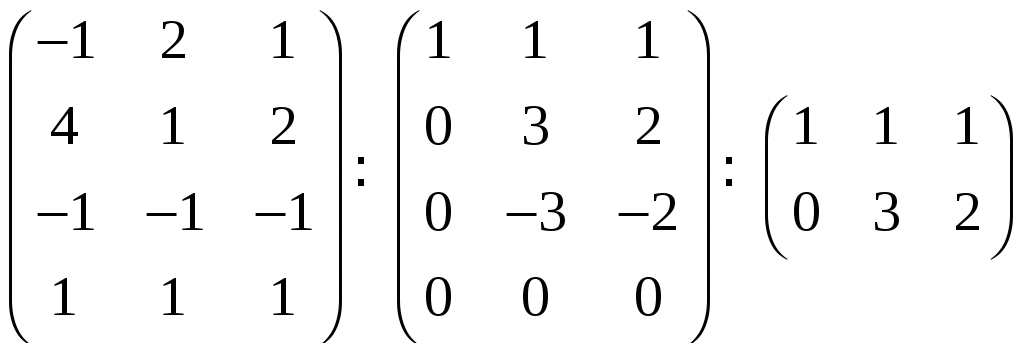
Получилась трапецеидальная система
уравнений. Она является неопределенной
и потому имеет ненулевые решения (кроме
нулевого). Таким образом, система
линейно зависима. Найдем коэффициенты
линейной зависимости. Для этого решаем
однородную систему линейных уравнений,
приведенную к трапецеидальному виду
Общее решение этой системы имеет вид
.
Найдем частное решение, придавая
произвольное значение, отличное от
нуля, например, -3. Получим
.
Таким образом,
.
Очевидно, коэффициенты линейной
зависимости определяются неоднозначно.
Пример 3. Найти какую-нибудь
максимальную линейно независимую
подсистему данной системы векторов, а
остальные векторы выразить через нее.
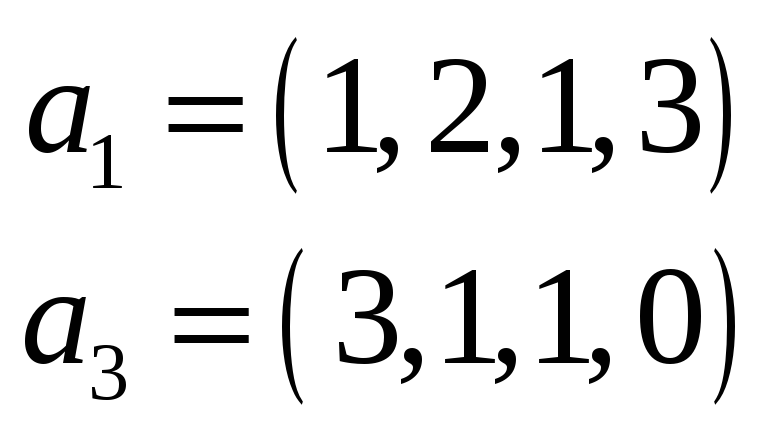
Решение. Составим матрицу
,
столбцами которой являются данные
векторы, и найдем ее ранг. Будем делать
элементарные преобразования только
над строками.
Первую строку, умноженную на соответствующие
числа -2, -1, -3, прибавили ко второй, третьей,
четвертой. Третью строку, умноженную
на соответствующие числа -2, -4, прибавили
ко второй и четвертой. И наконец, третью,
умноженную на 2, прибавили к четвертой.
Так как минор третьего порядка
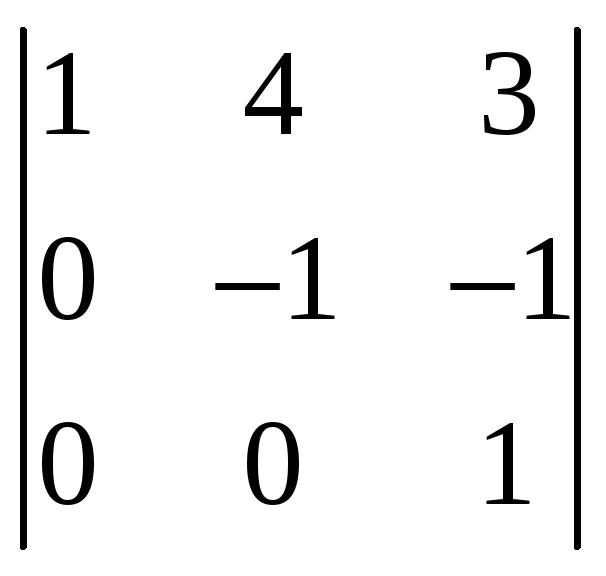
Отличен от нуля, а определитель четвертого
порядка равен нулю, то ранг последней
матрицы, а значит, ранг матрицы
равен 3. Отсюда следует, что ранг данной
системы равен 3.
Три вектора входят в максимальную
линейно независимую подсистему данной
системы. Очевидно, что это векторы
.Действительно,
выразим вектор
через
:
.
Подставим в это уравнение выражения
векторов
.
После выполнения операций над векторами
получим:
.
Приравнивая соответствующие координаты,
получим систему линейных уравнений:
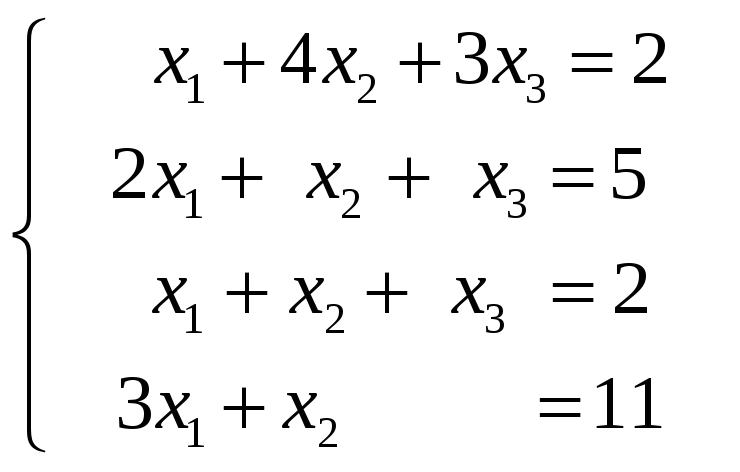
Решаем эту систему методом Гаусса.
Составим расширенную матрицу
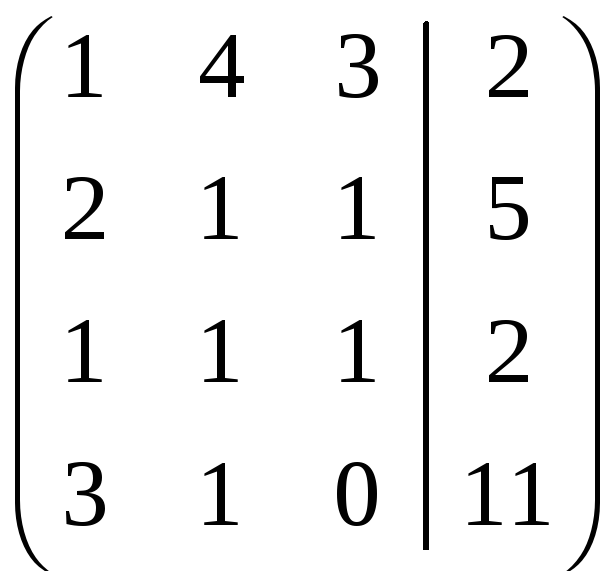
Эта матрица совпадает с матрицей
.
Так как мы проделываем элементарные
преобразования над строками матрицы
,
то эта система эквивалентна системе
линейных уравнений, соответствующей
последней матрице:
, то есть системе
, откуда
,
а следовательно,
.
Пример 4. Векторы
заданы своими координатами в некотором
базисе
.
Показать, что векторы
сами образуют базис, и найти координаты
вектора
в этом базисе.
Решение. Так как система любых трех
линейно независимых векторов является
базисом 3-мерного пространства, то
достаточно доказать, что система
линейно независима. Для этого составим
матрицу
,
столбцами которой являются координаты
векторов
,
и найдем ее ранг.
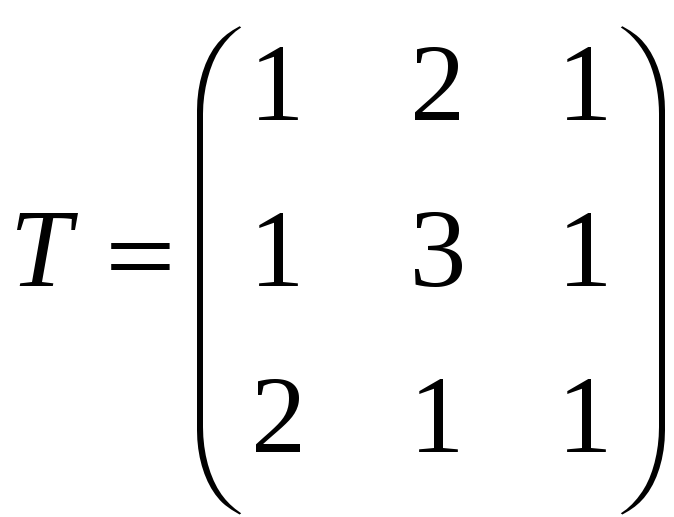
Определитель этой матрицы
,
а значит, по теореме о ранге, ранг матрицы
равен 3, что доказывает линейную
независимость системы
.
Таким образом,
образуют базис и
-матрица
перехода от базиса
к базису
.
Для нахождения координат вектора в
базисе
воспользуемся формулой преобразования
координат, приведенной в
:
, где
— матрица перехода от базиса
к базису
;
— координаты вектора в базисе
;
— координаты вектора
в базисе
.
Так как здесь
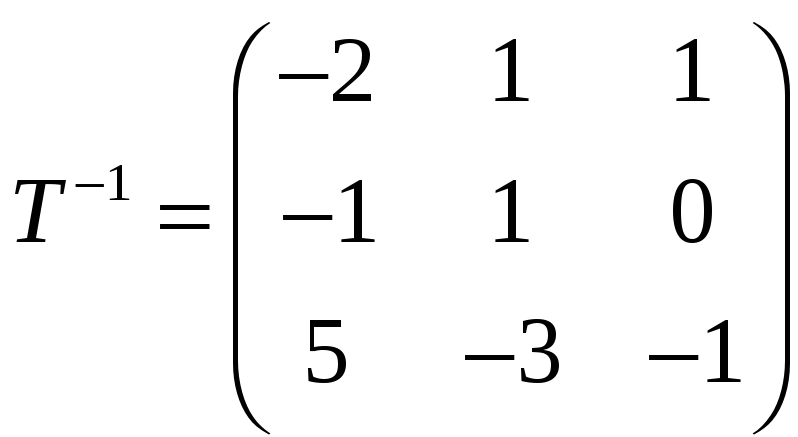
то
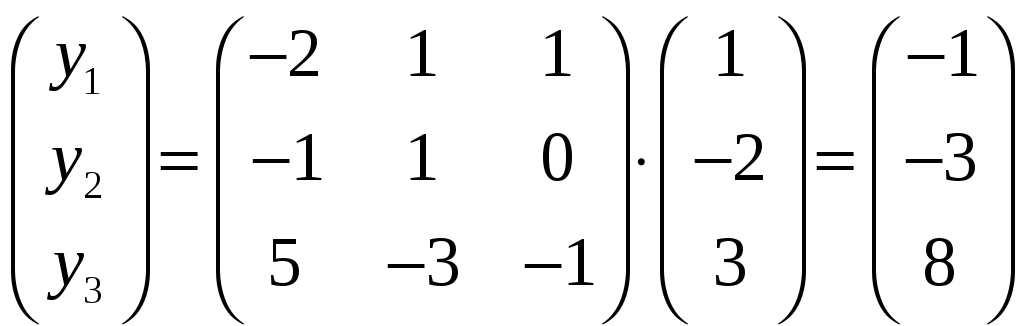
Откуда
,
то есть
.
Пример 5. Найти размерность и базис
линейного подпространства, натянутого
на векторы
Решение. Базис линейного подпространства
совпадает с максимальной линейно
независимой подсистемой системы векторов
(доказать!). Найдем эту подсистему, для
чего составим матрицу, столбцами которой
являются векторы
.
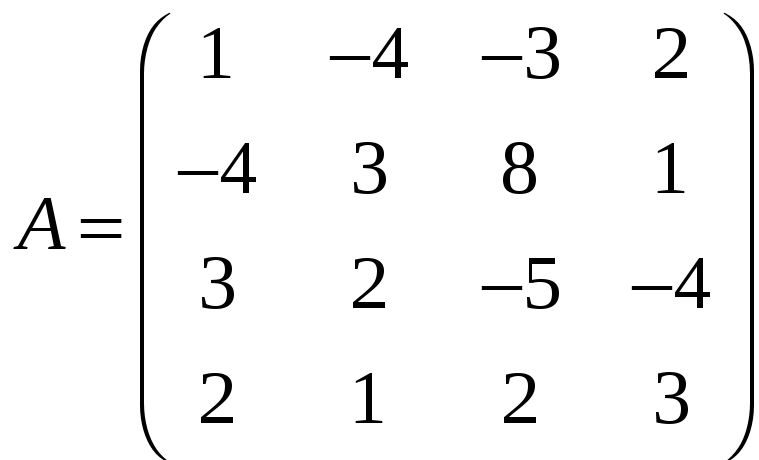
Найдем базисный минор этой матрицы. Так
как минор второго порядка
,
то рассмотрим минор 3-го порядка, его
окаймляющий
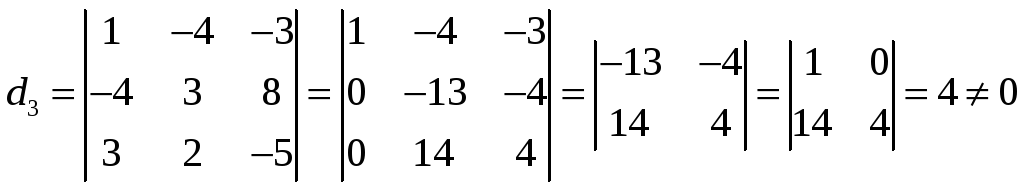
Теперь рассмотрим минор 4-го порядка,
окаймляющий минор 3-го порядка, отличный
от нуля. Это определитель матрицы
.
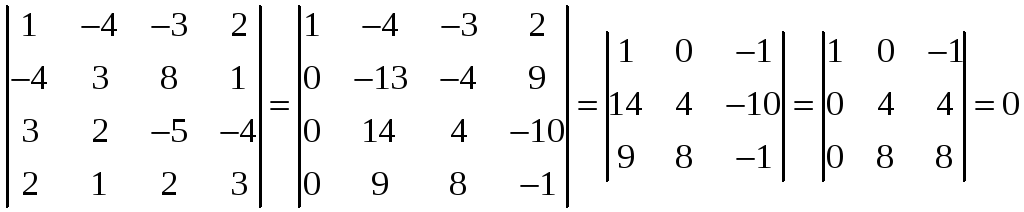
Он равен нулю. Значит,
является базисным минором, то есть
минором наибольшего порядка, отличным
от нуля. А тогда
образуют максимальную линейно-независимую
подсистему системы
и тем самым
образуют базис рассматриваемого
подпространства, причем размерность
подпространства равна 3.
Пример 6. Определить размерность и
базис пространства решений однородной
системы линейных уравнений.
Решение. Множество всех решений
однородной системы линейных уравнений
образует векторное пространство
размерности
,
где
— число неизвестных системы, а
— ранг матрицы этой системы. Базис
образует система из любых
линейно независимых частных решений.
Такая система решений называется
фундаментальной. Находим общее решение
системы методом Гаусса, для чего
составляем матрицу системы:
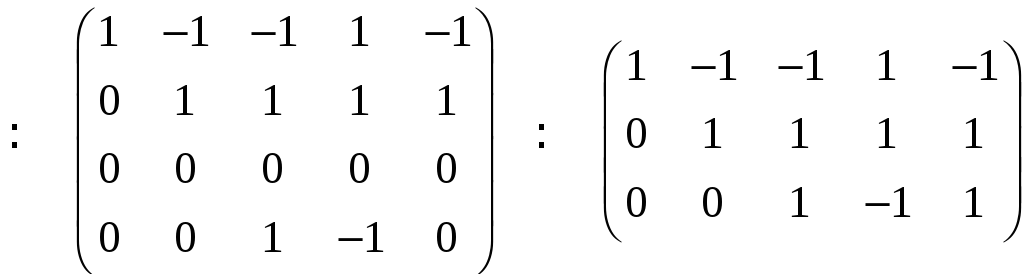
Ранг матрицы равен трем. Следовательно,
размерность пространства решений равна
2
.
Данную систему уравнений заменим
эквивалентной системой:
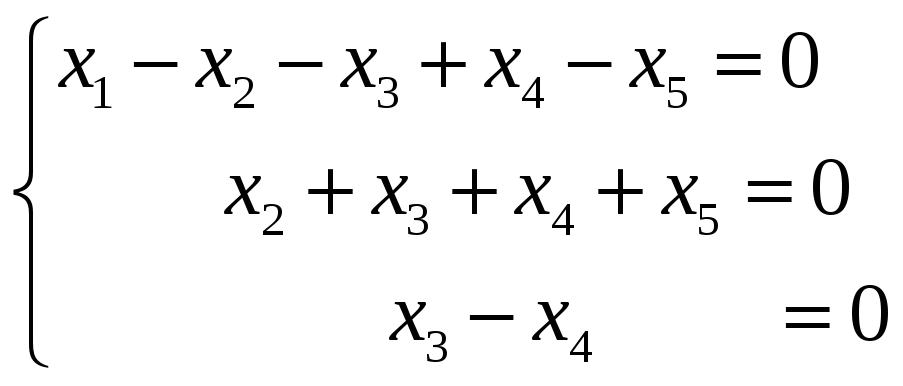
В качестве свободных неизвестных можно
взять
.
Тогда
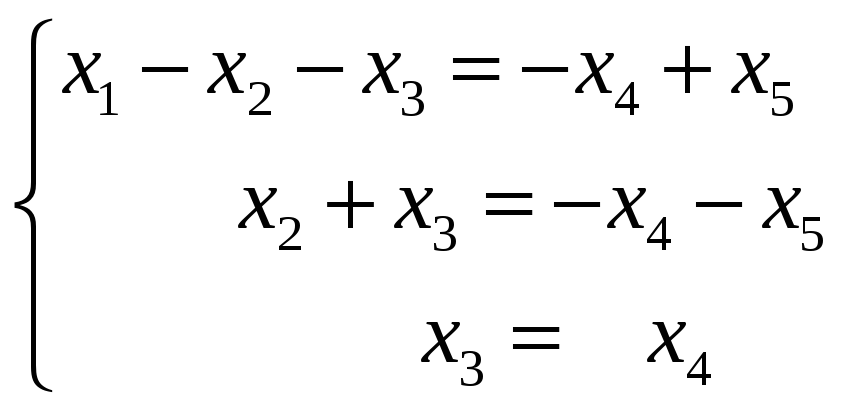
Общее решение системы имеет вид
.
Находим два линейно независимых частных
решения. Для их нахождения мы два раза
придаем
и
произвольные значения, но так, чтобы
определитель второго порядка, составленный
из этих значений, был отличен от нуля.
Положим
,
а затем
и найдем
Мы получим один из базисов пространства
решений данной однородной системы
уравнений.
Пример 7. Найти базис и размерность
пересечения подпространств
и
,
натянутых на системы векторов
и
соответственно, если векторы заданы
координатами в некотором базисе
пространства.
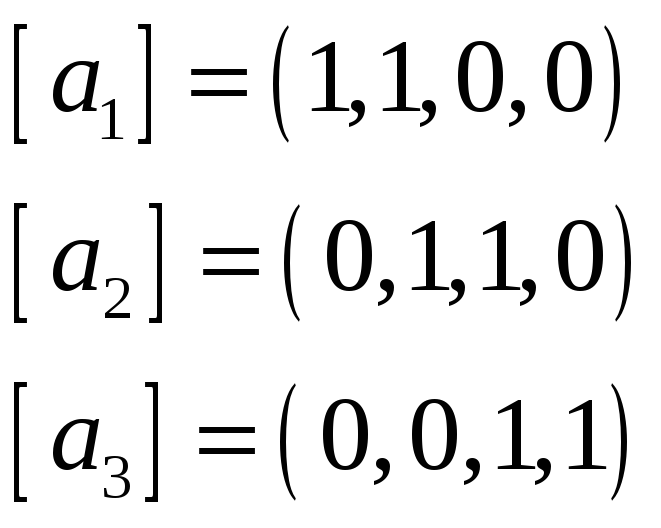
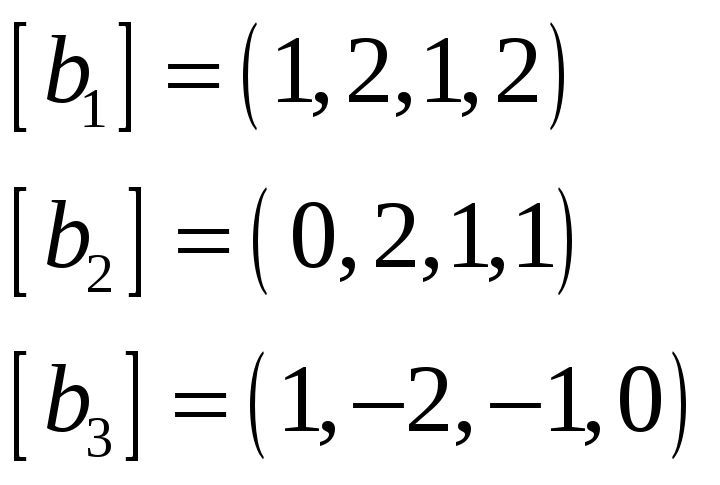
Решение. Вектор
тогда и только тогда, когда
линейно выражается через
и через
.
А для этого необходимо и достаточно,
чтобы ранг матрицы
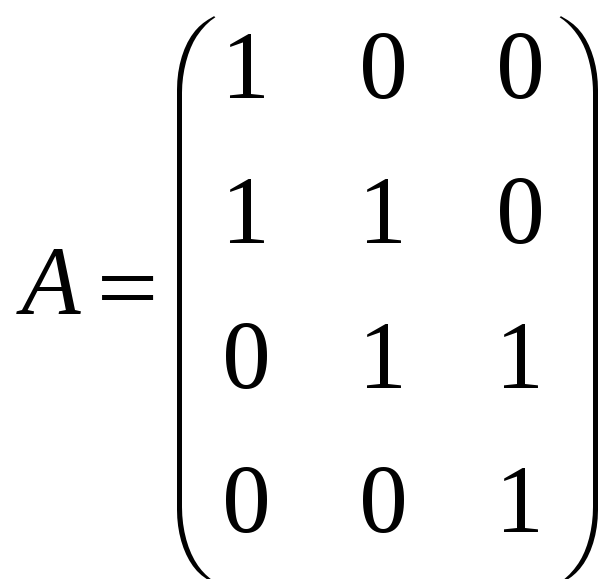
был равен рангу матрицы
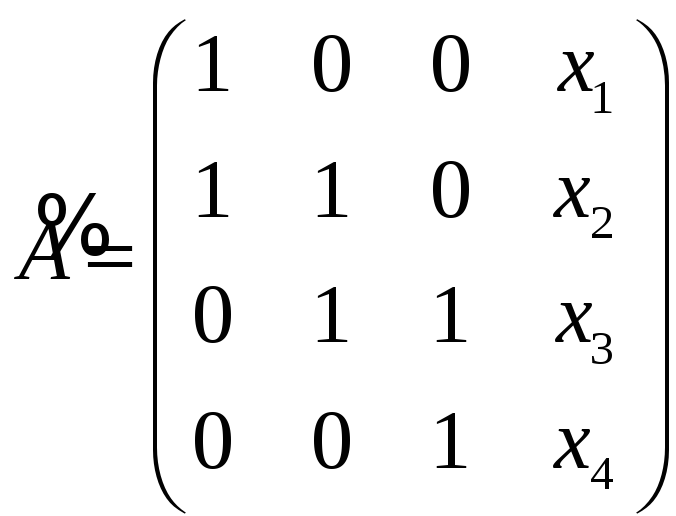
и ранг матрицы
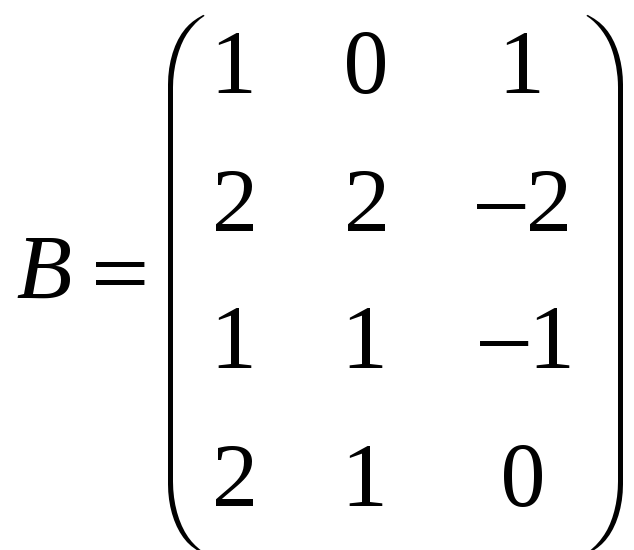
был равен рангу матрицы
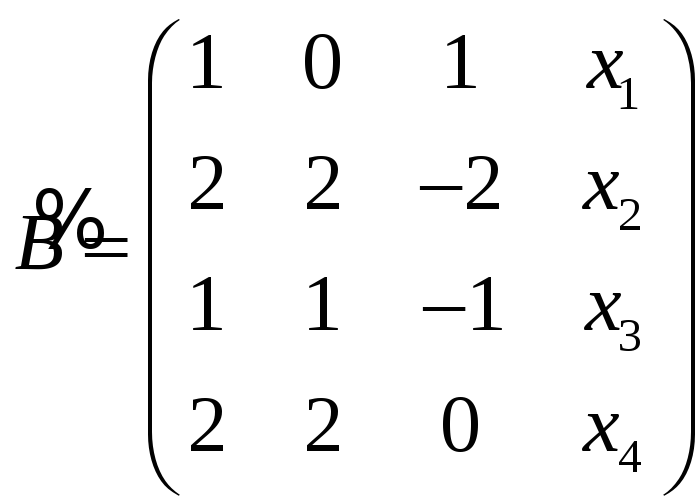
Выберем базисные миноры
и
матриц
и
соответственно. Для того, чтобы
и
,
необходимо и достаточно, чтобы
был базисным минором в
,
а
— в
.
Приравнивая нулю все миноры
и
,
окаймляющие соответственно
и
,
содержащие столбец
и имеющие порядок на единицу выше, чем
и
,
получим систему линейных уравнений.
Решаем эту систему методом Гаусса.

.
Общее решение имеет вид
.
Фундаментальная система состоит из
одного вектора
.
Следовательно, вектор
образует базис подпространства
.
Литература: 3 — §17,
18
5 — №№ 608-613, 624-626, 636-650, 652-655, 661-669, 672, 674,
681, 689-695, 702-704, 712-714, 724-727, 1277-1293, 1296-1305,
1309-1311, 1317, 1318, 1320, 1321.
Контрольная работа 2
Найти значение многочлена
и всех его производных в точке
.
1.
2.
3.
4.
5.
6.
Найти рациональные корни и определить
их кратность.
7.
8.
9.
10.
11.
.
12.
.
Разложить на неприводимые множители
над полем
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
Найти каноническое разложение многочлена
над полем путем отделения кратных
корней.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
Найти значение симметрического
многочлена
на корнях многочлена
.
25.
26.
27.
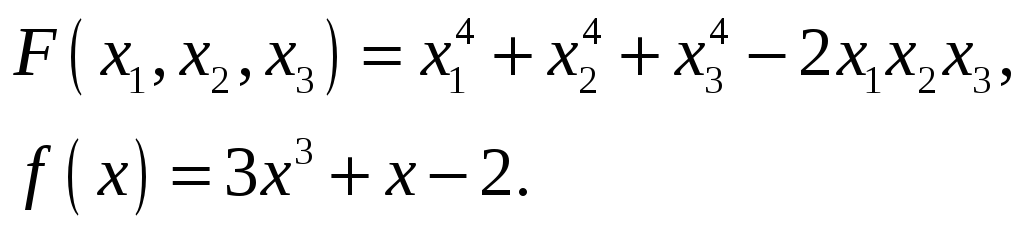
28.
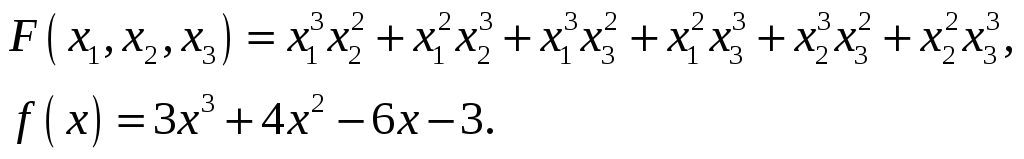
29.
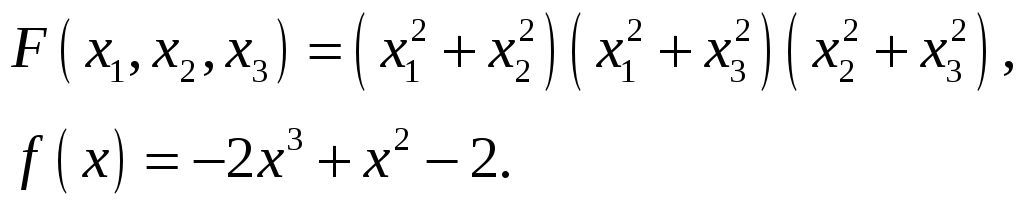
30.
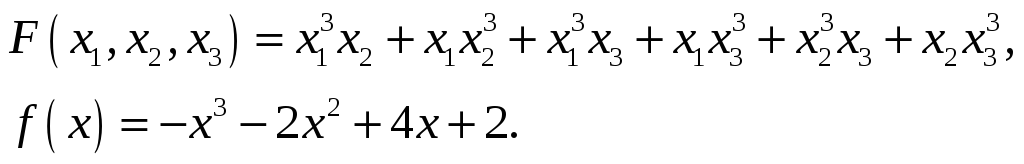
Доказать, что следующее множество
образует векторное пространство над
полем
.
Найти его базис и размерность.
31.
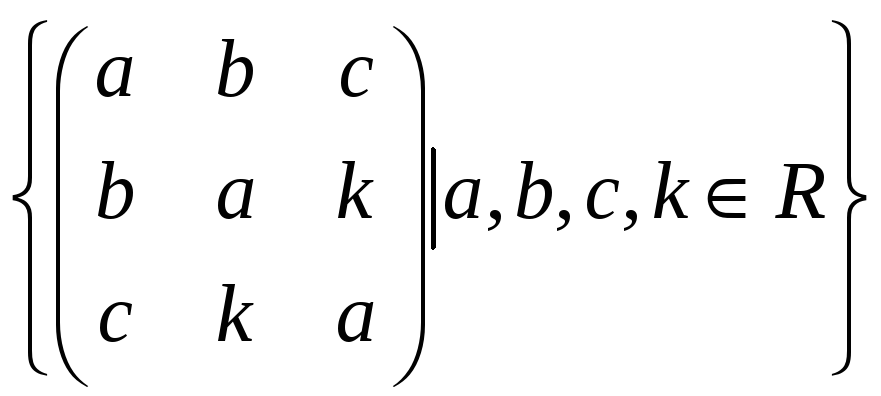
32.
.
33.
.
34.
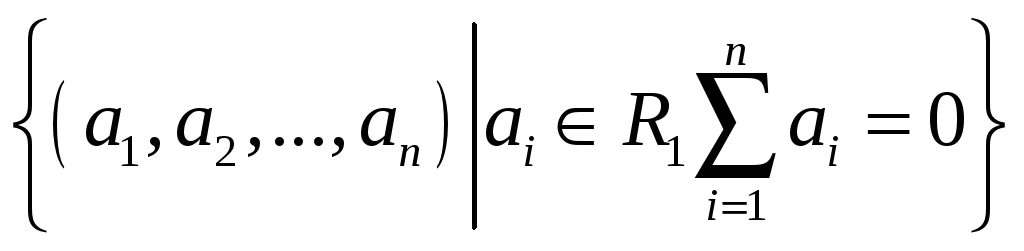
35.
.
36.
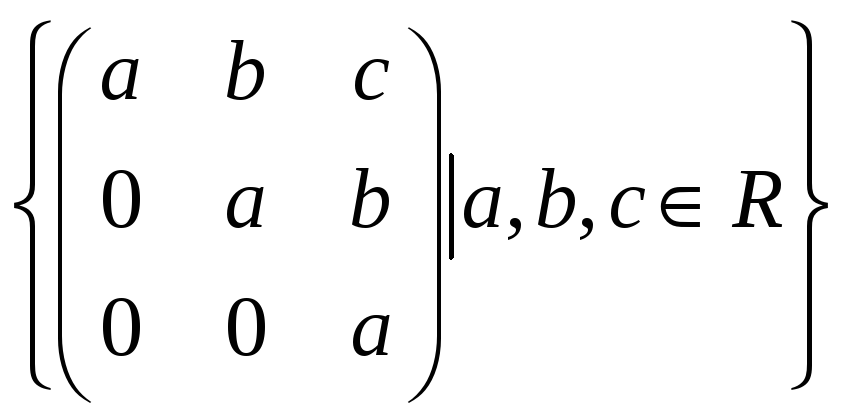
Выяснить, является ли система векторов
линейно зависимой. Найти коэффициенты
линейной зависимости.
37.
38.
39.
40.
41.
42.
Найти какую-нибудь максимальную
независимую подсистему данной системы
векторов, а остальные векторы выразить
через нее.
43.
44.
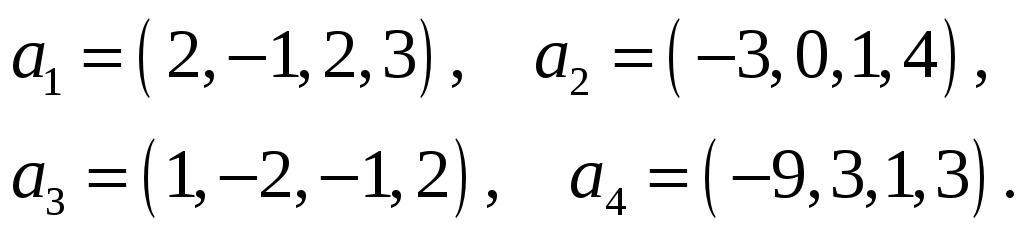
45.
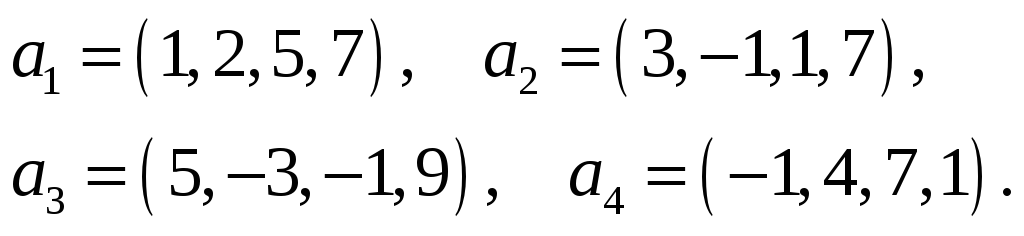
46.
47.
48.
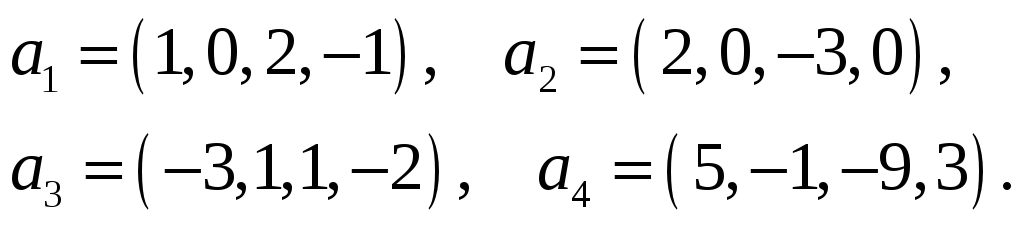
Векторы
и
заданы своими координатами в некотором
базисе
.
Показать, что векторы
сами образуют базис, и найти координаты
вектора
в этом базисе.
49.
50.
51.
52.
53.
54.
Найти размерность и базис пространства
решений однородной системы линейных
уравнений.
55.
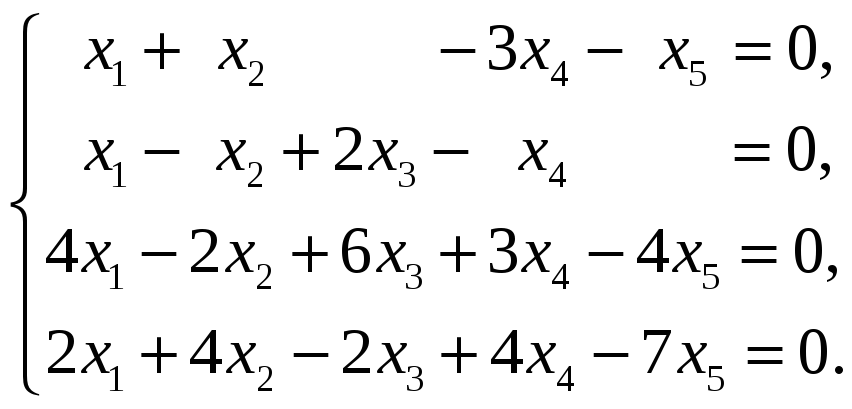
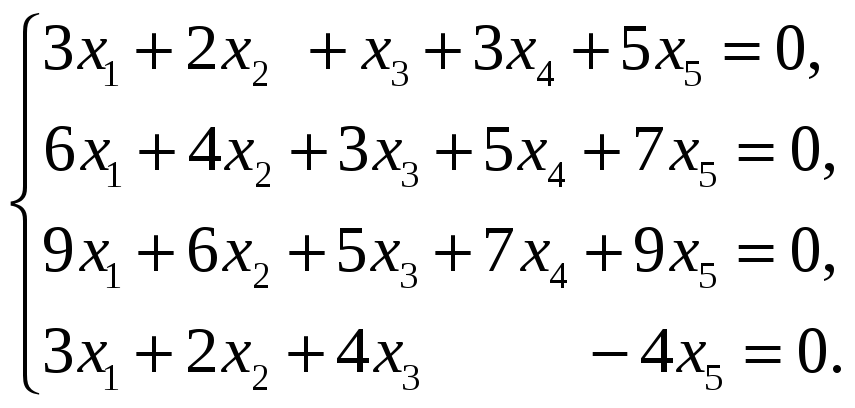
56.
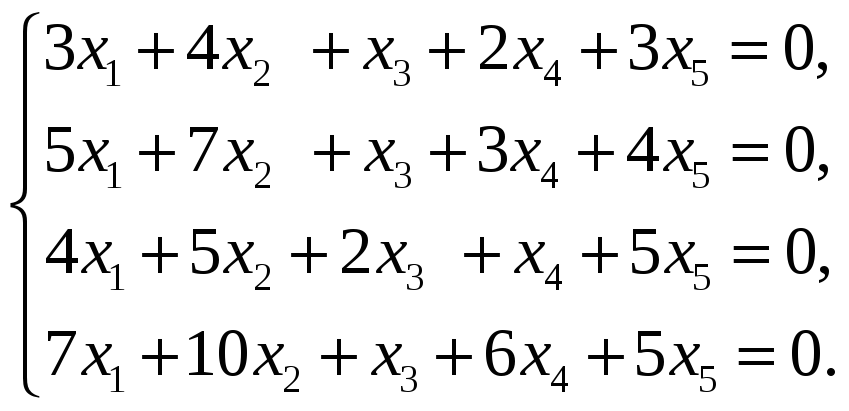
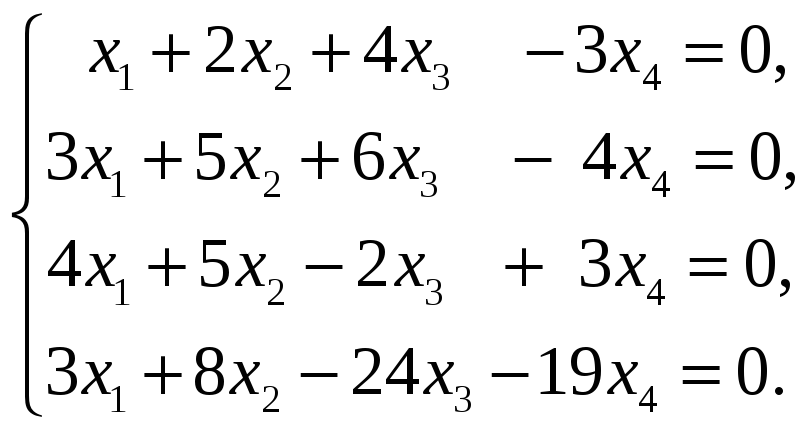
59.
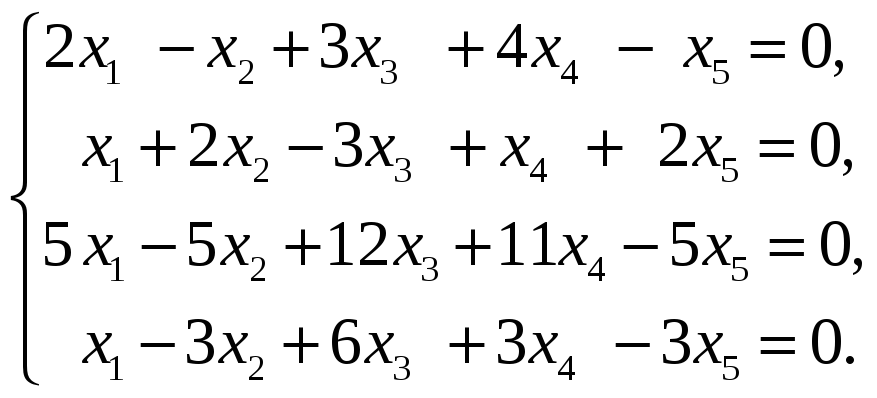
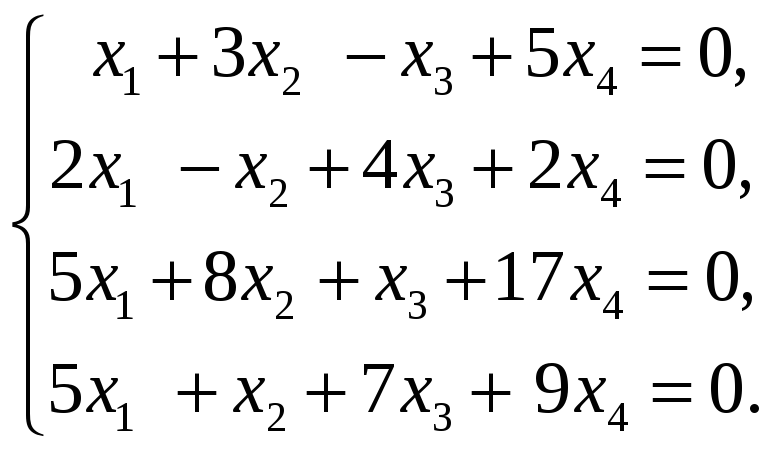
Найти базис пересечения подпространств
и
,
натянутых на векторы
и
соответственно, если все векторы заданы
своими координатами в некотором базисе
пространства.
61. 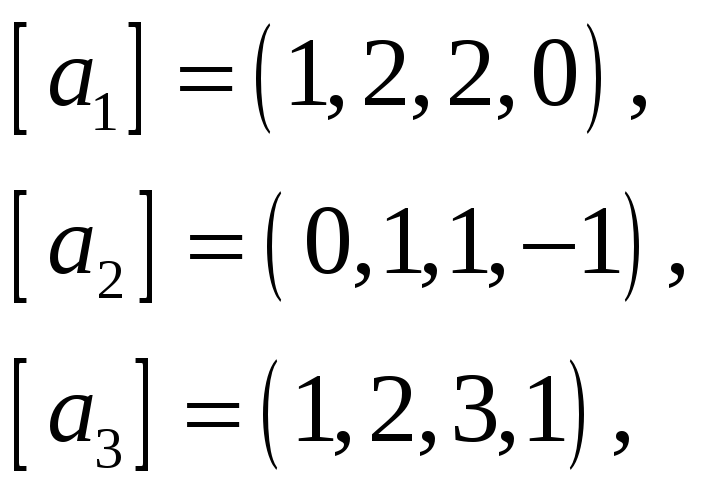
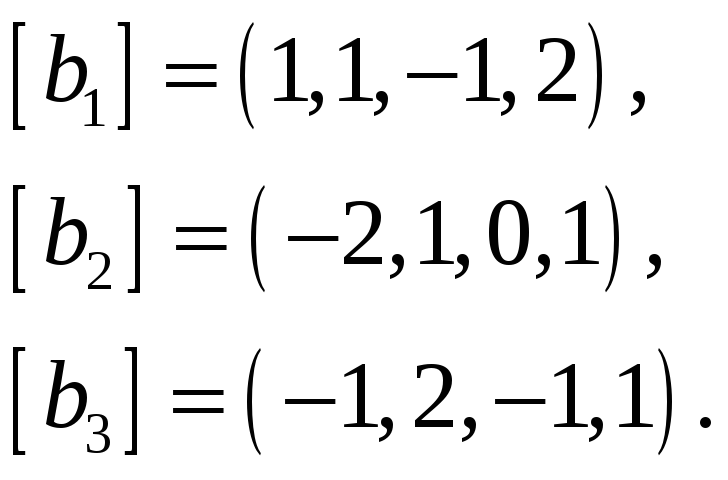
62. 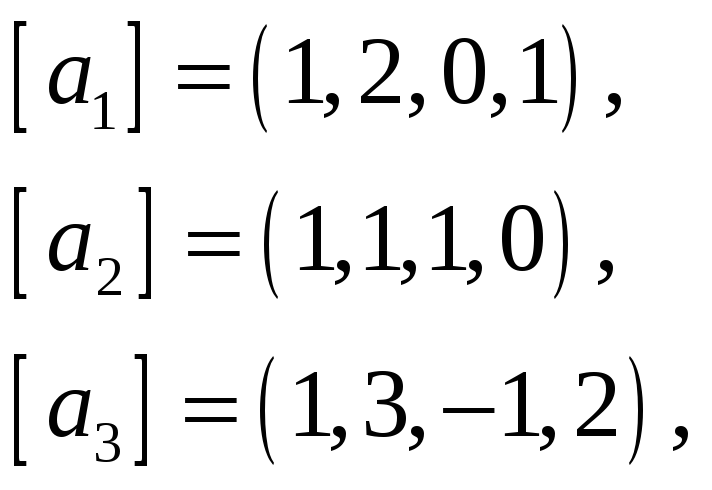
63. 
64. 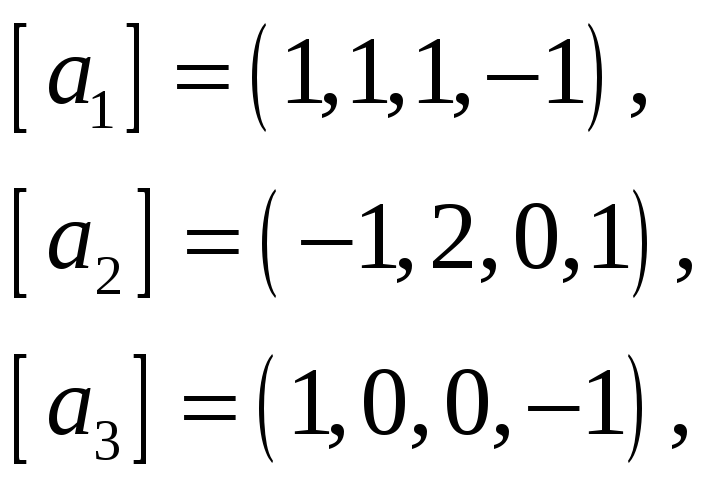
65. 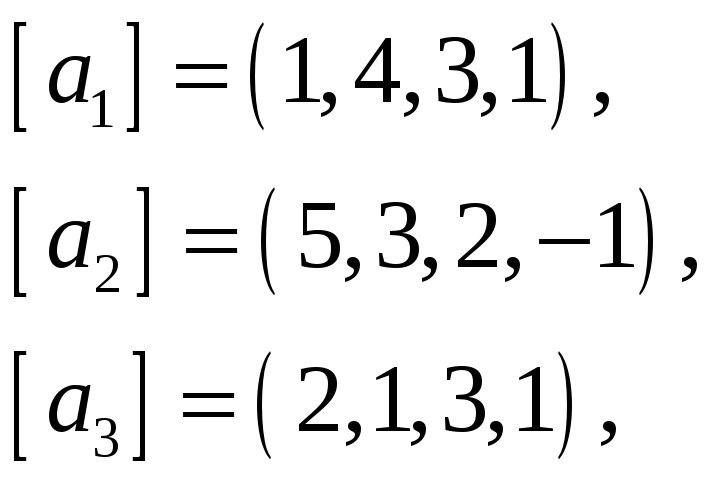
66. 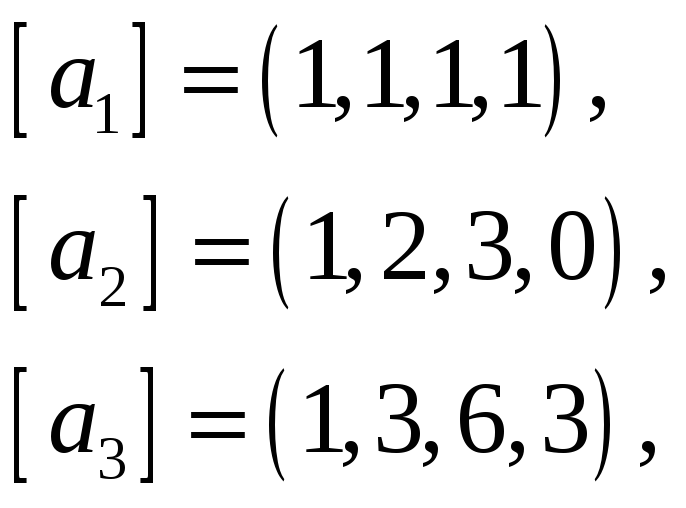
ЛИТЕРАТУРА
-
Курош А.Г. Курс высшей алгебры. 6-е изд.
М., 1971. -
Милованов М.В., Тышкевич Р.И., Феденко
А.С. Алгебра и аналитическая геометрия.
Часть I. Минск, 1984. -
Милованов М.В., Толкачев М.М., Тышкевич
Р.И., Феденко А.С. Алгебра и аналитическая
геометрия. Часть 2. Минск, 1981. -
Фаддеев Д.К., Соминский И.С. Сборник
задач по высшей алгебре. 3- изд. М.: Наука,
1974.
Учебное издание
ЖИГОТА АЛЛА ЭДУАРДОВНА
Методические указания и контрольные
работы
по курсу «Алгебра и теория чисел»
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 14.05.2011 Сообщений: 6 |
|
|
1 |
|
Найти подсистему системы векторов14.05.2011, 20:00. Показов 5888. Ответов 8
Найти максимальную линейно независимую подсистему данной системы векторов: a1=(1;1;-2;-2) a2=(-2;-2;1;1) ; a1 = (7;7;7;7) a1=(6;7;8;5) Я не понял последние 2 а,это опечатка или нет?я переписываю с листочка,там подряд две а1,как и тут,так и должно быть?помогите плиз!линейная алгебра,не разбираюсь из-за не желания,хотел убежать в вузе от математики навсегда,но до 3-его курса точно не убегу к сожалению Добавлено через 1 минуту
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
14.05.2011, 23:27 |
2 |
|
по-моему для линейно-независимой системы должно выполняться: если данная система имеет единственное решение, то максимальная подсистема состоит из всех этих четырёх векторов. иначе смотрите, сколько получается свободных членов, столько и векторов в максимальной подсистеме. Добавлено через 12 минут
1 |
|
0 / 0 / 0 Регистрация: 14.05.2011 Сообщений: 6 |
|
|
15.05.2011, 08:18 [ТС] |
3 |
|
Ну вот я нашел
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
15.05.2011, 21:03 |
4 |
|
так. это всё-таки лучше решать с помощью окаймляющих миноров, если вы такое проходили. у меня получилось, что максимальная подсистема должна состоять из 3 векторов.
1 |
|
0 / 0 / 0 Регистрация: 14.05.2011 Сообщений: 6 |
|
|
16.05.2011, 05:25 [ТС] |
5 |
|
Спасибо!
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
16.05.2011, 13:39 |
6 |
|
Aeristesia, вы знаете как это делается?
1 |
|
0 / 0 / 0 Регистрация: 14.05.2011 Сообщений: 6 |
|
|
16.05.2011, 15:12 [ТС] |
7 |
|
окаймляющие миноры?у меня даже от прочтения голова болит,куда там таким образом решать)))))я решал через онлайн решалки методом гаусса вроде Добавлено через 1 минуту
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
16.05.2011, 16:20 |
8 |
|
ох. записываем матрицу, строки которой – координаты данных векторов. минор 1 порядка – любой элемент данной матрицы. пусть будет Добавлено через 2 минуты
1 |
|
0 / 0 / 0 Регистрация: 14.09.2012 Сообщений: 6 |
|
|
11.10.2012, 22:03 |
9 |
|
(не вижу смысла добавлять отдельную тему) я еще вот в таком моменте сомневаюсь: можно ли в данном случае выполнять элементарные преобразования матрицы над столбцами? если да – нулевой столбец получается буквально через один цикл после приведения левой 4х4 части матрицы к диагональной а если нет – то нулевая строка не получится практически в любом случае далее, если вариант с нулевым столбцом подойдет – какой будет максимально линейно независимая подсистема? тот же нулевой вектор?
0 |


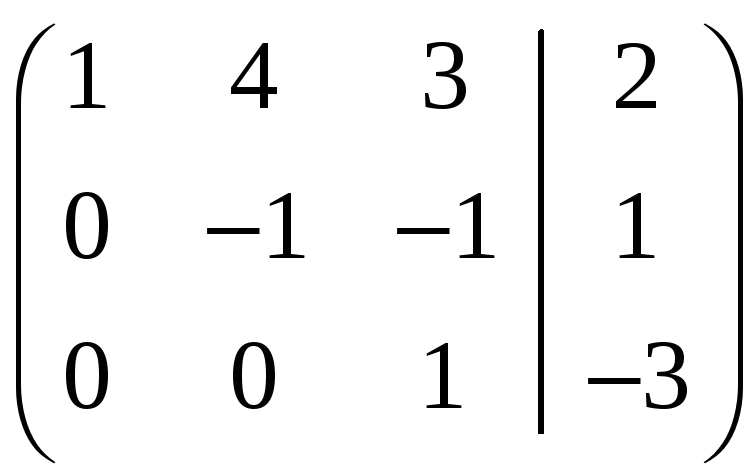
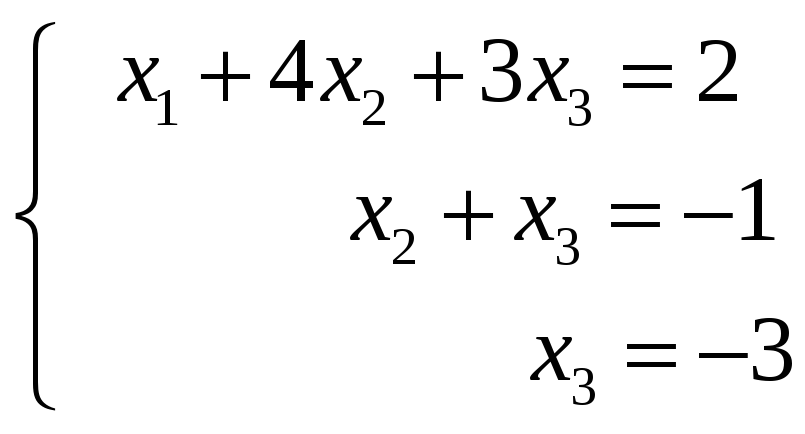
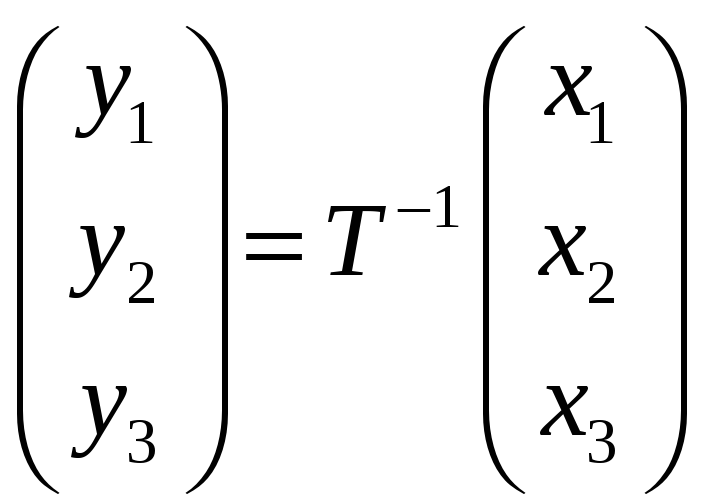
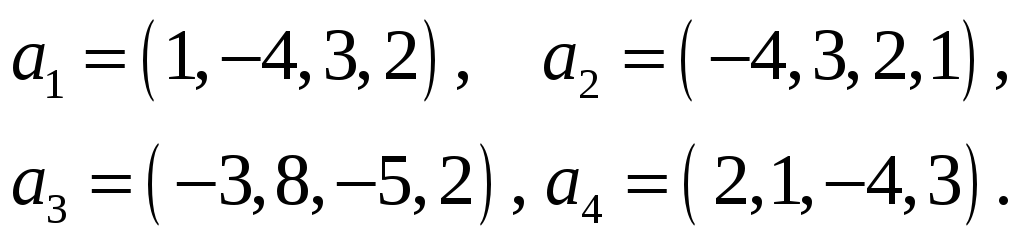
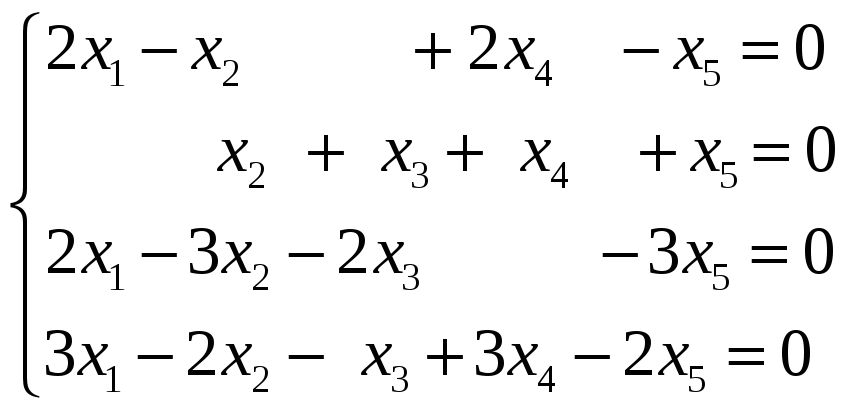
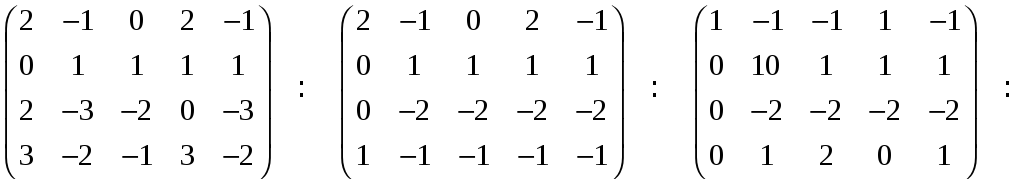
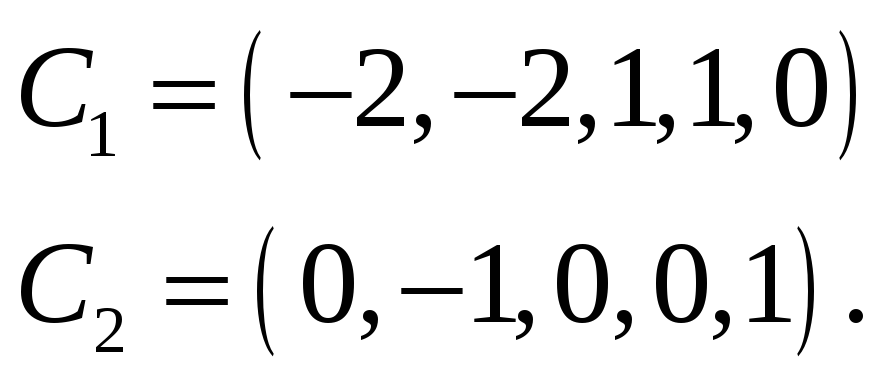
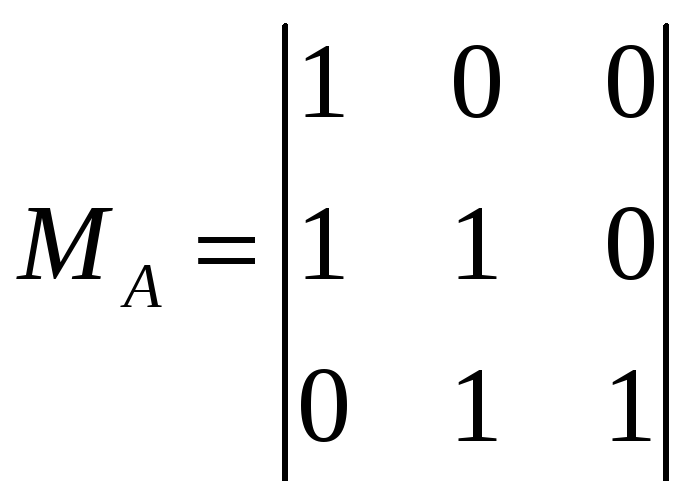
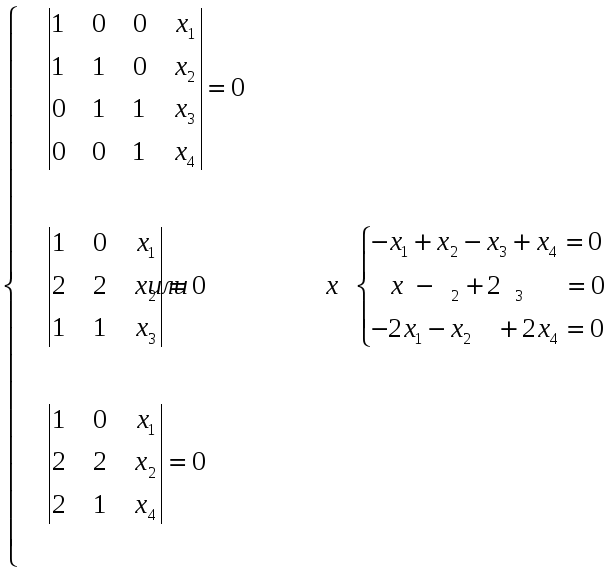
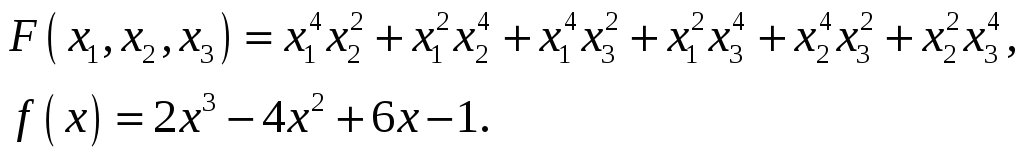
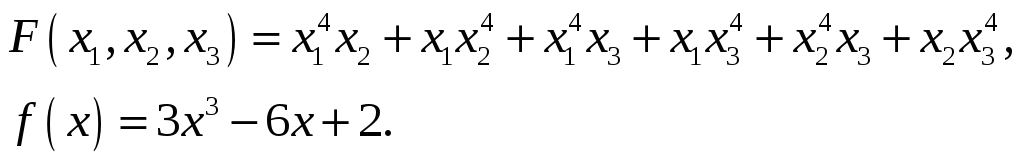
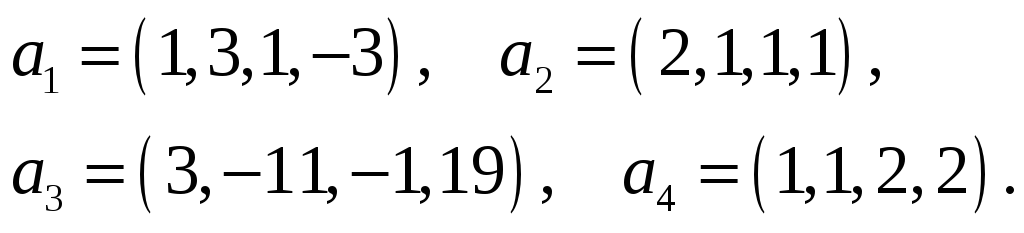
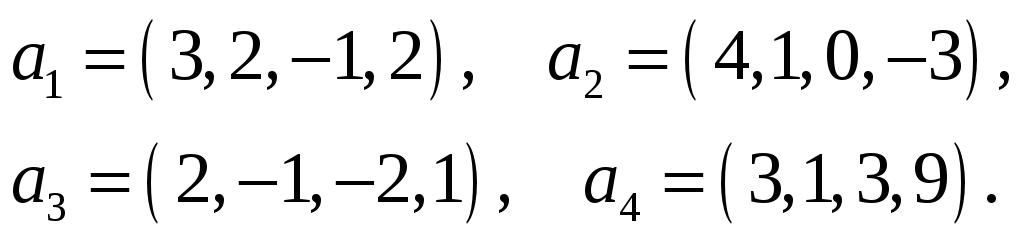
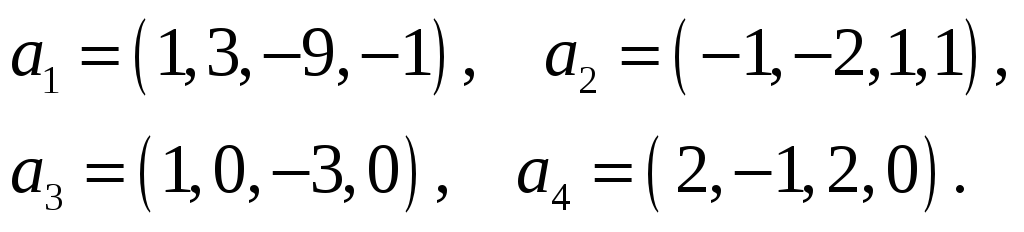
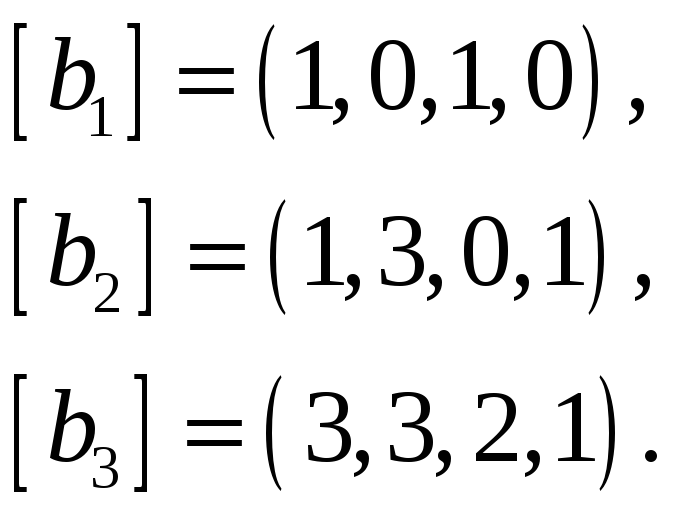
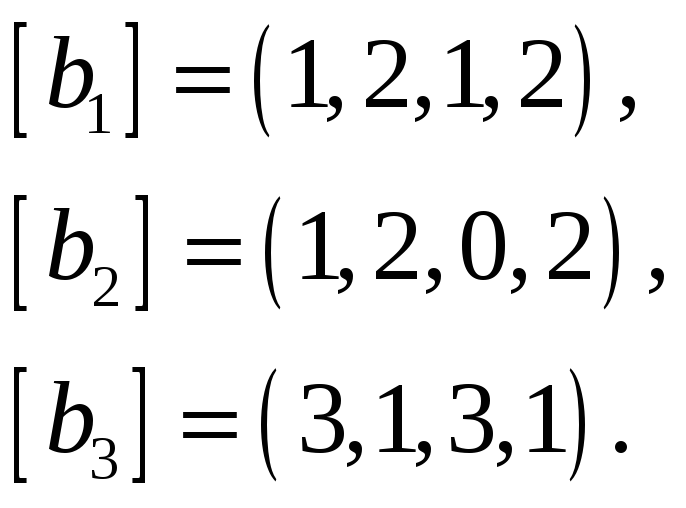
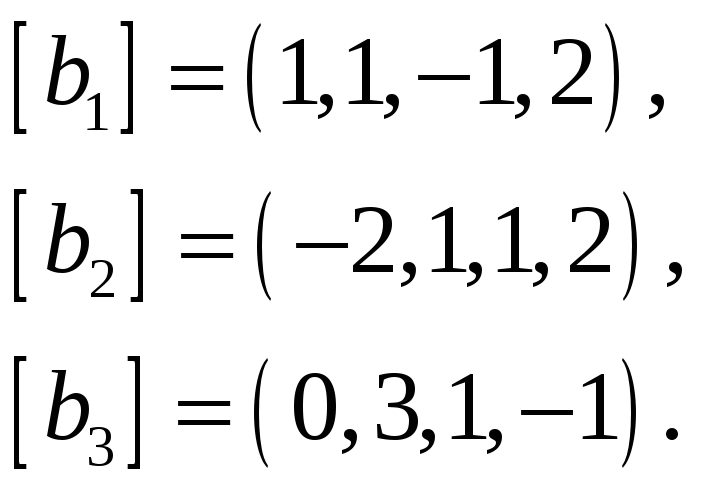
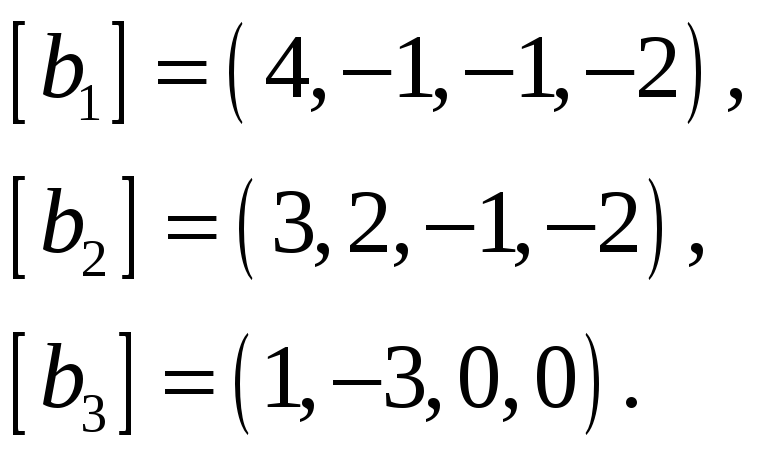
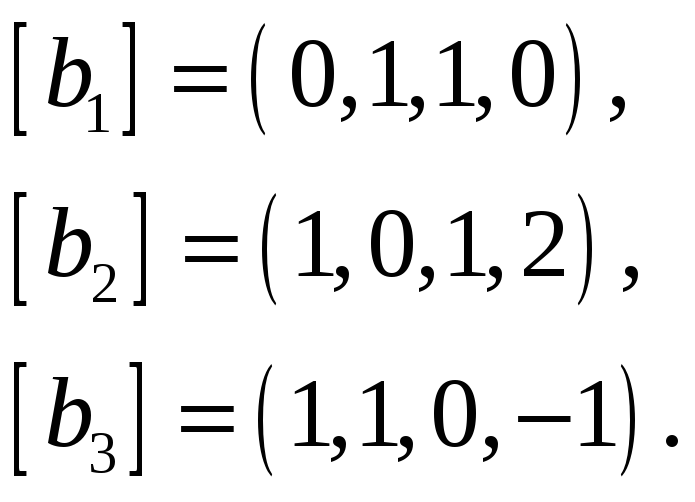

 ((
((