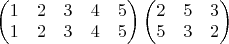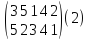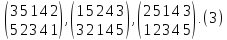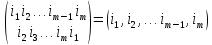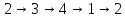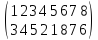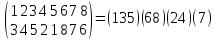Как найти подстановку в степени

Как найти подстановку в степени

Как возвести подстановку в степень

Определение 1. Подстановкой (перестановкой) множества M= n > состоящего из n первых натуральных чисел, называется взаимно-однозначное отображение множества M на себя. Число n в этом случае называется степенью подстановки (не путать с порядком подстановки!).

Подстановки будем записывать в виде таблицы, состоящей из двух строк и n столбцов следующим образом:

Пример. Примерами подстановок 5-го порядка будут подстановки:

Заметим,что порядок чисел в верхней строчке является несущественным, например,рассмотрим подстановку четвертой степени:

Поэтому эти подстановки тождественные.
Каждую подстановку можно записывать так, чтобы все числа в первой строке располагались в порядке возрастания. При такой записи подстановок любые две подстановки одной степени будут отличаться только перестановками во второй строке.

Отсюда следует довольно простой и важный вывод:

существует n! различных подстановок n – ой степени.

Научный форум dxdy

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Возвести подстановку в степень.

Последний раз редактировалось qwertz 04.05.2013, 21:57, всего редактировалось 3 раз(а).

$<begin<pmatrix>1 & 2 & 3 & 4 & 5 \ 4 & 5 & 2 & 1 & 3 end<pmatrix>>$^<100>» /></p> <p>Как это сделать?</p> <p><img decoding=что означает? Что будет, если применить его 2 раза? Три раза? Во что перейдут 1 и 4?

Последний раз редактировалось qwertz 05.05.2013, 10:09, всего редактировалось 2 раз(а).

Цикл $(1 4)$означает, что элемент '$отображается в $4$. Пробовал возводить цикл $(1 4)$во вторую степень (применить два раза), получилось, что '$перейдет в '$, а $4$в $4$, т.е тождественная подстановка. Если в третью (применить три раза), то $(1 4)^3 = (1 4)$, т.е получился сам же цикл. Стало быть, если цикл длины $n$возвести в степень $n$, то получится тождественная подстановка.
$((1 4) (2 5 3))^<100>= (1 4)^ <100>(2 5 3)^ <100>= ((1 4)^2)^ <50>((2 5 3)^3)^ <33>(2 5 3) = (1)(4)(2)(5)(3) cod (2 5 3)$» /> <br />Получилось, что тождественная подстановка <img decoding=умножается на цикл $(2 5 3)$, т.е:
$begin<pmatrix>1 & 2 & 3 & 4 & 5 \ 1 & 2 & 3 & 4 & 5 end <pmatrix>begin <pmatrix>2 & 5 & 3 \ 5 & 3 & 2 end<pmatrix>$» /><br />Никогда не умножал подстановки разных размеров, но полагаю, что получится: <br /> <img decoding=

Источник

Определение.
Всякое взаимно однозначное отображение
множества А первых n
натуральных чисел на себя называется
подстановкой
n-й
степени,
причем, очевидно, всякая подстановка А
может быть записана при помощи двух
перестановок, подписанных одна под
другой

(1)

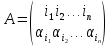
Через
αi
здесь обозначается то число, в которое
при подстановке А переходит число i
,
i
= 1, 2, …, n.

Запишем
одну под другой две перестановки из n
символов, беря полученные две строки в
скобки; например, n=5:

Мы скажем, что
число 3 переходит
в число 5,
число 5 переходит в 2, число 1 переходит
в 3, число 4 переходит в 4(или остаётся на
месте), и, наконец, число 2 переходит в
1. Таким образом, две перестановки,
записанные друг под другом в виде (2),
определяют некоторое взаимно
однозначное отображение
множества из первых пяти натуральных
чисел на себя, т. е. отображение, которое
каждому из натуральных чисел 1, 2, 3, 4, 5
ставит в соответствие одно из этих же
натуральных чисел, причем разным числам
ставятся в соответствие различные же
числа.

Ясно, что то взаимно
однозначное отображение множества их
первых пяти натуральных чисел, которые
мы получили при помощи (2), можно было
получить, записывая одну под другой и
некоторые другие пары перестановок из
пяти символов. Эти записи получаются
из (2) путем нескольких транспозиций
(перестановок) столбиков; таковы,
например,

Во
всех этих записях 3 переходит в 5, 5 в 2 и
т. д.

Подстановка А
обладает многими различными записями
вида (1). Так, (2) и (3) являются различными
записями одной и той же подстановки 5-й
степени.

Канонический вид подстановки

В частности, всякая
подстановка n-й
степени А может быть записана в
каноническом виде

(4)

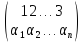
т.
е. с натуральным расположением чисел в
верхней строке. При такой записи различные
подстановки отличаются друг от друга
перестановками, стоящими в нижней
строке.

Примером
подстановки n-й
степени служит тождественная подстановка

,

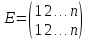
при
котором на месте остаются все символы.

Замечание.
Следует заметить, что верхняя и нижняя
строки в записи (1) подстановки А играют
разные роли и, переставив их, мы, вообще
говоря, получаем другую подстановку.

Цикловая структура подстановки

Подстановка
вида

(При
этом все числа i1,
i2,
…, im
– различны)

называется
циклом длины m.

Для
циклов вводят специальное обозначение:

Пример
1.

Цикл
(2 3 4 1) действует следующим образом

Циклы,
не содержащие общих элементов называются
независимыми(непересекающимися).

Теорема.
Каждую
подстановку можно разложить в произведение
независимых циклов. Это разложение
единственно с точностью до порядка
циклов.

Алгоритм
составления цикла:

1.Берем
подстановку, смотрим, во что переходит
первый элемент.

2.Полученный
элемент пишем за первым элементом и
находим его образ под действием
подстановки.

3.
Как только образ совпадает с элементом,
с которого началось построение цикла,
закрываем цикл.

4.
Дальше берем любой элемент, не входящий
в уже выписанные циклы и начинаем
построение нового цикла.

Пример
2.

Разложить
подстановку

в
произведение независимых циклов.

Решение.

Так
как
,
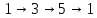
то получаем цикл (135). Цепочка 2→4→2
дает транспозицию (24). Так же 6→8→6
дает транспозицию (68). 7 остается на
месте.

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Тема: Как возвести подстановку в степень?  (Прочитано 6527 раз)

0 Пользователей и 1 Гость просматривают эту тему.

1 2 3 4 5 6 7 8
1 7 8 5 6 2 3 4    возвести в 19-ую степень

(1)^19 (2738456)^19

« Последнее редактирование: 25 Октября 2011, 00:38:32 от Asix »

19 раз умножить саму на себя

1 2 3 4 5 6 7 8
1 7 8 5 6 2 3 4    возвести в 19-ую степень
(1)^19 (2738456)^19

А попонятней можно задачу объяснить?

За жизнью надо тщательно следить, все время избегая с ней разлуки.

А попонятней можно задачу объяснить?

Т.е.?

(1) так и остается
а вот (2738456)^19 вроде находится так:

я делю степень на длину цикла
197 и беру остаток,т.е 5
(2738456)^19=(2738456)^5

и как возвести этот цикл в 5ую степень?

Источник

10:24

Степень подстановки что это

Определение 1. Подстановкой (перестановкой) множества  M={1,2,3,…n} состоящего из  n первых натуральных чисел, называется взаимно-однозначное отображение множества  M на себя. Число  n  в этом случае называется степенью подстановки (не путать с порядком подстановки!).

Подстановки будем записывать в виде таблицы, состоящей из двух строк и  n столбцов следующим образом:

Пример. Примерами подстановок 5-го порядка будут подстановки:

Заметим,что порядок чисел в верхней строчке является несущественным, например,рассмотрим подстановку четвертой степени:

Поэтому эти подстановки тождественные.
Каждую подстановку можно записывать так, чтобы все числа в первой строке располагались в порядке возрастания. При такой записи подстановок любые две подстановки одной степени будут отличаться только перестановками во второй строке.

Отсюда следует довольно простой и важный вывод:

существует n! различных подстановок n – ой степени.

P.S. Перестановку записанную в две строки обычно называют подстановкой.
  • 1
  • 2
  • 3
  • 4
  • 5

Категория: Комбинаторика | Просмотров: 4385 | | Теги: перестановки | Рейтинг: 3.0/2

Источник

Добавить комментарий