Как найти подстроку палиндром

Алгоритм поиска самой длинной подстроки-палиндрома

Один из самых прекрасных алгоритмов в информатике, который показывает, как можно получить большое ускорение от “вялого” O(n³) до молниеносного¹ O(n), просто посмотрев на проблему с другой точки зрения.

Задача состоит в том, чтобы найти самую длинную подстроку, которая является палиндромом (читается одинаково слева направо и справа налево, например, “racecar”). Так, самый длинный палиндром в строке “Fractions are never odd or even” это “never odd or even” (регистр букв и пробелы игнорируются). Это также имеет практическое применение в биохимии (ГААТТЦ или ЦТТААГ являются палиндромными последовательностями²). К тому же, эту задачу³ часто дают на собеседовании.

Самый простой и прямой подход (при этом самый медленный) – перебирать с начала все подстроки всех длин и проверять, является ли текущая палиндромом:

Псевдокод такого решения

ЦИКЛ по символам всей строки:
	ЦИКЛ по всем длинам, начиная с текущего символа:
		ЦИКЛ по символам в этой подстроке:

явно указывает, что метод со сложностью O(n³) (где n – это длина начальной строки) является быстровозрастающей функцией.

Если бы вместо перебора с самых начал подстрок, мы начинали перебор с середины, это позволило бы нам использовать результаты, которые мы получили на предыдущих шагах.

Например, если мы знаем, что “eve” – это палиндром, то нам потребуется всего одно сравнение, чтобы выяснить, что “level” тоже палиндром. В первом решении нам бы пришлось проверять все полностью с самого начала.

ЦИКЛ по символам строки до середины:
	ЦИКЛ по всем длинам, начиная с текущего символа:

В таком случае сложность составляет O(n²). Но существуют методы⁴, позволяющие сделать это еще быстрее.

Один из самых изящных – это алгоритм Манакера⁵. Он основан на методе, описанном выше, но его временная сложность сокращена до O(n).

Когда палиндромы в строке находятся далеко, оптимизировать нечего. Сложность и так O(n). Проблема появляется, когда они пересекаются, а худшим случаем является строка, состоящая из одной буквы.

Рассмотрим следующую ситуацию. Алгоритм нашел самый короткий зеленый палиндром, самый длинный голубой палиндром и остановился на букве “i”:

Внимательно посмотрев на картинку, можно заметить, что у нас нет необходимости обрабатывать правую часть голубого палиндрома. По определению, это зеркальное отражение левой части, так что полученную левую часть мы можем отразить на правую и получить ее, так сказать, “за бесплатно”.

Однако, это не единственный случай перекрытия. На следующей картинке зеленый палиндром пересекает границу голубого, поэтому его длина должна быть уменьшена.

Опять-таки нет нужды дважды проверять длину отраженного палиндрома: буквы b и x обязаны быть различными, иначе голубой палиндром был бы длиннее.

Наконец, один палиндром может “касаться” другого изнутри. В этом случае нет гарантий, что отраженный палиндром не имеет бОльшую длину, так как мы получаем нижнюю границу его длины:

В идеале мы должны пропускать как нулевые, так и строго ненулевые значения (= все случаи, кроме последнего) в дальнейшей обработке (код 1 ниже). Но в практике (если вообще можно говорить о практике в такой абстрактной задаче) разница между ≥ и = довольно мала (всего одно дополнительное сравнение), поэтому имеет смысл рассматривать все ненулевые значения с помощью ≥ для краткости и читаемости кода (код 2 ниже).

Одна из возможных реализаций алгоритма на питоне:

#код 1
def odd(s):
    n = len(s)
    h = [0] * n
    C = R = 0      # центр и радиус или крайний правый палиндром
    besti, bestj = 0, 0     # центр и радиус самого длинного палиндрома
    for i in range(n):
        if i < C + R:         # если есть пересечение
            j = h[C-(i-C)]       # отражение
            if j < C + R - i:    # случай A
                h[i] = j
                continue
            elif j > C + R - i:  # случай B 
                h[i] = C + R - i
                continue
            else:                # case C 
                pass
        else:                 # если нет пересечения
            j = 0
        while i-j > 0 and i+j<n-1 and s[i-j-1] == s[i+j+1]:
            j += 1
        h[i] = j
        if j > bestj:
            besti, bestj = i, j
        if i + j > C + R:
            C, R = i, j
    return s[besti-bestj : besti+bestj+1]

Сперва алгоритм пытается найти соответствующее отражение, как описано выше. Затем, если необходимо, последовательно ищет: как в алгоритме со сложностью O(n²), но принимая отраженное значения за начальную точку. В конце если новый палиндром перекрывает больше текста справа, чем предыдущий, то он становится новым крайним правым палиндромом.

Эта функция ищет палиндромы только нечетного размера. Общий подход для работы с палиндромами четного размера таков:

• вставлять произвольный символ между символами в оригинальной строке, к примеру ‘noon’ -> ‘|n|o|o|n|’,

• находить палиндром нечетного размера,

• удалять произвольные символы из результата.

Символ “|” необязательно должен отсутствовать в строке. Можно использовать любой символ.

def odd_or_even(s):
    return odd('|'+'|'.join(s)+'|').replace('|', '')

>>> odd_or_even('afternoon')
'noon'

Немного запутанная версия (труднее для понимания, немного медленнее, но короче) выглядит так:

#код 2
import re

def odd(s):
    n = len(s)
    h = [0] * n
    C = R = 0      # центр и радиус или крайний правый палиндром
    besti, bestj = 0, 0     # центр и радиус самого длинного палиндрома
    for i in range(n):
        j = 0 if i > C+R else min(h[C-(i-C)], C+R-i)
        while i-j > 0 and i+j<n-1 and s[i-j-1] == s[i+j+1]:
            j += 1
        h[i] = j
        if j > bestj:
            besti, bestj = i, j
        if i + j > C + R:
            C, R = i, j
    return s[besti-bestj : besti+bestj+1]

def manacher(s):
    clean = re.sub('W', '', s.lower())
    return odd('|'+'|'.join(clean)+'|')[1::2]

>>> manacher('He said: "Madam, I'm Adam!"')
'madamimadam'

Как видно, в коде есть два вложенных цикла. Тем не менее, интуитивно понятно, почему сложность O(n). На диаграмме показан массив h.

Внешний цикл соответствует горизонтальному перемещению, внутренний – вертикальному. Каждый шаг – это одно сравнение. Сплошные линии – расчет шагов, пунктирные – пропуск шагов.

Очевидно из диаграммы, что, когда палиндромы не пересекаются, число шагов “вверх” равно количеству горизонтальных “пропускающих” шагов. Для пересекающихся палиндромов чуть более заморочено, но если посчитать число шагов “вверх” и число горизонтальных “пропускающих шагов, то эти числа вновь совпадут. Так что общее число шагов ограничено 2n сравнениями. Не просто n , потому что, в отличие от вертикальных шагов, чтобы понять, пропускать ли горизонтальный шаг или нет, необходимо проделать некую работу (хотя можно изменить реализацию, чтобы пропускать их за постоянное время). Итого временная сложность – O(n).

Алгоритм Манакера позволяет найти самый длинный палиндром в строке (если быть точнее, не просто самый длинный палиндром, а самый длинный палиндром для всех возможных центров) за линейное время, используя очень интуитивный подход, лучше всего описываемый визуально.

Ссылки:

1. Сайт Big-O Cheat Sheet.

2. Статья на Википедии про палиндромные последовательности.

3. Задача на Leetcode про самый длинный палиндром в строке.

4. Статья на Википедии про самый длинный палиндром в строке.

5. Гленн Манакер (1975), “Новый линейный алгоритм для поиска самого длинного палиндрома строки”, журнал ACM.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июля 2020 года; проверки требуют 2 правки.

В разделе компьютерные науки, задача о самой длинной палиндромиальной подстроке — это задача отыскания самой длинной подстроки данной строки являющейся палиндромом. Например, самая длинная палиндромиальная подстрока «банана» это «анана». Самая длинная палиндромиальная подстрока не обязательно единственна; например в строке «абракадабра» нет палиндромиальной подстроки длиннее трёх символов, но есть состоящие в точности из трёх символов, а именно, «ака» и «ада». В некоторых приложениях требуется найти все максимальные палиндромиальные подстроки (а именно, все подстроки, которые сами по себе являются палиндромами и не могут быть дополнены до более длинных палиндромиальных подстрок) вместо того чтобы вернуть только одну подстроку или вернуть максимальную длину палиндромиальной подстроки.

Manacher (1975) изобрёл линейный по времени алгоритм перечисления всех палиндромов находящихся в начале данной строки. Однако, как было показано Apostolico, Breslauer & Galil (1995), этот же алгоритм может быть использован для нахождения всех самых длинных палиндромиальных подстрок в любом месте данной строки, опять-таки за линейное время. Поэтому он обеспечивает решение задачи нахождения максимальной палиндромиальной подстроки за линейное время. Альтернативные решения, работающие за линейное время, были предложены Jeuring (1994), и Gusfield (1997), который описал решение основанное на использовании суффиксных деревьев. Также известны эффективные параллельные алгоритмы решения этой задачи.^[1]

Задачу нахождения самой длинной палиндромиальной подстроки не следует путать с задачей нахождения самой длинной палиндромиальной подпоследовательности.

Алгоритм Манакера[править | править код]

Чтобы за линейное время найти в строке самый длинный палиндром, алгоритм может воспользоваться следующими свойствами палиндромов и подпалиндромов:

1. Левая часть палиндрома является зеркальным отражением его правой части
2. (Случай 1) Третий палиндром, чей центр лежит в правой части первого палиндрома, будет иметь в точности ту же длину, что и второй палиндром, центр которого зеркально отражен в левую часть, если второй палиндром лежит внутри первого, отступая от границы по крайней мере на один символ.
3. (Случай 2) Если второй палиндром имеет общую границу с первым палиндромом, или простирается за его пределы, то длина третьего палиндрома гарантировано не меньше расстояния от его центра до правой границы первого палиндрома. Эта длина совпадает с расстоянием от центра второго палиндрома до самого левого символа первого палиндрома.
4. Чтобы найти длину третьего палиндрома в случае 2, необходимо сравнивать символы, идущие за самым правым символом первого палиндрома с их зеркальным отражением относительно центра третьего палиндрома пока либо не исчерпается строка, либо не будет обнаружено неравенство символов.
5. (Случай 3) Ни первый, ни второй палиндромы не предоставляют информации, позволяющей определить длину четвёртого палиндрома, чей центр лежит за границей первого палиндрома.
6. Поэтому для определения слева направо палиндромиальных длин подстрок в строке желательно иметь опорный палиндром (исполняющий роль первого палиндрома), чьи символы занимают самые правые положения в строке (и, следовательно, третий палиндром в случае 2 и четвёртый палиндром в случае 3 могут заменять первый палиндром, чтобы стать новым опорным палиндромом).
7. Что касается оценки времени определения палиндромиальный длины для каждого символа строки: в Случае 1 сравнения символов не производится, в Случаях 2 и 3 кандидатами для сравнения являются только символы строки, лежащей за самым правым символом опорного палиндрома (и следовательно Случай 3 всегда приводит к смене опорного палиндрома, когда Случай 2 меняет опорный палиндром только если оказывается что длина третьего палиндрома в действительности больше чем его обещанная минимальная длина).
8. Для палиндромов чётной степени центр лежит между двумя центральными символами палиндрома.

Реализация[править | править код]

Пусть:

• s — строка из N символов
• s2 — производная от s строка, состоящая из N * 2 + 1 элементов, при этом каждый элемент соответствует одному из: N символам в s, N-1 промежутку между символами и границами, и промежуткам, идущим перед первым и за последним символами строки s соответственно
• Границы в s2 ничем не отличаются друг от друга в плане нахождения длины палиндрома
• Пусть p будет массивом радиусов палиндрома, то есть расстоянием от центра до любого из самых дальних символов палиндрома (то есть палиндром длиной 3 имеет палиндромиальный радиус 1)
• Пусть c будет положением центра палиндрома содержащего символ, ближайший к правому концу s2 (длина этого палиндрома p[c]*2+1)
• Пусть r будет положением самой правой границы этого палиндрома (то есть, r = c + p[c])
• Пусть i — положение элемента (то есть промежутка или символа) в s2, чей палиндромиальный радиус определяется, причём i всегда расположено правее c
• Пусть i_mir будет зеркальным отражением i относительно c (то есть, {i, i_mir} = {6, 4}, {7, 3}, {8, 2},… когда c = 5 (значит, i_mir = c * 2 — i))

Результат:
Максимально длинный палиндром, либо первый символ строки

#include <string>
#include <vector>
using namespace std;

string longestPalindrome(const string &s){
    vector<char> s2(s.size() * 2 + 1, '#');
    //создаем псевдостроку с границами в виде символа '#'
    for(int i = 0; i != s.size(); ++i){
        s2[i*2 + 1] = s[i];
    }

    int p[s2.size()];
    int r, c, index, i_mir;
    int maxLen = 1;
    i_mir = index = r = c = 0;

    for(int i = 1; i != s2.size() - 1; ++i){
        i_mir = 2*c-i;

        //Если мы попадаем в пределы радиуса прошлого результата,
        //то начальное значение текущего радиуса можно взять из зеркального результата
        p[i] = r > i ? min(p[i_mir], r-i) : 0;

        while(i > p[i] && (i + p[i] + 1) < s2.size() && s2[i - p[i] - 1] == s2[i + p[i] + 1])
            ++p[i];

        if(p[i] + i > r){
            c = i;
            r = i + p[i];
        }

        if(maxLen < p[i]){
            maxLen = p[i];
            index = i;
        }
    }

    //Отображаем найденные позиции на оригинальную строку
    return s.substr((index-maxLen)/2, maxLen);
}

Примечания[править | править код]

Литература[править | править код]

• Apostolico, Alberto; Breslauer, Dany & Galil, Zvi (1995), Parallel detection of all palindromes in a string, Theoretical Computer Science Т. 141 (1–2): 163–173, DOI 10.1016/0304-3975(94)00083-U.
• Crochemore, Maxime & Rytter, Wojciech (1991), Usefulness of the Karp–Miller–Rosenberg algorithm in parallel computations on strings and arrays, Theoretical Computer Science Т. 88 (1): 59–82, DOI 10.1016/0304-3975(91)90073-B.
• Crochemore, Maxime & Rytter, Wojciech (2003), 8.1 Searching for symmetric words, Jewels of Stringology: Text Algorithms, World Scientific, с. 111–114, ISBN 978-981-02-4897-0.
• Gusfield, Dan (1997), 9.2 Finding all maximal palindromes in linear time, Algorithms on Strings, Trees, and Sequences, Cambridge: Cambridge University Press, с. 197–199, ISBN 0-521-58519-8, DOI 10.1017/CBO9780511574931.
• Jeuring, Johan (1994), The derivation of on-line algorithms, with an application to finding palindromes, Algorithmica Т. 11 (2): 146–184, DOI 10.1007/BF01182773.
• Manacher, Glenn (1975), A new linear-time “on-line” algorithm for finding the smallest initial palindrome of a string, Journal of the ACM Т. 22 (3): 346–351, DOI 10.1145/321892.321896.

Ссылки[править | править код]

• Longest Palindromic Substring Part II., 2011-11-20, <http://leetcode.com/2011/11/longest-palindromic-substring-part-ii.html> Архивная копия от 2 февраля 2014 на Wayback Machine. A description of Manacher’s algorithm for finding the longest palindromic substring in linear time.
• Akalin, Fred (2007), Finding the longest palindromic substring in linear time, <http://www.akalin.cx/2007/11/28/finding-the-longest-palindromic-substring-in-linear-time/>. Проверено 22 ноября 2011.. An explanation and Python implementation of Manacher’s linear-time algorithm.
• Jeuring, Johan (2007–2010), Palindromes, <http://www.staff.science.uu.nl/~jeuri101/homepage/palindromes/index.html>. Проверено 22 ноября 2011.. Haskell implementation of Jeuring’s linear-time algorithm.
• Palindromes, <https://github.com/vvikas/palindromes/blob/master/src/LongestPalindromicSubString.java> (недоступная ссылка). Java implementation of Manacher’s linear-time algorithm.

This article incorporates text from Longest palindromic substring on PEGWiki under a Creative Commons Attribution (CC-BY-3.0) license.

Уточнение постановки

Легко увидеть, что таких подстрок в худшем случае будет . Значит, нужно найти компактный способ хранения информации о них. Пусть — количество палиндромов нечётной длины с центром в позиции , а — аналогичная величина для палиндромов чётной длины. Далее научимся вычислять значения этих массивов.

Наивный алгоритм

Идея

Рассмотрим сначала задачу поиска палиндромов нечётной длины. Центром строки нечётной длины назовём символ под индексом . Для каждой позиции в строке найдем длину наибольшего палиндрома с центром в этой позиции. Очевидно, что если строка является палиндромом, то строка полученная вычеркиванием первого и последнего символа из также является палиндромом, поэтому длину палиндрома можно искать бинарным поиском. Проверить совпадение левой и правой половины можно выполнить за , используя метод хеширования.

Для палиндромов чётной длины алгоритм такой же. Центр строки чётной длины — некий мнимый элемент между и . Только требуется проверять вторую строку со сдвигом на единицу. Следует заметить, что мы не посчитаем никакой палиндром дважды из-за четности-нечетности длин палиндромов.

Псевдокод

int binarySearch(s : string, center, shift : int):
    //shift = 0 при поиске палиндрома нечётной длины, иначе shift = 1
    int l = -1, r = min(center, s.length - center + shift), m = 0
    while r - l != 1
        m = l + (r - l) / 2
        //reversed_hash возвращает хэш развернутой строки s
        if hash(s[center - m..center]) == reversed_hash(s[center + shift..center + shift + m])
            l = m
        else
            r = m
    return r

int palindromesCount(s : string):
    int ans = 0
    for i = 0 to s.length
        ans += binarySearch(s, i, 0) + binarySearch(s, i, 1)
    return ans

Время работы

Изначальный подсчет хешей производится за . Каждая итерация будет выполняться за , всего итераций — . Итоговое время работы алгоритма .

Избавление от коллизий

У хешей есть один недостаток — коллизии: можно подобрать входные данные так, что хеши разных строк будут совпадать. Абсолютно точно проверить две подстроки на совпадение можно с помощью суффиксного массива, но с дополнительной памятью . Для этого построим суффиксный массив для строки , при этом сохраним промежуточные результаты классов эквивалентности . Пусть нам требуется проверить на совпадение подстроки и . Разобьем каждую нашу строку на две пересекающиеся подстроки длиной , где . Тогда наши строки совпадают, если и .

Итоговая асимптотика алгоритма: предподсчет за построение суффиксного массива и на запрос, если предподсчитать все , то .

Алгоритм Манакера

Идея

Алгоритм, который будет описан далее, отличается от наивного тем, что использует значения, посчитанные ранее.
Будем поддерживать границы самого правого из найденных палиндромов — . Итак, пусть мы хотим вычислить — т.е. длину наибольшего палиндрома с центром в позиции . При этом все предыдущие значения в массиве уже посчитаны. Возможны два случая:

1. , т.е. текущая позиция не попадает в границы самого правого из найденных палиндромов. Тогда просто запустим наивный алгоритм для позиции .
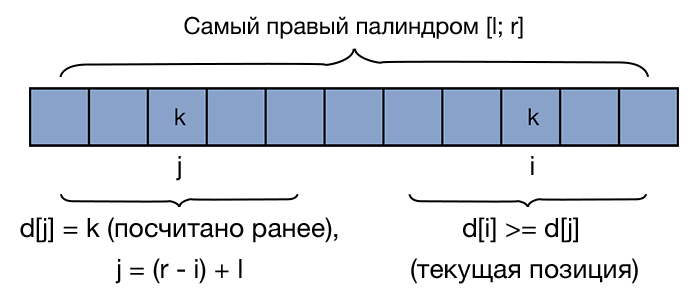
2. . Тогда попробуем воспользоваться значениями, посчитанным ранее. Отразим нашу текущую позицию внутри палиндрома . Поскольку и — симметричные позиции, то если , мы можем утверждать, что и . Это объясняется тем, что палиндром симметричен относительно своей центральной позиции. Т.е. если имеем некоторый палиндром длины с центром в позиции , то в позиции , симметричной относительно отрезка тоже может находиться палиндром длины . Это можно лучше понять, посмотрев на рисунок. Снизу фигурными скобками обозначены равные подстроки. Однако стоит не забыть про один граничный случай: что если выходит за границы самого правого палиндрома? Так как информации о том, что происходит за границами этого палиндрома у нас нет (а значит мы не можем утверждать, что симметрия сохраняется), то необходимо ограничить значение следующим образом: . После этого запустим наивный алгоритм, который будет увеличивать значение , пока это возможно.

После каждого шага важно не забывать обновлять значения .

Заметим, что массив считается аналогичным образом, нужно лишь немного изменить индексы.

Псевдокод

Приведем код, который вычисляет значения массива :

//  — исходная строка
int[] calculate1(string s):
  int l = 0
  int r = -1
  for i = 1 to n
    int k = 0
    if i <= r
       k = min(r - i, [r - i + l])
    while i + k + 1 <= n and i - k - 1 > 0 and s[i + k + 1] == s[i - k - 1]
       k++
     [i] = k
     if i + k > r
       l = i - k
       r = i + k
  return 

Вычисление значений массива :

//  — исходная строка
int[] calculate2(string s):
  int l = 0
  int r = -1
  for i = 1 to n
    int k = 0
    if i <= r
       k = min(r - i + 1, [r - i + l + 1])
    while i + k <= n and i - k - 1 > 0 and s[i + k] == s[i - k - 1]
       k++
     [i] = k
     if i + k - 1 > r
       l = i - k
       r = i + k - 1
  return 

Оценка сложности

Внешний цикл в приведенном алгоритме выполняется ровно раз, где — длина строки. Попытаемся понять, сколько раз будет выполнен внутренний цикл, ответственный за наивный подсчет значений. Заметим, что каждая итерация вложенного цикла приводит к увеличению на . Действительно, возможны следующие случаи:

1. , т.е. сразу будет запущен наивный алгоритм и каждая его итерация будет увеличивать значение хотя бы на .
2. . Здесь опять два случая:
   1. , но тогда, очевидно, ни одной итерации вложенного цикла выполнено не будет.
   2. , тогда каждая итерация вложенного цикла приведет к увеличению хотя бы на .

Т.к. значение не может увеличиваться более раз, то описанный выше алгоритм работает за время .

См. также

• Префикс-функция
• Z-функция
• Суффиксный массив
• Поиск наибольшей общей подстроки двух строк с использованием хеширования

Источники информации

• MAXimal :: algo :: Нахождение всех подпалиндромов
• Википедия — Поиск длиннейшей подстроки-палиндрома
• Алгоритмы для поиска палиндромов — Хабр
• MAXimal :: algo :: Суффиксный массив

There are two palindrome scenarios: Even palindromes (e.g. noon) and Odd palindromes (e.g. radar). There are only two possible (longest) palindromes for each position in the string. So, for each position, you only need to find the longest Even and Odd palindromes centred at that position by comparing characters forward and back.

s = "forgeeksskeegfor"

from os import path 
longest = ""
for i in range(1,len(s)-1):
    if min(i,len(s)-i)*2+1 <= len(longest): continue
    for odd in [1,0]:
        if s[i+odd] != s[i-1]: continue
        halfSize = len(path.commonprefix([s[i+odd:],s[:i][::-1]])) 
        if 2*halfSize + odd > len(longest):
            longest = s[i-halfSize:i+halfSize+odd];break
print(longest) # geeksskeeg

Note: this could be further optimized but will respond in O(n) time most of the time or up to O(n^2/2) in the worst case scenario where the string contains very long chains of identical characters (or only a single repeated character)

UPDATE

In order to minimize the impact of long chains of identical characters, the order of center positions for potential palindromes could follow a binary search pattern. The binRange() generator below can be used to replace range(1,len(s)-1) with binRange(1,len(s)-1) in the main loop. This will ensure that longer palindromes are found early and shorter embedded ones can be short circuited in subsequent iterations.

from itertools import zip_longest
def binRange(lo,hi=None):
    if hi is None: lo,hi = 0,lo
    if hi <= lo: return
    mid = (lo+hi-1)//2
    yield mid
    for a,b in zip_longest(binRange(lo,mid),binRange(mid+1,hi),fillvalue=None):
        if a is not None: yield a
        if b is not None: yield b