Страница 1 из 6
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ этой теме буду писать что-то вроде краткой шпаргалки по погрешностям. Опять же, данный текст ни в коей мере не официальный и ссылаться на него недопустимо. Буду признателен за исправление любых ошибок и неточностей, которые могут быть в этом тексте.
Что такое погрешность?
Запись результата эксперимента вида
![[IMG]](http://corum.mephist.ru/tex/images/b7cd22a4bb1c3d8abaa342cd2ada4701.gif) (
(![[IMG]](http://corum.mephist.ru/tex/images/48291f83278dbe78bb6d25c83d42b779.gif) ) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале
) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале ![[IMG]](http://corum.mephist.ru/tex/images/e52740eb8c1ca9095d2a4e17d036ebec.gif) , а в 30% – не будут.
, а в 30% – не будут.Или, что тоже самое, если мы повторим эксперимент, то новый результат ляжет в доверительный интервал
![[IMG]](http://corum.mephist.ru/tex/images/e52740eb8c1ca9095d2a4e17d036ebec.gif) с вероятностью, равной доверительной вероятности
с вероятностью, равной доверительной вероятности ![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) .
.Как округлять погрешность и результат?
Погрешность округляется до первой значащей цифры, если она не единица. Если единица – то до двух. При этом значащей цифрой называется любая цифра результата кроме нулей впереди.
Пример:
![[IMG]](http://corum.mephist.ru/tex/images/fe09543b974240017f246c36f0e20bad.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/a5cada5c2d1ccb4b76fbda0fb521adb3.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b4bebab07d35bbb43ec16714f5ed87c8.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/2e68c7fa8bf3791b61039377fa19d559.gif) но ни в коем случае не
но ни в коем случае не ![[IMG]](http://corum.mephist.ru/tex/images/f9c474b6e9e0acb125b588c2978f94e4.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/42a0f383586370bf8d25ece709fbb3e8.gif) , поскольку тут 2 значащие цифры – 2 и 0 после двойки.
, поскольку тут 2 значащие цифры – 2 и 0 после двойки. ![[IMG]](http://corum.mephist.ru/tex/images/d5d51f35586a0011459580a47c329c1c.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/bf7e5189fad7ab2880e4fc7c5411fea9.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/9182580f66fbbe10919734c8448a2b0e.gif)
![[IMG]](http://corum.mephist.ru/tex/images/74ccc55c5f11b678eee65f6d66b9a60d.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/60673e2250d177e624ad95b43064ca5e.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/af619a318dbcab2d7ff6c6654f907177.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b928ec2d5d3d00612d6b75b0024e52e6.gif)
Результат округляем таким образом, чтобы последняя значащая цифра результата соответствовала последней значащей цифре погрешности.
Примеры правильной записи:
![[IMG]](http://corum.mephist.ru/tex/images/5e73d4508bfbc87a12895031f6919e08.gif) мм
мм ![[IMG]](http://corum.mephist.ru/tex/images/e51638f79ed91c6edb4a330fbfeb683c.gif) мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности – единица.
мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности – единица. ![[IMG]](http://corum.mephist.ru/tex/images/03ffd1a1b9f618fd926a47a5ca0fc293.gif) мм
мм Примеры неправильной записи:
![[IMG]](http://corum.mephist.ru/tex/images/96072c008b0f5d6a865359f39cd1e082.gif) мм. Здесь лишний знак в результате. Правильно будет
мм. Здесь лишний знак в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/13bbbaf0c29b751a6c22008eb7f9f7b1.gif) мм.
мм. ![[IMG]](http://corum.mephist.ru/tex/images/2291014f831b0fd0257924da54867d23.gif) мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет
мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/13bbbaf0c29b751a6c22008eb7f9f7b1.gif) мм.
мм. В работе использую значение, данное мне просто в виде цифры. Например, масса грузиков. Какая у нее погрешность?
Если погрешность явно не указана, можно взять единицу в последнем разряде. То есть если написано m=1.35 г, то в качестве погрешность нужно взять 0.01 г.
Как считать погрешность сложной функции?
Есть функция от нескольких величин
![[IMG]](http://corum.mephist.ru/tex/images/27b6e5ddc95fcf2627e37957689fa579.gif) У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
![[IMG]](http://corum.mephist.ru/tex/images/cf5c3f00f8d2fe027241a59955d5ceae.gif)
символ
![[IMG]](http://corum.mephist.ru/tex/images/8fbdcb7dc81fe147175bc997b0fb2119.gif) означает частную производную f по x. Подробнее про частные производные здесь.
означает частную производную f по x. Подробнее про частные производные здесь.Как вообще правильно посчитать погрешность?
Положим, вы меряли одну и ту же величину x несколько (n) раз. Получили набор значений.
![[IMG]](http://corum.mephist.ru/tex/images/a0311888c35b344c57ef62341814562b.gif) . Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.
. Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.По пунктам.
1. Считаем погрешность разброса
Если все значения совпали – никакого разброса у вас нет. Иначе – есть погрешность разброса
![[IMG]](http://corum.mephist.ru/tex/images/693eacf86ab361cc13fe5e292519b7c3.gif) , которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:
, которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:![[IMG]](http://corum.mephist.ru/tex/images/c7f83b4f19066a525f2969ce1c8ce372.gif)
здесь
![[IMG]](http://corum.mephist.ru/tex/images/4c795de483c9c9897980b7ba74c847fc.gif) означает среднее по всем
означает среднее по всем ![[IMG]](http://corum.mephist.ru/tex/images/fac074461d1491da3757d3b266ebf89c.gif) .
.
Погрешность разброса![[IMG]](http://corum.mephist.ru/tex/images/693eacf86ab361cc13fe5e292519b7c3.gif) получается умножением среднеквадратичной погрешности среднего на коэффициент Стьюдента
получается умножением среднеквадратичной погрешности среднего на коэффициент Стьюдента ![[IMG]](http://corum.mephist.ru/tex/images/c5a8793748b3bf6f4c68fac5db40c651.gif) , который зависит от выбранной вами доверительной вероятности
, который зависит от выбранной вами доверительной вероятности ![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) и числа измерений n:
и числа измерений n:![[IMG]](http://corum.mephist.ru/tex/images/ceb95147a8605f55cd8513ecd26cc1fd.gif) .
. Коэффициенты Стьюдента
![[IMG]](http://corum.mephist.ru/tex/images/c5a8793748b3bf6f4c68fac5db40c651.gif) берем из нижеприведенной таблицы. Доверительная вероятность
берем из нижеприведенной таблицы. Доверительная вероятность ![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) выбитается произвольно, число измерений n мы также знаем.
выбитается произвольно, число измерений n мы также знаем. 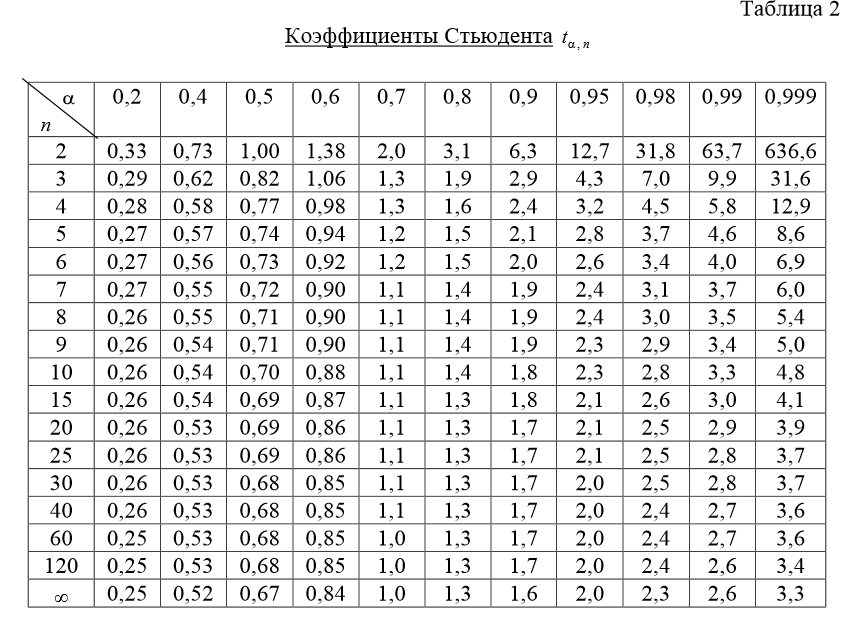
2. Считаем приборную погрешность среднего
Если погрешности разных точек разные, то по формуле
![[IMG]](http://corum.mephist.ru/tex/images/bb6c84165e61208b5b7b94e889085f7f.gif)
При этом естественно, у всех
![[IMG]](http://corum.mephist.ru/tex/images/80a15ae9b42d82e8676bae47fcab70b3.gif) доверительная вероятность должна быть одинаковой.
доверительная вероятность должна быть одинаковой. 3. Складываем среднее с разбросом
Погрешности всегда складываются как корень из квадратов:
![[IMG]](http://corum.mephist.ru/tex/images/b853078084cb450336d8305ee3ff0051.gif)
При этом нужно убедиться, что доверительные вероятности с которыми были вычислены
![[IMG]](http://corum.mephist.ru/tex/images/c391ad2e2574b7c9ffb7f64916b97dc2.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/e3f04bbaaa490a4d496e19c05c63f31e.gif) совпадают.
совпадают.
Как по графику определить приборную погрешность среднего? Ну т.е., используя метод парных точек или метод наименьших квадратов, мы найдем погрешность разброса среднего сопротивления. Как найти приборную погрешность среднего сопротивления?
И в МНК и в методе парных точек можно дать строгий ответ на этот вопрос. Для МНК форума в Светозарове есть (“Основы…”, раздел про метод наименьших квадратов), а для парных точек первое, что приходит в голову (в лоб, что называется) это посчитать приборную погрешность каждого углового коэффициента. Ну и далее по всем пунктам…

Если же не хочешь мучиться, то в лабниках дан простой способ для оценки приборной погрешности углового коэффициента, именно из МНК следующий (например перед работой 1 в лабнике “Электроизмерительные приборы. …” последняя страница Метод.рекомендаций).
![[IMG]](http://corum.mephist.ru/tex/images/59b6fc687986871e08a4def089688bbf.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/a5f06e8811bf82a53ff629bd97e8417e.gif) – величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
– величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
На магазине сопротивлений написан класс точности: 0,05/4*10^-6? Как из этого найти погрешность прибора?Это означает, что предельная относительная погрешность прибора (в процентах) имеет вид:
![[IMG]](http://corum.mephist.ru/tex/images/fd7f8eb5a1972f4158afd23480837110.gif) , где
, где
![[IMG]](http://corum.mephist.ru/tex/images/8f29cb2c179bfc115aa33e7730d3954d.gif) – наибольшее значение сопротивления магазина, а
– наибольшее значение сопротивления магазина, а ![[IMG]](http://corum.mephist.ru/tex/images/7d47b66519d27f5821540aa071c3d561.gif) – номинальное значение включённого сопротивления.
– номинальное значение включённого сопротивления.
Легко видеть, что второе слагаемое важно тогда, когда мы работаем на очень малых сопротивлениях.Подробнее всегда можно посмотреть в паспорте прибора. Паспорт можно найти в интернете, забив марку прибора в гугл.
Литература про погрешности
Рецептурная информация про то как считать погрешности дана во введениях к практикумам, в частности, во вводной части к практикуму “Измерительные приборы”.
Гораздо больше информации по этому поводу можно найти в рекомендованной для первокурсников книге:
В.В. Светозаров “Элементарная обработка результатов измерений”В качестве дополнительной (для первокурсников дополнительной) литературы можно порекомендовать:
В.В.Светозаров “Основы статистической обработки результатов измерений”И уж тем кто хочет окончательно во всем разобраться непременно стоит заглянуть сюда:
Дж. Тейлор. “Введение в теорию ошибок”Спасибо Lexxus’у за нахождение и размещение у себя на сайте этих замечательных книжек.
-

Lexxus
Немного великий
Администратор
VIPА разве не
![[IMG]](http://corum.mephist.ru/tex/images/e1b00eb5241498c481dfb7468c96e465.gif)
? -

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторНеа. Последняя значащая цифра результата должна отвечать последней значащей цифре погрешности.
Если мы держим миллиметры в погрешности, то почему их надо убирать в результате? -
0,98 можно округлить так:
![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
-

Lexxus
Немного великий
Администратор
VIP[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
[/quote]
0.98 можно округлять до 1.0, если погрешность получилась 0.195 и более.
В противном случае, округлять до 1.0 нельзя. -

Lexxus
Немного великий
Администратор
VIPlamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность – скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае – до десятков), т.е. записать![[IMG]](http://corum.mephist.ru/tex/images/d482ffddae86743b780638e2194d1cb2.gif) ?
?
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
[/quote]0,98 это результат или погрешность?

[quote name=’Lexxus’ post=’379428′ date=’Oct 5 2010, 16:53′]
lamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность – скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае – до десятков), т.е. записать![[IMG]](http://corum.mephist.ru/tex/images/d482ffddae86743b780638e2194d1cb2.gif) ?
?
[/quote]
Да, именно так, если я правильно понимаю. Связано, как я понимаю, с тем, что погрешность округления самой погрешности в этом случае превысит результат .
. То есть я понимаю, что четверка несет в себе некую информацию, которая убивается округлением. Но по сравнению с самой погрешностью, и с ее ошибкой округления, это уже все мало.
-
А в чем разница 2х примеров? Во втором случае оба числа просто на порядок меньше. Нельзя их записать как-то типа
![[IMG]](http://corum.mephist.ru/tex/images/795e28a5ddba8232883f37576bbf11cf.gif) . Это, разве, не полностью аналогичный случай к правильному варианту записи?
. Это, разве, не полностью аналогичный случай к правильному варианту записи?
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ первом случае первая цифра в погрешности – единица. Из-за этого мы держим в погрешности 2 знака, чтобы минимизировать ошибку округления погрешности. Во втором – четверка. И мы оставляем только один знак.
-
Т.е.
![[IMG]](http://corum.mephist.ru/tex/images/e7493bf11a89e41c4c62b4e8aee498a5.gif) – правильно?
– правильно?Думаю, тогда стоит в инструкции более ясно написать, почему предыдущее не правильно.
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторДа. А +- 4.2 – неправильно.Предлагай. У меня-то глаз замылен, мне все кажется понятным
 .
.
-
результат

-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379443′ date=’Oct 5 2010, 17:41′]
результат
[/quote]
Тогда тебе Lexxus ответил.[quote name=’Chameleon’ post=’379445′ date=’Oct 5 2010, 17:42′]
как так “завернуто”
[/quote]Слишком сложно для восприятия, имхо. Смешано в кучу правильное и неправильное. Я чуть выше, в примерах правильной записи, добавил строчку, поясняющую различие. И, кстати, про единицу сказано выше.
-
т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9

-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор -
[quote name=’Silver MC’s’ date=’Oct 5 2010, 18:19′]
[snapback]379453[/snapback]т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9[/quote]
Нет. Если погрешность 0,1, то дадо писать так: $0.98pm0.10
Если в погрешности 1я значащая цифра 1, то второй знак обязателен.
PS Если преподаватели немного посвирепствуют, то никакие мануалы и не нужны. Кстати в Светозарове то же самое написано, что и тут. -
Мне кажется, стоит еще написать:
1. как округлять пятерку в последнем разряде (у преподавателей разных кафедр похоже требования разные)
1.56
1.54
1.55
1.52. на пальцах объяснить что значит частная производная с простеньким примерчиком
Если надо – текст попозже напишу
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторNick_, а надо ли тут так вдаваться в математику? тем более в элементарную, вроде правил округления?
-

Lexxus
Немного великий
Администратор
VIPПроблема в том, что функции многих переменных и частные производные в курсе матанализа, кажется, где-то ближе к концу первого семестра.
Страница 1 из 6
Поделиться этой страницей

Оценим
погрешности методов вычисления. Для
разностных правой и левой производных
будут справедливы следующие выражения
![]() (5.16)
(5.16)
и
![]() , (5.17)
, (5.17)
а
для центральной
![]() . (5.18)
. (5.18)
Для
оценки погрешностей левых и правых
разностных производных первую производную
можно получить из разложения в ряд
Тейлора в виде
![]() . (5.19)
. (5.19)
Здесь
и ниже
![]()
и
![]()
– некоторые точки, расположенные на
интервалах
![]()
и
![]()
соответственно. Откуда погрешности
этих методов будут иметь вид
![]() , (5.20)
, (5.20)
а
оценка абсолютных погрешностей будет
удовлетворять неравенству ![]() , (5.21)
, (5.21)
где ![]() . (5.22)
. (5.22)
Таким
образом, формулы (5.2) и (5.3) вычисления
правой и левой разностных производных
имеют первый порядок точности по
![]() .
.
Для
центральной разностной производной
соответствующие разложения функций
![]()
в ряд Тейлора должны учитывать и
производную третьего порядка (вторая
производная при вычитании исчезает)
![]() . (5.23)
. (5.23)
Отсюда
получим
![]() (5.24)
(5.24)
и
для оценки абсолютной погрешности будет
справедливо неравенство
![]() (5.25)
(5.25)
где
![]()
(5.26)
Таким
образом, производная
![]()
вычисляется при помощи формул центральной
разностной производной со вторым
порядком точности по
![]() ,
,
т.е. точнее, чем по формулам (5.2) и (5.3).
Очень
часто уменьшение погрешности метода,
в данном случае метода численного
дифференцирования, сопровождается
ростом влияния погрешности исходных
данных и вычислительной погрешности.
Численное дифференцирование относится
именно к таким задачам, которые обычно
называют плохо обусловленными.
Оценим
совместное влияния погрешностей
вычисления и метода для вычисления
первой производной. Пусть значение
производной вычисляется по формуле
(5.3), тогда погрешность метода можно
оценить по соотношению (5.21). Если значения
функции
![]()
известны с некоторой погрешностью
![]()
(![]() ),
),
то погрешность вычисления
![]()
будет содержать дополнительное слагаемое
 ,(5.27)
,(5.27)
Пренебрегая
для простоты погрешностью округления,
имеем оценку погрешности в следующем
виде
![]()
.(5.28)
Из
формулы (5.28) очевидно, что уменьшение
![]()
не приводит к увеличению точности
вычисления производной, так как возрастает
ошибка, связанная с погрешностью
определения функции (рисунок 5.1).
Погрешности
![]()
возникают вследствие ошибок измерения
или предыдущего вычисления по приближенным
формулам. Из соотношения (5.28) можно найти
оптимальное значение разбиения, находя
экстремум правой части, такое
![]()
будет равно
![]() .(5.29)
.(5.29)
Отметим,
что повышение точности метода лишь
отчасти повышает точность вычисления
производной.

Рисунок
5.1. Зависимость погрешности вычисления
первой производной от величины шага.
5.3.
Численное интегрирование. Простейшие
методы К
численному интегрированию прибегают
в тех случаях, когда невозможно
аналитически получить первообразную,
или когда такая первообразная имеет
неудобный или слишком сложный для
вычисления вид. Основной задачей
численного интегрирования является
вычисление интеграла вида
![]() ,(5.29)
,(5.29)
где
![]()
и
![]()
– нижний и верхний пределы интегрирования,
а функция
![]()
– непрерывная на отрезке
![]() .
.
Сущность
большинства методов вычисления
определенных интегралов состоит в
замене подынтегральной функции
![]()
аппроксимирующей функцией
![]() ,
,
для которой можно легко записать
первообразную в элементарных функциях,
т.е.
![]() ,(5.30)
,(5.30)
где
![]()
– погрешность вычисления.
Используемые
на практике методы численного
интегрирования можно условно сгруппировать
в зависимости от способа аппроксимации
подынтегральной функции.
-
Методы
полиномиальной аппроксимации
 ,
,
которые отличаются друг от друга
степенью используемого полинома, что
определяет количество узлов, где
необходимо вычислить подынтегральную
функцию. Это достаточно простые для
реализации методы. В частности к этим
методам относятся простейшие формулы
– прямоугольников, трапеций, Симпсона,
которые обобщаются формулами
Ньютона-Котеса. -
Сплайновые
методы базируются на аппроксимации

сплайнами. Методы этого класса отличаются
по типу выбранных сплайнов и используются
в основном там, где применяются алгоритмы
сплайновой аппроксимации для обработки
данных. -
Методы
наивысшей алгебраической точности,
использующие неравноотстоящие узлы,
расположенные по алгоритму, обеспечивающую
минимальную погрешность интегрирования,
используются для наиболее сложных
функций при заданном количестве узлов
вычисления функции
 .
. -
Методы,
основанные на случайном выборе узлов,
где определяются значения интегрируемой
функции. Эти методы (методы Монте-Карло)
используются для вычисления кратных
интегралов, для которых они наиболее
эффективны.
В
дальнейшем ограничимся методами первой
и второй группы, а также рассмотрим
алгоритмы метода Монте-Карло для кратных
интегралов.
Наиболее
широко на практике для вычисления
определенных интегралов используются
квадратурные формулы – приближенные
равенства вида
 , (5.31)
, (5.31)
что
соответствует разбиению полного
интеграла на сумму интегралов от функции
по элементарным отрезкам. Здесь
![]()
– некоторые точки (узлы) из отрезка
![]() ,
,
разбитого на
![]()
элементарных отрезков
![]() ,
,
при этом
![]() ,
,
а
![]() ,
,
а
![]()
– некоторые коэффициенты. Сумма, стоящая
в правой части выражения (5.31) называется
квадратурной суммой. Погрешность
вычисления по этой формуле определяется
выражением
![]() . (5.32)
. (5.32)
Заметим,
что интеграл вида (5.29) определяет площадь
фигуры ограниченной прямыми
![]() ,
,
![]() ,
,
![]()
и графиком функции
![]() .
.
Для вычисления этой и площади и
соответственно интеграла ее можно
разбить на простые фигуры. На этом и
основаны простейшие методы вычисления
интеграла (5.29).
Формулы
прямоугольников.
Рассмотрим разбиение отрезка
![]()
на
![]()
элементарных отрезков
![]() ,
,
пусть для простоты
![]() ,
,
тогда каждому значению
![]()
можно поставить в соответствие значение
функции
![]() .
.
Рассматривая
![]()
как высоту прямоугольника с основанием
![]()
можно получить две формулы: формулу
левых прямоугольников (рисунок 5.2)
![]() (5.33)
(5.33)
и
формулу правых прямоугольников
![]() .(5.34)
.(5.34)
Аналогичным
образом за высоту прямоугольника можно
взять его середину. В этом случае отрезок
обычно разбивают на
![]()
отрезков и рассматривают только нечетные
узлы, что эквивалентно рассмотрению
прямоугольников высотой, равной значению
функции в середине элементарного
отрезка. Квадратурная формула называется
формулой средних прямоугольников
(рисунок 5.3) и имеет вид
![]() .(5.35)
.(5.35)
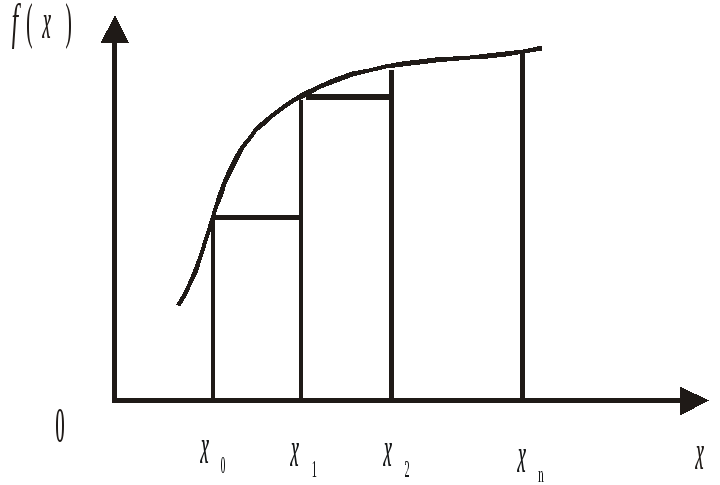
Рисунок
5.2. Интегрирование по формуле левых
прямоугольников
Интересно
отметить, что формулы левых и правых
прямоугольников фактически заменяют
интеграл верхними и нижними суммами
Дарбу и, к сожалению, имеют высокую
погрешность. Это в равной степени
относится и к формуле средних
прямоугольников.
Формула
трапеций.
Следующая простейшая формула получается,
если рассматривать в качестве приближения
не прямоугольник, а трапецию с высотами
![]()
и
![]()
(рисунок 5.4). В этом случае площадь
![]() -ой
-ой
элементарной трапеции с основанием
![]()
будет иметь вид
![]() . (5.36)
. (5.36)

Рисунок
5.3. Интегрирование по формуле средних
прямоугольников
Приближенное
значение интеграла в свою очередь будет
определяться как
 . (5.37)
. (5.37)
Эта
формула соответствует приближенной
замене площади исходной криволинейной
трапеции площадью фигуры, ограниченной
ломаной линией.
Рисунок
5.4. Интегрирование по формуле трапеций
В
качестве примера приведена программа
вычисления интеграла от функции
![]()
на отрезке [-5,5] по формуле правых
прямоугольников.
В математике для приближённого вычисления производных заданной таблично функции можно искать выражение значений производных через известные значения функции с помощью подходящего набора коэффициентов. Для этого можно использовать различные интерполяционные формулы или метод неопределённых коэффициентов.
Равноотстоящие узлы[править | править код]
Пусть 





В зависимости от расположения точки 
Симметричные коэффициенты[править | править код]
Для получения симметричных коэффициентов число узлов в сетке должно быть нечётным. Тогда порядок погрешности приближения будет чётным числом.
| Порядок производной | Порядок погрешности | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | −1/2 | 0 | 1/2 | ||||||||
| 4 | 1/12 | −2/3 | 0 | 2/3 | −1/12 | |||||||
| 6 | −1/60 | 3/20 | −3/4 | 0 | 3/4 | −3/20 | 1/60 | |||||
| 8 | 1/280 | −4/105 | 1/5 | −4/5 | 0 | 4/5 | −1/5 | 4/105 | −1/280 | |||
| 2 | 2 | 1 | −2 | 1 | ||||||||
| 4 | −1/12 | 4/3 | −5/2 | 4/3 | −1/12 | |||||||
| 6 | 1/90 | −3/20 | 3/2 | −49/18 | 3/2 | −3/20 | 1/90 | |||||
| 8 | −1/560 | 8/315 | −1/5 | 8/5 | −205/72 | 8/5 | −1/5 | 8/315 | −1/560 | |||
| 3 | 2 | −1/2 | 1 | 0 | −1 | 1/2 | ||||||
| 4 | 1/8 | −1 | 13/8 | 0 | −13/8 | 1 | −1/8 | |||||
| 6 | −7/240 | 3/10 | −169/120 | 61/30 | 0 | −61/30 | 169/120 | −3/10 | 7/240 | |||
| 4 | 2 | 1 | −4 | 6 | −4 | 1 | ||||||
| 4 | −1/6 | 2 | −13/2 | 28/3 | −13/2 | 2 | −1/6 | |||||
| 6 | 7/240 | −2/5 | 169/60 | −122/15 | 91/8 | −122/15 | 169/60 | −2/5 | 7/240 | |||
| 5 | 2 | −1/2 | 2 | −5/2 | 0 | 5/2 | −2 | 1/2 | ||||
| 4 | 1/6 | −3/2 | 13/3 | −29/6 | 0 | 29/6 | −13/3 | 3/2 | −1/6 | |||
| 6 | −13/288 | 19/36 | −87/32 | 13/2 | −323/48 | 0 | 323/48 | −13/2 | 87/32 | −19/36 | 13/288 | |
| 6 | 2 | 1 | −6 | 15 | −20 | 15 | −6 | 1 | ||||
| 4 | −1/4 | 3 | −13 | 29 | −75/2 | 29 | −13 | 3 | −1/4 | |||
| 6 | 13/240 | −19/24 | 87/16 | −39/2 | 323/8 | −1023/20 | 323/8 | −39/2 | 87/16 | −19/24 | 13/240 |
Например, третья производная с погрешностью второго порядка вычисляется как
Коэффициенты вперёд[править | править код]
| Порядок производной | Порядок погрешности | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 1 | |||||||
| 2 | −3/2 | 2 | −1/2 | |||||||
| 3 | −11/6 | 3 | −3/2 | 1/3 | ||||||
| 4 | −25/12 | 4 | −3 | 4/3 | −1/4 | |||||
| 5 | −137/60 | 5 | −5 | 10/3 | −5/4 | 1/5 | ||||
| 6 | −49/20 | 6 | −15/2 | 20/3 | −15/4 | 6/5 | −1/6 | |||
| 2 | 1 | 1 | −2 | 1 | ||||||
| 2 | 2 | −5 | 4 | −1 | ||||||
| 3 | 35/12 | −26/3 | 19/2 | −14/3 | 11/12 | |||||
| 4 | 15/4 | −77/6 | 107/6 | −13 | 61/12 | −5/6 | ||||
| 5 | 203/45 | −87/5 | 117/4 | −254/9 | 33/2 | −27/5 | 137/180 | |||
| 6 | 469/90 | −223/10 | 879/20 | −949/18 | 41 | −201/10 | 1019/180 | −7/10 | ||
| 3 | 1 | −1 | 3 | −3 | 1 | |||||
| 2 | −5/2 | 9 | −12 | 7 | −3/2 | |||||
| 3 | −17/4 | 71/4 | −59/2 | 49/2 | −41/4 | 7/4 | ||||
| 4 | −49/8 | 29 | −461/8 | 62 | −307/8 | 13 | −15/8 | |||
| 5 | −967/120 | 638/15 | −3929/40 | 389/3 | −2545/24 | 268/5 | −1849/120 | 29/15 | ||
| 6 | −801/80 | 349/6 | −18353/120 | 2391/10 | −1457/6 | 4891/30 | −561/8 | 527/30 | −469/240 | |
| 4 | 1 | 1 | −4 | 6 | −4 | 1 | ||||
| 2 | 3 | −14 | 26 | −24 | 11 | −2 | ||||
| 3 | 35/6 | −31 | 137/2 | −242/3 | 107/2 | −19 | 17/6 | |||
| 4 | 28/3 | −111/2 | 142 | −1219/6 | 176 | −185/2 | 82/3 | −7/2 | ||
| 5 | 1069/80 | −1316/15 | 15289/60 | −2144/5 | 10993/24 | −4772/15 | 2803/20 | −536/15 | 967/240 |
Например, первая производная с погрешностью третьего порядка и вторая производная с погрешностью второго порядка вычисляются как
Нетрудно видеть, что коэффициенты для погрешности первого порядка представляют собой биномиальные коэффициенты с меняющимися знаками, что соответствует общей формуле для восходящих конечных разностей.
Коэффициенты назад[править | править код]
Для получения коэффициентов назад необходимо обратить знаки у коэффициентов вперёд для производных нечётных порядков и зеркально отразить таблицу коэффициентов справа налево:
| Порядок производной | Порядок погрешности | −5 | −4 | −3 | −2 | −1 | 0 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 1 | ||||
| 2 | 1/2 | −2 | 3/2 | ||||
| 3 | −1/3 | 3/2 | −3 | 11/6 | |||
| 2 | 1 | 1 | −2 | 1 | |||
| 2 | −1 | 4 | −5 | 2 | |||
| 3 | 1 | −1 | 3 | −3 | 1 | ||
| 2 | 3/2 | −7 | 12 | −9 | 5/2 | ||
| 4 | 1 | 1 | −4 | 6 | −4 | 1 | |
| 2 | −2 | 11 | −24 | 26 | −14 | 3 |
Например, первая производная с погрешностью третьего порядка и вторая производная с погрешностью второго порядка вычисляются как
Произвольная сетка узлов[править | править код]
Для получения коэффициентов для произвольно расположенных узлов 


где
— неизвестные коэффициенты,
— остаточный член интерполяции.
Коэффициенты 





В этом случае погрешность вычислений будет иметь порядок 
Матрица системы является матрицей Вандермонда, которая также возникает при решении общей задачи интерполяции многочленами.
Примечания[править | править код]
- ↑ Березин, Жидков, 1962, с. 230.
- ↑ Березин, Жидков, 1962, с. 234.
Литература[править | править код]
- Березин, И. С., Жидков Н. П. Методы вычислений. — 2-е изд. — М.: Физматлит, 1962. — Т. I.
- . Generation of Finite Difference Formulas on Arbitrarily Spaced Grids (англ.) // Mathematics of Computation. — 1988. — Vol. 51. — P. 699—706. — doi:10.1090/S0025-5718-1988-0935077-0.
Ссылки[править | править код]
- Калькулятор коэффициентов для произвольных сеток узлов (численно)
См. также[править | править код]
- Метод конечных разностей







