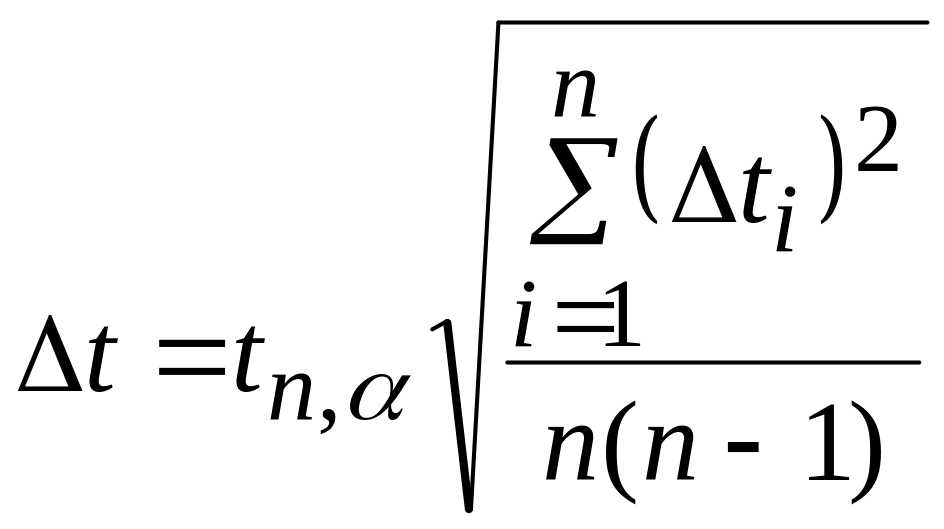
,
(8.31)
где
коэффициент Стьюдента для числа опытов
n=5
и доверительной вероятности α=0.95 равен:
tn
α=2.78;
Δti=|tср.-
ti|.
Замечание
2: погрешности
ε
и М
рассчитываются, исходя из формул (8.28) и
(8.29) соответственно, по стандартной
методике расчета погрешностей при
косвенных измерениях:
![]()
,
где
![]()
,
![]()
,
![]()
.
![]()
,
где
производные равны:
![]()
,
![]()
,
![]()
,
![]()
.
Замечание
3: погрешность
рассчитывается,
исходя из формулы (8.14) по стандартной
методике расчета погрешностей при
косвенных измерениях:
![]()
.
Задание
2.
Проверка
теоремы Штейнера.
-
Оставив
грузы
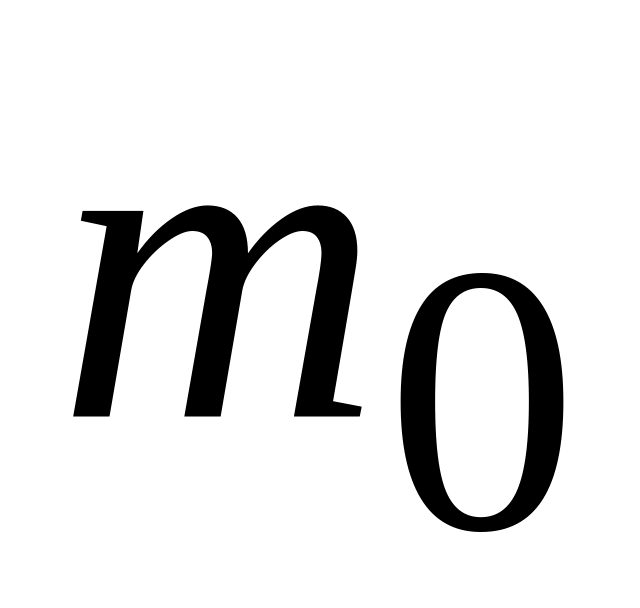
на концах стержней, измерьте расстояние
R1
от центра
тяжести грузов на стержнях до оси
вращения. -
Занесите
в таблицу 8.2 из таблицы 8.1 значения
времени

.
Таблица
8.2
|
, |
||||||
|
№ |
Грузы R1=…м |
Грузы R3=…м |
|
|
||
|
t1, с |
, кг.м2 |
t3, с |
кг.м2 |
|||
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
4 |
||||||
|
5 |
||||||
|
t1ср.=… |
t3ср.=… |
-
Положите
на тарелочку гирьку массой.
-
Передвиньте
грузына середину стержней, измерьте расстояние
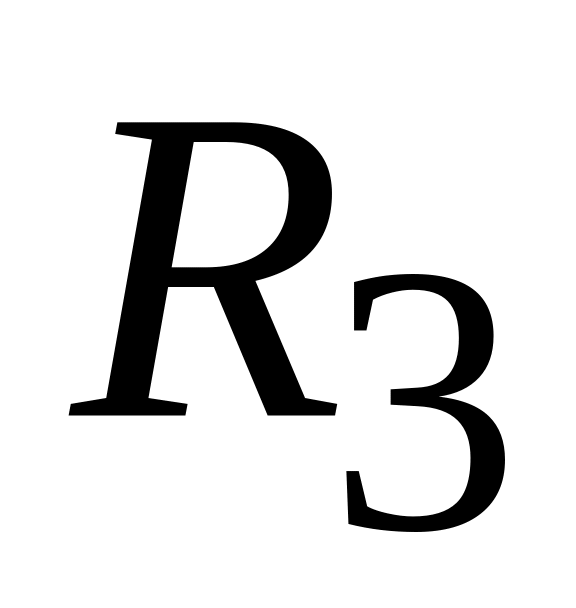
от центра тяжести грузов на стержнях
до оси вращения. -
Повторите
измерения времени

движения груза
5 раз (аналогично заданию 1), рассчитайте
среднее время и момент инерциикрестовины для нового положения грузиков
на стержнях по формуле (8.27). -
Все
результаты занесите в таблицу 8.2. -
Рассчитайте
изменение момента инерции маятника
Обербека при передвижении грузов с
конца стержней на середину по формуле
(8.32).
![]()
,
(8.32)
где
m0
= 0.12 кг.
-
Сравните
изменение момента инерции маятника
Обербека, рассчитанного с использованием
теоремы Штейнера по формуле (8.32), и
полученного экспериментально по данным
табл. 8.2:
![]()
.
-
Сделайте
выводы.
Контрольные вопросы
-
Дайте
определение углового перемещения,
угловой скорости и ускорения. Как
направлены эти вектора? -
Запишите
формулы, связывающие линейные и угловые
величины перемещения, скорости,
ускорения. -
Что
такое момент силы относительно точки?
Относительно оси? От чего он зависит?
Как направлен вектор момента силы? -
Что
такое момент инерции материальной
точки; твердого тела? От чего он зависит? -
Сформулируйте
и докажите основной закон динамики
вращательного движения (8.18). -
Сформулируйте
теорему Штейнера и покажите, где в
работе она используется. -
Как
и почему изменяется время движения
гири, если грузы на спицах передвинуть
ближе к оси вращения? -
При
каком расположении грузов на крестовине
их можно считать точечными, при каком
– нельзя? -
Выведите
формулы (8.27), (8.28), (8.29). -
Докажите
(8.32).
Используемая
литература
[5]
§1.5; 2.8; 3.2; 4.8; 7.1; [3] §2.4; 4.1; 4.2; 4.3; 5.3; 5.6; [1] §
3-5, 9, 36-39; [6] §1.2; 1.4; 1.9-1.13; 1.19; 1.31-1.34; [7]
§2-7; 16-19.
Лабораторная
работа 1-09
Определение
момента инерции маховика
Цель
работы: определение
момента инерции твердого тела с помощью
закона сохранения энергии.
Теоретическое
введение
В
![]()
работе изучаются такие движения в
механике, при которых существенна
конечная протяженность тел – их нельзя
рассматривать в данных условиях как
материальные точки. Если тело является
настолько жестким, что деформациями,
возникающими при его движении, можно
пренебречь, то тело можно рассматривать
как недеформируемое, абсолютно твердое
(или просто твердое) тело. Взаимное
расположение частей абсолютно твёрдого
тела остается неизменным во время
движения.
Простейшим
движением твердого тела является
поступательное. Тело перемещается
параллельно самому себе; все точки его
имеют одинаковую скорость и описывают
траектории одинаковой формы, только
смещенные по отношению друг к другу.
При этом кинетическая энергия равна:
![]()

,
(9.1)
где
![]()
– скорость тела,
– его масса.
Другим
простейшим видом движения твердого
тела является вращение тела вокруг оси.
Определим кинетическую энергию твердого
тела, закрепленного на неподвижной оси,
вокруг которой оно может свободно
вращаться (рис.9.1); точка О – след этой
оси. К одной из точек тела А приложена
внешняя сила
![]()
.
Мысленно разделим тело на отдельные
элементарные части, настолько малые,
чтобы их можно было считать движущимися
как материальные точки.
– масса этого элемента,
![]()
– его расстояние до оси вращения. При
вращении различные точки тела описывают
окружности, лежащие в плоскостях,
перпендикулярных оси вращения. Если за
время
тело поворачивается на угол
![]()
,
то путь
![]()
,
проходимый за это время i-той
точкой тела, будет равен
![]()
.
Разделив
на
,
найдем скорость i-той
точки:
![]()
.
(9.2)
Величина
![]()
есть угловая скорость. Она одинакова
для всех точек тела и представляет собой
угловое перемещение тела за единицу
времени. Величина скорости i-того
элемента равна:
![]()
,
(9.3)
а
его кинетическая энергия:
![]()
(9.4)
Просуммировав
эти энергии по всем элементам тела,
получим полную кинетическую энергию
вращающегося твердого тела:
![]()
(9.5)
Стоящая
в скобках сумма зависит от того, с каким
именно твердым телом мы имеем дело (от
его формы, размеров и распределения
массы в нем), а также от того, как
расположена в нем ось вращения. Эта
величина, характеризующая твердое тело
и выбранную ось вращения, называется
моментом инерции относительно данной
оси и обозначается буквой
![]()
(9.6)
Если
твердое тело – сплошное, то его нужно
разделить на бесконечно большое
количество бесконечно малых частей.
Суммирование в (9.6) заменяем интегрированием:
![]()
.
(9.7)
Так
как
![]()
(
– плотность тела), то вычисление момента
инерции сводится к тройному интеглалу
по координатам:
![]()
.
(9.8)
Вычисление
таких интегралов в общем случае
представляет собой сложную задачу. Лишь
для тел симметричной формы при однородном
распределении массы по объему тела их
моменты инерции определить достаточно
просто, если ось вращения проходит через
центр масс (шар, цилиндр, диск, стержень).
Поэтому моменты инерции сложных тел
проще определять экспериментально.
Таким
образом, кинетическая энергия вращающегося
тела может быть записана в виде:
![]()
(9.9)
Это
выражение формально похоже на выражение
для энергии поступательного движения
(9.1), отличаясь от него тем, что вместо
скорости
стоит угловая скорость
,
а вместо массы
– момент инерции
.
Так что при вращении момент инерции
играет роль, аналогичную массе при
поступательном движении.
Далее
кинетическую энергию произвольно
движущегося твердого тела можно
представить в виде суммы энергий
поступательного и вращательного
движений, если ось вращения проходит
через центр инерции тела. Тогда для
полной кинетической энергии произвольно
движущегося тела имеем:
![]()
.
(9.10)
Здесь
первое слагаемое – кинетическая энергия
поступательного движения,
– скорость перемещения центра инерции;
второе слагаемое – кинетическая энергия
вращения тела вокруг оси, проходящей
через центр инерции;
![]()
– момент инерции тела относительно
этой оси.
Независимо
от характера движения тел (поступательного
или вращательного) для замкнутых систем
справедлив закон сохранения механической
энергии (суммы кинетической и потенциальной
энергий), если между телами действуют
только консервативные силы. Если в
замкнутой системе тел действуют и не
консервативные силы, например, силы
трения, то изменение полной механической
энергии системы
![]()
равно работе неконсервативных сил:
![]()
.
(9.11)
В
данной лабораторной работе используется
именно этот закон. Необходимо еще дать
определение работы при вращении твердого
тела. Выражение для работы
при вращении твердого тела вокруг оси
легко представить, если продолжить
отмеченную аналогию между соотношениями
динамики поступательного движения и
динамики твердого тела: вместо линейной
скорости
– угловая скорость
;
вместо массы
– момент инерции
;
вместо силы
![]()
– момент силы
,
вместо пути
– угол поворота
.
Тогда вместо соотношения
![]()
,
определяющего работу при поступательном
движении, для вращательного движения
получим:
![]()
.
(9.12)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
кто знает физику??? как определить относительную погрешность измерения времени????
Ученик
(128),
закрыт
12 лет назад
*чел*
Гуру
(3279)
13 лет назад
разность между результатом отдельного измерения и средним результатом, взятую по модулю называют абсолютной погрешностью измерения. относительная погрешность равна отношению абсолютной погреш. к среднему результаты и выражается в % это всё чем могу помочь) Пусть N1 N2 N3 …Nn -результаты отдельных измерений тогда средний рез. вычисляется по фотмуле N =N1+N2+N3….Делённое на N
УДК 389.004.12
Полякова Л.В., Гладкова С.С.
ПОГРЕШНОСТИ ИЗМЕРЕНИЯ ВРЕМЕНИ, ЭТАЛОНЫ ИЗМЕРЕНИЯ ВРЕМЕНИ
Полякова Людмила Васильевна, Российский химико-технологический университет им. Д.И. Менделеева, доцент кафедры Инновационных материалов и защиты от коррозии. Адрес:125047, Москва, Миусская пл., д.9. Тел.+79651814143, e-mail:polyakova1803@mail.ru
Гладкова Софья Сергеевна, Российский химико-технологический университет им. Д.И. Менделеева, Студентка кафедры Инновационных материалов и защиты от коррозии. Адрес:125047, Москва, Миусская пл., д.9. ,e-mail sofi2103@list.ru
Известно, что во все времена проблема определения времени была актуальна. Важным показателем измерений являетсяя их точность, которая представляет собой ту степень близости итогов измерения к некоторому действительному значению, которая используется для качественного сравнения измерительных операций. В качестве количественной оценки, как правило, используется погрешность измерений.
Ключевые слова: Время, эталон времени, измерение, погрешность Измерения
TIME MEASUREMENT ERRORS, TIME MEASUREMENT STANDARDS
Lyudmila V. Polyakova, D. I. Mendeleev Russian University of Chemical Technology, Associate Professor of the Department of Innovative Materials and Corrosion Protection. Address:9 Miusskaya pl., Moscow, 125047. Tel.+79651814143, e-mail:polyakova1803@mail.ru
Sofia S. Gladkova, D. I. Mendeleev Russian University of Chemical Technology, Associate Professor of the Department of Innovative Materials and Corrosion Protection. Address: 9 Miusskaya pl., Moscow, 125047, e-mail sofi2103@list.ru
It is known that at all times the problem of determining time was relevant. An important indicator of measurements is their accuracy, which is the degree of proximity of the measurement results to a certain actual value, which is used for qualitative comparison of measurement operations. As a rule, the measurement error is used as a quantitative assessment.
Keywords: Time, time standard, measurement, measurement Error
Что такое время? До сих пор понятие «время» является неразрешимой проблемой философии и естествознания. И во все времена на него отвечали по – разному. В самом общем виде можно сказать, что время – это форма существования материи, выражающая изменения объектов и явлений действительности. Проблема определения времени была актуальна и остаётся актуальной для человечества на протяжении существования бытия . В практике использования измерений очень важным показателем становится их точность, которая представляет собой ту степень близости итогов измерения к некоторому действительному значению, которая используется для качественного сравнения измерительных операций. А в качестве количественной оценки, как правило, используется погрешность измерений.
Погрешности связанные со временем всего две:
Статическая погрешность – это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины. Динамическая погрешность – это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при
измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).
Гравитационное (или эфемеридное) время и атомное время.
Равномерное время называется ньютоновским или эфемеридным временем. Начиная с 1960 г., в астрономических ежегодниках эфемериды Солнца, Луны, планет и их спутников даются в системе эфемеридного времени. В связи с использованием системы эфемеридного времени в астрономии и физике введено новое определение производной единицы времени — секунды.
Использование атомной секунды в качестве эталонной единицы времени было принято 12-й Международной конференцией по мерам и весам в Париже в 1964. Она определяется на основе цезиевого эталона. С помощью электронных устройств осуществляется подсчет колебаний цезиевого генератора, и время, за которое
происходит 9 192 631 770 колебаний, принимается за эталон секунды.
Эфемеридное время устанавливается по данным астрономических наблюдений и подчиняется законам гравитационного взаимодействия небесных тел. Определение времени с помощью квантовых стандартов частоты основано на электрических и ядерных взаимодействиях внутри атома. Вполне возможно несовпадение масштабов атомного и гравитационного времени. В таком случае частота колебаний, генерируемых атомом цезия, будет изменяться по отношению к секунде эфемеридного времени в течение года, и это изменение нельзя отнести за счет ошибки наблюдения.
Самые точные наручные или настенные часы грешат против эталонного времени в миллиарды раз. Впрочем, в быту и не нужна точность до долей микросекунды. Но она совершенно необходима в исследовании космоса, для создания систем навигации, управления воздушным движением, повышения качества теле- и радиопередач и многих других целей.
Эталон времени — особенный. Все остальные эталоны вводятся в действие периодически, для сличения с ними вторичных и рабочих эталонов. Но эталон, хранящий шкалу времени, нельзя остановить, как нельзя остановить время. Он работает всегда. Есть такой афоризм: время — очень простое понятие, пока вы не пытаетесь объяснить его кому-нибудь. С полным основанием эти слова можно отнести и к
эталону времени. Меньше всего он напоминает часы, а оборудование и научные подразделения, которые обеспечивают эксплуатацию эталона, занимают большое здание. Находится оно во Всероссийском научно-исследовательском институте физико-технических и радиотехнических измерений (ВНИИФТРИ) под Москвой.
Эталон времени — это сложный комплекс, в который входят цезиевые реперы (генераторы, дающие строго определенную частоту) и водородные хранители частоты, хранители шкал времени, приборы для измерения временных интервалов и другая аппаратура. Некоторые составляющие эталона уникальны, например, радиооптический частотный мост, который служит для измерения частот излучения лазеров. В мире кроме России такой мост есть только в Канаде, во Франции, в США и Великобритании. Российский государственный эталон времени входит в группу лучших мировых эталонов, его относительная погрешность не превышает 5.10-14, то есть 0,00000000000005 секунды. За полмиллиона лет эталон даст погрешность в одну секунду.
Библиография
1. Полякова Л.В., Василенко О.А. Методы оценивания погоешностей измерений, методические указания/ -М.:РХТУ им. Д.И. Менделеева, 2021 – 36 с.
2. https://mydocx.ru/6-38900.html
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим:  . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
 (5.1)
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0  0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
 и указывает на качество измерения. Ее можно выразить в процентах.
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
- Для линейки 1:
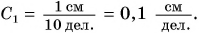
- Для линейки 2:
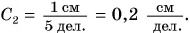
- Для линейки 3:
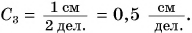
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:


А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы  ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления
), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления  ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:
1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10°  определенный по средней шкале с точностью до 5°
определенный по средней шкале с точностью до 5°  определенный по верхней шкале с точностью до 1°
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Измерение длины, площади, объема и времени
- Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
- Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
п.1. Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
Цель работы
Научиться измерять длину с помощью линейки, определять площадь поверхности и объем прямоугольного параллелепипеда, находить абсолютные и относительные погрешности косвенных измерений.
Теоретические сведения
 |
Прямоугольный параллелепипед – это многогранник с шестью гранями, каждая из которых является прямоугольником. Прямоугольный параллелепипед имеет три измерения: длину, ширину и высоту. |
Пусть
длина (AD=BC=A_1 D_1=B_1 C_1=a)
ширина (AB=CD=A_1 B_1=C_1 D_1=b)
высота (AA_1=BB_1=CC_1=DD_1=c)
Площади верхней и нижней грани равны (S_1=ab), площади передней и задней граней равны (S_2=ac), площади левой и правой граней равны (S_3=bc).
Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех шести граней: $$ S_{пов}=2S_1+2S_2+2S_3=2(ab+ac+bc) $$ Объем прямоугольного параллелепипеда равен произведению всех трех измерений: $$ V=abc $$
Пусть измерения проводятся ученической линейкой с ценой деления (triangle=1 мм).
Тогда инструментальная погрешность измерений равна половине цены деления: $$ d=frac{triangle}{2}=0,5 мм $$ Абсолютная погрешность измерений при работе с линейкой равна инструментальной погрешности, поэтому для всех измерений: (triangle a=triangle b=triangle c=d=0,5 мм)
Относительные погрешности измерений (в долях, без процентов): $$ delta_a=frac{triangle a}{a}=frac da, delta_b=frac{triangle b}{b}=frac db, delta_c=frac{triangle c}{c}=frac dc $$ Выведем необходимые формулы.
Рассмотрим нижнюю грань. Её площадь (S_1=ab) является произведением двух длин.
Значит, относительная погрешность измерения площади равна сумме относительных погрешностей длин: $$ delta_{S1}=delta_a+delta_b $$ Аналогично для остальных граней: $$ delta_{S2}=delta_a+delta_c, delta_{S3}=delta_b+delta_c $$ Абсолютная погрешность измерения площади нижней грани: $$ triangle S_1=S_1cdotdelta_{S1}=abcdot(delta_a+delta_b)=abcdotleft(frac da+frac dbright)=abdcdotleft(frac ab+frac1bright)=abdcdotfrac{b+a}{ab}= d(a+b) $$ Аналогично для остальных граней: $$ triangle S_2=S_2cdotdelta_{S2}=d(a+c), triangle S_3=S_3cdotdelta_{S3}=d(b+c) $$ Абсолютная погрешность суммы измерений равна сумме абсолютных погрешностей. Получаем для площади поверхности: begin{gather*} triangle S_{пов}=2(triangle S_1+triangle S_2+triangle S_3)=2(d(a+b)+d(a+c)+d(b+c))=\ =2d(a+b+a+c+b+c)=4d(a+b+c) end{gather*}
Абсолютная погрешность определения площади поверхности прямоугольного параллелепипеда равна: $$ triangle S_{пов}=4d(a+b+c) $$ где (d) – инструментальная погрешность линейки, (a,b,c) – измеренные значения длины, ширины и высоты.
Найдем погрешность определения объема.
Объем равен произведению трех измерений, значит, относительная погрешность для объема равна сумме относительных погрешностей измерений: $$ delta_v=delta_a+delta_b+delta_c=frac da+frac db+frac dc=dleft(frac 1a+frac 1b+frac 1cright)=dcdotfrac{bc+ac+ab}{abc} $$ Абсолютная погрешность для объема: $$ triangle V=vcdotdelta_v=abccdot dcdotfrac{bc+ac+ab}{abc} = d(bc+ac+ab)=dcdotfrac{S_{пов}}{2} $$
Абсолютная погрешность определения объема прямоугольного параллелепипеда равна: $$ triangle V=dcdotfrac{S_{пов}}{2} $$ где (d) – инструментальная погрешность линейки, (S_{пов}) – площадь поверхности.
Приборы и материалы
Ученическая линейка, книга (или деревянный брусок).
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Измерьте длину, ширину и высоту книги (бруска), (a,b,c).
3. Найдите площадь поверхности (S_{пов}) и объем (V).
4. Найдите абсолютные погрешности (triangle S_{пов}) и (triangle V).
5. Найдите относительные погрешности в процентах: $$ delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}, delta_V=frac{triangle V}{V}cdot 100text{%} $$ 6. Дополнительное задание. Определите толщину одного листа книги, абсолютную и относительную погрешность этой величины.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Инструментальная погрешность линейки (d=frac{1 мм}{2}=0,5 мм)
Результаты измерений:
a=218 мм
b=147 мм
c=32 мм
Площадь поверхности: begin{gather*} S_{пов}=2(ab+ac+bc)=2(218cdot 147+218cdot 32+147cdot 32)=\ =2(32046+6976+4704)=87452 (мм^2) end{gather*} Объем: $$ V=abc=218cdot 147cdot 32=1025472 (мм^2) $$ Абсолютная погрешность определения площади поверхности (округляем до двух значащих цифр с избытком): $$ triangle S_{пов}=4d(a+b+c)=4cdot 0,5cdot (218+147+32)=2cdot 397=794 (мм^2)approx 800 (мм^2) $$ Полученную величину площади поверхности также округляем до сотен. Получаем: $$ S_{пов}=(87500pm 800) (мм^2) $$ Абсолютная погрешность определения объема: $$ triangle V=dcdotfrac{S_{пов}}{2}=0,5cdotfrac{87452}{2}=21863 (мм^3)approx 22000 (мм^3) $$ Полученную величину объема также округляем до тысяч. Получаем: $$ V=(1025000pm 22000) (мм^3) $$
Относительные погрешности (округляем до двух значащих цифр с избытком): begin{gather*} delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}=frac{800}{87500}cdot 100text{%} approx 0,92text{%}\ delta_v=frac{triangle V}{V}cdot 100text{%}=frac{22000}{1025000}cdot 100text{%}approx 2,2text{%} end{gather*} Измеряем толщину книги между обложками: (h=23 мм)
Количество страниц в книге (N=688)
Количество листов в 2 раза меньше. Получаем толщину одного листа: $$ t=frac{h}{N/2}=frac{2h}{N}=frac{2cdot 23}{688}approx 0,0669 (мм)=66,9 (мк) $$ Количество листов – величина точная, без погрешностей.
Абсолютная погрешность для толщины листа зависит только от (triangle h): $$ triangle t=frac 2Ntriangle h=frac 2N d=frac{2}{688}cdot 0,5approx 0,0015 (мм)=1,5 (мк) $$ Толщина листа: $$ t=(66,9pm 1,5) мк $$ Относительная погрешность: $$ delta_t=frac{triangle t}{t}cdot 100text{%}=frac{1,5}{66,9}cdot 100text{%}approx 2,3text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью линейки с инструментальной погрешностью (d=0,5 мм).
Получена площадь поверхности книги $$ S_{пов}=(87500pm 800) мм^2, delta_{S_{пов}}approx 0,92text{%} $$ Объем книги: $$ V=(1025000pm 22000) мм^3, delta_Vapprox 2,2text{%} $$ Определяя толщину листа, мы использовали способ рядов и увеличили абсолютную точность измерений от 0,5 мм до 1,5 мк. Толщина листа: $$ t=(66,9pm 1,5) мк, delta_tapprox 2,3text{%} $$ С наибольшей точностью определена площадь поверхности, т.к. для нее относительная погрешность меньше всех.
С наименьшей относительной точностью определена толщина листа, зато абсолютная точность для этой величины очень высока – 1,5 микрона.
п.2. Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
Цель работы
Научиться измерять время с помощью секундомера, определять абсолютную и относительную погрешность величины, полученной в серии прямых измерений.
Теоретические сведения
Математическим маятником называют груз небольших размеров, подвешенный на тонкой невесомой нерастяжимой нити.
Периодом колебаний математического маятника называют время, за которое он возвращается в исходную точку.
При отклонении математического маятника на малые углы (до 20°) период его колебаний (T) остается постоянной величиной. В действительности колебания постепенно затухают, но при достаточно длинной нити и тяжелом грузике, затухания происходят медленно.
Приборы и материалы
Секундомер, штатив, грузик на длинной нитке (не менее 50 см).
Ход работы
1. Закрепите нитку с грузиком в лапке штатива, как показано на рисунке.
2. Определите цену деления секундомера.
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний.
4. Повторите опыт 5 раз.
5. С помощью алгоритма определения истинного значения и абсолютной погрешности в серии измерений (см. §3 данного справочника) найдите точное значение и абсолютную погрешность времени 10 колебаний.
6. Найдите точное значение и абсолютную погрешность периода колебаний (T), рассчитайте относительную погрешность результата измерений.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Определение цены деления секундомера
 |
Два ближайших пронумерованных деления на основной шкале: begin{gather*} a=5 с\ b=10 с end{gather*} Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.
Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
Инструментальная погрешность секундомера равна половине цены деления: (d=frac{triangle}{2}=0,1 c)
Измерения времени 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 15,3 | 14,9 | 15,2 | 15,5 | 15,1 | 76,0 |
| (triangle c) | 0,1 | 0,3 | 0 | 0,3 | 0,1 | 0,8 |
Найдем среднее время для 10 колебаний: begin{gather*} t_0=frac{15,3+14,9+15,2+15,5+15,1}{5}=frac{76,0}{5}=15,2 (c) end{gather*} Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_0): $$ triangle_1=|15,3-15,2|=0,1; triangle_2=|14,9-15,2|=0,3 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,1+0,3+0+0,3+0,1}{5}=frac{0,8}{5}=0,16 (c) $$ Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,16right}=0,16 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(15,20pm 0,16) c end{gather*} Период колебаний в 10 раз меньше: $$ T=frac{1}{10}(t_0pmtriangle t), T=(1,520pm 0,016) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_0}cdot 100text{%}=frac{0,016}{1,520}cdot 100text{%}approx 1,1text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью секундомера, для которого была определена цена деления (triangle=0,2 с) и соответствующая инструментальная погрешность (d=frac{triangle}{2}=0,1 с).
В данном случае абсолютная погрешность может быть заметно больше инструментальной, и поэтому для ее определения потребовалась серия экспериментов.
Полученный в серии из 5 экспериментов результат измерения времени 10 колебаний: $$ t=(15,20pm 0,16) c $$ Искомый период колебаний маятника: $$ T=(1,520pm 0,016) c, delta_T=1,1text{%} $$
