Определение погрешности измерения на электроизмерительных приборах. Класс точности прибора
Следует помнить,
что никакое измерение, т.е. сравнение с
эталонной величиной, не может быть
выполнено абсолютно точно. Результат
измерения всегда содержит некоторую
ошибку. Кроме того, надо учесть, что
измерение проводится не путем сравнения
с самим эталоном, а с помощью измерительного
прибора (который при поверке был сравнен
с эталоном). Очевидно, что, измеряя с
помощью этого измерительного прибора,
мы не можем сделать ошибки меньшей, чем
та, которая определяется погрешностью
измерительного устройства.
Разность между
показаниями прибора и действительным
значением измеряемой величины называется
абсолютной погрешностью А.
|
А |
(1) |
Отношение
абсолютной погрешности к действительному
значению измеряемой величины, выраженное
в процентах, называется относительной
погрешностью:
|
|
(2) |
Приведенные
определения относительной и абсолютной
погрешности не дают возможности узнать
их величину, так как действительное
значение измеряемой величины нам
неизвестно. Определить величины
погрешностей при электрических измерениях
становится возможным, если известен
класс
точности
прибора (КЛ
Т).
Он дает предельную абсолютную погрешность,
выраженную в процентах от номинального
показания прибора (максимального при
данном пределе измерения) АНОМ:
|
КЛ |
(3) |
Класс
точности указан на шкале прибора (рис.
6).
Зная класс точности
прибора, можно легко определить абсолютную
погрешность измерения А:
|
А |
(4) |
Например,
для катушки сопротивления в 1000 Ом класса
точности 0,05 абсолютная погрешность:
|
А |
Относительную
погрешность также можно вычислить через
класс точности прибора. По определению
относительная
погрешность:
|
|
(5) |
Учитывая,
что действительное значение измеряемой
величины АДЕЙСТ
и показания прибора АИЗМ
примерно равны (АДЕЙСТ
АИЗМ),
и, используя формулу (4), получаем:
|
|
(6) |
Видно,
что относительная погрешность измерений
будет тем меньше, чем ближе снимаемые
показания к номинальному значению для
данного прибора, т.е. к концу
шкалы.
Следовательно, при работе с многопредельными
ЭИП нужно так выбирать предел измерения
прибора, чтобы показания считывались
со второй половины шкалы. Следует
помнить, что номинальное значение
многопредельного ЭИП определяется
положением, в котором стоит переключатель
пределов при данном измерении.
При работе с
многопредельными приборами нужно
внимательно рассчитывать цену одного
деления шкалы ЦД. Под делением
следует понимать не разность между
штрихами, а разность между ними в
соответствии с оцифровкой шкалы. Цена
деления равномерной шкалы равна
отношению номинального значения
показания прибора (предела измерения)
к общему числу делений N
на шкале прибора: ЦД =
![]() .
.
Численное значение измеряемой величины
АИЗМ равно цене деления ЦД,
умноженной на измеренное число делений
NИЗМ
по шкале:
|
АИЗМ |
(7) |
Рассмотрим
примеры определения погрешностей для
многопредельных ЭИП.
|
Пример 1. |
||||
|
Переключатель измерения |
→ |
|
← ← |
Шкала
Класс |
|
Рис. 6. |
На рис. 6 изображен
многопредельный вольтметр. Вычислить
абсолютную и относительную погрешности
определения напряжения. Класс точности
вольтметра 0,5.
Номинальное
значение напряжения 300 В (определяется
положением переключателя пределов
напряжения).
Цена деления
данного предела измерения ЦД =![]() =
=
2 В/дел.
Измеренное значение
напряжения UИЗМ = 2 В/дел.·75
дел. = 150 В.
Абсолютная
погрешность измерения U
=
![]()
= 1,5 (В).
Относительная
погрешность измерения 0
=
![]()
= 1,0%.
Пример 2

Рис. 7.
На рис. 7 изображен
тот же многопредельный вольтметр при
другом положении переключателя пределов
измерений. Вычислить абсолютную и
относительную погрешности определения
напряжения.
Номинальное
значение напряжения 150 В.
Цена деления
данного предела измерения ЦД =
150 В / 150 дел. =
1 В/дел.
Измеренное значение
напряжения UИЗМ = 1 В/дел.×150
дел. =
150 В.
Абсолютная
погрешность измерения U
=
![]()
= 0,75 (В).
Относительная
погрешность измерения 0
=
![]()
= 0,5%.
Таким образом,
выбор наиболее подходящего предела
измерения приводит к уменьшению как
абсолютной, так и относительной
погрешности.
Масштабные
измерительные преобразователи (МИП)
При необходимости
измерения токов и напряжений, превышающих
верхний предел измерения используемого
прибора, используются МИПы.
Для приборов
постоянного тока в качестве МИП
используются шунты и добавочные
сопротивления. Для приборов переменного
тока – добавочные резисторы (для
напряжений до 30 кВ и частот от 10 Гц до
20 кГц) и измерительные трансформаторы
тока и напряжения.
Расчет шунта к
амперметру
При измерении тока
амперметр включается последовательно
с нагрузкой. Если амперметром требуется
измерить ток, превышающий верхний предел
измерения, то параллельно амперметру
включается шунт с сопротивлением RШ
(рис. 8). Шунт представляет собой
толстую константановую или манганиновую
пластину. Применение этих сплавов для
изготовления шунтов связано с тем, что
их сопротивление слабо зависит от
температуры.

Рис. 8.
На рис. 8 показана
схема подключения шунта RШ к
амперметру. RА – внутреннее
сопротивление амперметра, которое мало
по сравнению с сопротивлением нагрузки
RН для того, чтобы включение
амперметра последовательно с нагрузкой
не приводило к существенным изменениям
тока в цепи нагрузки. I – ток через
сопротивление нагрузки RН; IШ
– ток через шунт с сопротивлением RШ;
IА – ток через амперметр с
сопротивлением RА.
По первому правилу
Кирхгофа алгебраическая сумма токов
в узле равна нулю:
I =
IА
+ IШ
и, следовательно,
IШ = I
– IА.
Падение напряжения
между точками а и b:
Uаb
= IА·RА
= IШ·RШ.
Таким образом, для
того, чтобы с помощью данного амперметра
измерить ток I, сопротивление шунта
должно быть
|
RШ |
(8) |
где
I/IA
= n
– коэффициент
шунтирования,
показывающий, во сколько раз расширяется
предел измерения амперметра при
подключении шунта.
Фактический ток
в цепи определяется произведением
показаний прибора и множителя n.

Рис. 9.
Реальный шунт
(рис. 9) должен иметь четыре контакта: к
двум из них подключается прибор, а к
двум другим – соединительные провода
электрической цепи.
Пример 3.
Рассчитать шунт
к миллиамперметру на 10 mА с внутренним
сопротивлением 500 Ом, если надо измерить
ток 10 А.
Воспользуемся
формулой (8):
![]()
Соседние файлы в папке Переменный ток
- #
- #
- #
- #
- #
- #
Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность.
Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок.
Все остальные погрешности являются случайными.
Промахи – грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.
Приборные погрешности определяются двумя факторами:
1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия.
Абсолютная погрешность через класс точности оценивается следующим образом:
(Dx) к.т.= (g/100)A,
где g – класс точности в %, указанный на панели прибора,
А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;
2. ценой делений шкалы прибора:
(Dx) ц.д.= ![]() h,
h,
где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения.
Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда, который предписывает следующий образ действий, если физическая величина х измерена n раз:
1) имея х1 , …,хn – значений измеряемой величины х, выбираем из ![]() хmax и хmin и находим среднее значение х:
хmax и хmin и находим среднее значение х:
![]() ;
;
2) находим абсолютную погрешность Dxр =![]()
3) Записываем результат в виде: ![]() с
с ![]() , где a – доверительная вероятность того, что истинное значение измеренной величины находится на отрезке
, где a – доверительная вероятность того, что истинное значение измеренной величины находится на отрезке ![]() .
.
Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.)
Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:
1) Вы измерили и получили несколько i = 1,…,m значений случайной
величины ![]() i. Сначала исключаем промахи, то есть заведомо неверные
i. Сначала исключаем промахи, то есть заведомо неверные
результаты.
2) По оставшимся n значениям определяем среднее значение величины ![]() :
:
.gif) i
i
3) Определяем среднеквадратичную погрешность среднего значения ![]() :
:

i
4) Задаемся доверительной вероятностью a. По таблице коэффициентов
Стьюдента (Приложение 1) определяем по известному значению
числа измерений n и доверительной вероятности a коэффициент
Стьюдента tan.
5) Определяем погрешность среднего значения величины ![]() (доверительный интервал)
(доверительный интервал) ![]()
D![]() = tan s<X>
= tan s<X>
6) Записываем результат
![]() = (
= (![]() ± D
± D![]() ) с указанием доверительной вероятности a.
) с указанием доверительной вероятности a.
В научных статьях обычно приводят доверительный интервал
D![]() = s<X>,
= s<X>,
соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора.
Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым.
В теории ошибок показывается, что результирующая погрешность ![]() , если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее – погрешность) эксперимента (подробнее см. в работе [1]).
, если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее – погрешность) эксперимента (подробнее см. в работе [1]).
Содержание материала
- Класс точности
- Класс точности
- Что такое класс точности прибора?
- Виды маркирования
- Пределы
- Вопрос выбора
- ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- Как определить класс точности электроизмерительного прибора, формулы расчета
- Нормирование
- Для чего используются
- Измерение
- Защита
- Разновидности амперметров
- Как определить класс точности манометра
- Какие классы точности бывают, как обозначаются
- Определение погрешности
Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.

Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.

Что такое класс точности прибора?
Класс точности – это характеристика прибора, которая определяется границами допускаемых основной и дополнительной погрешностей, а также другими свойствами, предусмотренными стандартами на данный вид изделия, которые оказывают влияние на точность. Этот параметр присутствует в технических характеристиках многих приборов, которые имеют эталонные выходные параметры, будь то электронные или механические измерительные устройства. Класс точности является основной характеристикой измерительной техники: весов, мультиметров, осциллографов, КИПовского оборудования и прочего. Чем выше это значение у прибора, тем больше стоит такое устройство, это связано со сложностью производства таких изделий.

Нормированная погрешность
Класс точности приборов измерений характеризует свойства таких изделий по отношению к точности, но при этом не является показателем точности этих измерений, выполненных при помощи данного устройства. С целью преждевременного выявления погрешности прибора, которую данное средство внесет в измеряемый результат, используют нормированные значения погрешностей. Значение этого параметра у каждого технического приспособления одной группы является индивидуальным, оно имеет отличные друг от друга случайные и систематические составляющие, но такая погрешность любого измерительного прибора одного класса не должна превышать установленное нормированное значение. Границы главной погрешности и коэффициента влияния заносятся в паспорт любого измерительного прибора. Все основные методы нормирования допустимых погрешностей и обозначения класса измеряющих устройств установлены ГОСТом, например, класс точности весов предусмотрен ГОСТом 24104-2001, который вступил в силу 01.07.2002.

Виды маркирования
Класс точности любого измерительного прибора маркируется на шкале устройства в виде числа. Это значение указывает нормированную величину погрешности, выраженную в процентном отношении. Если класс точности на шкале прибора обведен кружком, например 2,5, то это значит, что величина погрешности чувствительности устройства составляет 2,5 процента. По такому принципу нормируют погрешность масштабных преобразователей (измерительных шунтов, делителей напряжения, измерителей трансформаторов напряжения и тока и т. п.). Если значение класса точности на шкале прибора не подчеркнуто, например 0,7, это значит, что устройство нормируется погрешностью нуля равным 0,7. Эти приборы при любых з начениях Х имеют абсолютную погрешность нуля, равную константе. В случае степенной или равномерной отметки класса точности на шкале устройства принимается верхний предел измерения. В том случае, когда нулевая отметка расположена по центру шкалы, то это значение принимается равным протяженности измеряемого диапазона. При этом будет неправильным считать, что амперметр с классом точности 0,7 обеспечит во всем измеряемом диапазоне погрешность результата 0,7%. В таком случае относительная погрешность будет равна классу точности только на последнем значении шкалы. На приборах с неравномерной шкалой (омметры) класс точности маркируют в долях от длины шкалы, его обозначают ниже значения знака «угол». В случае если класс точности указан в дробном виде (например, 0,03/0,02), это значит, что погрешность в конце измеряемого диапазона составит 0,03, а в начале 0,01. Такими приборами являются постоянные потенциометры, цифровые вольтметры и другие высокоточные измерительные приборы.
Виды маркирования
Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.
Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.
Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.
Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.
Пределы
Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.
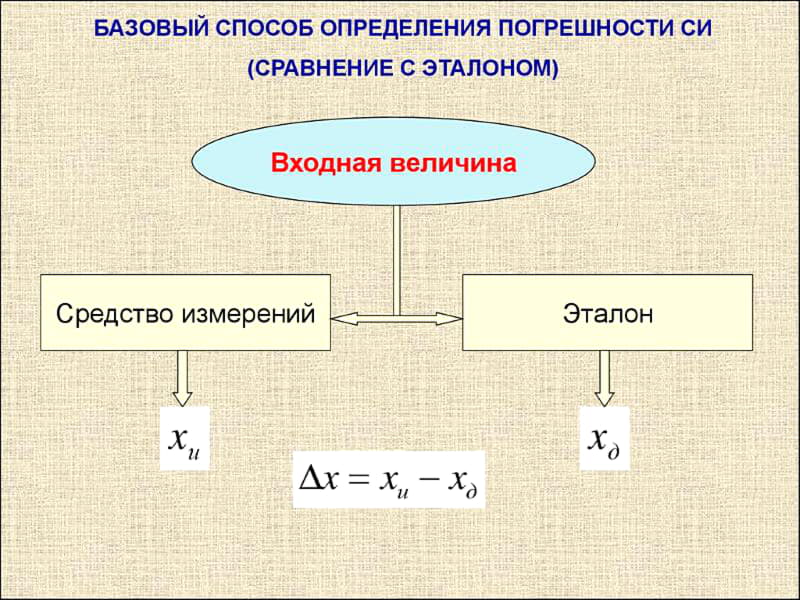
Базовый способ определения погрешности
При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.
Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.
Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5
Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.
Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.
Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.
Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.
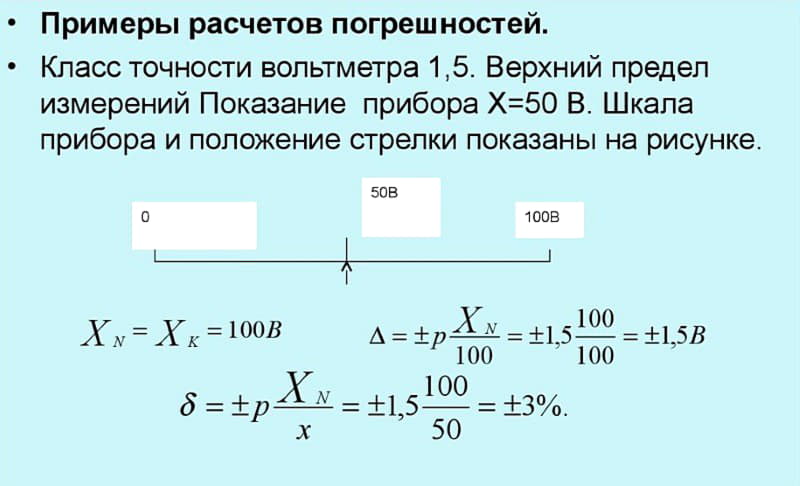
Пример расчета погрешности
Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.
Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.
Вопрос выбора
Для установки электросчётчика в частном доме или квартире подойдут модели, которые имеют класс не менее 2.
Кроме этого, отправляясь за электрическим счётчиком в магазин, следует точно знать следующие характеристики:
- Фазность электрической сети. Если электрическая сеть, которая подведена к счётчику, является однофазной, то устройство должно быть также для однофазной сети. Трёхфазный электросчётчик также можно установить для подсчёта использования электроэнергии, но такие устройства, как правило, имеют более высокую стоимость. Когда счётчик устанавливается для измерения трёхфазного тока, то на нём обязательно указывается соответствующая надпись. Для подсчёта трёхфазного тока однофазные приборы не используются.
- Нагрузка, при которой будет эксплуатироваться данное устройство. В зависимости от максимальной нагрузки, которая будет подключена к устройству подсчёта электроэнергии, выбирается модель, на корпусе которой обозначается такой показатель. Для стандартной нагрузки, которая используется в частном доме, применяются модели электросчётчиков рассчитанных на максимальный ток – 60 А. Если планируется подключать мощные отопительные электрические котлы, то электросчётчик выбирается с показателем не менее – 100 А.
- Если поставщик электроэнергии может продавать электроэнергию по 2 тарифам, то тарифность счётчика также учитывается при покупке. Значительно экономить на оплате электричества позволяет двухтарифные устройства. При использовании электроэнергии в ночное время такой счётчик будет регистрировать расход отдельно. Если поставщик электроэнергии позволяет производить такую оплату, то установка многотарифного счётчика позволит использовать электричество более рационально.
- Способ крепления. Позволяет установить прибор в уже имеющийся короб, или на место прибора который был установлен ранее.
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ Измеренная прибором величина всегда отличается от истинного значения на некоторое число, называемое погрешностью прибора. Погрешности измерительных приборов определяют поверкой, т. е. сравнением показаний поверяемого прибора с показаниями более точного, образцового прибора при измерении ими одной и той же величины. Значение измеряемой величины, определенное по образцовому прибору, принято считать действительным. Однако действительное значение отличается от истинного на погрешность, присущую данному образцовому прибору. Различают абсолютную, относительную и приведенную погрешности измерения.
Как определить класс точности электроизмерительного прибора, формулы расчета
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.

Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12
Находим относительную погрешность:
Y= 100×0,025/12=0,208 или 2,08%
(вывод: класс точности – 2,5).
Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:
Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12
Предел абсолютной допустимой погрешности:
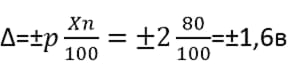
Относительная погрешность одного деления:
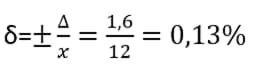 Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.
Нормирование
Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й
Нормирование осуществляется по:
- абсолютной;
- относительной;
- приведенной.

Формулы расчета абсолютной погрешности по ГОСТ 8.401
Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.
Скачать ГОСТ 8.401-80
Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.
Для чего используются
Разнообразные виды измерительных трансформаторов встречаются как в небольших приборах размером со спичечный коробок, так и в крупных энергетических установках. Их основное назначение – понижать первичные токи и напряжения до значений, необходимых для измерительных устройств, защитных реле и автоматики. Применение понижающих катушек обеспечивает защиту цепи низшего и высшего ранга, поскольку они разделены между собой.
Понижающие средства разделяют по признакам эксплуатации и предназначены для:
- измерений. Они передают вторичный ток на приборы;
- защиты токовых цепей;
- применения в лабораториях. Такие понижающие средства имеют высокую классность точности;
- повторного конвертирования, они относятся к промежуточным инструментам.

Измерение
Измерительный трансформатор необходим для понижения высокого тока основного напряжения и передачу его на измерительные устройства. Для подключения стандартных приборов к высоковольтной сети потребовались бы громоздкие установки. Реализовывать инструменты таких размеров экономически не выгодно и не целесообразно.
Использование понижающих трансформаторов позволяет применять обычные устройства измерения в обычном режиме, что расширяет спектр их применения. Благодаря снижению напряжения, они не требуют дополнительных модификаций. Трансформатор отделяет высоковольтное напряжение сети от питающего напряжения приборов, обеспечивая безопасность из использования. От их классности зависит точность учета электрической энергии.
Защита
Кроме питания измерительных приборов понижающие трансформаторы подают напряжение на системы защиты и автоматической блокировки. Поскольку в сетевой электросети происходят перепады и скачки напряжения, которое губительно для высокоточного оборудования цепи.

В энергетических установках оборудование делится на силовое и вторичное, которое контролирует процессы первичной схемы подключения устройств. Высоковольтная аппаратура располагается на открытых площадках или устройствах. Вторичное оборудование находится на релейных планках внутри распределительных шкафов.
Промежуточным элементом передачи информации между силовыми агрегатами и средствами измерения, управления, контроля и защиты являются понижающие или измерительные трансформаторы. Они разделяют первичную и вторичную цепь от пагубного воздействия силовых агрегатов на чувствительные измерительные приборы, а также защищают обслуживающий персонал от повреждений.
Разновидности амперметров
Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.

Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.
Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.
Как определить класс точности манометра
Манометр — измерительный прибор, который позволяет установить значение избыточного давления, действующего в трубопроводе или в рабочих частях различных видов оборудования. Такие приборы широко применяются в системах отопления, водоснабжения, газоснабжения, других инженерных сетях коммунального и промышленного назначения. В зависимости от условий эксплуатации измерителя существуют определенные ограничения по допустимому пределу его погрешности. Поэтому важно знать, как определить класс точности манометра.
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже

Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Приборы, способные выполнять множество различных замеров, могут быть одновременно более двух классов.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.

- 0,1, 0,2 – считается самым высоким классом
- 0,5, 1 – чаще применяется для устройств средней ценовой категории, например, бытовых
- 1,5, 2,5 – используется для приборов измерения с низкой точностью или индикаторов, аналоговых датчиков
Примечание. На корпусе высокоточных измерителей, класс может не наносится. Обозначение таких устройств как правило выполняется особыми знаками.
Определение погрешности
Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления. Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа. 
Необходимо отметить, что таким способом можно посчитать только основную погрешность. Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.
Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений. Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.
Источник:
Теги
Измерительные приборы: вольтметры, амперметры, токовые клещи, осциллографы и другие — это устройства, предназначенные для определения искомых величин в заданном диапазоне, каждый из них имеет свою точность, причем устройства, измеряющие одну и ту же величину, в зависимости от модели, могут отличаться по точности и классу.
В каких-то ситуациях достаточно просто определить значение, например, вольтаж батарейки, а в других необходимо выполнить многократное повторение измерений высокоточными приборами для получения максимально достоверного результата, так в чем отличие таких измерительных устройств, что означает класс точности, сколько их бывает, как его определить и многое другое читайте далее в нашей статье.

Содержание:
- 1 Что такое класс точности
- 2 Какие классы точности бывают, как обозначаются
- 3 Каким ГОСТом регламентируется точность приборов?
- 4 Как определить класс точности электроизмерительного прибора, формулы расчета
- 5 Поверка приборов, для чего она нужна
- 6 Видео на тему относительная погрешность прибора
- 7 Заключение
Что такое класс точности
Определение: «Класс точности измерения — это общая характеристика точности средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими факторами, влияющими на нее».
Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.
Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.
Устаревание, несовершенство изготовления измерителей, внешние воздействия — это основной показатель отклонения погрешностей.
Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.
Абсолютная погрешность рассчитывается следующим образом:
∆=±a или ∆=(a+bx)
x — число делений, нормирующее значение величины
a, b – положительные числа, не зависящие от х
Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже

Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Приборы, способные выполнять множество различных замеров, могут быть одновременно более двух классов.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.

- 0,1, 0,2 – считается самым высоким классом
- 0,5, 1 – чаще применяется для устройств средней ценовой категории, например, бытовых
- 1,5, 2,5 – используется для приборов измерения с низкой точностью или индикаторов, аналоговых датчиков
Примечание. На корпусе высокоточных измерителей, класс может не наносится. Обозначение таких устройств как правило выполняется особыми знаками.
Каким ГОСТом регламентируется точность приборов?
ГОСТ 8.401-80 «Классы точности средств измерений» общие требования. Нормативным документом устанавливаются общие положения классификации точностей измерительных приборов.
Как определить класс точности электроизмерительного прибора, формулы расчета
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.

Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12
Находим относительную погрешность:
Y= 100×0,025/12=0,208 или 2,08%
(вывод: класс точности — 2,5).
Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:
Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12
Предел абсолютной допустимой погрешности:
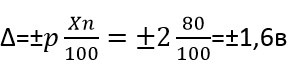
Относительная погрешность одного деления:
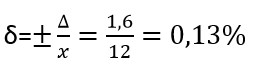
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.
Поверка приборов, для чего она нужна
Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.
Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.

Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.
Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.
Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.
Видео на тему относительная погрешность прибора
Заключение
Класс точности является важным показателем для каждого прибора, при выборе всегда обращайте внимание на него. Если вам нужен, например, электрический счетчик, важно чтобы он измерял потребление энергии с максимальной точностью, благодаря этому за весь период эксплуатации, вы сможете сэкономить приличную сумму средств.
Но, а если вам необходимо просто периодически проверять напряжение в розетке, для этого не стоит переплачивать за дорогостоящую покупку.
Для любого прибора характерно отклонение показаний от фактического значения измеряемой величины. Данное диапазон характеризуется приборной погрешностью.
Не известно точно, чему равна приборная погрешность, и как именно она искажает конкретное измерение. Тем самым по своей сути она близка к случайной погрешности, не смотря на то, что является систематической.
Для оценки систематической приборной погрешности также применяют методы математической статистики:
Здесь дельта − приборная погрешность, соответствующая выбранной доверительной вероятности “а”; t – коэффициент Стьюдента при выбранной доверительной вероятности “a” и числе измерений n, стремящемся к бесконечности; б – максимальная приборная погрешность.
Величина максимальной приборной погрешности зависит от прибора.
1. Для стрелочных электроизмерительные приборов, у которых указан класс точности:
где A наибольшее значение, которое может быть измерено по шкале прибора; K – класс точности прибора.
2. Для цифровых приборов максимальная приборная погрешность обычно указывается в паспорте прибора.
3. Если при измерениях используется прибор, у которого класс точности неизвестен или прибор не имеет класса точности (например, измерительная линейка или секундомер), максимальную приборную погрешность принимают равной цене наименьшего деления его шкалы.
В существенном числе лабораторных задач, при величине доверительной вероятности 95%, погрешность измерительного прибора можно принять равной половине цены деления.

