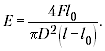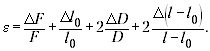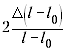В чем смысл оценки погрешности измерения? В том, что мы задаем границы истинного значения величины, которого мы не знаем, и никогда не сможем узнать, т.к. все измерения всегда делаются с
погрешностью. Если, например, значение силы задано вот таким образом:

это означает, что истинное значение лежит между значениями 2,3 Н и 2,5 Н. Эти значения можно назвать “границами” значения этой величины.
При проведении прямых измерений абсолютная погрешность измерения определяется прибором и методом измерения (погрешность отсчета).
Возникает вопрос: как найти погрешность результата косвенных измерений? Ответ вполне логичен: надо найти верхнюю и нижнюю границу результата, используя верхние и нижние границы значений
величин, входящих в формулу для нахождения искомой величины. Т.е., смотря на формулу, вы должны понять, как максимально увеличить результат, подставляя верхние или нижние границы измеренных
значений. Знания арифметики должны нам подсказать, что, чтобы получить больше, в числитель дроби надо поставить верхнюю границу, а в знаменатель – нижнюю, это приведет к увеличению дроби; чтобы
получить больше, надо уменьшаемое сделать больше, а вычитаемое – меньше. Рассмотрим пример.
Допустим, при смешивании горячей и холодной воды мы имеем следующие результаты измерений:
·
температура холодной воды t1 = (16,0 ± 1,5) °С,
·
температура горячей воды t1 = (66,0 ± 1,5) °С
·
температура смеси t = (43,0 ± 1,5) °С,
·
масса холодной воды mх = (80 ± 2) г = (80 ± 2) ∙
10–3 кг,
·
масса горячей воды mг = (100 ± 5) г = (100 ± 5) ∙ 10–3 кг.
Надо рассчитать количества теплоты, полученное холодной водой и отданное горячей при смешивании и сравнить полученные значения в пределах погрешности.
При расчёте количества теплоты, полученного холодной водой, получаем значение:

А для количества теплоты, отданного горячей:

Вычислим верхнюю границу количества теплоты, полученного холодной водой.
Так как количество теплоты определяется умножением, то максимальное количество теплоты получится, если взять для каждого из множителей максимальное значение, то есть верхние границы
интервалов значений с погрешностью. А максимальное значение разности получится, если для уменьшаемого взять верхнюю границу значения, а для вычитаемого – нижнюю. Полученное значение будет верхней
границей значения количества теплоты:

Аналогично вычисляем нижнюю границу значения количества теплоты:

Округлять раньше времени результаты не надо, ведь мы еще не знаем, с какой точностью (погрешностью) мы определили значение количества теплоты. Но и переписывать все цифры с калькулятора, если
ответ получается в виде бесконечной дроби, тоже не надо. Поскольку в эксперименте мы редко измеряем значения с точностью меньше 1 процента, но и держать цифры, которые «поправляют» значение
меньше, чем на процент, наверно, не стоит. Если первая значащая цифра дает 100% результата, то третья – как раз 1%. Так что достаточно оставлять в промежуточных вычислениях 3 значащие цифры. У
нас получены целые числа, но мы могли бы округлить и их:

В полученных границах для Qпол и лежит искомое значение. Чтобы сравнивать это значение с количеством теплоты, отданным горячей водой методом
интервалов, оценим

абсолютную погрешность найденного значения количества теплоты. Из рисунка видно, что

Найденное нами прежде значение для Qпол близко к значению, найденному как среднее значение границ:

Кроме того, нам все равно придется округлить эти значения в соответствии с вычисленной погрешностью. Поэтому вычислять среднее в дальнейшем не обязательно.
А вот для погрешности найдём следующее значение:

Кстати, если бы мы предварительно округлили бы значения границ, как описывалось, значение погрешности не изменилось бы (проверьте!).
Произведем необходимые округления (до разряда сотен) и запишем значение количества теплоты, полученного холодной водой:
Qпол = 9100 Дж ± 1200 Дж.
Значит, полученное значение лежит округлённо между 7900 Дж и 10 300 Дж.
Попробуйте рассчитать таким же образом границы значения количества теплоты, отданного горячей водой. Если не получится сделать это самим, посмотрите еще раз,
как это делается.
Вычисляем верхнюю границу:

Вычисляем нижнюю границу значения количества теплоты:


Итак, мы выяснили, что количество теплоты, полученное холодной водой, лежит между 7900 Дж и 10300 Дж, а количество
отданного горячей водой – между 8000 и

11400 Дж. Как сделать вывод о том, равны ли эти значения? Очень просто: надо нанести интервалы значений на числовую
ось и посмотреть, перекрываются ли эти интервалы. Из рисунка можно видеть, что эти количества теплоты совпадают в пределах погрешности эксперимента.
Следует пояснить правила округления при записи результатов с погрешностью. Обычно во всех пособиях предлагается в
значении абсолютной погрешности оставлять одну значащую цифру. Так, число 0,63 следует округлить до 0,6. Однако надо быть осторожным в случае, если в процессе округления полученная одна значащая
цифра является единицей. В этом случае при округлении числа 1,49 до 1 погрешность округления может составить (1,49 – 1)/1 0,49 = 49% от неокруглённого значения, поскольку интервал округления по
величине близок к самому значению погрешности. Даже когда единственная значащая цифра после округления 2, погрешность может составить до 25% от самого значения. Поэтому в вузе обычно объясняют
студентам, что значение погрешности окончательного результата округляется до одной значащей цифры, но если эта значащая цифра 1 или 2, то до двух. В школьном эксперименте абсолютная погрешность
результата около 30% вполне обычное дело, поэтому в значении погрешности рекомендуется оставлять две значащие цифры только в том случае, если первая из них – единица. В значении результата следует
оставлять столько десятичных знаков (или разрядов), сколько их в значении погрешности, так как погрешность «поправляет» «неверные» цифры результата.
Общий подход к
вычислению границ
Если известны
границы числовой величины, то можно по
формуле (1.2.5) наилучшим образом вычислить
ее приближенное значение и по формуле
(1.2.6) получить его предельную абсолютную
погрешность.
Пусть дана функция
.
Точные значения аргументови функции
неизвестны, но известны границы ее
аргументов,
.
Найдем точные границы величиныu.
По формуле (1.2.2) можно получить множества
принадлежности точных значений аргументов
,
.
(1.7.1)
Точные значения
аргументов
должны этим отрезкам принадлежать.
Составим из них прямое декартово
произведение.
Очевидно,и
.
Отсюда следует, что
в качестве
можно выбрать
–
множество значений функции
,
когда ее аргумент (точка
)
принимает всевозможные значения из
множества
.
Тогда, согласно
определению, (см. формулу (1.2.1)), можно
получить точные границывеличиныu:
;
(1.7.2)
;
(1.7.3)
После вычисления
границ величины u
можно наилучшим образом вычислить
по формуле
(1.7.4)
и
найти его предельную абсолютную
погрешность
.
(1.7.5)
Наиболее сложным
моментом в применении описанного подхода
к вычислению приближенного значения
функции и оценки его погрешности является
вычисление точных границ по формулам
(1.7.2), (1.7.3). Для преодоления этих трудностей
можно использовать пооперационное
вычисление границ величины u
и обобщенный метод границ.
Пооперационное
вычисление границ
Основные формулы
метода границ.
Процесс вычислений по заданной формуле
представляется в виде цепочки отдельных
элементарных операций: суммы, разности,
произведения, частного и функции одного
переменного. Зная границы результатов
этих элементарных операций, можно
получить искомые границы окончательного
результата.
Получим границы
результатов пяти описанных элементарных
операций. Пусть имеются величины x,
y
и известны их
границы
,
,
,
.
Введем величины,
,
,
,
.
Здесь
– заданная функция одной переменной.
Тогда будут
справедливы формулы
для определения границ результатов
элементарных операций (суммы, разности,
произведения, частного и функции одной
переменной)
,
;(1.7.6)
,
; (1.7.7)
,
;
(1.7.8)
,
;(1.7.9)
;
.(1.7.10)
Если на отрезке
функция
является непрерывной или монотонной,
то будут существовать,
и ими можно заменить точные грани:
,
.
(1.7.11)
Если на отрезке
функция
является монотонной, то минимум и
максимум функции будут достигаться на
концах отрезка. Поэтому вместо формул
(1.7.11) можно использовать либо формулы
,
,
(1.7.12)
если функция
неубывающая, либо формулы
,
,
(1.7.13)
если
функция
невозрастающая.
Формулы (1.7.8)
справедливы только при
и
,
а формулы (1.7.9)–
при
и
.
Докажем формулы
(1.7.6) – (1.7.10) . Согласно формуле (1.2.3),
,
.
(1.7.14)
Сложим почленно
эти неравенства:
.
Отсюда следуют
формулы (1.7.6).
Умножим на (-1) все
части второго неравенства (1.7.14) и сложим
его почленно с первым неравенством
(1.7.14):
.
Отсюда следуют
формулы (1.7.7).
Рассмотрим частный
случай, когда
и
.
Тогда в неравенствах (1.7.14) все члены
неотрицательные и эти неравенства можно
перемножить:
.
Отсюда следуют
формулы (1.7.8).
Рассмотрим частный
случай, когда
и
.
Тогда в первом неравенстве (1.7.14) все
члены будут неотрицательные, а во втором
– положительные. Применим ко всем частям
второго неравенства (1.7.14) функцию:
,
а
теперь перемножим это неравенство с
первым неравенством (1.7.14):
.
Отсюда следуют
формулы (1.7.9).
Формулы (1.7.10)
следуют из формул (1.7.2) и (1.7.3) при
.
Пример 1
Пусть
,
,
,
,
,
,
.
Применяя формулы (1.7.6) – (1.7.13), (1.7.4),
(1.7.5), требуется найти,
,
,
.
Для определения
границ числителя и функции
воспользуемся формулами (1.7.12) – (1.7.13).
Так как функциявозрастает на отрезке
,
ее наименьшее значение достигается на
левом конце этого отрезка, а наибольшее
– на правом:,
.
Функциятакже является возрастающей, поэтому
,
.
Далее находим границы знаменателя по
формулам (1.7.6):,
.
Применяя формулы (1.7.9), получим,
.
И наконец, применяя
формулы (1.7.4), (1.7.5), окончательно получим
,
.
Запишем результат в соответствии с
первым правилом верных знаков:.
Сравним полученные
результаты с результатами примеров 1
из параграфов 1.5 и 1.6. Они существенно
отличаются (прежние результаты:
).
Исходя из вычисленных точных граници
найдем предельную абсолютную погрешность
приближенного значения:
.
Каким же результатам верить? Прежние
результаты, полученные с помощью линейных
оценок являются приближенными, а
результаты, полученные методом границ
– точные, если не учитывать погрешности
округлений при вычислениях. Поэтому
верить необходимо именно им. Сравнение
показывает, что для рассмотренного
примера линейные оценки занижают оценку
погрешности в 2 раза. Это связано с тем,
что погрешности аргументов оказались
слишком велики и условия применимости
линейных оценок не выполняются.
Особые случаи
вычисления границ
Замена
переменных.
Если в формулу
входят операции умножения или деления
и выполняются условия применимости
формул (1.7.8), (1.7.9), то можно вычислять
границы результатаu
с помощью формул (1.7.6) – (1.7.13). В тех же
случаях, когда эти условия не выполняются,
для вычисления границ произведения и
частного можно использовать либо замены
переменных, либо вычислять эти границы,
пользуясь определением, по формулам
(1.7.2) и (1.7.3). Рассмотрим применение замен
переменных на конкретном примере.
П

ример 2
Пусть
,
,
,
,
.
Требуется найти,
.
Переменные x
и u
принимают отрицательные значения.
Введем новые переменные
,
,
которые будут принимать положительные
значения. Очевидно,
причем все условия применимости формулы
(1.7.8) для этого случая выполнены.
,
(рис. 1.3). По формуле (1.7.8) находим:
,
.
Далее аналогично вычисляем границы
результата:,
.
Вычисление
границ произведения и частного.
Способ замены переменных не годится,
если нижняя и верхняя границы хотя бы
одного из аргументов оказываются разных
знаков. В этом случае можно вычислять
границы произведения и частного
непосредственно по формулам (1.7.2),
(1.7.3).
Пример 3
Пусть
,
,
,
,
.
Требуется найти,
.
По формулам (1.7.2),
(1.7.3)
,
,
где
,
,
(рис. 1.4).
В
Рис. 1.4
еличинаy
не обращается в 0, если
точка
.
Поэтому функциянепрерывна на множествеЕ
и достигает своих точных граней.
Следовательно, существуют максимум и
минимум функции
на множествеЕ
и ими можно заменить точные грани:
,
.
Координатная ось
разбивает множество Е
на два прямоугольника
и
(рис. 1.7.2). Найдем минимум и максимум
функциив каждом из них в отдельности. В
прямоугольникевеличиныx
и u
неотрицательны, а величина y
положительна. Поэтому дробь
принимает наибольшее значение в точке
,
когда величинаx
принимает наибольшее, а величина y
– наименьшее возможное значение.
Соответственно, наименьшее значение
эта дробь принимает в точке
.
Таким образом,
,
.
В прямоугольнике
величиныx
и u
отрицательны,
а величина y
положительна. Поэтому положительная
дробь
будет принимать наибольшее значение в
точке,когда величина
принимает наибольшее, а величинаy
– наименьшее возможное значение.
Соответственно, наименьшее значение
этадробь будет
принимать в точке
.
Тогда отрицательная дробьпринимает наименьшее и наибольшее
значения, соответственно, в точкахи
.
Таким образом,
,
.
Объединяя оба
рассмотренные случая, окончательно
получим
,
.
Обобщенный метод
границ
Вычисление границ
по формулам (1.7.2), (1.7.3) в общем случае
представляет собой сложную задачу, но
при оценке погрешностей длины отрезков
(1.7.1) часто бывают малы. Учет этого
обстоятельства во многих случаях
позволяет значительно упростить
вычисление границ.
Множество
представляет
собой n-мерный
прямоугольник. Функцию
назовеммонотонной
по каждому из своих аргументов на
множестве Е,
если для любого аргумента
и для любой точки
функция одной переменной
либо не убывает, либо не возрастает на
отрезке.
Будем считать, что
условия монотонности функции
по каждому аргументу на множествеЕ
выполняются. Тогда функция
будет иметь наименьшее и наибольшее
значение на множествеЕ
и они будут достигаться в вершинах
множества Е.
Координаты точки минимума
,
точки максимумафункции и границыu
определяются по формулам


,
.
(1.7.17)
Замечание. Условия
монотонности функции
по каждому из аргументов на множествеЕ
выполняются во многих случаях, поскольку
размеры прямоугольника Е,
как правило, малы. Если же эти условия
не выполняются на всем прямоугольнике
Е,
то часто его можно разбить на более
мелкие прямоугольники, на которых
условия монотонности будут выполняться.
Пример 4
Пусть
,
,
,
,
,
,
.
Требуется найти,
.
Множество
представляет
собой трехмерный прямоугольник. Зададим
произвольную точку
.
Функция одной
переменной
,
где
.
Эта функция, очевидно, возрастает на
отрезке.
Функция одной
переменной
,
где
,
.
Эта функция, очевидно, убывает на отрезке.
Функция одной
переменной
,
где
,
.
Эта функция, очевидно, убывает на отрезке.
Таким образом,
наша функция является монотонной по
каждой из своих переменных и ее минимум
и максимум достигаются в точках
и
, соответственно. Отсюда
,
.
Сравните полученные
результаты с результатами примера 1,
этого параграфа.
Соседние файлы в папке ВМ_УЧЕБНИК
- #
- #
- #
- #
- #
- #
- #
- #
- #
И снова о погрешностях
Окончание. См. № 15/07
Д.А.ИВАШКИНА,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
И снова о погрешностях
4. Учёт случайных погрешностей при
прямых измерениях
Если, проведя одно и то же измерение
несколько раз, вы видите, что результат остаётся
одним и тем же, то случайные погрешности
эксперимента малы, их не следует учитывать. Но
если при повторении измерения получаются разные
значения, то следует взять среднее значение из
серии измерений:
где n – число измерений. Как
узнать, какова погрешность результата? Логично, и
ученики сами обычно предлагают это, определить
среднее отклонение результата от среднего
значения. Полученная величина носит название средней
арифметической ошибки: Она показывает, на сколько в
среднем каждое измеренное значение отклоняется
от среднего значения. Но эта величина слабо
зависит от количества проведённых измерений. В
чём же тогда смысл многократных измерений?
Для среднеквадратичной погрешности,
которая определяется немного сложнее:
есть простое правило: средняя
квадратичная погрешность среднего
арифметического равна средней квадратичной
погрешности отдельного результата, делённой на
корень квадратный из числа измерений: Из формулы ясно,
что с увеличением числа измерений случайная
погрешность среднего значения уменьшается.
Поэтому необходимо проводить столько измерений,
чтобы случайная погрешность стала меньше
значения систематической погрешности данного
измерения.
К сожалению, в лабораторных работах и
при любых других экспериментах в школе провести
достаточное количество измерений невозможно в
силу нехватки времени. Как поступать, может
решить сам учитель. На мой взгляд, для нахождения
средней арифметической погрешности среднего
значения можно использовать формулу,
аналогичную формуле для средней квадратичной
ошибки:
Хотя эта формула и неверна, она
помогает понять смысл проведения большого числа
измерений. Использоваться же она будет всего в
нескольких работах, и, следовательно, нет нужды
специально обучать нахождению погрешности
среднего значения. Зато, получив в этих работах
случайную погрешность меньше погрешности
систематической, ученик запомнит, что каждое
измерение следует производить несколько раз при
малейшем подозрении, что в данном эксперименте
имеется случайная погрешность. Как правило, уже
при пяти измерениях достигается необходимая
малость случайной погрешности по сравнению с
систематической.
5. Определение погрешности
результата косвенных измерений
К определению погрешности результата
косвенных измерений учащиеся готовы, на мой
взгляд, уже к 8-му классу. В зависимости от уровня
класса впервые метод границ [1, 12] можно
применить или в работе по сравнению количеств
теплоты при смешивании воды, или при нахождении
сопротивления проводника. Поясню на примерах.
-
Допустим, при нагревании холодной
воды в процессе смешивания мы имеем следующие
результаты измерений:
– температура холодной воды t1
= (16,0 ± 1,5) °С;
– температура смеси t = (43,0 ± 1,5) °С;
– объём холодной воды V1 = (80
± 2) мл = (80 ± 2) • 10–6 м3.
Получаем количество теплоты,
полученное холодной водой:
Q = 4190 Дж/(кг • °С) • 1000 кг/м3
• 80 • 10–6 м3 (43 – 16) °С = 9050,4 Дж.
(1)
Возникает вопрос: а какова погрешность
полученного значения? Другими словами, на
сколько мы можем ошибиться, если точные значения
не равны измеренным, а лежат где-то в интервале,
даваемом погрешностью? Например, начальная
температура воды может быть равна 16,5 °С, 17,0 °С и
т.д. Тогда вычисленное количество теплоты будет
меньше. Логично посмотреть, на сколько мы можем
ошибиться по максимуму. Максимальное количество
теплоты получится, если взять для всех
сомножителей максимальные значения, т.е. верхние
границы интервалов значений с погрешностью, для
уменьшаемого взять верхнюю границу значения, а
для вычитаемого – нижнюю:
Qв = 4190 Дж/(кг • °С) • 1000
кг/м3 • 82 • 10–6 м3 (44,5 – 14,5)°С = 10 307,4 Дж.
Аналогично вычисляем нижнюю границу
значения количества теплоты:
Qн = 4190 Дж/(кг • °С) • 1000
кг/м3 • 78 • 10–6 м3 (41,5 – 17,5) °С = 7843,68
Дж.
В данных пределах и лежит искомое
значение. Чтобы сравнивать методом интервалов
это значение с количеством теплоты, отданным
горячей водой, надо округлить значения верхней и
нижней границ. Лучше это сделать, оценив
абсолютную погрешность найденного значения
количества теплоты.
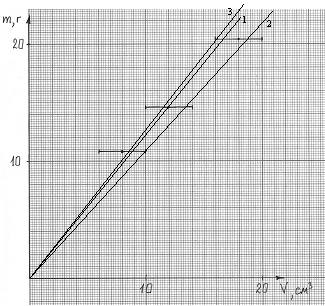
Рис. 2
Из рис. 2 видно, что
Найденное выше значение (1) близко к (3),
поэтому его не стоит находить ещё раз. А вот для
погрешности найдём с помощью (2):
(две
значащие цифры, т.к. первая «1»). Поэтому
количество теплоты, полученное холодной водой,
можно округлить: Qполуч = 9000 Дж ±
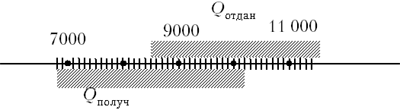
1200 Дж (т.е. между 7800 Дж и 10 200 Дж). Если количество
теплоты, отданное горячей водой, лежит между 8500
Дж и 11 500 Дж (Qотдан = 10 000 Дж ± 1500 Дж), то
можно видеть, что эти количества теплоты
совпадают в пределах погрешности эксперимента
(рис. 3).
Рис.3
-
Определение сопротивления резистора.
Пусть измеренные значения напряжения и силы тока
следующие:
– U = 2,60 В ± 0,15 В (инструментальная
погрешность 0,15 В; погрешность отсчёта может быть
взята равной 0,05 В, т.е. в 3 раза меньше
инструментальной, поэтому ею можно пренебречь);
– I = 1,2 А ± 0,1 А (инструментальная
погрешность 0,05 А, погрешность отсчёта 0,05 А).
Тогда для сопротивления получаем:
Но на самом резисторе написано: «2 ± 0,1 ». Получается, что
мы неверно определили сопротивление? Рассчитаем
погрешность нашего определения значения
сопротивления:
Uв = 2,75 В; Uн = 2,45 В; Iв
= 1,3 А, Iн = 1,1 А;
Полученное экспериментально значение
сопротивления R = (2,2 ± 0,3) Ом совпадает в
пределах погрешности со значением R = (2,0 ± 0,1)
Ом, указанным на резисторе.
С помощью метода границ можно вывести
и формулы для погрешности при обобщении темы
«Определение погрешности косвенных измерений»,
но уже в 9-м классе.
Определение погрешности разности. Пусть
А = В – С. Рассчитаем погрешность А в
общем виде:
Ав = Вв – Сн
= (В + В)
– (С – С)
= (В – С) + (В
+ С);
Ан = Вн – Св
= (В – В)
– (С + С)
= (В – С) – (В
+ С);
Полученное очень важно: в некоторых
работах в формулах для вычисления результата
встречается разность двух близких по значению
величин, что приводит к большой относительной
погрешности результата.
-
В cтарой работе «Определение модуля
Юнга резины» [11] удлинение резинового жгута
находилось как разность его результирующей и
начальной длин. Если условия опыта таковы, что
эта разность мала, например, составляет 1,5 см, то
относительная погрешность определения разности(погрешность
отсчёта взята гораздо меньше инструментальной
погрешности). Ясно, что такое измерение
использовать для определения модуля Юнга
нежелательно, – может получиться погрешность
больше 100%. Лучше увеличить нагрузку на жгут.
Аналогичная проблема возникает в работе
«Измерение ЭДС и внутреннего сопротивления
источника» [2] (одно сопротивление должно быть в
несколько раз больше другого) и др.
Определение погрешности частного
двух величин. Пусть Рассчитаем погрешность в общем виде:
Такую формулу трудно запоминать.
Поэтому найдём относительную погрешность
величины А:
Итак, относительная погрешность
частного равна сумме относительных погрешностей
величин, входящих в него. Такая же формула
получается и для относительной погрешности
произведения.
Важным я считаю не сам процесс расчёта
погрешности. Эти формулы дают мощный инструмент
для оценки обоснованности проведения
эксперимента. При их использовании легко
объяснить, при измерении какой из величин
следует увеличить точность, чтобы получить
лучший результат.
Рассмотрим формулу для нахождения
модуля Юнга:
Если воспользоваться для расчёта погрешности
результата методом границ, то неясным останется,
какая из величин в формуле вносит наибольшую
погрешность.
Для нахождения относительной
погрешности результата лучше воспользоваться
формулой:
При подстановке значений оказывается,
что слагаемое
даёт максимальный вклад в сумму, а остальные
слагаемые в несколько раз меньше, так что ими
можно пренебречь. Если l – l0 будет
невелико, то значение относительной погрешности
окажется очень большим, порой выше 100%. Какой
вывод сделают в таком случае ученики?
Такая ситуация – пример того, как
применение упрощённого способа вычисления
погрешностей может привести к большим ошибкам.
Конечно же, этот эксперимент совершенно
обоснован, с помощью него можно найти модуль
Юнга. Только следует выбрать те измерения, где l
– l0 достаточно велико, и не забыть
пренебречь малыми слагаемыми при расчёте
погрешности.
6. Определение коэффициента
прямой пропорциональности
В лабораторных работах нередко
встречается ситуация, когда необходимо по
графику определить коэффициент
пропорциональности в зависимости одной величины
от другой. И здесь в учебниках встречаются две
ситуации.
В работе «Определение модуля Юнга» [13]
после нахождения модуля Юнга для измерений с
тремя различными нагрузками учащимся
предлагается найти среднее арифметическое трёх
полученных значений. Такой подход ошибочен, т.к.
каждое значение получено с различными
систематическими погрешностями, т.е. с разной
степенью точности. Нельзя суммировать эти
значения «с одинаковым весом». При подобных
вычислениях в теории ошибок находится сумма этих
значений с разными коэффициентами.
Далее, в работе «Измерение жёсткости
пружины» [7] в аналогичной ситуации совершенно
справедливо отмечено, что, поскольку жёсткость
пружины в каждом из опытов получена при разных
условиях, среднее арифметическое этих значений
находить нельзя. И предлагается найти среднее
значение коэффициента жёсткости по графику как
коэффициент пропорциональности. Однако,
поскольку учащиеся не могут найти погрешность
найденного таким образом коэффициента
пропорциональности, предлагается взять в
качестве этой погрешности погрешность
наихудшего результата. Я считаю, что такой подход
не оправдан. Зачем брать погрешность самого
ненадёжного результата, если сам способ
нахождения коэффициента жёсткости из графика
применяется для того, чтобы определить этот
коэффициент наиболее точно? Думаю, авторы просто
не хотели заострять внимание на этом вопросе.
На мой взгляд, для определения
коэффициента пропорциональности по графику
можно предложить несколько вариантов.
Вариант 1. Самый простой, а потому
пригодный для младших классов. Отмечаем на
графике экспериментальные значения с указанием
погрешности. Обращаем внимание учащихся на то,
что если бы мы не нанесли погрешности на графики,
то провести прямую было бы затруднительно. В 7-м
классе достаточно просто отметить тот факт, что
зависимость между двумя величинами прямо
пропорциональна. Но если всё-таки необходимо
найти значение коэффициента пропорциональности,
можно обойтись без расчёта погрешности, отметив
только, что этот способ (многократные измерения
при различных условиях и построение графика)
используется именно для того, чтобы уменьшить
погрешность результата.
Вариант 2. Чертим прямую, находим
экспериментальную точку, которая лежит ближе
всего к прямой, и именно эту точку и считаем самой
точной. Остаётся вычислить результат для неё по
обычным формулам, рассчитав также и погрешность.
Вариант 3. Самый логичный. Пробуем
провести через точки вместе с их погрешностями
две прямые: с наибольшим и с наименьшим наклоном.
Значения коэффициентов для них и будут верхней и
нижней границами для результата. Зная границы,
рассчитываем среднее значение коэффициента и
погрешность. Данная погрешность неявно будет
содержать в себе как систематическую
погрешность экспериментально измеренных
величин, так и случайную погрешность определения
среднего, но уже с учётом точности каждого
результата. Этот вариант годится для
использования в экспериментах, когда
коэффициент должен быть оценён достаточно точно.
Но он достаточно сложен, поэтому не стоит его
использовать во всех случаях.
Вариант 4. Использование
встроенных программ в калькуляторах или готовых
компьютерных программ для вычисления
коэффициентов по методу наименьших квадратов.
Этот способ пригоден для практикума в старших
классах и/или в классах физматпрофиля. К
сожалению, в такие программы, как правило,
встроен метод наименьших квадратов, не
учитывающий погрешностей экспериментальных
точек. Применение имеет смысл в случаях, когда
погрешности всех точек практически одинаковы
или когда доминирующей является случайная
погрешность. Она и будет учтена.
Какой из этих вариантов выбрать, может
решать сам учитель. К счастью, таких работ
довольно мало. Продемонстрируем все эти варианты
на примере.
-
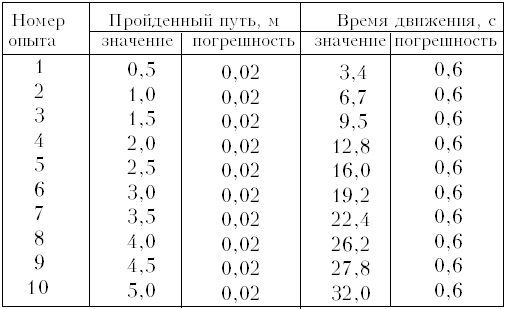
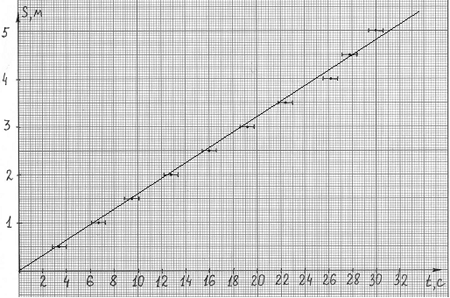
Возьмём данные эксперимента по
зависимости пути от времени равномерного
движения (машинка из конструктора с
электрическим приводом):
Действуя так, как описано в варианте 1,
строим график (рис. 4).
Рис. 4
Так как точек на графике много, можно с
уверенностью утверждать, что 8-я и 10-я точки
являются «выбросами», т.е. измерены небрежно.
Учитывая погрешность эксперимента, можно
провести прямую практически единственным
способом: соответствующая скорость 0,16 м/с. Если
воспользоваться методом наименьших квадратов
(например, встроенной функцией ЛИНЕЙН в
программе MicrosoftExcel), то для коэффициента мы
получим значение 0,158 ± 0,002 м/с (вариант 4).
Для варианта 2 подходит 3-я точка.
Скорость, вычисленная по данным для этой точки,
0,158 м/с. Рассчитаем погрешность: Так как относительная
погрешность пути мала по сравнению с
относительной погрешностью времени,
пренебрегаем ею. Абсолютная погрешность
результата: 0,063
• 0,158 = 0,010 м/с. То есть скорость, вычисленная в
варианте 2: (0,158 ± 0,010) м/с.
Из приведённого примера видно, что
значения коэффициента пропорциональности
получаются очень близкими. В этом примере
погрешности отдельных измерений были достаточно
малы, а точек, наоборот, было много. Рассмотрим
пример, когда погрешности, напротив, велики, а
количество опытов в силу объективных причин
мало.
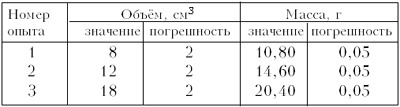
-
Найдём плотности пластмассы путём
измерения массы и объёмов тел.
В случае варианта 1 прямую проводим
так, чтобы количество точек над и под прямой было
одинаково (рис. 5), т.е. в данном случае – одна
сверху, одна снизу (прямая 1). Плотность в
этом случае равна 1,23 г/см3.
Рис. 5
В случае варианта 2 пригодна 2-я точка.
Для неё значение плотности (1,2 ± 0,2) г/см3.
Вариант 3: проведём прямые 2 и 3.
Для прямой 2 коэффициент пропорциональности
1,09 г/см3 является нижней границей
искомого значения плотности, а для прямой 3
(1,27 г/см3) – верхней. Полусумма этих
значений есть значение плотности (1,18 г/см3),
а полуразность – значение погрешности (0,09 г/см3).
Вариант 4 в данном случае менее
пригоден, т.к. не учитывает больших значений
погрешностей при измерении объёма с помощью
мерного цилиндра, но и в этом варианте плотность
(1,18 ± 0,05) г/см3.
Следует заметить, что в двух последних
примерах на графиках были обозначены только
погрешности вдоль горизонтальной оси, т.к.
погрешности значений второй переменной были
очень малы.
Послесловие
Научиться обрабатывать результаты
экспериментов учащиеся могут, лишь обрабатывая
результаты экспериментов. Это означает, что
помимо стандартного набора лабораторных работ
необходимо проводить много фронтальных и
демонстрационных экспериментов с обработкой
результатов. Это большая работа, и я хочу
пожелать успехов всем учителям, кто вступит на
этот путь или уже стоит на нём.
Литература
1. Анофрикова С.В., Стефанова Г.П.
Практическая методика преподавания физики.
Часть первая. – Астрахань: Издательство
Астраханского ГПИ, 1995.
2. Физика: Под ред. А.А.Пинского: Учебник
для 10 кл. школ и классов с угл. изучением физики. –
М.: Просвещение, 2002.
3. Попова О.Н. Обучение учащихся
выявлению устойчивых связей и отношений между
физическими величинами: Методическое пособие
для учителей физики. – Элиста: Элистинский лицей,
1998.
4. Анофрикова С.В. Азбука
учительской деятельности, иллюстрированная
примерами деятельности учителя физики. Ч. 1.
Разработка уроков. – М.: МПГУ, 2001.
5. Пёрышкин А.В. Физика-8. – М.:
Дрофа, 2004.
6. Громов С.В., Родина Н.А. Физика-8.
– М.: Просвещение, 2000.
7. Кикоин И.К., Кикоин А.К. Физика-10.
Механика. – М.: Просвещение, 2001.
8. Фронтальные лабораторные занятия по
физике в 7–11 классах общеобразовательных
учреждений. Книга для учителя: Под ред. В.А.Бурова,
Г.Г.Никифорова. – М.: Просвещение, Учебная
литература, 1996.
9. Зайдель А.Н. Элементарные оценки
ошибок измерений. – Л.: Наука, 1967.
10. Хорозов С.А. Работа над
ошибками: В кн. «Энциклопедия для детей», т. 16
«Физика», ч. 1 «Биография физики. Путешествие в
глубь материи. Механистическая картина мира». –
М.: Аванта+, 2000.
11. Мякишев Г.Я., Буховцев Б.Б., Сотский
Н.Н. Физика-10. – М.: Просвещение, 2004.
12. Кирик Л.А. Физика-9: Методические
материалы. – М.: Илекса, 2003.
13. Шахмаев Н.М., Шахмаев С.Н., Шодиев
Д.Ш. Физика-10. – М.: Просвещение, 1994.

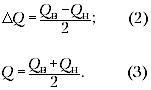
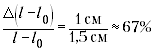 (погрешность
(погрешность