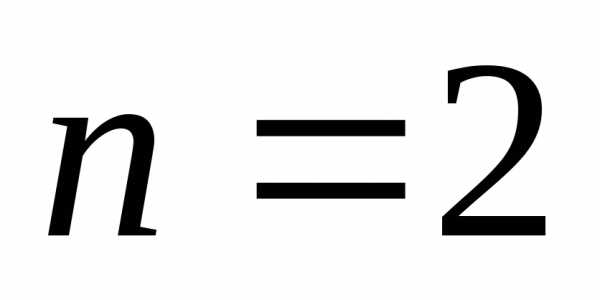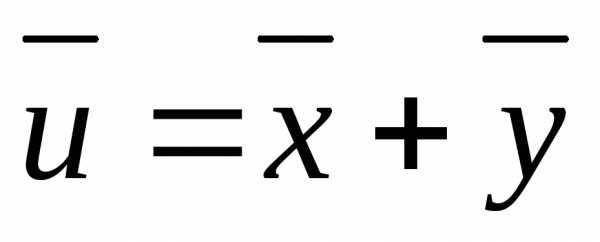Определение случайных погрешностей прямых измерений Метод Стьюдента
В
теории ошибок считается, что
случайные погрешности подчиняются
вероятностным закономерностям. При
постоянном числе измерений,
чем
больше ошибка по абсолютной величине,
тем меньше ее вероятность. Зависимость
плотности распределения вероятностей
измеряемой величиныот измеренного значения
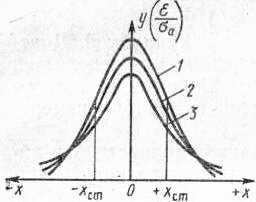
описывается кривой (рис. 2), называемой
кривой нормального распределения
Гаусса. Площадь, отвечающая какому-либо
интервалу оси абсцисс, изображает
вероятность попадания случайного
результата в данный интервал. По
распределению Гаусса наиболее вероятным
значением измеряемой величины является
ее среднее значение.
Вид
кривой распределения определяется
величиной
,
называемой среднеквадратической ошибкой
(стандартное отклонение):

С
увеличением
точность измерения уменьшается, и кривая
нормального закона распределения имеет
более пологий вид (см. рис. 2).
Величина
характеризует разброс отклонений от
среднего значения. На практике число
измерений ограничено (чаще всего не
более 5-7). В этом случае пользуются
распределением Стьюдента.
Английский
математик и химик В.С. Госсет (псевдоним
Стьюдент) в 1908 г. предложил методику
обработки результатов многократных
измерений одной и той же величины.
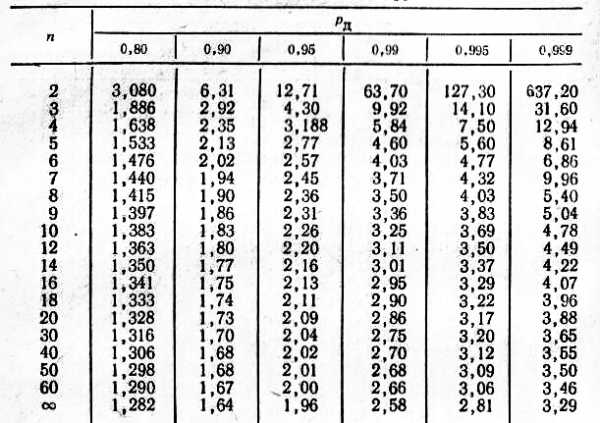
Существуют
специальные таблицы, в которых приведены
коэффициенты
Стьюдента
,
определяемые доверительной вероятностьюи числом измерений
.
Например, придля доверительной вероятности
получим
(см. таблицу в приложении 1).
Согласно
методике Стьюдента средняя квадратическая
погрешность результата измерений
среднего арифметического определяется
формулой:

где
– абсолютная погрешность каждого
измерения,
–
число
измерений.
Границы
средней квадратической погрешности:
.
Абсолютная
погрешность измерений:
,
где
– приборная погрешность.
Если
,
то;
если
,
то.
Окончательный
результат записывается в виде:
.
Определение
погрешностей косвенных измерений
-
Взять
натуральный логарифм от левой и правой
частей формулы, помня, что
,
,
.
-
Найти
полный дифференциал полученного
выражения, помня, что
.
-
Заменить
знаки дифференциала
на
знаки
.
-
Знаки
«–»,
стоящие перед дифференциалами, заменить
на знаки «+», так как суммарная погрешность
всегда больше погрешности отдельных
измерений. -
В
полученную формулу подставить средние
арифметические значения прямо измеренных
величин и их абсолютные погрешности. -
Вычислить
относительную и абсолютную погрешности
косвенно измеряемой величины. -
Записать
окончательный результат в виде
.
ПРИМЕР:
Найдём
относительную и абсолютную погрешности
для ускорения при поступательном
движении.
,
,
,
.
–
относительная погрешность величины
ускорения
.
Абсолютная
погрешность равна
.
Окончательный
результат:
.
Кинематические характеристики равнопеременного движения
Если
тело, поднятое на высоту
(рис.
3), движется поступательно вниз без
начальной скорости с ускорением,
то
.
Отсюда
(1)
Максимальная
скорость тела, движущегося без начальной
скорости, в нижней точке траектории
движения равна:
.
(2)
Максимальная
угловая скорость блока (шкива, оси)
радиуса
:
.
(3)
Т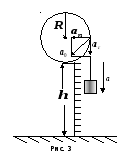
расположенные на ободе колеса, движутся
с полным ускорением(см. рис. 3), где
– тангенциальная составляющая ускорения,
направленная по касательной, равная по
модулю ускорению поступательного
движения тела, т.е.;
– нормальная составляющая ускорения,
направленная к центру окружности равная
по модулю
.
(4)
Модуль
полного ускорения
.
(5)
Угловое
ускорение маховика (блока, шкива) радиуса
:
.
(6)
Соседние файлы в папке UBA_11
- #
- #
- #
В статье представлен метод расчета случайной погрешности прямого измерения. К прямым измерениям относят нахождение величины из опытных данных с помощью прибора. К прямым измерениям можно отнести измерение длины линейкой, времени секундомером, объема цилиндром и так далее.
1. Измерим n раз некоторую величину X при одинаковых условиях. В результате получим набор значений X1, X2, X3,…,Xn.
2. Далее вычислим среднее арифметическое значение величины X по формуле:
Для увеличения точности измерений необходимо увеличить количество измерений. При многократном увеличении числа измерений среднее арифметическое значение измеряемой величины будет стремиться к её истинному значению. То есть следует учитывать, что при конечном числе они будут равны друг другу лишь приближенно. Поэтому необходимо определять степень этого приближения, чтобы данное количество было достаточным для оценки результата.
3. Найдем среднее квадратичное отклонение среднего арифметического:
При этом значение случайной погрешности в случае небольшого числа измерений можно представить в виде
где t – это коэффициент Стьюдента, зависящий от доверительной вероятности и числа измерений . Значения коэффициента Стьюдента для доверительной вероятности приведены в таблице.
Таблица 1
Значения коэффициента Стьюдента.
Надежность результата многократных измерений. Коэффициент Стьюдента.
Доверительной
вероятностью или надежностью
P
серии измерений называется вероятность
попадания истинного значения измеряемой
величины в данный интервал (выражается
в долях единицы или в процентах).
Интервал
(<x>±-
∆x)
в который попадает истинное значение
искомой величины с заданной доверительной
вероятностью P(∆x)
, называют доверительным
интервалом или интервалом надежности
и для краткости обозначают как ∆x.
Чем
больше доверительный интервал, тем
больше доверительная вероятность того,
что результат измерения попадет в него.
Величина доверительного интервала,
рассчитывается методами теории
вероятностей и математической статистики
и определяется выбором вида функции
распределения случайных величин f(∆x).
Для
всех функций распределения, базовым
является распределение
Гаусса,
справедливое для большого количества
равноточных
измерений

[1.5]
где
величина
называется среднеквадратичным
или стандартным отклонением
от среднего
значения <x>
а,
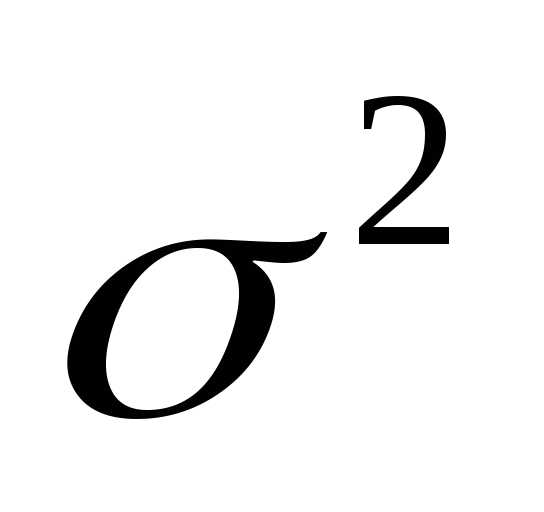
распределения.
Распределение
Гаусса показывает, что вероятность
появления малых случайных погрешностей
больше вероятности появления больших
погрешностей, при этом случайные
погрешности равные по абсолютной
величине, но противоположные по знаку
встречаются одинаково часто.
При
лабораторных измерениях (n
< 20) для расчета интервала надежности
используется распределение
Стьюдента (при
распределение Стьюдента переходит в
распределение Гаусса),
которое
позволяет по заданной величине надежности
P(∆x)
найти величину доверительного интервала
∆x,
с помощью поправочных коэффициентов
Стьюдента:
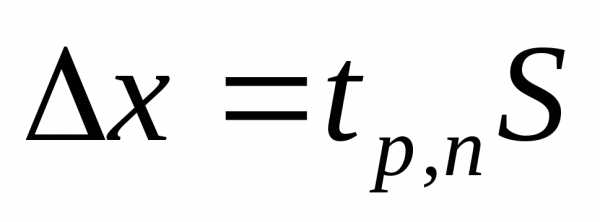
где
— коэффициент
Стьюдента, зависящий от выбора
доверительной вероятности p
и числа измерений n,
S
– среднеквадратичное отклонение –
(СКО), вычисляемое по формуле:
[1.7]
Величина
интервала ∆x,
рассчитанная при помощи формулы [1.6]
стремится к нулю при увеличении числа
опытов.
Коэффициенты Стьюдента
|
Число измерений n |
Доверительная |
|||
|
0,90 |
0,95 |
0,99 |
0,999 |
|
|
2 |
6,314 |
12,706 |
63,657 |
636,619 |
|
3 |
2,920 |
4,303 |
9,925 |
31,598 |
|
4 |
2,353 |
3,182 |
5,841 |
12,941 |
|
5 |
2,132 |
2,776 |
4,604 |
8,610 |
|
6 |
2,015 |
2,571 |
4,032 |
6,859 |
|
7 |
1,943 |
2,447 |
3,707 |
5,959 |
|
8 |
1,895 |
2,365 |
3,499 |
5,405 |
|
9 |
1,860 |
2,306 |
3,355 |
5,041 |
|
10 |
1,833 |
2,262 |
3,250 |
4,781 |
Очевидно, что число
опытов имеет смысл выбрать таким, чтобы
случайная погрешность среднего сравнялась
с погрешностью прибора либо стала меньше
ее. Дальнейшее увеличение числа измерений
теряет смысл, так как не увеличит точность
получаемого результата
Расчет погрешности прямых измерений
Прежде,
чем приступить к измерениям, необходимо
предварительно определить пределы
точности данных приборов (инструментальные
погрешности
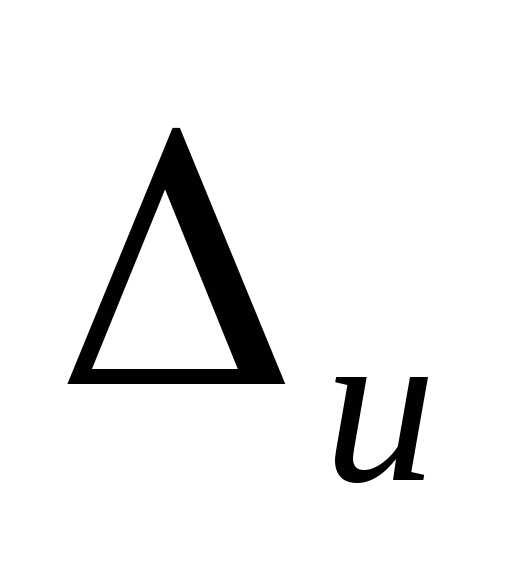
Равноточные
измерения любой физической величины
делаются не менее трех раз и заносятся
в таблицу, с учетом инструментальной
погрешности. В зависимости от поведения
значений результатов измерения, возникают
две различные схемы:
Случайная
погрешность много меньше инструментальной
Если
оказывается, что все время получается
один и тот же результат (нет разброса),
то в качестве интервала надежности
берется стандартная (инструментальная)
погрешность прибора ∆и,
рассчитанная по его классу точности
(или погрешность градуировки прибора)
и результат записывается в виде:
При
этом доверительная вероятность
(надежность) равна
и, как правило, не указывается.
Случайная
погрешность сравнима с инструментальной
Если
разброс значений физической величины
x
превышает погрешность градуировки, то
количество измерений n
увеличивают до тех пор, пока они не
окажутся величинами одного порядка.
Интервал надежности вычисляют в следующей
последовательности:
-
Находят
среднее значение: -
Оценивают
среднеквадратичное отклонение — СКО:
-
По
заданному значению надежности p
и числу измерений n,
находят
случайную составляющую погрешности:
-
Полную
погрешность вычисляют как корень
квадратный из суммы квадратов случайной
∆хсл
и инструментальной ∆xи
составляющих:
-
Находят
относительную погрешность: -
Результат
записывают в виде: ,
,
р
= …
studfiles.net
Коэффициент Стьюдента
Пример
Определить
достоверность
измерений для
установленного доверительного интервала.
По формуле (1.2)
имеем:
.
По табл.1.1для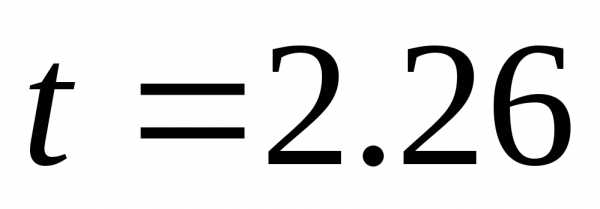
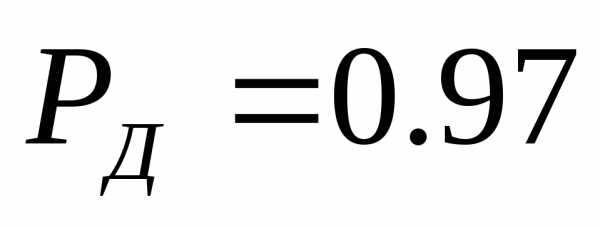
Это означает, что
в заданный доверительный интервал из
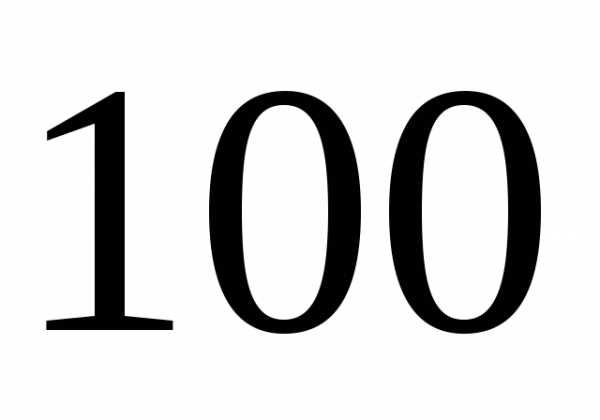

Значение
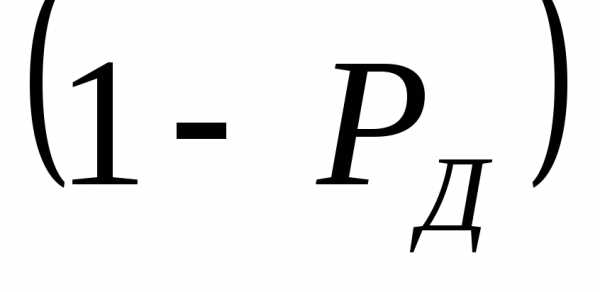
уровнем
значимости.
Из него следует,
что при нормальном законе распределения
погрешность, превышающая доверительный
интервал, будет встречаться один раз
из
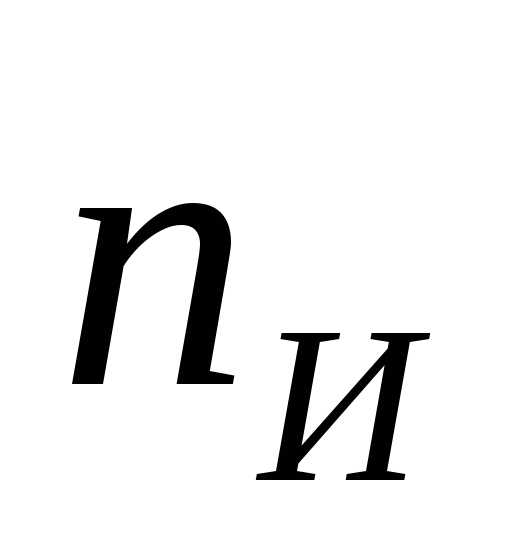
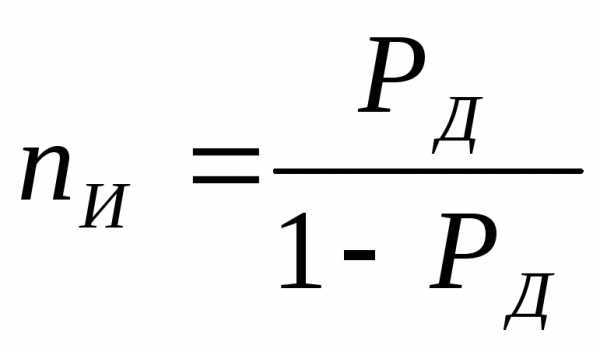
(1.4)
Это означает, что
приходится браковать одно из
измерений.
По данным приведенных
выше примеров можно вычислить количество
измерений, из которых одно измерение
превышает доверительный интервал.
Если
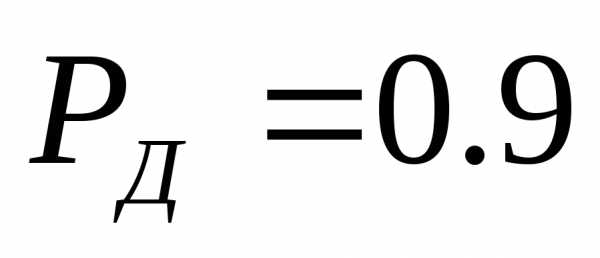
то по формуле (1.4) определяетсяизмерений.
Если
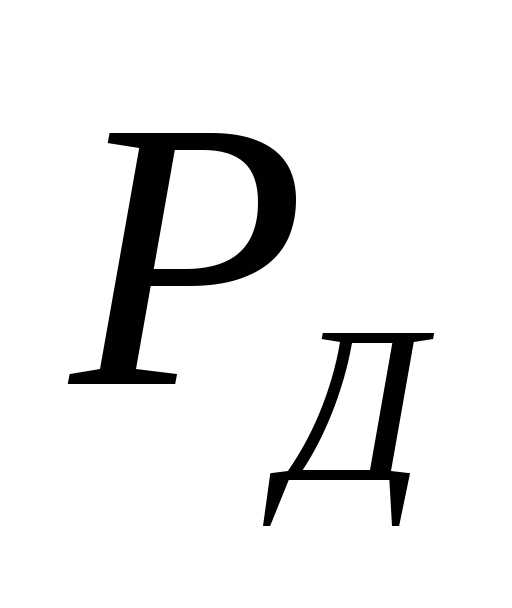
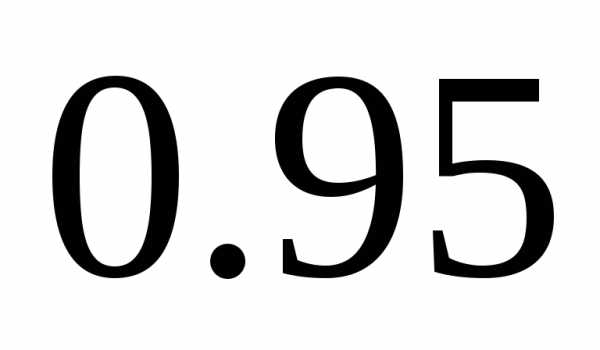
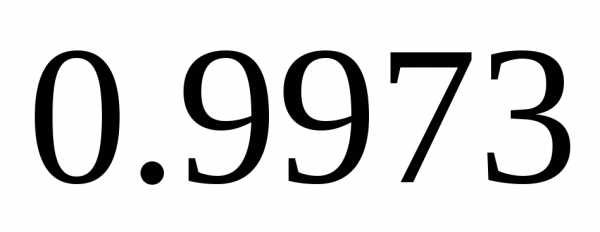
соответственно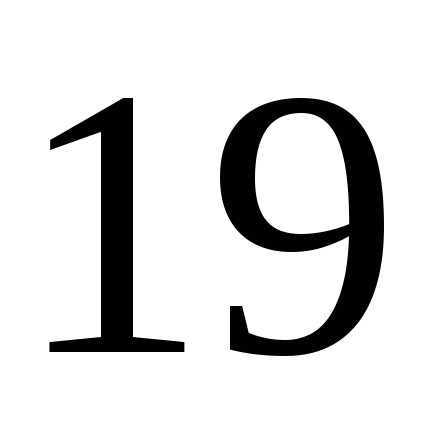

2. Определение минимального количества измерений
Для проведения
опытов с заданной точностью и достоверностью
необходимо знать то количество измерений,
при котором экспериментатор уверен в
положительном исходе.
В связи с этим
одной из первоочередных задач при
статистических методах оценки является
установление минимального, но достаточного
числа измерении для данных условий.
Задача сводится
к установлению минимального объема
выборки (числа измерении)
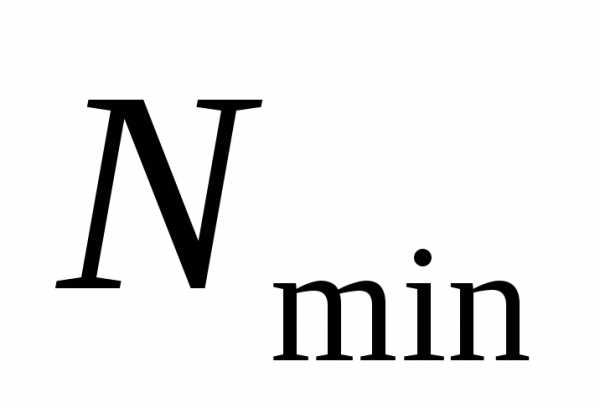
интервала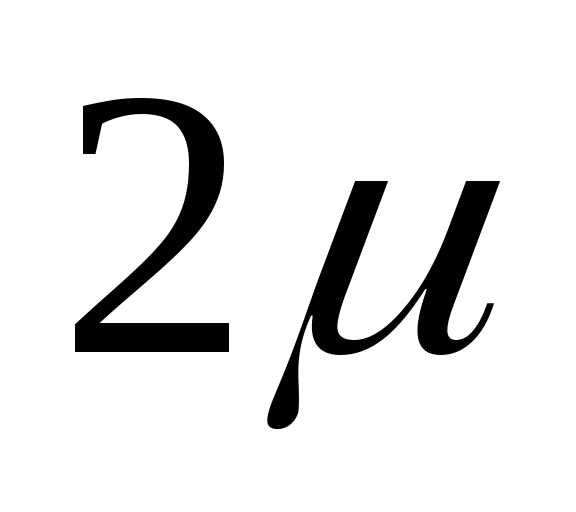
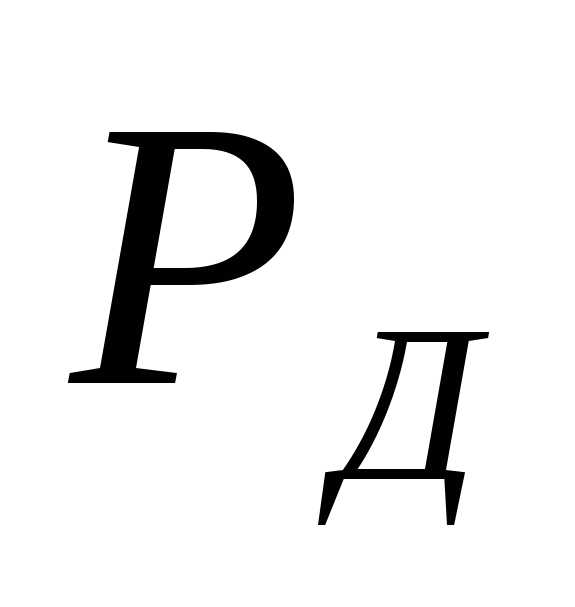
При выполнении
измерений необходимо знать их точность:
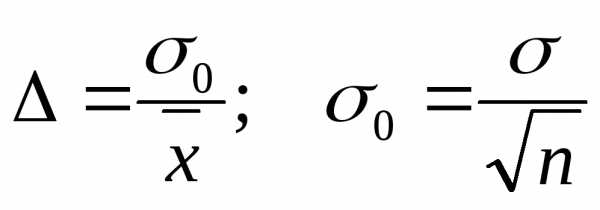
(2.1)
где
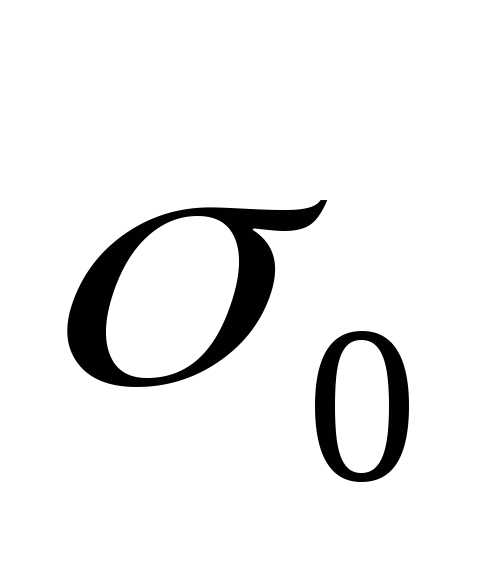
среднеквадратического отклонения
Значение
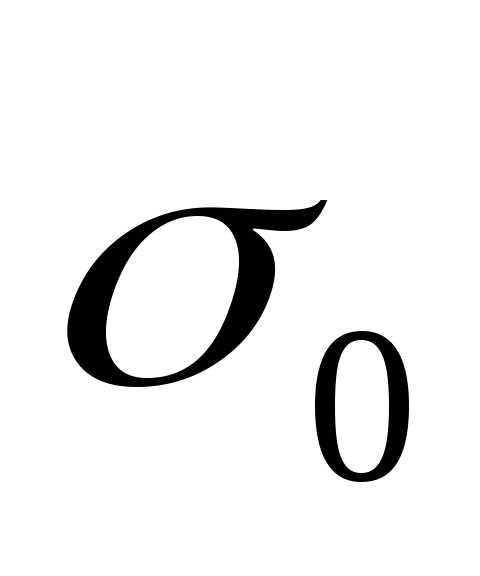
ошибкой.
Доверительный
интервал ошибки измерения

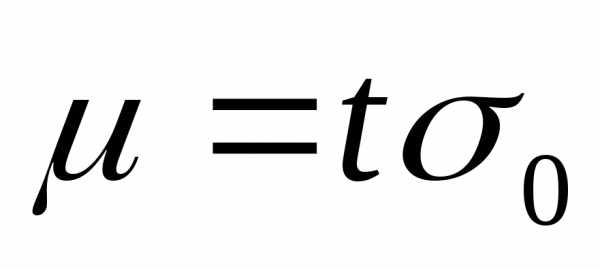
С помощью
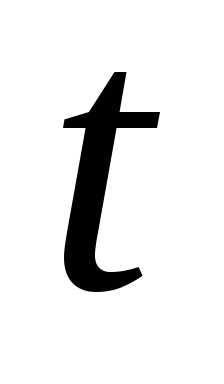
вероятность ошибки измерений потабл.1.1.
В исследованиях
часто по заданной точности

определяют минимальное количество
измерений, гарантирующих требуемые
значения
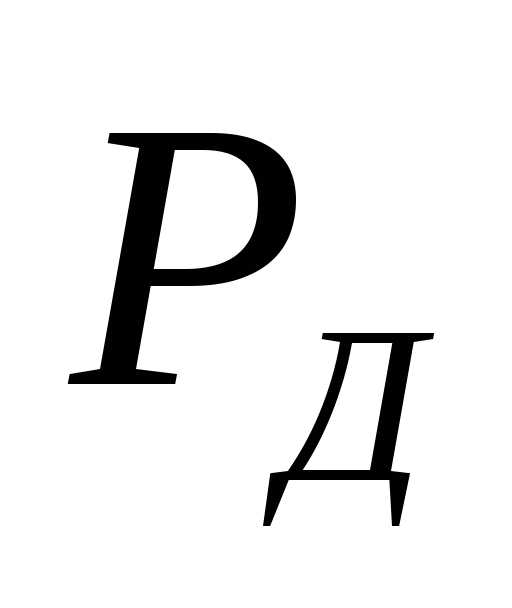
При получаем
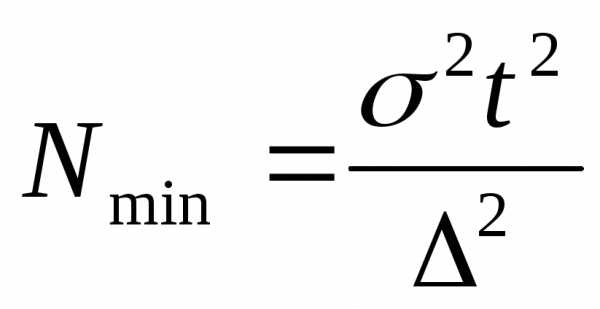
(2.2)
Для определения
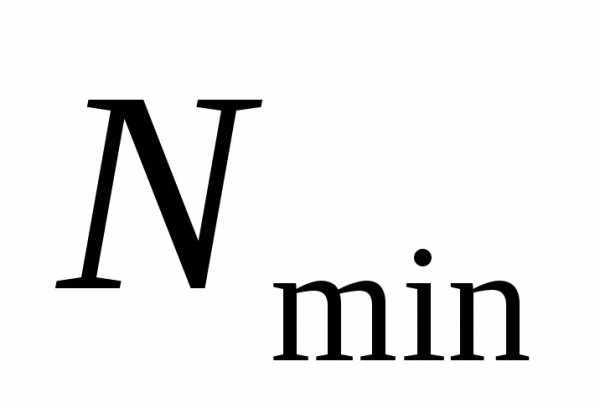
вычислений.
1.
Проводится предварительный эксперимент
с количеством измерений
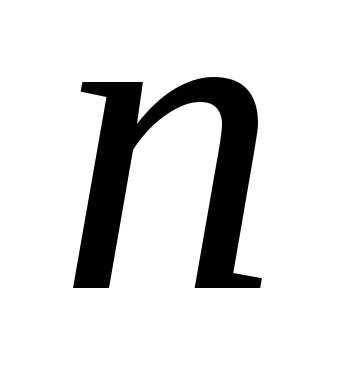
которое составляет в зависимости от
трудоемкости опыта от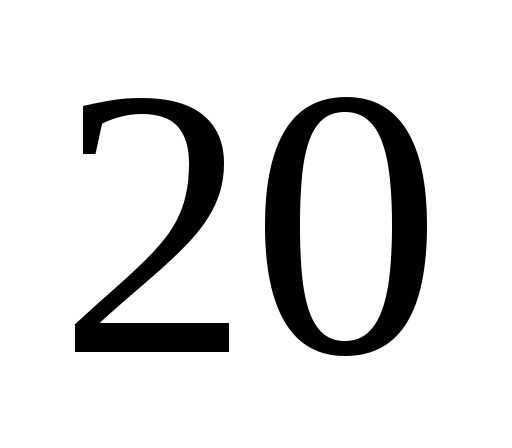

2.
Вычисляется среднеквадратическое
отклонение

3.
В соответствии с поставленными задачами
эксперимента устанавливается требуемая
точность измерений

которая не должна превышать точности
прибора.
4.
Устанавливается нормированное отклонение
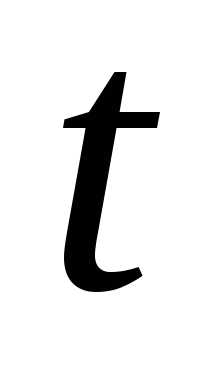
значение которого обычно задается
(зависит также от точности метода).
5.
По формуле (2.2) определяют
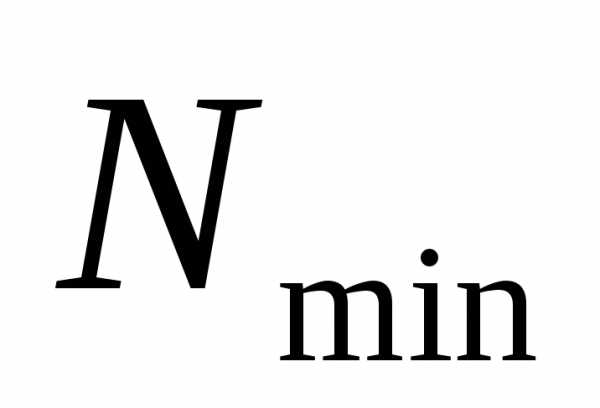
число измерений не должно быть меньше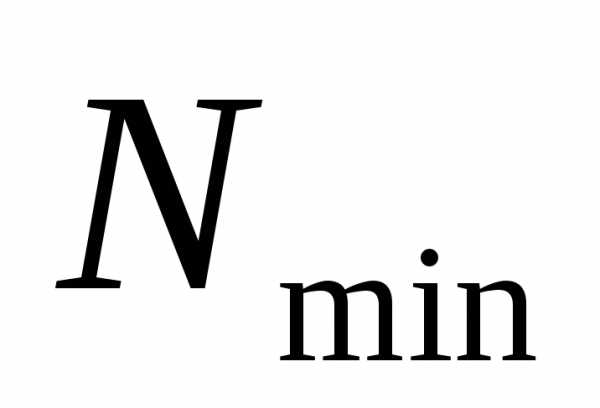
Пример
При приемке
сооружений комиссия в качестве одного
из параметров замеряет их ширину.
Согласно инструкции требуется выполнять

параметра.
Если предварительно вычисленное значение,
то можно определить, с какой достоверностью
комиссия оценивает данный параметр.
Из формулы (2.2)
можно записать
.
В соответствии с
табл.10.1
доверительная вероятность для
.
Это низкая
вероятность.
Погрешность,
превышающая доверительный интервал
,
согласно выражению (1.4) будет встречаться
один раз из,
т.е. из четырех измерений. Это недопустимо.
В связи с этим
необходимо вычислить минимальное
количество измерений с доверительной
вероятностью
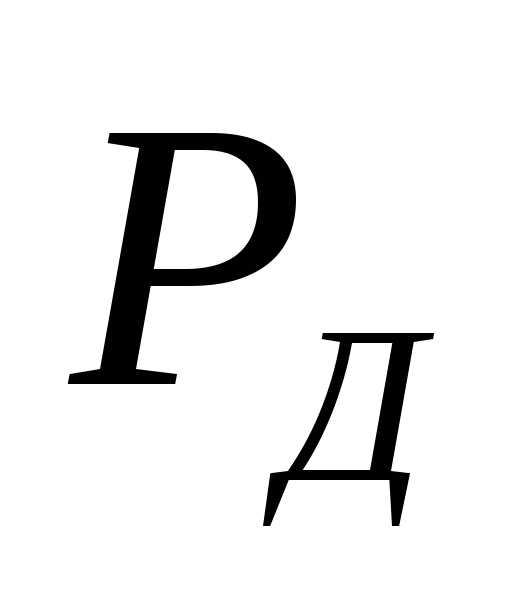
равной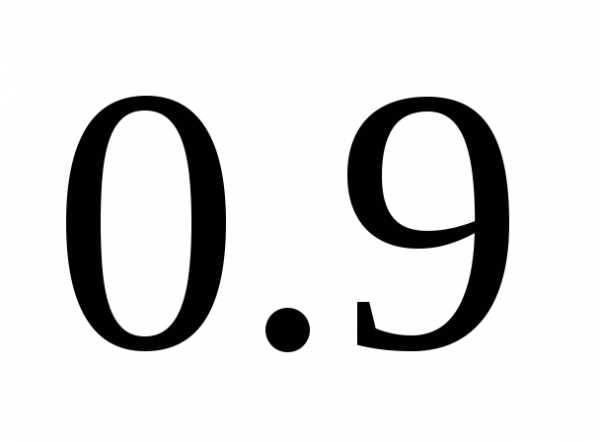
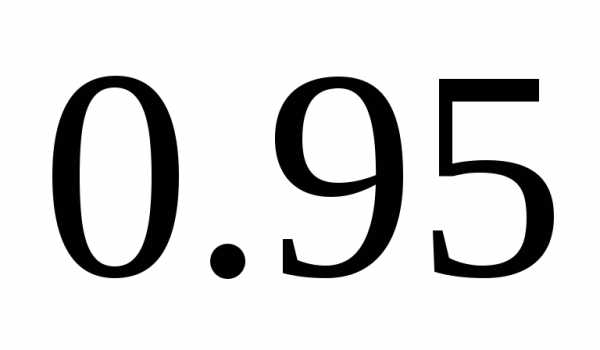
По формуле (2.2)
имеем
измерения при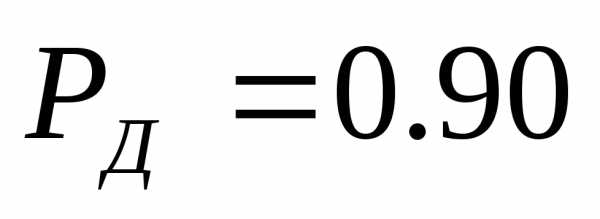

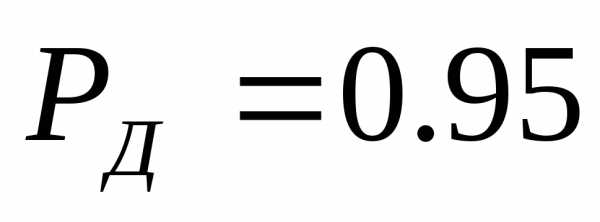
что значительно превышает установленные
Для нахождения
границы доверительного интервала при
малых значениях (
применяют метод, предложенный в 1908 г.
английским математиком Госсетом В.С.
(псевдоним Стьюдент).
Кривые распределения
Стьюдента в случае
(практически при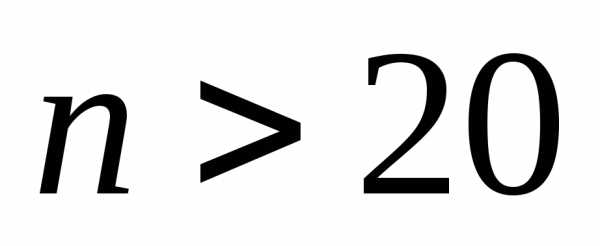
переходят в кривые нормального
распределения (рис.10.1).
Рис.2.1. Кривые
распределения Стьюдента для различных
значений:
1
— при
;2
— при
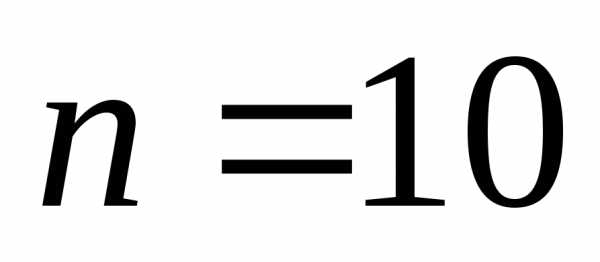
— при
studfiles.net
Коэффициенты Стьюдента
|
Число |
Надежность Р |
||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,99 |
|
|
2 |
1,00 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
637 |
|
3 |
0,82 |
1,06 |
1,5 |
1,9 |
2,9 |
4,3 |
35 |
|
4 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
12,9 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
8,6 |
|
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
6,9 |
|
7 |
0,72 |
0,91 |
1,1 |
1,4 |
1,9 |
2,4 |
6,0 |
|
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
5,4 |
|
9 |
0,71 |
0,89 |
1,1 |
1,4 |
1,9 |
2,3 |
5,0 |
|
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
4,8 |
2.2. Расчет случайной погрешности
При обработке прямых измерений результаты
наблюдений и вычислений удобно оформлять
в виде табл. 2.
Таблица 2
Расчет среднего значения и случайной погрешности по методу Стьюдента
|
№ |
ai |
|
ai |
ai2 |
|
P |
tPN |
aсл |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
||||||||
|
2 |
||||||||
|
3 |
В колонке 1указывается номер опыта
по порядку (обычно проводится 3-7
измерений).
В колонке 2 записываютсязначения
измеряемой величины.
В колонку 3вноситсясреднее
значениеизмеряемой величины,
рассчитанное по формуле:
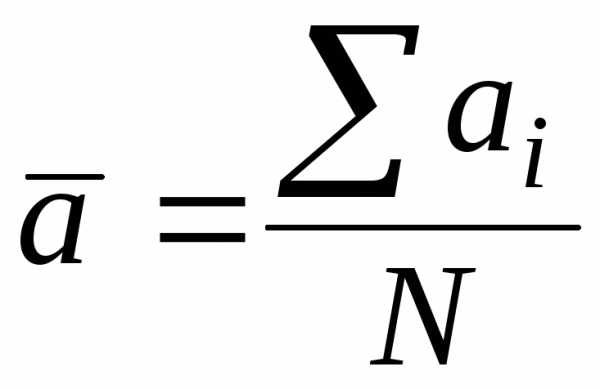
В колонке 4представленыотклонениякаждого значенияизмеряемой величины от среднего:
.
(2)
Каждый результат, полученный по последней
формуле, возводится в квадрат и заносится
в колонку 5.
В колонке 6следует расположитьсреднеквадратичную погрешность ,
рассчитанную по формуле:
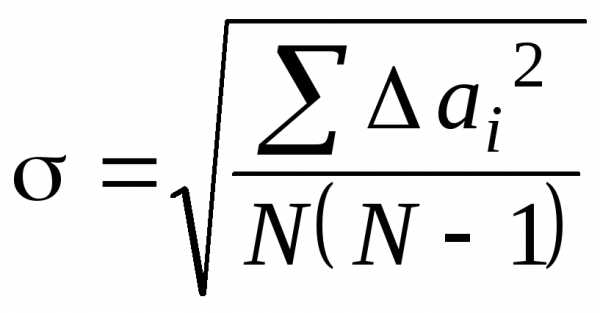
Она характеризует разброс средних
значений измеряемой величины.
Среднеквадратичная погрешность тем
больше, чем сильнее измеренные величины
отличаются друг от друга.
В колонку 7заносится значение
доверительной вероятности (или надежности)
Обычно достаточно выбрать значениеР= 0,95 (или, что то же самое, 95%).
Коэффициент Стьюдента, учитывающий
заданную доверительную вероятность и
число измерений tPN
,находится по табл. 1 и располагаетсяв
колонке 8.
Случайная погрешностьрассчитывается
по формуле
aсл=tPN
S(4)
и заносится в колонку 9.
2.3. Учет систематических погрешностей
К учитываемым систематическим погрешностям
относятся погрешности средств измерения
и погрешности отсчета.
В форме абсолютных погрешностейзадаются погрешности линеек,
штангенциркулей, секундомеров, термометров
и т.п. Абсолютная погрешность средства
измерения в этом случае может быть
вычислена по формуле
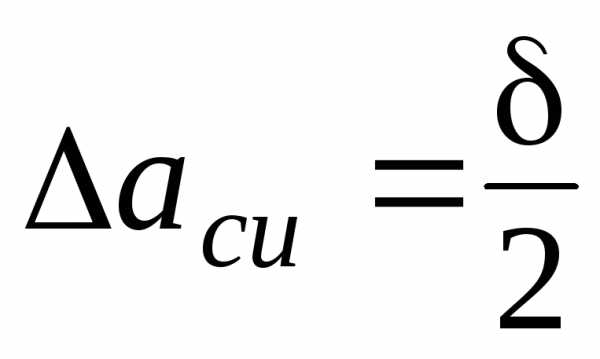
где -
цена деления прибора.
В форме приведенных погрешностейзадаются пределы допускаемых погрешностей
электроизмерительных приборов,
манометров. Этим приборам присваиваются
классы точности.Класс точностиравен пределу допускаемой приведенной
погрешности, выраженной в процентах,
которая определяется по формуле
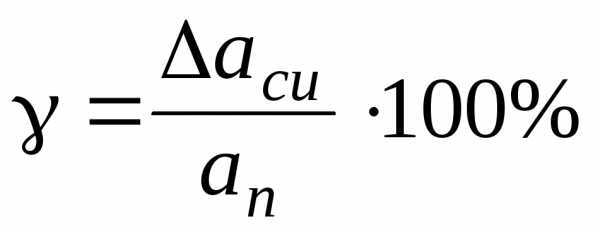
где ап—нормирующее
значениеприбора илипредел измерений;
— предел допускаемой приведенной
погрешности прибора в процентах от
нормирующего значения;
аси— абсолютная погрешность
прибора.
Пользуясь этой формулой, можно определить
абсолютную погрешность измерительного
прибора:
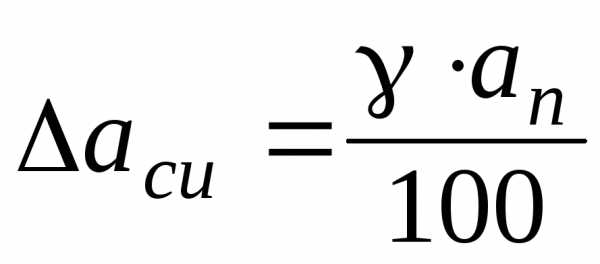
Полная абсолютная погрешностьпрямых измерений рассчитывается по
формуле
. (7)
Чаще всего случайная погрешность и
погрешность средств измерения — величины
разных порядков; в таких случаях меньшей
погрешностью пренебрегают. Например,
если
,
то
studfiles.net
Коэффициенты Стьюдента — это… Что такое Коэффициенты Стьюдента?
- Коэффициенты Стьюдента
-
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Определение
Пусть Fn — функция распределения Стьюдента t(n) с n степенями свободы, и . Тогда α-квантилью этого распределения называется число tα,n такое, что
- .
Замечания
- .
- Функция не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение t(n) симметрично. Следовательно,
- t1 − α,n = − tα,n.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета tα,n, необходимо найти строку, соответствующую нужному n, и колонку, соответствующую нужному α. Искомое число находится в таблице на их пересечении.
Пример
- t0.2,4 = 0.2707;
- t0.8,4 = − t0.2,4 = − 0.2707.
См. также
Квантили tα,n
two-tailed test 1-0.9/2 1-0.8/2 1-0.7/2 1-0.6/2 1-0.5/2 1-0.4/2 1-0.3/2 1-0.2/2 1-0.1/2 1-0.05/2 1-0.02/2 one-tailed test 1-0.9 1-0.8 1-0.7 1-0.6 1-0.5 1-0.4 1-0.3 1-0.2 1-0.1 1-0.05 1-0.02 1 0.1584 0.3249 0.5095 0.7265 1.0000 1.3764 1.9626 3.0777 6.3138 12.7062 31.8205 2 0.1421 0.2887 0.4447 0.6172 0.8165 1.0607 1.3862 1.8856 2.9200 4.3027 6.9646 3 0.1366 0.2767 0.4242 0.5844 0.7649 0.9785 1.2498 1.6377 2.3534 3.1824 4.5407 4 0.1338 0.2707 0.4142 0.5686 0.7407 0.9410 1.1896 1.5332 2.1318 2.7764 3.7469 5 0.1322 0.2672 0.4082 0.5594 0.7267 0.9195 1.1558 1.4759 2.0150 2.5706 3.3649 6 0.1311 0.2648 0.4043 0.5534 0.7176 0.9057 1.1342 1.4398 1.9432 2.4469 3.1427 7 0.1303 0.2632 0.4015 0.5491 0.7111 0.8960 1.1192 1.4149 1.8946 2.3646 2.9980 8 0.1297 0.2619 0.3995 0.5459 0.7064 0.8889 1.1081 1.3968 1.8595 2.3060 2.8965 9 0.1293 0.2610 0.3979 0.5435 0.7027 0.8834 1.0997 1.3830 1.8331 2.2622 2.8214 10 0.1289 0.2602 0.3966 0.5415 0.6998 0.8791 1.0931 1.3722 1.8125 2.2281 2.7638 11 0.1286 0.2596 0.3956 0.5399 0.6974 0.8755 1.0877 1.3634 1.7959 2.2010 2.7181 12 0.1283 0.2590 0.3947 0.5386 0.6955 0.8726 1.0832 1.3562 1.7823 2.1788 2.6810 13 0.1281 0.2586 0.3940 0.5375 0.6938 0.8702 1.0795 1.3502 1.7709 2.1604 2.6503 14 0.1280 0.2582 0.3933 0.5366 0.6924 0.8681 1.0763 1.3450 1.7613 2.1448 2.6245 15 0.1278 0.2579 0.3928 0.5357 0.6912 0.8662 1.0735 1.3406 1.7531 2.1314 2.6025 16 0.1277 0.2576 0.3923 0.5350 0.6901 0.8647 1.0711 1.3368 1.7459 2.1199 2.5835 17 0.1276 0.2573 0.3919 0.5344 0.6892 0.8633 1.0690 1.3334 1.7396 2.1098 2.5669 18 0.1274 0.2571 0.3915 0.5338 0.6884 0.8620 1.0672 1.3304 1.7341 2.1009 2.5524 19 0.1274 0.2569 0.3912 0.5333 0.6876 0.8610 1.0655 1.3277 1.7291 2.0930 2.5395 20 0.1273 0.2567 0.3909 0.5329 0.6870 0.8600 1.0640 1.3253 1.7247 2.0860 2.5280 21 0.1272 0.2566 0.3906 0.5325 0.6864 0.8591 1.0627 1.3232 1.7207 2.0796 2.5176 22 0.1271 0.2564 0.3904 0.5321 0.6858 0.8583 1.0614 1.3212 1.7171 2.0739 2.5083 23 0.1271 0.2563 0.3902 0.5317 0.6853 0.8575 1.0603 1.3195 1.7139 2.0687 2.4999 24 0.1270 0.2562 0.3900 0.5314 0.6848 0.8569 1.0593 1.3178 1.7109 2.0639 2.4922 25 0.1269 0.2561 0.3898 0.5312 0.6844 0.8562 1.0584 1.3163 1.7081 2.0595 2.4851 26 0.1269 0.2560 0.3896 0.5309 0.6840 0.8557 1.0575 1.3150 1.7056 2.0555 2.4786 27 0.1268 0.2559 0.3894 0.5306 0.6837 0.8551 1.0567 1.3137 1.7033 2.0518 2.4727 28 0.1268 0.2558 0.3893 0.5304 0.6834 0.8546 1.0560 1.3125 1.7011 2.0484 2.4671 29 0.1268 0.2557 0.3892 0.5302 0.6830 0.8542 1.0553 1.3114 1.6991 2.0452 2.4620 30 0.1267 0.2556 0.3890 0.5300 0.6828 0.8538 1.0547 1.3104 1.6973 2.0423 2.4573 31 0.1267 0.2555 0.3889 0.5298 0.6825 0.8534 1.0541 1.3095 1.6955 2.0395 2.4528 32 0.1267 0.2555 0.3888 0.5297 0.6822 0.8530 1.0535 1.3086 1.6939 2.0369 2.4487 33 0.1266 0.2554 0.3887 0.5295 0.6820 0.8526 1.0530 1.3077 1.6924 2.0345 2.4448 34 0.1266 0.2553 0.3886 0.5294 0.6818 0.8523 1.0525 1.3070 1.6909 2.0322 2.4411 35 0.1266 0.2553 0.3885 0.5292 0.6816 0.8520 1.0520 1.3062 1.6896 2.0301 2.4377 36 0.1266 0.2552 0.3884 0.5291 0.6814 0.8517 1.0516 1.3055 1.6883 2.0281 2.4345 37 0.1265 0.2552 0.3883 0.5289 0.6812 0.8514 1.0512 1.3049 1.6871 2.0262 2.4314 38 0.1265 0.2551 0.3882 0.5288 0.6810 0.8512 1.0508 1.3042 1.6860 2.0244 2.4286 39 0.1265 0.2551 0.3882 0.5287 0.6808 0.8509 1.0504 1.3036 1.6849 2.0227 2.4258 40 0.1265 0.2550 0.3881 0.5286 0.6807 0.8507 1.0500 1.3031 1.6839 2.0211 2.4233 41 0.1264 0.2550 0.3880 0.5285 0.6805 0.8505 1.0497 1.3025 1.6829 2.0195 2.4208 42 0.1264 0.2550 0.3880 0.5284 0.6804 0.8503 1.0494 1.3020 1.6820 2.0181 2.4185 43 0.1264 0.2549 0.3879 0.5283 0.6802 0.8501 1.0491 1.3016 1.6811 2.0167 2.4163 44 0.1264 0.2549 0.3878 0.5282 0.6801 0.8499 1.0488 1.3011 1.6802 2.0154 2.4141 45 0.1264 0.2549 0.3878 0.5281 0.6800 0.8497 1.0485 1.3006 1.6794 2.0141 2.4121 46 0.1264 0.2548 0.3877 0.5281 0.6799 0.8495 1.0483 1.3002 1.6787 2.0129 2.4102 47 0.1263 0.2548 0.3877 0.5280 0.6797 0.8493 1.0480 1.2998 1.6779 2.0117 2.4083 48 0.1263 0.2548 0.3876 0.5279 0.6796 0.8492 1.0478 1.2994 1.6772 2.0106 2.4066 49 0.1263 0.2547 0.3876 0.5278 0.6795 0.8490 1.0475 1.2991 1.6766 2.0096 2.4049 50 0.1263 0.2547 0.3875 0.5278 0.6794 0.8489 1.0473 1.2987 1.6759 2.0086 2.4033 100 0.1260 0.2540 0.3864 0.5261 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 1000 0.1257 0.2534 0.3854 0.5246 0.6747 0.8420 1.0370 1.2824 1.6464 1.9623 2.3301
Wikimedia Foundation.
2010.
- Коэффициенты Ламэ
- Коялович, Войцех
Смотреть что такое «Коэффициенты Стьюдента» в других словарях:
-
Процентили распределения Стьюдента — Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез. Содержание 1 … Википедия
-
Квантили распределения Стьюдента — Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.… … Википедия
-
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
-
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
-
Наименьших квадратов метод — один из методов ошибок теории (См. Ошибок теория) для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближённого представления заданной функции другими (более простыми)… … Большая советская энциклопедия
-
Математи́ческие ме́тоды — в медицине совокупность методов количественного изучения и анализа состояния и (или) поведения объектов и систем, относящихся к медицине и здравоохранению. В биологии, медицине и здравоохранении в круг явлений, изучаемых с помощью М.м., входят… … Медицинская энциклопедия
-
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
-
РДМУ 109-77: Методические указания. Методика выбора и оптимизации контролируемых параметров технологических процессов — Терминология РДМУ 109 77: Методические указания. Методика выбора и оптимизации контролируемых параметров технологических процессов: 73. Адекватность модели Соответствие модели с экспериментальными данными по выбранному параметру оптимизации с… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации
-
Нахождение дисперсии ошибки определения коэффициента регрессии — 3.9.3. Нахождение дисперсии ошибки определения коэффициента регрессии При равном числе параллельных опытов (m0) во всех точках плана матрицы дисперсию ошибки определения коэффициента регрессии определяют по формуле… … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
КОЭФФИЦИЕНТЫ Стьюдента t p 2
КОЭФФИЦИЕНТЫ
СТЬЮДЕНТА tp,n
(n от 1 до 30)
р — надежность,
n – число измерений
|
n |
p |
|||||||
|
0,80 |
0,90 |
0,95 |
0,98 |
0,99 |
0,995 |
0,998 |
0,999 |
|
|
2 |
3,077 |
6,313 |
12,706 |
31,820 |
63,656 |
127,656 |
318,306 |
636,619 |
|
3 |
1,885 |
2,920 |
4,302 |
6,964 |
9,924 |
14,089 |
22,327 |
31,599 |
|
4 |
1,638 |
2,353 |
3,182 |
4,540 |
5,840 |
7,458 |
10,214 |
12,924 |
|
5 |
1,533 |
2,132 |
2,776 |
3,746 |
4,604 |
5,597 |
7,173 |
8,610 |
|
6 |
1,476 |
2,015 |
2,570 |
3,649 |
4,032 |
4,773 |
5,893 |
6,863 |
|
7 |
1,439 |
1,943 |
2,446 |
3,142 |
3,707 |
4,316 |
5,207 |
5,958 |
|
8 |
1,415 |
1,895 |
2,365 |
2,998 |
3,500 |
4,229 |
4,785 |
5,408 |
|
9 |
1,397 |
1,860 |
2,306 |
2,897 |
3,355 |
3,832 |
4,501 |
5,041 |
|
10 |
1,383 |
1,833 |
2,262 |
2,821 |
3,250 |
3,690 |
4,297 |
4,780 |
|
11 |
1,372 |
1,813 |
2,228 |
2,764 |
3,169 |
3,581 |
4,144 |
4,587 |
|
12 |
1,363 |
1,795 |
2,201 |
2,718 |
3,105 |
3,496 |
4,024 |
4,437 |
|
13 |
1,356 |
1,782 |
2,179 |
2,681 |
3,085 |
3,428 |
3,929 |
4,178 |
|
14 |
1,350 |
1,771 |
2,160 |
2,650 |
3,112 |
3,373 |
3,852 |
4,220 |
|
15 |
1,345 |
1,761 |
2,145 |
2,625 |
2,976 |
3,326 |
3,787 |
4,140 |
|
16 |
1,341 |
1,753 |
2,131 |
2,603 |
2,947 |
3,286 |
3,732 |
4,072 |
|
17 |
1,336 |
1,745 |
2,119 |
2,583 |
2,920 |
3,252 |
3,686 |
4,015 |
|
18 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
3,222 |
3,646 |
3,965 |
|
19 |
1,330 |
1,734 |
2,101 |
2,551 |
2,878 |
3,197 |
3,611 |
3,922 |
|
20 |
1,328 |
1,729 |
2,093 |
2,540 |
2,861 |
3,174 |
3,579 |
3,883 |
|
21 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
3,153 |
3,552 |
3,850 |
|
22 |
1,323 |
1,720 |
2,079 |
2,517 |
2,831 |
3,135 |
3,527 |
3,819 |
|
23 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
3,119 |
3,505 |
3,792 |
|
24 |
1,320 |
1,714 |
2,069 |
2,500 |
2,807 |
3,104 |
3,485 |
3,768 |
|
25 |
1,138 |
1,711 |
2,064 |
2,492 |
2,797 |
3,091 |
3,467 |
3,745 |
|
26 |
1,316 |
1,708 |
2,060 |
2,485 |
2,787 |
3,078 |
3,450 |
3,725 |
|
27 |
1,315 |
1,705 |
2,056 |
2,478 |
2,778 |
3,066 |
3,436 |
3,706 |
|
28 |
1,314 |
1,703 |
2,052 |
2,473 |
2,771 |
3,057 |
3,421 |
3,690 |
|
29 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
3,047 |
3,408 |
3,674 |
|
30 |
1,311 |
1,699 |
2,045 |
2,462 |
2,756 |
3,036 |
3,396 |
3,849 |
КОЭФФИЦИЕНТЫ
СТЬЮДЕНТА tp,n
(n от 30 до 500)
р — надежность,
n – число измерений
|
N |
p |
|||||||
|
0,80 |
0,90 |
0,95 |
0,98 |
0,99 |
0,995 |
0,998 |
0,999 |
|
|
31 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
3,030 |
3,385 |
3,646 |
|
33 |
1,308 |
1,693 |
2,036 |
2,440 |
2,738 |
3,014 |
3,365 |
3,621 |
|
35 |
1,307 |
1,691 |
2,032 |
2,441 |
2,728 |
3,952 |
3,348 |
3,601 |
|
37 |
1,305 |
1,688 |
2,028 |
2,435 |
2,720 |
9,490 |
3,333 |
3,582 |
|
39 |
1,304 |
1,686 |
2,024 |
2,429 |
2,712 |
3,981 |
3,319 |
3,566 |
|
41 |
1,303 |
1,684 |
2,021 |
2,423 |
2,705 |
3,971 |
3,307 |
3,551 |
|
43 |
1,320 |
1,682 |
2,018 |
2,418 |
2,698 |
2,693 |
3,296 |
3,537 |
|
45 |
1,301 |
1,680 |
2,015 |
2,414 |
2,692 |
3,956 |
3,286 |
3,526 |
|
47 |
1,300 |
1,677 |
2,013 |
2,410 |
2,687 |
3,949 |
3,277 |
3,515 |
|
49 |
1,299 |
1,677 |
2,011 |
2,406 |
2,682 |
3,943 |
3,269 |
3,505 |
|
51 |
1,298 |
1,676 |
2,009 |
2,403 |
2,678 |
3,937 |
3,261 |
3,406 |
|
56 |
1,297 |
1,673 |
2,004 |
2,396 |
2,668 |
2,924 |
3,256 |
3,476 |
|
61 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
3,915 |
3,232 |
3,460 |
|
66 |
1,295 |
1,669 |
1,997 |
2,385 |
2,654 |
3,906 |
3,220 |
3,447 |
|
71 |
1,294 |
1,669 |
1,994 |
2,381 |
2,648 |
3,899 |
3,211 |
3,435 |
|
81 |
1,292 |
1,664 |
1,990 |
2,373 |
2,638 |
2,887 |
3,195 |
3,416 |
|
91 |
1,291 |
1,662 |
1,987 |
2,389 |
2,632 |
2,878 |
3,183 |
3,402 |
|
101 |
1,290 |
1,660 |
1,984 |
2,364 |
2,626 |
2,871 |
3,174 |
3,391 |
|
121 |
1,289 |
1,658 |
1,972 |
2,358 |
2,617 |
2,860 |
3,160 |
3,374 |
|
151 |
1,287 |
1,655 |
1,976 |
2,352 |
2,609 |
2,848 |
3,146 |
3,357 |
|
201 |
1,286 |
1,653 |
1,972 |
2,345 |
2,601 |
2,839 |
3,132 |
3,340 |
|
251 |
1,285 |
1,651 |
1,970 |
2,341 |
2,597 |
2,822 |
3,123 |
3,330 |
|
301 |
1,284 |
1,650 |
1,968 |
2,339 |
2,592 |
2,828 |
3,118 |
3,323 |
|
401 |
1,284 |
1,649 |
1,966 |
2,336 |
2,588 |
2,823 |
3,111 |
3,315 |
|
501 |
1,283 |
1,647 |
1,964 |
2,333 |
2,785 |
2,819 |
3,106 |
3,310 |
studfiles.net
Коэффициент Стьюдента
|
n |
a |
||||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
|
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
31,6 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
8,6 |
|
10 |
0,7 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
3,3 |
4,8 |
Таким образом,
порядок расчета случайной ошибки
измерения должен быть следующим:
а) производят n
измерений искомой физической величины
и вычисляют ее среднее значение
;
б) находят абсолютные
погрешности отдельных измерений
;
в) рассчитывают
среднюю квадратическую погрешность
среднего арифметического
;
г)
по заданной доверительной вероятности
a
и числу измерений n
находят из табл. 1.1 коэффициент Стьюдента
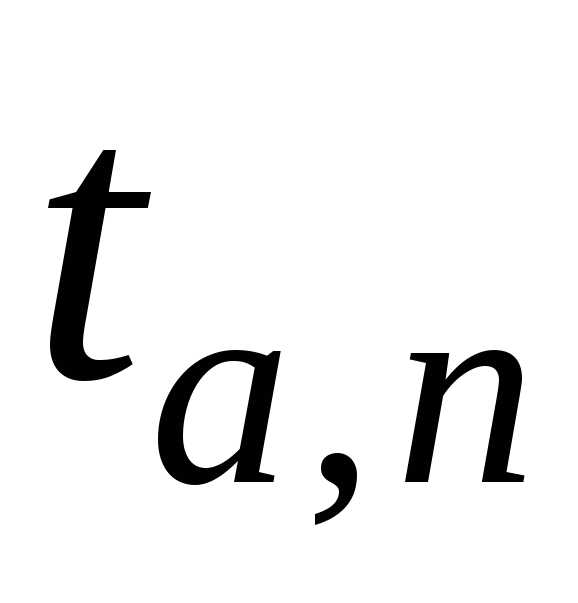
д) рассчитывают
доверительный интервал
;
е) окончательный
результат записывают в виде
при
.
Замечания.
Так как при малом числе измерений
является
случайной величиной и определяется с
большой погрешностью, то при записи
числового значения доверительного
интервала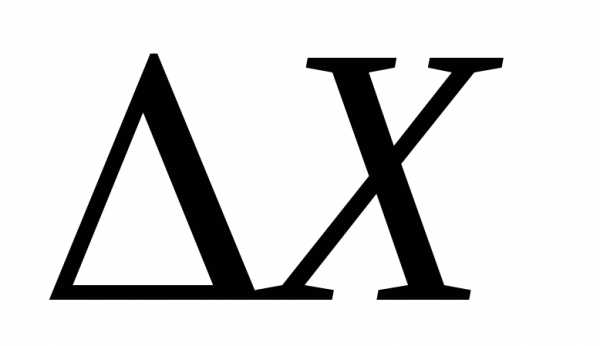
учитывать это обстоятельство. В теории
ошибок доказано, что при числе измеренийn
£
10
в числовом значении
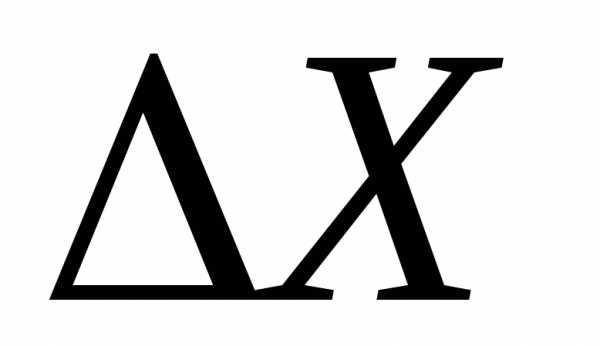
оставить одну значащую цифру, если она
больше трех (),
и две, если первая из них меньше четырех
().
Затем числовое значение <X
>
округляют до разряда ошибки, например:
.
Точность вычислений
при обработке результатов измерений
нужно согласовать с точностью самих
измерений, ошибка вычислений должна
быть на порядок меньше ошибки измерений.
Систематические ошибки. Соотношение случайной и систематической ошибок
Систематические
ошибки могут существенно исказить
результат измерения, поэтому перед
началом измерений необходимо выявить
систематические ошибки и, если возможно,
исключить их. С этой целью проверяют
исправность используемых приборов,
правильность их установки, анализируют
метод измерения и т. д. Чаще всего
источником систематических погрешностей
являются неточности, допущенные при
изготовлении измерительных приборов,
такие погрешности называют инструментальными,
или приборными. Эти ошибки при изготовлении
приборов не определяют, а лишь
устанавливают, не превышают ли они
допустимые пределы. Предельная погрешность
d
обычно указывается в паспорте или
обозначается соответствующим условным
знаком на шкале прибора. Например, для
микрометра предельная погрешность
равна 0,004 мм,
для штангенциркуля –
0,05 мм
и
т. д.
Таким
образом, в результате обработки данных,
полученных при измерении, мы находим
случайную ошибку, величина которой
определяется полушириной доверительного
интервала
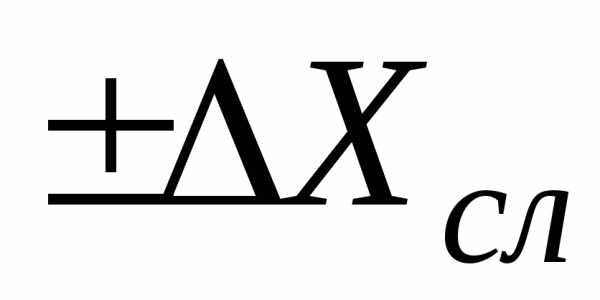
и ситематическую ошибку, равную предельной
погрешности:Если предельная допустимая погрешность
измерительного прибора не указана, то∆Хпр
берут равной половине цены наименьшего
деления шкалы прибора.
К
какому же отношению между величинами
случайной и систематической погрешностей
следует стремиться при проведении
измерений? По-видимому, определяющей
должна быть систематическая ошибка,
т.е., выбирая метод измерения и необходимое
число измерений, нужно добиваться, чтобы
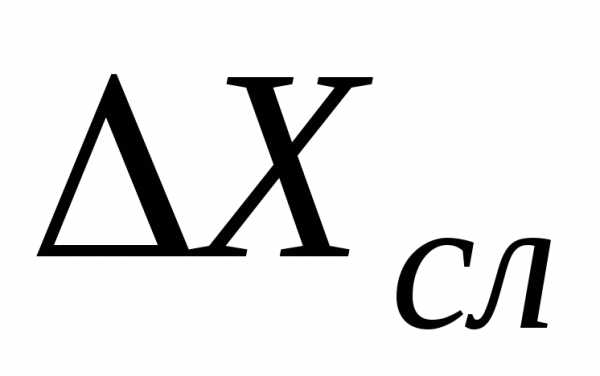
меньше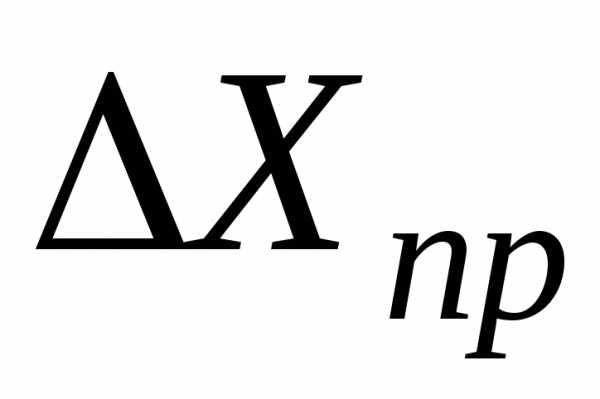
Если,
то пренебрегают систематической ошибкой,
прирассматривают только систематическую
ошибку. Может оказаться, что случайная
ошибка сравнима по величине с
систематической, тогда находят суммарную
ошибку
.
studfiles.net
Значения коэффициентов Стьюдента
|
n |
0,9 |
0,95 |
0,99 |
0,999 |
|
1 |
2 |
3 |
4 |
5 |
|
2 3 4 5 6 7 8 9 10 ∞ |
6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,65 |
12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 1,96 |
63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 2,58 |
636,62 31,60 12,84 8,61 6,86 5,96 5,40 5,04 4,78 3,29 |
Например,
задавая доверительную вероятность δ
=0.95, по числу проведенных измерений n=5
по табл. 2 можно найти
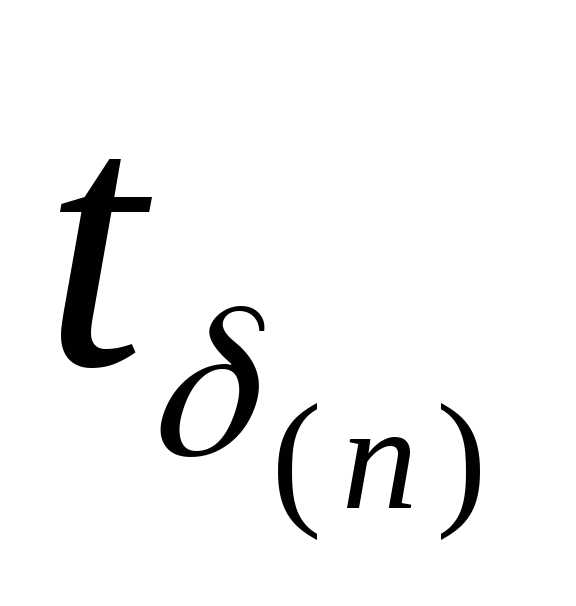
2,78. Тогда, определив предварительно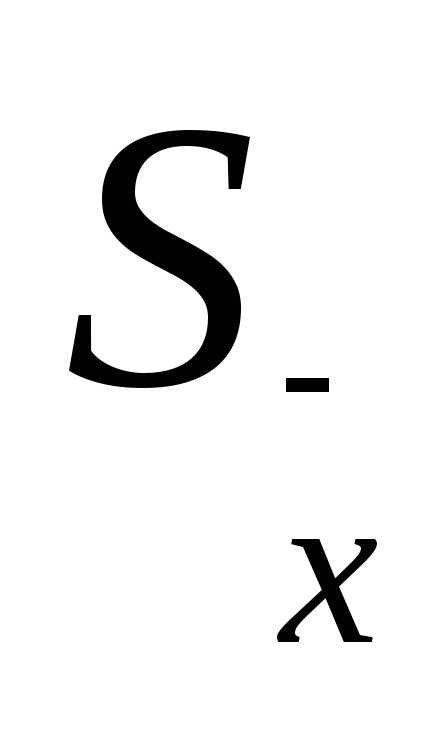
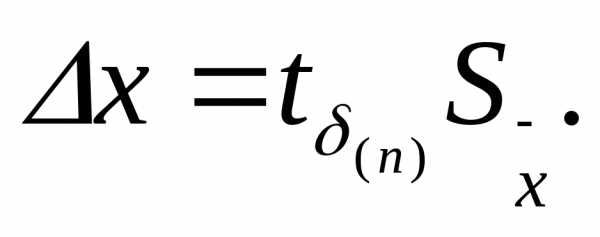
Выражение
(41) ввиду малого объема информации дает
границы доверительного интервала более
широкими.
Результат
измерения можно представить в виде:
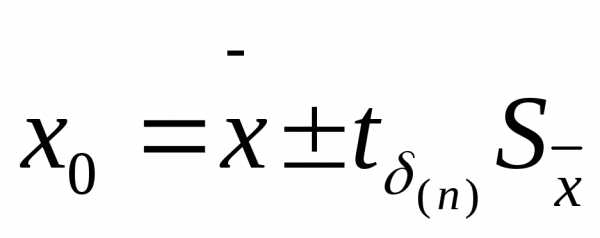
δ=0,95, n=5.
(42)
Конечно,
оценка (42) еще не дает представления об
общей погрешности измерения, в
которую
входит и систематическая ошибка.
Совместный
учет случайных
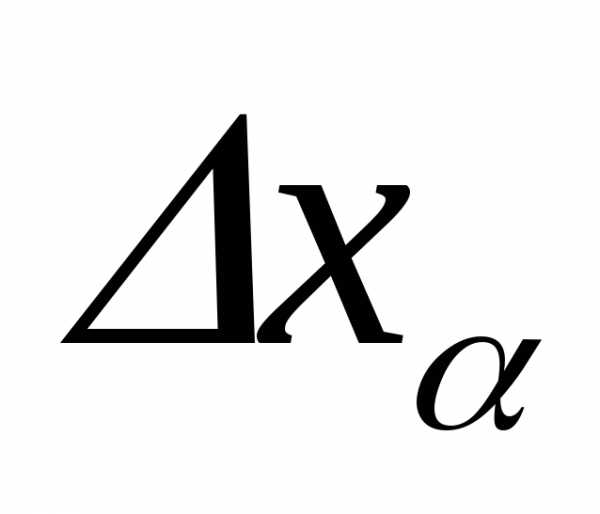
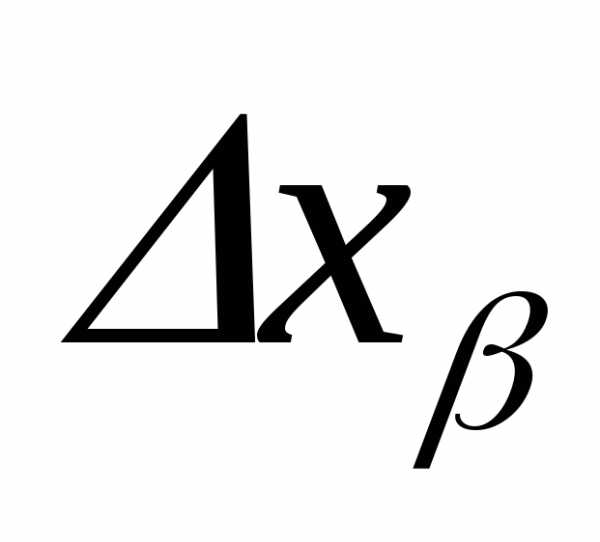
При
этом следует принять во внимание, что
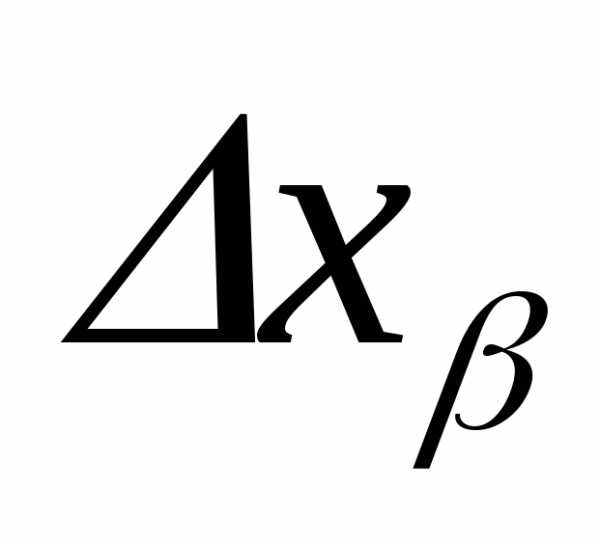
Максимальное же значение случайных
ошибок равно 3σ . Следовательно, для их
равноправного учета необходимо
предположить, что приборная погрешность
β (или ∆пр)
равна утроенной дисперсии распределения
погрешностей прибора 3σпр
,т.е. погрешности соответствующей
надежности δ =0.997. Тогда за систематическую
ошибку можно принять
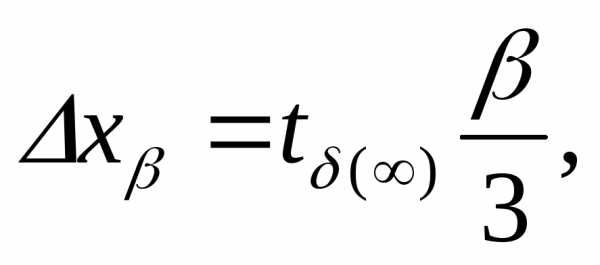
(43)
Коэффициенты
Стьюдента для проведенного числа
измерений


заданной надежности
δ.
Погрешности косвенных измерений
Часто
приходится вычислять искомую величину
по результатам измерений других величин,
связанных с этой величиной определенной
функциональной зависимостью. Например,
объем шара
можно вычислить, измерив его радиусR
. Также измерения называются косвенными.
Рассмотрим
конкретный пример. Допустим, что величины
Х0,
У0
и U0
связаны равенством
.
(44)
Непосредственно
измеряются величины Х0
и У0,
и по этим измерениям мы судим об U0,
считая
(45)
измерением
величины U0.
Предполагается,
что измерения Хi
и yi
независимы друг
от
друга, и распределены нормально с
дисперсиями
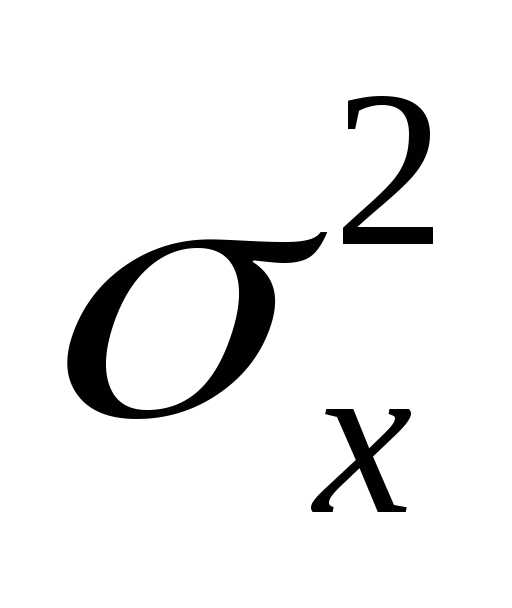
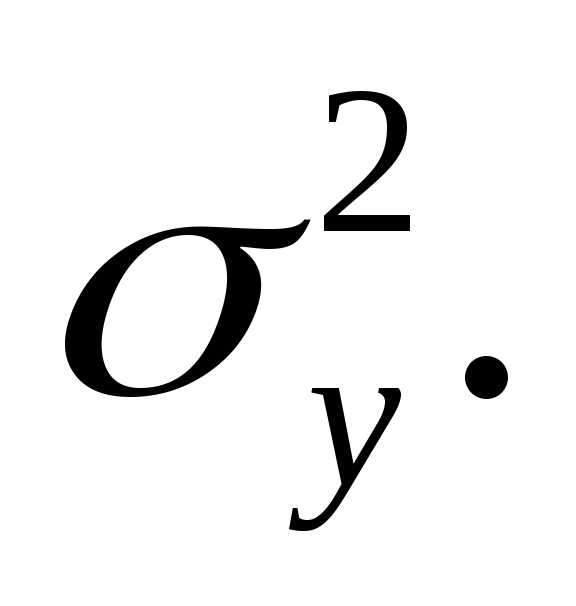
заключается в том, как по известным
значениям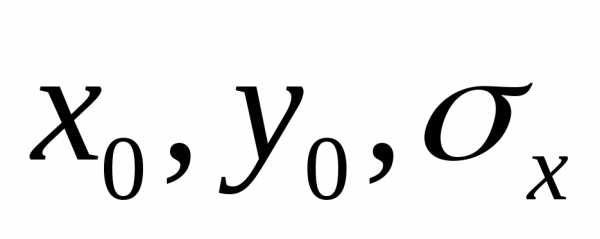

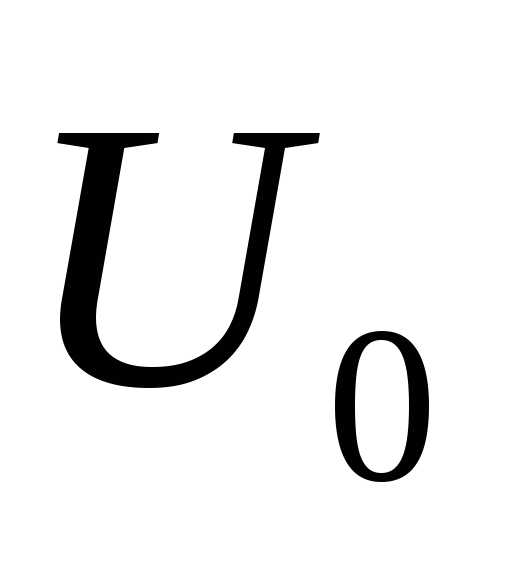
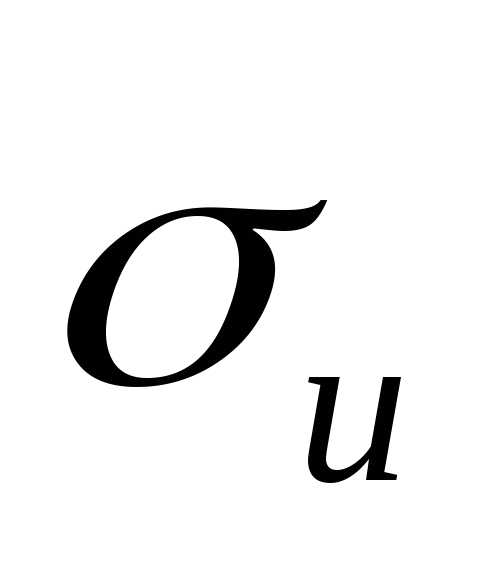
Очевидно,
что погрешность косвенного измерения
обусловлена
погрешностями отдельных измерений
и.
Поэтому выражение (45) можно переписать
в виде:
(46)
Вычитая
почленно левые и правые части уравнений
(46) и (44). для погрешности косвенного
измерения получим:
(47)
Тогда
для дисперсии результатов косвенного
измерения можно записать выражение:
Здесь
член
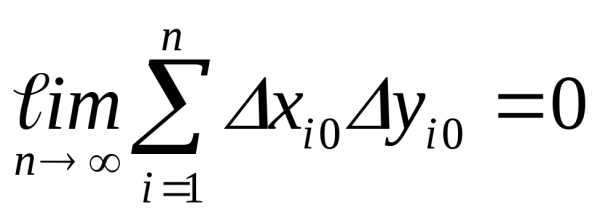
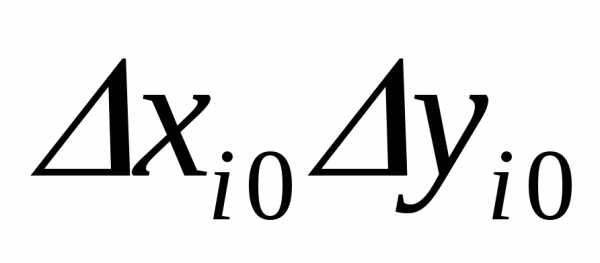
положительным, или отрицательным.
Учитывая,
что
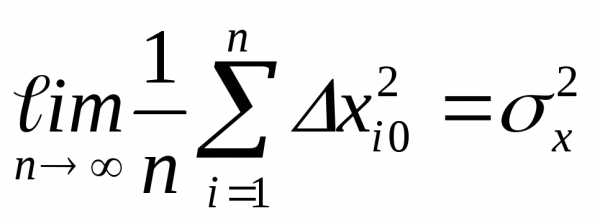
получим
(48)
или
(49)
Равенство
(49) определяет соотношение средних
квадратичных ошибок прямых и косвенных
измерений. Это выражение для частного
случая имеет весьма общий характер и
называется законом сложения дисперсий.
Следовательно,
при измерении нескольких неизвестных
величин складываются дисперсии этих
величин (не ошибки, а именно дисперсии).
Средние
квадратичные ошибки средних арифметических
связаны
аналогичным образом
(50)
Рассмотрим
общий случай, когда u
— функция двух переменных х и y:
(51)
Ошибки
в величинах х и у такова:
,
где Х0
и У0
— истинные значения величин Х в У. Тогда
для результата отдельного измерения
можно записать
(52)
Если
‘та функция непрерывна и имеет
производные, то ее можно разложить в
ряд Тейлора. Рассматривая только члены
c
нулевыми и первыми степенями малых
погрешностей

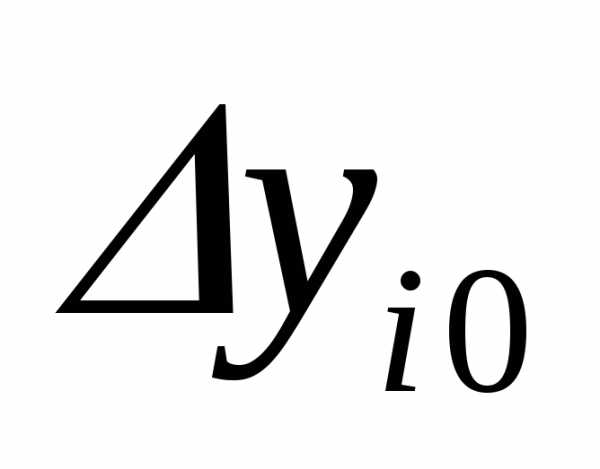
получим:
или
поскольку
(53)
Частные
производные здесь вычисляются при Х=Х0
и У=У0.
Запишем выражение для дисперсии
результатов косвенного измерения:
Учитывая,
что
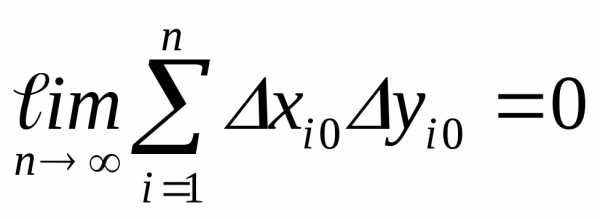
получим
(54)
или
(55)
Для
относительной погрешности косвенного
измерения
учитывая,
что
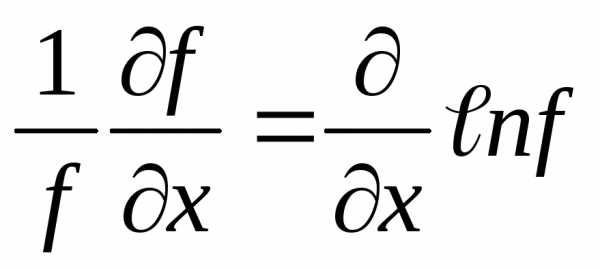
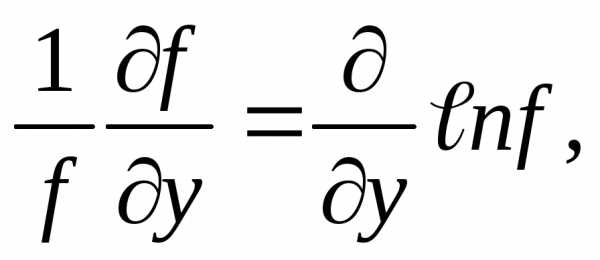
(56)
studfiles.net
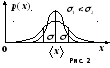

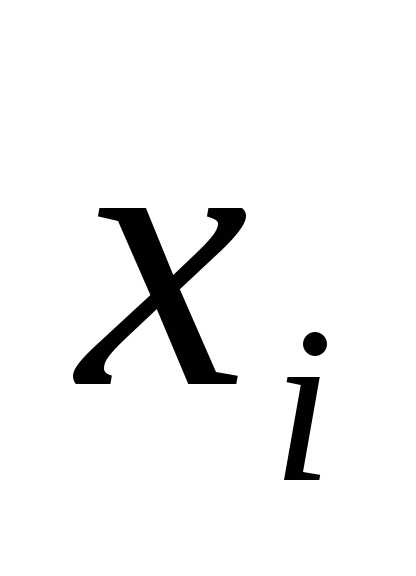
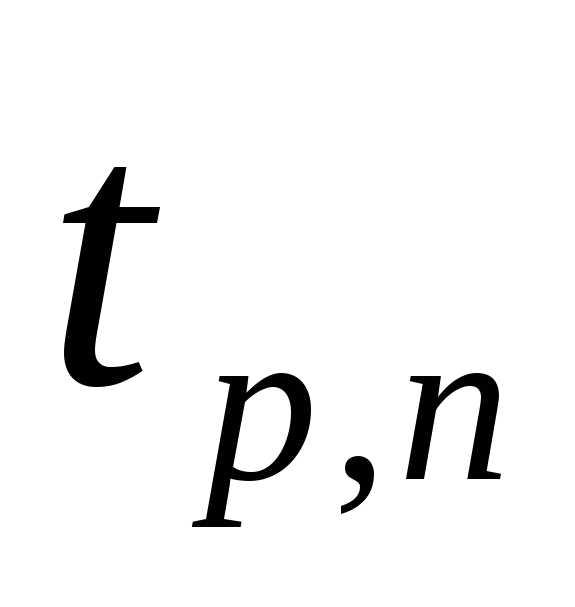
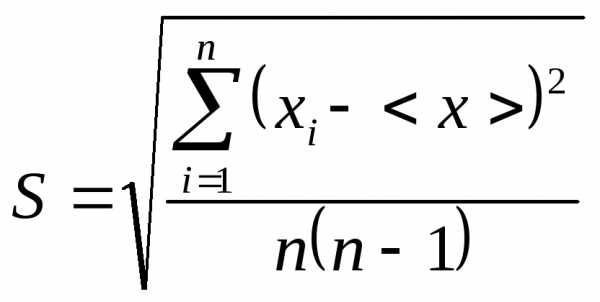
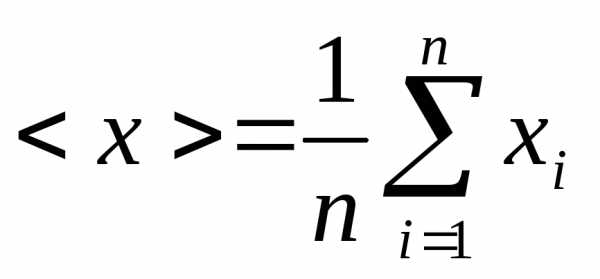
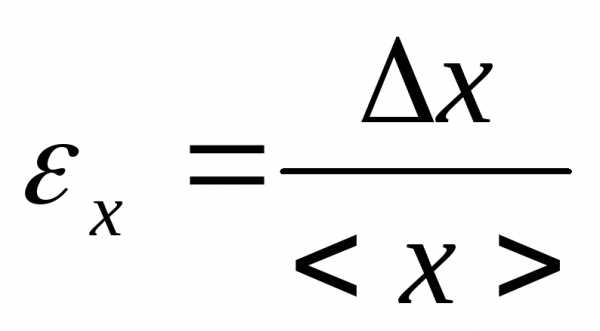
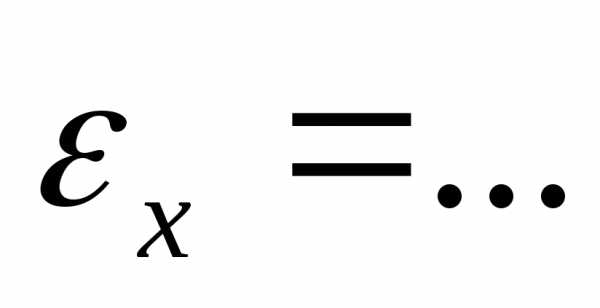 ,
,