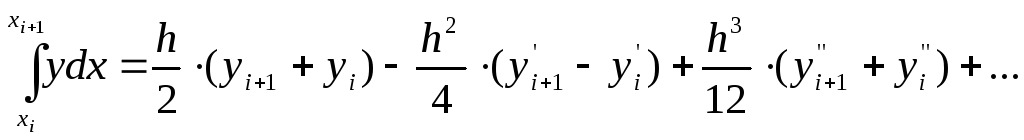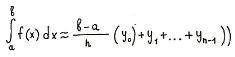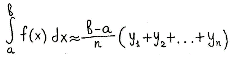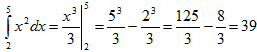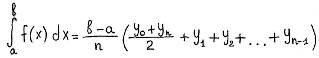Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.
Метод трапеций
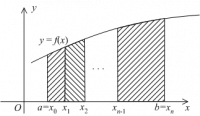
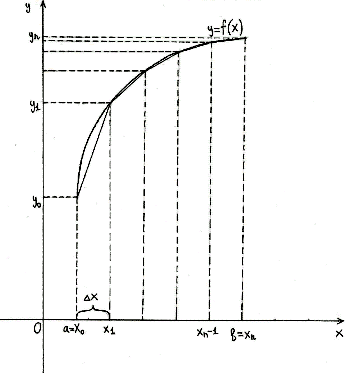
Предположим, что нам нужно приближенно вычислить определенный интеграл ∫abf(x)dx, подынтегральная функция которого y=f(x) непрерывна на отрезке [a;b]. Для этого разделим отрезок [a;b] на несколько равных интервалов длины h точками a=x0<x1<x2<…<xn-1<xn=b. Обозначим количество полученных интервалов как n.
Найдем шаг разбиения: h=b-an. Определим узлы из равенства xi=a+i·h, i=0, 1,…, n.
На элементарных отрезках рассмотрим подынтегральную функцию xi-1; xi, i=1, 2,.., n.
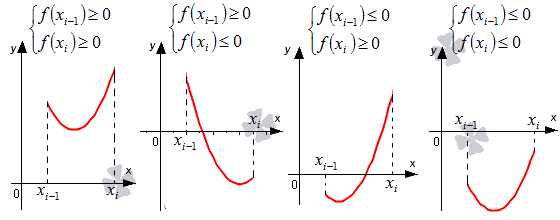
При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:
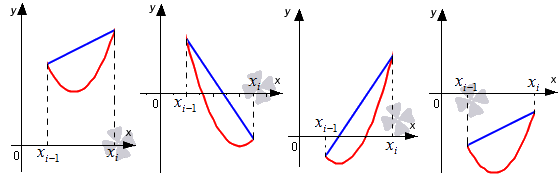
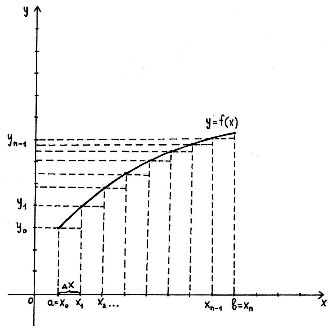
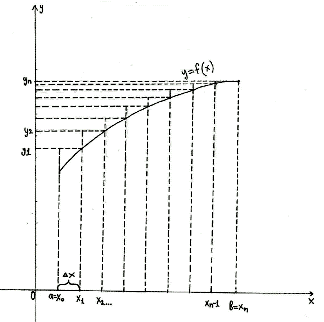
Выделим отрезки xi-1; xi, i=1, 2,…, n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.
Возьмем выражение f(xi-1)+f(xi)2·h в качестве приближенного значения интеграла ∫xi-1xif(x)dx. Т.е. примем ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.
Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.
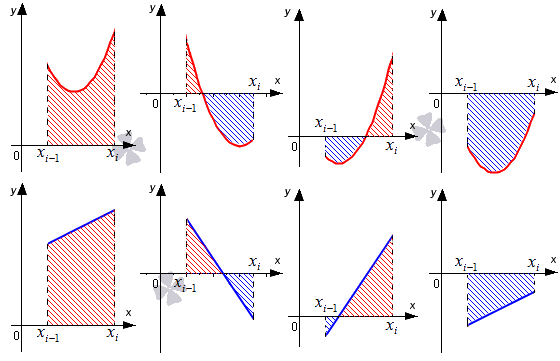
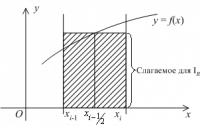
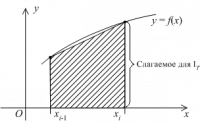
Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями f(xi-1), f(xi) высотой h. В четвертом из рассматриваемых нами случаев заданный интеграл ∫xi-1xf(x)dx приближенно равен площади трапеции с основаниями -f(xi-1), -f(xi) и высотой h, которую необходимо взять со знаком «-». Для того, чтобы вычислить приближенное значение определенного интеграла ∫xi-1xif(x)dx во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.
Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫abf(x)dx в виде суммы интегралов вида ∫xi-1xif(x)dx на каждом элементарном отрезке и в последующей приближенной замене ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.
Формула метода трапеций
Вспомним пятое свойство определенного интеграла: ∫abf(x)dx=∑i=1n∫xi-1xif(x)dx. Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫xi-1xif(x)dx подставить их приближенные значения: ∫xi-1xif(x)dx=∑i=1n∫xi-1xif(x)dx≈∑i=1nf(xi-1)+f(xi)2·h==h2·(f(x0)+f(x1)+f(x1)+f(x2)+f(x2)+f(x3)+…+f(xn))==h2·f(x0)+2∑i=1n-1f(xi)+f(xn)⇒∫xi-1xif(x)dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)
Формула метода трапеций: ∫xi-1xif(x)dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)
Оценка абсолютной погрешности метода трапеций
Оценим абсолютную погрешность метода трапеций следующим образом:
δn≤maxx∈[a;b]f”(x)·n·h312=maxx∈[a;b]f”(x)·b-a312n2
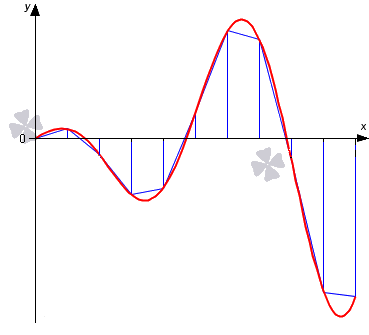
Графическая иллюстрация метода трапеций
Графическая иллюстрация метода трапеций приведена на рисунке:
Примеры вычислений
Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов. Особое внимание уделим двум разновидностям заданий:
- вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
- нахождение приближенного значения определенного интеграла с оговоренной точностью.
При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n.
Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0,01, то промежуточные вычисления мы проводим с точностью до 0,0001 или 0,00001. При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.
Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.
Итак, ∫057dxx2+1=7arctg(x)05=7arctg 5≈9,613805.
Вычислим по методу трапеций определенный интеграл ∫057×2+1dx для n равным 10.
Решение
Формула метода трапеций имеет вид ∫xi-1xif(x)dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)
Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h=b-an , определить узлы xi=a+i·h, i=0, 1,…, n, вычислить значения подынтегральной функции f(x)=7×2+1.
Шаг разбиения вычисляется следующим образом: h=b-an=5-010=0.5. Для вычисления подынтегральной функции в узлах xi=a+i·h, i=0, 1,…, n будем брать четыре знака после запятой:
i=0: x0=0+0·0.5=0⇒f(x0)=f(0)=702+1=7i=1: x1=0+1·0.5=0.5⇒f(x1)=f(0.5)=70,52+1=5,6…i=10: x10=0+10·0.5=5⇒f(x10)=f(5)=752+1≈0,2692
Внесем результаты вычислений в таблицу:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | 0 | 0.5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| f(xi) | 7 | 5,6 | 3,5 | 2,1538 | 1,4 | 0,9655 | 0,7 | 0,5283 | 0,4117 | 0,3294 | 0,2692 |
Подставим полученные значения в формулу метода трапеций: ∫057dxx2+1≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)==0,52·7+2·5,6+3,5+2,1538+1,4+0,9655+0,7+0,5283+0,4117+0,3294+0,2692=9,6117
Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница. Полученные значения совпадают до сотых.
Ответ: ∫057dxx2+1=9,6117
Вычислим по методу трапеций значение определенного интеграла ∫12112×4+13x-160dx с точностью до 0,01.
Решение
Согласно условию задачи a = 1; b = 2, f(x)=112×4+13x-160; δn≤0,01.
Найдем n, которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δn≤maxx∈[a;b]f”(x)·(b-a)312n2. Сделаем мы это следующим образом: мы найдем значения n, для которых будет выполняться неравенство maxx∈[a;b]f”(x)·(b-a)312n2≤0,01. При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.
Для начала найдем наибольшее значение модуля второй производной функции на отрезке [1; 2].
f'(x)=112×4+13x-160’=13×3+13⇒f”(x)=13×3+13’=x2
Вторая производная функция является квадратичной параболой f”(x)=x2. Из ее свойств мы знаем, что она положительная и возрастает на отрезке [1; 2]. В связи с этим maxx∈[a;b]f”(x)=f”(2)=22=4.
В приведенном примере процесс нахождения maxx∈[a;b]f”(x) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения maxx∈[a;b]f”(x).
Подставим полученное значение в неравенство maxx∈[a;b]f”(x)·(b-a)312n2≤0,01
4·(2-1)312n2≤0,01⇒n2≥1003⇒n≥5,7735
Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.
Вычислим шаг: h=b-an=2-16=16.
Найдем узлы xi=a+i·h, i=1, 0,…, n, определим значения подынтегральной функции в этих узлах:
i=0: x0=1+0·16=1⇒f(x0)=f(1)=112·14+13·1-160=0,4i=1: x1=1+1·16=76⇒f(x1)=f76=112·764+13·76-160≈0,5266…i=6: x10=1+6·16=2⇒f(x6)=f(2)=112·24+13·2-160≈1,9833
Результаты вычислений запишем в виде таблицы:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| xi | 1 | 76 | 43 | 32 | 53 | 116 | 2 |
| fxi | 0,4 | 0,5266 | 0,6911 | 0,9052 | 1,1819 | 1,5359 | 1,9833 |
Подставим полученные результаты в формулу трапеций:
∫12112×4+13x-160dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)==112·0,4+2·0,5266+0,6911+0,9052+1,1819+1,5359+1,9833≈1,0054
Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:
∫12112×4+13x-160dx=x560+x26-x6012=1
Как видим, полученной точности вычислений мы достигли.
Ответ: ∫12112×4+13x-160dx≈1,0054
Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.
Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как In. Выберем произвольное число n. По формуле метода трапеций вычислим исходный интеграл при одинарном (n=10) и удвоенном (n=20) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I20-I10.
Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I20-I10<δn, то мы прекращаем вычисления и выбираем значение I20 , которое можно округлить до требуемого порядка точности.
Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов (n=40).
Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.
Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.
Необходимо вычислить определенный интеграл ∫02xexdx по методу трапеций с точностью до 0,001.
Решение
Возьмем n равное 10 и 20. По формуле трапеций получим I10=8,4595380, I20=8,4066906.
I20-I10=8,4066906-8,4595380=0,0528474>0,001, что требует продолжения вычислений.
Возьмем n равное 40: I40=8,3934656.
I40-I20=8,3934656-8,4066906=0,013225>0,001, что также требует продолжения вычислений.
Возьмем n равное 80: I80=8,3901585.
I80-I40=8,3901585-8,3934656=0,0033071>0,001, что требует проведения еще одного удвоения числа узлов.
Возьмем n равное 160: I160=8,3893317.
I160-I80=8,3893317-8,3901585=0,0008268<0,001
Получить приближенное значение исходного интеграла можно округлив I160=8,3893317 до тысячных: ∫02xexdx≈8,389.
Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫02xexdx=ex·(x-1)02=e2+1≈8,3890561. Требуемая точность достигнута.
Ответ: ∫02xexdx≈8,389
Погрешности
Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.
Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:
δn≤maxx∈[a;b]f”(x)n·h312=maxx∈[a;b]f”(x)·b-a312n2δn≤maxx∈[a;b]f”(x)n·h324=maxx∈[a;b]f”(x)·b-a324n2.
Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.
В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.
Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.
При использовании
метода трапеций возникает ошибка, равная
сумме площадей между кривой y=f(x)
и хордами, соединяющими точки yi
и yi+1.
Для оценки этой
погрешности можно разложить функцию
y=f(x)
в ряд Тейлора в точках xi
и xi+1.
Это разложение позволит получить
уравнение исходной кривой в виде, удобном
для сравнения точного значения интеграла
с приближенным, вычисленным по методу
трапеций.
Разложим функцию
y=f(x)
в ряд Тейлора в окрестности точки x=xi:
Аналогично, разлагая
функцию в ряд в окрестности точки xi+1
= xi
+ h :
Обе эти формулы
справедливы, но ни одна из них в отдельности
не позволяет получить нужный результат.
Поэтому берут среднее значение из обеих
формул:
Интегрируя y
dx от xi
до xi+1
,
получают:
Это выражение
представляет собой оценку истинного
значения интеграла. Оценка может быть
сделана как угодно точной, потому что
можно взять сколь угодно большое
количество членов в разложении функции
в ряд Тейлора.
Правило трапеций
получается, если в этой формуле отбросить
все члены, содержащие h
в степенях выше первой. Поэтому можно
записать:
где
Для малых h
первый член гораздо больше всех остальных,
поэтому можно предположить, что ошибка
как раз им и определяется. Поэтому можно
записать:
где константу К
необходимо определить. Конечно, это
будет только некоторое приближение,
основанное на допущении о постоянстве
К;
такое приближение справедливо только
до тех пор, пока y’’
и производные высших порядков не
изменяются сильно между xi
и xi+1.
При определении
К
необходимо помнить, что формула
справедлива для любой
функции. Поэтому можно взять любую
функцию, для которой погрешность при
интегрировании по методу трапеций не
будет равна нулю. Результат будет
справедлив для всех функций. Если взять
функцию y
= x, то можно
легко убедиться, что погрешность равна
нулю, т.е. метод трапеций дает точный
результат при интегрировании линейных
функций.
Возьмем y
= x2.
В этом случае:
Но, с другой стороны,
если в формулу
подставить yi
= xi2
и yi+1
= (xi
+
h)2,
то можно получить:
Приравнивая два
последних уравнения, легко получить:
Но так как y’
= 2x, то
можно получить
Поэтому для К
получают
И окончательно
Полную погрешность
можно оценить из соотношения
где yb’
равно
значению df/dx
при x
= b и ya’
равно
значению df/dx
при x
= a.
Чаще погрешность
для метода трапеций выражают с помощью
несколько преобразованной формулы. На
основании теоремы о среднем в интегральном
исчислении
,
где a £
x
£
b
можно, положив ,
записать f(x)
= y’(x). Отсюда
yb
– ya
= (b-a)×y’(x)
После еще одного
дифференцирования можно получить
где a
£
x
£
b, так что
Более того, если
в интервале a
£
x
£
b имеется
M = max { y’’(x)
}, то
10.4 Метод парабол
В этом методе
вершины каждых трех ординат соединяются
дугами квадратичных парабол, оси которых
параллельны оси y.
Таким образом, вместо двух прямоугольных
трапеций рассматривают одну элементарную
трапецию, ограниченную параболической
дугой. Исходя из этого можно видеть, что
число разбиений n
в методе Симпсона должно быть четным.
Площади полученных
трапеций можно обозначить как s12,
s34,
… , sn-1,n.
Рассмотрим первую из этих трапеций. Для
упрощения вычислений можно перенести
ось ординат параллельно самой себе так,
чтобы она шла вдоль ординаты yo
. Ясно, что от этого величина площади не
изменится.
Уравнение квадратичной
параболы , ось которой параллельна
оси y, есть
y = A0
+ A1*x
+ A2*x2
Чтобы парабола
проходила через точки подынтегральной
кривой (xo,yo),
(x1,y1),
(x2,y2)
нужно правильно подобрать коэффициенты
А0,
А1
и А2:
Так как xo
= 0, x1
= h и
x2
= 2h, то,
подставив эти значения в приведенное
выше уравнение можно получить:
После решения этой
системы можно найти:
;
;
Площадь s12
определяется
интегралом:
Подставив найденные
значения А0,
А1
и
А2
в это уравнения
и приведя свободные члены, получим:
Аналогично
. . . . . . . .
. .
Следовательно,
Отсюда можно найти
формулу метода парабол (или метода
Симпсона):
Или, в более
компактном виде:
где cj
= 1, 4,
2,
4,
2,
… ,2,
4,
1 .
Предельная
абсолютная погрешность метода Симпсона:
, где
Пример 1:
вычислить приближенно по формуле
Симпсона
с точностью до 0.001.
Решение:
нужно вычислить какой шаг h
нужно взять для достижения заданной
точности. Для этого вычисляют
;
;
;
Наибольшее значение
½f
IV(x)½
на отрезке [ 0;1 ] достигается в точке х=0:
½f
IV(x)½
= 3. Значит:
Так как эта
погрешность должна быть меньше 0.001, то
h4/60
£
0.001, т.е. h4
£
0.06. Можно
принять h =
0.5 (если h =
0.5, то h4
= 0.0625), т.е. несколько больше нужной
величины. Итак, для достижения требуемой
точности достаточно разбить интервал
пополам.
Вычисления нужно
провести с одним запасным знаком:
Округляя последний
член можно получить I
»
1.148 .
Можно вычислить точное значение этого
интеграла по формуле Ньютона-Лейбница:
Таким образом, значение этого интеграла,
вычисленное по методу Симпсона, имеет
четыре верных знака после запятой.
Если вычисление
четвертой производной подынтегральной
функции затруднительно, то для оценки
погрешности вычисления интеграла по
методу Симпсона можно использовать
следующую стратегию.
-
Пусть интеграл
вычислен по формуле Симпсона дважды
при различных значениях h.
Пусть I1,
h1,
d1
– соответственно обозначают найденный
результат, значение шага и погрешность
первого вычисления, а I2,
h2,
d2
– то же при втором вычислении. -
Согласно формуле
оценки погрешности, имеем

или
-
Отсюда, в частности
если h2
= h1/2,
то получают, что d1
= 16*d2
и для точного
значения интеграла S
при двух вычислениях с шагом h1
и
h2
= h1/2,
имеют
S = I1
+ d1
= I1
+ 16*d2
S = I2
+ d2
-
Отсюда, отняв
верхнее уравнение от нижнего, находят
,
или, применяя более общие выражения,
.
Следовательно,
если по формуле Симпсона вычислить
интеграл
разделив отрезок [
a,b ] первый
раз на n
частей, а второй – на 2n
частей, то для второго результата I2n
погрешность приблизительно будет
равняться 1/15
разности результатов I2n
и
In
.
Этот способ называют
оценкой погрешности формулы Симпсона
по методу удвоения шага вычислений.
Пример 2:
вычислить по формуле Симпсона
, приняв n =
8. Вычисления
вести с шестью знаками после запятой.
Оценить погрешность полученного
результата, пользуясь способом удвоения
шага вычислений; сравнить результат с
истинным значением интеграла, взяв
последнее с одним запасным (седьмым)
знаком.
Решение:
находим значение подынтегральной
функции:
|
I |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
x |
0 |
0.125 |
0.250 |
0.375 |
0.500 |
0.625 |
0.750 |
0.875 |
1 |
|
f(x) |
1.000000 |
0.984625 |
0.941176 |
0.876712 |
0.800000 |
0.719101 |
0.640000 |
0.566389 |
0.500000 |
Нужно подставить
эти значения в формулу Симпсона при h1
= 0.250 и h2
= 0.125:
Отсюда
Таким образом, все
шесть знаков I2n
должны быть точными.
Истинное значение
интеграла равно:
что подтверждает
полученный результат.
Рассмотренные
методы прямоугольников, трапеций и
парабол, являются частным случаем (при
m=0,
m=1
и m=2)
общей квадратурной
формулы Ньютона-Котеса,
которую получают, заменив подынтегральную
функцию полиномом m-ой
степени. Кроме формулы Ньютона-Котеса
есть ряд других квадратурных функций.
Наиболее точной из них является формула
Гаусса,
которая при n
точках промежутка интегрирования
обеспечивает совершенно точные результаты
для полинома (2n+1)-й
степени. Точки деления в формуле Гаусса
берут не на равных расстояниях одна от
другой, а выбирают по определенному
правилу.
Соседние файлы в папке 2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Введение
- 2 Метод прямоугольников
- 2.1 Формула прямоугольников на частичном отрезке и ее погрешность
- 2.2 Составная формула прямоугольников и ее погрешность
- 2.3 Применимость метода к функции, заданной в конечном числе точек
- 3 Метод трапеций
- 3.1 Формула трапеций на частичном отрезке и ее погрешность
- 3.2 Составная формула трапеций и ее погрешность
- 3.3 Применимость метода к функции, заданной в конечном числе точек
- 4 Числовой пример
- 5 Рекомендации программисту
- 5.1 Оценка погрешности
- 5.2 Пример программы на языке C++
- 6 Заключение
- 7 Список литературы
Введение
Рис.1
Задача численного интегрирования состоит в нахождении приближенного значения интеграла
( 1 )
где – заданная и интегрируемая на отрезке
функция.
Если один или оба предела равны или
, то с помощью трюков с заменой переменных можно осуществить переход к конечному отрезку от луча или всей числовой прямой.
Введем на сетку с переменным шагом
, т.е. множество точек
, и представим интеграл (1) в виде суммы интегралов по частичным отрезкам:
( 3 )
Для построения формулы численного интегрирования на всем отрезке достаточно построить квадратурную формулу для интеграла
( 4 )
на частичном отрезке и воспользоваться свойством (3).
Метод прямоугольников
Формула прямоугольников на частичном отрезке и ее погрешность
Рис.2
Заменим интеграл (3) выражением , где
Тогда получим формулу
( 5 )
которая называется формулой прямоугольников на частичном отрезке
Погрешность метода (5) определяется величиной
которую легко оценить с помощью формулы Тейлора. Действительно, запишем в виде
( 6 )
и воспользуемся разложением
где . Тогда из (6) получим
Обозначая , оценим
следующим образом:
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка
( 7 )
т.е. формула имеет погрешность при
.
Заметим,что оценка (7) является неулучшаемой, т.е. существует функция , для которой (7) выполняется со знаком равенства. Действительно, для
имеем
и
Составная формула прямоугольников и ее погрешность
Суммируя равенства (5) по от
до
, получим составную формулу прямоугольников
( 8 )
Погрешность этой формулы
равна сумме погрешностей по всем частичным отрезкам,
Отсюда, обозначая , получим
( 9 )
т.е. погрешность формулы прямоугольников на всем отрезке есть велицина .
Видим, что квадратурная формула имеет второй порядок точности.
Применимость метода к функции, заданной в конечном числе точек
Заметим, что метод прямоугольников в том виде,в котором он описан выше, не применим в общем случае к функциям,значения которых мы знаем в конечном числе точек, так как, например, мы не всегда можем разбить отрезкок интегрирования на подотрезки, серединами которых являются точки,в которых нам известно значение функции.
Метод трапеций
Формула трапеций на частичном отрезке и ее погрешность
Рис.3
На частичном отрезке эта формула имеет вид
( 10 )
и получается путем замены подынтегральной функции интерполяционным многочленом первой степени,постоенным по узлам
, т.е. функцией
Для оценки погрешности достаточно вспомнить,что
Отсюда получим
и,следовательно,
( 11 )
Оценка (11) неулучшаема, так как в ней достигается равенство, например, для .
Составная формула трапеций и ее погрешность
Составная формула трапеций имеет вид
( 12 )
где .
Погрешность этой формулы оценивается следующим образом:
( 13 )
где
Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности,, но ее погрешность оценивается величиной в два раза большей.
Применимость метода к функции, заданной в конечном числе точек
В отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как мы всегда можем взять в качесве узлов интегрирования данные точки.
Числовой пример
Вычислим по формулам прямоугольников и трапеций при интеграл
( 14 )
В данном случае
Зная точный ответ (14), найдем погрешности
( 15 )
Вторая производная функции на отрезке
отрицательна, ее модуль не превышает единицы:
. Величина погрешностей (15) удовлетворяет неравенствам (9) и (13):
Рекомендации программисту
Оценка погрешности
Величина погрешности численного интегрирования зависит как от шага сетки , так и от гладкости подынтегральной функции
. Например, в оценку (11), наряду с
, входит величина
которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке . Для этого прежде всего надо уметь апостериорно, т.е. после проведения расчета, оценивать погрешность.
Апостериорную оценку погрешности можно осуществить методом Рунге. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности , т.е.
. Тогда
откуда получим
( 16 )
( 17 )
Пусть используется составная квадратурная формула
где – квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций). Проведем на каждом частичном отрезке
все вычисления дважды, один раз – с шагом
и второй раз – с шагом
и оценим погрешность по правилу Рунге (17):
Пример программы на языке C++
- Исходный текст программы
В программе интеграруемая функция задается в функции . В данном примере интегрируется логарифм и эта функция выглядит так:
double function(double x)
{
return log(x);
}
Функция реализует метод прямоугольников, а
– метод трапеций.
Эти функции имеют следующие параметры:
double trapezium(double left, double right, double step)
double rectangles(double left, double right, double step)
где left - левый предел интегрирования,
right - правй предел интегрирования,
step - шаг интегрирования.
Заключение
Методы прямоугольников и трапеций являются одними из простейших методов интегрирования (запрограммировать их не составляет особого труда). Но эти методы имеют лишь второй порядок точности,в то время как есть методы более высоких порядков.
Если же сравнивать эти два метода между собой, то метод прямоугольников, который относится к методам Гаусса – Кристоффеля, является точнее метода трапеций, относящегося к методам Ньютона – Котеса. Но в то же время метод трапеций может применяться с произвольным шагом, в отличие от метода прямоугольников, который, как мы увидели, не применим, например, к функциям,заданным в конечном числе точек.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- А.А.Самарский. Введение в численные методы М.: Наука, 1982.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Метод трапеций — это метод приближённого интегрирования, полезный в тех случаях, когда нет возможности найти первообразную функции и вычислить интеграл через неё.
Помимо метода трапеций существуют другие методы приближённого интегрирования, например, метод прямоугольников и метод парабол.
Метод трапеций по сути похож на метод прямоугольников, но при этом он менее точный, чем метод средних прямоугольников.
Сущность метода трапеций
Рисунок 1. Метод трапеций для вычисления интегралов
Предположим, требуется вычислить интеграл от функции $f(x)$ на отрезке $left[a;bright]$.
Также как и в случае с методом прямоугольников разобьём график кривой на элементарные сегменты c помощью точек с абсциссами $x_i$, и получим ломаную с вершинами в точках $(x_i;y_i)$, при этом $y_i=f(x_i)$, а $i$ принимает значения от $0$ до $n-1$.
Для этого выберем количество отрезков, на которые разбиваем исследуемый интервал и воспользуемся формулой для вычисления длины одного такого отрезка, которую мы уже использовали для метода прямоугольников:
$∆x=frac{b-a}{n}$
Для вычисления по методу трапеций между собой соединяются две рядом стоящие точки разбиения, в результате образуя элементарные сегменты. Как видно дальше, значение функции $f(x)$ берётся на границах исследуемого отрезка.
Площадь первой такой трапеции составит:
$S_1=frac{b-a}{n} cdot frac{y_1+y_2}{2}$,
а площадь $i$-ой трапеции составит:
$S_i=frac{b-a}{n} cdot frac{y_{i-1}+y_i}{2}$,
Сложим площади всех элементарных трапеций:
$int^b_a f(x)dx =frac{b-a}{n}(frac{y_0+y_n}{2}+y_1+y_2+…+y_{n-1})$
Таким образом, площади всех элементарных трапеций, сложенные вместе, являются приближённой площадью фигуры, ограниченной линиями $x=a$, $x=b$, осью абсцисс и графиком кривой $f(x)$.
«Метод трапеций» 👇
Определение 1
Формула для приближённого вычисления интеграла методом трапеций:
$int_a^b f(x)dx ≈frac{x_i-x_{i-1}}{2} cdot(f(x_0)+2sum^{n-1}_{i=1}f(x_i)+f(x_n))$
Погрешность при использовании метода трапеций
Погрешность метода составляет:
Определение 2
$|δ_n|≤max_{x inleft[a;bright]}|f’’(x)| cdot frac{ncdot(frac{x_i-x_{i-1}}{2})^3}{12}=max_{x inleft[a;bright]}|f’’(x)| cdot (frac{(b-a)^3}{12n^2})$
Как видно из вышеприведённой формулы, здесь погрешность несколько больше чем погрешность метода средних прямоугольников, однако, не всегда удобно использовать именно этот метод. Метод трапеции удобен если самого графика функции нет, но есть значения, которые принимает функция $f(x)$ в точках разбиения. В случаях же когда всё же есть график, целесообразнее пользоваться методом средних прямоугольников.
Также при невозможности определения максимума функции сложно определить вычисляемую погрешность. В этом случае можно прибегнуть к следующему: сначала провести численное интегрирование методом трапеций для $n=10$, а затем на том же отрезке провести вычисление при $n=20$. Если разница двух полученных значений интегралов составляет меньше чем требуемая по условию погрешность, то в качестве ответа выбирают приближённое значение интеграла при $n=20$, а вычисления заканчивают. В противном случае если требуемая точность не достигнута, продолжают удваивать дальше количество отрезков.
Пример 1
Посчитайте интеграл $int_1^2 frac{dx}{x}=ln2$ с точностью до $0, 001$, используя метод трапеций.
Разобьём нашу функцию на 10 равных сегментов.
В начале оценим погрешность вычисления:
$|δ_n|≤max_{xin left[1;2right]}|(frac{1}{x})’’| cdot frac{(2-1)^3}{12 cdot 10^2}$
В данном случае погрешность составляет $|δ_n|≤0.00008$, следовательно, для разбиения можно использовать 10 сегментов.
Также как и с методом прямоугольников, разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=frac{2-1}{10}=0,1$ и вычислим значение подынтегральной функции $y(x)=frac{1}{x}$ на границах каждого отрезка:
$x_0=1,0;y_0=1,0000;$
$x_1=1,1; y_1=0,9091;$
$x_2=1,2; y_2=0,8333;$
$x_3=1,3; y_3=0,7692;$
$x_4=1,4; y_4=0,7143;$
$x_5=1,5; y_5=0,6667;$
$x_6=1,6; y_6=0,6250;$
$x_7=1,7; y_7=0,5882;$
$x_8=1,8; y_8=0,5556;$
$x_9=1,9; y_9=0,5263;$
$x_{10}=2,0; y_{10}=0,5000;$
Сумма всех вычисленных значений функции $f(x)$ от первого до девятого включительно составит $6.1877$, а само значение интеграла составит:
$int_1^2 frac{dx}{x}=0,1 cdot (frac{1,5000}{2})+ 6,1877=0.69377$
Данное значение отвечает необходимой точности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Учебно-воспитательные задачи:
- Дидактическая цель. Познакомить учащихся с методами
приближённого вычисления определённого интеграла. - Воспитательная цель. Тема данного занятия имеет большое
практическое и воспитательное значение. Наиболее просто к идее численного
интегрирования можно подойти, опираясь на определение определённого
интеграла как предела интегральных сумм. Например, если взять какое-либо
достаточно мелкое разбиение отрезка [a; b] и построить для
него интегральную сумму, то её значение можно приближённо принять за
значение соответствующего интеграла. При этом важно быстро и правильно
производить вычисления с привлечением вычислительной техники.
Основные знания и умения. Иметь понятие о приближённых методах
вычисления определённого интеграла по формулам прямоугольников и трапеций.
Обеспечение занятия
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод
прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора). - Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится
вычислять определённые интегралы, для которых невозможно найти первообразную. В
этом случае применяют приближённые методы вычисления определённых интегралов.
Иногда приближённый метод применяют и для “берущихся” интегралов, если
вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого
вычисления интеграла заключается в том, что кривая
заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.
Последовательность занятия.
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
План занятия
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных
методов интегрирования, геометрический смысл определённого интеграла.
- Выполнение практической работы.
Решение многих технических задач сводится к вычислению определённых
интегралов, точное выражение которых сложно, требует длительных вычислений и не
всегда оправдано практически. Здесь бывает вполне достаточно их приближённого
значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение
которой неизвестно. В этом случае можно заменить данную линию более простой,
уравнение которой известно. Площадь полученной таким образом криволинейной
трапеции принимается за приближённое значение искомого интеграла.
Простейшим приближённым методом является метод прямоугольников. Геометрически
идея способа вычисления определённого интеграла по формуле прямоугольников
состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой
площадей прямоугольников, одна сторона которых равна
, а друга –
.
Если суммировать площади прямоугольников, которые показывают площадь
криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
[Рисунок1]
то получим формулу:
Если с избытком
[Рисунок2],
то
Значения у0, у1,…, уn находят из
равенств ,
к
=
0, 1…,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла
, нужно:
- разделить отрезок интегрирования [a, b] на n равных частей
точками х0=а,
х1, х2,…, х
n
-1,
х
n
=
b
; - вычислить значения подынтегральной функции
в
точках деления, т.е. найтиу
0
=
f (x0),
у
1
=
f (x1),
у
2
=
f (x2),
у
n
-1
=
f (xn-1),
у
n
=
f (xn)
; - воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Пример 1. Вычислить по формуле прямоугольников
. Найти
абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных
частей. Тогда а
=
0,
b =
3
,
х
k = a + k
х
х0 = 2 + 0
= 2
х1 = 2 + 1
= 2,5
х2 = 2 + 2
=3
х3 = 2 + 3
= 3
х4 = 2 + 4
= 4
х5 = 2 + 5
= 4,5
f (x0) = 22 = 4
f
(x
1
)
= 2
,5
2
=
6,25
f
(x
2
)
=
32
=
9
f
(x
3
)
=
3,52
=
12,25
f
(x
4
)
=
42
=
16
f
(x
5
)
=
4,52
=
20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти
точное значение интеграла:
Вычисления проходили долго и мы получили довольно-таки грубое округление.
Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться
техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х
[2
;5
]
с заданным шагом
х = 0,1.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (2). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (2,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А32, до значения х=5). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской
раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется
4. Теперь необходимо скопировать функцию из ячейки В2.
Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В33 может быть найдено приближённое значение интеграла.
Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции (f(x)).
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция – функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В
ячейке В33 появляется приближённое значение искомого интеграла с недостатком
(37,955) .
Сравнивая полученное приближённое значение с истинным значением интеграла (39),
можно видеть, что ошибка приближения метода прямоугольников в данном случае
равна
=
|39 – 37
,
955| = 1
,045
Пример 2. Используя метод прямоугольников, вычислить
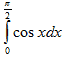
заданным шагом х =
0,05.
Решение:
- Для нахождения определённого интеграла значения подынтегральной функции
f(x) должны быть введены в рабочую таблицу Excel в диапазоне
с
заданным шагомх
= 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
интегрирования (0). В ячейку А3 вводится второе значение аргумента –
левая граница диапазона плюс шаг построения (0,05). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=1,55). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2. Здесь должно оказаться значение косинуса, соответствующее
значению аргумента в ячейке А2. Для получения значения косинуса
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку
Вставка функции (
f
х
)
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция – функцию COS.
Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя
указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле
вправо, чтобы открыть столбец данных (А). Указываем значение
аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В
ячейке В2 появляется 1. Теперь необходимо скопировать функцию из
ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В
результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла.
Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции(
(
f
х
))
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция – функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В
ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).
Сравнивая полученное приближённое значение с истинным значением интеграла
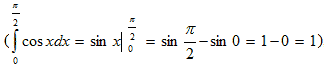
видеть, что ошибка приближения метода прямоугольников в данном случае равна
Метод трапеций обычно даёт более точное значение интеграла, чем метод
прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций
и приближённое значение определённого интеграла находится как сумма площадей
трапеций
[Рисунок3]
Пример 3. Методом трапеций найти
с шагом
х = 0,1.
Решение.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (0). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (0,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=3,1). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение (в примере синуса). Для этого табличный курсор
необходимо установить в ячейку В2. Здесь должно оказаться значение синуса,
соответствующее значению аргумента в ячейке А2. Для получения значения
синуса воспользуемся специальной функцией: нажимаем на панели инструментов
кнопку Вставка функции f(x). В появившемся диалоговом окне
Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические.
Справа в поле Функция – функцию SIN. Нажимаем кнопку ОК.
Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле
окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец
данных (А). Указываем значение аргумента синуса щелчком мыши на
ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
формулу в диапазон В2:В33. В результате должна быть получена таблица данных
для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла
по методу трапеций. Для этого в ячейку В34 вводим формулу =
0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели
инструментов кнопки Вставка функции (f(x)). В появившемся
диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем
Математические. Справа в поле Функция – функцию Сумм. Нажимаем кнопку ОК.
Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон
суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке
В34 появляется приближённое значение искомого интеграла с недостатком (1,997)
.
Сравнивая полученное приближённое значение с истинным значением интеграла
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
- Решение упражнений.
- Вычислить
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить
разделив отрезок [0;4] на 40 равных частей. - Вычислить
разделив отрезок [0;8] на 40 равных частей. - Вычислить