Как найти погрешность при делении

Погрешность произведения

Пусть в результате измерений получено:

$$ x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x, y gt 0 $$

Найдём границы для произведения этих величин: z = xy

$$ {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow (x_0- Delta x)(y_0-Delta y) le xy le (x_0+ Delta x)(y_0+ Delta y) Rightarrow $$

$$ Rightarrow x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y+ Delta x Delta y) $$

(О правилах умножения двух неравенств, см. §36 данного справочника).

Абсолютные погрешности $Delta x ≪ x_0, Delta y≪y_0$ заметно меньше $x_0$ и $ y_0$, поэтому будем считать, что произведение $Delta x Delta y approx 0$, и им можно пренебречь. Получаем:

$$ x_0 y_0-( Delta xy_0+x_0 Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y) $$

$$ z = z_0 pm Delta z: z_0 = x_0 y_0, quad Delta z = Delta xy_0+x_0 Delta y $$

$$ δ_z = frac{Delta z}{z_0} = frac{Delta xy_0+x_0 Delta y}{x_0 y_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$

$$ δ_{xy} = δ_x+δ_y $$

При умножении приближенных величин их относительные погрешности складываются.

Погрешность степени

Пусть в результате измерений получено: $x = x_0 pm Delta x, x gt 0$

Тогда, для квадрата x из выражения для относительной погрешности произведения получаем: $δ_{x^2} = δ_x+δ_x = 2δ_x$.

Для куба: $δ_{x^3 } = δ_{x^2}+δ_x = 2δ_x+δ_x = 3δ_x$.

Для произвольной степени n:

$$ δ_{x^n} = n δ_x $$

При возведении приближенной величины в натуральную степень n, её относительная погрешность увеличивается в n раз.

Погрешность частного

Пусть в результате измерений получено:

$$x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x,y gt 0 $$

Найдём границы для частного этих величин: $z = frac{x}{y}$

$$ {left{ begin{array}{c} x_0- Delta x le x le x_0 + Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow {left{ begin{array}{c}x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0-Delta y} ge frac{1}{y} ge frac{1}{y_0+ Delta y} end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0+ Delta y} le frac{1}{y} le frac{1}{y_0- Delta y} end{array} right.} Rightarrow frac{x_0- Delta x}{y_0+ Delta y} le frac{x}{y} le frac{x_0+ Delta x}{y_0- Delta y} Rightarrow $$

$$ Rightarrow frac{ (x_0- Delta x)(y_0- Delta y)}{(y_0+ Delta y)(y_0- Delta y)} le frac{x}{y} le frac{(x_0+ Delta x)(y_0+ Delta y)}{(y_0- Delta y)(y_0+ Delta y)} Rightarrow $$

$$ Rightarrow frac{x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y)}{y_0^2- Delta y^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y+ Delta x Delta y)}{y_0^2- Delta y^2} $$

О правилах умножения двух неравенств и обращения положительных сторон, см. §36 данного справочника.

Считаем произведения и квадраты абсолютных погрешностей малыми величинами $Delta x Delta y approx 0, quad Delta y^2 approx 0$, которыми можно пренебречь. Получаем:

$$ frac{x_0 y_0-( Delta xy_0+x_0 Delta y)}{y_0^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y)}{y_0^2} $$

$$frac{x_0}{y_0} – left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) le frac{x}{y} le frac{x_0}{y_0} + left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) $$

$$ z = z_0 pm Delta z: z_0 = frac{x_0}{y_0}, Delta z = frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}$$

$$ δ_z = frac{Delta z}{z_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) : frac{x_0}{y_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) cdot frac{y_0}{x_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$

$$ δ_{frac{x}{y}} = δ_x+δ_y $$

При делении приближенных величин их относительные погрешности складываются.

Примеры

Пример 1. Точное значение выражения:

$$5,31 cdot 4,16+2,19 cdot 1,51 = 22,0896+3,3069 = 25,3965 $$

Считая все величины, входящие в выражение, приближёнными с абсолютной погрешностью $Delta$ x = 0,01, выясните, нужно ли округлять ответ.

Во сколько раз абсолютная погрешность результата больше абсолютной погрешности исходных данных? Во сколько раз относительная погрешность результата больше относительной погрешности сомножителя 5,31?

Обозначим a = 5,31, b = 4,16, c = 2,19, d = 1,51.

Относительные погрешности (округление с избытком):

$$δ_a = frac{0,01}{5,31} cdot 100 text{%} = 0,19 text{%}, quad δ_b = frac{0,01}{4,16} cdot 100 text{%} = 0,25 text{%} $$

$$δ_c = frac{0,01}{2,19} cdot 100 text{%} = 0,46 text{%}, quad δ_d = frac{0,01}{1,51} cdot 100 text{%} = 0,67 text{%} $$

Относительные погрешности произведений:

$$ δ_{ab} = δ_a+δ_b = 0,19 text{%} + 0,25 text{%} = 0,44 text{%} $$

$$ δ_{cd} = δ_c+δ_d = 0,46 text{%} +0,67 text{%} = 1,13 text{%} approx ↑ 1,2 text{%} $$

Абсолютные погрешности произведений:

$$ Delta_{ab} = δ_{ab} cdot ab = 0,0044 cdot 22,0896 approx 0,09719 approx ↑ 0,098 $$

$$ Delta_{cd} = δ_{cd} cdot cd = 0,012 cdot 3,3069 approx 0,03968 approx 0,040 $$

Оставляем в промежуточных оценках 2 значащие цифры для последующего округления. Абсолютная погрешность выражения:

$$ Delta_{ab+cd} = Delta_{ab} + Delta_{cd} = 0,098+0,040 = 0,138 approx ↑ 0,2 $$

Таким образом, ответ нужно округлить до десятых:

$$ 5,31 cdot 4,16+2,19 cdot 1,51 approx 25,4 ± 0,2 $$

Отношение абсолютной погрешности результата к погрешности исходных данных:

$ frac{0,2}{0,01} = 20$ – абсолютная погрешность увеличилась в 20 раз.

Относительная погрешность результата: $δ = frac{0,2}{25,4} cdot 100 text{%} approx 0,79 text{%} $

По отношению к $δ_a: frac{δ}{δ_a} = frac{0,79}{0,19} approx 4,2$ – относительная погрешность результата в 4,2 раза больше.

Пример 2. а) Границы приближенных величин $5 le x le 6,6 le y le 7$. Оцените сумму, разность, произведение и частное этих величин.

б) Считая x и y точными величинами, принимающими значения на заданных отрезках, найдите границы суммы, разности и произведения этих величин.

а) По условию:

$$ {left{ begin{array}{c} x_0-Delta x = 5 \ x_0+Delta x = 6 end{array} right.} Rightarrow {left{ begin{array}{c} 2x_0 = 5+6 = 11 \ 2 Delta x = 6-5 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} x_0 = 5,5 \ Delta x = 0,5 end{array} right.} Rightarrow δ_x = frac{0,5}{5,5} cdot 100 text{%} approx 9,1 text{%} $$

$$ {left{ begin{array}{c} y_0- Delta y = 6 \ y_0+ Delta y = 7 end{array} right.} Rightarrow {left{ begin{array}{c} 2y_0 = 6+7 = 13 \ 2 Delta y = 7-6 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} y_0 = 6,5 \ Delta y = 0,5 end{array} right.} Rightarrow δ_y = frac{0,5}{6,5} cdot 100 text{%} approx 7,7 text{%} $$

Абсолютная погрешность суммы: $Delta_{x+y} = Delta_x+Delta_y = 0,5+0,5 = 1$

$$ x+y = (5,5+6,5) pm 1 = 12 pm 1 $$

Границы суммы: $ 11 le x+y le 13$

Абсолютная погрешность разности: $Delta _{x-y} = Delta _x + Delta _y = 0,5+0,5 = 1$

$$ x-y = (5,5-6,5) pm 1 = -1 pm 1 $$

Границы разности: $-2 le x-y le 0$

Относительная погрешность произведения:

$$δ_{xy} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%}$$

Абсолютная погрешность произведения:

$$ Delta_{xy} = δ_{xy} cdot x_0 y_0 = 0,17 cdot 5,5 cdot 6,5 = 6,0775 approx ↑ 7 $$

$$ xy = (5,5 cdot 6,5) pm 7 approx 36 pm 7 $$

Границы произведения: $29 le xy le 43$

Относительная погрешность частного:

$$ δ_{x/y} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%} $$

Абсолютная погрешность частного:

$$ Delta_{frac{x}{y}} = δ_{frac{x}{y}} cdot frac{x_0}{y_0} = 0,17 cdot frac{5,5}{6,5} approx 0,14 approx ↑ 0,2 $$

$$ frac{x}{y} = left( frac{5,5}{6,5} right) pm 0,2 approx 0,8 pm 0,2 $$

Границы частного: $0,6 le frac{x}{y} le 1,0$

б) Для точных величин получаем следующие границы:

Границы суммы:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5+6 le x+y le 6+7 Rightarrow 11 le x+y le 13 $$

Границы разности:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ -7 le -y le -6 end{array} right.} Rightarrow 5-7 le x-y le 6-6 Rightarrow -2 le x-y le 0 $$

Границы произведения:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5 cdot 6 le xy le 6 cdot 7 Rightarrow 30 le xy le 42 $$

Границы частного:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ frac{1}{7} le frac{1}{y} le frac{1}{6} end{array} right.} Rightarrow frac{5}{7} le frac{x}{y} le 1 $$

Пример 3. В эксперименте по определению плотности вещества получен объём V = 9, 7 $pm$ 0,05 мл и масса m = 107 $pm$ 2 г. Найдите плотность.

Это свинец или железо?

Плотность:

$$ ρ = frac{m}{V}, ρ_0 = frac{m_0}{V_0} = frac{107 cdot 10^{-3} кг}{9,7 cdot 10^{-6} м^3} approx 11031 frac{кг}{м^3} $$

Относительные погрешности (округление с избытком):

$$ δ_V = frac{0,05}{9,7} cdot 100 text{%} approx 5,2 text{%}, δ_m = frac{2}{107} cdot 100 text{%} approx 1,9 text{%} $$

$$ δ_ρ = δ_V+δ_m = 5,2 text{%} +1,9 text{%} = 7,1 text{%} $$

Абсолютная погрешность для плотности (округление с избытком):

$$ Δ_ρ = δ_ρ cdot ρ_0 = 0,071 cdot 11031 approx 800 frac{кг}{м^3} $$

$$ ρ = 11000 pm 800 frac{кг}{м^3} $$

Это – свинец (табличное значение $ρ_{таб} = 11340 frac{кг}{м^3}$ ).

Погрешность
частного:
относительная погрешность частного
не превышает суммы относительных
погрешностей делимого и делителя.

Пример.
Найти частное u = 25.7 / 3.6, если все написанные
знаки делимого и делителя верны.

Решение.
u = 25.7 / 3.6 = 7.14 . du = dx1 + dx2 = 0.05/25.7 + 0.05/3.6 =
0.002 + 0.014 = 0.016 . Так как u = 7.14, то Du = 0.016 ·
7.14 = 0.11 . Поэтому u = 7.14 ± 0.11 .

21. Абсолютная и относительная погрешности деления.

Для
частного двух чисел вычисления будут
аналогичными.

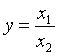
Находим
натуральный логарифм и его частные
производные

,

, 

следовательно, предельная
относительная погрешность частного
равна сумме предельных относительных
погрешностей делимого и делителя.

Абсолютная
погрешность результата
вычисления функции нескольких
приближенных чисел равна сумме
произведений модуля частной производной
функции на абсолютную
погрешность
приближенного числа.

24. Методы центральных прямоугольников, трапеций и Симпсона вычисления определенных интегралов: расчетные формулы, порядок точности, оценка погрешности, вычисление погрешности по правилу Рунге.

Требуется
найти

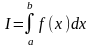
с
той или иной степенью точности. Известны
три классических способа сделать это.

Способ
№ 1: метод
прямоугольников.
Отрезок

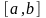
разбивается на

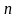
равных частей:

длиной

,
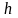
где

.

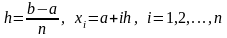
Затем
на каждом участке

функция

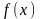
заменяется на константу

,
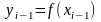
после чего искомый интеграл заменяется
на интеграл от новой ступенчатой
функции, т.е. на число

.

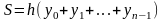
Можно
доказать, что справедлива следующая
оценка:

,

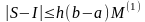
где

– максимум модуля первой производной
функции

на отрезке

.

Способ
№ 2: метод
трапеций.

В
этом методе искомый интеграл после
разбиения отрезка на равные части
заменяется на следующую сумму (суммируются
площади трапеций, а не прямоугольников,
как в предыду-щем случае):

,

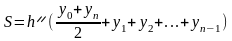
где

Можно доказать, что если

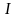
– исходный обсуждаемый интеграл,то

,

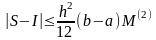
где

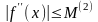
на отрезке

.

: Способ
№ 3: метод
парабол(Cимпсона).
В этой ситуации отрезок

разбивается на

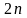
равных частей:

,
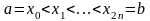
где


.
На участках

,
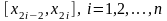
функцию

заменяют
на параболу, проходящую через точки

и интегралом от этой параболы на участке

заменяют интеграл от функции

на этом же участке, после чего все эти
интегралы суммируют и результаты
принимают за интеграл от

по всему отрезку

.
Полученная приближенная формула
называется формулой
парабол или
формулой
Симпсона.
Вот ее окончательный

вид:

.

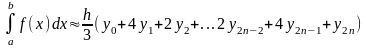
Если
левую часть этого приближенного
равенства обозначить через I
а правую – через S,
то окажется выполненной следующая
формула для оценки погрешности:

,

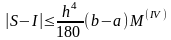
где

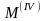
– максимум на интервале

четвертой
производной функции

.

существует
еще один широко применяемый метод –
метод Рунге-Кутта, который, как правило,
быстрее приводит к числу

,
чем метод Эйлера. Сформулируем действия
по методу Рунге-Кутта:

1й
шаг. Фиксируем
точность, с которой нужно найти значение

.
Обозначим это число через

.
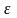
Поясним, что это означает, что числа,
отличающиеся меньше, чем на

,
считаются одинаковыми.

2й
шаг. Фиксируем
произвольное

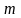
и разделим отрезок

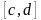
на

равных частей:

,
где

.

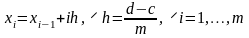
3й
шаг. Построим
последовательность чисел

,
где

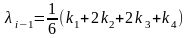
и

в
которой, напомним,

.
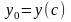
Обозначим

через

.

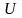
4й
шаг. Заменим

на

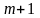
и повторим шаги 2 и 3. Полученное число

(т.е. послед-нее из вычисляемых на шаге
3) обозначим теперь через

.

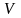
5й
шаг. Если
окажется, что числа

и

отличаются друг от друга меньше, чем
на

,
то число

считается найденным и равным

.
В противном случае переобозначим

через

и вернемся к шагу 4.

Можно
доказать, что когда
функция

из
(7.4.1) имеет
непрерывные частные производные,
описанный процесс обязательно конечен
и ответ находится действительно с любой
наперед заданной точностью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #