Как найти погрешность приближения числа десятичной дробью

Математика

6 класс

Урок № 68

Приближение десятичных дробей

Перечень рассматриваемых вопросов:

1. Десятичная дробь, приближённое значение, округление.
2. Значащая цифра десятичной дроби.

Тезаурус

Округление десятичной дроби – нахождение приближённого значения.

Десятичная дробь – дробь, записанная в десятичной форме.

Значащая цифра десятичной дроби – это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.

Теоретический материал для самостоятельного изучения

Не всегда возможно и нужно найти точные ответы на некоторые вопросы. Например, сколько кубических метров воды содержит Каспийское море? Сколько тонн снега выпало зимой? Сколько волос на голове человека? Поэтому, вместо точных берут другие значения, близкие к искомым, приближённые.

Рассмотрим несколько чисел. 1,3; 1,5; 1,8

Все эти числа имеют целую часть – единицу, значит, находятся между соседними натуральными числами 1 и 2.

При этом 1,3 находится ближе к 1, а 1,8 ближе к 2.

Поэтому можно сказать, что 1,3 приближённо равно 1,

а 1,8 приближённо равно 2.

Число 1,5 находится точно в середине, его можно приблизить и к единице, и к двум.

1,3 ≈ 1

1,8 ≈ 2

1,5≈1; 1,5≈2

Но если следовать правилам округления чисел, то 1,5 приближённо равно 2.

Приближение десятичных дробей, которое мы выполнили, называется округлением десятичной дроби до единиц.

Округление десятичной дроби – нахождение приближённого значения.

Если число А мало отличается от числа Б, то говорят, что число А приближённо равно числу Б. А ≈ Б; ≈ – знак приближённого равенства.

Если при этом Б меньше, чем А, то Б называют приближением А с недостатком.

Если Б больше, чем А, то его называют приближением А с избытком.

Рассмотрим на примере произвольной десятичной дроби.

А = 3,42845

Оборвём эту дробь на цифре второго разряда после запятой.

3,42845

Получим число, меньшее, чем А. 3,42 < А

Если увеличить число сотых на единицу, получим число, большее, чем А. 3,43 > А

Таким образом, первоначальное число А находится между данными числами. 3,42 < А < 3,43

Поэтому получаем, что 3,42 – приближение числа А с точностью до одной сотой с недостатком.

А ≈ 3,42 с точностью до 0,01 с недостатком.

3,43 – приближение числа А с точностью до одной сотой с избытком.

А ≈ 3,43 с точностью до 0,01 с избытком.

Так как третья цифра после запятой у числа А больше пяти, то оно ближе к 3,43, чем к 3,42. Поэтому говорят, что 3,43 есть приближение А с точностью до одной сотой с округлением.

Введём понятие значащей цифры десятичной дроби. Это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.

Например,

0,403 – все цифры после запятой значащие.

0,00256 – все цифры, начиная с двойки – значащие.

Округлим некоторые числа до третьей значащей цифры. Это означает, что округляем до того разряда, где находится третья значащая цифра, заменив следующие цифры нулями.

3,14159 ≈ 3,14000 = 3,14

0,046052 ≈ 0,046100 = 0,0461

– 0,023039 ≈ – 0,023000 = – 0,0230

Разбор заданий тренировочного модуля

Тип 1. Зачеркивания элементов.

Зачеркните неверный ответ.

Задание. Округлите число 1037,9301 до четырёх значащих цифр.

Варианты ответов: 1037,9; 1038

Решение. Значащие цифры – это первая отличная от нуля цифра, а также все следующие за ней. Значащими цифрами в данном числе являются все цифры, начиная с первой. Четыре значащие – это вся целая часть дроби. После запятой в разряде десятых стоит цифра 9, значит, при округлении к цифре разряда единиц мы прибавим 1. Получим 1038.

Ответ: 1038

Тип 2. Ввод с клавиатуры в пропуски в тексте.

Задание. Впишите в пропуски цифры, чтобы получилось верное округление

А) 383,_75 ≈ 383,6

Б) 2_9,746 ≈ 210

В) 548,_77 ≈ 548,18

Решение.

А) Дробь округлена до десятых. Следующая цифра после разряда десятых – 7. Значит, при округлении к цифре десятых прибавили единицу. Получилось 6. Значит, исходная цифра — 5.

Ответ: 383,575 ≈ 383,6

Б) Дробь округлена до десятков. Следующая цифра после разряда десятков – 9. Значит, при округлении к цифре десятков прибавили единицу. Получилось 1. Значит, исходная цифра десятков – 0.

Ответ: 209,746 ≈ 210

В) Дробь округлена до сотых. При этом количество десятых не менялось, и в конечном числе равно 1. Значит. И в исходном числе количество десятых – 1.

Ответ: 548,177 ≈ 548,18

Абсолютная и относительная погрешности

Абсолютная погрешность приближения

Имея дело в вычислениях с бесконечными десятичными дробями, приходится для удобства выполнять приближение этих чисел, т. е. округлять их. Приблизительные числа получаются также при различных измерениях.

Бывает полезно узнать, как сильно приближенное значение числа отличается от его точного значения. Понятно, что чем это различие меньше, тем лучше, тем точнее выполнено измерение или вычисление.

Для определения точности измерений (вычислений) вводят такое понятие как погрешность приближения. По-другому его называют абсолютной погрешностью.

Абсолютной погрешностью приближения называется модуль разности между точным значением числа и его приближенным значением.

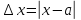
где х — это точное значение числа, а — его приближенное значение.

Например, в результате измерений было получено число 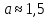. Однако в результате вычисления по формуле точное значение этого числа 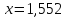. Тогда абсолютная погрешность приближения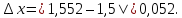

В случае с бесконечными дробями погрешность приближения определяется по той же формуле. На месте точного числа записывается сама бесконечная дробь. Например, 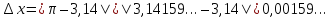. Здесь получается, что абсолютная погрешность приближения выражена иррациональным числом.

Приближение может выполняться как по недостатку, так и по избытку.

То же число π при приближении по недостатку с точностью до 0,01 равно 3,14, а при приближении по избытку с точностью до 0,01 равно 3,15.

Правило округления: если первая отбрасываемая цифра равна пяти или больше пяти, то выполняется приближение по избытку; если же меньше пяти, то по недостатку.

Например, т.к. третьей цифрой после запятой у числа π является 1, то при приближении с точностью до 0,01 оно выполняется по недостатку.

Вычислим абсолютные погрешности приближения до 0,01 числа π по недостатку и по избытку:

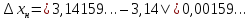
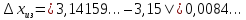
Как видим, абсолютная погрешность приближения по недостатку меньше, чем по избытку. Значит, приближение по недостатку в этом случае обладает более высокой точностью.

Относительная погрешность приближения

Абсолютная погрешность обладает одним важным недостатком – оно не позволяет оценить степень важности ошибки.

Например, покупаем мы на рынке 5 кг картофеля, а недобросовестный продавец при измерении веса ошибся на 50 г в свою пользу. Т.е. абсолютная погрешность составила 50 г. Для нас такая оплошность будет сущей мелочью и мы даже не обратим на неё внимания. А если при приготовлении лекарства произойдёт подобная ошибка? Тут уже всё будет намного серьёзней. А при загрузке товарного вагона наверняка возникают отклонения намного больше данного значения.

Поэтому сама по себе абсолютная погрешность малоинформативная. Кроме неё очень часто дополнительно рассчитывают относительное отклонение.

Относительной погрешностью приближения называется отношение абсолютной погрешности к точному значению числа.

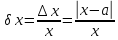
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

Приведём несколько примеров.

Пример 1.  На предприятии 1284 рабочих и служащих. Округлить количество работающих до целых с избытком и с недостатком. Найти их абсолютные и относительные погрешности (в процентах). Сделать вывод.

Итак, , .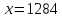

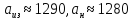Абсолютная погрешность: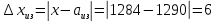

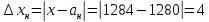
Относительная погрешность: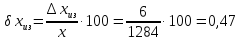

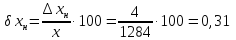
Значит, точность приближения с недостатком выше, чем точность приближения с избытком.

Пример 2. В школе 197 учащихся. Округлить количество учащихся до целых с избытком и с недостатком. Найти их абсолютные и относительные погрешности (в процентах). Сделать вывод.

Итак, , .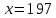

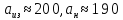Абсолютная погрешность: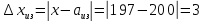

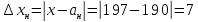
Относительная погрешность: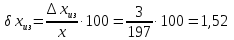

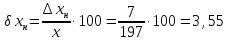
Значит, точность приближения с избытком выше, чем точность приближения с недостатком.

1. Найдите абсолютную погрешность приближения:

1. числа 2,87 числом 2,9; числом 2,8;

2. числа 0,6595 числом 0,7; числом 0,6;

3. числа 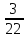числом ;

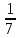4. числа 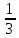числом 0,3;

5. числа 4,63 числом 4,6; числом 4,7;

6. числа 0,8535 числом 0,8; числом 0,9;

7. число 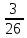числом ;

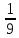8. число числом 0,2.

1. Приближённое значение числа х равно а. Найдите абсолютную погрешность приближения, если:

1. Запишите в виде двойного неравенства:

1. Найдите приближённое значение числа х, равное среднему арифметическому приближений с недостатком и избытком, если:

1. Докажите, что среднее арифметическое чисел а и b является приближённым значением каждого из этих чисел с точностью до .

1. Округлите числа:

до десятков	до единиц	до десятых
до тысячных	до тысяч	до стотысячных
до единиц	до десятков	до десятых
до тысячных	до сотен	до десятитысячных

1. Представьте обыкновенную дробь в виде десятичной и округлите её до тысячных и найдите абсолютную погрешность:

1. Докажите, что каждое из чисел 0,368 и 0,369 является приближённым значением числа с точностью до 0,001. Какое из них является приближённым значением числа с точностью до 0,0005?

1. Докажите, что каждое из чисел 0,38 и 0,39 является приближённым значением числа с точностью до 0,01. Какое из них является приближённым значением числа с точностью до 0,005?

1. Округлите число до единиц и найдите относительную погрешность округления:

2,1	5,12	9,736	49,54
1,7	9,85	5,314	99,83

1. Представьте каждое из чисел и в виде десятичной дроби. Округлив полученные дроби до десятых, найдите абсолютную и относительную погрешности приближений.

1. Представьте каждое из чисел и в виде десятичной дроби. Округлив полученные дроби до десятых, найдите абсолютную и относительную погрешности приближений.

1. Радиус Земли равен 6380 км с точностью до 10 км. Оцените относительную погрешность приближённого значения.

1. Наименьшее расстояние от Земли до Луны равно 356400 км с точностью до 100 км. Оцените относительную погрешность приближения.

1. Сравните качества измерения массы М электровоза и массы т таблетки лекарства, если т (с точностью до 0,5 т), а г (с точностью до 0,01 г).

1. Сравните качества измерения длины реки Волги и диаметра мячика для настольного тенниса, если км (с точностью до 5 км) и мм (с точностью до 1 мм).

3

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.

ЗАПИСЬ ПРИБЛИЖЕННОГО ЧИСЛА.

ВЕРНЫЕ И ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА

х – точное число

а – приближенное число

Разность   х – а    между точным числом х и приближенным числом а называется погрешностью приближения.

Модуль погрешности называется абсолютной погрешностью и обозначается ∆:

| х – а | = ∆

Погрешность и абсолютная погрешность имеют ту же размерность, что и рассматриваемая величина

Граница абсолютной погрешности ∆а – положительное число, которое больше или равно абсолютной погрешности или:

| х – а | ≤ ∆а

Если задана граница абсолютной погрешности ∆а, то число а есть приближенное значение числа х с точностью до ∆а и записывают

х = а ± ∆а, например: 94,5 ± 0,3

В отличие от абсолютной погрешности, граница абсолютной погрешности не определяется однозначно, поэтому на практике выбирается такое значение границы абсолютной погрешности, которое удобно для вычислений и обеспечивает максимальную точность.

Цифра приближенного числа а, записанного в виде десятичной дроби, называется верной (точной), если граница абсолютной погрешности числа не превышает (меньше или равно) единицы того разряда, в котором стоит эта цифра. В противном случае она называется сомнительной, например:

25,63 ± 0,2

Граница погрешности 0,2 , поэтому рассмотрим

цифру 5, разряд единицы, единица разряда 1 и 0,2 < 1 (граница погрешности не превышает единицу разряда), значит цифра 5 – верная, тогда цифра десятков – 2  данного числа тоже верная.

Цифра 6, разряд десятые, единица разряда 0,1 и 0,2 > 0,1  (граница погрешности превышает единицу разряда), значит цифра 6 – сомнительная. Значит и цифра 3 (сотые) будет также сомнительной

2 и 5 – верные цифры, 6 и 3 – сомнительные цифры числа

Запись чисел с сохранением только верных цифр широко используется во всех математических таблицах, в справочниках (физика, астрономия, техника). При этом, по записи приближенного числа можно оценить погрешность приближения, например:

табличные данные: температура кипения золота – 2700 ºС, значит граница абсолютной погрешности 1 ºС, температура кипения йода – 182,8 ºС, значит граница абсолютной погрешности 0,1 ºС.

Записи приближенных чисел 0,3; 0,30; 0,300 – неравносильны, т.к. приближенное число 0,3 имеет погрешность не более 0,1;

приближенное число 0,30 имеет погрешность не более 0,01;

приближенное число 0,300 имеет погрешность не более 0,001.

Если целое число содержит в конце нули, не являющиеся верными цифрами, то их заменяют множителем 10^р, где р – число таких нулей.

В записи приближенных чисел принято соблюдать следующие правила:

• Оставлять в записи приближенного числа только верные цифры;
• Если в десятичной дроби последние верные цифры нули, то их надо выписать;
• Если число содержит в конце нули, не являющиеся верными цифрами, то они должны быть заменены на 10^р , где р – число нулей, которые надо заменить

Например,

Записать правильно следующие приближенные числа:  

1. а = 0,075 ± 0,000005 – здесь погрешность меньше, чем 0,00001 (0,000005<0,00001), значит а = 0,07500 (последние верные цифры нули и их надо выписать, см. правило)
2. а = 746000000 ± 5000 здесь погрешность меньше, чем 10000 (5000<10000), значит последние четыре нуля не являются верными цифрами и их надо заменить на  10^р  а = 74600·10⁴
3. а = 0,35  ∆а = 0,00005 – здесь погрешность меньше, чем 0,0001 значит

а = 0,3500 (последние верные цифры нули)

1. а = 765000  ∆а = 5 – здесь погрешность  5<10  значит а = 76500·10, т.к. последний нуль не является верной цифрой
2. а = 0,3700  ∆а = 0,05 – здесь погрешность 0,05<0,1 и цифра 7 не является верной, она отбрасывается, значит а = 0,4

В некоторых заданиях необходимо наоборот определить абсолютную погрешность по записи приближенного числа, например,

Указать абсолютную погрешность приближенных чисел:

1. а = 14,5 ·10, значит ∆а = 10
2. а = 34,20 т.к. последний нуль является верной цифрой, то ∆а = 0,01
3. а = 263·10⁴ , значит ∆а = 10000

Число в стандартном виде записывают так:

а = а_0, а₁ а₂ … а_k  ·10^m , где 1 ≤ а₀ ≤ 10,

а_0, а₁ а₂ … а_k  –  все верные цифры числа,

показатель m – называется порядком числа.

Если число, записанное в виде десятичной дроби содержит все верные цифры, то все его цифры, начиная с первой слева отличной от нуля, называют значащими, например:

7,03 – три значащие цифры

4400 – четыре значащие цифры

0,000270 – три значащие цифры (нули, расположенные левее первой, отличной   от нуля цифры, не считаются значащими  0,000270).

Округление числа – это замена его числом с меньшим количеством значащих цифр. При округлении числа до m значащих цифр отбрасывают все цифры, стоящие правее m-ой значащей цифры, заменяя их на нули (при сохранении разряда). При этом, если первая из отбрасываемых цифр ≥ 5, то последнюю оставшуюся цифру увеличивают на единицу,

например:

Округлить число с заданной точностью:

• с точностью до 10^-3   (10^-3  = 0,001)

1,5783

Значащие цифры – 1, 5, 7  и 8, цифра 3 – сомнительная, т.к. 0,001 > 0,0001 (единицы разряда)

1,5783 ≈ 1,578 (последняя из отбрасываемых цифр 3<5, значит предыдущую оставляем без изменений)

23,4997

Значащие цифры – 2, 3, 4, 9 и 9, цифра 7 – сомнительная

7>5, значит предыдущую увеличиваем на 1, получим

23,4997 ≈ 23,500

• с точностью до 10^-2  (10^-2  = 0,01)

4,761 ≈ 4,76

31,009 ≈ 31,01

• с точностью до 10³  (10³ = 1000)

159734 ≈ 160000 = 160·10³

28,34 ≈ 0 – ни одна из цифр не является значащей 1000 > 10, т.к. задана точность 1000, а заданное число меньше, чем погрешность.

Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие)