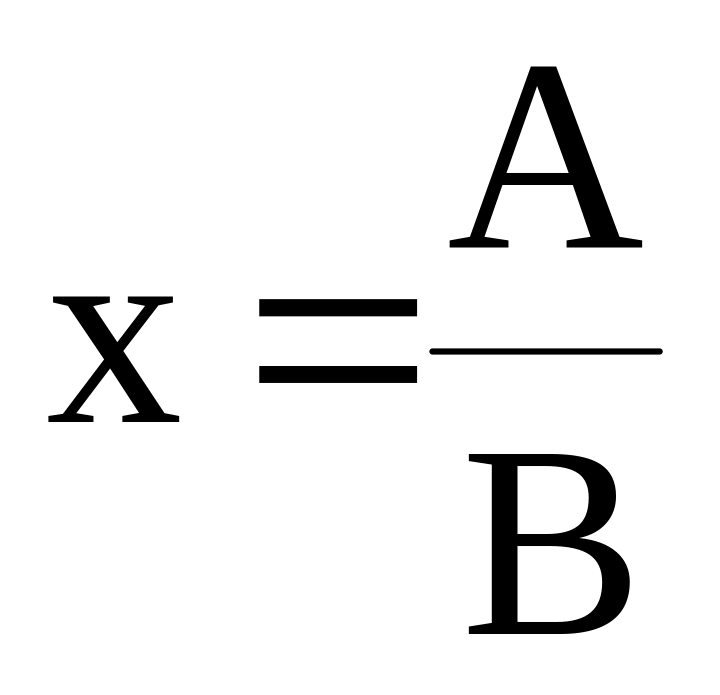Погрешности косвенных измерений
Если результат
эксперимента определяется на основе
расчетов, то измерения называются
косвенными. Например, при определении
импульса тела p
= mv, скорости
равноускоренного движении V
= V0
+ at и т.п. Однако
нам не удастся подсчитать погрешность
полученного результата косвенных
измерений так же просто, как при проведении
прямых измерениях.
Предположим, что нам
необходимо определить периметр и площадь
прямоугольника. Произведя измерения
линейкой, мы получим длины его сторон.
Пусть длина одной стороны прямоугольника
будет равна a,
другой – b.
Тогда периметр р
прямоугольника будет равен p=2(a + b), а
его площадь s = ab. Можно ли утверждать,
что погрешности результатов расчета
периметра прямоугольника и его площади
будут одинаковыми? Вряд ли, ведь формулы,
которыми пользовались при расчете
разные: при нахождении периметра
величины, полученные при измерении, мы
складывали, а при подсчете его площади
– перемножали.
При расчете погрешности
результатов косвенных измерений нам
придется учитывать, как выглядит формула,
по которой производился расчет искомой
величины. В теории погрешностей
доказывается, как это можно сделать в
общем виде. Мы же воспользуемся набором
готовых формул для вычисления относительной
погрешности результатов косвенных
измерений. Формулы расчета относительных
погрешностей для различных случаев
приведены в таблице
3.
Таблица
2
Как
пользоваться этой таблицей?
|
Вид функции |
Относительная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть, например,
некоторая физическая величина х
рассчитывается по формуле:
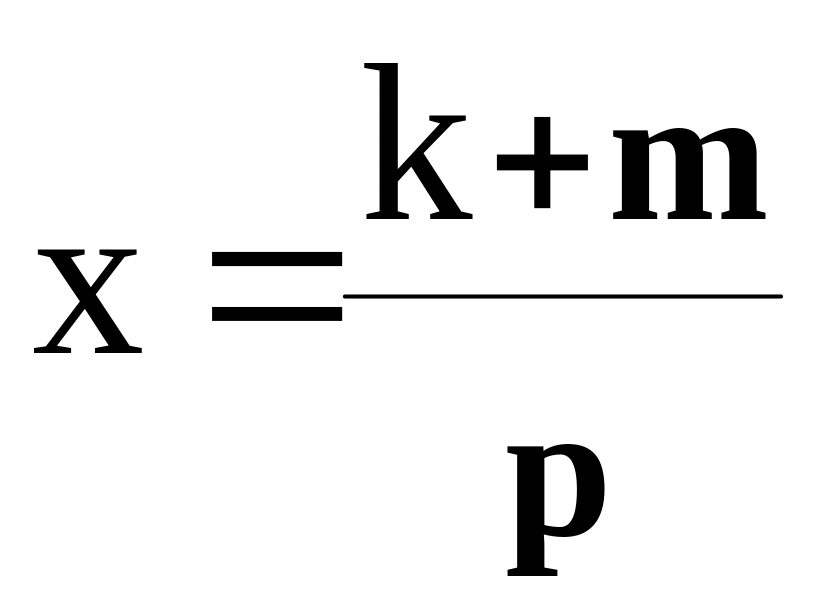
.
Значения k,
m
и p
найдены прямыми измерениями во время
проведения эксперимента. Их абсолютные
погрешности соответственно равны
![]()
.
Подставляя полученные значения в
формулу, получим приближенное значение
![]()
.
Затем следует рассчитать
относительную погрешность результата
косвенных измерений –
![]()
,
воспользовавшись соответствующей
формулой из таблицы 3.
На первый взгляд может
показаться, что такой формулы в таблице
нет. При более внимательном анализе
ситуации заметим, что в нашем случае
искомое значение находится как отношение
двух величин k
+ m = А и
р = В, поэтому
нам можно воспользоваться формулой Х
= А : В.
В нашем случае из
таблицы 3 имеем для отношения А
: В:
![]()
или
![]()
Из этой же таблицы мы
можем узнать, как рассчитать относительную
погрешность суммы:

.
Следовательно,
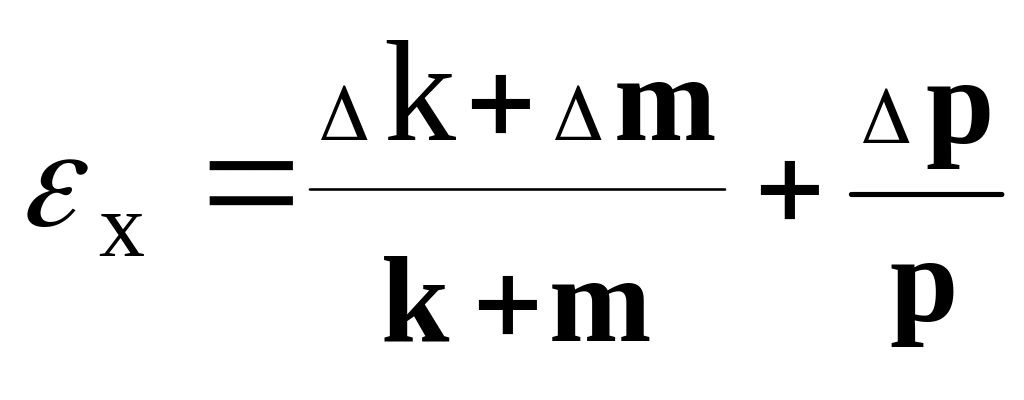
.
Теперь можно найти
значение границе абсолютной погрешности
результатов косвенных измерений, которая
рассчитывается несколько иначе, чем
при проведении прямых измерений. Для
вычисления абсолютной погрешности
результатов косвенных обычно измерений
используют формулу для расчета
относительной погрешности
.
Откуда
![]()
..
Окончательный результат
косвенных измерений записывают в виде:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Mikhail Levin
Искусственный Интеллект
(614566)
10 лет назад
никак. Надо хотя бы стороны знать. У квадрата и длинной-длинной полоски погрешность будет разная.
если погрешность измерения длины dl
S’=S+ds=(a+dl)(b+dl)=ab + a*dl +b*dl + dl*dl ~ S + (a+b)*dl
ds ~= (a+b)*dl
мне по работе приходилось считать для произвольную участков? там все хуже…
000Мыслитель (5459)
10 лет назад
Спасибо!!
Только у меня нет сторон. Известна только погрешность измерения сторон – 0,01м, периметр – 11,98м и площадь 8,94м2. И ответ – 0,06м2. Но как он получается?
По периметру я же не могу узнать точно, какова длина сторон.
Assafriend
Мудрец
(18996)
10 лет назад
вычесть из максимальной площади прямоугольника минимальную – это и будет абс погрещность по площади ессно для каждого прямоугольника – своя!
например квадрат 1м +/-0.1м имеем 1.21-0.81=0.4 кв. м. т. е. 1 +/- 0,2 кв. м.
000Мыслитель (5459)
10 лет назад
Только тогда надо стороны знать, а я их не знаю. Знаю только периметр и площадь. И неизвестно, квадрат ли это.
AssafriendМудрец (18996)
10 лет назад
ваши стороны х и у
2х+2у=11.98 отсюда х=11.98/2-у
х*у=8.94 отсюда х=8.94/у
графики этих двух функций пересекутся в единственной точке так можно узнать стороны!
Вольный ветер
Искусственный Интеллект
(283261)
10 лет назад
Компьютер способен решать задачки не только по высшей математике, но и более сложные! А молодежь только играет, на компе работать не научились, а на калькуляторе уже разучились, вот дяди и решают вам элементарные примеры, и задачки, хотя своя ЭВМ у вас под носом….))))
1. Найти абсолютные и относительные погрешности числа ![]() , заданного двумя и тремя цифрами после запятой.
, заданного двумя и тремя цифрами после запятой.
Решение. а) Пусть ![]() . Тогда справедливо
. Тогда справедливо
![]() ;
; ![]() ;
;
Б) если ![]() , то
, то
![]() ;
; ![]()
Ответ: а) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() .
.
2. Округлить число ![]() до семи, шести, пяти и т. д. десятичных знаков и до целого числа.
до семи, шести, пяти и т. д. десятичных знаков и до целого числа.
Решение. Округляем по порядку: ![]() (так как первая из отброшенных цифр равна 5, остальные нулевые, а последняя оставшаяся нечетная);
(так как первая из отброшенных цифр равна 5, остальные нулевые, а последняя оставшаяся нечетная); ![]() (первая из отброшенных больше 5);
(первая из отброшенных больше 5); ![]() (первая
(первая
из отброшенных 5, а среди остальных есть ненулевые); ![]() (первая отброшенная меньше 5);
(первая отброшенная меньше 5); ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
3. Вычислить верные значащие цифры чисел: а) X = 0,004507; ![]() ; б) X = 9,999785;
; б) X = 9,999785; ![]() ; в) X = 0,0208700;
; в) X = 0,0208700; ![]() .
.
Решение. В записи рассматриваемых чисел подчеркнем верные значащие цифры:
А) 0,004507![]() , так как
, так как ![]() ;
;
Б) 9,999785![]() , так как
, так как ![]() ;
;
В) 0,0208700![]() , так как
, так как ![]() .
.
4. Стороны треугольника A = 17,3 см, B = 23,6 см, C = 14,2 см измерены с абсолютной погрешностью ![]() см. Определить абсолютную погрешность и пределы относительной погрешности периметра
см. Определить абсолютную погрешность и пределы относительной погрешности периметра ![]() треугольника.
треугольника.
Решение. ![]() См,
См, ![]() . Таким образом,
. Таким образом, ![]() (последняя цифра в числе 55,1 сомнительная, так как
(последняя цифра в числе 55,1 сомнительная, так как ![]() ). Теперь вычислим относительные погрешности сторон
). Теперь вычислим относительные погрешности сторон
![]() Пределы изменения относительной погрешности равны:
Пределы изменения относительной погрешности равны: ![]() .
.
5. Ребра прямоугольного параллелепипеда A = 4,3 см, B = 1,6 см,
C = 2,8 см измерены с абсолютной погрешностью ![]() см. Определить абсолютную и относительную погрешность вычисления его объема
см. Определить абсолютную и относительную погрешность вычисления его объема ![]() .
.
Решение. ![]() ;
; ![]()
Тогда ![]()
![]() . Так как
. Так как ![]() ,
,
то в ![]() верна лишь цифра десятков, а остальные цифры сомнительные.
верна лишь цифра десятков, а остальные цифры сомнительные.
Задачи для самостоятельного решения по теме 1
1. Найти абсолютные и относительные погрешности числа ![]() , заданного двумя и тремя цифрами после запятой.
, заданного двумя и тремя цифрами после запятой.
2. Округлить число ![]() до шести, пяти и т. д. десятичных знаков и до целого числа.
до шести, пяти и т. д. десятичных знаков и до целого числа.
3. Вычислить верные значащие цифры чисел: а) X = 0,004507; ![]() ; б) X = 12,396;
; б) X = 12,396; ![]() ; в) X = 0,037862;
; в) X = 0,037862; ![]() .
.
4. Стороны прямоугольника равны A = 3,3 см, B = 5,2 см. Найти
а) абсолютную погрешность периметра и площади прямоугольника;
б) определить пределы изменения относительной погрешности периметра.
| < Предыдущая | Следующая > |
|---|
Формула прямоугольника


4.4
Средняя оценка: 4.4
Всего получено оценок: 141.
4.4
Средняя оценка: 4.4
Всего получено оценок: 141.
Формул прямоугольника не так много, но все их стоит знать, поскольку это базовые формулы математики. Прямоугольник – первая фигура, поэтому не знать основные формулы прямоугольника это пробел, который нужно устранить как можно быстрее.
Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы прямые. Что такое параллелограмм? Это выпуклый четырехугольник, у которого все стороны попарно равны и параллельны.
Различают выпуклые и невыпуклые четырехугольники. Различить их можно используя метод сторон. Для этого через две смежные произвольные вершины проводят прямую. Если существует хоть одна такая прямая, которая делит фигуру на две части, то четырехугольник невыпуклый. Если таких прямых нет, то фигура считается выпуклой.
Частным случаем прямоугольника является квадрат. У квадрата все стороны равны и попарно параллельны. Кстати, сам прямоугольник является частным случаем параллелограмма.
Чтобы доказать, что параллелограмм является прямоугольником нужно всего лишь доказать, что один из углов параллелограмма равен 90 градусом. Дело в том, что в параллелограмме противоположные углы равны – это одно из свойств этой фигуры. Если противоположные углы равны, а в любом четырехугольнике сумма углов равна 360 градусам, то если один угол равен 90 градусам, противоположный ему так же 90.
Сумма оставшихся углов составляет 180 градусов, но они так же равны, т.е. каждый из углов составляет 180:2=90 градусов.
Выходит для доказательства того, что перед нами прямоугольник требуется выполнение двух условий:
- Четырехугольник является параллелограммом.
- Один из углов параллелограмма равен 90 градусам.
Формулы прямоугольника
У прямоугольника не так много формул. Перечислим все из них:
- Формула площади
- Формула периметра
- Формула диагонали
Формула площади всем давно знакома: это произведение длины на ширину:
S=a*b
Периметр это всегда сумма всех сторон фигуры, но в случае с периметром прямоугольника все стороны равны и параллельны, то есть:
P=2*(a+b)
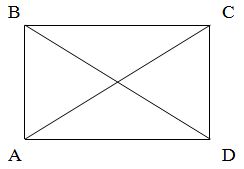
Особой формулы диагонали нет, но ее, как правило, выражают из теоремы Пифагора. Ведь ,если провести диагональ, то она разделит прямоугольник на два равных прямоугольных треугольника. Диагональ в этом случае будет равна корню квадратному из суммы квадратов катета:
$$d=sqrt{a^2+b^2}$$
Чему же равна вторая диагональ? Она будет такой же, так как в прямоугольнике диагонали равны. Погрешности у формул прямоугольника нет, поэтому результаты можно смело округлять – это не особо скажется на отклонении конечного результата от реальности.
Все эти формулы выведены на основании логических выводов. Поэтому лучше просто запомнить эти формулы. Не имеет смысла запоминать процесс вывода , это слишком сложно, проще заучить и использовать готовые формулы.

Что мы узнали?
Мы узнали, что прямоугольник – это параллелограмм, у которого все углы прямые. Поговорили о признаках прямоугольников и выделили основные формулы прямоугольника – формулу площади, формулу периметра и формулу диагонали.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 141.
А какая ваша оценка?
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим задачу, в которой требуется вычислить определённый интеграл $int^b_a f(x)dx$, при этом функция $f(x)$ является непрерывной на промежутке $left[a;bright]$. Обычно, если существует возможность, интегралы вычисляются через нахождение первообразной, но так как это не всегда возможно, прибегают к использованию приближённых методов.
К наиболее часто используемым приближённым методам относят:
- Метод прямоугольников;
- Метод трапеций;
- Метод Симпсона или иначе метод парабол.
В данной статье мы подробно расcмотрим метод прямоугольников.
Сущность метода прямоугольников
Рассмотрим нахождение определённого интеграла от функции $f(x)$ с точки зрения геометрии. Интеграл $int^b_a f(x)dx$ в данном случае есть не что иное, как площадь фигуры, ограниченной сверху графиком $f(x)$, по бокам прямыми $x=a$ и $x=b$, а снизу осью абсцисс.

Рисунок 1. Метод средних прямоугольников
Для того чтобы найти площадь всей фигуры, можно воспользоваться определением интеграла и разбить всю фигуру на равные сегменты одной и той же длины. Точки на оси абсцисс, которые будут разбивать фигуру, обозначим как $x_i$. Нулевая точка при разбиении $x_0=a$, а конечная точка $x_n=b$. Для того чтобы вычислить длину одного сегмента, воспользуемся формулой:
$Δx_i=frac{b-a}{n}$
В методе средних прямоугольников каждый сегмент заменяется на прямоугольник, за высоту которого принимается ордината середины отрезка. Получается, что площадь одного такого прямоугольника равна $S_i= frac{b-a}{n} cdot f(ξ_i)$, а площадь всей фигуры будет равна:
«Метод прямоугольников» 👇
$int^b_a f(x)dx=frac{b-a}{n}cdot (f( ξ_0)+f( ξ_1)+…+f( ξ_{n-1})$, где $x_i≤ ξ_i≤x_{i+1}$
Эта формула позволяет не вычислять напрямую площадь искомой фигуры, ограниченной кривой линией, а заменить её приблизительной площадью ступенчатой фигуры, состоящей из прямоугольников.
При использовании метода средних прямоугольников так как $ξ_i=frac{x_i+x_{i+1}}{2}=x_{i+frac{1}{2}}$, тогда $f( ξ_i)=f(x_{i+frac{1}{2}})$ обозначим как $y_{i+ frac{1}{2}}$,
и формула примет вид:
Определение 1
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_{frac{1}{2}} + y_{frac{3}{2}} + y_{n- frac{1}{2}}left(1right)$
Эта формула называется формулой средних прямоугольников.
Методы левых и правых прямоугольников
Данные методы отличаются от метода средних прямоугольников тем, что здесь в качестве ординаты для элементарного прямоугольника выбирается либо крайнее левое значение функции $f(x)$ (и тогда метод называется методом левых прямоугольников), либо крайнее правое, и тогда метод носит название метода правых прямоугольников.
Определение 2
Формула для применения метода левых прямоугольников выглядит так:
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_0 + y_1 + y_{n- 1})left(2right)$
Определение 3
Формула для метода правых прямоугольников:
$int^b_a f(x)dx=frac{b-a}{n}cdot (y_1 + y_2 + y_n)left(3right)$
Формулы $(1), (2), (3)$ иначе также называются квадратурными составными формулами.
Погрешность метода прямоугольников
Для того чтобы оценить общую погрешность метода прямоугольников, необходимо рассмотреть каждый из элементарных сегментов кривой по отдельности. Общая погрешность в таком случае представляет собой сумму погрешностей всех погрешностей сегментов.
Итак, рассмотрим, чему равна погрешность на одном сегменте.
Площадь одного сегмента вычисляется по приближённой формуле:
$int^{x_i}_{x_{i-1}} f(x)dx≈f(x_{i-1}+frac{x_i-x_{i-1}}{2}) cdot (x_i-x_{i-1})left(4right)$
Погрешность будем определять по разнице со значением первообразной, вычисленной с помощью формулы Ньютона-Лейбница:
$δ_i= int^{x_i}_{x_{i-1}} f(x)dx – f(x_{i-1}+frac{x_{i}-x_{i-1}}{2}) cdot (x_i-x_{i-1})left(5right)$
Так как в левой части равенства $x_{i}-x_{i-1}$ есть не что иное как $int^x{i}_{x_{i-1}}dx$ — длина элементарного отрезка, его можно заменить на $dx$. Перепишем правую часть равенства $(4)$, используя это:
$f(x_{i-1}+frac{x_i-x_{i-1}}{2}) cdot (x_i-x_{i-1})=int^{x_i}_{x_{i-1}} f(x_{i-1}+ frac{x_{i}-x_{i-1}}{2})dx$
$δ_i=int^{x_i}_{x_{i-1}} f(x)dx – int^{x_i}_{x_{i-1}} f(x_{i-1}+ frac{x_{i}-x_{i-1}}{2})dx =int^{x_i}_{x_{i-1}}(f(x)-f(x_{i-1}+ frac{x_i-x_{i-1}}{2})dx left(6right)$
Допуская, что фунцкия $f(x)$ дважды дифференцируема в точке $x=x_{i}-x_{i-1}$ и вокруг неё, разложим её в бесконечную сумму степенных функций, используя ряды Тейлора и формулу Лагранжа:
$f(x)=f(x_{i-1}+frac{Δx}{2})+f’(x_{i-1}+frac{Δx}{2}) cdot (x-(x_{i-1}+frac{Δx}{2}))+f’’(ε_i) cdot frac{(x-(x_{i-1}+frac{Δx}{2}))^2}{2}$
Применим полученное для подстановки:
$f(x)-f(x_{i-1}+ frac{Δx}{2})=f’(x_{i-1}+frac{Δx}{2}) cdot(x-(x_{i-1} + frac{Δx}{2}))+f’’(ε_i) cdot frac{(x-(x_{i-1}+frac{Δx}{2}))^2}{2}left(7right)$
Проинтегрируем $(7)$:
$int^{x_{i}}_{x_{i-1}}(f(x)-f(x_{i-1}+ frac{Δx}{2})dx= int^{x_{i}}_{x_{i-1}}f’(x_{i-1}+frac{Δx}{2}) cdot(x-(x_{i-1}+frac{ Δx}{2}))dx+ int^{x_{i}}_{x_{i-1}} f’’(ε_i) cdot frac{x-(x_{i-1}+ frac{Δx}{2}))^2}{2}dx$
В конечном итоге для элементарного сегмента $left[x_{i-1};x_iright]$ имеем:
$δ_i=int^x{i}_{x_{i-1}} (f(x)-f(x_{i-1}+frac{Δx}{2}))=frac{f’’(ε_i) cdot h^3}{24}$ и наконец,
$|δ_i|≤max_{xin left[x_{i-1};x_iright]}|f’’(x)| cdot frac{h^3}{24}.$
Для всей же фигуры погрешность полученной площади составит:
$δ_i=sum^n_{i=1}int^{x_i}_{x_{i-1}}(f(x)-f(x_{i-1}+frac{Δx}{2}))dx$
и в конечном виде:
Определение 4
$|δ_i|≤max_{xin left[a;bright]}|f’’(x)| cdot frac{(b-a)^3}{24n^2}$
Данная формула используется для получения погрешности при использовании формулы для средних прямоугольников.
Формула для погрешности методов правых и левых прямоугольников выводится аналогичным способом и имеет следующий вид:
Определение 5
$|δ_i|≤max_{xin left[a;bright]}|f’(x)| cdot frac{(b-a)^2}{2n}$
Погрешность, полученная с использованием метода правых или левых прямоугольников для вычисления интегралов больше, чем погрешность при использовании метода средних прямоугольников. Поэтому более предпочтительным для приближённого интегрирования является именно метод средних прямоугольников.
Пример 1
Вычислить интеграл $int_1^2 frac{dx}{x}=ln2$ с точностью до $0, 001$ используя формулу средних прямоугольников.
Разобьём нашу функцию на 10 равных сегментов.
В начале оценим погрешность вычисления:
$|δ_n|≤max_{xin left[a;bright]}|(frac{1}{x})’| cdot frac{(2-1)^3}{24 cdot 10^2}$
В данном случае погрешность меньше либо равна:
$|δ_n|≤0.000042$, следовательно, в данном случае для разбиения можно использовать 10 сегментов.
Разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=frac{2-1}{10}=0,1$ и вычислим значение подынтегральной функции $y(x)=frac{1}{x}$ в середине каждого отрезка:
$x_frac{1}{2}=1,05; y_frac{1}{2}=0,9524;$
$x_frac{3}{2}=1,15; y_frac{3}{2}=0,8696;$
$x_frac{5}{2}=1,25; y_frac{5}{2}=0,8;$
$x_frac{7}{2}=1,35; y_frac{7}{2}=0,7407;$
$x_frac{9}{2}=1,45; y_frac{9}{2}=0,6897;$
$x_frac{11}{2}=1,55; y_frac{11}{2}=0,6452;$
$x_frac{13}{2}=1,65; y_frac{13}{2}=0,6061;$
$x_frac{15}{2}=1,75; y_frac{15}{2}=0,5714;$
$x_frac{17}{2}=1,85; y_frac{17}{2}=0,5405;$
$x_frac{19}{2}=1,95; y_frac{19}{2}=0,5128;$
Сумма всех вычисленных значений функции $f(x)$ составит $6.9284$, а само значение составит:
$int_1^2 frac{dx}{x}=frac{6,9284}{10}=0.69284$ — что отвечает требуемому условию о погрешности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме