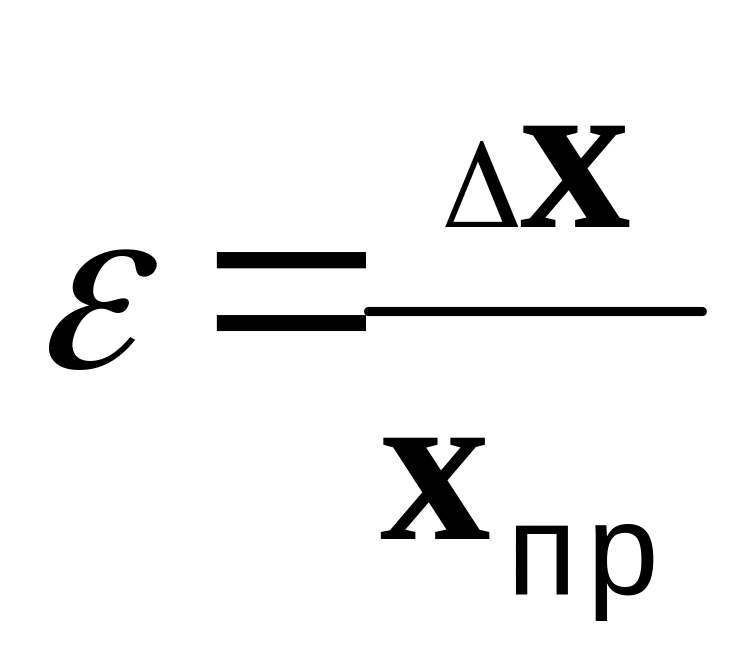Оценка погрешностей измерений при выполнении лабораторных работ по физике
Выполнение лабораторных
работ связано с измерением различных
физических величин и последующей
обработкой полученных результатов.
Поскольку не существует абсолютно
точных приборов и других средств
измерения, следовательно, не бывает
и абсолютно точных результатов измерения.
Погрешности возникают при любых
измерениях, и только правильная оценка
погрешностей проведенных измерений и
расчетов позволяет выяснить степень
достоверности полученных результатов.
Абсолютная погрешность измерения
Рисунок
1
Предположим, что
диаметр стержня, измеренный штангенциркулем,
оказался равным 14 мм. Можно ли быть
уверенным, что он пройдет в “идеальное”
отверстие того же диаметра? Если бы этот
вопрос был поставлен чисто ”теоретически“,
то ответ был бы утвердительным, но на
практике может получиться иначе. Диаметр
стержня был определен с помощью реального
измерительного прибора, следовательно,
с некоторой погрешностью. Значит 14 мм
– это приближенное
значение диаметра
– Xпр.
Определить его истинное значение
невозможно, можно только указать
некоторые границы достоверности
полученного приближенного результата,
внутри которых находится истинное
значение диаметра нашего стержня. Эта
граница называется границей
абсолютной погрешности
и обозначается ΔX
(её часто называют просто абсолютной
погрешностью).
Поэтому наш стержень может пройти в
отверстие, а так же может и не пройти в
него: все зависит от того, в каком месте
интервала [Xпр
– ΔX,
Xпр
+ ΔX]
находится
истинное значение диаметра нашего
стержня. На рисунке 1 показан случай,
когда стержень в отверстие не пройдет.
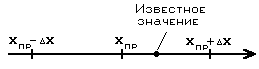
Итак, абсолютная
погрешность показывает, насколько
неизвестное экспериментатору истинное
значение измеряемой величины может
отличаться от измеренного значения.
Результат измерения
с учетом абсолютной погрешности
записывают так:
Относительная погрешность измерения
Значение абсолютной
погрешности все же не позволяет в полной
мере оценить качество наших измерений.
Если, например, в результате измерений
установлено, что длина стола с учетом
абсолютной погрешности равна (100±
1) см, а толщина
его крышки равна (2
± 1) см, то качество
измерений в первом случае выше (хотя
граница абсолютной погрешности измерений
в обоих случаях одинакова). Качество
измерений характеризуется относительной
погрешностью ε,
равной отношению абсолютной погрешности
ΔX к значению
величины Xпр,
получаемой в результате измерения:
.
При выполнении
лабораторных работ выделяют следующие
виды погрешностей:
погрешности прямых измерений; погрешности
косвенных измерений; случайные погрешности
и систематические погрешности.
Погрешности прямых измерений
Прямое измерение
– это такое
измерение, при котором его результат
определяется непосредственно в процессе
считывания со шкалы прибора. В нашем
первом примере с определением диаметра
стержня речь шла как раз о таком измерении.
Погрешность прямого измерения обозначается
значком Δ. Если вы умеете правильно
пользоваться измерительным прибором,
то погрешность прямого измерения зависит
только от его качества и равна сумме
инструментальной
погрешности
прибора (Δ и)
и погрешности
отсчета (Δ 9).
Таким образом: Δ = Δ и
+ Δ о
Инструментальная
погрешность
измерительного прибора (Δи)
определяется на заводе-изготовителе.
Абсолютные инструментальные погрешности
измерительных приборов, чаще всего
используемых для проведения лабораторных
работ, приведены в таблице 1.
Таблица
1
|
Средства измерения |
Предел измерения |
Цена деления |
Инструментальная погрешность |
|
Линейка ученическая |
До 30 см |
1 мм |
|
|
Линейка чертежная |
До 50 см |
1 мм |
0,2 |
|
Линейка инструментальная |
До 30 см |
1 мм |
0,1 |
|
Линейка демонстрационная |
100 см |
1 см |
0,5 |
|
Лента измерительная |
150 см |
0,5 см |
0,25 |
|
Измерительный |
до 250 мл |
1 мл |
1 |
|
Штангенциркуль |
150 мм |
0,1 мм |
0,05 |
|
Микрометр |
25 мм |
0,01 мм |
0,005 |
|
Динамометр учебный |
4 Н |
0,1 Н |
0,05 |
|
Секундомер электронный |
100 с |
0,01 с |
0,01 |
|
Барометр-анероид |
720-780 мм.рт.ст |
1 мм.рт.ст. |
3 |
|
Термометр спиртовой |
0-100оС |
1оС |
1оС |
|
Термометр ртутный |
До 250оС |
1оС |
0,5оС |
|
Амперметр школьный |
2 А |
0,1 А |
0,05 |
|
Вольтметр школьный |
6 В |
0,2 В |
0,15 |
Погрешность отсчета
измерительного прибора (Δ
о)
связана с тем, что указатель прибора
не всегда точно совпадает с делениями
шкалы. В этом случае погрешность отсчета
не превосходит половины цены деления
шкалы.
Поэтому абсолютную
погрешность прямого измерения находят
по формуле
.,
где с – цена деления шкалы измерительного
прибора.
Учитывать погрешность
отсчета надо только в тех случаях, когда
указатель прибора при измерении находится
между нанесенными на шкалу прибора
делениями. Не имеет смысла учитывать,
погрешности отсчета у цифровых
измерительных приборов.
Одновременно
учитывать обе составляющие погрешности
прямого измерения следует лишь в том
случае, если их значения близки друг к
другу. Любым из
этих слагаемых можно пренебречь, если
оно не превосходит одной трети или
одной четверти второго. В этом состоит
так называемое правило “ничтожных
погрешностей“.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лабораторная
работа №
«Название
лабораторной работы»
Цель работы: (ознакомление с методами
измерения физических величин; изучение физических явлений и законов …).
Приборы и материалы: (перечислить все
используемое в лабораторной работе оборудование).
Теоретическое обоснование: (Выводятся основные
расчетные формулы, проводится краткое (схематическое) обоснование
эксперимента).
Ход работы: (Кратко описываются
основные этапы выполнения лабораторной работы. Результаты измерений и расчета
погрешностей заносят в таблицу).
Расчет погрешностей:
Результат измерения физической величины
всегда отличается от ее истинного значения, наиболее точно отражающего
соответствующую физическую характеристику. Действительное значение –
значение физической величины, найденное экспериментально. Точность измерения
определяется близостью действительного значения физической величины к
истинному. Отклонение результата измерения от истинного значения называется погрешностью
измерений. Качество измерений физической величины характеризуется абсолютной
и относительной погрешностью.
Абсолютная погрешность (Δа) при однократном прямом измерении равна приборной
погрешности.
Инструментальные погрешности мер и измерительных приборов
|
Деревянная линейка (мм) |
Линейка (мм) |
Мерная лента (см) |
Весы учебные (г) |
Гири 4 класса |
Измерительный цилиндр (мл) |
|||||||||||
|
Номинальное значение |
300 – 350 |
200 – 250 |
150 |
200 |
100 г |
50 г |
20 г |
10 г |
5 г |
2 г |
1 г |
мг |
500 |
250 |
100 |
50 |
|
Цена деления |
1 |
1 |
0,5 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
5 |
5 |
1 |
1 |
|
Погрешность |
0,5 |
1 |
0,25 |
0,1 |
0,04 |
0,03 |
0,02 |
0,012 |
0,008 |
0,006 |
0,004 |
0,001 |
5 |
2,5 |
1 |
0,5 |
|
Класс точности |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
|
Динамометр уч. (Н) |
Термометр лабораторный ртутный (0С) |
Термометр (не ртутный (0С)) |
Амперметр (А) |
Вольтметр (В) |
Барометр анероид (мм.рт.ст.) |
Набор сопротивлений (Ом) |
Секундомер (с) |
Транспортир (рад) |
Штангенциркуль (мм) |
|||||
|
Номинальное значение |
4 |
– |
– |
2 |
4 |
720 – 780 |
1 |
2 |
4 |
0 – 30 |
3,14 |
– |
||
|
Цена деления |
0,1 |
1 |
– |
0,1 |
0,2 |
1 |
– |
– |
– |
0,2 |
0,017 |
– |
||
|
Погрешность |
0,05 |
1 |
ЦД |
0,08 |
0,1 |
0,16 |
0,2 |
3 |
– |
– |
– |
0,1 |
0,02 |
– |
|
Класс точности |
– |
– |
– |
4% |
5% |
4% |
5% |
– |
– |
– |
– |
– |
– |
– |
Результат однократного измерения принято
записывать в виде : а = аизмеренное Δа.
Затем результат откладывают на числовой оси:
Относительная погрешность (ε) при однократном измерении – безразмерная физическая величина,
равная отношению абсолютной погрешности к измеренному значению физической
величины:
Точность измерений различных физических
величин сравнивают по их относительным погрешностям. Чем меньше относительная
погрешность, тем выше точность измерения.
Погрешность справочных и табличных величин (если погрешность не указана) составляет пять единиц разряда,
следующего после последней значащей цифры (Например: g = 9,8 м/с2; Δg = 0,05 м/с2).
Погрешности при прямых измерениях физической величины:
Прямое измерение – нахождение числового
значения искомой физической величины непосредственно средствами измерения.
Точность результата однократного измерения
значения физической величины невелика, вследствие двух погрешностей, которые
невозможно исключить в процессе опыта:
Случайная погрешность – погрешность,
изменяющаяся случайным образом при повторных измерениях. Она вызывается
непостоянством внешних условий и несовершенными действиями экспериментатора.
Грубая погрешность (промах) – погрешность,
существенно превышающая ожидаемую при данных условиях. Грубая погрешность
обусловлена ошибочным отсчетом или временной неисправностью измерительного
прибора.
Для уменьшения влияния случайных факторов
проводят многократные измерения данной физической величины а1, а2,
а3, … аn. При этом результаты
измерений, содержащих промахи, исключаются из дальнейшей обработки результатов.
В качестве действительного значения
физической величины принимают среднее арифметическое измеряемой величины:
, где n – число
измерений.
Случайную погрешность оценивают как модуль отклонения результатов измерений то среднего
арифметического значения:
Результирующая абсолютная погрешность Δа при
прямых измерениях физической величины а учитывает как приборную Δапр,
так и случайную Δасл погрешность и находится как их сумма:
Δа = Δапр+ Δасл
Значение физической величины, полученное в
результате прямого измерения, записывается в виде:
а = аср Δа и откладывается на
числовой оси.
Относительная погрешность при прямых
измерениях высчитывается по формуле:
Существуют определенные правила записи окончательного
результата измерений физической величины. Абсолютная погрешность приводится с
одной значащей цифрой после запятой. Две значащие цифры необходимо сохранять,
если первой значащей цифрой после запятой, характеризующей величину
погрешности, будет 1. (Например: значение 11, 394576 округляем до 11,4;
значение 11,001346 округляем до 11,0013). При записи окончательного результата
значения измеряемой величины, разряд последней значащей цифры должен совпадать
с разрядом последней значащей цифры абсолютной погрешности. (Например:
а = (12,6 0,4)м; а = (12,64
0,14)м).
Расчет погрешностей при косвенных измерениях физической величины
Косвенное измерение – нахождение числового
значения искомой физической величины по формуле, связывающей ее с другими
физическими величинами, определяемыми в результате прямых измерений.
Погрешности косвенно измеряемой величины
зависит от погрешностей всех величин, входящих в расчетную формулу. В таблице
представлены выражения для расчета относительной погрешности физической
величины а, измеряемой косвенно и зависящей от величин x и
y, имеющих абсолютные погрешности Δx и
Δy:
|
а |
ε |
|
С(x |
|
|
C(x – y) |
|
|
Cxy; |
|
|
C xk yn |
|
Абсолютная погрешность Δа
величины а находится по формуле Δа = аср ε.
Окончательный результат записывают в виде а = аср Δа и откладывают на числовой оси.
Вывод: (Записываются основные результаты эксперимента,
и делается логическое заключение).
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.