Загрузить PDF
Загрузить PDF
Погрешность измерения, выраженная в процентах (далее процентная погрешность) — это разность между истинным и измеренным значением, деленная на истинное значение и умноженная на 100. Процентная погрешность позволяет представить, насколько (в процентах) измеренное значение отличается от истинного. Погрешность может быть вызвана ошибками в измерениях (неточными инструментами или человеческим фактором) или из-за округлением значений. При этом формула для вычисления процентной погрешности довольно простая.
-

1
Запишите формулу для вычисления процентной погрешности. Формула: [(|Измеренное значение — Истинное значение|) / Истинное значение] x 100. В эту формулу необходимо подставить два значения — измеренное и истинное.[1]
- Измеренное значение — это оценочное (приблизительное) значение; истинное значение — это точное значение.
- Например, если вы думаете, что в сумке лежат 9 апельсинов, но на самом деле их 10, число 9 — это приблизительное значение, а 10 — точное значение.
-

2
Вычтите точное значение из оценочного. В нашем примере вычтите 10 (точное значение) из 9 (оценочное значение): 9 – 10 = -1.[2]
- Эта разность характеризует различие между приблизительным и точным значениями, то есть насколько точное значение отличается от оценочного.
-

3
Найдите абсолютное значение этой разности. Так как в формулу нужно подставить абсолютное значение разности, знаком «минус» можно пренебречь. То есть в нашем примере -1 превратится в 1.[3]
- В нашем примере: 9 – 10 = -1. Абсолютное значение -1 записывается так: |-1| = 1.
- Если разность положительная, не меняйте ее. Например: 12 яблок (приблизительное значение) – 10 яблок (точное значение) = 2. Абсолютное значение 2: |2| = 2.
- В статистике абсолютное значение означает, что вас не интересует, в каком направлении отклоняется оценочное значение (слишком большое, то есть положительное, или слишком маленькое, то есть отрицательное). Вы просто хотите знать, на какую величину оценочное значение отличается от истинного.
-

4
Разделите найденную разность на абсолютную величину истинного значения. Сделайте это на калькуляторе или вручную. В нашем примере точное значение уже положительное, поэтому просто разделите 1 (полученная разность) на 10 (точное значение).[4]
- В нашем примере: 1/|10|= 1/10.
- В некоторых случаях точное значение может быть отрицательным числом. Если это так, знак «минус» можно проигнорировать (то есть работайте с абсолютной величиной точного значения).[5]
Реклама
-

1
Преобразуйте обычную дробь в десятичную. В проценты проще преобразовать десятичную дробь. В нашем примере 1/10 = 0,1. Более сложные вычисления выполните на калькуляторе.
- Если под рукой калькулятора нет, разделите числа в столбик, чтобы получить десятичную дробь. Как правило, достаточно 4–5 цифр после десятичной запятой, чтобы округлить дробь.
- При преобразовании обычной дроби в десятичную всегда делите положительное число на положительное число.
-

2
Умножьте полученную десятичную дробь на 100. В нашем примере умножьте 0,1 на 100, а затем к результату припишите символ «%». Так вы получите процентную погрешность.[6]
- В нашем примере: 0,1 x 100 = 10 %.
-

3
Проверьте результат, чтобы убедиться, что он правильный. Иногда замена знаков (положительный/отрицательный) и деление могут привести к незначительным ошибкам в расчетах. Поэтому лучше проверить ответ.
- В нашем примере необходимо убедиться, что оценочное значение (9 апельсинов) отличается от истинного значения (10 апельсинов) на 10 %. 10 % (10 % = 0,1) от 10 апельсинов равно 1 (0,1 × 10 = 1).
- 9 апельсинов + 1 = 10 апельсинов. Это подтверждает, что оценочное значение (9) действительно отличается от истинного значения (10) на 1 (то есть на 10 %).
Реклама
Советы
- Иногда измеренное (оценочное, приблизительное) значение называется экспериментальным, а истинное (точное) значение называется теоретическим. Обязательно используйте значение, с которым сравнивается данное значение, как точное значение.
- Так как в данном методе используются абсолютные величины приблизительных и точных значений, нет разницы, в каком порядке вычитать числа. Например,|8 – 4| = 4 и |4 – 8| = |-4|= 4. Результаты одинаковые!
Реклама
Об этой статье
Эту страницу просматривали 64 675 раз.
Была ли эта статья полезной?
1) Абсолютная погрешность.
Абсолютную погрешность принято обозначать прописной греческой буквой дельта (Δ).
Чтобы найти абсолютную погрешность, следует воспользоваться формулой:
Δ = |x – x0|
где
Δ — абсолютная погрешность;
x — приближённое (практическое) значение измеряемой величины;
x0 — точное (истинное/теоретическое) значение измеряемой величины.
Абсолютная погрешность имеет ту же единицу измерения, что и измеряемая величина. Например: если измеряемая величина измеряется в метрах, то и абсолютная погрешность будет измеряться в метрах; если изм. величину мы измеряем в килограммах, то и абсолютную погрешность — тоже в килограммах. И так далее.
2) Относительная погрешность.
Относительная погрешность, как правило, обозначается строчной греческой буквой дельта (δ).
Чтобы найти относительную погрешность, следует воспользоваться формулой:
δ = |x – x0|/x0
где
δ — относительная погрешность;
x — приближённое (практическое) значение измеряемой величины;
x0 — точное (истинное/теоретическое) значение измеряемой величины.
Относительная погрешность является безразмерной величиной. Относительная погрешность либо имеет единицу измерения 1 (доли единицы), либо измеряется в процентах.
Чтобы перевести относительную погрешность из долей единицы в проценты, необходимо умножить её на 100.
δ (%) = δ * 100 = (|x – x0|/x0) * 100
Для примера рассмотрим такую задачу.
Ученик измерял линейкой длину карандаша. В результате измерений ученик получил результат, равный 152 мм. Истинная же длина карандаша, измеренная штангенциркулем, равняется 151,7 мм. Вопрос: чему равна абсолютная и относительная погрешность результата измерений ученика?
Дано:
x = 152 мм;
x0 = 151,7 мм.
Найти:
Δ — ?
δ — ?
Решение.
1) Найдём абсолютную погрешность.
Δ = |x – x0| = |152 мм – 151,7 мм| = |0,3 мм| = 0,3 мм.
2) Найдём относительную погрешность.
δ = |x – x0|/x0 = (|152 мм – 151,7 мм|/151,7 мм) * 100% = (0,3 мм : 151,7 мм) * 100% = 0,198 %.
Ответ: Δ = 0,3 мм; δ = ок. 0,198 % (приближённое значение).
Percentage error is an estimation of the inconsistency between a noticed and a valid or acknowledged esteem. While estimating information, the outcome regularly shifts from genuine worth. The error can emerge because of a wide range of reasons that are regularly connected with human error yet can likewise be because of assessments and limits of gadgets utilized in the estimation. Notwithstanding, in such cases, it becomes essential to ascertain the percentage error. The calculation of percentage error includes the outright error, which is basically the contrast between the noticed and the genuine worth. The absolute error is then partitioned by the exact value, bringing about the general error duplicated by 100 to get the percentage error.
The percentage error value is a lot of significant under test computations. It permits us to perceive how far separated the evaluations and the exact value was, concerning a percentage. Hence we really want to process percentage errors experiencing the same thing.
Percent error
Percent/Percentage error is the distinction between the actual value and the estimated value contrasted with the actual value and is communicated in a percentage design. All in all, you track down the distinction between the actual response and the speculated reply, partition it by the actual response, and express it as a percentage. Percent errors demonstrate how gigantic our errors are at the point at which we measure something. For example, a 3% error demonstrates that we got extremely near the acknowledged value, while 80% implies that we were very a long way from the actual value
In simple words, Percentage error is the contrast between a deliberate and exact value, isolated by the known value, and subsequently increased by 100 percent. For some applications, percentage error is communicated as a positive value. Regularly, the absolute value of the error is partitioned by an accepted value and given as a percent.
Percent error formula
The formula for finding percent error,
Percent Error = (Actual Value – Estimated Value)/(Exact value) × 100
Most of the time, the percentage error is expressed as a positive value.
Actual value can be a few times named as true value or exact value.
Finding the Percent Error
Percentage error can be determined utilizing three straightforward advances,
- Work out the error (Deduct assessed esteem from the real worth) and disregard any negative (-) sign. i.e., take the absolute worth of error.
Absolute Error = Approximate Value – Exact Value
- Partition the error by the real worth (in some cases, we might get a decimal number).
Relative Error = (Approximate Value – Exact Value )/( Exact Value)
- Convert that to a percentage (by increasing by 100 connect “%” sign)
Percent Error = {(Approximate Value – Exact Value )/( Exact Value)} × 100 percent.
The absolute worth of the error is separated by a genuine worth and displayed as a percent.
Sample Questions
Question 1: Mr. Raju measured his height and found 6 feet. But later on, by careful observation, he has found his actual height to be 5.5 ft. Find the percent error Raju made in measuring his height.
Solution:
Before solving the problem, let us identify the information,
Actual value = 5.5 ft and Estimated value = 6 ft.
Now,
Step 1: Subtract one value from others to get the absolute value]e of error.
Error = 6 – 5.5
= 0.5
Step 2: Divide the error by actual value.
0.5/5.5 = 0.0909 (up to 4 decimal places)
Step 3: Multiply that answer by 100 and attach the % symbol to express the answer as a percentage
0.0909 × 100 = 9.09%
Therefore Percentage error measured is 9.09%
Question 2: Lakshmi’s mathematical class had 34 children yesterday. She miscounted the class total and recorded it as 28 children. What is Lakshmi’s percent error?
Solution:
The actual number of students = 34
Recorded number of students = 28
Absolute Error = 34 – 28 = 6
Percent Error = 6/28 = 0.21
= 0.21 × 100 = 21%
Lakshmi’s percent error is 21%
Question 3: A boy measured the area of a rectangle plot to be 450 cm². But the actual area of the plot has been recorded as 455 cm². Calculate the percent error of his measurement.
Solution:
Given,
Measured area value = 450 cm²
Actual area value = 455 cm²
Steps of calculation,
Step 1: Subtract one value from another; 455 – 450 = 5
the difference is 5, which is the error.
Step 2: Divide the error by actual value; 5/455 = 0.0109
Step 3: Multiply this value by 100
0.0109 × 100 = 0.109% (expressing it in two decimal points)
Hence, 0.10% is the percent error.
Question 4: A scale measures wrongly a value as 21 cm due to some marginal errors. Calculate the percentage error if the actual measurement of the value is 17 cm.
Solution:
Given in the problem,
Recorded measurement = 21 cm
Actual measurement = 17 cm
Error = Recorded measurement – Actual measurement
= 21 – 17 = 4
Applying the formula for the computation,
Percentage Error = (Error) / (Actual measurement) × 100
= (4/17) × 100 = 0.235 × 100 = 23.5
Percentage Error calculated as 23.5%
Question 5: John expected 30 people to turn up for a job interview, but only 24 did. What was the percentage error?
Solution:
The actual number of people attended = 24
Number of people expected = 30
Absolute Error = 30 – 24 = 6
Percent Error = 6/30 = 0.20
= 0.20 × 100 = 20%
John’s percent error is 20%
Question 6: Sam thought 90 people would turn up to the concert, but in fact, 100 did. What would be Sam’s percent error?
Solution:
The actual number of people came to concert = 100
Number of people Sam expected = 90
Error = Expected number of people attended – Actual number of people
= 100 – 90 = 10
Applying the formula for the computation,
Percentage Error = (Error) / (Actual measurement) × 100
= (10/90) × 100 = 0.235 × 100 = 23.5
Percentage Error calculated as 23.5%
Question 7: Shreya is attempting the precision of a scale in her science lab. She took a weight that she knew had a mass of 30 kg and weighed it. The scale read that the weight weighed 30.4 kg. What is the absolute error of the mass of the weight that Shreya recorded? And also find percent error?
Solution:
Use the absolute error formula to determine this,
Absolute Error = |Actual Value – Measured Value|
Absolute Error = x
Actual Value = 30
Measured Value = 30.4
= |30 – 30.4| = |−0.4| = 0.4
The absolute error was 0.4 kg.
Percentage Error = (Error) / (Actual value) × 100
= (0.4/30) × 100
=1.3333% (Considering upto 2 decimal points)
Therefore Shreya’s percent error is 1.33%
Last Updated :
02 Jun, 2022
Like Article
Save Article
Как рассчитать процент ошибки
На чтение 4 мин. Просмотров 1.8k. Опубликовано 05.06.2021
Ошибка в процентах или ошибка в процентах выражает в процентах разницу между приблизительным или измеренным значением и точным или известным значением. Он используется в науке для сообщения о разнице между измеренным или экспериментальным значением и истинным или точным значением. Вот как вычислить процентную ошибку с примером вычисления.
Содержание
- Ключевые моменты: процентная ошибка
- Формула процентной ошибки
- Шаги вычисления процентной ошибки
- Пример вычисления процента ошибки
- Процент Ошибка в сравнении с абсолютной и относительной ошибкой
- Источники
Ключевые моменты: процентная ошибка
- Цель вычисления процентной ошибки – определить, насколько близко измеренное значение к истинному значению.
- Ошибка в процентах (ошибка в процентах) – это разница между экспериментальное и теоретическое значение, разделенное на теоретическое значение, умноженное на 100, чтобы получить процент.
- В некоторых полях процентная погрешность всегда выражается как положительное число. В других случаях правильно иметь либо положительное, либо отрицательное значение. Знак может быть сохранен, чтобы определить, постоянно ли записанные значения оказываются выше или ниже ожидаемых значений.
- Ошибка в процентах – это один из типов вычисления ошибок. Абсолютная и относительная погрешности – два других общих вычисления. Процентная ошибка является частью комплексного анализа ошибок.
- Ключом к правильному сообщению процентной ошибки является знание того, следует ли опускать знак (положительный или отрицательный) при вычислении, и сообщать значение, используя правильное количество значащих цифр.
Формула процентной ошибки
Процентная ошибка – это разница между измеренным или экспериментальным значение и принятое или известное значение, разделенное на известное значение, умноженное на 100%.
Для многих приложений процентная ошибка всегда выражается как положительное значение . Абсолютное значение ошибки делится на допустимое значение и выражается в процентах.
| принятое значение – экспериментальное значение | принятое значение x 100%
Для химии и других наук принято оставлять отрицательное значение, если оно произойдет. Важно, является ли ошибка положительной или отрицательной. Например, вы не ожидаете получить положительную процентную ошибку при сравнении фактического выхода с теоретическим в химической реакции. Если было вычислено положительное значение, это дало бы подсказку относительно потенциальных проблем с процедурой или неучтенных реакций.
При сохранении знака ошибки вычисление будет экспериментальное или измеренное значение минус известное или теоретическое значение, разделенное на теоретическое значение и умноженное на 100%.
ошибка в процентах = [ экспериментальное значение – теоретическое значение]/теоретическое значение x 100%
Шаги вычисления процентной ошибки
- Вычтите одно значение из другого. Порядок не имеет значения, если вы опускаете знак (беря абсолютное значение. Вычтите теоретическое значение из экспериментального значения, если вы сохраняете отрицательные знаки. Это значение является вашей «ошибкой».
- Разделить погрешность точным или идеальным значением (не вашим экспериментальным или измеренным значением). В результате будет получено десятичное число.
- Преобразуйте десятичное число в процент, умножив его на 100.
- Добавьте символ процента или%, чтобы сообщить значение процентной ошибки. .
Пример вычисления процента ошибки
В лаборатории вам дают блок алюминия. Вы измеряете размеры блока и его объем в емкости с водой известного объема. Вы рассчитываете, что плотность алюминиевого блока составляет 2,68 г/см 3 . Вы проверяете плотность алюминиевого блока при комнатной температуре и обнаруживаете, что она составляет 2,70 г/см 3 . Вычислите процентную ошибку вашего измерения.
- Вычтите одно значение из другого:
2,68 – 2,70 = -0,02 - В зависимости от того, что вам нужно, вы можете отбросить любой отрицательный знак (взять абсолютное значение): 0,02
Это ошибка. - Разделите ошибку на истинное значение: 0,02/2,70 = 0,0074074
- Умножьте это значение на 100%, чтобы получить процентную ошибку:
0,0074074 x 100% = 0,74% (выражается с использованием 2 значащих цифр) .
В науке важны значительные цифры. Если вы сообщите об ответе, используя слишком много или слишком мало ответов, это может быть сочтено неправильным, даже если вы правильно настроили проблему.
Процент Ошибка в сравнении с абсолютной и относительной ошибкой
Ошибка в процентах связана с абсолютной ошибкой и относительной ошибкой. Разница между экспериментальным и известным значением – это абсолютная ошибка. Когда вы разделите это число на известное значение, вы получите относительную ошибку. Ошибка в процентах – это относительная ошибка, умноженная на 100%. Во всех случаях сообщайте значения, используя соответствующее количество значащих цифр.
Источники
- Беннет, Джеффри; Бриггс, Уильям (2005), Использование и понимание математики: подход количественного мышления (3-е изд.), Boston: Pearson.
- Торнквист, Лео; Вартия, Пентти; Вартия, Юрьё (1985), «Как следует измерять относительные изменения?», Американский статистик , 39 (1): 43–46.
Процентная ошибка в наборе данных — это разница между точным и приблизительным значениями по сравнению с исходным значением. Эта процентная ошибка выражается в процентах и, следовательно, умножается на 100.
Вы можете выразить процентную ошибку как абсолютную ошибку или относительную ошибку. Ошибки могут возникать из-за ошибки точности в машине, ошибки вычислений, ошибки измерения или условий окружающей среды.
Процентные ошибки помогают нам определить, насколько значительны наши ошибки во время любого анализа. Более мелкие процентные ошибки означают, что мы близки к исходному значению, в то время как более существенные процентные ошибки означают значительное расхождение между фактическим значением и приблизительным значением.
Например, ошибка в 2% будет означать, что мы очень близки к исходному значению, а ошибка в 56% будет означать огромную разницу между фактическим и приблизительным значением.
Ошибки при измерении широко распространены, потому что руки могут трястись во время измерений, инструменты могут быть неисправны, материал может быть неточным и т. д.
Расчет процента ошибки
Для расчета процентной ошибки необходимо иметь два доступных значения. Одно точное значение, а второе приблизительное значение. Вычтите оба этих значения, а затем разделите их на исходное значение. Поскольку процентная ошибка выражается в виде процентов, умножьте полученное таким образом число на 100. Другими словами, процентная ошибка — это относительная ошибка, умноженная на 100.
Процентная ошибка = [(Actual Value – Expected Value) / Expected Value] × 100
Компоненты формулы
Фактическое значение: Фактическое значение указывает числовое значение конкретного показания. Фактическое значение должно было быть записано при снятии показаний, но из-за некоторых ошибок мы не смогли записать это значение. Это обычное значение, которое идеально подходит для проведения расчетов.
Ожидаемое значение: Ожидаемое значение указывает на показания, записанные во время эксперимента. В большинстве случаев оно не похоже на фактическое значение из-за ошибки. Ошибки могут быть вызваны неисправностью машины, ошибкой при снятии показаний или факторами окружающей среды, такими как воздух или сломанные и поврежденные инструменты.
Некоторые примеры
Пример 1
Мальчик измерял площадь треугольника и, по его словам, получил 462 кв.см. Однако первоначальная площадь квадрата равна 465 кв.см. Вычислите процент ошибки.
Решение
Значение измеряемой площади = 462 кв.см
Значение фактической площади = 465 кв. см.
Расчет
Разница фактического значения – измеренного значения: 465-462 = 3
Итак, 3 — это ошибка измерения.
Разделите ошибку на фактическое значение – 3/465 = 0,00645.
Умножив полученное значение на 100 – 0,00645 X 100 = 0,64%.
Следовательно, процентная ошибка при вычислении площади треугольника составляет 0,64%.
Пример 2
Предположим, вы планировали вечеринку, на которой должно было присутствовать около 20 человек, а успели прийти только 18 человек. Вычислите процент ошибки в вашей оценке.
Решение
Первоначальное ожидаемое количество людей = 20
Пришедших = 18
Расчет
Разница фактического значения – конечного значения = 20 – 18 = 2
Итак, 2 — это ошибка здесь.
Разделите ошибку на фактическое значение – 2/20 = 0,1.
Умножение значения на 100 – 0,1 X 100 = 10%
Следовательно, процентная ошибка в оценке количества гостей составляет 10%.
Пример 3
Предположим, вы провели эксперимент по измерению температуры кипения воды и в ходе эксперимента обнаружили, что результат равен 102 °C. Фактическая температура замерзания воды составляет 100°С.
Решение
Фактическая температура кипения воды = 100°С.
Зарегистрированная температура кипения воды = 102°C
Расчет
Разница между фактическим значением и расчетным значением = 100 -102 = 2°C (процентная ошибка никогда не может быть отрицательной, поэтому мы оставляем ее только положительной).
Итак, 2 — это ошибка здесь.
Разделите ошибку на фактическое значение – 2/100 = 0,02.
Умножение полученного значения на 100 – 0,02 X 100 = 2%
Следовательно, процентная погрешность измерения температуры кипения воды составляет 2%.
Реальные сценарии, в которых важна процентная ошибка
- Процентная ошибка играет важную роль, помогая вам определить, была ли конкретная задача, которую вы выполнили, на должном уровне или нет. Это поможет вам указать на ваши ошибки.
- Процентная погрешность может быть полезной в лабораторных процедурах и на крупных предприятиях, где недопустима малейшая ошибка.
- Процентная ошибка также находит свое применение, когда нам нужно выполнить оптовый заказ, и в его выполнении не может быть никаких ошибок.
- В научных лабораториях использование процентной ошибки имеет решающее значение.
Процентная ошибка против абсолютной ошибки
Абсолютная погрешность измерения – это разница между фактическим и расчетным значениями. Единица основной ошибки такая же, как и начальное значение.
Пример
Предположим, вы планировали купить 2 кг манго, а продавец отмерил для вас 1,98 кг. Абсолютная ошибка в этом случае составит 2 – 1,98 = 0,02.
С другой стороны, процентная ошибка рассчитывается путем деления абсолютной ошибки на исходное значение, а затем умножения полученного ответа на 100. Процентная ошибка является безразмерной величиной.
В приведенном выше примере абсолютная ошибка составляет 0,02.
Теперь, чтобы вычислить процентную ошибку, мы разделим ее на 20.
0,02/20 = 0,001
Таким образом, процентная ошибка в этом случае составляет 0,001 X 100 = 0,1%.
Процентная ошибка против относительной ошибки
Относительная ошибка в любом расчете — это абсолютная ошибка, деленная на фактическое значение. Это означает, что процентная ошибка представляет собой разницу между истинным значением и наблюдаемым значением, деленную на фактическое значение.
Пример
Синоптики ожидали, что температура сегодня будет 38°C. Однако она поднялась до 42°C.
Сначала мы находим разницу между двумя числами, т. е. ожидаемым значением и фактическим значением.
42° – 38° = 4°С
Теперь для расчета относительной погрешности мы делим это число на фактическое число, то есть на 38°C.
4/38 = 0,1052
С другой стороны, процентная ошибка — это относительная ошибка, умноженная на 100.
В приведенном выше примере процентная ошибка составит 0,1052 X 100 = 10,52%.
Теперь вы можете обнаружить, что довольно легко вычислить процентную ошибку, относительную ошибку или абсолютную ошибку.
Вы можете упростить расчет процентных ошибок, воспользовавшись помощью нескольких онлайн-калькуляторов процентных ошибок. Теперь вам не придется задаваться вопросом, как рассчитать процентную ошибку, потому что эти калькуляторы могут сделать все это за вас.
Инструменты расчета погрешности
№1. Калькулятор Суп
В Калькулятор Суп помогает рассчитать процентную ошибку между экспериментальным значением и фактическим значением. Все, что вам нужно сделать, это ввести значения и дождаться результатов. Калькулятор сам производит все расчеты и выдает точные результаты.
На странице отображаются два разных столбца, в которых вы вводите значения чисел, для которых хотите рассчитать процентную ошибку, и позволяете калькулятору делать остальную часть магии.
№ 2. Калькулятор.net
Калькулятор.net имеет два столбца, в которые вы вводите фактические и оценочные значения, а остальные расчеты выполняет калькулятор. Это удобно, когда есть много выборок данных, которые вы хотите рассчитать, и у вас нет времени вручную вычислять процентную ошибку в каждом случае. Калькулятор упрощает процесс и дает ответ сразу, без особых задержек.

Процентные ошибки неизбежны. Вы можете только уменьшить их значение, но не будет никакого инцидента, когда показание процентной ошибки станет равным нулю. Он может быть приблизительно равен нулю, но никогда не может быть точным нулем.
№3. Хорошие калькуляторы
Многие онлайн-калькуляторы могут помочь вам решить проблемы с процентной ошибкой. Из них одним из самых удобных является Хорошие калькуляторы. В этом калькуляторе вы просто вводите оценочное и исходное значение, и он автоматически выдает результаты.
Это избавит вас от хлопот, связанных с выполнением обширных вычислений, и сбережет ваше время. Вы можете быстро решить комплексные расчеты за считанные секунды и сэкономить много времени.
Таким образом, калькулятор идеально подходит для расчета процентной ошибки, когда у вас есть под рукой обширные данные, но у вас мало времени.
Вывод
Ошибки в расчетах могут полностью испортить любой проект или исследование. Здесь вы можете воспользоваться помощью онлайн-калькуляторов процентных ошибок, чтобы выполнить работу более эффективно и без человеческих ошибок.
Если вы занимаетесь финансами, вы можете взглянуть на некоторые из этих калькуляторов процента прибыли.
Как рассчитать процент ошибки
Как рассчитать процент ошибки

Процентная ошибка или процентная ошибка выражает в процентах разницу между приблизительным или измеренным значением и точным или известным значением. Это используется в науке, чтобы сообщить разницу между измеренным или экспериментальным значением и истинным или точным значением. Вот как рассчитать процент ошибки, с примером расчета.
Ключевые моменты: процент ошибок
- Цель расчета процентной погрешности состоит в том, чтобы измерить, насколько близко измеренное значение к истинному значению.
- Процентная ошибка (процентная ошибка) — это разница между экспериментальным и теоретическим значением, деленная на теоретическое значение, умноженное на 100, чтобы получить процент.
- В некоторых полях процентная ошибка всегда выражается как положительное число. В других случаях правильно иметь положительное или отрицательное значение. Знак может быть сохранен, чтобы определить, падают ли записанные значения выше или ниже ожидаемых значений.
- Процент ошибок является одним из типов ошибок. Абсолютная и относительная погрешность — два других распространенных вычисления. Процент ошибок является частью всестороннего анализа ошибок.
- Ключом к правильному сообщению процентной ошибки является то, чтобы знать, нужно ли сбрасывать знак (положительный или отрицательный) в расчете, и сообщать значение, используя правильное количество значащих цифр.
Формула процентной ошибки
Процентная ошибка — это разница между измеренным и известным значением, деленная на известное значение, умноженное на 100%.
Для многих приложений процент ошибки выражается как положительное значение. Абсолютное значение ошибки делится на принятое значение и выражается в процентах.
| принятое значение — экспериментальное значение | принятое значение х 100%
Для химии и других наук принято сохранять отрицательное значение. Важна ли ошибка положительная или отрицательная. Например, вы не ожидаете, что будет иметь место положительная процентная ошибка при сравнении фактического теоретического выхода в химической реакции. Если бы было рассчитано положительное значение, это дало бы подсказки относительно потенциальных проблем с процедурой или неучтенных реакций.
При сохранении знака ошибки вычисление представляет собой экспериментальное или измеренное значение минус известное или теоретическое значение, деленное на теоретическое значение и умноженное на 100%.
процентная ошибка = экспериментальное значение — теоретическое значение / теоретическое значение х 100%
Этапы расчета процента ошибок
- Вычтите одно значение из другого. Порядок не имеет значения, если вы отбрасываете знак, но вы вычитаете теоретическое значение из экспериментального значения, если сохраняете отрицательные знаки. Это значение является вашей «ошибкой».
- Разделите ошибку на точное или идеальное значение (не на ваше экспериментальное или измеренное значение). Это даст десятичное число.
- Преобразуйте десятичное число в процент, умножив его на 100.
- Добавьте символ процента или%, чтобы сообщить о вашем процентном значении ошибки.
Пример расчета процента ошибок
В лаборатории вам дают блок алюминия. Вы измеряете размеры блока и его смещение в контейнере с известным объемом воды. Вы рассчитываете плотность блока из алюминия равной 2,68 г / см. 3 , Вы посмотрите на плотность алюминиевого блока при комнатной температуре и обнаружите, что она составляет 2,70 г / см. 3 , Рассчитайте процентную погрешность вашего измерения.
- Вычтите одно значение из другого:
2.68 — 2.70 = -0.02 - В зависимости от того, что вам нужно, вы можете отказаться от любого отрицательного знака (принять абсолютное значение): 0,02
Это ошибка. - Разделите ошибку на истинное значение: 0,02 / 2,70 = 0,0074074
- Умножьте это значение на 100%, чтобы получить процентную ошибку:
0,0074074 х 100% = 0,74% (выражено с использованием 2 значащих цифр).
Значимые цифры важны в науке. Если вы сообщаете об ответе, используя слишком много или слишком мало, он может считаться неправильным, даже если вы правильно настроили проблему.
Процент ошибок по сравнению с абсолютной и относительной ошибкой
Процентная ошибка связана с абсолютной ошибкой и относительной ошибкой. Разница между экспериментальным и известным значением является абсолютной ошибкой. Когда вы делите это число на известное значение, вы получаете относительную ошибку. Процентная ошибка — это относительная ошибка, умноженная на 100%.
MPE – средняя процентная ошибка в Excel
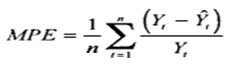 Из данной статьи вы узнаете:
Из данной статьи вы узнаете:
- Для чего нужна средняя процентная ошибка;
- Как она рассчитывается.
+ сможете скачать пример расчета в Excel.
MPE (mean percentage error) — средняя процентная ошибка прогноза.
MPE – средняя процентная ошибка прогноза используется в случаях, когда надо определить модель прогноза дает последовательно завышенные прогнозы или последовательно заниженные прогнозы.
Если значение больше нуля, то прогнозы последовательно занижены, т.е. в среднем меньше факта.
Если ошибка меньше нуля, то прогнозы последовательно завышены, т.е. модель делает прогноз в среднем выше факта.
Как рассчитать среднюю процентную ошибку?
- Рассчитываем ошибку для каждого значения модели;
- Делим на фактические данные ошибку в каждый момент времени.
Рассчитываем среднее по пункту 2, и получает среднюю процентную ошибку — MPE:
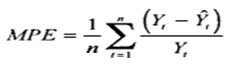
Рассчитаем на примере прогноза объема продаж:
1. Ошибка = фактические продаж минус значения прогнозной модели для каждого момента времени:
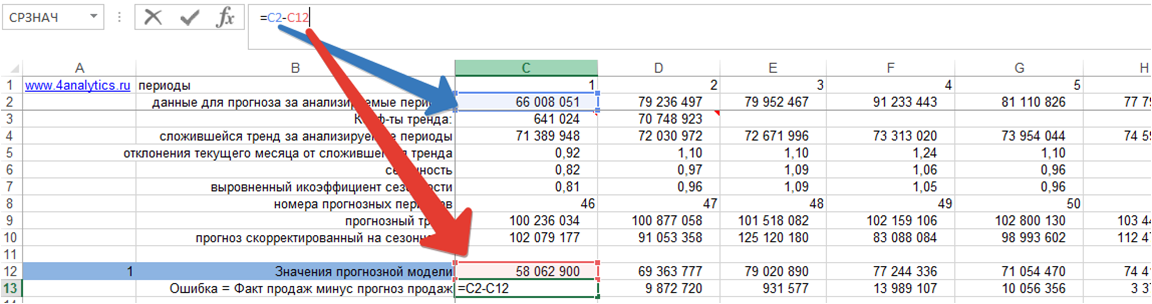
2. Делим ошибку на фактические продажи для каждого периода времени:
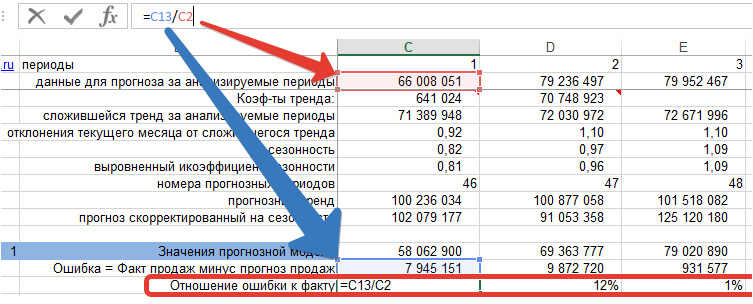
3. Рассчитываем среднее значение % ошибки — MPE:
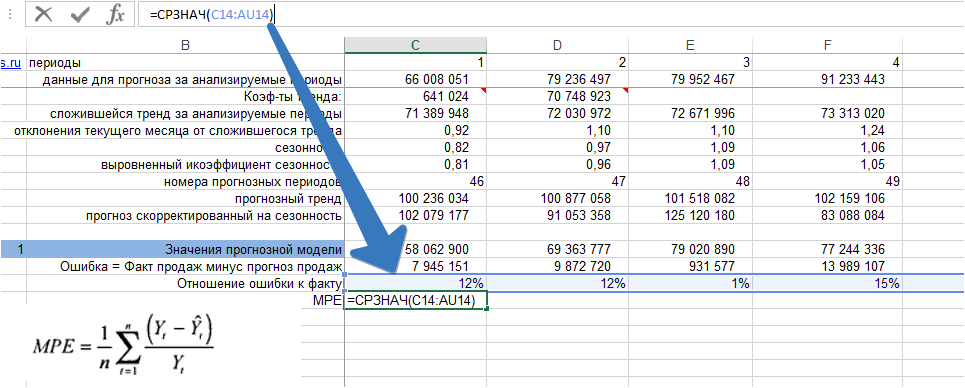
Мы видим, что средняя процентная ошибка у нас получилась -0,65% — это говорит о том, что модель прогноза в среднем дает завышенные прогноза на 0,65%:
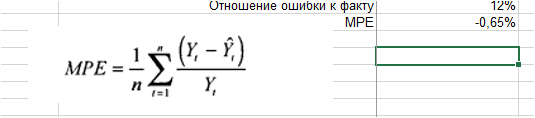
Из данной статьи вы узнали, для чего использовать среднюю процентную ошибку прогноза — MPE и как ее рассчитать в Excel.
Если у вас остались вопросы, пожалуйста, задавайте в комментариях, буду рад помочь!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
6 способов посчитать проценты от суммы с калькулятором и без
Простейшие формулы помогут узнать, выгодны ли скидки, и не нарушить пропорцию классного рецепта.
1. Как посчитать проценты, разделив число на 100
Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.
Пример 1
Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.
Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.
Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.
Умножьте 4,58 на 7, и вы получите 32,06 рубля.
Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.
Пример 2
Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.
Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.
Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.
100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.
2. Как посчитать проценты, разделив число на 10
Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.
Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.
Пример
Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.
В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.
Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.
Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.
В любом случае такими крупными числами оперировать довольно просто.
3. Как посчитать проценты, составив пропорцию
Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:
сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.
Или можно записать её так: a : b = c : d.
Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.
Пример 1
Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.
Сначала вычисляем процентную долю оставшегося шоколада.
90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.
Х = 70 × 100 / 90 = 77,7%.
Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:
200 г : 100% = Х : 77,7%, где Х — нужное количество масла.
Х = 77,7 × 200 / 100 = 155,4.
Следовательно, в тесто нужно положить примерно 155 г масла.
Пример 2
Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.
Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.
Составьте пропорцию: 1 499 : 100 = Х : 87.
Х = 87 × 1 499 / 100.
Заплатите 1 304,13 рубля и носите блузку с удовольствием.
4. Как посчитать проценты с помощью соотношений
В некоторых случаях можно воспользоваться простыми дробями. Например, 10% — это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.
- 20% — 1/5, то есть нужно делить число на 5;
- 25% — 1/4;
- 50% — 1/2;
- 12,5% — 1/8;
- 75% — это 3/4. Значит, придётся разделить число на 4 и умножить на 3.
Пример
Вы нашли брюки за 2 400 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:
100% — 25% = 75% — стоимость брюк в процентах от первоначальной цены после применения скидки.
2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.
5. Как посчитать проценты с помощью калькулятора
Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.
- Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
- Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
- Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.
6. Как посчитать проценты с помощью онлайн-сервисов
Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.
Planetcalc
На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.
Калькулятор — справочный портал
Ещё один сервис с калькуляторами на любой вкус.
Allcalc
Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.
Как рассчитать процент ошибки
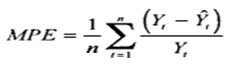 Из данной статьи вы узнаете:
Из данной статьи вы узнаете:
- Для чего нужна средняя процентная ошибка;
- Как она рассчитывается.
+ сможете скачать пример расчета в Excel.
MPE (mean percentage error) — средняя процентная ошибка прогноза.
MPE – средняя процентная ошибка прогноза используется в случаях, когда надо определить модель прогноза дает последовательно завышенные прогнозы или последовательно заниженные прогнозы.
Если значение больше нуля, то прогнозы последовательно занижены, т.е. в среднем меньше факта.
Если ошибка меньше нуля, то прогнозы последовательно завышены, т.е. модель делает прогноз в среднем выше факта.
Как рассчитать среднюю процентную ошибку?
- Рассчитываем ошибку для каждого значения модели;
- Делим на фактические данные ошибку в каждый момент времени.
Рассчитываем среднее по пункту 2, и получает среднюю процентную ошибку — MPE:
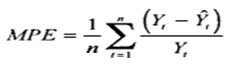
Рассчитаем на примере прогноза объема продаж:
1. Ошибка = фактические продаж минус значения прогнозной модели для каждого момента времени:

2. Делим ошибку на фактические продажи для каждого периода времени:

3. Рассчитываем среднее значение % ошибки — MPE:

Мы видим, что средняя процентная ошибка у нас получилась -0,65% — это говорит о том, что модель прогноза в среднем дает завышенные прогноза на 0,65%:
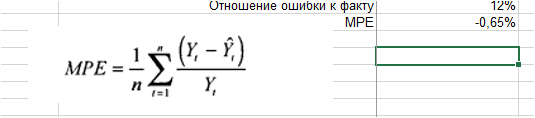
Из данной статьи вы узнали, для чего использовать среднюю процентную ошибку прогноза — MPE и как ее рассчитать в Excel.
Если у вас остались вопросы, пожалуйста, задавайте в комментариях, буду рад помочь!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Как определить существенность ошибки в бухгалтерской отчетности
Ошибиться при составлении бухгалтерской отчетности может каждый. Главное — исправить ошибку. А порядок ее исправления зависит от двух моментов: является ли ошибка существенной и в каком периоде она обнаружен а пп. 3, 5— 11, 14 ПБУ 22/2010 .
Существенная ошибка — ошибка, которая в отдельности или вместе с другими ошибками за тот же период может повлиять на экономические решения пользователей, принимаемые ими на основе бухотчетности этого период а пп. 3, 5— 11, 14 ПБУ 22/2010 .
Как вносить исправления в учет
Что такое существенность ошибки
Критерий существенности ошибки вы определяете и устанавливаете сами, прописав его в учетной политик е п. 3 ПБУ 22/2010 ; п. 4 ПБУ 1/2008 . Он должен быть обоснованным.
ВАРИАНТ 1. Можно ориентироваться на те же правила определения существенности показателя, что содержатся в ПБУ 9/99 о доходах и ПБУ 10/99 о расходах. Напомним, там сказано, что доход (расход) по определенному виду деятельности показывается в отчетности отдельно, если он составляет 5% и более от общей суммы доходов (расходов) за отчетный перио д п. 18.1 ПБУ 9/99 ; п. 21.1 ПБУ 10/99 . По аналогии можно закрепить в учетной политике, что ошибка является существенной, если она искажает показатель за отчетный период более чем на 5%.
ВАРИАНТ 2. Можно оценивать существенность ошибки исходя из удельного веса статьи баланса, при отражении которой допущена ошибка, в валюте баланса. К примеру, неправильно определен срок полезного использования ОС. Его цена не превышает сотни тысяч рублей. А стоимость всех активов компании исчисляется миллионами. Понятно, что допущенная ошибка не повлияет на принятие собственниками компании решений по этой бухотчетности. Другое дело, если компания купила недвижимость, но несвоевременно отразила ее стоимость на балансе, а других ОС у компании нет. Такую ошибку уже нужно признать существенной.
ВАРИАНТ 3. Может быть использован такой качественный показатель, как вид деятельности. Например, ваш основной вид деятельности — торговля, неосновной — аренда. Можно установить, что ошибки, допущенные в учете по аренде, всегда несущественны.
ВАРИАНТ 4. Можно прописать, что существенность ошибки будет оцениваться по каждому конкретному случаю отдельно исходя из влияния этой ошибки на финансовый результат и имущественное положение организации. То есть какой-либо единый критерий не устанавливать.
ВАРИАНТ 5. Если вы составляете отчетность исключительно для сдачи в инспекцию (собственники ею не интересуются), то можно ориентироваться на норму КоАП: если показатель какой-либо статьи (строки) бухотчетности искажен в результате ошибки на 10% и более, то это грубое нарушение правил бухучета, за которое руководителю грозит штраф от 2 тыс. до 3 тыс. руб . ст. 15.11 КоАП РФ То есть можно установить, что существенной будет ошибка, искажающая показатель строки бухотчетности не менее чем на 10%.
Пример. Определение вида допущенной ошибки
/ условие / Организация за декабрь 2011 г. ошибочно начислила амортизацию в размере 200 000 руб. вместо 250 000 руб.
При этом до выявления ошибки показатели, на которые влияет эта ошибка, были следующие:
- остаточная стоимость основных средств (из баланса) — 900 000 руб.;
- прибыль от продаж (из отчета о прибылях и убытках) — 1 000 000 руб.;
- прибыль до налогообложения (из отчета о прибылях и убытках) — 270 000 руб.;
- чистая прибыль (из отчета о прибылях и убытках) — 216 000 руб.;
- себестоимость продаж (из отчета о прибылях и убытках) — 700 000 руб.;
- сумма налога на прибыль (из отчета о прибылях и убытках) — 54 000 руб.
В налоговом учете допущена такая же ошибка — разниц нет.
В учетной политике организация установила, что существенной является ошибка, приводящая к искажению любой строки бухотчетности не менее чем на 10%.
/ решение / Посмотрим, является ли ошибка существенной.
ШАГ 1. Рассчитаем сумму ошибки: 250 000 руб. – 200 000 руб. = 50 000 руб.
ШАГ 2. Рассчитаем процент искажения каждой строки бухгалтерского баланса и отчета о прибылях и убытках, на которые влияет отражение амортизации.
Ошибки, такие как неисправные приборы, помещения или наблюдения, могут возникать по нескольким причинам в математике и естествознании. Определение процента ошибки может выразить, насколько точными были ваши расчеты. Вам необходимо знать две переменные: оценочное или прогнозируемое значение и известное или наблюдаемое значение. Вычтите первое из второго, затем разделите результат на известное значение и преобразуйте эту цифру в процент. В этой формуле Y1 представляет расчетное значение, а Y2 — известное значение: х 100 процентов.
Применяя формулу
Лабораторное руководство факультета физики и астрономии Университета Айовы содержит исторический пример процента ошибки: расчет скорости света Оле Ромера. Ромер оценил скорость света в 220 000 километров в секунду, хотя фактическая константа намного выше, 299 800 километров в секунду. Используя формулу выше, вы можете вычесть оценку Ромера из фактического значения, чтобы получить 79 800; деление этого результата на фактическое значение дает результат.26618, что составляет 26, 618 процента. Более мирские применения формулы могут предсказывать высокие температуры на неделю, а затем сравнивать этот прогноз с фактическими наблюдаемыми температурами. Социологи и маркетологи могут также использовать формулу; Например, вы можете предсказать, что 5000 человек посетят публичное мероприятие, а затем сравнить это с 4550 людьми, которые на самом деле присутствовали. Процентная ошибка в этом случае будет минус-9 процентов.



