Страница 1 из 6
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ этой теме буду писать что-то вроде краткой шпаргалки по погрешностям. Опять же, данный текст ни в коей мере не официальный и ссылаться на него недопустимо. Буду признателен за исправление любых ошибок и неточностей, которые могут быть в этом тексте.
Что такое погрешность?
Запись результата эксперимента вида
![[IMG]](http://corum.mephist.ru/tex/images/b7cd22a4bb1c3d8abaa342cd2ada4701.gif) (
(![[IMG]](http://corum.mephist.ru/tex/images/48291f83278dbe78bb6d25c83d42b779.gif) ) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале
) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале ![[IMG]](http://corum.mephist.ru/tex/images/e52740eb8c1ca9095d2a4e17d036ebec.gif) , а в 30% – не будут.
, а в 30% – не будут.Или, что тоже самое, если мы повторим эксперимент, то новый результат ляжет в доверительный интервал
![[IMG]](http://corum.mephist.ru/tex/images/e52740eb8c1ca9095d2a4e17d036ebec.gif) с вероятностью, равной доверительной вероятности
с вероятностью, равной доверительной вероятности ![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) .
.Как округлять погрешность и результат?
Погрешность округляется до первой значащей цифры, если она не единица. Если единица – то до двух. При этом значащей цифрой называется любая цифра результата кроме нулей впереди.
Пример:
![[IMG]](http://corum.mephist.ru/tex/images/fe09543b974240017f246c36f0e20bad.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/a5cada5c2d1ccb4b76fbda0fb521adb3.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b4bebab07d35bbb43ec16714f5ed87c8.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/2e68c7fa8bf3791b61039377fa19d559.gif) но ни в коем случае не
но ни в коем случае не ![[IMG]](http://corum.mephist.ru/tex/images/f9c474b6e9e0acb125b588c2978f94e4.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/42a0f383586370bf8d25ece709fbb3e8.gif) , поскольку тут 2 значащие цифры – 2 и 0 после двойки.
, поскольку тут 2 значащие цифры – 2 и 0 после двойки. ![[IMG]](http://corum.mephist.ru/tex/images/d5d51f35586a0011459580a47c329c1c.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/bf7e5189fad7ab2880e4fc7c5411fea9.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/9182580f66fbbe10919734c8448a2b0e.gif)
![[IMG]](http://corum.mephist.ru/tex/images/74ccc55c5f11b678eee65f6d66b9a60d.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/60673e2250d177e624ad95b43064ca5e.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/af619a318dbcab2d7ff6c6654f907177.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b928ec2d5d3d00612d6b75b0024e52e6.gif)
Результат округляем таким образом, чтобы последняя значащая цифра результата соответствовала последней значащей цифре погрешности.
Примеры правильной записи:
![[IMG]](http://corum.mephist.ru/tex/images/5e73d4508bfbc87a12895031f6919e08.gif) мм
мм ![[IMG]](http://corum.mephist.ru/tex/images/e51638f79ed91c6edb4a330fbfeb683c.gif) мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности – единица.
мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности – единица. ![[IMG]](http://corum.mephist.ru/tex/images/03ffd1a1b9f618fd926a47a5ca0fc293.gif) мм
мм Примеры неправильной записи:
![[IMG]](http://corum.mephist.ru/tex/images/96072c008b0f5d6a865359f39cd1e082.gif) мм. Здесь лишний знак в результате. Правильно будет
мм. Здесь лишний знак в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/13bbbaf0c29b751a6c22008eb7f9f7b1.gif) мм.
мм. ![[IMG]](http://corum.mephist.ru/tex/images/2291014f831b0fd0257924da54867d23.gif) мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет
мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/13bbbaf0c29b751a6c22008eb7f9f7b1.gif) мм.
мм. В работе использую значение, данное мне просто в виде цифры. Например, масса грузиков. Какая у нее погрешность?
Если погрешность явно не указана, можно взять единицу в последнем разряде. То есть если написано m=1.35 г, то в качестве погрешность нужно взять 0.01 г.
Как считать погрешность сложной функции?
Есть функция от нескольких величин
![[IMG]](http://corum.mephist.ru/tex/images/27b6e5ddc95fcf2627e37957689fa579.gif) У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
![[IMG]](http://corum.mephist.ru/tex/images/cf5c3f00f8d2fe027241a59955d5ceae.gif)
символ
![[IMG]](http://corum.mephist.ru/tex/images/8fbdcb7dc81fe147175bc997b0fb2119.gif) означает частную производную f по x. Подробнее про частные производные здесь.
означает частную производную f по x. Подробнее про частные производные здесь.Как вообще правильно посчитать погрешность?
Положим, вы меряли одну и ту же величину x несколько (n) раз. Получили набор значений.
![[IMG]](http://corum.mephist.ru/tex/images/a0311888c35b344c57ef62341814562b.gif) . Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.
. Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.По пунктам.
1. Считаем погрешность разброса
Если все значения совпали – никакого разброса у вас нет. Иначе – есть погрешность разброса
![[IMG]](http://corum.mephist.ru/tex/images/693eacf86ab361cc13fe5e292519b7c3.gif) , которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:
, которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:![[IMG]](http://corum.mephist.ru/tex/images/c7f83b4f19066a525f2969ce1c8ce372.gif)
здесь
![[IMG]](http://corum.mephist.ru/tex/images/4c795de483c9c9897980b7ba74c847fc.gif) означает среднее по всем
означает среднее по всем ![[IMG]](http://corum.mephist.ru/tex/images/fac074461d1491da3757d3b266ebf89c.gif) .
.
Погрешность разброса![[IMG]](http://corum.mephist.ru/tex/images/693eacf86ab361cc13fe5e292519b7c3.gif) получается умножением среднеквадратичной погрешности среднего на коэффициент Стьюдента
получается умножением среднеквадратичной погрешности среднего на коэффициент Стьюдента ![[IMG]](http://corum.mephist.ru/tex/images/c5a8793748b3bf6f4c68fac5db40c651.gif) , который зависит от выбранной вами доверительной вероятности
, который зависит от выбранной вами доверительной вероятности ![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) и числа измерений n:
и числа измерений n:![[IMG]](http://corum.mephist.ru/tex/images/ceb95147a8605f55cd8513ecd26cc1fd.gif) .
. Коэффициенты Стьюдента
![[IMG]](http://corum.mephist.ru/tex/images/c5a8793748b3bf6f4c68fac5db40c651.gif) берем из нижеприведенной таблицы. Доверительная вероятность
берем из нижеприведенной таблицы. Доверительная вероятность ![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) выбитается произвольно, число измерений n мы также знаем.
выбитается произвольно, число измерений n мы также знаем. 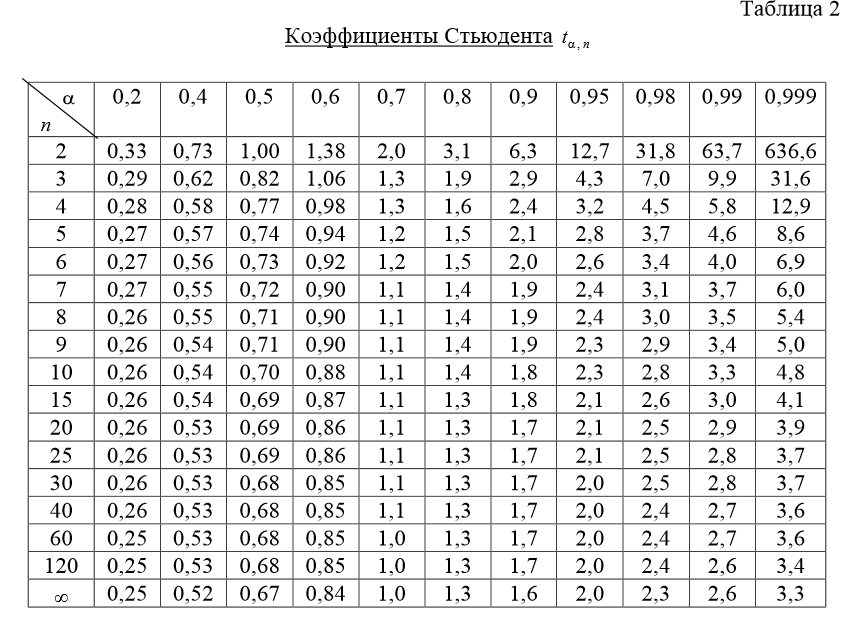
2. Считаем приборную погрешность среднего
Если погрешности разных точек разные, то по формуле
![[IMG]](http://corum.mephist.ru/tex/images/bb6c84165e61208b5b7b94e889085f7f.gif)
При этом естественно, у всех
![[IMG]](http://corum.mephist.ru/tex/images/80a15ae9b42d82e8676bae47fcab70b3.gif) доверительная вероятность должна быть одинаковой.
доверительная вероятность должна быть одинаковой. 3. Складываем среднее с разбросом
Погрешности всегда складываются как корень из квадратов:
![[IMG]](http://corum.mephist.ru/tex/images/b853078084cb450336d8305ee3ff0051.gif)
При этом нужно убедиться, что доверительные вероятности с которыми были вычислены
![[IMG]](http://corum.mephist.ru/tex/images/c391ad2e2574b7c9ffb7f64916b97dc2.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/e3f04bbaaa490a4d496e19c05c63f31e.gif) совпадают.
совпадают.
Как по графику определить приборную погрешность среднего? Ну т.е., используя метод парных точек или метод наименьших квадратов, мы найдем погрешность разброса среднего сопротивления. Как найти приборную погрешность среднего сопротивления?
И в МНК и в методе парных точек можно дать строгий ответ на этот вопрос. Для МНК форума в Светозарове есть (“Основы…”, раздел про метод наименьших квадратов), а для парных точек первое, что приходит в голову (в лоб, что называется) это посчитать приборную погрешность каждого углового коэффициента. Ну и далее по всем пунктам…

Если же не хочешь мучиться, то в лабниках дан простой способ для оценки приборной погрешности углового коэффициента, именно из МНК следующий (например перед работой 1 в лабнике “Электроизмерительные приборы. …” последняя страница Метод.рекомендаций).
![[IMG]](http://corum.mephist.ru/tex/images/59b6fc687986871e08a4def089688bbf.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/a5f06e8811bf82a53ff629bd97e8417e.gif) – величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
– величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
На магазине сопротивлений написан класс точности: 0,05/4*10^-6? Как из этого найти погрешность прибора?Это означает, что предельная относительная погрешность прибора (в процентах) имеет вид:
![[IMG]](http://corum.mephist.ru/tex/images/fd7f8eb5a1972f4158afd23480837110.gif) , где
, где
![[IMG]](http://corum.mephist.ru/tex/images/8f29cb2c179bfc115aa33e7730d3954d.gif) – наибольшее значение сопротивления магазина, а
– наибольшее значение сопротивления магазина, а ![[IMG]](http://corum.mephist.ru/tex/images/7d47b66519d27f5821540aa071c3d561.gif) – номинальное значение включённого сопротивления.
– номинальное значение включённого сопротивления.
Легко видеть, что второе слагаемое важно тогда, когда мы работаем на очень малых сопротивлениях.Подробнее всегда можно посмотреть в паспорте прибора. Паспорт можно найти в интернете, забив марку прибора в гугл.
Литература про погрешности
Рецептурная информация про то как считать погрешности дана во введениях к практикумам, в частности, во вводной части к практикуму “Измерительные приборы”.
Гораздо больше информации по этому поводу можно найти в рекомендованной для первокурсников книге:
В.В. Светозаров “Элементарная обработка результатов измерений”В качестве дополнительной (для первокурсников дополнительной) литературы можно порекомендовать:
В.В.Светозаров “Основы статистической обработки результатов измерений”И уж тем кто хочет окончательно во всем разобраться непременно стоит заглянуть сюда:
Дж. Тейлор. “Введение в теорию ошибок”Спасибо Lexxus’у за нахождение и размещение у себя на сайте этих замечательных книжек.
-

Lexxus
Немного великий
Администратор
VIPА разве не
![[IMG]](http://corum.mephist.ru/tex/images/e1b00eb5241498c481dfb7468c96e465.gif)
? -

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторНеа. Последняя значащая цифра результата должна отвечать последней значащей цифре погрешности.
Если мы держим миллиметры в погрешности, то почему их надо убирать в результате? -
0,98 можно округлить так:
![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
-

Lexxus
Немного великий
Администратор
VIP[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
[/quote]
0.98 можно округлять до 1.0, если погрешность получилась 0.195 и более.
В противном случае, округлять до 1.0 нельзя. -

Lexxus
Немного великий
Администратор
VIPlamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность – скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае – до десятков), т.е. записать![[IMG]](http://corum.mephist.ru/tex/images/d482ffddae86743b780638e2194d1cb2.gif) ?
?
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
[/quote]0,98 это результат или погрешность?

[quote name=’Lexxus’ post=’379428′ date=’Oct 5 2010, 16:53′]
lamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность – скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае – до десятков), т.е. записать![[IMG]](http://corum.mephist.ru/tex/images/d482ffddae86743b780638e2194d1cb2.gif) ?
?
[/quote]
Да, именно так, если я правильно понимаю. Связано, как я понимаю, с тем, что погрешность округления самой погрешности в этом случае превысит результат .
. То есть я понимаю, что четверка несет в себе некую информацию, которая убивается округлением. Но по сравнению с самой погрешностью, и с ее ошибкой округления, это уже все мало.
-
А в чем разница 2х примеров? Во втором случае оба числа просто на порядок меньше. Нельзя их записать как-то типа
![[IMG]](http://corum.mephist.ru/tex/images/795e28a5ddba8232883f37576bbf11cf.gif) . Это, разве, не полностью аналогичный случай к правильному варианту записи?
. Это, разве, не полностью аналогичный случай к правильному варианту записи?
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ первом случае первая цифра в погрешности – единица. Из-за этого мы держим в погрешности 2 знака, чтобы минимизировать ошибку округления погрешности. Во втором – четверка. И мы оставляем только один знак.
-
Т.е.
![[IMG]](http://corum.mephist.ru/tex/images/e7493bf11a89e41c4c62b4e8aee498a5.gif) – правильно?
– правильно?Думаю, тогда стоит в инструкции более ясно написать, почему предыдущее не правильно.
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторДа. А +- 4.2 – неправильно.Предлагай. У меня-то глаз замылен, мне все кажется понятным
 .
.
-
результат

-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379443′ date=’Oct 5 2010, 17:41′]
результат
[/quote]
Тогда тебе Lexxus ответил.[quote name=’Chameleon’ post=’379445′ date=’Oct 5 2010, 17:42′]
как так “завернуто”
[/quote]Слишком сложно для восприятия, имхо. Смешано в кучу правильное и неправильное. Я чуть выше, в примерах правильной записи, добавил строчку, поясняющую различие. И, кстати, про единицу сказано выше.
-
т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9

-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор -
[quote name=’Silver MC’s’ date=’Oct 5 2010, 18:19′]
[snapback]379453[/snapback]т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9[/quote]
Нет. Если погрешность 0,1, то дадо писать так: $0.98pm0.10
Если в погрешности 1я значащая цифра 1, то второй знак обязателен.
PS Если преподаватели немного посвирепствуют, то никакие мануалы и не нужны. Кстати в Светозарове то же самое написано, что и тут. -
Мне кажется, стоит еще написать:
1. как округлять пятерку в последнем разряде (у преподавателей разных кафедр похоже требования разные)
1.56
1.54
1.55
1.52. на пальцах объяснить что значит частная производная с простеньким примерчиком
Если надо – текст попозже напишу
-

lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторNick_, а надо ли тут так вдаваться в математику? тем более в элементарную, вроде правил округления?
-

Lexxus
Немного великий
Администратор
VIPПроблема в том, что функции многих переменных и частные производные в курсе матанализа, кажется, где-то ближе к концу первого семестра.
Страница 1 из 6
Поделиться этой страницей

Если
изучается зависимость одной величины
от другой, то результаты могут быть
представлены в виде графика.
При
вычерчивании графика руководствуются
следующими правилами9:
Выбор
бумаги. График
строят только на миллиметровой бумаге
или на бумаге со специальными координатными
сетками. При их отсутствии иногда
приходится (хотя это крайне нежелательно!)
пользоваться бумагой «в клеточку»
или белой бумагой, на которой карандашом
нанесена сетка.
Выбор
координатных осей.
Общепринято по оси абсцисс откладывать
ту величину, изменения которой являются
причиной изменения другой (т. е. по оси
абсцисс – аргумент, по оси ординат
– функцию).
Выбор
масштабов.
Масштаб графика определяется погрешностью
измерения величин, отложенных по осям:
погрешность должна быть видна на графике,
т. е. должна представляться в выбранном
масштабе отрезком достаточной длины,
иначе график не отражает всех деталей
эксперимента и не может быть использован
для графической обработки данных без
потери точности.
Шкала
должна легко читаться, поэтому одна
клетка масштабной сетки должна
соответствовать удобному числу – 0,1;
0,2; 0,5; 1; 2; 5;
10; … (но не 2,5; 3; 4; 7; 1,13; и т.д.) единиц
изображаемой на графике величины.
При неудобном
масштабе нанесение экспериментальных
точек на график и использование графика
требуют неоправданно большого времени
и нередко сопровождаются досадными
ошибками.
Масштабы
по обеим осям выбираются независимо
друг от друга. Однако следует помнить,
что график получается более наглядным,
если основная часть кривой имеет наклон,
не слишком отличающийся от 45°. В этом
случае наиболее удобно анализировать
форму кривой.
Если
при выборе масштабов для обеих осей на
основе величин погрешностей график
получается слишком растянутым в
каком-либо направлении, то это означает,
что измерения соответствующей
величины проведены с излишне высокой
точностью. При таких условиях разумно
несколько увеличить масштаб по оси, для
которой точность измерений меньше, а
затем выбрать масштаб для второй оси
так, чтобы график имел удобную форму,
уже не обращая внимания на величину
погрешности.
Нанесение
шкал по осям.
Оси графика
должны иметь ясные, четкие обозначения.
Рядом с делениями – на удобных расстояниях
– должны быть нанесены цифры, позволяющие
установить значения, соответствующие
делениям шкалы. Масштаб
наносится на осях графика в виде
равноотстоящих «круглых» чисел, например
6; 8; 10; … или 4,74; 4,76; 4,78; … (чтобы не
загромождать график, можно опускать
целую часть числа: 4,74; ,76; ,78; и т.д.). Не
следует расставлять эти числа слишком
густо – достаточно нанести их через 2
или даже через 5 см.
Это не вызывает неудобств, так как при
рассмотрении графика можно легко
восстановить пропущенные значения.
Круглые значения
цифр располагаются на жирных линиях
сетки (на миллиметровой бумаге такие
линии идут через 5 см).
На
оси обязательно указываются обозначение
и единицы измерения соответствующей
величины. При этом множитель, определяющий
порядок величины, включается обычно
в единицы измерения, например: I,
мА;
I,
103
А
или, иногда, I·103,
А.
Выбор
интервала.
При построении
графиков следует разумно выбирать
интервал, чтобы измеренные точки
располагались на всей площади листа.
Поэтому на графике приводится только
та область изменения измеренных величин,
которая была исследована на опыте.
Не
следует стремиться к тому, чтобы на
графике обязательно поместилось
начало координат (точка 0,0). Даже в том
случае, когда требуется найти точку
пересечения какой-либо прямой на графике
с одной из координатных осей, нет
необходимости, чтобы эта ось помещалась
на графике; точку пересечения легко
найти расчетом, пользуясь подобием
треугольников. Начало координат помещают
на графике только в том случае, когда
это не требует большого увеличения его
размеров.
Следует
помнить, однако, что иногда точка (0,0)
есть результат измерения, причем
часто – наиболее надежный результат
(например, при определении сопротивления
точка I
= 0; U=
0).
Нанесение
точек на график.
Точки должны
наноситься на график очень тщательно
и аккуратно, чтобы график получился
более точным. Их следует отмечать
карандашом, так как иначе ошибочно
нанесенную точку нельзя удалить с
графика, не испортив его.
Никаких
выносных линий и отметок, поясняющих
построение точек,
на
график наносить
нельзя (так как они загромождают рисунок
и мешают анализировать результаты).
Выносная линия может в виде исключения
быть нанесена, только если какую-либо
точку хотят особо выделить на графике
(например, положение максимума).
Если
на один и тот же график наносятся
различные группы данных (результаты
измерения разных величин; одной величины,
но полученные в разных условиях или
разными авторами и т. п.), то точки,
относящиеся к разным группам, должны
быть помечены различными символами
(кружки, треугольники, звездочки и
т. п.) или нанесены разными цветами,
чтобы их нельзя было спутать.
Изображение
погрешности.
Способ
изображения на графике экспериментальных
результатов зависит от того, известна
ли их случайная погрешность. Если
она неизвестна (что чаще всего и бывает),
то результаты изображаются точками,
а если известна, то лучше изображать их
с помощью крестиков соответствующих
размеров, нанесенных поверх точек.
Полуразмер
креста по горизонтали должен быть равен
стандартной погрешности по оси абсцисс,
а его вертикальный полуразмер –
погрешности по оси ординат.
В том случае, если одна из ошибок – из-за
своей малости – не может быть изображена
графически, результаты изображаются
черточками, вытянутыми на ± σ
в том направлении, где погрешность не
мала.
Можно
также указывать погрешность размером
точек, для этого точки рисуют либо в
виде эллипсов с длиной полуосей, равной
в масштабе графика величине погрешности,
либо в виде прямоугольников таких
же размеров. Нет необходимости указывать
погрешность для каждой точки, но если
погрешность изменяется вдоль кривой,
следует показать это на нескольких
точках.
Проведение
кривых через экспериментальные точки.
Кривую на графике проводят плавно,
избегая изломов и перегибов. Кривая
должна проходить насколько возможно
ближе ко всем нанесенным точкам, но
ни в коем случае не следует стремиться
провести ее через каждую точку. Через
экспериментальные точки всегда следует
проводить самую простую кривую,
совместимую с этими точками,
т. е. кривую, от которой экспериментальные
данные отступают, как правило (в 2/3
случаев), не более чем на стандартную
ошибку. Не следует придавать кривым
никаких изгибов, если экспериментальным
данным – в пределах ошибок – можно
удовлетворить и без этого.
Излом
на кривой можно рисовать только в том
случае, если он не может быть объяснен
погрешностью измерений и если при этом
на его существование указывает большое
число точек. Кроме того, нужно быть
уверенным в отсутствии систематических
ошибок (изломы часто появляются, например,
когда сначала работают на одной шкале
прибора, а затем переходят на другую).
Помните, что
всякая
особенность на кривой (излом, резкое
изменение кривизны и пр.) требует либо
специального экспериментального
доказательства, либо теоретического
объяснения.
При
проведении кривой нужно следить за тем,
чтобы на каждом достаточно большом
ее участке экспериментальные точки
располагались как выше, так и ниже
кривой.
Во
всех случаях кривая должна быть проведена
так, чтобы она не закрывала экспериментальных
точек.
Выбор
наиболее наглядной зависимости.
При построении графика нужно стремиться
к тому, чтобы он наиболее четко отражал
все особенности представляемой
зависимости. Для этого часто бывают
удобны функциональные масштабы – по
осям откладываются не сами измеряемые
величины, а их функции, подобранные в
соответствии с решаемой задачей.
При
графической обработке результатов
следует помнить, что на глаз можно точно
провести через экспериментальные точки
только прямую линию. Поэтому при
построении графика следует стремиться
к тому, чтобы ожидаемая зависимость
имела вид прямой линии.
К
логарифмическому масштабу без особой
необходимости прибегать не следует.
Одна из наиболее часто встречающихся
погрешностей опыта – смещение нуля
отсчета – приводит в этом случае к
сильному искажению прямолинейного
характера кривой.
Бывают,
однако, случаи, когда логарифмический
масштаб необходим. Это происходит,
например, если исследуемая величина
очень сильно изменяется, причем
одновременно интересны очень малые и
очень большие ее значения. Логарифмический
масштаб позволяет все точки уместить
на одном чертеже и исследовать совместно.
Логарифмический масштаб выбирают и в
том случае, если имеются основания
ожидать, что искомая зависимость
является степенной, но показатель
степени неизвестен. Иногда применяют
также полулогарифмический (логарифм
откладывается только по одной из осей)
масштаб. Надо помнить, однако,
что логарифмический
масштаб можно применять без потери
точности, только если относительная
погрешность постоянна для всей кривой.
Оформление
графиков.
Готовый график снабжается заголовком,
который должен содержать точное описание
того, что показывает график.
Разные
группы точек (разные символы) или разные
кривые на графике также должны быть
объяснены. Эти объяснения приводятся
в подписи к графику (внизу листа или на
свободном, не занятом кривой, месте
на самом графике).
Основное
достоинство графиков – их наглядность.
Посмотрев на график, можно получить
качественное представление о
полученной зависимости и отметить
наличие различных особенностей:
максимумов, минимумов, точек перегиба,
областей наибольшей и наименьшей
скорости изменения, периодичности и
т. п. График позволяет также легко
судить о соответствии экспериментальных
данных той или иной теоретической
зависимости и вообще облегчает обработку
измерений.
С
помощью графика можно вести обработку
экспериментальных данных. Графическая
обработка не так точна, как численная,
использующая строгие методы, например
метод наименьших квадратов (см. ниже),
но зато проста, наглядна и в большинстве
случаев не требует длинных вычислений,
давая в то же время очень неплохие
результаты. Более того, на графике обычно
хорошо видны особенности, которые
легко пропустить при формальном
применении численных методов. Поэтому
первичную обработку данных (особенно,
если она проводится непосредственно
во время эксперимента) желательно делать
графически. Конечно, если полученной
точности окажется недостаточно, то
нужно использовать более точные методы.
Очень
часто бывает нужно выразить найденную
из опыта зависимость в виде уравнения
(например, представить ее в виде полинома
у = a+bx+cx2+…,
показательной функции у = аеbx
и т. п.). Вид этого уравнения может
быть подобран произвольно или получен
на основании каких-либо теоретических
соображений. В обоих случаях необходимо
проверить, пригодна ли данная формула
для представления совокупности
экспериментальных данных, и подобрать
наилучшим образом значения неизвестных
параметров а,
b,
с, …, входящих
в формулу.
Особенно
просто задача решается для линейной
функции
у = а + bх.
(32)
(т. е.
для простых
формул, содержащих один или два неизвестных
параметра).
В этом случае график у(х) – прямая
линия и необходимо найти параметры а
и b
в формуле (32).
Значение
b
находится как угловой коэффициент
полученной прямой 10,
а значение а
– как величина
отрезка, отсекаемого ею на оси ординат
[6].
Чтобы
найти погрешность в определении параметра
а,
нужно смещать прямую вниз параллельно
самой себе, пока выше нее не окажется
вдвое больше точек, чем снизу. Затем
следует сместить ее вверх, пока снизу
не окажется вдвое больше точек, чем
сверху. Пусть расстояние между этими
прямыми ровно Δ а
(см. рис. 1).
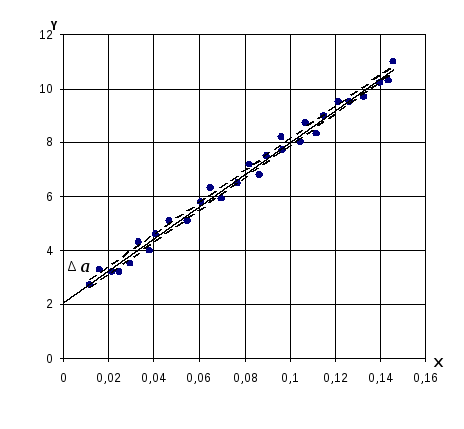

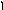
Рис.
1. Графический метод обработки результатов.
Оценка погрешности в определении
параметра a
[6].
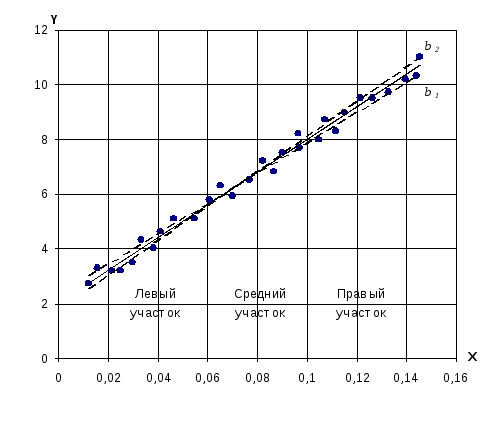


Рис.
2. Графический
метод обработки результатов. Оценка
погрешности в определении параметра b
[6].
Погрешность
в определении а
равна [6]
![]() ,
,
(33)
где
п —
полное число точек на графике.
Погрешность
в определении параметра b
находится аналогичным образом (рис.
2). «Рабочий участок» оси абсцисс (участок,
на котором расположены экспериментальные
точки) делится на три равные части.
Средний участок в дальнейшей работе не
участвует. Для определения
![]() прямая поворачивается так, чтобы на
прямая поворачивается так, чтобы на
левом участке выше нее оказалось вдвое
больше точек, чем под ней, а на правом
участке – наоборот. Затем кривая
поворачивается так, чтобы на левом
участке 2/3 точек лежали ниже прямой, а
на правом – ниже нее. Обозначим разницу
в угловых коэффициентах этих прямых
через Δb.
Тогда
![]() ,
,
(34)
где
п —
полное число точек на графике.
Часто
случается, что начальная точка искомой
зависимости хорошо известна и лежит
в начале координат. Как бы ни была сложна
зависимость тока, проходящего через
проводник, от приложенного к нему
напряжения, можно быть уверенным, что
при отсутствии напряжения нет и тока
(мы предполагаем, что в цепи не возникает
термо-э.д.с.). Если чайник не нагревать
и не охлаждать, то изменение его
температуры равно нулю, и т. д. Во всех
этих случаях нулевая точка не просто
известна,— она является самой надежной
из всех, которые используются при
обработке результатов. Задача о
проведении наилучшей прямой сводится
в этом случае к подбору параметра в
формуле
у
= k
x.
(35)
Стандартная
погрешность при определении параметра
![]() в
в
формуле (35) находится следующим образом.
«Рабочим» участком в этом случае является
весь диапазон по оси Х
от нуля до последней точки. Его следует
разбить на три части и самую левую –
ближнюю к началу координат – часть во
внимание не принимать. Затем нужно
провести через начало координат две
вспомогательные прямые так, чтобы выше
одной из них лежало 2/3 точек, а выше
другой – 1/3. Различие в
![]() между
между
этими прямыми определяет
![]() .
.
Стандартная погрешность находится по
формуле
![]() ,
,
(36)
где
п —
полное число точек на графике.
Если
функция у
=f(x)
нелинейна, удобно использовать
функциональный масштаб – график
перечерчивается в новых координатах,
выбранных так, чтобы получить линейную
зависимость.
Зависимость
вида у
= a xn,
например, можно исследовать на графике
![]() =f(x)
=f(x)
или у
= f(xn),
если п
известно. Если же п,
как и а,
подлежит определению из экспериментальных
данных, применяется логарифмический
масштаб lg y = f(lg x),
в котором подбираемая функция
представится прямой lg y = lg a + n lg x;
параметры функции легко определяются
из наклона и начальной ординаты прямой.
Функция вида у = а + b х2
подбирается
на графике у = f(x2).
Экспоненциальная функция вида
y = a x2 e–bx
(температурная зависимость тока
термоэлектронной эмиссии) изобразится
прямой в координатах lg y/x2
и 1/х.
Если
применяется такой метод обработки
результатов, то, как правило, строят два
графика – график в функциональном
масштабе для количественной обработки
и график в натуральном масштабе для
наглядного представления функции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определить погрешность по графику?
аня с.
27 октября 2018 · 928
ОтветитьУточнить
Иван Воробьёв16,6 K
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас активно… · 21 янв 2019
Провести границу по самой высокой и самой низкой точкам графика, в это коридоре, который образуется между границами, полуширина коридора – коридора ошибок и будет погрешностью.
469
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
скрыт(Почему?)
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
1 |
|
Оценка погрешности по графику. Как?10.06.2012, 00:33. Показов 25924. Ответов 15
Выполняю лабораторную.
0 |
|
4444 / 2448 / 227 Регистрация: 20.08.2011 Сообщений: 3,108 |
|
|
10.06.2012, 02:48 |
2 |
|
.. получилась прямая .. как оценить погрешности из графика? Да не прямая получилась, а только примерно прямая. Там же точки были разбросаны, и не лежали на прямой. И можно было построить коридор, в котором могут лежать такие прямые. Вот полуширина этого коридора ошибок и дает погрешность измерения.
1 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
10.06.2012, 16:37 [ТС] |
3 |
|
а понял.
0 |
|
4444 / 2448 / 227 Регистрация: 20.08.2011 Сообщений: 3,108 |
|
|
10.06.2012, 22:17 |
4 |
|
а понял. .. в этом конусе могут лежать точки, так?.. Нет, не понял! Не конус, а коридор.
0 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
10.06.2012, 22:41 [ТС] |
5 |
|
Как должен выглядеть ответ? Миниатюры
0 |
|
11 / 11 / 0 Регистрация: 19.03.2010 Сообщений: 101 |
|
|
15.06.2012, 00:31 |
6 |
|
На простом языке можно ознакомиться в курсе ОФП ФФ и в методичке “Обработка результатов физического эксперимента” Митин, Русаков
0 |
|
240Volt |
|
15.06.2012, 20:46
|
|
Не по теме:
Ну-ну! Не первый раз уже натыкаюсь на форуме на рекламу этих пособий. Только вот в Митине нет ни одного графика, а Амосов не имеет отношения к обработке экспериментальных данных.
0 |
|
11 / 11 / 0 Регистрация: 19.03.2010 Сообщений: 101 |
|
|
15.06.2012, 23:22 |
8 |
|
Только вот в Митине нет ни одного графика Как это нет? Там же учат находить прямую по точкам? Там коэффициент корреляции ищут. y = Ax+b, не? Или вам нужно чтобы там вам на координатной сетке нарисовали точки? Специально скачал методичку – пункт 2в. Страница 31. Для непонятливых там про Сидорова написано. пункт 3. Ну если вы еще всю методичку не прочитали – прочитайте всю, найдете много полезного. А если вам нужно с доказательствами – математический подход изложен в чм и неплохо бы почитать матстатистику. МНК нужно знать любому инженеру, хотя бы на пальцах. Хи квадрат распределение и коэффициенты чебышОва, можно изучить попозже.
коридор Покажите хоть одно определение “коридора”.
0 |
|
240Volt |
|
16.06.2012, 14:37
|
|
Не по теме:
Как это нет? Там же учат находить прямую по точкам? .. Да так это нет! Ни одного графика в вашем Митине нет. И вообше ни о построении графиков, ни о том, как снимать с графиков точки, ни о том, как по графикам определять погрешности, ничего этого в ней нет. МНК есть, но здесь речь не о нем. Автор темы совсем о другом спрашивал. Одно дело определение параметров линейной зависимости, а другое – построение графика и его обработка. Если, конечно, вы понимаете разницу.
0 |
|
Sanyur |
|
16.06.2012, 15:34
|
|
Не по теме:
построение графика и его обработка ГОСТ вам в руки. Читайте. Если вы считаете, что я рекламирую что то, то вы ошибаетесь. Хоть бы сами подумали: вам дают знания, а вы не пользуетесь ими. Совершенно бесплатно. Не нравится не читайте. График строится так: обрабатывается по МНК. Анализируется коэффициент корреляции. Строится на графике прямая, которая получилась по МНК. В каждой точке эксперимента, строится отрезок погрешности(точка +- ошибка. можно в виде I). На основание коэффициента и построений делается вывод о соответствии зависимости прямой и правильности результатов измерений экспериментов. А для того чтобы
Выполняю лабораторную. выше написанного хватит.
0 |
|
240Volt |
|
16.06.2012, 23:30
|
|
Не по теме: Уважаемый Sanyur! Дискуссия с вами в чужой теме не представляет для меня интереса. Как и знания, которые, как вам кажется, вы мне предлагаете. Не пытаюсь вас обидеть. Просто у меня свои представления об этой теме. Если у вас есть, что посоветовать ТС конкретного, посоветуйте ему, а меня не стоит пытаться убедить. Предлагаю на этом дискуссию закончить.
0 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
18.06.2012, 01:00 [ТС] |
12 |
|
Видите график в 5 посте этой темы? там ваш “коридор” нарисован. я нашел ширину этого коридора, нашел полуширину.
0 |
|
11 / 11 / 0 Регистрация: 19.03.2010 Сообщений: 101 |
|
|
18.06.2012, 01:39 |
13 |
|
VladSharikov, если вам не сложно, то напишите полностью задание. Или описание того, чем вы занимались. Спасибо.
0 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
18.06.2012, 01:45 [ТС] |
14 |
|
Все, что есть это провести сравнение теоретической и экспериментальной кривых и анализ полученных результатов, включая оценку погрешности измерений из графика.
0 |
|
11 / 11 / 0 Регистрация: 19.03.2010 Сообщений: 101 |
|
|
18.06.2012, 01:51 |
15 |
|
VladSharikov, вы меня не так поняли. Опишите, пожалуйста, как вы получали зависимость экспериментально, какая кривая должна быть теоретически, наконец, сам эксперимент. И задание. Желательно как написано в лабнике, или откуда вы задачу эту взяли.
0 |
|
25 / 25 / 7 Регистрация: 02.12.2010 Сообщений: 824 |
|
|
18.06.2012, 01:56 [ТС] |
16 |
|
1. зарисовывали дифракционную картину “как есть” теоретически кривая должна быть 45 градусов.
0 |


