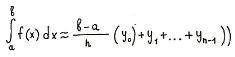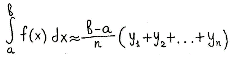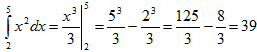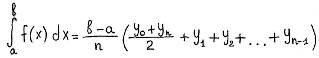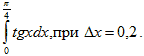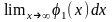Как найти погрешность вычисления интеграла

Как найти погрешность вычисления интеграла

Учебно-воспитательные задачи:

  • Дидактическая цель. Познакомить учащихся с методами
    приближённого вычисления определённого интеграла.
  • Воспитательная цель. Тема данного занятия имеет большое
    практическое и воспитательное значение. Наиболее просто к идее численного
    интегрирования можно подойти, опираясь на определение определённого
    интеграла как предела интегральных сумм. Например, если взять какое-либо
    достаточно мелкое разбиение отрезка [a; b] и построить для
    него интегральную сумму, то её значение можно приближённо принять за
    значение соответствующего интеграла. При этом важно быстро и правильно
    производить вычисления с привлечением вычислительной техники.

Основные знания и умения. Иметь понятие о приближённых методах
вычисления определённого интеграла по формулам прямоугольников и трапеций.

Обеспечение занятия

  • Раздаточный материал. Карточки-задания для самостоятельной работы.
  • ТСО. Мультипроектор, ПК, ноутбуки.
  • Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод
    прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора).
  • Вычислительные средства: ПК, микрокалькуляторы.
  • Методические рекомендации

Вид занятия. Интегрированное практическое.

Мотивация познавательной деятельности учащихся. Очень часто приходится
вычислять определённые интегралы, для которых невозможно найти первообразную. В
этом случае применяют приближённые методы вычисления определённых интегралов.
Иногда приближённый метод применяют и для “берущихся” интегралов, если
вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого
вычисления интеграла заключается в том, что кривая
заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.

Последовательность занятия.

  1. Формула прямоугольников.
  2. Формула трапеций.
  3. Решение упражнений.

План занятия

  1. Повторение опорных знаний учащихся.

Повторить с учащимися: основные формулы интегрирования, сущность изученных
методов интегрирования, геометрический смысл определённого интеграла.

  1. Выполнение практической работы.

Решение многих технических задач сводится к вычислению определённых
интегралов, точное выражение которых сложно, требует длительных вычислений и не
всегда оправдано практически. Здесь бывает вполне достаточно их приближённого
значения.

Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение
которой неизвестно. В этом случае можно заменить данную линию более простой,
уравнение которой известно. Площадь полученной таким образом криволинейной
трапеции принимается за приближённое значение искомого интеграла.

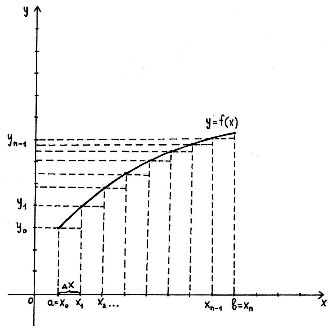
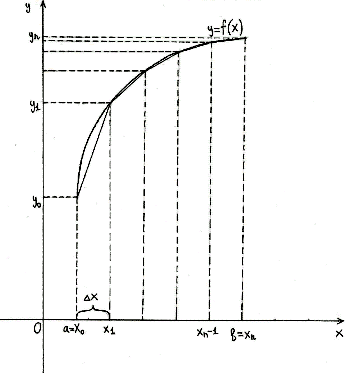
Простейшим приближённым методом является метод прямоугольников. Геометрически
идея способа вычисления определённого интеграла по формуле прямоугольников
состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой
площадей прямоугольников, одна сторона которых равна
, а друга –
.

Если суммировать площади прямоугольников, которые показывают площадь
криволинейной трапеции с недостатком [Рисунок1], то получим формулу:

[Рисунок1]

то получим формулу:

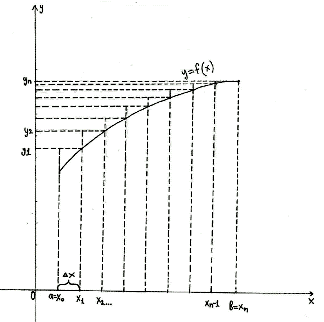
Если с избытком

[Рисунок2],

то

Значения у0, у1,…, уn находят из
равенств ,
к
=
0, 1…,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.

Итак, чтобы найти приближённое значение интеграла
, нужно:

  • разделить отрезок интегрирования [a, b] на n равных частей
    точками х0=

    а,

    х1, х2,…, х
    n
    -1    ,
    х
    n
    =
    b
    ;

  • вычислить значения подынтегральной функции
    в
    точках деления, т.е. найти

    у
    0

    =
    f (x0),
    у
    1

    =
    f (x1),
    у
    2

    =
    f (x2),
    у
    n
    -1
    =
    f (xn-1),
    у
    n

    =
    f (xn)
    ;

  • воспользоваться одной из приближённых формул.

Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:


Пример 1. Вычислить по формуле прямоугольников
. Найти
абсолютную и относительную погрешности вычислений.

Решение:

Разобьём отрезок [a, b] на несколько (например, на 6) равных
частей. Тогда а

=

0,

b =

3
,

х
k = a + k


х
х0 = 2 + 0

= 2
х1 = 2 + 1

= 2,5
х2 = 2 + 2

=3
х3 = 2 + 3

= 3
х4 = 2 + 4

= 4
х5 = 2 + 5

= 4,5

f (x0) = 22 = 4

f

(x
1
)
= 2
,5
2

=

6,25

f

(x
2
)
=
32

=

9

f

(x
3
)
=
3,52


=

12,25

f

(x
4
)
=
42


=
16

f

(x
5
)
=
4,52


=

20,25.

х 2 2,5 3 3,5 4 4,5
у 4 6,25 9 12,25 16 20,25

По формуле (1):

Для того, чтобы вычислить относительную погрешность вычислений, надо найти
точное значение интеграла:



Вычисления проходили долго и мы получили довольно-таки грубое округление.
Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться
техническими возможностями компьютера.

Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х

[2
;5
]
с заданным шагом
х = 0,1.

  1. Открываем чистый рабочий лист.
  2. Составляем таблицу данных (х и f(x)). Пусть первый столбец
    будет значениями х, а второй соответствующими показателями f(x).
    Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
    слово Функция. В ячейку А2 вводится первое значение аргумента – левая
    граница диапазона (2). В ячейку А3 вводится второе значение аргумента
    – левая граница диапазона плюс шаг построения (2,1). Затем, выделив
    блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
    нижний угол блока протягиваем до ячейки А32, до значения х=5).
  3. Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
    записать её уравнение. Для этого табличный курсор необходимо установить в
    ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской
    раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется
    4. Теперь необходимо скопировать функцию из ячейки В2.
    Автозаполнением копируем эту формулу в диапазон В2:В32.
    В результате должна быть получена таблица данных для нахождения интеграла.
  4. Теперь в ячейке В33 может быть найдено приближённое значение интеграла.
    Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер
    функций (нажатием на панели инструментов кнопки Вставка функции (f(x)).
    В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
    Категория выбираем Математические. Справа в поле Функция – функцию Сумм.
    Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
    мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В
    ячейке В33 появляется приближённое значение искомого интеграла с недостатком
    (37,955) .

Сравнивая полученное приближённое значение с истинным значением интеграла (39),
можно видеть, что ошибка приближения метода прямоугольников в данном случае
равна

=

|39 – 37
,
955| = 1
,045

Пример 2. Используя метод прямоугольников, вычислить
с
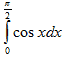
заданным шагом х =
0,05.

Решение:

  1. Для нахождения определённого интеграла значения подынтегральной функции
    f(x) должны быть введены в рабочую таблицу Excel в диапазоне 
    с
    заданным шагом х
    = 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
    интегрирования (0). В ячейку А3 вводится второе значение аргумента –
    левая граница диапазона плюс шаг построения (0,05). Затем, выделив
    блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
    нижний угол блока протягиваем до ячейки А33, до значения х=1,55).
  2. Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
    записать её уравнение. Для этого табличный курсор необходимо установить в
    ячейку В2. Здесь должно оказаться значение косинуса, соответствующее
    значению аргумента в ячейке А2. Для получения значения косинуса
    воспользуемся специальной функцией: нажимаем на панели инструментов кнопку
    Вставка функции (
    f
    х
    )
    .
    В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
    Категория выбираем Математические. Справа в поле Функция – функцию COS.
    Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя
    указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле
    вправо, чтобы открыть столбец данных (А). Указываем значение
    аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В
    ячейке В2 появляется 1. Теперь необходимо скопировать функцию из
    ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В
    результате должна быть получена таблица данных для нахождения интеграла.
  3. Теперь в ячейке В34 может быть найдено приближённое значение интеграла.
    Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер
    функций (нажатием на панели инструментов кнопки Вставка функции

    (
    (
    f
    х
    ))
    .
    В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
    Категория выбираем Математические. Справа в поле Функция – функцию Сумм.
    Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
    мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В
    ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).

Сравнивая полученное приближённое значение с истинным значением интеграла
, можно
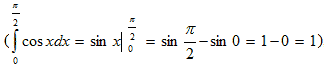
видеть, что ошибка приближения метода прямоугольников в данном случае равна


Метод трапеций обычно даёт более точное значение интеграла, чем метод
прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций
и приближённое значение определённого интеграла находится как сумма площадей
трапеций

[Рисунок3]

Пример 3. Методом трапеций найти
с шагом
х = 0,1.

Решение.

  1. Открываем чистый рабочий лист.
  2. Составляем таблицу данных (х и f(x)). Пусть первый столбец
    будет значениями х, а второй соответствующими показателями f(x).
    Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
    слово Функция. В ячейку А2 вводится первое значение аргумента – левая
    граница диапазона (0). В ячейку А3 вводится второе значение аргумента
    – левая граница диапазона плюс шаг построения (0,1). Затем, выделив
    блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
    нижний угол блока протягиваем до ячейки А33, до значения х=3,1).
  3. Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
    записать её уравнение (в примере синуса). Для этого табличный курсор
    необходимо установить в ячейку В2. Здесь должно оказаться значение синуса,
    соответствующее значению аргумента в ячейке А2. Для получения значения
    синуса воспользуемся специальной функцией: нажимаем на панели инструментов
    кнопку Вставка функции  f(x). В появившемся диалоговом окне
    Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические.
    Справа в поле Функция – функцию SIN. Нажимаем кнопку ОК.
    Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле
    окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец
    данных (А). Указываем значение аргумента синуса щелчком мыши на
    ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
    необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
    формулу в диапазон В2:В33. В результате должна быть получена таблица данных
    для нахождения интеграла.
  4. Теперь в ячейке В34 может быть найдено приближённое значение интеграла
    по методу трапеций. Для этого в ячейку В34 вводим формулу =
    0,1*((В2+В33)/2+,     затем вызываем Мастер функций (нажатием на панели
    инструментов кнопки Вставка функции  (f(x)). В появившемся
    диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем
    Математические. Справа в поле Функция – функцию Сумм. Нажимаем кнопку ОК.
    Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон
    суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке
    В34 появляется приближённое значение искомого интеграла с недостатком (1,997)
    .

Сравнивая полученное приближённое значение с истинным значением интеграла
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.


  1. Решение упражнений.
  1. Вычислить

    методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
  2. Вычислить методом трапеций
       
  3. Вычислить методом трапеций
  4. Вычислить методом трапеций
  5. Вычислить 

    разделив отрезок [0;4] на 40 равных частей.
  6. Вычислить
     
    разделив отрезок [0;8] на 40 равных частей.
  7. Вычислить 
Источник

Оценка точности вычисления определённого интеграла

Интеграл
вычисляется по выбранной формуле
(прямоугольников, трапеций, парабол
Симпсона) при числе шагов, равном n, а
затем при числе шагов, равном 2n.
Погрешность вычисления значения
интеграла при числе шагов, равном 2n,
определяется по формуле Рунге:


,
для формул прямоугольников и трапеций 
,
а для формулы Симпсона 
.

Таким
образом, интеграл вычисляется для
последовательных значений числа
шагов 
,
где n0 —
начальное число шагов. Процесс вычислений
заканчивается, когда для очередного
значения N будет выполнено условие 
,
где ε — заданная точность.

Вопрос 11

Определённый
интеграл называется несобственным,
если выполняется, по крайней мере, одно
из следующих условий:

  • Предел a
    или b (или оба предела) являются
    бесконечными;

  • Функция
    f(x) имеет одну или несколько точек
    разрыва внутри отрезка [a, b].

Несоб.
Интеграл 1 рода: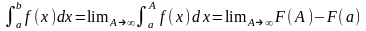

Если
предел конечен, то интеграл сходится,
иначе (илил несущ., бесконеч.) расходится

Несоб.
Интеграл 2 рода: (?????????????????)

3
признака сходимости не соб. интегралов
1 рода от неотриц. ф-й.

  1. 0≤f1(x)≤f2(x),
    x[a,∞)

Если
сх.

=>сх.

2)
Если расх.

=>расх.

3)
0≤φ1(x),
0≤φ2(x)

(≠0 ≠∞)


,

– одинаково

Приложения:

Существует
и др. методы приближ. Вычисления
интегралов. Например, подынт. ф-ю можно
заменить многочленом Тейлора, получится
квадратурная формула. Для получения
оценки погрешности от замены интеграла
квадратурной формулой, надо проинтегрировать
остаток ф-лы Тейлора и ост. Оценить.

Вопрос 14

В математическом
анализе, производная
по направлению —
это обобщение понятия производной на
случай функции нескольких
переменных. Производная по направлению
показывает, насколько быстро функция
изменяется при движении вдоль заданного
направления.

Производная
функции одной переменной показывает,
как изменяется её значение при малом
изменении аргумента.
Если мы попытаемся по аналогии определить
производную функции многих переменных,
то столкнёмся с трудностью: в этом
случае изменение аргумента (то есть
точки в пространстве) может происходить
в разных направлениях, и при этом будут
получаться разные значения производной.
Именно это соображение и приводит к
определению производной
по направлению.

Рассмотрим
функцию 
 от 
 аргументов
в окрестности точки 
.
Для любого единичного вектора 
 определим
производную функции 
 в
точке 
 по
направлению 
 следующим
образом:

Значение
этого выражения показывает, как быстро
меняется значение функции при сдвиге
аргумента в направлении вектора 
.

Если
направление сонаправленно с координатной
осью, то производная по направлению
совпадает с частной
производной по
этой координате.

Связь
с градиентом

Производную
по направлению дифференциируемой по
совокупности переменных функции можно
рассматривать как проекцию градиента
функции на это направление, или иначе,
как скалярное произведение градиента
на орт направления:


,

где 
 —
орт направления. Отсюда следует, что
максимальное значение в точке производная
по направлению принимает, если направление
совпадает с направлением градиента функции
в данной точке. Также видно, что значение
производной по направлению не зависит
от длины вектора 
.

Производные
высших порядков

Если
функция U
= f 
(x, y,
z) имеет в некоторой (открытой)
области x0y0 частную
производную по одной из переменных, то
названная производная, тоже являясь
функцией от аргументов x, y,
z, может, в свою очередь, в некоторой
точке x0, y0,
z0 иметь
частные производные по той же или по
любой другой переменной. Для исходной
функции U
= f  
(x, y,
z) эти последние производные будут
частными производными второго порядка.
Если была взята первая производная
по x (
),
то её вторые производные по x, y,
z, будут записаны так:

Заметим,
что частная производная высших порядков,
взятая по разным переменным, называется
смешанной производной.

Формула
Тейлра (вопрос 6)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.

Метод трапеций

Предположим, что нам нужно приближенно вычислить определенный интеграл ∫abf(x)dx, подынтегральная функция которого y=f(x) непрерывна на отрезке [a;b]. Для этого разделим отрезок [a;b] на несколько равных интервалов длины h точками  a=x0<x1<x2<…<xn-1<xn=b. Обозначим количество полученных интервалов как n.

Найдем шаг разбиения: h=b-an. Определим узлы из равенства xi=a+i·h, i=0, 1,…, n.

На элементарных отрезках рассмотрим подынтегральную функцию xi-1; xi, i=1, 2,.., n.

При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:

Метод трапеций

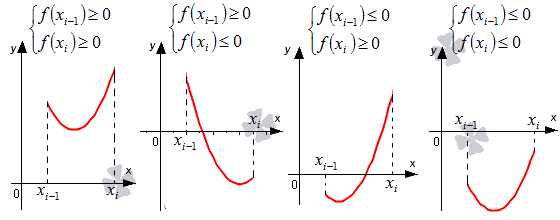
Выделим отрезки xi-1; xi, i=1, 2,…, n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.

Метод трапеций

Возьмем выражение f(xi-1)+f(xi)2·h в качестве приближенного значения интеграла ∫xi-1xif(x)dx. Т.е. примем ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.

Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.

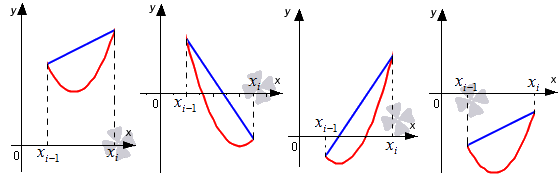
Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями  f(xi-1), f(xi) высотой h. В четвертом из рассматриваемых нами случаев заданный интеграл ∫xi-1xf(x)dx приближенно равен площади трапеции с основаниями -f(xi-1), -f(xi)  и высотой h, которую необходимо взять со знаком «-». Для того, чтобы вычислить приближенное значение определенного интеграла ∫xi-1xif(x)dx во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.

Метод трапеций

Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫abf(x)dx  в виде суммы интегралов вида ∫xi-1xif(x)dx на каждом элементарном отрезке и в последующей приближенной замене ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.

Формула метода трапеций

Вспомним пятое свойство определенного интеграла: ∫abf(x)dx=∑i=1n∫xi-1xif(x)dx. Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫xi-1xif(x)dx подставить их приближенные значения: ∫xi-1xif(x)dx=∑i=1n∫xi-1xif(x)dx≈∑i=1nf(xi-1)+f(xi)2·h==h2·(f(x0)+f(x1)+f(x1)+f(x2)+f(x2)+f(x3)+…+f(xn))==h2·f(x0)+2∑i=1n-1f(xi)+f(xn)⇒∫xi-1xif(x)dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)

Определение 1

Формула метода трапеций: ∫xi-1xif(x)dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)

Оценка абсолютной погрешности метода трапеций

Оценим абсолютную погрешность метода трапеций следующим образом:

Определение 2

δn≤maxx∈[a;b]f”(x)·n·h312=maxx∈[a;b]f”(x)·b-a312n2

Графическая иллюстрация метода трапеций

Графическая иллюстрация метода трапеций приведена на рисунке:

Графическая иллюстрация метода трапеций

Примеры вычислений

Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов. Особое внимание уделим двум разновидностям заданий:

  • вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
  • нахождение приближенного значения определенного интеграла с оговоренной точностью.

При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n.

Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0,01, то промежуточные вычисления мы проводим с точностью до 0,0001 или 0,00001. При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.

Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.

Итак, ∫057dxx2+1=7arctg(x)05=7arctg 5≈9,613805.

Пример 1

Вычислим по методу трапеций определенный интеграл ∫057×2+1dx для n равным 10.

Решение

Формула метода трапеций имеет вид ∫xi-1xif(x)dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)

Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h=b-an , определить узлы xi=a+i·h, i=0, 1,…, n, вычислить значения подынтегральной функции f(x)=7×2+1.

Шаг разбиения вычисляется следующим образом: h=b-an=5-010=0.5. Для вычисления подынтегральной функции в узлах xi=a+i·h, i=0, 1,…, n будем брать четыре знака после запятой:

i=0: x0=0+0·0.5=0⇒f(x0)=f(0)=702+1=7i=1: x1=0+1·0.5=0.5⇒f(x1)=f(0.5)=70,52+1=5,6…i=10: x10=0+10·0.5=5⇒f(x10)=f(5)=752+1≈0,2692

Внесем результаты вычислений в таблицу:

i 0 1 2 3 4 5 6 7 8 9 10
xi 0 0.5 1 1,5 2 2,5 3 3,5 4 4,5 5
f(xi) 7 5,6 3,5 2,1538 1,4 0,9655 0,7 0,5283 0,4117 0,3294 0,2692

Подставим полученные значения в формулу метода трапеций: ∫057dxx2+1≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)==0,52·7+2·5,6+3,5+2,1538+1,4+0,9655+0,7+0,5283+0,4117+0,3294+0,2692=9,6117

Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница. Полученные значения совпадают до сотых.

Ответ: ∫057dxx2+1=9,6117

Пример 2

Вычислим по методу трапеций значение определенного интеграла ∫12112×4+13x-160dx с точностью до 0,01.

Решение

Согласно условию задачи a = 1; b = 2, f(x)=112×4+13x-160; δn≤0,01.

Найдем n, которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δn≤maxx∈[a;b]f”(x)·(b-a)312n2. Сделаем мы это следующим образом: мы найдем значения n, для которых будет выполняться неравенство maxx∈[a;b]f”(x)·(b-a)312n2≤0,01. При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.

Для начала найдем наибольшее значение модуля второй производной функции на отрезке [1; 2].

f'(x)=112×4+13x-160’=13×3+13⇒f”(x)=13×3+13’=x2

Вторая производная функция является квадратичной параболой f”(x)=x2. Из ее свойств мы знаем, что она положительная и возрастает на отрезке [1; 2]. В связи с этим maxx∈[a;b]f”(x)=f”(2)=22=4.

В приведенном примере процесс нахождения maxx∈[a;b]f”(x) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения maxx∈[a;b]f”(x).

Подставим полученное значение в неравенство maxx∈[a;b]f”(x)·(b-a)312n2≤0,01

4·(2-1)312n2≤0,01⇒n2≥1003⇒n≥5,7735

Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.

Вычислим шаг: h=b-an=2-16=16.

Найдем узлы xi=a+i·h, i=1, 0,…, n, определим значения подынтегральной функции в этих узлах:

i=0: x0=1+0·16=1⇒f(x0)=f(1)=112·14+13·1-160=0,4i=1: x1=1+1·16=76⇒f(x1)=f76=112·764+13·76-160≈0,5266…i=6: x10=1+6·16=2⇒f(x6)=f(2)=112·24+13·2-160≈1,9833

Результаты вычислений запишем в виде таблицы:

i 0 1 2 3 4 5 6
xi 1 76 43 32 53 116 2
fxi 0,4 0,5266 0,6911 0,9052 1,1819 1,5359 1,9833

Подставим полученные результаты в формулу трапеций:

∫12112×4+13x-160dx≈h2·f(x0)+2∑i=1n-1f(xi)+f(xn)==112·0,4+2·0,5266+0,6911+0,9052+1,1819+1,5359+1,9833≈1,0054

Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:

∫12112×4+13x-160dx=x560+x26-x6012=1

Как видим, полученной точности вычислений мы достигли.

Ответ: ∫12112×4+13x-160dx≈1,0054

Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.

Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как In. Выберем произвольное число n. По формуле метода трапеций вычислим исходный интеграл при одинарном (n=10) и удвоенном (n=20) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I20-I10.

Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I20-I10<δn, то мы прекращаем вычисления и выбираем значение  I20 , которое можно округлить до требуемого порядка точности.

Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов (n=40).

Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.

Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.

Пример 3

Необходимо вычислить определенный интеграл ∫02xexdx по методу трапеций с точностью до 0,001.

Решение

Возьмем n равное 10 и 20. По формуле трапеций получим  I10=8,4595380, I20=8,4066906.

I20-I10=8,4066906-8,4595380=0,0528474>0,001, что требует продолжения вычислений.

Возьмем n равное 40: I40=8,3934656.

I40-I20=8,3934656-8,4066906=0,013225>0,001, что также требует продолжения вычислений.

Возьмем n равное 80: I80=8,3901585.

I80-I40=8,3901585-8,3934656=0,0033071>0,001, что требует проведения еще одного удвоения числа узлов.

Возьмем n равное 160: I160=8,3893317.

I160-I80=8,3893317-8,3901585=0,0008268<0,001

Получить приближенное значение исходного интеграла можно округлив I160=8,3893317 до тысячных: ∫02xexdx≈8,389.

Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫02xexdx=ex·(x-1)02=e2+1≈8,3890561. Требуемая точность достигнута.

Ответ: ∫02xexdx≈8,389

Погрешности

Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.

Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:

δn≤maxx∈[a;b]f”(x)n·h312=maxx∈[a;b]f”(x)·b-a312n2δn≤maxx∈[a;b]f”(x)n·h324=maxx∈[a;b]f”(x)·b-a324n2.

Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.

В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.

Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.

Источник

Вычисление определённых интегралов: базовые алгоритмы

Время на прочтение
13 мин

Количество просмотров 82K

image
В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают “под капотом”, и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.

Определение интеграла

Интегралом (по Риману) от функции $f(x)$ на отрезке $[a;b]$ называется следующий предел:

$int_a^b f(x)dx = lim_{Delta x to 0} sum_{i=0}^{n-1} f(xi_i)(x_{i+1} - x_i),~~(1)$

где $Delta x = maxlbrace x_{i+1} - x_irbrace$ — мелкость разбиения, $x_0 = a$, $x_n = b$, $xi_i$ — произвольное число на отрезке $[x_i; x_{i+1}]$.

Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким.
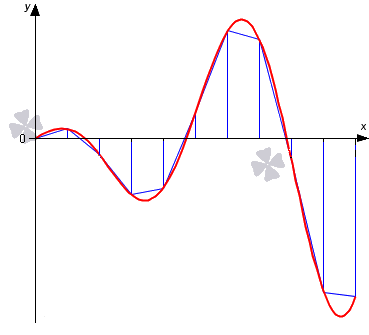
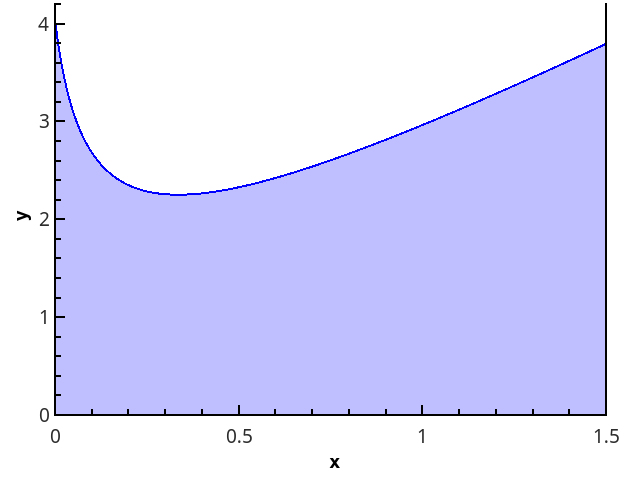
image
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).

Квадратурные формулы

Определение интеграла (1) можно переписать в виде

$I = int_a^b f(x)dx approx I_n = (b - a)sum_{i=0}^{n-1} w_i f(xi_i),~~(2)$

где $w_i$ — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа $n$ точек, в которых вычисляется функция.

Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки $lbrace xi_i rbrace$ и веса $w_i$ таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.

Вычислительная задача

Задана функция $f(x)$, для которой есть алгоритм вычисления значений в любой точке отрезка $[a;b]$ (имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).

Требуется найти приближённое значение интеграла $int_a^b f(x)dx$.
Решения будут реализованы на языке Python 3.6.

Для проверки методов используется интеграл $int_0^{3/2} left[ 2x + frac{1}{sqrt{x + 1/16}}right]dx = 17/4$.

Кусочно-постоянная аппроксимация

Идейно простейшие квадратурные формулы возникают из применения выражения (1) “в лоб”:

$I_n = sum_{i=0}^{n-1} f(xi_i) (x_{i+1} - x_i)$

Т.к. от метода разбиения отрезка точками $lbrace x_irbrace$ и выбора точек $lbracexi_irbrace$ значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1) $xi_i = x_i$; 2) $xi_i = x_{i+1}$; 3) $xi_i = (x_i + x_{i+1}) / 2$.

Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.

Реализация

def _rectangle_rule(func, a, b, nseg, frac):
    """Обобщённое правило прямоугольников."""
    dx = 1.0 * (b - a) / nseg
    sum = 0.0
    xstart = a + frac * dx # 0 <= frac <= 1 задаёт долю смещения точки, 
                           # в которой вычисляется функция,
                           # от левого края отрезка dx
    for i in range(npoints):
        sum += func(xstart + i * dx)

    return sum * dx

def left_rectangle_rule(func, a, b, nseg):
    """Правило левых прямоугольников"""
    return _rectangle_rule(func, a, b, nseg, 0.0)

def right_rectangle_rule(func, a, b, nseg):
    """Правило правых прямоугольников"""
    return _rectangle_rule(func, a, b, npoints, 1.0)

def midpoint_rectangle_rule(func, a, b, nseg):
    """Правило прямоугольников со средней точкой"""
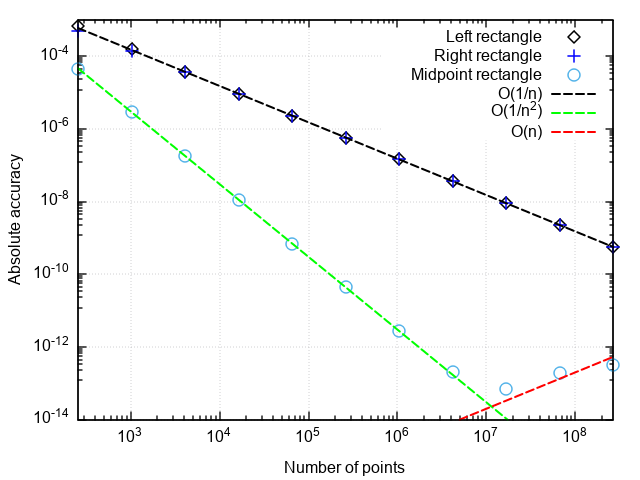
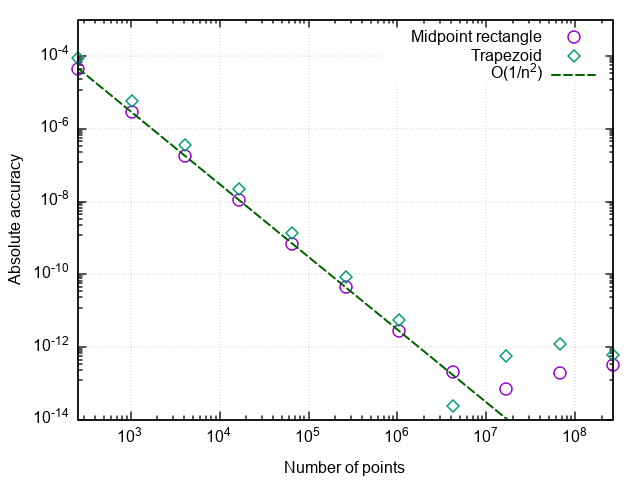
    return _rectangle_rule(func, a, b, nseg, 0.5)

Для анализа производительности квадратурных формул построим график погрешности в координатах “число точек — отличие численного результата от точного”.

image

Что можно заметить:

  1. Формула со средней точкой гораздо точнее, чем с правой или левой точками
  2. Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
  3. При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
    Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е. $|I_n - I| = O( 1/n^2)$, а формулы правых и левых прямоугольников — первый порядок, т.е. $|I_n - I| = O(1/n)$.
    Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как $|I_n - I| = O(1/n)$, что не даёт при интегрировании достигнуть машинной точности.
    Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).

Кусочно-линейная аппроксимация

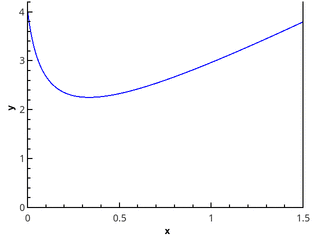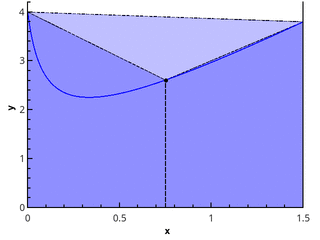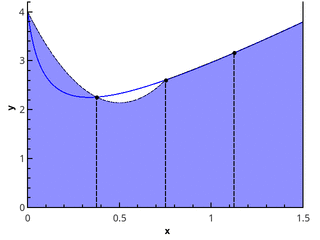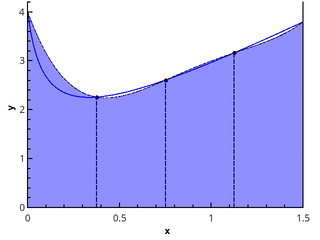
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:

$I_n = sum_{i=0}^{n-1} frac{f(x_i) + f(x_{i+1})}{2}(x_{i+1} - x_i)~~(3)$

image
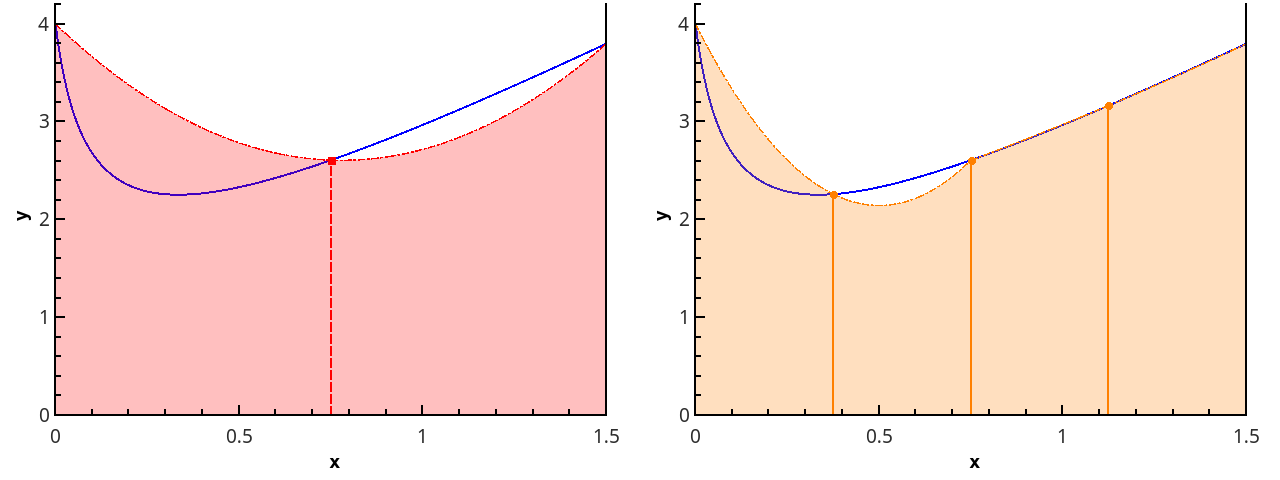
Иллюстрация метода трапеций для n=1 и n=2.

В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид

$I_n = hleft(frac{f(a) + f(b)}{2} + sum_{i=1}^{n-1} f(a + ih)right),~h=frac{b-a}{n}~~(3a)$

Реализация

def trapezoid_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    dx = 1.0 * (b - a) / nseg
    sum = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        sum += func(a + i * dx)

    return sum * dx

Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).
image

Контроль точности вычисления

Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.

Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: $Delta_{2n} approx |I_{2n} - I_n|$. Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.

Чем ещё хорош метод прямоугольников

Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x-1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.

Отсюда получаем следующий код для метода трапеций с контролем точности:

def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1):
    """Правило трапеций
       rtol - желаемая относительная точность вычислений
       nseg0 - начальное число отрезков разбиения"""
    nseg = nseg0
    old_ans = 0.0
    dx = 1.0 * (b - a) / nseg
    ans = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        ans += func(a + i * dx)

    ans *= dx
    err_est = max(1, abs(ans))
    while (err_est > abs(rtol * ans)):
        old_ans = ans
        ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) # новые точки для уточнения интеграла
                                                                      # добавляются ровно в середины предыдущих отрезков
        nseg *= 2
        err_est = abs(ans - old_ans)

    return ans

С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.

Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.

Кусочно-параболическая аппроксимация

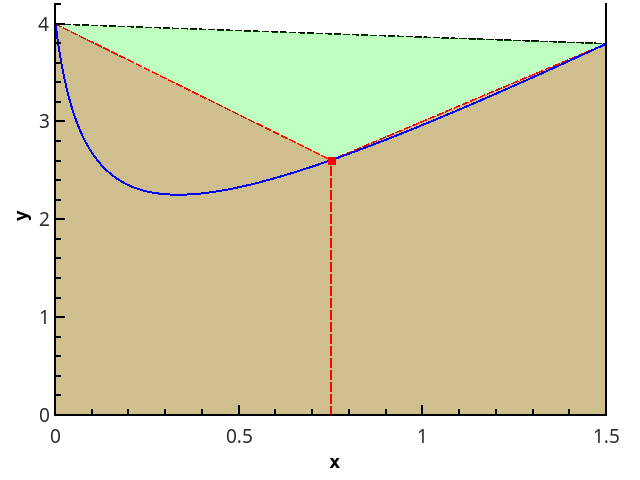
Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами {(x0=a, x1, x2), (x2, x3, x4), …, (xn-2, xn-1, xn=b)}.


Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).

Приближая интеграл от функции на каждом из отрезков [xk;xk+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (xk+1=xk+h), получаем формулу Симпсона:

$I_{Simps, n} = sum_{i=0}^{n/2-1}frac{h}{3}[f(x_{2i})+4f(x_{2i+1})+f(x_{2i + 2})] = \ =frac{h}{3}[f(a)+4f(a+h)+2f(a+2h) + ... +4f(b-h) + f(b)]~~(4)$

Из формулы (4) напрямую получается “наивная” реализация метода Симпсона:

Заголовок спойлера

def simpson_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    if nseg%2 = 1:
        nseg += 1
    dx = 1.0 * (b - a) / nseg
    sum = (func(a) + 4 * func(a + dx) + func(b))
    for i in range(1, nseg / 2):
        sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx)

    return sum * dx / 3

Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.

Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам $(a, f_0),~(a+h, f_1),~(a+2h, f_2)$:

$I_{Simps,2} = frac{h}{3}(f_0 + 4f_1 + f_2) = frac{4}{3}hleft(frac{f_0 + f_1}{2} + frac{f_1 + f_2}{2}right) - frac{1}{3}cdot2hfrac{f_0 + f_2}{2} = \ =frac{4I_{trap,2} - I_{trap,1}}{3}$

Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.

Как-то так…

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным числом отрезков разбиения nseg0
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1):
        """Интегрирование методом трапеций с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        ans = Quadrature.__restart(func, x0, x1, nseg0)
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            ans = Quadrature.__double_nseg(func, x0, x1)
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

    def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1):
        """Интегрирование методом парабол с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0)
        new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
        ans = (4 * new_trapez_sum - old_trapez_sum) / 3
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            old_trapez_sum = new_trapez_sum
            new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
            ans = (4 * new_trapez_sum - old_trapez_sum) / 3
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Сравним эффективность метода трапеций и парабол:

>>> import math
>>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 65537
4.250000001385811
>>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 2049
4.2500000000490985

Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!

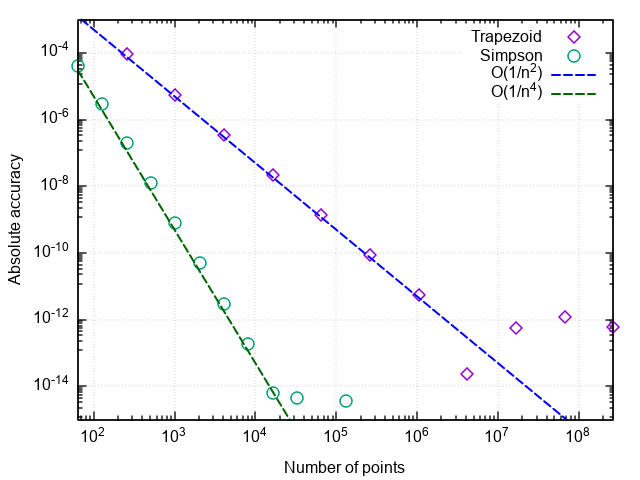
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования $|I_{Simps, n} - I| = O(1/n^4)$ (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).
image
Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.

Что дальше?

Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов wi в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.

Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:

$I_{trap,n}[f, a, b] = int_a^b f(x)dx + C_2h^2 + C_4h^4 + C_6h^6 + ...,~h = frac{b-a}{n}~~~(5)$

На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла $I(h)$ строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.

Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.

Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.

$I_{trap,n} - I approx C_2h^2;~I_{trap,2n} - I approx C_2left(frac{h}{2}right)^2$

Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:

$I = I_{trap,2n} - C_2left(frac{h}{2}right)^2 + O(h^4) approx I_{trap,2n} - frac{I_{trap,2n}-I_{trap,n}}{1-2^2} = I_{Simps,2n}$

Повторяя аналогичную процедуру для формулы Симпсона, получаем:

$I_{Simps,2n} - I approx C_4left(frac{h}{2}right)^4;~I_{Simps,n} - I approx C_4h^4$

$I = I_{Simps,2n} - C_4left(frac{h}{2}right)^4 + O(h^6) approx I_{Simps,2n} - frac{I_{Simps,2n}-I_{Simps,n}}{1-2^4}$

Если продолжить, вырисовывается такая таблица:

2 порядок 4 порядок 6 порядок …
I0,0
I1,0 I1,1
I2,0 I2,1 I2,2
… … …

В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).

Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:

$I_{i,j} = I_{i,j-1} - frac{I_{i,j-1}-I_{i-1,j-1}}{1-left(frac{h_{i-j}}{h_i}right)^2} = I_{i,j-1} - frac{I_{i,j-1}-I_{i-1,j-1}}{1-2^{2j}}~~~(6)$

Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.

$Delta_{i,j} approx I_{i,j} - I_{i,j-1}$

Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.

Реализация

Дополнительный метод добавляется в класс Quadrature

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным разбиением на nseg0 отрезков
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True):
        """Интегрирование методом Ромберга
           nseg0 - начальное число отрезков разбиения
           maxcol - максимальный столбец таблицы"""
        # инициализация таблицы
        Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]]
        i = 0
        maxcol = max(0, maxcol)
        ans = Itable[i][i]
        error_est = max(1, abs(ans))
        while (error_est > abs(rtol * ans)):
            old_ans = ans
            i += 1
            d = 4.0
            ans_col = min(i, maxcol)
            Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1))
            for j in range(0, ans_col):
                diff = Itable[i][j] - Itable[i - 1][j]
                Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0)
                d *= 4.0

            ans = Itable[i][ans_col]
            if (maxcol <= 1): # методы трапеций и парабол обрабатываются отдельно
                error_est = abs(ans - Itable[i - 1][-1])
            elif (i > maxcol):
                error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)])
            else:
                error_est = abs(ans - Itable[i - 1][i - 1])

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Проверим, как работает аппроксимация высокого порядка:

>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) # трапеции
Total function calls: 65537
4.250000001385811
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) # параболы
Total function calls: 2049
4.2500000000490985
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4)
Total function calls: 257
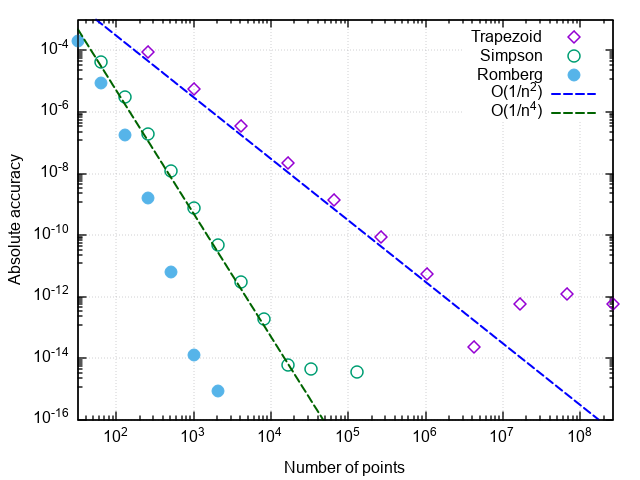
4.250000001644076

Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:
image

Некоторые замечания

Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5×10-15, метод парабол — при желаемой точности 2×10-16(что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.

Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.

Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:

>>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5)
Total function calls: 9
5.0
>>> Quadrature.simpson(abs, -1, 3, rtol=1e-5)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3)
Total function calls: 33
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4)
Total function calls: 33
5.000001383269357

Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4j. Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/ni)2j ~ 4–ij. C учётом деления получается ~4-(i+1)j ~ 4–j2. Т.е. при j~7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.

Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла $int_0^1sqrt{x}sin{x}dx$ и эквивалентного ему $int_0^1 2t^2sin{t^2}dt$. Как говорится, почувствуйте разницу.

Заключение

Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования “обычных” функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.

Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).

Литература

  1. А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука. 1989.
  2. J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
  3. W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 мая 2019 года; проверки требуют 14 правок.

Правило Рунге — правило оценки погрешности численных методов, было предложено К. Рунге в начале 20 века.[1]

Основная идея (для методов Рунге-Кутты решения ОДУ) состоит в вычислении приближения выбранным методом с шагом h, а затем с шагом h/2, и дальнейшем рассмотрении разностей погрешностей для этих двух вычислений.

Применение правила Рунге[править | править код]

Оценка точности вычисления определённого интеграла[править | править код]

Интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном 2n. Погрешность вычисления значения интеграла при числе шагов, равном 2n, определяется по формуле Рунге:
Delta _{{2n}}approx Theta |I_{{2n}}-I_{{n}}|, для формул левых и правых прямоугольников {displaystyle Theta =1}, для формул средних прямоугольников и трапеций Theta ={frac {1}{3}}, а для формулы Симпсона Theta ={frac {1}{15}}.[2] В общем случае {displaystyle Theta ={{1} over {2^{p}-1}}}. Под p понимается порядок погрешности использованного численного метода.

Таким образом, интеграл вычисляется для последовательных значений числа шагов N=n_{0},2n_{0},4n_{0},dots , где n_{0} — начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения N будет выполнено условие {displaystyle Delta _{2n}<varepsilon }, где varepsilon  — заданная точность.

Оценка точности численного решения ОДУ[править | править код]

Также применяется для оценки точности решений обыкновенных дифференциальных уравнений на регулярных сетках. Для оценки требуется решить задачу на 2 сетках, один раз с шагом h (y_{{i,h}}) и второй — с шагом h/2 (y_{{i,h/2}}). Формула[3]

{displaystyle {|y_{i,h}-y_{i,h/2}|} over {2^{p}-1}}

дает погрешность решения y_{{i,h/2}}. Под p понимается порядок точности использованного численного метода.
Например, для численного метода, имеющего четвёртый порядок точности, формула принимает вид:

{1 over 15}|y_{{i,h}}-y_{{i,h/2}}|

Примечания[править | править код]

  1. ↑ Ivan P. Gavrilyuk, «2.4 A posteriori error estimation and automatic grid generation.» // Exact and Truncated Difference Schemes for Boundary Value ODEs, Springer, 2011, ISBN 9783034801072, pages 76-77: «The first possibility is the classic technique which has been proposed by Carl Runge.»
  2. ↑ Огородников А. С., Орлов О. В.,6. Правило Рунге оценки погрешности интегрирования Архивная копия от 14 сентября 2013 на Wayback Machine // Лабораторная работа № 4. Численное интегрирование, Лабораторный практикум по курсу «Численные методы» (ЭНИН) Архивная копия от 8 декабря 2015 на Wayback Machine, Томский политехнический университет
  3. ↑ П. В. Виноградова, А. Г. Ереклинцев, 8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА Архивная копия от 14 сентября 2013 на Wayback Machine // ЧИСЛЕННЫЕ МЕТОДЫ Архивная копия от 4 марта 2016 на Wayback Machine, Дальневосточный государственный университет путей сообщения, 2011

Литература[править | править код]

  • РУНГЕ ПРАВИЛО // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
  • Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; 2 изд., т. 2, М., 1962;
  • Современные численные методы решения обыкновенных дифференциальных уравнений, пер. с англ., М., 1979. А. Б. Иванов.

Ссылки[править | править код]

  • Осокин А. Е., 4.7 Правило Рунге оценки погрешности. Экстраполяция Ричардсона. Архивная копия от 24 мая 2013 на Wayback Machine // ВВЕДЕНИЕ В ЧИСЛЕННЫЕ МЕТОДЫ АНАЛИЗА И ЛИНЕЙНОЙ АЛГЕБРЫ Архивная копия от 1 января 2013 на Wayback Machine, Горно-Алтайский государственный университет, 2002
Источник

Добавить комментарий