Для треугольника:
![]() .
.
![]() , (37)
, (37)
т.е. квадрат
относительной погрешности вычисления
площади треугольника, прямоугольника,
параллелограмма равен сумме квадратов
относительных погрешностей измерений
основания и высоты фигуры.
Для трапеции:
![]() ,
,
относительная СКП
вычисления площади составит
![]() (38)
(38)
Если принять, что
относительные погрешности измерения
основания и высоты фигуры одинаковые
и равны
![]() ,
,
то из (45) найдем
![]() . (39)
. (39)
Пример: Основание
и высоту фигуры площадью P=100га,
измерили на местности с относительной
погрешностью
![]() ,
,
СКП площади составит![]() .
.
Для четырехугольника
по форме близкого к квадрату, в котором
измерены все стороны и два угла, т.е.
![]()
![]()
![]() и
и![]()
![]()
![]() ,
,
справедливо выражение
![]() (40)
(40)
Если для вычисления
площади четырехугольника, использовались
три известные стороны и два угла (40), то
![]() (41)
(41)
Пример: При
относительной погрешности измерений
![]() и СКП измерений угла
и СКП измерений угла![]() ,
,
относительная погрешность определения
площади составит![]() .
.
Из приведенных
примеров, очевидно, что относительная
погрешность вычисления площади
аналитическим способом несколько больше
относительной погрешности измеренных
линий и зависит не только от точности
измерений на местности, но и от применяемых
формул.
8.3. Вычисление площадей графическим способом
На плане контур,
площадь которого хотят определить
разбивают на геометрические фигуры, в
которых измеряют длины сторон и высоты.
Далее по формулам (38-44) находят площадь.
Существует ряд
условий при вычислении площадей
графическим способом, к которым относятся:
-
для вычисления
площадей участков, имеющих большое
количество углов, целесообразнее
вычислять площадь по графическим
координатам точек; -
при выборе
разбиваемой на плане фигуры, предпочтение
отдают треугольникам, причем наилучшим
вариантом являются равносторонние
треугольники
 ;
; -
если высоты или
основания представляют собой линии,
измеренные на местности (стороны
теодолитного хода), то для повышения
точности вычисления площадей, длины
этих линий не измеряют на плане, а берут
из результатов непосредственных
измерений; -
точность вычисления
площади неравностороннего треугольника
выше, если короткое основание (высота)
измерено на местности, а длинная высота
(основание) получена с плана -
для контроля и
повышения точности площадь определяют
дважды: по двум различным основаниям
и двум высотам. Затем сравнивают
расхождение полученных площадей и при
их допустимости
![]() ,
,
вычисляют среднее
значение.
8.4. Точность вычисления площадей графическим способом
Если в треугольнике
измерено по плану основание
![]() и
и
высота![]() ,
,
то погрешность вычисления площади можно
найти из выражения
![]() (42)
(42)
Погрешности
измерения основания и высоты по плану
можно считать одинаковыми
![]() ,
,
тогда с учетом![]() ,
,
получим погрешность вычисления площади
треугольника
![]() (43)
(43)
В случае если
![]() получим
получим![]() ,
,
но![]() ,
,
тогда
![]() (44)
(44)
Для трапеции,
прямоугольника и параллелограмма
обозначим
![]() и
и![]() ,
,
тогда погрешность вычисления площади
данных фигур составит
![]() (45)
(45)
В случае если
![]() получим
получим![]() ,
,
но![]() ,
,
тогда
![]() (46)
(46)
Из сравнения формул
очевидно, что погрешность вычисления
площади треугольника меньше погрешности
определения площадей других фигур.
Обозначив
![]() ,
,
гдеK
– коэффициент вытянутости фигуры, то
из (46) получим
![]() . (47)
. (47)
Так как площадь
треугольника
![]() и
и![]() ,
,
то
![]()
откуда.
Подставив выражение
![]() в (50) найдем
в (50) найдем
![]() (48)
(48)
Из анализа формул
(47) и (51) видно, что погрешность определения
площади вытянутого треугольника по
плану больше погрешности определения
площади треугольника при
![]() в
в![]() раз. Это заключение верно и для
раз. Это заключение верно и для
прямоугольника, трапеции и параллелограмма.
Пример. На плане
масштаба 1:500 измерены
![]() ,
,![]() .
.
Площадь треугольника![]() ,
,![]() ,
,
или в масштабе плана0,2м.,
![]() .
.
По формуле (51) найдем
![]() ,
,
или
![]() .
.
Если основание
![]() измерено на местности рулеткой с
измерено на местности рулеткой с
относительной погрешностью![]() ,
,
по формуле (44) получим

Следовательно,
погрешность измерения на плане короткого
основания
![]() снизило точность вычисления площади
снизило точность вычисления площади
треугольника в пять раз.
Если площадь
многоугольника разбита на
![]() треугольников с соотношением
треугольников с соотношением![]() ,
,
т.е.![]() ,
,
то погрешность определения его площади,
составит
![]() .
.
СКП площади каждого
треугольника определим по формуле
![]() ,
,
тогда
![]() .
.
Следовательно, на
точность определения площади контура
на плане не влияет на сколько треугольников
разбит этот контур. Нет необходимости
стремиться к тому, чтобы число треугольников
было наименьшим, а надо стараться, чтобы
выполнялось условие
![]() .
.
Погрешность
площади, вычисленной по графическим
координатам точек можно рассчитать по
формуле
![]() ,
,
в которой СКП
измерения координат на плане с помощью
измерителя принимают равной
![]() .
.
При измерении
площади контура с помощью квадратной
или параллельной палетками ее погрешность
характеризуется эмпирической формулой
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
РЕКОМЕНДУЕМЫЕ ФОРМУЛЫ
РАСЧЕТА ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ (ВЫЧИСЛЕНИЯ) ПЛОЩАДИ ЗДАНИЯ,
СООРУЖЕНИЯ, ПОМЕЩЕНИЯ, МАШИНО-МЕСТА
1. В случае если здание, сооружение, помещение, мащино-место имеет простейшую геометрическую фигуру в форме квадрата, прямоугольника, параллелограмма, среднюю квадратическую погрешность определения площади здания, сооружения, помещения, машино-места (mp) рекомендуется вычислять по формуле:
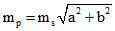 ,
,
где:
a и b – длина и ширина прямоугольника, у квадрата – длина сторон, у параллелограмма – длина основания и высота соответственно;
ms – средняя квадратическая погрешность определения линейных измерений.
2. В случае если здание, сооружение, помещение имеет простейшую геометрическую фигуру в форме треугольника, а площадь его определяется через произведение высоты на основание, то среднюю квадратическую погрешность определения площади здания, сооружения, помещения рекомендуется вычислять по формуле:
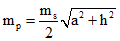 ,
,
где:
a – длина основания треугольника;
h – высота треугольника;
ms – средняя квадратическая погрешность определения линейных измерений.
3. При определении площади здания, сооружения, помещения путем разбивки такого объекта на простейшие геометрические фигуры и суммирования площадей таких фигур или площади помещения путем суммирования площадей всех частей такого помещения среднюю квадратическую погрешность определения площади здания, сооружения, помещения в пределах одного этажа, а также в случае одноэтажности объекта недвижимости рекомендуется вычислять по формуле:
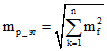 ,
,
где:
mf – средняя квадратическая погрешность определения площади простейшей фигуры или одной части помещения;
n – количество простейших геометрических фигур, на которые был разбит объект для определения площади, или количество частей, из которых состоит помещение.
4. В случае наличия нескольких этажей у здания, сооружения, расположения помещения на нескольких этажах и (или) наличия эксплуатируемой кровли среднюю квадратическую погрешность определения площади здания, сооружения, помещения рекомендуется вычислять по формуле:
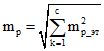 ,
,
где:
mp_эт – средняя квадратическая погрешность определения площади здания, сооружения, помещения в пределах одного этажа, а также эксплуатируемой кровли;
c – количество этажей у здания, сооружения, помещения, также при необходимости учитывается эксплуатируемая кровля.
5. Среднюю квадратическую погрешность определения площади застройки сооружения рекомендуется вычислять по формуле:
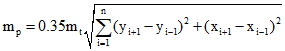 ,
,
где:
xi, yi – координаты характерных точек контура застройки сооружения;
mt – средняя квадратическая погрешность измерений положения точек контура застройки сооружения;
n – число характерных точек контура застройки сооружения.
Скачать документ целиком в формате PDF
Mikhail Levin
Искусственный Интеллект
(614566)
10 лет назад
никак. Надо хотя бы стороны знать. У квадрата и длинной-длинной полоски погрешность будет разная.
если погрешность измерения длины dl
S’=S+ds=(a+dl)(b+dl)=ab + a*dl +b*dl + dl*dl ~ S + (a+b)*dl
ds ~= (a+b)*dl
мне по работе приходилось считать для произвольную участков? там все хуже…
000Мыслитель (5459)
10 лет назад
Спасибо!!
Только у меня нет сторон. Известна только погрешность измерения сторон – 0,01м, периметр – 11,98м и площадь 8,94м2. И ответ – 0,06м2. Но как он получается?
По периметру я же не могу узнать точно, какова длина сторон.
Assafriend
Мудрец
(18996)
10 лет назад
вычесть из максимальной площади прямоугольника минимальную – это и будет абс погрещность по площади ессно для каждого прямоугольника – своя!
например квадрат 1м +/-0.1м имеем 1.21-0.81=0.4 кв. м. т. е. 1 +/- 0,2 кв. м.
000Мыслитель (5459)
10 лет назад
Только тогда надо стороны знать, а я их не знаю. Знаю только периметр и площадь. И неизвестно, квадрат ли это.
AssafriendМудрец (18996)
10 лет назад
ваши стороны х и у
2х+2у=11.98 отсюда х=11.98/2-у
х*у=8.94 отсюда х=8.94/у
графики этих двух функций пересекутся в единственной точке так можно узнать стороны!
Вольный ветер
Искусственный Интеллект
(283261)
10 лет назад
Компьютер способен решать задачки не только по высшей математике, но и более сложные! А молодежь только играет, на компе работать не научились, а на калькуляторе уже разучились, вот дяди и решают вам элементарные примеры, и задачки, хотя своя ЭВМ у вас под носом….))))
При выполнении обмеров помещений с целью подготовки технического плана всегда возникают ошибки, связанные с погрешностями измерений. Непосредственно выполняются линейные измерения размеров помещений, а площадь помещений является расчетной величиной, которая имеет погрешность, зависимую от погрешностей прямых (линейных) измерений.
Допустимые ошибки измерений линий при технической инвентаризации установлены пунктом 11.10 Рекомендаций по технической инвентаризации и регистрации зданий гражданского назначения (Приняты Росжилкоммунсоюзом к введению в действие с 1 января 1991 года) и составляют:
для линий до 1 м +/- 1 см (1:100);
для линий до 6 м +/- 3 см (1:150);
для линий до 12 м +/- 5 см (1:200);
для линий до 24 м +/- 8 см (1:300);
для линий до 100 м +/- 30 см (1:400).
Применительно к квартирам почти все измеряемые линии находятся в пределах от 1 до 6 метров. Следовательно, возможно принять предельную ошибку измерения линии в среднем 3 см.
По правилам математической статистики для перехода от предельных ошибок (при принятии доверительного интервала равным 95%) к средним квадратическим погрешностям следует предельную ошибку разделить на 2. В этом случае средняя квадратическая погрешность измерения линии составит 1.5 см, или 0.015 м.
Погрешность измерения площади помещения целесообразно рассчитать по упрощенной методике. Для этого следует принять, что типичное помещение в квартире имеет прямоугольную форму и его площадь определяется произведением длины помещения на его ширину:
При этом погрешность измерения длины помещения – линии a (Da) обусловит погрешность площади в зависимости от длины помещения (DPa), а погрешность измерения ширины помещения – линии b (Db) обусловит погрешность площади в зависимости от ширины помещения (DPb). Графически эти погрешности будут выглядеть следующим образом:
Из рисунка очевидно, что
DPa= b * Da,
DPb= a * Db.
Величины DPa и DPb являются независимыми случайными величинами, поскольку они являются производными от независимых случайных величин (погрешностей измерения). В связи с этим общая погрешность определения площади согласно правилам сложения независимых случайных величин определяется путем их геометрического суммирования:
DP = √((DPa)2 + (DPb)2)
Выразив DPa и DPb через длину и ширину помещения и погрешности их измерения и приняв во внимание, что погрешность измерения ранее определена равной 0.015 м, получим:
DP = √(( b * Da)2 + (a * Db)2) = √(( b * 0.015)2 + (a * 0.015)2) = √(0.0152*( a2 + b2)) = 0.015 * √( a2 + b2)
В случае, если помещение представляет собой квадрат и a = b, P = a2, формула погрешности сводится к следующему:
DP = 0.015 * √( a2 + a2) =0.015 * √(2*a2) = 0.015 *√2 * √P
При подстановке в формулу различных значений соотношения a и b, можно найти зависимость между отношением a/b=K и погрешностью площади.
DP = 0.015 * √( b2 + (К*b)2) =0.015 * √(( 1+К2) *b2)
Принимая во внимание, что a = b*K, получим:
P=a*b = b2*K
или
b2 = P/K
Подставив последнее соотношение в формулу для погрешности определения площади, получим
DP = 0.015 * √(( 1+К2) *b2) = 0.015 * √(( 1+К2) *P/K) = 0.015 * √((( 1+К2)/K) *P)
Величина K = a/b, выражающая отношение длины помещения к его ширине, называется коэффициентом вытянутости геометрической фигуры. Для упрощения расчетов целесообразно не определять ее отдельно для каждого объекта, а определить ее среднее значение по представительной выборке и в дальнейшем пользоваться полученным результатом.
В качестве типичного объекта взята типовая секция дома проекта П44Т и выполнен расчет среднего весового значения этого коэффициента (за вес единичного определения коэффициента принята площадь данного помещения, вычисленная упрощенно, без учета сложной конфигурации). Полученный результат равен 1.67.
Для такого значения К получим
DP = 0.015 * √(( 1+К2)/K) *P) = 0.015 * √(( 1+1.672)/1.67) *P) = 0.015 * 1.506 * √P = 0.0226 * √P
Для перехода от средних квадратических значений погрешности к предельно допустимым применяется коэффициент 2 (при доверительном интервале 95%). В этом случае
DP предельн = 0.0451 * √P, кв. м.
Для упрощения расчетов возможно округлить коэффициент:
DP предельн = 0.05 * √P, кв. м.
Таким образом определяется предельная погрешность определения площади элементарного прямоугольника. Для перехода к предельной погрешности площади квартиры (как совокупности помещений) нужно провести геометрическое суммирование погрешностей по помещениям. Эта операция сводится к подстановке значения общей площади квартиры в последнюю формулу.
Возможно составить таблицу значений погрешности определения площади для квартир различной площади. Результаты приведены ниже.
Приведенная таблица погрешностей не учитывает возможные погрешности при возведении некапитальных стен, в результате чего измерения длины помещения по разным стенам могут дать различные результаты. Таблица применима только в отношении домов, построенных из типовых сборных ж/б элементов (как дома серии П44Т). Для монолитных домов, домов серии П111М (с легкобетонными перегородками) необходимо учитывать в расчетах указанную выше погрешность.
Для таких домов погрешность прямых измерений была определена по выборке натурных измерений помещений. В тестовом объекте (монолитный многоквартирный жилой дом) обмеры были выполнены по всему периметру всех помещений. Выла взята случайная выборка из 50 помещений прямоугольной формы. Погрешность измерений была определена по абсолютным отклонениям между измеренными длинами противолежащих сторон прямоугольника (всего 100 пар измерений, по 2 пары на помещение).
Значение средней квадратической погрешности по выборке составило 0.024 м. Это значение подставлено в формулу расчета погрешности площади вместо величины 0.015 м:
DP = 0.024 * 1.506 * √P = 0.036 * √P
предельная погрешность определения площади в этом случае составляет
DPпредельн = 2 * 0.036 * √P = 0.072 * √P
Для упрощения расчетов возможно округлить коэффициент:
DP предельн = 0.07 * √P, кв. м.
Таблица погрешностей определения площади для квартир различной площади для указанного случая приведена ниже.![[IMG]](https://img-fotki.yandex.ru/get/98971/13421369.2/0_bbfa5_ea7cf4e0_orig)
При проведении землеустроительных работ используются различные способы вычисления площадей участков земли. Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.
СодержаниеПоказать
- Основные способы
- Аналитический способ
- Графический метод
- Механический способ
- Погрешность определения площади
- Определение площади участка на ПКК
Основные способы
Существует три основных способа определения площадей:
- аналитический;
- графический;
- механический.
 При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.
При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.
Для графического способа используются данные измерений на плане и карте.
Такой способ чаще всего используется при отсутствии информации полевых измерений.
При механическом способе площадь определяется по плану с помощью специального устройства – планиметра.
Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.
Эти три метода имеют различные показатели точности.
Наиболее точным является аналитический метод. На точность этого метода влияют только погрешности полевых измерений.
Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.
 Аналитический способ
Аналитический способ
Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.
В соответствии с ними площадь многоугольника S может быть определена по формуле:
S= 0,5*∑(Xi*(Yi+1-Yi-1), где:
- Xi и Yi – координаты i-той характерной точки участка, имеющего вид многоугольника;
- i – порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
- n – число характерных точек.
Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.
Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:
Sт=0,5*(a+b)*h, где:
- a и b – основания фигуры;
- h – высота трапеции.
При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:
р=0,5(а+B+c+d), где:
a,b,c,d – величины сторон.
Тогда площадь участка Sу будет равна:
Sy=√(p-a)(p-b)(p-c)(p-d).
В некоторых случаях, когда имеется много точек поворота, аналитический расчет площади участка производится с использованием данных об углах азимута.
При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.
 Графический метод
Графический метод
При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.
Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.
Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.
В некоторых случаях участки имеют криволинейную форму, которую трудно аппроксимировать простыми фигурами. В таких случаях могут использоваться палетки.
Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.
Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.
Механический способ
Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.
Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
Точность метода зависит от размеров участка и свойств плана.
Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность – это разность между вычисленной величиной площади участка и ее истинной величиной.
Для различных методов определения площади такие погрешности могут быть различными.
Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:
mp= mt*√ P, где:
- mt – СКП расположения поворотных точек;
- P – площадь участка.
Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.
Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:
mpс= 0,2*√600=4,89 м.
При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.
Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.
В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.
Определение площади участка на ПКК
Публичная кадастровая карта (ПКК) – это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).
Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.
Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.
Среди этих данных имеется площадь данного участка, которая является официальной величиной, так как она введена в ЕГРН.
Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: “обл. Московская, р-н Зарайский, снт “Изобретатель”, уч-к 116″.
 Однако при обращении к ПКК с использованием этого адреса система дает сбой. Подобный результат получается и при обращении к ПКК на других страницах.
Однако при обращении к ПКК с использованием этого адреса система дает сбой. Подобный результат получается и при обращении к ПКК на других страницах.
Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.
Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.
Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.
По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.
![[IMG]](https://img-fotki.yandex.ru/get/55905/13421369.2/0_bbf9f_194a810_orig)
![[IMG]](https://img-fotki.yandex.ru/get/28982/13421369.2/0_bbfa0_f0d5a6f3_orig)
![[IMG]](https://img-fotki.yandex.ru/get/98971/13421369.2/0_bbfa1_4538c891_orig)
![[IMG]](https://img-fotki.yandex.ru/get/58454/13421369.2/0_bbfa2_6c5c2a6a_orig)
![[IMG]](https://img-fotki.yandex.ru/get/93451/13421369.2/0_bbfa3_4956c37b_orig)
![[IMG]](https://img-fotki.yandex.ru/get/93451/13421369.2/0_bbfa4_3711ce17_orig)
