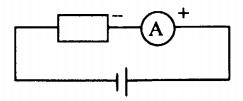
Как найти показания вольтметра по напряжению - Сайт, где вы сможете решить свои вопросы

Амперметр

Для измерения силы тока используется амперметр. В идеале собственное сопротивление амперметра стремится к нулю, и оно никак не влияет на значение силы тока. Он включается в цепь последовательно с соблюдением полярности:

Вольтметр

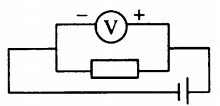
Для измерения напряжения участка цепи используется вольтметр. В идеале собственное сопротивление вольтметра стремится к бесконечности, и устройство не проводит через себя ток. Он включается в электрическую цепь параллельно участку, в котором будет измеряться напряжение, с соблюдением полярности:

Как правильно записывать показания измерительных приборов с учетом погрешности

При записи величин (с учетом погрешности) следует пользоваться формулой:

A=a±Δa

где A — измеряемая величина, a — результат измерений, Δa — погрешность измерений.

Важно!

Погрешность измерений равна половине цены деления шкалы измерительного прибора, если в задаче не указана другая величина погрешности.

Цена деления шкалы — разность значений величины, соответствующих двум соседним отметкам шкалы. Чтобы найти цену деления шкалы, нужно:

Найти два ближайших штриха шкалы, возле которых написаны значения величин.
Вычесть из большего значения меньшее.
Полученное число разделить на число делений (промежутков), находящихся между ними.

Пример №1. Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.

Видно, что стрелка вольтметра встала на значении «2,0» Вольт. Она немного не дотягивает до штриха «2», но к нему она находится ближе, чем к предыдущему штриху.

Два ближайших штриха шкалы с указанными значениями имеют значения 1 и 2 В. Всего между ними 5 промежутков. Следовательно, цена деления шкалы равна: (2 – 1)/5 = 0,2 (Вольт).

Так как по условию задачи погрешность равна половине цене деления шкалы, то она равна 0,1 Вольтам. Следовательно, вольтметр показывает: 2,0 ± 0,1 В.

Задание EF18821

Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения равна цене деления вольтметра.

Ответ: (____± ____) В.

Алгоритм решения

1.Определить цену деления шкалы измерительного прибора.

2.Определить погрешность измерений.

3.Определить показания прибора.

4.Записать показания прибора с учетом погрешности измерений.

Решение

Так как два ближайших штриха, обозначенными числовыми значениями, показывают 1 и 2 Вольта, а между ними 5 делений, то цена деления шкалы равна:

2−15=0,2 (В)

Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка вольтметра стоит в трех делениях от штриха, обозначенном цифрой «1». 3 деления по 0,2 Вольта равны 0,6 Вольтам. Следовательно, вольтметр показывает 1,6 В. С учетом погрешности: V = 1,6 ± 0,2 В.

Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».

Ответ: 1,60,2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18883

Определите показания амперметра (см. рисунок), если погрешность прямого измерения силы тока равна цене деления амперметра.

Ответ: ( ____± ____) А.

Алгоритм решения

1.Определить цену деления шкалы измерительного прибора.

2.Определить погрешность измерений.

3.Определить показания прибора.

4.Записать показания прибора с учетом погрешности измерений.

Решение

Так как два ближайших штриха, обозначенными числовыми значениями, показывают 0 и 0,2 Ампера, а между ними 10 делений, то цена деления шкалы равна:

0,2−010=0,02 (А)

Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка амперметра стоит на штрихе, обозначенном числом «0,2». Следовательно, амперметр показывает 0,2 А. Так как при измерении учитываются сотые доли Амперов, правильно результат измерения записывается так: I = 0,20 А. С учетом погрешности: I = 0,20 ± 0,02 А.

Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».

Ответ: 0,200,02

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19038

Определите напряжение на лампочке (см. рисунок), если погрешность прямого измерения напряжения равна цене деления вольтметра.

Ответ: ( ____±____ ) В.

Алгоритм решения

1.Определить цену деления шкалы измерительного прибора.

2.Определить погрешность измерений.

3.Определить показания прибора.

4.Записать показания прибора с учетом погрешности измерений.

Решение

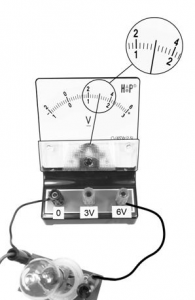
Так как два ближайших штриха, обозначенными числовыми значениями, показывают 2 и 4 Вольта, а между ними 10 делений, то цена деления шкалы равна:

4−210=0,2 (В)

Согласно условию задачи, погрешность измерений равна цене деления шкалы. Стрелка вольтметра стоит в пяти делениях от штриха, обозначенном цифрой «2». 5 делени1 по 0,2 Вольта равны 1 Вольту. Следовательно, вольтметр показывает 3 В. Так как при измерении учитываются сотые доли Вольтов, правильно результат измерения записывается так: U = 3 В.С учетом погрешности: U = 3,0 ± 0,2 В.

Внимание! При записи ответа нужно использовать только десятичные числа без пробелов и знака «±».

Ответ: 3,00,2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.3k

Источник

Я в школе учился давно, поэтому не совсем уверен, что правильно понимаю термины “идеальный вольтметр” и ” идеальный источник тока”. Возможно это означает, что сопротивление вольтметра – бесконечно, а внутреннее сопротивление источника тока равно нулю. Если это так, то задачу можно решать так:

В приведённой схеме резистор R2 и сопротивление вольтметра (обозначим его R3, хотя оно и не очень нужно, просто для ясности) соединены параллельно. Их эквивалентное сопротивление (R) определяется по формуле 1/R=1/R2+1/R3, Получаем, что R=160 Ом. Ток в цепи равен 32/160=0,2 А. Полное сопротивление цепи 160+240=400 Ом, ЭДС источника*0,2=80 В.

Если сопротивление вольтметра R3 – бесконечное, то он не влияет на параметры цепи. Тогда полное сопротивление цепи равно 240+200=440 Ом, Ток в цепи равен 80/440=(2/11) А, Падение напряжения на резисторе R2 (именно это и покажет вольтметр) составит (2/11)*200=400/11 В, или приблизительно 36,(36) В. (36) обозначает 36 в периоде, т.е. 36,36363636… , или округлённо 36,37 В.

Источник

Как определить показания вольтметра в цепи постоянного тока

Измерение тока и напряжения. Вольтметр и амперметр.

Приветствую всех читателей на нашем сайте и сегодня в рамках курса “Основы электроники” мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр и амперметр.

Меры безопасности

Поскольку сам прибор имеет большое сопротивление, а в сеть он подключается параллельно, вероятность того, что при работе с ним человек получит сильный удар током, минимальна. Однако если вольтметры используются в промышленности, часто приходится иметь дело с большими значениями напряжения и других величин, характеризующих электрический ток.

Нужно быть очень осторожным, измеряя напряжение в сети посредством этого электроизмерительного прибора. Ни в коем случае нельзя прикасаться к прибору голыми руками. Избежать несчастного случая помогут перчатки из непроводящего ток материала, например, из резины.

Нельзя прикасаться к оголенным проводам, даже если уже известно, что напряжение в них не очень велико, например, Вольт или еще меньше.

Измерение тока. Амперметр.

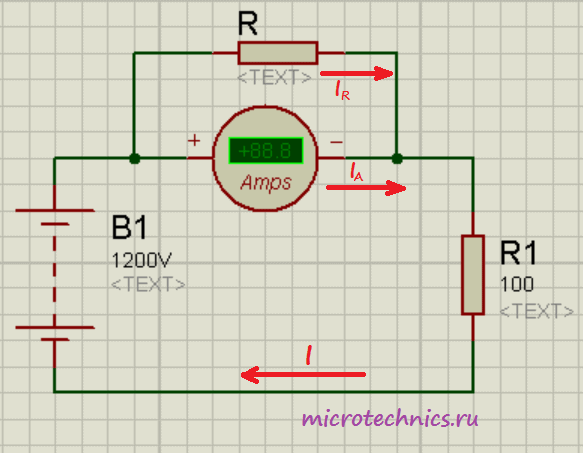
И начнем мы с измерения тока. Прибор, используемый для этих целей, называется амперметр и в цепь он включается последовательно. Рассмотрим небольшой примерчик:

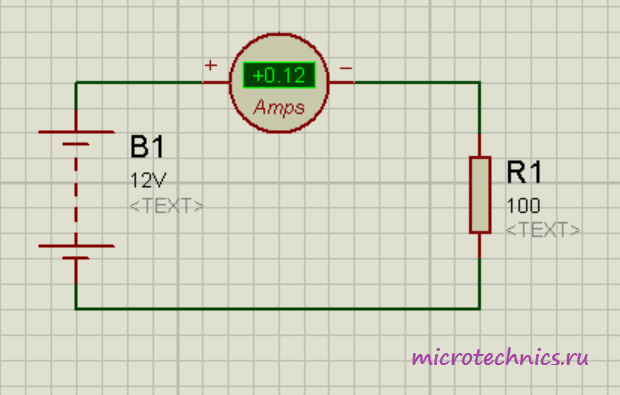
Как видите, здесь источник питания подключен напрямую к резистору. Кроме того, в цепи присутствует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи должна быть равна:

Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи

Источник

Измерение тока и напряжения. Вольтметр и амперметр.

Приветствую всех читателей на нашем сайте и сегодня в рамках курса «Основы электроники» мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр и амперметр.

Измерение тока. Амперметр.

Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 🙂

Важным параметром этого прибора является его внутреннее сопротивление r_А . Почему это так важно? Смотрите сами — при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:

Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.

При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:

В этой формуле n — это коэффициент шунтирования — число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.

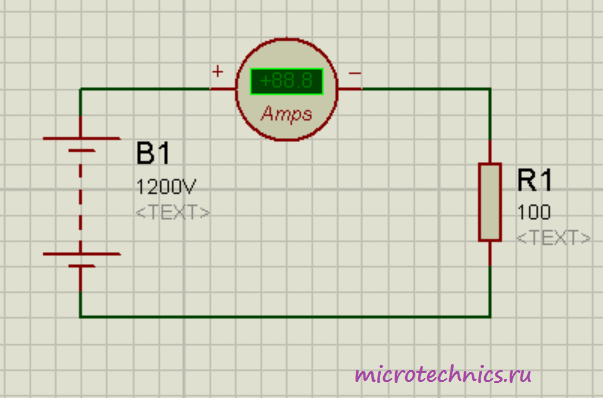
Пусть максимальное значение, которое может измерить амперметр составляет 1 А. А схема, силу тока в которой нам нужно определить имеет следующий вид:

Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:

В данной задаче нам необходимо измерить ток I . Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:

В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.

Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:

Выразим ток шунта через ток амперметра:

Подставим в это уравнение предыдущее выражение для тока шунта:

Но сопротивление шунта нам также известно ( R = frac ). В итоге мы получаем:

Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нам и нужно измерить 🙂

С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.

Измерение напряжения. Вольтметр.

Прибор, предназначенный для измерения напряжения называется вольтметр. И, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся с чем это связано:

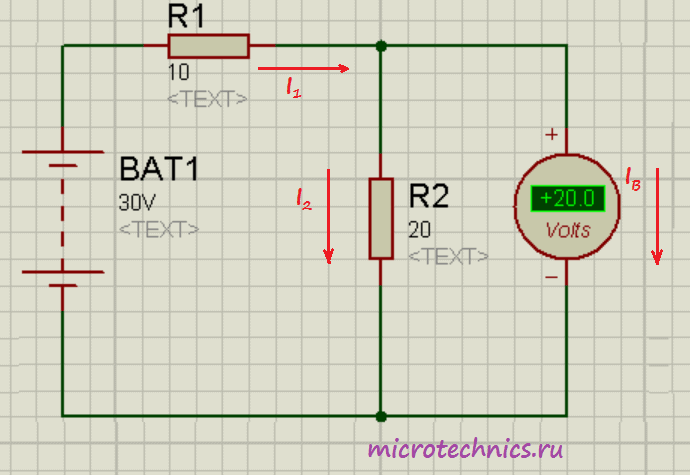
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:

Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с R_2 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток ( I_B = 0 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку r_В имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток. В связи с этим напряжение на резисторе R_2 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.

Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:

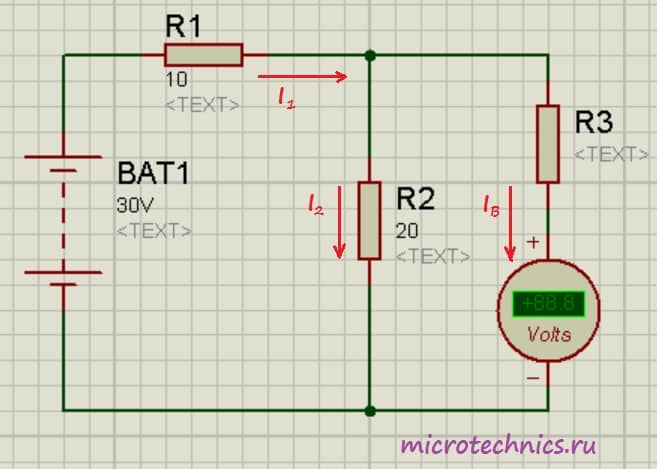
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример:

Здесь мы добавили в цепь добавочное сопротивление R_3 . Перед нами стоит задача измерить напряжение на резисторе R_2:medspace U_2 = R_2medspace I_2 . Давайте определим, какой результат при таком включении выдаст нам вольтметр:

Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:

Таким образом: U_В = frac . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра!

В завершении статьи пару слов об измерении сопротивления и мощности.

Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи — омметр — и мощности — ваттметр.

В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями и заходите к нам на сайт! До скорых встреч!

Источник

Амперметр и вольтметр. Правила включения.

теория по физике 🧲 постоянный ток

Как правильно записывать показания измерительных приборов с учетом погрешности

При записи величин (с учетом погрешности) следует пользоваться формулой:

где A — измеряемая величина, a — результат измерений, Δa — погрешность измерений.

Найти два ближайших штриха шкалы, возле которых написаны значения величин.
Вычесть из большего значения меньшее.
Полученное число разделить на число делений (промежутков), находящихся между ними.

Источник

Как найти показания вольтметра?

Нужно найти показания вольтметра

(Возникает проблема с преобразованием треугольник — звезда)

Напряжение узла «2» относительно «земля», (смотри табл. )

Между точкой «+» и «3» падает 140 вольт. Следовательно, в точке «1» получается плечо делителя из R1 = 20 Ом и параллельного соединения 20 Ом и 30 Ом = 12 Ом.
Получается, что на комбинированном плече делителя падает 140*(12/32) = 52.5 Ом. Скобки поставил для наглядности. Это напряжение делится пополам делителем R2+R4. Получаем 26.25 вольта.

Теперь отнимаем их от 140 и получаем 113.75.
Вуаля.

А про звезду с треугольником — не понял. Простите.

Если про делитель напряжения на сопротивлениях непонятно, то либо продолжайте изучать закон Ома, либо в поиск.
Можно в личку.

сумма сопрот w=R2+R3+R4 = 50. напротив узла 1:
r1= R2*R3/w =300/50 = 6;
2: r2 = 4.5; 3: r3 = 6;
Это сопротивления звезды .
Цепочка : R1;r2;r3 (r1 для напряжения V роли не играет)

V = U*(R1+r2)/(R1+r2+r3) = 112.4590164

Лично меня всегда учили сначала «разворачивать» схему более удобно (в сложных задачах)
Выбираем самую длинную «дорогу»(от + к -) и рисуем на 2 схеме ее прямо, обозначаем узлы и ответвления

Дальше легко, по закону ома.

У меня получилось так же, как и у Алексея ответ

Правда я решал там «числами» и плохо понятно.

Источник

Определение показаний вольтметров.

На рис.3 представлена схема с
вольтметрами и с соединением R6
и E6.

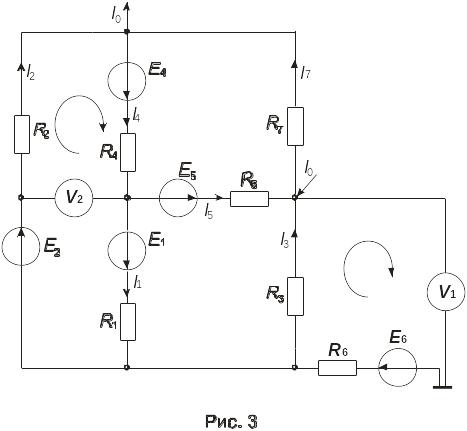
Рассмотрим контур a–R3-d–V1-o–E6-R6-a
и составим для него уравнение по второму
закону Кирхгофа:

E6
= I3R3
+ Udo,
здесь Udo
и есть показание вольтметра V1,

Udo
= E6
– I3R3.

Для нахождения показания второго
вольтметра, рассмотрим контур

f–R2-c–E4-R4-b–V2-f
и составим для него уравнение по второму
закону Кирхгофа:

E4
= I2R2
+ I4R4
+ Ubf,
здесь Ubf
и есть показание вольтметра V2,

Ubf
= E4
– I2R2
– I4R4.

Определение методом эквивалентного
генератора

величины дополнительной э.д.с.,

которую нужно включить во вторую
ветвь,

чтобы ток в ней увеличился в два раза

и сменил направление.

Составим схему, состоящую из
эквивалентного генератора и второй
ветви. Она представлена на рис.4:

Здесь Г – эквивалентный генератор,

Eг
и Rг
– э.д.с. и собственное сопротивление,
соответственно,

эквивалентного генератора,

E2
и R2
– э.д.с. и резистор второй ветви,

Ex
– искомая э.д.с.,

2I2
– ток во второй ветви, равный удвоенному
значению ранее

найденного тока I2,
и имеющий противоположное ему

направление.

Уравнение по второму закону Кирхгофа
для этой схемы будет иметь вид:

E2
+ EГ
– Ex
= -2I2(R2
+ RГ),

отсюда следует:

Ex
= E2
+ EГ
+ 2I2(R2
+ RГ).

Для того, чтобы найти Ex,
нужно найти э.д.с. эквивалентного
генератора EГ
и его собственное сопротивление RГ.

Определение э.Д.С. Эквивалентного генератора методом узловых потенциалов.

Рассмотрим схему эквивалентного
генератора. Она представлена на рис.5.

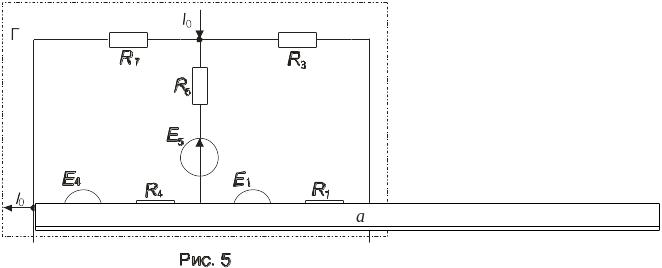
Э.д.с. эквивалентного генератора EГ,
которое равно падению напряжения Uac,
при отсоединённой второй ветви, т.е. при
режиме холостого хода эквивалентного
генератора. Для того, чтобы найти Uac,
достаточно знать потенциалы точек a
и c:

Uac
= φa
– φс, здесь
φa
и φс –
потенциалы точек a и
c.

При отсоединённой второй ветви a
и c не являются узлами,
но будем учитывать их узлами при
составлении уравнений по методу узловых
потенциалов. Источник тока I0
преобразуем в источник э.д.с. (рис.6) EI,
хотя в данной схеме это преобразование
не приведёт к уменьшению числа узлов:
EI
= I0R7.

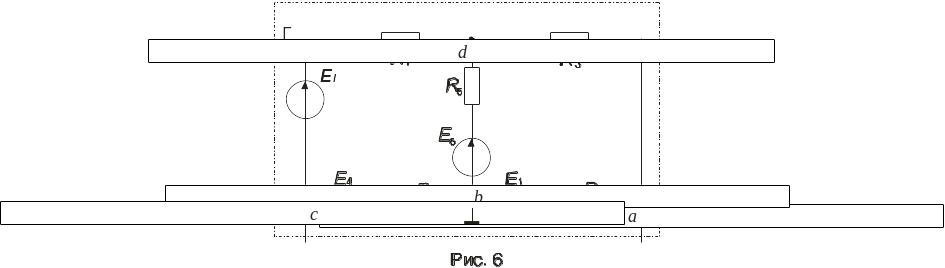
Примем потенциал узла b
за базовый (φb
= 0), а для определения потенциалов других
узлов, записываем уравнения:

a)
φa(G1
+ G3)
– φdG3
= E1G1,

φс(G4
+ G7)
– φdG7
= –E4G4
– EIG7,
φd(G3
+ G5
+ G7)
– φaG3
– φсG7
= E5G5
+ EIG7,

здесь G1,
G3,
G4,
G5,
G7,
проводимости соответствующих ветвей,

G1
= 1/R1,…,
G7
= 1/R7.
Подставим численные значения в уравнения:

a)
φa(0,2
+ 0,25) – φd0,25
= 130×0,2,

φс(0,2
+ 0,5) – φd0,5
= -60×0,2 -8×0,5,
φd(0,25+
0,33 +0,5) – φa0,25
– φс0,5
= 50×0,33+ 8×0,5,

сформируем матрицу из коэффициентов
при φa,
φс и φd
и столбец из правых частей:

0,45 0 -0,25 26

0 0,7 -0,5 -16

-0,25 -0,5 1,08 20,5.

В результате решения системы уравнений
получены значения:

φa
= 80,15 В, φb
= 0 В, φс =
5,906 В, φd
= 40,27 В,

Uac
= φa
– φс =
74,244 В, EГ
= 74,244 В.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определите показания вольтметра в цепи, изображенной на рис., если E = 15 В, R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, R4 = 12 Ом, R5 = 2 Ом.

Определить показания вольтметра, ток

Re: определить показания вольтметра, ток КЗ?

Решение:
первый пункт:
Согласно предложенной схеме, сопротивление R5 соединено последовательно с участком, на котором вольтметр измеряет напряжение.
На этом участке цепи сопротивления R1, R2, R3 соединены параллельно с сопротивлением R4.
Общее сопротивление цепи (Ом):

R=R5+(1R1+R2+R3+1R4)−1=8.

Согласно закона Ома для полной цепи (в первом условии о внутреннем сопротивлении нет речи, поэтому считаем его равным нулю: r = 0) (А):

I=ER+r=ER=158.

Показания вольтметра (В):

U=I⋅(1R1+R2+R3+1R4)−1=158⋅122=11,25.

Второй пункт:
Ток короткого замыкания:

Iк=E/r.

Согласно закона Ома:

I=ER+r,I⋅(R+r)=E,Ik=I⋅(R+r)r=3,6.

Источник

Как правильно записывать показания измерительных приборов с учетом погрешности

Как определить показания вольтметра в цепи постоянного тока

Измерение тока и напряжения. Вольтметр и амперметр.

Меры безопасности

Измерение тока. Амперметр.

Измерение тока и напряжения. Вольтметр и амперметр.

Измерение тока. Амперметр.

Измерение напряжения. Вольтметр.

Амперметр и вольтметр. Правила включения.

теория по физике 🧲 постоянный ток

Как правильно записывать показания измерительных приборов с учетом погрешности

Как найти показания вольтметра?

Определение показаний вольтметров.

Определение э.Д.С. Эквивалентного генератора методом узловых потенциалов.

Вам также может понравиться

Как найти сумму элементов массива после максимального

Как исправить фото на памятнике

Как найти деепричастный оборот 6 класс

Добавить комментарий Отменить ответ