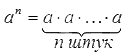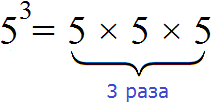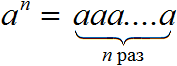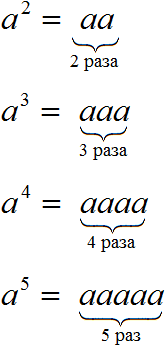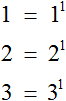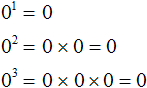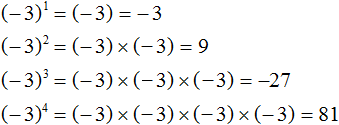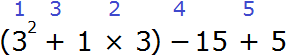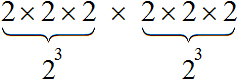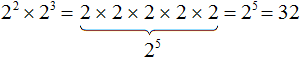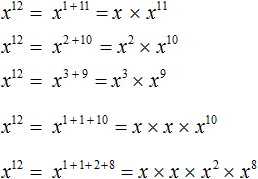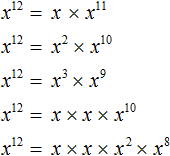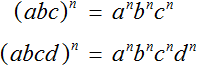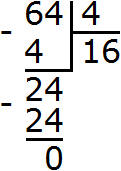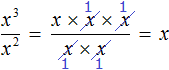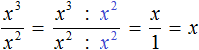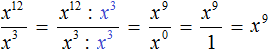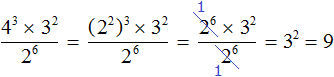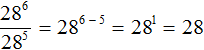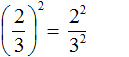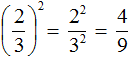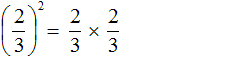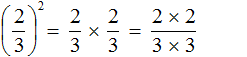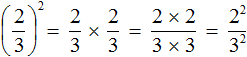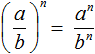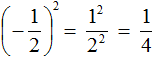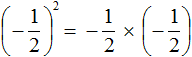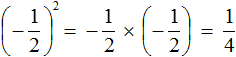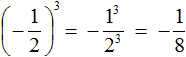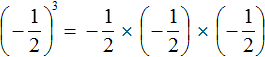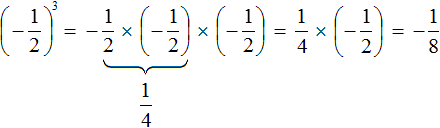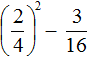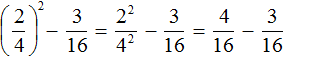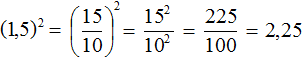В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a), а в качестве показателя – натуральное (обозначим буквой n).
Степень числа a с натуральным показателем n – это произведение n-ного числа множителей, каждый из которых равен числу а. Записывается степень так: an, а в виде формулы ее состав можно представить следующим образом:
Например, если показатель степени равен 1, а основание – a, то первая степень числа a записывается как a1. Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a1=a.
В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8·8·8·8 можно сократить до 84. Примерно так же произведение помогает нам избежать записи большого числа слагаемых (8+8+8+8=8·4); мы это уже разбирали в статье, посвященной умножению натуральных чисел.
Как же верно прочесть запись степени? Общепринятый вариант – «a в степени n». Или можно сказать «n-ная степень a» либо «a n-ной степени». Если, скажем, в примере встретилась запись 812, мы можем прочесть «8 в 12-й степени», «8 в степени 12» или «12-я степень 8-ми».
Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа 7(72), то мы можем сказать «7 в квадрате» или «квадрат числа 7». Аналогично третья степень читается так: 53 – это «куб числа 5» или «5 в кубе». Впрочем, употреблять стандартную формулировку «во второй/третьей степени» тоже можно, это не будет ошибкой.
Разберем пример степени с натуральным показателем: для 57 пятерка будет основанием, а семерка – показателем.
В основании не обязательно должно стоять целое число: для степени (4,32)9 основанием будет дробь 4,32, а показателем – девятка. Обратите внимание на скобки: такая запись делается для всех степеней, основания которых отличаются от натуральных чисел.
Например: 123, (-3)12, -2352, 2,4355, 73.
Для чего нужны скобки? Они помогают избежать ошибок в расчетах. Скажем, у нас есть две записи: (−2)3 и −23. Первая из них означает отрицательное число минус два, возведенное в степень с натуральным показателем три; вторая – число, соответствующее противоположному значению степени 23.
Иногда в книгах можно встретить немного другое написание степени числа – a^n (где а – основание, а n – показатель). То есть 4^9 – это то же самое, что и 49. В случае, если n представляет собой многозначное число, оно берется в скобки. Например, 15^ (21), (−3,1) ^ (156). Но мы будем использовать обозначение an как более употребительное.
О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a n-ное число раз. Подробнее об этом мы писали в другой статье.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 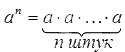
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Равенство am:an=am−n будет верно при условиях: m и n – натуральные числа, m <n, a≠0.
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: an:an=an−n=a0
Но при этом an:an=1 – частное равных чисел an и a. Выходит, что нулевая степень любого отличного от нуля числа равна единице.
Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: am·an=am+n .
Если n у нас равен 0, то am·a0=am (такое равенство также доказывает нам, что a0=1). Но если а также равно нулю, наше равенство приобретает вид 0m·00=0m, Оно будет верным при любом натуральном значении n, и неважно при этом, чему именно равно значение степени 00, то есть оно может быть равно любому числу, и на верность равенства это не повлияет. Следовательно, запись вида 00 своего особенного смысла не имеет, и мы не будем ему его приписывать.
При желании легко проверить, что a0=1 сходится со свойством степени (am)n=am·n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Разберем пример с конкретными числами: Так, 50 – единица, (33,3)0=1, -4590=1, а значение 00 не определено.
После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: am·an=am+n.
Введем условие: m=−n, тогда a не должно быть равно нулю. Из этого следует, что a−n·an=a−n+n=a0=1. Выходит, что an и a−n у нас являются взаимно обратными числами.
В итоге a в целой отрицательной степени есть не что иное, как дробь 1an.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Степень a с целым отрицательным показателем n можно представить в виде дроби 1an. Таким образом, a-n=1an при условии a≠0 и n – любое натуральное число.
Проиллюстрируем нашу мысль конкретными примерами:
3-2=132, (-4.2)-5=1(-4.2)5, 1137-1=111371
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Степень числа a с натуральным показателем z – это: az=az, eсли z-целое положительное число1, z=0 и a≠0, (при z=0 и a=0 получается 00, значения выражения 00 не определяется) 1az, если z – целое отрицательное число и a≠0 (если z – целое отрицательное число и a=0 получается 0z, его значение не определяется)
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа a с дробным показателем m/n, где n – натуральное число, а m – целое.
У нас есть некоторая степень с дробным показателем amn. Для того, чтобы свойство степени в степени выполнялось, равенство amnn=amn·n=am должно быть верным.
Учитывая определение корня n-ной степени и что amnn=am, мы можем принять условие amn=amn, если amn имеет смысл при данных значениях m, n и a.
Приведенные выше свойства степени с целым показателем будут верными при условии amn=amn.
Основной вывод из наших рассуждений таков: степень некоторого числа a с дробным показателем m/n – это корень n-ой степени из числа a в степени m. Это справедливо в том случае, если при данных значениях m, n и a выражение amn сохраняет смысл.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
1. Мы можем ограничить значение основания степени: возьмем a, которое при положительных значениях m будет больше или равно 0, а для отрицательных – строго меньше (поскольку при m≤0 мы получаем 0m, а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом:
Степень с дробным показателем m/n для некоторого положительного числа a есть корень n-ной степени из a, возведенного в степень m. В виде формулы это можно изобразить так:
amn=amn
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m/n можно выразить как
0mn=0mn=0 при условии целого положительного m и натурального n.
При отрицательном отношении mn<0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Выражение amn иногда все же имеет смысл при некоторых отрицательных значениях a и некоторых m. Так, верны записи (-5)23, (-1,2)57, -12-84, в которых основание отрицательно.
2. Второй подход – это рассмотреть отдельно корень amn с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень a, в показателе которой стоит сократимая обыкновенная дробь, считается степенью a, в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись am·kn·k, то мы можем свести ее к amn и упростить расчеты.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то amn имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Для любой обыкновенной сократимой дроби m·kn·k степень можно заменить на amn.
Степень числа a с несократимым дробным показателем m/n – можно выразить в виде amn в следующих случаях: – для любых действительных a, целых положительных значений m и нечетных натуральных значений n. Пример: 253=253, (-5,1)27=(-5,1)-27, 0519=0519.
– для любых отличных от нуля действительных a, целых отрицательных значений m и нечетных значений n, например, 2-53=2-53, (-5,1)-27=(-5,1)-27
– для любых неотрицательных a, целых положительных значений m и четных n, например, 214=214, (5,1)32=(5,1)3, 0718=0718.
– для любых положительных a, целых отрицательных m и четных n, например, 2-14=2-14, (5,1)-32=(5,1)-3, .
В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: -2116, -21232, 0-25.
Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, 6/10=3/5. Тогда должно быть верным (-1)610=-135, но -1610=(-1)610=110=11010=1, а (-1)35=(-1)35=-15=-155=-1.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
Таким образом, степень положительного числа a с дробным показателем m/n определяется как 0mn=0mn=0. В случае отрицательных a запись amn не имеет смысла. Степень нуля для положительных дробных показателей m/n определяется как 0mn=0mn=0, для отрицательных дробных показателей мы степень нуля не определяем.
В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: 51,7, 325-237.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
51,7=51710=5710325-237=325-177=325-177
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
Допустим, что у нас есть иррациональное число a и последовательность его десятичных приближений a0, a1, a2, …. Например, возьмем значение a=1,67175331…,тогда
a0=1,6, a1=1,67, a2=1,671, …,a0=1,67, a1=1,6717, a2=1,671753, …
и так далее (при этом сами приближения являются рациональными числами).
Последовательности приближений мы можем поставить в соответствие последовательность степеней aa0, aa1, aa2, …. Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.
Возьмем для примера a=3, тогда aa0=31,67, aa1=31,6717, aa2=31,671753, … и т.д.
Последовательность степеней можно свести к числу, которое и будет значением степени c основанием a и иррациональным показателем a. В итоге : степень с иррациональным показателем вида 31,67175331.. можно свести к числу 6,27.
Степень положительного числа a с иррациональным показателем a записывается как aa. Его значение – это предел последовательности aa0, aa1, aa2, …, где a0, a1, a2, … являются последовательными десятичными приближениями иррационального числа a. Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом 0a=0 Так, 06=0,02133=0. А для отрицательных этого сделать нельзя, поскольку, например, значение 0-5, 0-2π не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и 12, 15в2 и 1-5 будут равны 1.
В статье мы введём понятие степени числа, на простых и понятных примерах объясним, что такое степень с целым показателем, натуральным, рациональным, действительным и иррациональным. Заодно покажем несколько поучительных примеров и задач, которые помогут читателю лучше понять и полнее уяснить тему.
Степень с натуральным показателем
Определение 1 + формула
Степенью числа a с натуральным показателем n называют число, полученное в результате умножения числа a самого на себя n количество раз. В виде формулы выше сказанное можно записать так:
[a^{n}=a*a* ldots * a]
Читается запись, как «a» в степени «n». Для a2 и для a3 можно сказать «a в степени два» и «a в степени три» или «a во второй степени» и «a в третьей степени». Однако гораздо чаще говорят: «a в квадрате» и «a в кубе». Это устоявшиеся, общеупотребительные названия. Например, «3 в квадрате» или «7 в кубе». Формулировки типа «3 в степени два» и «7 в степени три» ошибочными не считаются, но употребляются гораздо реже, a называется основанием степени.
Запомните, n обозначает количество множителей, то, сколько раз a нужно само на себя перемножить.
Примеры 1 — 6
47 читается, как «четыре в седьмой степени». В виде произведения 47 может быть записано, как 4*4*4*4*4*4*4. При этом 4 является основанием, а 7 её показателем.
193. Может быть прочтено, как «19 в кубе». Оба прочтения будут одинаково верными.
(8,234)5. Читается, как «8,234 в пятой степени». Обратите внимание, в данном случае основанием является десятичная дробь.
(2/5)9 . Здесь основанием будет обычная дробь, она правильная.
(43/7)3 тоже отвечает определению. Из указанного примера видно, что основанием может быть и не правильная дробь.
Записи (8(3/7))8, (-5/9)5. (√3)7, (-√8)2 есть степени с целым n. Однако надо понимать разницу между (-5)3 и –53. Первое является степенью отрицательного числа, а второе можно записать как –(53). Оно соответствует числу, которое противоположно 53.
Отдельно рассмотрим пример, когда n равен 1. Любое число с ним можно записать в виде a1. Некоторые почему-то считают, что этом случае следует выполнить умножение столько раз, сколько указано в показателе. На самом деле ничего умножать не нужно. Степень любого числа с n равным 1 будет самим этим числом.
Т. е. 561 = 56, (1/456)1 равно 1/456, (-86)1 равно -86.
Запись 0n тоже имеет право на существование. По сути она означает, что нуль нужно помножить на себя самого n раз. Умножение на нуль всегда даёт нуль. Получается, любая степень с основанием нуль, независимо от её показателя всегда будет равна нулю.
Значительно реже всех выше перечисленных случаев встречается запись типа a^n. Она соответствует записи an.
Примеры 7 — 9
9^8 читается, как «9 в восьмой степени», n может быть и многозначным числом.
5^(237). Читается, как «5 в двести тридцать седьмой степени».
Выражения 78,4, (3/56)1/2, 8 √3 не являются степенями с натуральным показателем.
Запомните, основанием степени с натуральным n может быть практически любое число (хоть дробь, хоть корень и т. д.), а вот в показателе должно обязательно находиться натуральное число, т. е. не дробное и не отрицательное.
Основные свойства степени с натуральным показателем
Они следующие:
- Когда происходит умножение степеней с равным основанием, то оно остаётся прежним. Показатели при этом складываются.
am*an = am+n
- Когда степени с одинаковыми основаниями делятся, то основание сохраняется прежним, а показатели вычитаются.
am/an = am-n При этом m > n и a не равно нулю.
- Когда степень возводят в степень, то основание не меняют, а сами степени перемножаются.
(am)n = am*n
- Если в степень возводится дробь, то в неё возводится как числитель дроби, так и её знаменатель.
(a/b)n = an/bn При этом b не должно быть равно нулю.
Примеры 10 — 12
21*22*23. Складываем 1, 2 и 3. В итоге 21+2+3=26
(-3/7)5: (-3/7)3. Из 5 вычитаем 3. В результате имеем (-3/7)5-3 = (-3/7)2.
Нужно возвести в степень выражение (a2*b3)4. Сначала на 4 умножаем 2, затем 3. Итогом будет выражение a8b12.
О сравнении степеней
Если сравниваемые степени имеют равные основания, большие числа 1, то большим считается та из них, у которой показатель степени выше.
Примеры 13 — 16
Какое из чисел больше: 217 или 227. Основания одинаковые, но 27 больше, чем 17. 27>17. Значит 227 больше, чем 217.
Если n одинаковые, но основание находится в промежутке от 0 до 1, то большим будет степень, у которой показатель меньше.
Сравнить числа (0,3)11 и (0,3)7. Основание больше ноля, но не доходит до единицы. Значит, в отличие от предыдущего примера, здесь всё наоборот. Большим будет считаться число, с меньшим показателем. Т. к. 11>7, то (0,3)11<(0,3)7.
Если n одинаковые, а основания разные, то большим будет то, у которого больше основание.
Сравнить между собой числа 73 и 153. 15 >7, значит 153 больше, чем 73.
Если различаются и показатели, и основания, то числа, посредством тех или иных преобразований, сначала приводят к вида, когда у них либо то, либо другое одинаково, а уже потом сравнивают по приведённым выше правилам.
Выясните, какое из чисел больше 3200 или 2300.
2300 = 23*100 = (23)100 =8100
3200 = 32*100 = (32)100 = 9100
9 больше, чем 8. Значит 9100 больше 8100.
Соответственно 3200 будет больше, чем 2300.
Степень с целым показателем
Определение 2
Степенью с целым показателем называется степень, показателем которой является любое целое число. Это своего рода расширение множества чисел с натуральным показателем. К последним прибавляются числа с отрицательным значением и ноль.
Рассмотрим степень с целым отрицательным n. Любое число вида a-n можно представить в виде 1/an. При этом a не должно быть равно нулю. n может быть любым натуральным числом.
Примеры 17 — 18
7-5 не является степенью с натуральным показателем, но в то же самое время является степенью с целым показателем. Примечательно, что равное ему число (1/7)5 будет степенью с целым n. Мы рассматриваем 7-5 и (1/7)5, как равные, но, всё-таки, разные числа.
(4/5)-1 можно представить как 1/(4/5)1.
Сложнее дело обстоит с понятием нулевой степени. Чтобы её объяснить, ещё раз приведём правило по делению степеней с равными основаниями.
Правило 1
Равенство am/an = am-n остаётся верным лишь в том случае, когда m и n будут натуральными числами, m < n и a не равно нулю. Последнее условие позволяет нам избежать деления на нуль. Если m и n окажутся равными, то мы придём к результату (an/an) = an-n = a0
Т. е. при делении степеней, которые имеют одно и тоже основание из показателя делимого следует вычесть n делителя. В случае, когда и они одинаковы, например, если a3 разделить на a3, мы получим a0.
Как известно из курса элементарной математики, частное от деления любого числа на самого себя всегда равно единице. Из этого напрямую следует, что нулевая степень любого числа всегда равна 1.
Пример 19
70= 1, -50= 1, (3/5)0 = 1, (√8)0 = 1, (7567776)0 = 1.
Несколько неожиданным для многих является тот факт, что ноль в степени ноль тоже равен единице 00 = 1. Положение осложняет тот факт, что на ноль делить нельзя. Так откуда же тогда взяли, что нулевая степень нуля есть 1.
На самом деле, хотя на ноль никакое число не делится, оно может делится на сколь угодно малое, т. е. близкое к нулю число. В высшей математике доказывается, что предел (a/a), когда a является бесконечно малой величиной, действительно стремится к 1.
Свойства степени с целым показателем практически ничем не отличаются от её свойств с натуральным. Нужно только помнить, что в показателе появляются отрицательные числа и их следует складывать и вычитать по строго определённым для этого правилам.
Примеры 20 — 21
57* 5-3= 57-3 = 54.
84/8-2 = 84-(-2)= 86.
Нет времени решать самому?
Наши эксперты помогут!
Степень с рациональным показателем
Определение 3
Степенью с рациональным показателем называется степень, показатель которой, есть рациональное число, т. е. помимо целых и отрицательных значений, может иметь ещё и дробные. Записывается это в виде am/n. Из определения дробной степени известно, что am/n можно записать в виде n√am. n не должно быть равно нулю, ведь на ноль делить нельзя.
Если m и n делятся нацело, то получаем степень с целым показателем. Если при этом ещё и частное от деления больше нуля, то получим степень с натуральным.
Правило 2
Любое число am * k/n *k можно заменить на am/n.
Теперь о том, почему в дроби требуется замена сократимого показателя на несократимый. Если этого не делать, то может возникнуть, например, следующая ситуация:
(-1)6/10 = (-1)2/5, однако, если посчитать получится
(-1)6/10 = 10√(-1)6 = 10√1 = 1.
(-1)3/5 = 5√(-1)3 = 5√(-1) = -1
Примеры степеней с рациональным n: (31/2), 75/4, 74/2. Основание может быть и многозначным числом, в частности, 128-2/7 тоже степень с рациональным.
Примеры 22 — 24
-161/4 является степенью с рациональным показателем.
(-16)1/4 смысла не имеет. Оно равносильно выражению 4√(-16). Какое число нужно возвести в четвёртую степень, чтобы получить -16 ? Ответ – никакое. Такого числа не существует.
Казалось бы, √(-8) имеет право на существование. Оно равно -2 И действительно, можно записать (-8)1/3= -2. Однако, если мы запишем 1/3.
по-другому, то результат окажется совершенно иным. Смотрите:
(-8)1/3 = (-8)2/6 = 6√(-8)2 = 6√(64) = 2.
Получается парадокс, поэтому запись √(-8) лишено смысла.
Из примеров выше становится ясно, что извлечение чётных корней из отрицательных чисел категорически запрещено.
Не будет ошибкой замена любого из дробных показателей смешанным (например, 52,1 на 52(1/10), однако, чтобы не запутаться, при проведении вычислений, всегда, когда это возможно, лучше заменяйте подобные числа и корень числа дробной степенью. Это делает запись более наглядной и позволяет избежать многих ошибок.
Свойства степени с рациональным показателем аналогичны с натуральным или целым n, только дело приходится иметь с дробями. В первую очередь это касается деления и перемножения степеней с одинаковыми основаниями, а также их сравнения. Вспомните, как оно проводится для обыкновенных дробей.
пример 25
72/3 * 78/4 = 732/12 = 716/6
Степень числа с иррациональным показателем
Чтобы разобраться в этом вопросе, нужно разобраться в том, что является иррациональным числом. Любое рациональное число допускает его представление в виде бесконечной периодической десятичной дроби либо как обыкновенную дробь типа (m/n). Об иррациональных числах этого не скажешь. Десятичные дроби, с помощью которых выражаются иррациональные числа, бесконечны и апериодичны. Примерами иррациональных чисел являются √7, число [pi], √2 + √3.
Строится степень с рациональным n с помощью так называемого предельного перехода по последовательностям степеней с рациональными показателями. Они с недостатком либо с избытком приближаются к степени иррациональным n.
Покажем как это происходит. Пусть нам дано иррациональное число a.
a0 = 1,6 , a1 = 1,67, a2 = 1,671…
a0 = 1,67, a1 = 1,6717, a2 = 1,671753…
И т. д. Заметьте – сами приближения, это рациональные числа.
Последовательности приближений нам нужно поставить в соответствие последовательность степеней αa0, αa1, αa2. Значения этих степеней можно подсчитать.
a = 1,67175331. Пусть для примера у нас будет α = 3
Тогда получается αa0 = 3,167; αa1 = 3,16717; αa2= 3,1671753 и т. д.
Указанная последовательность сводится к числу, которое окажется значением степени с основанием α и иррациональным показателем a. После некоторой работы в итоге получаем 31,67175331 = 6,27.
Свойства у степени с иррациональным n в целом такие же, как рациональным. В частности, сложение показателей при перемножении, сравнение иррациональных степеней происходят аналогичным образом. Нужно только иметь в виду, что при бесконечности и апериодичности иррациональной дроби вы имеете дело с приближёнными с той или иной точностью значениями. Впрочем, в зависимости от поставленной задачи, нужной точности достичь можно в любом случае. Очень осторожны будьте с приближениями. У новичков здесь очень часто случаются ошибки. После некоторого опыта и практики действия совершаются автоматически. Старайтесь на первых порах порешать как можно больше примеров. Пусть они кажутся вам однотипным, но навык отточить и закрепить позволяют.
Что такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
23 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 53, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.
Число, которое повторяется называют основанием степени. В выражении 53 основанием степени является число 5.
А число, которое надписано над числом 5 называют показателем степени. В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень.
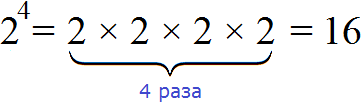
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 00 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
32 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
24 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
23 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
102
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
102 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
102 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
103 = 1000
Пример 3. Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
104 = 10000
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
101 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 101
10 = 101
Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 102
100 = 102
Пример 3. Представим число 1 000 в виде степени с основанием 10.
1 000 = 103
Пример 4. Представим число 10 000 в виде степени с основанием 10.
10 000 = 104
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2)2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −22, которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −22 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −22 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−22 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2)3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5)3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1. Найти значение выражения 2 + 52
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 52 = 2 + 25 = 27
Пример 10. Найти значение выражения −62 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−62 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−62 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 22
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 22 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12. Найти значение выражения (32 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 53 + 5 × 23
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (23)2. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(23)2 это произведение двух степеней, каждая из которых равна 23
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (23)2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (23)2 можно перемножить и записать это произведение над основанием 2
Получили 26. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 23 это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:
(an)m = an × m
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (32)2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 34. А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 22 на 33.
22 это число 4, а 33 это число 27. Перемножаем числа 4 и 27, получаем 108
22 × 33 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 22 на 23
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 22 и 23. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 25. Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 22 это произведение 2 × 2, а 23 это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2. Это произведение представимо в виде 25
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 21 × 22 × 23. Основание 2 оставим без изменений, а показатели сложим:
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 58 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 58 × 25 получилась одна степень.
Число 25 можно представить в виде 52. Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 58 × 25 в виде одной степени, а именно в виде степени 510.
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 29 × 32
Число 32 можно представить в виде 25. Тогда получим выражение 29 × 25. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 31 и 31
31 × 31
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
31 × 31 = 32
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
31 × 31 = 32 = 9
Пример 4. Вычислите произведение 2 × 2 × 32 × 33, используя основное свойство степени.
Произведение 2 × 2 заменим на 21 × 21, затем на 21 + 1, а затем на 22. Произведение 32 × 33 заменим на 32 + 3, а затем на 35
Далее вычисляем значение каждой степени и находим произведение:
Пример 5. Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7. Выполнить умножение y3y2y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8. Выполнить умножение aa3a2a5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9. Представить степень 38 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 38 в виде произведения степеней 35 и 33
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 35 × 33 можно записать как 35 + 3, откуда 38.
Конечно можно было представить степень 38 в виде произведения других степеней. Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x12 в виде различных произведений степеней с основаниями x.
Воспользуемся основным свойство степени. Представим x12 в виде произведений с основаниями x, и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 22, а произведение 3 × 3 можно заменить на 32. Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 22 × 32.
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4)2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz)3
Возведём в третью степень каждый множитель данного произведения:
(3xyz)3 = 33x3y3z3
Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 52 × 32. Возведем каждое число во вторую степень и перемножим полученные результаты:
52 × 32 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)2. Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
52 × 32 = (5 × 3)2 = (15)2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)n = an × bn, то an × bn = (a × b)n. То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(an)m = an × m
К примеру, выражение (23)2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(23)2 = 23 × 2 = 26
Далее вычислить степень 26, которая равна 64
(23)2 = 23 × 2 = 26 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (23)2. Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
(2 × 2 × 2)2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2)2 = 22 × 22 × 22
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
Как и раньше получили 26. Значение этой степени равно 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (22 × 32)3. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 21 × 41. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
Пример 2. Найти значение выражения (33)2
Основание оставляем без изменений, а показатели перемножаем:
Получили 36. Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax)3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)3 — получится −8. Буквенная часть останется без изменений:
Пример 6. Выполнить возведение в степень в выражении (10xy)2
Пример 7. Выполнить возведение в степень в выражении (−5x)3
Пример 8. Выполнить возведение в степень в выражении (−3y)4
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
Пример 10. Упростите выражение x5 × (x2)3
Степень x5 пока оставим без изменений, а в выражении (x2)3 выполним возведение степени в степени:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Теперь выполним умножение x5× x6. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Пример 9. Найти значение выражения 43 × 22, используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 43. Основание у этой степени есть число 4, которое можно представить в виде 22. Тогда исходное выражение примет вид (22)3 × 22. Выполнив возведение степени в степень в выражении (22)3, мы получим 26. Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 43 на 22.
Вычислим 43, получим 64. Вычислим 22, получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 23 : 22
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 23 : 22 равно 2.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 23 : 22. Здесь делимое это 23, а делитель 22.
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 23 на 22 означает найти такую степень, которая при умножении на делитель 22 даст в результате 23. А какую степень можно умножить на 22, чтобы получить 23 ? Очевидно, что только степень 21. Из основного свойства степени имеем:
Убедиться, что значение выражения 23 : 22 равно 21 можно непосредственно вычислив само выражение 23 : 22. Для этого сначала найдём значение степени 23, получим 8. Затем найдём значение степени 22, получим 4. Разделим 8 на 4, получим 2 или 21, поскольку 2 = 21.
23 : 22 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
Например, найдём значение выражения 22 : 22. Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 22 : 22 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 22 и 22 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 22 : 22 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 412 : 410
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
412 : 410 = 412 − 10 = 42 = 16
Пример 3. Представить частное x3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Пример 4. Представить частное x3 : x2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x3 можно записать как x × x × x, а степень x2 как x × x. Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x2. Чтобы сократить дробь
на x2 нужно числитель и знаменатель дроби
разделить на x2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5. Выполнить деление x12 : x3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 72
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (23)4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями:
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 43 запишем в виде возведения степени в степень (22)3. Тогда получим следующее выражение:
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (22)3
В числителе и в знаменателе получившегося выражения содержится степень 26, которую можно сократить на 26
Видим, что в результате осталась единственная степень 32, значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 75 × 45 можно представить в виде степени с одним показателем (7 × 4)5. Далее перемножим выражение в скобках, получим 285. В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
Значит, значение выражения 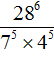
Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как
.
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности
Значит обыкновенная дробь во второй степени равна дроби
.
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 22 и 32 соответственно:
Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение 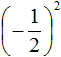
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение 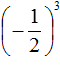
Сначала перемножили и
, получили
, но затем умножив
на
мы получим отрицательный ответ
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
Далее вычислим значение получившегося выражения:
Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
Пример 2. Найти значение степени (−1,5)3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
Пример 3. Найти значение степени (−2,4)2
Показатель степени является чётным числом. Значит ответ будет положительным:
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Представьте в виде степени произведение:
Решение:
Задание 8. Представьте в виде степени произведение:
Решение:
Задание 9. Представьте в виде степени произведение:
Решение:
Задание 10. Представьте в виде степени произведение:
Решение:
Задание 11. Представьте в виде степени произведение:
Решение:
Задание 12. Представьте в виде степени произведение:
Решение:
Задание 13. Представьте в виде степени частное:
Решение:
Задание 14. Представьте в виде степени частное:
Решение:
Задание 15. Представьте в виде степени частное:
Решение:
Задание 16. Представьте в виде степени частное:
Решение:
Задание 17. Представьте в виде степени частное:
Решение:
Задание 18. Представьте в виде степени частное 
Решение:
Задание 19. Представьте в виде степени частное:
Решение:
Задание 20. Сократите дробь 
Решение:
Задание 21. Представьте в виде степени следующее произведение:
Решение:
Задание 22. Представьте в виде степени следующее произведение:
Решение:
Задание 23. Представьте в виде степени следующее произведение:
Решение:
Задание 24. Представьте в виде степени следующее произведение:
Решение:
Задание 25. Представьте в виде степени следующее произведение:
Решение:
Задание 26. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 27. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 28. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 32. Представьте в виде степени следующее выражение:
Решение:
Задание 33. Представьте в виде степени следующее выражение:
Решение:
Задание 34. Представьте в виде степени следующее выражение:
Решение:
Задание 35. Представьте в виде степени следующее выражение:
Решение:
Задание 36. Представьте в виде степени следующее выражение:
Решение:
Задание 37. Представьте в виде степени следующее выражение:
Решение:
Задание 38. Найдите значение следующего выражения:
Решение:
Задание 39. Найдите значение следующего выражения:
Решение:
Задание 40. Найдите значение следующего выражения:
Решение:
Задание 41. Найдите значение следующего выражения:
Решение:
Задание 42. Найдите значение следующего выражения:
Решение:
Задание 43. Найдите значение следующего выражения:
Решение:
Задание 44. Найдите значение следующего выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Степень числа
- Возведение в степень
- Выражения со степенями. Порядок действий
- Калькулятор возведения в степень
Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.
Рассмотрим умножение одинаковых чисел, например:
5 · 5 · 5 = 125.
Произведение 5 · 5 · 5 можно записать так: 53 (пять в третьей степени). Выражение 53 — это степень. Следовательно,
5 · 5 · 5 = 53 = 125.
Рассмотрим выражение 53 . В этом выражении число 5 — основание степени, а число 3 — показатель степени.
Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.
Читаются степени так:
- 72 —
семь во второй степени
.Вторую степень числа также называют квадратом этого числа. Следовательно, выражение 72 можно прочесть так:
семь в квадрате
иликвадрат числа семь
. - 23 —
два в третьей степени
.Третью степень числа также называют кубом этого числа. Следовательно, выражение 23 можно прочесть так:
два в кубе
илидва куб
. - 64 —
шесть в четвёртой степени
. - 1015 —
десять в пятнадцатой степени
. - an —
a в энной степени
илиa в степени эн
.
Пример. Записать в виде степени:
a) 5 · 5;
б) 10 · 10 · 10 · 10;
в) 8 · 8 · 8.
Решение:
a) 5 · 5 = 52;
б) 10 · 10 · 10 · 10 = 104;
в) 8 · 8 · 8 = 83.
Возведение в степень
Возведение числа в степень — это вычисление произведения одинаковых множителей. Например, возвести число 2 в третью степень (23) — это значит найти произведение 2 · 2 · 2 , то есть
23 = 2 · 2 · 2 = 8.
Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:
23 = 8,
2 — это основание степени, 3 — показатель степени, 8 — степень.
Пример. Вычислите:
a) 112;
б) 25;
в) 104.
Решение:
a) 112 = 11 · 11 = 121;
б) 25 = 2 · 2 · 2 · 2 · 2 = 32;
в) 104 = 10 · 10 · 10 · 10 = 10000.
Выражения со степенями. Порядок действий
Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия. Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.
Рассмотрим два выражения:
52 + 22
и
(5 + 2)2
В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.
52 + 22 = 25 + 4 = 29,
(5 + 2)2 = 72 = 49.
Пример 1. Найти значение выражения:
5 · (10 – 8)3.
Решение: Сначала выполняется действие, заключённое в скобки:
1) 10 – 8 = 2.
Затем, по правилам порядка действий, выполняется возведение в степень:
2) 23 = 2 · 2 · 2 = 8.
И последним действием вычисляется произведение:
3) 5 · 8 = 40.
Ответ: 5 · (10 – 8)3 = 40.
Пример 2. Вычислить:
a) (4 + 2) · 32;
б) 3 · 52 – 50;
в) 3 · 4 + 62.
Решение:
a) (4 + 2) · 32 = 54
- 4 + 2 = 6
- 32 = 9
- 6 · 9 = 54
б) 3 · 52 – 50 = 25
- 52 = 25
- 3 · 25 = 75
- 75 – 50 = 25
в) 3 · 4 + 62 = 48
- 62 = 36
- 3 · 4 = 12
- 12 + 36 = 48
Калькулятор возведения в степень
Данный калькулятор поможет вам выполнить возведение в степень. Просто введите основание с показателем степени и нажмите кнопку Вычислить
.
Математика – точная наука, и математический язык приветствует употребление более кратких записей.

А запись 5 · 5 · 5 · 5 · 5 · 5 математик заменит записью 56, потому что шесть одинаковых множителей. Конечно, при необходимости можно использовать обратные записи.
Мы знаем, что 76 есть произведение шести множителей, каждый из которых равен 7:
76 = 7 · 7 · 7 · 7 · 7.
Число 7 – основание степени, число 6 – показатель степени, выражение 76 – степень.
Дадим определение степени для любого основания и любого натурального показателя.
Степенью числа а с натуральным показателем n большим 1, называется произведение n множителей, каждый из которых равен а.
Для степени числа а с показателем n принято обозначение: аn.
По определению аn = а · а · а · а… а. (n раз)
В определение не включён случай, когда показатель n = 1, так как не имеет смысла говорить о произведении, состоящем из одного множителя. Степень с показателем 1 определяется особо.
Степенью числа а с показателем 1 называется само число а: а1 = а.
Вычисление значения степени называют действием возведения в степень. Это действие выполняется первым при вычислении значения выражения.
Рассмотрим примеры вычислений значений выражений, содержащих степени.
Пример 1. Найдём значение степеней (-4)4 (-4)3.
(-4)4 = (-4) · (-4) · (-4) · (-4) = 256
(-4)3 = (-4) · (-4) · (-4) = -64
Обратим внимание, при возведении в степень отрицательного числа, положительное число получается, если число возводится в чётную степень, если же отрицательное число возводится в нечётную степень, то получается отрицательное число.
(3/4)3 = 3/4 · 3/4 · 3/4 = 27/64.
Пример 3. Найдем значение выражения 6 · 33.
Чтобы найти значение этого выражения, достаточно сначала найти значение степени 33, а затем выполнить умножение:
1) 33 = 3 · 3 · 3 = 27
2) 6 · 27 = 162.
Значение степени можно найти с помощью вычислительной техники, а можно воспользоваться таблицей степеней.
Пример 4. Рассмотрим ещё один пример. Найдём значение выражения 0,5 · 482.
0,5 · 482 = 0,5 · 2304 = 1152
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.