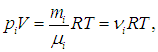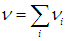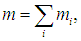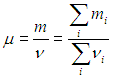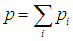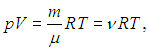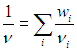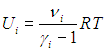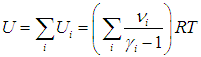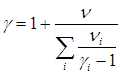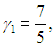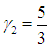Как найти показатель адиабаты для смеси газов - Сайт, где вы сможете решить свои вопросы

Иное название этого понятия — «коэффициент Пуассона»; о параметре, характеризующем упругие свойства материала, см. Коэффициент Пуассона.

Термодинамика
Статья является частью одноименной серии.

Уравнение состояния Идеальный газ Термодинамические величины Термодинамические потенциалы Термодинамические циклы Фазовые переходы
См. также «Физический портал»

Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении ( C_P ) к теплоёмкости при постоянном объёме ( C_V ). Иногда его ещё называют фактором изоэнтропийного расширения. Обозначается греческой буквой gamma (гамма) или kappa (каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква ^[1].

Уравнение:

${displaystyle gamma ={frac {C_{P}}{C_{V}}}={frac {c_{P}}{c_{V}}},}$

где

— теплоёмкость газа,

— удельная теплоёмкость (отношение теплоёмкости к единице массы) газа,

индексы

обозначают условие постоянства давления или постоянства объёма, соответственно.

Для показателя адиабаты справедлива теорема Реша (1854)^[2]^[3]:

${displaystyle gamma ={frac {chi _{t}}{chi _{s}}},}$

где $chi _{t}$ и ${displaystyle chi _{s}}$ — изотермический и адиабатический (изоэнтропический) коэффициенты всестороннего сжатия.

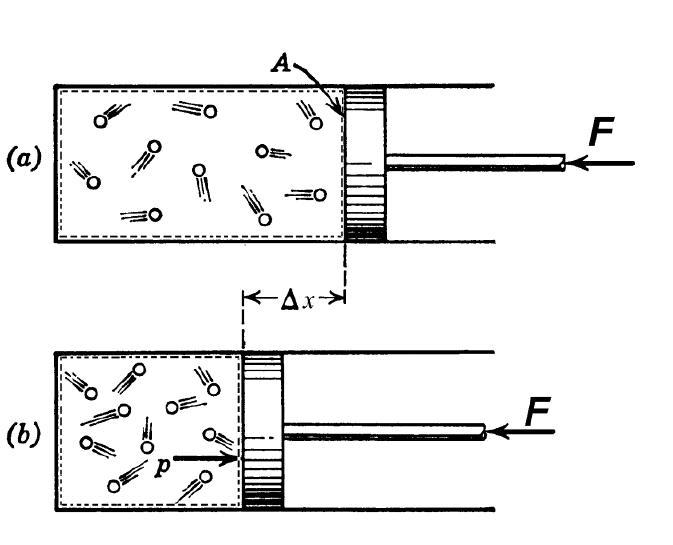
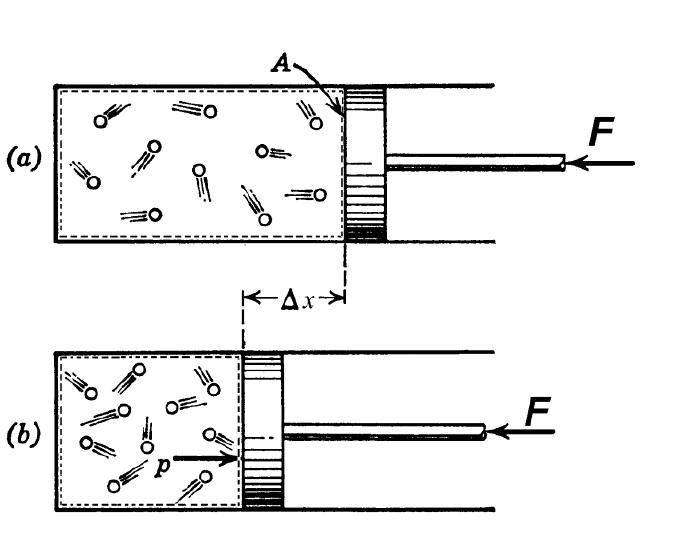
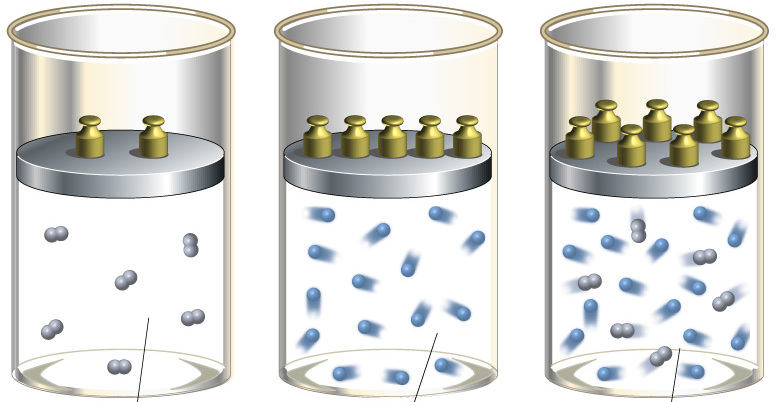
Для понимания этого соотношения можно рассмотреть следующий эксперимент. Закрытый цилиндр с закреплённым неподвижно поршнем содержит воздух. Давление внутри равно давлению снаружи. Этот цилиндр нагревается до определённой, требуемой температуры. До тех пор, пока поршень закреплён в неподвижном состоянии, объём воздуха в цилиндре остаётся неизменным, в то время как температура и давление возрастают. Когда требуемая температура будет достигнута, нагревание прекращается. В этот момент поршень «освобождается» и, благодаря этому, начинает перемещаться под давлением воздуха в цилиндре без теплообмена с окружающей средой (воздух расширяется адиабатически). Совершая работу, воздух внутри цилиндра охлаждается ниже достигнутой ранее температуры. Чтобы вернуть воздух к состоянию, когда его температура опять достигнет упомянутого выше требуемого значения (при всё ещё «освобождённом» поршне) воздух необходимо нагреть. Для этого нагревания извне необходимо подвести примерно на 40 % (для двухатомного газа — воздуха) большее количество теплоты, чем было подведено при предыдущем нагревании (с закреплённым поршнем). В этом примере количество теплоты, подведённое к цилиндру при закреплённом поршне, пропорционально C_V , тогда как общее количество подведённой теплоты пропорционально C_P . Таким образом, показатель адиабаты в этом примере равен 1,4.

Другой путь для понимания разницы между C_P и C_V состоит в том, что C_P применяется тогда, когда работа совершается над системой, которую принуждают к изменению своего объёма (то есть путём движения поршня, который сжимает содержимое цилиндра), или если работа совершается системой с изменением её температуры (то есть нагреванием газа в цилиндре, что вынуждает поршень двигаться). C_V применяется только если P dV — а это выражение обозначает совершённую газом работу — равно нулю. Рассмотрим разницу между подведением тепла при закреплённом поршне и подведением тепла при освобождённом поршне. Во втором случае давление газа в цилиндре остаётся постоянным, и газ будет как расширяться, совершая работу над атмосферой, так и увеличивать свою внутреннюю энергию (с увеличением температуры); теплота, которая подводится извне, лишь частично идёт на изменение внутренней энергии газа, в то время как остальное тепло идёт на совершение газом работы.

показатели адиабаты для различных температур и газов^[4]^[5]
темп.	газ			темп.	газ			темп.	газ
20 °C	He	1,660	20 °C	NO	1,400	20 °C	H₂O	1,330
19 °C	Ne	1,640	−181 °C	O₂	1,450	100 °C	1,324
−180 °C	Ar	1,760	−76 °C	1,415	200 °C	1,310
20 °C	1,670	20 °C	1,400	0 °C	сухой воздух	1,403
19 °C	Kr	1,680	100 °C	1,399	20 °C	1,400
19 °C	Xe	1,660	200 °C	1,397	100 °C	1,401
360 °C	Hg	1,670	400 °C	1,394	200 °C	1,398
−181 °C	H₂	1,597	20 °C	CO	1,400	400 °C	1,393
−76 °C	1,453	20 °C	Cl₂	1,340	1000 °C	1,365
20 °C	1,410	0 °C	CO₂	1,310	2000 °C	1,088
100 °C	1,404	20 °C	1,300	15 °C	SO₂	1,290
400 °C	1,387	100 °C	1,281	−115 °C	CH₄	1,410
1000 °C	1,358	400 °C	1,235	−74 °C	1,350
2000 °C	1,318	1000 °C	1,195	20 °C	1,320
−181 °C	N₂	1,470	15 °C	NH₃	1,310	15 °C	C₂H₆	1,220
15 °C	1,404	20 °C	N₂O	1,310	16 °C	C₃H₈	1,130

Соотношения для идеального газа[править | править код]

Для идеального газа теплоёмкость не зависит от температуры. Соответственно, можно выразить энтальпию как ${displaystyle H=C_{P}T}$ и внутренняя энергия может быть представлена как . Таким образом, можно также сказать, что показатель адиабаты — это отношение энтальпии к внутренней энергии:

${displaystyle gamma ={frac {H}{U}}.}$

С другой стороны, теплоёмкости могут быть выражены также через показатель адиабаты ( gamma ) и универсальную газовую постоянную ():

${displaystyle C_{P}=nu {frac {gamma R}{gamma -1}}qquad }$

и ${displaystyle qquad C_{V}=nu {frac {R}{gamma -1}}.}$

Может оказаться достаточно трудным найти информацию о табличных значениях C_V , в то время как табличные значения C_P приводятся чаще. В этом случае можно использовать следующую формулу для определения C_V :

${displaystyle C_{V}=C_{P}-nu R,}$

где — количество вещества в молях. Для молярных теплоёмкостей, соответственно,

${displaystyle C_{P}={frac {gamma R}{gamma -1}},qquad C_{V}={frac {R}{gamma -1}}=C_{P}-R.}$

Соотношения с использованием количества степеней свободы[править | править код]

Показатель адиабаты ( gamma ) для идеального газа может быть выражен через количество степеней свободы () молекул газа:

$gamma = frac{i+2}{i}qquad$

или $qquad i = frac{2}{gamma - 1}.$

Таким образом, для одноатомного идеального газа (три степени свободы) показатель адиабаты равен:

${displaystyle gamma ={frac {5}{3}}approx 1{,}67,}$

в то время как для двуатомного идеального газа (пять степеней свободы) (при комнатной температуре):

${displaystyle gamma ={frac {7}{5}}=1{,}4.}$

Для многоатомного идеального газа (шесть степеней свободы) показатель адиабаты равен:

${displaystyle gamma ={frac {6+2}{6}}={frac {4}{3}}approx 1{,}33.}$

Воздух на земле представляет собой в основном смесь двухатомных газов (около 78 % азота — N₂, и около 21 % кислорода — O₂), и при нормальных условиях его можно рассматривать как идеальный. Двухатомный газ имеет пять степеней свободы (три поступательных и две вращательных степени свободы; колебательная степень свободы не задействована, за исключением высоких температур). Как следствие, теоретически, показатель адиабаты для воздуха имеет величину:

${displaystyle gamma ={frac {5+2}{5}}={frac {7}{5}}=1{,}4.}$

Это хорошо согласуется с экспериментальными измерениями показателя адиабаты воздуха, которые приблизительно дают значение 1,403 (приведённое выше в таблице).

Соотношения для реальных газов[править | править код]

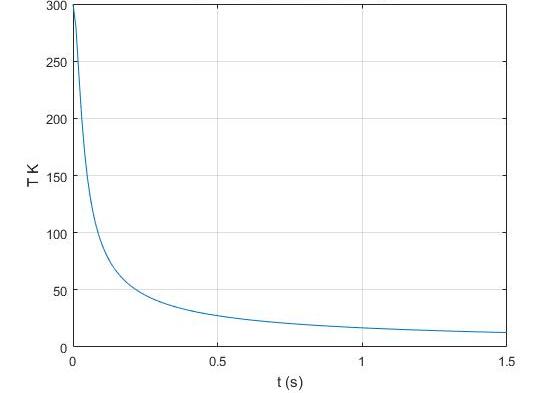
По мере того, как температура возрастает, более высокоэнергетические вращательные и колебательные состояния становятся достижимыми для молекулярных газов, и таким образом, количество степеней свободы возрастает, и уменьшается показатель адиабаты gamma .

Для реальных газов, как C_P , так и C_V возрастают с увеличением температуры, при этом разность между ними остаётся неизменной (согласно приведённой выше формуле C_P = C_V + R ), и эта разность отражает постоянство величины , то есть работы, совершаемой при расширении. Величина представляет собой разницу между количествами подведённой теплоты при постоянном давлении и при постоянном объёме. Следовательно, отношение двух величин, gamma , возрастает при увеличении температуры. См. также удельная теплоёмкость.

Термодинамические выражения[править | править код]

Значения, полученные с помощью приближённых соотношений (в частности, ), во многих случаях являются недостаточно точными для практических инженерных расчётов, таких, как расчёты расходов через трубопроводы и клапаны. Предпочтительнее использовать экспериментальные значения, чем те, которые получены с помощью приближённых формул. Строгие значения соотношения $frac{C_p}{C_v}$ может быть вычислено путём определения C_v из свойств, выраженных как:

${displaystyle C_{p}-C_{v} = -T{frac {left({frac {partial V}{partial T}}right)_{P}^{2}}{left({frac {partial V}{partial P}}right)_{T}}} = -T{frac {{left({frac {partial P}{partial T}}right)}^{2}}{frac {partial P}{partial V}}}.}$

Значения C_p не составляет труда измерить, в то время как значения для C_v необходимо определять из формул, подобных этой. См. здесь^[en] для получения более подробной информации о соотношениях между теплоёмкостями.

Вышеприведённые соотношения отражают подход, основанный на развитии строгих уравнений состояния (таких, как уравнение Пенга — Робинсона^[en]), которые настолько хорошо согласуются с экспериментом, что для их применения требуется лишь незначительно развивать базу данных соотношений или значений C_v . Значения могут быть также определены с помощью метода конечных разностей.

Адиабатический процесс[править | править код]

Для изоэнтропийного, квазистатического, обратимого адиабатного процесса, происходящего в простом сжимаемом идеальном газе:

${displaystyle PV^{gamma }={text{constant}},}$

где — это давление и — объём газа.

Экспериментальное определение величины показателя адиабаты[править | править код]

Поскольку процессы, происходящие в небольших объёмах газа при прохождении звуковой волны, близки к адиабатическим^[6], показатель адиабаты можно определить, измерив скорость звука в газе. В этом случае показатель адиабаты и скорость звука в газе будут связаны следующим выражением:

${displaystyle c={sqrt {frac {gamma kT}{m}}}={sqrt {frac {gamma RT}{M}}},}$

где gamma — показатель адиабаты; — постоянная Больцмана; — универсальная газовая постоянная; — абсолютная температура в кельвинах; — молекулярная масса; — молярная масса.

Другим способом экспериментального определения величины показателя адиабаты является метод Клемана — Дезорма, который часто используется в учебных целях при выполнении лабораторных работ. Метод основан на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами: адиабатическим и изохорическим.^[7]

Лабораторная установка включает стеклянный баллон, соединённый с манометром, краном и резиновой грушей. Груша служит для нагнетания воздуха в баллон. Специальный зажим предотвращает утечку воздуха из баллона. Манометр измеряет разность давлений внутри и вне баллона. Кран может выпускать воздух из баллона в атмосферу.

Пусть первоначально в баллоне было атмосферное давление и комнатная температура. Процесс выполнения работы можно условно разбить на два этапа, каждый из которых включает в себя адиабатный и изохорный процесс.

1-й этап:
При закрытом кране накачиваем в баллон небольшое количество воздуха и зажимаем шланг зажимом. При этом давление и температура в баллоне повысятся. Это адиабатический процесс. Со временем давление в баллоне начнёт уменьшаться вследствие того, что газ в баллоне начнёт охлаждаться за счёт теплообмена через стенки баллона. При этом давление будет уменьшаться при постоянном объёме. Это изохорный процесс. Выждав, когда температура воздуха внутри баллона сравняется с температурой окружающего воздуха, запишем показания манометра h_1 .

2-й этап:
Теперь откроем кран 3 на 1—2 секунды. Воздух в баллоне будет адиабатно расширяться до атмосферного давления. При этом температура в баллоне понизится. Затем кран закроем. Со временем давление в баллоне начнёт увеличиваться вследствие того, что газ в баллоне начнёт нагреваться за счёт теплообмена через стенки баллона. При этом снова будет увеличиваться давление при постоянном объёме. Это изохорный процесс. Выждав, когда температура воздуха внутри баллона сравнится с температурой окружающего воздуха, запишем показание манометра h_2 . Для каждой ветви 2-х этапов можно написать соответствующие уравнения адиабаты и изохоры. Получится система уравнений, которые включают в себя показатель адиабаты. Их приближённое решение приводит к следующей расчётной формуле для искомой величины:

${displaystyle gamma ={h_{1} over {h_{1}-h_{2}}}.}$

Недостатком данного метода является то, что процессы быстрого расширения газа в ходе лабораторной работы не являются чисто адиабатическими ввиду теплообмена через стенку сосудов, а рассматриваемый газ заведомо не является идеальным. И хотя полученная в ходе лабораторной работы величина будет заведомо содержать методическую погрешность, всё же существуют различные способы её устранения, например, за счёт учёта времени расширения и количества подведенного за это время тепла.^[8]

См. также[править | править код]

Теплоёмкость
Удельная теплоёмкость
Скорость звука
Термодинамические уравнения^[en]
Термодинамика
Объёмная теплоёмкость

Примечания[править | править код]

↑ Fox, R., A. McDonald, P. Pritchard: Introduction to Fluid Mechanics 6th ed. Wiley
↑ Толпыго К. Б., Термодинамика и статистическая физика, 1966, с. 83.
↑ Партингтон Дж. Р., Раковский А. В., Курс химической термодинамики, 1932, с. 41.
↑ White, Frank M.: Fluid Mechanics 4th ed. McGraw Hill
↑ Lange’s Handbook of Chemistry, 10th ed. page 1524
↑ Савельев, 2001, с. 30—32.
↑ physdep.isu.ru
↑ physchem.msu.ru (недоступная ссылка)

Литература[править | править код]

Партингтон Дж. Р., Раковский А. В. Курс химической термодинамики / Пер. с англ. Я. В. Герасимова, проработка и дополнения проф. А. В. Раковского. — 2-е изд., стереотипное. — М.—Л.: Госхимтехиздат, 1932. — 383 с.
Толпыго К. Б. Термодинамика и статистическая физика. — Киев: Изд-во Киевского ун-та, 1966. — 364 с.
Савельев И. В. Курс общей физики: Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.

Источник

Решение
Показатель адиабаты определяется по формуле [ gamma =frac{{{c}_{p}}}{{{c}_{V}}}(1). ]
Найдем молярную теплоемкость при постоянном объеме
[ begin{align}
& Delta Q={{c}_{V}}mDelta T,m={{m}_{1}}+{{m}_{2}}, \
& Delta Q=Delta {{Q}_{1}}+Delta {{Q}_{2}}, \
& Delta {{Q}_{1}}={{c}_{V1}}{{m}_{1}}Delta T,Delta {{Q}_{2}}={{c}_{V2}}{{m}_{2}}Delta T, \
& {{c}_{V}}mDelta T={{c}_{V1}}{{m}_{1}}Delta T+{{c}_{V2}}{{m}_{2}}Delta T, \
& {{c}_{V}}=frac{{{c}_{V1}}{{m}_{1}}+{{c}_{V2}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}},(2) \
& {{c}_{V1}}=frac{{{i}_{1}}}{2}frac{R}{{{M}_{1}}},{{c}_{V2}}=frac{{{i}_{2}}}{2}frac{R}{{{M}_{2}}}, \
& {{c}_{V}}=frac{R}{2({{m}_{1}}+{{m}_{2}})}left( frac{{{i}_{1}}{{m}_{1}}}{{{M}_{1}}}+frac{{{i}_{2}}{{m}_{2}}}{{{M}_{2}}} right).(3) \
end{align} ]
По аналогии с (2) и (3) получим молярную теплоемкость при постоянном давлении
[ begin{align}
& {{c}_{p}}=frac{{{c}_{p1}}{{m}_{1}}+{{c}_{p2}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}, \
& {{c}_{p1}}=frac{({{i}_{1}}+2)}{2}frac{R}{{{M}_{1}}},{{c}_{p2}}=frac{({{i}_{2}}+2)}{2}frac{R}{{{M}_{2}}}, \
& {{c}_{p}}=frac{R}{2({{m}_{1}}+{{m}_{2}})}left( frac{({{i}_{1}}+2){{m}_{1}}}{{{M}_{1}}}+frac{({{i}_{2}}+2){{m}_{2}}}{{{M}_{2}}} right).(4) \
end{align} ]
Подставляем (3) и (4) в (1)
[ gamma =frac{{{c}_{p}}}{{{c}_{V}}}=frac{frac{R}{2({{m}_{1}}+{{m}_{2}})}left( frac{({{i}_{1}}+2){{m}_{1}}}{{{M}_{1}}}+frac{({{i}_{2}}+2){{m}_{2}}}{{{M}_{2}}} right)}{frac{R}{2({{m}_{1}}+{{m}_{2}})}left( frac{{{i}_{1}}{{m}_{1}}}{{{M}_{1}}}+frac{{{i}_{2}}{{m}_{2}}}{{{M}_{2}}} right)}=frac{frac{({{i}_{1}}+2){{m}_{1}}}{{{M}_{1}}}+frac{({{i}_{2}}+2){{m}_{2}}}{{{M}_{2}}}}{frac{{{i}_{1}}{{m}_{1}}}{{{M}_{1}}}+frac{{{i}_{2}}{{m}_{2}}}{{{M}_{2}}}}.(5) ]
Для кислорода O₂ – i₁=5, для углекислого газа CO₂ – i₂=6. Подставляем все данные в (6)
[ gamma =frac{frac{({{i}_{1}}+2){{m}_{1}}}{{{M}_{1}}}+frac{({{i}_{2}}+2){{m}_{2}}}{{{M}_{2}}}}{frac{{{i}_{1}}{{m}_{1}}}{{{M}_{1}}}+frac{{{i}_{2}}{{m}_{2}}}{{{M}_{2}}}}=frac{frac{(5+2)3,2}{32cdot {{10}^{-3}}}+frac{(6+2)4,4}{44cdot {{10}^{-3}}}}{frac{5cdot 3,2}{32cdot {{10}^{-3}}}+frac{6cdot 4,4}{44cdot {{10}^{-3}}}}=frac{700+800}{500+600}=1,36. ]
Ответ: 1,36.

Источник

Показатели адиабаты: определение и процесс

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Адиабатический процесс

Вам будет интересно: Задачи социологии: предметы, основные методы, цели и развитие

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

теплопроводность между внешней средой и системой по той или иной причине является низкой;
скорость процесса велика, поэтому обмен теплом не успевает происходить.

В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Уравнение Пуассона для адиабаты идеального газа

Вам будет интересно: Что такое плиз? Молодежный сленг

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Теплоемкости CP и CV

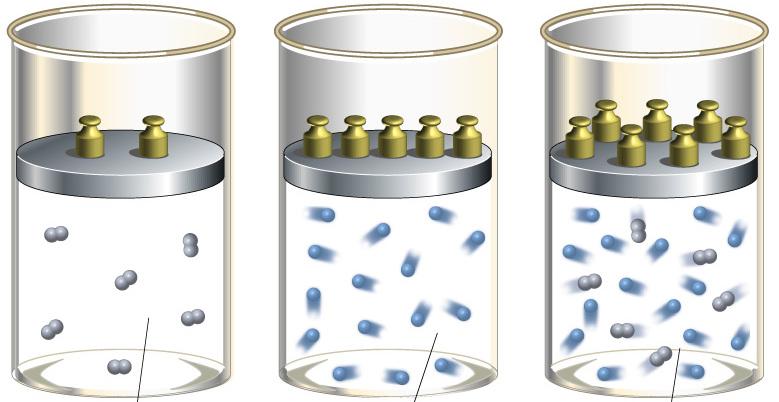
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

CP*dT = CV*dT + P*dV.

Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

Откуда можно определить значение изохорной теплоемкости CV:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:

Тогда значение γ будет равно:

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Где γi — это величина γ для i-го компонента.

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Уравнение Пуассона

Определение и формула уравнения Пуассона

Уравнение Пуассона описывает адиабатический процесс, происходящий в идеальном газе. Адиабатический процесс — это процесс, в котором нет теплообмена между рассматриваемой системой и окружающей средой:

Уравнение Пуассона имеет вид:

Здесь V — объем, занимаемый газом, P — его давление, а значение k называется адиабатическим индексом.

Адиабатический индекс в уравнении Пуассона

Адиабатический индекс можно рассчитать как отношение изобарной теплоемкости газа к его изохорной теплоемкости:

В практических расчетах удобно помнить, что для идеального газа адиабатический индекс равен для двухатомного и для трехатомного .

Что относительно реальных газов, когда силы взаимодействия между молекулами начинают играть важную роль? В этом случае адиабатический индекс для каждого испытательного газа может быть получен экспериментально. Один из таких методов был предложен в 1819 году Климентом и Дезормом. Мы наполняем цилиндр холодным газом, пока давление в нем не достигнет Р1. Затем мы открываем клапан, газ начинает адиабатически расширяться, а давление в цилиндре падает до атмосферного ПА. После того, как изохорный газ нагрелся до температуры окружающей среды, давление в цилиндре повысится до P2. Тогда адиабатический индекс можно вычислить по формуле:

Адиабатический индекс всегда больше 1, поэтому при адиабатическом сжатии газа — как идеального, так и реального — температура газа всегда поднимается до меньшего объема, а при расширении газ охлаждается. Это свойство адиабатического процесса, называемого пневматическим кремнем, используется в дизельных двигателях, где горючая смесь сжимается в цилиндре и воспламеняется теплом. Напомним первый закон термодинамики: , где — внутренняя энергия системы, а А — выполненная на ней работа. Поскольку работа, выполняемая газом, идет только для изменения ее внутренней энергии — и, следовательно, температуры. Из уравнения Пуассона можно получить формулу для расчета газовой операции в адиабатическом процессе:

Здесь n — количество газа в молях, R — универсальная газовая постоянная, T — абсолютная температура газа.

Уравнение Пуассона для адиабатического процесса используется не только при расчетах двигателей внутреннего сгорания, но и при проектировании холодильных машин.

Стоит вспомнить, что уравнение Пуассона точно описывает только равновесный адиабатический процесс, состоящий из непрерывно меняющихся состояний равновесия. Если на самом деле мы открываем клапан в цилиндре так, чтобы газ расширялся адиабатически, то возникнет нестационарный переходный процесс с газовой турбулентностью, который будет испаряться из-за макроскопического трения.

Примеры решения проблем

Одноатомный идеальный газ был адиабатически сжат, так что его объем увеличился в 2 раза. Как изменится давление газа?

Адиабатический индекс для одноатомного газа равен . Однако его можно вычислить по формуле:

где R — универсальная газовая постоянная, а і — степень свободы молекулы газа. Для одноатомного газа степень свободы равна 3: это означает, что центр молекулы может выполнять поступательное движение вдоль трех координатных осей.

Поэтому адиабатический индекс:

Представьте себе состояние газа в начале и конце адиабатического процесса через уравнение Пуассона:

Давление уменьшится в 3.175 раз.

100 молей двухатомного идеального газа было адиабатически сжато при 300 К. В то же время давление газа увеличилось в 3 раза. Как изменился газ?

Степень свободы двухатомной молекулы равна i = 5, так как молекула может двигаться постепенно вдоль трех координатных осей и вращаться вокруг двух осей.

Рассчитайте диатомический адиабатический индекс:

Определите, как изменяется объем газа при адиабатическом сжатии, из уравнения Пуассона:

Это означает, что объем газа уменьшился в 2,19 раза.

Вычислите работу газа, используя следующую формулу:

1.5. Смеси газов

Возникает естественный вопрос: какими уравнениями описываются смеси идеальных газов? Ведь с чистыми газами нам редко приходится встречаться в природе. Например, наша естественная среда обитания — воздух — состоит из азота N₂ (78,08 %), кислорода O₂ (20,95 %), инертных газов (0,94 %), углекислого газа СO₂ (0,03 %).

Пусть в некотором объеме V при некоторой температуре Т содержится смесь газов (которые мы будем нумеровать
индексом i ). Роль каждого компонента смеси будем характеризовать массовой долей:

где m_i — масса i-го компонента. Наша задача — написать уравнение, подобное уравнению Клапейрона — Менделеева, и разобраться с эффективным числом степеней свободы смеси, где могут содержаться и одноатомные, и многоатомные молекулы.

Прежде всего, заметим, что мы рассматриваем идеальные газы. Молекулы не взаимодействуют друг с другом, и потому каждый компонент не мешает любому другому «жить» в том же общем сосуде. Различные газы в сосуде, в силу их предполагаемой идеальности, просто «не замечают» друг друга. Поэтому для каждого из компонентов справедливо одно и то же уравнение Клапейрона — Менделеева:

где n_i — число молей вещества в i -м компоненте. Полное число n молей в смеси равно сумме числа молей n_i в каждом из компонентов:

Аналогично, полная масса смеси равна сумме масс каждого из компонентов

и естественно определить молярную массу смеси m как массу одного моля смеси:

Введем величину, называемую парциальным давлением.

Парциальное давление p_i — это давление, оказываемое i-м компонентом газовой смеси.

Имеет место закон Дальтона для газовой смеси:

Полное давление газовой смеси равно сумме всех парциальных давлений

Суммируя левые и правые части (1.21), приходим к стандартной форме уравнения Клапейрона — Менделеева

где m, μ, n определяются из условия конкретной задачи. Например, если заданы массовые доли компонентов, то молярную массу смеси находим из соотношения

Внутренняя энергия U_i i-го компонента смеси определяется в соответствии с формулами (1.16) и (1.19):

С одной стороны, полная внутренняя энергия смеси равна сумме энергий каждого компонента:

С другой стороны, запишем стандартное выражение вида (1.25)

Сравнивая (1.26) и (1.27), получаем формулу для показателя адиабаты смеси

Найдя массу моля и показатель адиабаты смеси, мы можем пользоваться всеми формулами, полученными ранее для «чистых» идеальных газов.

Пример. Дана смесь кислорода O₂ (компонент 1) и аргона Ar (компонент 2), причем количества вещества обоих компонентов одинаковы n₁ = n₂. Найдем показатель адиабаты смеси.

Показатель адиабаты двухатомного кислорода равен

а одноатомного аргона

Поэтому для смеси газов на основании (1.29) получаем

источники:

http://www.homework.ru/spravochnik/uravnenie-puassona/

http://online.mephi.ru/courses/physics/molecular_physics/data/course/1/1.5.1.html

Источник

Адиабатический процесс

теплопроводность между внешней средой и системой по той или иной причине является низкой;
скорость процесса велика, поэтому обмен теплом не успевает происходить.

Уравнение Пуассона для адиабаты идеального газа

dU = -P*dV.

P*V^γ = const.

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом C_P изобарную теплоемкость, а символом C_V – изохорную. Тогда для γ справедливо равенство:

γ = C_P/C_V.

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин C_Pи C_V. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

dU = C_V*dT.

Величина C_V определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

C_P*dT = C_V*dT + P*dV.

Отсюда видно, что C_P>C_V, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

C_P = C_V + R.

Откуда можно определить значение изохорной теплоемкости C_V:

γ = C_P/C_V;

C_V = R/(γ-1).

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

C_V = 3/2*R.

Из последних двух равенств следует значение показателя адиабаты:

3/2*R = R/(γ-1) =>

γ = 5/3 ≈ 1,67.

Зависимость γ от числа степеней свободы

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для C_V приобретает вид:

C_V = 5/2*R.

Тогда значение γ будет равно:

γ = 7/5 = 1,4.

γ = 4/3 ≈ 1,33.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна a_i. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

γ = ∑_i=1^N(a_i*γ_i).

Где γ_i – это величина γ для i-го компонента.

Источник

Примеры решения задач

Пример 1
Баллон вместимостью V
= 5 л содержит
смесь гелия и водорода при давлении P
= 600 кПа. Масса m
смеси равна 4 г, массовая w₁
доля гелия равна 0,6. Определить температуру
смеси, парциальные давления P₁
и
P₂, молярную
массу смеси.

Решение.

Массовая доля
w
– отношение
массы компонента смеси к массе смеси,
т.е.

.
Аналогично,

.
Следовательно,

и

.

Найдем молярную
массу смеси:

Здесь М₁
и М₂
– молярные
массы компонентов смеси; М₁= 410^³
кг/моль, М₂= 210^³
кг/моль. Получаем:

Запишем уравнение
Клапейрона – Менделеева для смеси:

Отсюда выразим и
найдем температуру смеси:

Парциальное
давление – давление, создаваемое
компонентом смеси в сосуде. Таким
образом, для нахождения можно использовать
уравнение Клапейрона – Менделеева:

Отсюда выразим и
найдем парциальное давление Р₁:

Используя закон
Дальтона Р
= P₁
+
P₂,
находим P₂:

Р₂
= P
– P₁= 600 –
257,3 = 342,7 кПа.

Ответ:
258 К; 257,3 кПа; 342,7 кПа; 2,8610^³
кг/моль.

Пример 2
Определить кинетическую энергию

вращательного движения одной молекулы
кислорода при температуре Т
= 286 К, а также кинетическую энергию

вращательного движения всех молекул
этого газа, если его масса равна 4 г.

Решение.

На каждую степень
свободы молекул газа приходится
одинаковая средняя энергия

,
где k
= 1,3810^²³
Дж/К – постоянная Больцмана. Так как
молекула кислорода двухатомная, то
имеет 3 степени поступательного движения
и 2 степени вращательного движения.
Таким образом,

Кинетическая
энергия вращательного движения всех
молекул этого газа:

где N
– число молекул газа, определяемое по
формуле

.

Таким образом,
получаем

Ответ:
297Дж.

Пример 3
В центрифуге находится азот при
температуре 17⁰С.
Центрифуга, внутренний радиус которой
0,5 м, вращается вместе с азотом с частотой
80 с^-1.
Во сколько раз давление в центре
центрифуги меньше давления на расстоянии
0,4 м от оси вращения?

Решение.

Используем для
решения распределение Больцмана в виде

где U
– потенциальная энергия поля. Учтем,
что вместо концентрации можем записать
давление, так как

и

.
В этом случае получим

На частицы газа в
центрифуге действует центробежная сила
инерции

Используем связь
между потенциальной энергией и силой:

Тогда получим вид
потенциального поля в центрифуге

Примем постоянную
интегрирования С
= 0. Тогда получим выражение для расчета
давления газа в центрифуге:

Отсюда находим
искомое отношение:

Учтем, что

– масса молекулы кислорода,

– угловая скорость вращения,

– универсальная газовая постоянная.

В итоге получаем

Ответ:
в 1,26 раз.

Пример 4
Рассчитать среднее число столкновений,
испытываемых за 5 с молекулой азота при
температуре 17⁰С
и давлении 10⁵
Па.

Решение.

Среднее число
столкновений, испытываемых одной
молекулой за единицу времени, равно

где d
– эффективный диаметр молекулы; n
– концентрация молекул;

– средняя арифметическая скорость
теплового движения молекул.

За время t
число столкновений составит

(1)

Средняя арифметическая
скорость определяется выражением

Найдем концентрацию
молекул:

Из уравнения
Клапейрона – Менделеева выразим

Подставив полученные
выражения в (1), получим:

Ответ:
3,7510¹⁰.

Пример 5
Найти показатель адиабаты 
для смеси газов, состоящей из количества
₁
= 5 моль гелия и количества ₂
= 3 моль азота.

Решение.

Показателем
адиабаты 
называется отношение удельных
теплоемкостей смеси газа c_v
(при постоянном
объеме) и
с_р
(при постоянном
давлении)

Удельную теплоемкость
смеси газа c_v
при постоянном
объеме найдем из уравнения теплового
баланса: количество теплоты, затраченное
на нагрев смеси, равно количеству
теплоты, идущему на нагрев компонент
смеси, т.е.

Учтем, что

,

,

,

,
а t
одинаково, тогда получим

Отсюда выражаем
c_v:

Гелий – одноатомный
газ, поэтому у него число степеней
свободы i₁= 3, молярная
масса гелия М₁= 410^³
кг/моль. Азот – двухатомный газ, поэтому
у него число степеней свободы i₂= 5, молярная
масса азота М₂= 2810^³
кг/моль.

Проводя аналогичные
выкладки для расчета удельной теплоемкости
смеси газа с_р
при постоянном
давлении, с учетом того, что

и

,
получаем:

Тогда показателем
адиабаты 
будет определяться выражением

Подставляя числовые
значения, получим

Ответ:
1,53.

Пример 6
Кислород занимает объем V₁= 1л и находится
под давлением Р₁= =200 кПа.
Газ нагрели сначала при постоянном
давлении до объема V₂= 3л, а затем
при постоянном объеме до давления Р₃= 500 кПа.
Найти: изменение
U
внутренней энергии газа; совершенную
им работу А;
количество теплоты Q,
переданное газу.

Решение.

Изменение внутренней
энергии газа при его переходе из состояния
1 в состояние 3 найдем по формуле

Выразим температуры
из уравнения Клапейрона – Менделеева
с учетом того, что V₂=
V₃
и Р₁=
Р₂:

;

.

Получаем в итоге
выражение для расчета внутренней
энергии:

Так как кислород
– двухатомный газ, то i
= 5. Подставим
числовые значения:

Работа , совершаемая
газом, равна А=А₁₂+А₂₃,
где А₁₂
– работа,
совершаемая на участке 1-2 (при постоянном
давлении), А₂₃
– работа,
совершаемая на участке 2-3 (при постоянном
объеме).

А₁₂=PV=P₁(V₂–
V₁)=210⁵(310^³– 110^³)
= 400 Дж.

А₂₃=0,
т.к. объем
газа не меняется.

В итоге полная
работа А =
А₁₂=
400 Дж.

По первому началу
термодинамики определим количество
теплоты:

Q=U+A=3250+400=3650
Дж.

Ответ:
3250Дж; 400 Дж;
3650 Дж.

Пример 7
Идеальная тепловая машина работает по
циклу Карно и получает от нагревателя
за цикл 5 кДж тепла. Рассчитать работу
машины за цикл и количество теплоты,
отдаваемое холодильнику, если температура
нагревателя 600⁰С,
а холодильника 20⁰С.

Решение.

Работа тепловой
машины за цикл равна