Как найти показатель корня

Корень из числа

• Квадратный корень
• Арифметический квадратный корень

Корень  n-ой  степени из числа  a  — это число,  n-ая  степень которого равна  a.  Например, корнем второй степени из  36  будет число  6,  так как:

6² = 36.

Для записи корня используется знак  √    (знак корня  или  радикал). Под чертой знака записывается подкоренное число, а над знаком, в левом верхнем углу, показатель корня:

²√36.

Подкоренное число — это степень, показатель корня — это показатель степени, корень — основание степени. Если

,

то

.

Эта запись читается так: корень  n-ой  степени из числа  a  равен  x.

Извлечение корня — это действие, обратное возведению в степень, с помощью которого по данной степени и по данному показателю степени находят основание степени.

Квадратный корень

Квадратным корнем из числа  a  называется число, квадрат которого равен  a.

Например, квадратными корнями из числа  16  являются числа  4  и  -4:

²√16 = 4   или   ²√16 = -4.

Рассмотрим уравнение

x² = a

при различных значениях   a:

1. a < 0:

   В данном случае уравнение не будет иметь решений, так как квадрат любого числа всегда является положительным числом или нулём. Следовательно,  x²  не может быть равен отрицательному числу.

2. a = 0:

   В этом случае уравнение имеет единственное решение:

   x = 0.

3. a > 0:

   В этом случае уравнение имеет два корня: положительный и отрицательный, модули которых равны. Так как вторая степень отрицательного числа является числом положительным:

   x = ±√a .

Из рассмотренного примера можно сделать вывод, что для того чтобы из числа можно было извлечь квадратный корень, необходимо, чтобы оно было числом положительным или нулём.

Арифметический квадратный корень

Арифметический квадратный корень из положительного числа  a  — это положительное число  x,  квадрат которого равен  a:

²√a = x,   следовательно   x² = a.

При обозначении квадратного корня показатель корня опускается, то есть квадратный корень обозначается знаком корня без показателя. Например:

√a  — квадратный корень из  a.

Обратите внимание, что при чтении выражения слово арифметический опускается.

Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня.

Извлечение квадратного корня — действие обратное возведению в квадрат (или возведению числа во вторую степень). При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число.

Поэтому для проверки полученного результата можно найденный корень возвести во вторую степень, если степень будет равна подкоренному числу, значит корень был найден правильно.

Рассмотрим извлечение арифметического квадратного корня и его проверку на примере. Найдём  √36,  для этого надо найти число, при возведении которого во вторую степень получится  36.  Таким числом является  6,  так как

6² = 36.

Значит,  √36 = 6.  Корень  -6  мы не рассматриваем, потому что арифметический корень является положительным числом.

Это статья об извлечении корней. См. также Корень уравнения и Корень многочлена.

Корень -й степени из числа определяется^[1] как такое число , что Здесь  — натуральное число, называемое показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай не представляет интереса.

Обозначение: символ (знак корня) в правой части называется радикалом. Число (подкоренное выражение) чаще всего вещественное или комплексное, но существуют и обобщения для других математических объектов, например, вычетов, матриц и операторов, см. ниже #Вариации и обобщения.

Примеры для вещественных чисел:

Как видно из первого примера, у вещественного корня чётной степени могут быть два значения (положительное и отрицательное), и это затрудняет работу с такими корнями, не позволяя использовать их в арифметических вычислениях. Чтобы обеспечить однозначность, вводится понятие арифметического корня^[⇨] (из неотрицательного вещественного числа), значение которого всегда неотрицательно, в первом примере это число Кроме того, принято соглашение, по которому знак корня чётной степени из вещественного числа всегда обозначает арифметический корень^[2][3]: Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус^[2]; например, так делается в формуле решения квадратного уравнения :

Вещественные корни чётной степени из отрицательных чисел не существуют. Из комплексного числа всегда можно извлечь корень любой степени, но результат определён неоднозначно — комплексный корень -й степени из ненулевого числа имеет различных значений (см. #Корни из комплексных чисел).

Операция извлечения корня и алгоритмы её реализации появились в глубокой древности в связи с практическими потребностями геометрии и астрономии, см. #История.

Определение и связанные понятия[править | править код]

Кроме приведенного выше, можно дать два равносильных определения корня^[4]:

Операция вычисления называется «извлечением корня -й степени» из числа . Это одна из двух операций, обратных по отношению к возведению в степень^[5], а именно — нахождение основания степени по известному показателю и результату возведения в степень . Вторая обратная операция, логарифмирование, находит показатель степени по известным основанию и результату.

Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия^[5].

Корни из вещественных чисел[править | править код]

В данном разделе всюду — натуральное число, — вещественные числа. Корень -й степени из вещественного числа , в зависимости от чётности и знака , может иметь от 0 до 2 вещественных значений.

Общие свойства[править | править код]

• Корень нечётной степени из положительного числа — положительное число, однозначно определенное.

Например,

• Корень нечётной степени из отрицательного числа — отрицательное число, однозначно определенное.

Например,

• Корень чётной степени из положительного числа имеет два значения с противоположными знаками, но равными по модулю.

Например,

• Корень чётной степени из отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число. Ниже будет показано, как извлекать такие корни в более широкой системе — множестве комплексных чисел (тогда значениями корня будут комплексных чисел).

• Корень любой натуральной степени из нуля — ноль.

Предостережение[править | править код]

Как сказано выше: «Корень чётной степени из отрицательного числа не существует в области вещественных чисел». При этом в области комплексных чисел такой корень существует. Поэтому следует всегда учитывать, в какой числовой системе (вещественных или комплексных чисел) мы извлекаем корень.

1. Пример. В области вещественных чисел, квадратный корень из не существует.
2. Пример. В области комплексных чисел, квадратный корень из равен

Арифметический корень[править | править код]

Выше уже говорилось, что корни чётной степени определены, вообще говоря, неоднозначно, и этот факт создаёт неудобства при их использовании. Поэтому было введено практически важное ограничение этого понятия^[6].

Арифметический корень -й степени из неотрицательного вещественного числа  — это неотрицательное число , для которого Обозначается арифметический корень знаком радикала.

Таким образом, арифметический корень, в отличие от корня общего вида (алгебраического), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно^[7] и неотрицательно. Например, квадратный корень из числа имеет два значения: и , из них арифметическим является первое.

Алгебраические свойства[править | править код]

Приведённые ниже формулы верны, прежде всего, для арифметических корней любой степени (кроме особо оговоренных случаев). Они справедливы также для корней нечётной степени, у которых допускаются и отрицательные подкоренные выражения^[8].

Корень из произведения равен произведению корней из сомножителей:

• 

Аналогично для деления:

• 

Следующее равенство есть определение возведения в дробную степень^[10]:

• 

Величина корня не изменится, если его показатель и степень подкоренного выражения разделить на одно и то же число (множитель показателя степени и показатель степени подкоренного выражения):

Для корней нечётной степени укажем дополнительное свойство:

• 

Извлечение корня и возведение в дробную степень[править | править код]

Операция возведения в степень первоначально была введена как сокращённая запись операции умножения натуральных чисел: . Следующим шагом было определение возведения в произвольную целую, в том числе отрицательную, степень:

Операция извлечения арифметического корня позволяет определить возведение положительного числа в любую рациональную (дробную) степень^[10]:

   

При этом числитель дроби может иметь знак. Свойства расширенной операции в основном аналогичны возведению в целую степень.

Это определение означает, что извлечение корня и обратное к нему возведение в степень фактически объединяются в одну алгебраическую операцию. В частности:

Попытки возведения в рациональную степень отрицательных чисел могут привести к ошибкам, поскольку значение алгебраического корня неоднозначно, а область значений арифметического корня ограничена неотрицательными числами. Пример возможной ошибки:

Функция корня[править | править код]

• Графики функций корня

• 

  Функции корня:
  — арифметический, чётные степени 2, 4, 6
  — общий, нечётные степени 3, 5, 7

Если рассматривать подкоренное выражение как переменную, мы получим функцию корня -й степени: . Функция корня относится к категории алгебраических функций. График любой функции корня проходит через начало координат и точку .

Как сказано выше, для корня чётной степени, чтобы обеспечить однозначность функции, корень должен быть арифметическим, так что аргумент неотрицателен. Функция корня нечётной степени однозначна и существует для любого вещественного значения аргумента.

Тип функции корня	Область определения	Область значений	Другие свойства
Чётной степени			Функция выпукла вверх на всей области определения
Нечётной степени			Функция нечётна

Для любой степени функция корня строго возрастает, непрерывна всюду внутри своей области определения. Неограниченно дифференцируема всюду, кроме начала координат, где производная обращается в бесконечность^{[11] [12]}. Производная определяется по формуле^[13]:

   . В частности,   .

Функция неограниченно интегрируема во всей области определения. Неопределенный интеграл ищется по формуле:

   . В частности,      , где    — произвольная постоянная.

Предельные соотношения[править | править код]

Приведём несколько полезных пределов, содержащих корни^[16].

Практическое вычисление корней[править | править код]

Функция вычисления квадратных и кубических корней предусмотрена во многих калькуляторах; например, калькулятор Windows показывает соответствующие кнопки в режиме «Инженерный» (Научный). Если на электронном калькуляторе есть клавиша возведения в степень: то для извлечения корня из текущего числа надо нажать следующие клавиши^[17].

Набрать показатель корня

Нажать клавишу

Нажать клавишу

Для расчёта вручную можно использовать быстро сходящийся метод, изложенный в статье «Алгоритм нахождения корня n-ной степени». Для степеней выше третьей можно использовать логарифмическое тождество:

Для извлечения корня надо найти логарифм подкоренного выражения, разделить на степень корня и найти антилогарифм результата.

Корни из комплексных чисел[править | править код]

Зарождение понятия комплексного числа исторически было связано с желанием «легализовать» квадратные корни из отрицательных чисел. Как постепенно выяснилось, комплексные числа обладают богатыми алгебраическими и аналитическими свойствами; в частности, извлечение корней из них всегда возможно, хотя и неоднозначно. Для корней в комплексной области знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней; в последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Пример возможной ошибки:

(что, конечно, неверно)

Ошибка возникла из-за того, что неарифметический квадратный корень является многозначной функцией, и его нельзя использовать в арифметических действиях.

Способы нахождения[править | править код]

Запишем комплексное число в тригонометрической форме:

.

Тогда корни -й степени из определяются формулой Муавра (тригонометрическая форма)^[18]:

или в показательной форме:

Корень степени из ненулевого комплексного числа имеет значений (это следствие основной теоремы алгебры), и все они различны. Значение корня, получаемое при , часто называется главным.

Поскольку для всех значений корня величина модуля одинакова (он определяется как арифметический корень из модуля изначального комплексного числа), а меняется лишь его аргумент, все значений корня располагаются на комплексной плоскости на окружности радиуса c центром в начале координат. Корни делят эту окружность на равных частей.

Примеры[править | править код]

Найдём . Поскольку по формуле получаем:

При получим первый корень , при получим второй корень

Другой пример: найдём . Представим подкоренное выражение в тригонометрической форме:

По формуле Муавра получаем:

В итоге имеем четыре значения корня^[19]:

Можно записать сводный ответ в виде:

Комплексная функция корня и риманова поверхность[править | править код]

Рассмотрим комплексную функцию корня -й степени: Согласно сказанному выше, эта функция является многозначной (точнее, -значной) функцией, и это создаёт неудобства при её исследовании и применении. В комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определённую не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью^[20].

• 

  Риманова поверхность для комплексного квадратного корня

• 

  Риманова поверхность для комплексного корня 4-й степени

Для комплексной функции корня -й степени её риманова поверхность (см. рисунки) состоит из ветвей (листов), связанных винтообразно, причём последний лист связан с первым. Эта поверхность непрерывна и односвязна. Один из листов содержит главные значения корня, получаемые как аналитическое продолжение вещественного корня с положительного луча вещественной оси.

Опишем для простоты комплексную функцию квадратного корня. Её риманова поверхность состоит из двух листов. Первый лист можно представить как комплексную плоскость, у которой вырезан положительный луч вещественной оси. Значения функции корня на этом листе имеют вдвое меньший аргумент, чем , и поэтому они заполняют верхнюю часть комплексной плоскости значений. На разрезе первый лист склеен со вторым, и функция непрерывно продолжается через разрез на второй лист, где её значения заполняют нижнюю часть комплексной плоскости значений. Оставшиеся свободными начало первого листа и конец второго тоже склеим, после чего полученная функция на римановой поверхности становится однозначной и всюду непрерывной^[20].

Единственный нуль у функции (первого порядка) получается при . Особые точки: и (точки разветвления бесконечного порядка)^[20]. Понятие точки разветвления означает, что замкнутый контур в окрестности нуля неизбежно содержит переход с листа на лист.

В силу односвязности риманова поверхность корня является универсальной накрывающей^[21] для комплексной плоскости без точки .

Вариации и обобщения[править | править код]

Корень -й степени из есть решение уравнения , и его в принципе можно определить всюду, где такое уравнение имеет смысл. Чаще всего рассматривают такие обобщения в алгебраических кольцах. Лучше всего исследованы обобщённые квадратные корни.

Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня то откуда: , то есть, в силу отсутствия делителей нуля, . В более общем случае, когда в кольце имеются делители нуля или оно некоммутативно, число корней может быть любым.

В теории чисел рассматривается конечное кольцо вычетов по модулю : если сравнение имеет решение, то целое число называется вычетом степени n (в противном случае — невычетом степени n). Решение , если оно существует, является полным аналогом корня n-й степени из целого числа . Чаще всего используются случаи^[22]:

Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из образуют трёхмерную сферу, определяемую формулой^[23]:

Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен^[24]. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).

Квадратные корни вводятся также для функций^[25], операторов^[26] и других математических объектов.

История[править | править код]

Развитие понятия[править | править код]

Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков (о достижениях древнего Египта в этом отношении ничего не известно). Среди таких задач^[27]:

• Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
• Нахождение стороны квадрата, площадь которого задана.
• Решение квадратных уравнений.

Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод. Начальное приближение для рассчитывалось исходя из ближайшего к корню (в меньшую сторону) натурального числа . Представив подкоренное выражение в виде: , получаем: , затем применялся итеративный процесс уточнения, соответствующий методу Ньютона^[28]:

Итерации в этом методе очень быстро сходятся. Для , например, и мы получаем последовательность приближений:

В заключительном значении верны все цифры, кроме последней.

Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах»^[29]. Древние греки сделали важное открытие:  — иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально^[30].

Греки сформулировали проблему удвоения куба, которая сводилась к построению кубического корня с помощью циркуля и линейки. Проблема оказалась неразрешимой. Численные алгоритмы извлечения кубического корня опубликовали Герон (в трактате «Метрика», I век н. э.) и индийский математик Ариабхата I (V век)^[31].

Алгоритмы извлечения корней любой степени из целого числа, разработанные индийскими и исламскими математиками, были усовершенствованы в средневековой Европе. Николай Орем (XIV век) впервые истолковал^[32] корень -й степени как возведение в степень .

После появления формулы Кардано (XVI век) началось применение в математике мнимых чисел, понимаемых как квадратные корни из отрицательных чисел^[33]. Основы техники работы с комплексными числами разработал в XVI веке Рафаэль Бомбелли, который также предложил оригинальный метод вычисления корней (с помощью цепных дробей). Открытие формулы Муавра (1707) показало, что извлечение корня любой степени из комплексного числа всегда возможно и не приводит к новому типу чисел^[34].

Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру^[35]. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корня^[36].

Этимология термина и происхождение символики[править | править код]

Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически: как нахождение стороны квадрата по известной его площади. После перевода на санскрит греческое слово «сторона» превратилась в «мула» (основание). Слово «мула» имело также значение «корень», поэтому при переводе индийских сиддхант на арабский использовался термин «джизр» (корень растения). Впоследствии аналогичное по смыслу слово «radix» закрепилось в латинских переводах с арабского, а через них и в русской математической терминологии («корень», «радикал»)^[37].

Средневековые математики (например, Кардано) обозначали квадратный корень^[38] символом R_x, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году^[39]. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт (1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.

Показатель степени появился в знаке корня благодаря Валлису и «Универсальной арифметике» Ньютона (XVIII век)^[40].

См. также[править | править код]

• Алгоритм нахождения корня n-ной степени
• Возведение в степень
• Квадратный корень
• Корни из единицы
• Кубический корень
• Логарифм
• Основная теорема алгебры
• Степенная функция

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
• Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М.: Мнемозина, 2003. — 376 с.
• Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.

Примечания[править | править код]

15 января 2017

Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)

Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)

Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.

Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:

Корни бывают чётной степени (наш любимый $sqrt{a}$, а также всякие $sqrt[4]{a}$ и даже $sqrt[116]{a}$ ) и нечётной степени (всякие $sqrt[3]{a}$, $sqrt[7]{a}$ и т.д.). И определение корня нечётной степени несколько отличается от чётной.

Вот в этом грёбаном «несколько отличается» скрыто, наверное, 95% всех ошибок и недопонимания, связанного с корнями. Поэтому давайте раз и навсегда разберёмся с терминологией:

Определение. Корень чётной степени n из числа $a$ — это любое неотрицательное число $b$ такое, что ${{b}^{n}}=a$. А корень нечётной степени из того же числа $a$ — это вообще любое число $b$, для которого выполняется всё то же равенство: ${{b}^{n}}=a$.

В любом случае корень обозначается вот так:

[b=sqrt[n]{a}]

Число $n$ в такой записи называется показателем корня, а число $a$ — подкоренным выражением. В частности, при $n=2$ получим наш «любимый» квадратный корень (кстати, это корень чётной степени), а при $n=3$ — кубический (степень нечётная), который тоже часто встречается в задачах и уравнениях.

Примеры. Классические примеры квадратных корней:

[begin{align} & sqrt{4}=2; \ & sqrt{81}=9; \ & sqrt{256}=16. \ end{align}]

Кстати, $sqrt{0}=0$, а $sqrt{1}=1$. Это вполне логично, поскольку ${{0}^{2}}=0$ и ${{1}^{2}}=1$.

Кубические корни тоже часто встречаются — не надо их бояться:

[begin{align} & sqrt[3]{27}=3; \ & sqrt[3]{-64}=-4; \ & sqrt[3]{343}=7. \ end{align}]

Ну, и парочка «экзотических примеров»:

[begin{align} & sqrt[4]{81}=3; \ & sqrt[5]{-32}=-2. \ end{align}]

Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!

А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.

Зачем вообще нужны корни?

Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?

Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:

[begin{align} & 5cdot 5=25; \ & 5cdot 5cdot 5=125; \ & 5cdot 5cdot 5cdot 5=625; \ & 5cdot 5cdot 5cdot 5cdot 5=3125; \ & 5cdot 5cdot 5cdot 5cdot 5cdot 5=15 625. end{align}]

Ну и так далее. Ладно, ладно: последние две строчки я считал на калькуляторе.:)

Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:

[5cdot 5cdot 5cdot 5cdot 5cdot 5=15 625]

Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:

[5cdot 5cdot 5cdot 5cdot 5cdot 5={{5}^{6}}=15 625]

Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5¹⁸³. Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.

После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?

Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. Потому что выяснилось, что для большинства «готовых» степеней таких «исходных» чисел нет. Судите сами:

[begin{align} & {{b}^{3}}=27Rightarrow b=3cdot 3cdot 3Rightarrow b=3; \ & {{b}^{3}}=64Rightarrow b=4cdot 4cdot 4Rightarrow b=4. \ end{align}]

А, что если ${{b}^{3}}=50$? Получается, что нужно найти некое число, которое будучи трижды умноженное само на себя даст нам 50. Но что это за число? Оно явно больше 3, поскольку 3³ = 27 < 50. С тем же успехом оно меньше 4, поскольку 4³ = 64 > 50. Т.е. это число лежит где-то между тройкой и четвёркой, но чему оно равно — фиг поймёшь.

Именно для этого математики и придумали корни $n$-й степени. Именно для этого ввели значок радикала $sqrt{*}$. Чтобы обозначить то самое число $b$, которое в указанной степени даст нам заранее известную величину

[sqrt[n]{a}=bRightarrow {{b}^{n}}=a]

Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.

Да что там! Даже самый простой и всем знакомый $sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:

[sqrt{2}=1,414213562…]

Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:

[sqrt{2}=1,4142…approx 1,4 lt 1,5]

Или вот ещё пример:

[sqrt{3}=1,73205…approx 1,7 gt 1,5]

Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).

Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $mathbb{R}$, как и давно знакомые нам дроби и целые числа.

Невозможность представить корень в виде дроби вида $frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.

Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.

Пример.

[begin{align} & sqrt{2+sqrt[3]{27}}=sqrt{2+3}=sqrt{5}approx 2,236… \ & sqrt[3]{sqrt[5]{-32}}=sqrt[3]{-2}approx -1,2599… \ end{align}]

Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. Впрочем, можно, посчитать на калькуляторе, но даже самый совершенный калькулятор дат нам лишь несколько первых цифр иррационального числа. Поэтому гораздо правильнее записать ответы в виде $sqrt{5}$ и $sqrt[3]{-2}$.

Именно для этого их и придумали. Чтобы удобно записывать ответы.

Почему нужны два определения?

Внимательный читатель уже наверняка заметил, что все квадратные корни, приведённые в примерах, извлекаются из положительных чисел. Ну, в крайнем случае из нуля. А вот кубические корни невозмутимо извлекаются абсолютно из любого числа — хоть положительного, хоть отрицательного.

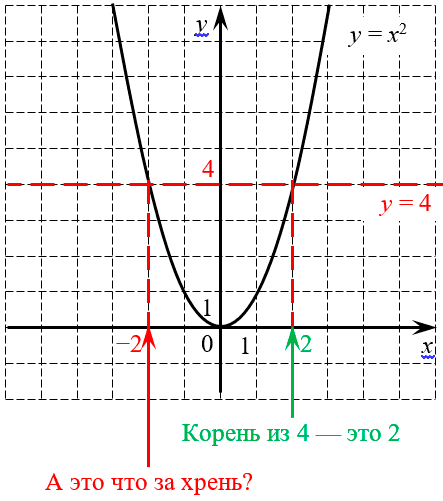
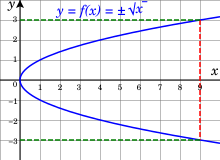
Почему так происходит? Взгляните на график функции $y={{x}^{2}}$:

Попробуем с помощью этого графика посчитать $sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку

[x=pm 2Rightarrow {{x}^{2}}=4]

С первым числом всё понятно — оно положительное, поэтому оно и есть корень:

[sqrt{4}=2]

Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)

В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.

Подобная проблема возникает у всех корней с чётным показателем:

1. Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
2. Из отрицательных чисел корень с чётным $n$ вообще не извлекается.

Именно поэтому в определении корня чётной степени $n$ специально оговаривается, что ответ должен быть неотрицательным числом. Так мы избавляемся от неоднозначности.

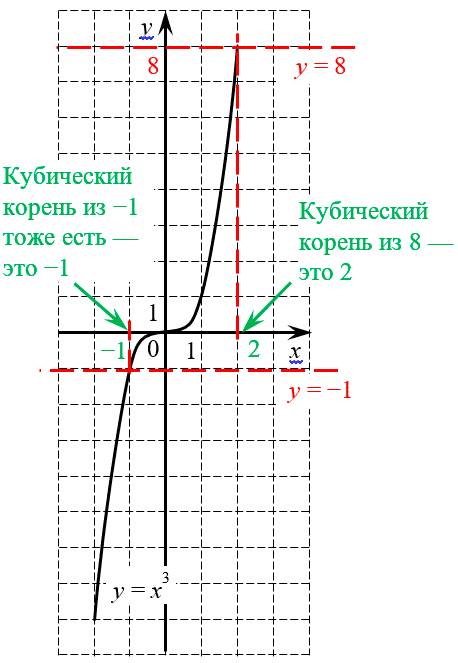
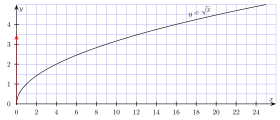
Зато для нечётных $n$ такой проблемы нет. Чтобы убедиться в этом, давайте взглянем на график функции $y={{x}^{3}}$:

Из этого графика можно сделать два вывода:

1. Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
2. Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).

Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.

Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.

Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.

А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:

1. Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
2. А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.

Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.

Основные свойства и ограничения

У корней много странных свойств и ограничений — об этом будет отдельный урок. Поэтому сейчас мы рассмотрим лишь самую важную «фишку», которая относится лишь к корням с чётным показателем. Запишем это свойство в виде формулы:

[sqrt[2n]{{{x}^{2n}}}=left| x right|]

Другими словами, если возвести число в чётную степень, а затем из этого извлечь корень той же степени, мы получим не исходное число, а его модуль. Это простая теорема, которая легко доказывается (достаточно отдельно рассмотреть неотрицательные $x$, а затем отдельно — отрицательные). О ней постоянно талдычат учителя, её дают в каждом школьном учебнике. Но как только дело доходит до решения иррациональных уравнений (т.е. уравнений, содержащих знак радикала), ученики дружно забывают эту формулу.

Чтобы детально разобраться в вопросе, давайте на минуту забудем все формулы и попробуем посчитать два числа напролом:

[sqrt[4]{{{3}^{4}}}=?quad sqrt[4]{{{left( -3 right)}^{4}}}=?]

Это очень простые примеры. Первый пример решит большинство людишек, а вот на втором многие залипают. Чтобы без проблем решить любую подобную хрень, всегда учитывайте порядок действий:

1. Сначала число возводится в четвёртую степень. Ну, это как бы несложно. Получится новое число, которое даже в таблице умножения можно найти;
2. И вот уже из этого нового числа необходимо извлечь корень четвёртой степени. Т.е. никакого «сокращения» корней и степеней не происходит — это последовательные действия.

Раберёмся с первым выражением: $sqrt[4]{{{3}^{4}}}$. Очевидно, что сначала надо посчитать выражение, стоящее под корнем:

[{{3}^{4}}=3cdot 3cdot 3cdot 3=81]

Затем извлекаем корень четвёртой степени из числа 81:

[sqrt[4]{81}=3]

Теперь сделаем то же самое со вторым выражением. Сначала возводим число −3 в четвёртую степени, для чего потребуется умножить его само на себя 4 раза:

[{{left( -3 right)}^{4}}=left( -3 right)cdot left( -3 right)cdot left( -3 right)cdot left( -3 right)=81]

Получили положительное число, поскольку общее количество минусов в произведении — 4 штуки, и они все взаимно уничтожится (ведь минус на минус даёт плюс). Дальше вновь извлекаем корень:

[sqrt[4]{81}=3]

В принципе, эту строчку можно было не писать, поскольку и ежу понятно, что ответ получится один и тот же. Т.е. чётный корень из той же чётной степени «сжигает» минусы, и в этом смысле результат неотличим от обычного модуля:

[begin{align} & sqrt[4]{{{3}^{4}}}=left| 3 right|=3; \ & sqrt[4]{{{left( -3 right)}^{4}}}=left| -3 right|=3. \ end{align}]

Эти вычисления хорошо согласуются с определением корня чётной степени: результат всегда неотрицателен, да и под знаком радикала тоже всегда стоит неотрицательное число. В противном случае корень не определён.

Замечание по поводу порядка действий

Прежде чем мы двинемся дальше, хотел бы отметить, что выражения $sqrt{{{a}^{2}}}$ и ${{left( sqrt{a} right)}^{2}}$, столь похожие на первый взгляд, на самом деле имеют принципиально разный смысл. Судите сами:

1. Запись $sqrt{{{a}^{2}}}$ означает, что мы сначала возводим число $a$ в квадрат, а затем извлекаем из полученного значения квадратный корень. Следовательно, мы можем быть уверены, что под знаком корня всегда сидит неотрицательное число, поскольку ${{a}^{2}}ge 0$ в любом случае;
2. А вот запись ${{left( sqrt{a} right)}^{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.

Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.

Впрочем, все эти проблемы актуальны лишь для чётных показателей.

Вынесение минуса из-под знака корня

Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:

[sqrt[2n+1]{-a}=-sqrt[2n+1]{a}]

Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:

[begin{align} & sqrt[3]{-8}=-sqrt[3]{8}=-2; \ & sqrt[3]{-27}cdot sqrt[5]{-32}=-sqrt[3]{27}cdot left( -sqrt[5]{32} right)= \ & =sqrt[3]{27}cdot sqrt[5]{32}= \ & =3cdot 2=6. end{align}]

Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.

И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!

Арифметический корень

Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?

А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них.

Определение. Арифметическим корнем $n$-й степени из неотрицательного числа $a$ называется такое неотрицательное число $b$, что ${{b}^{n}}=a$.

Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.

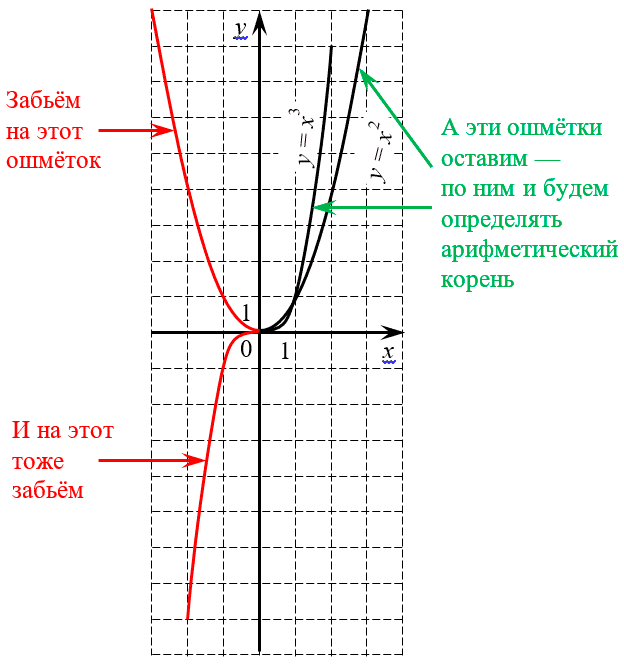
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:

Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.

Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»

Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. Например, правило возведения в степень:

[sqrt[n]{a}=sqrt[ncdot k]{{{a}^{k}}}]

Обратите внимание: мы можем возвести подкоренное выражение в любую степень и одновременно умножить на эту же степень показатель корня — и в результате получится то же самое число! Вот примеры:

[begin{align} & sqrt[3]{5}=sqrt[3cdot 2]{{{5}^{2}}}=sqrt[6]{25} \ & sqrt{2}=sqrt[2cdot 4]{{{2}^{4}}}=sqrt[8]{16} \ end{align}]

Ну и что в этом такого? Почему мы не могли сделать это раньше? А вот почему. Рассмотрим простое выражение: $sqrt[3]{-2}$ — это число вполне нормальное в нашем классическом понимании, но абсолютно недопустимо с точки зрения арифметического корня. Попробуем преобразовать его:

$begin{align} & sqrt[3]{-2}=-sqrt[3]{2}=-sqrt[3cdot 2]{{{2}^{2}}}=-sqrt[6]{4} lt 0; \ & sqrt[3]{-2}=sqrt[3cdot 2]{{{left( -2 right)}^{2}}}=sqrt[6]{4} gt 0. \ end{align}$

Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.

WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.

Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.

Алгебраический корень: для тех, кто хочет знать больше

Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному.

Так вот: помимо «классического» определения корня $n$-й степени из числа и связанного с ним разделения на чётные и нечётные показатели есть более «взрослое» определение, которое вообще не зависит от чётности и прочих тонкостей. Это называется алгебраическим корнем.

Определение. Алгебраический корень $n$-й степени из числа любого $a$ — это множество всех чисел $b$ таких, что ${{b}^{n}}=a$. Для таких корней нет устоявшегося обозначения, поэтому просто поставим чёрточку сверху:

[overline{sqrt[n]{a}}=left{ bleft| bin mathbb{R};{{b}^{n}}=a right. right}]

Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:

1. Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
2. Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
3. Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.

Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.

Пример. Вычислите выражения:

[overline{sqrt{4}};quad overline{sqrt[3]{-27}};quad overline{sqrt[4]{-16}}.]

Решение. С первым выражением всё просто:

[overline{sqrt{4}}=left{ 2;-2 right}]

Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.

[overline{sqrt[3]{-27}}=left{ -3 right}]

Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.

Наконец, последнее выражение:

[overline{sqrt[4]{-16}}=varnothing ]

Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.

Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $sqrt[4]{-16}$, и многие другие странные вещи.

Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».

На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)

Смотрите также:

1. Умножение корней n-й степени
2. Свойства арифметического квадратного корня
3. Тест к уроку «Знаки тригонометрических функций» (1 вариант)
4. Тест по методу интервалов для строгих неравенств
5. Вебинар по задачам 18: модуль и окружности
6. Решение задач на движение по воде

Что такое корень n-й степени из действительного числа

Чтобы научиться работать с корнями степени (n), необходимо знать, что такое арифметический КВАДРАТНЫЙ корень и его свойства.

Корнем n-й степени ((n=2, 3, 4, 5, 6… )) некоторого числа (a) называют такое неотрицательное число (b), которое при возведении в степень (n in N) дает (a). Корень n-ой степени обозначается при помощи знака радикала (sqrt[n]{a}):

$$ sqrt[n]{a}=b; $$
$$ b^{n}=underbrace{b*b*b*…*b}_{n ; раз}=a. $$

Число (n in N) при этом называют показателем корня, а число (a) подкоренным выражением.

Если (n=2), то перед вами корень 2-й степени или, другими словами, обычный арифметический квадратный корень, который все проходили в 8-м классе.

Если (n=3), то это корень 3-й степени, (sqrt[3]{a}). Его обычно называют кубическим корнем. Чтобы его вычислить, нужно найти такое число, которое умноженное на само себя три раза, даст подкоренное выражение.

Если (n=4), то корень 4-й степени, (sqrt[4]{a}) и т.д.

Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень. Для того, чтобы вычислить корень n-й степени от (a), нужно сообразить какое число в степени (n) будет давать (a).

Пример 1
$$ sqrt[3]{27}=3 $$

Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.

Пример 2
$$ sqrt[4]{16}=2 $$

Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.

Пример 3
$$ sqrt[n]{0}=0 $$

Если извлечь корень n-й степени из 0, всегда будет 0.

Пример 4
$$ sqrt[n]{1}=1 $$

Если извлечь корень n-й степени из 1, всегда будет 1.

Пример 5
$$ sqrt[3]{19}= ? $$

Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим (2,668…) – иррациональное число с бесконечным количеством знаков после запятой.

Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть (sqrt[3]{19}).

Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева ближайшие числа, корень из которых посчитать можно:

$$ sqrt[3]{8} le sqrt[3]{19} le sqrt[3]{27} $$
$$ 2 le sqrt[3]{19} le 3 $$

Получается, что наш корень лежит между числами 2 и 3.

Пример 6

Оценить значение (sqrt[4]{15}= ?)
$$ sqrt[4]{1} le sqrt[4]{15} le sqrt[4]{16}; $$
$$ 1 le sqrt[4]{15} le 2; $$

Корень четной и нечетной степеней

Надо четко различать правила работы c четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из неотрицательного числа. Из отрицательных чисел корень четной степени не существует.

Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:

Пример 7
$$ sqrt[3]{-27}=-3 $$

Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного. Напоминаю, что извлечь корень 3-й степени, значит найти такое число, которое при возведении в 3-ю степень даст покоренное выражение. Если ((-3)) умножить на само себя три раза, то мы получим покоренное выражение (-27=(-3)*(-3)*(-3)).

Пример 8
$$ sqrt[4]{-27} $$

Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. Невозможно найти число, которое при умножении на само себя четыре раза, даст отрицательное значение.

Из-под знака нечетного показателя корня можно выносить минус. Это упрощает процесс подсчета.

$$sqrt[5]{-32}=-sqrt[5]{32}=-2;$$

Свойства корня n-й степени

Пусть есть два числа a и b, для них будут выполняться следующие свойства:

$$ (sqrt[n]{a})^n=a $$
$$ sqrt[n]{a^n}=a $$
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
$$ (sqrt[n]{a})^k=sqrt[n]{a^k} $$
$$sqrt[n] {sqrt[k]{a}}=sqrt[n*k]{a} $$
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$

При использовании вышеперечисленных свойств важно помнить: корень четной степени не существует из отрицательных чисел, и сам корень четной степени всегда положителен. Надо быть внимательным и следить, чтобы в ходе преобразований эти ограничения не нарушались.

Рассмотрим примеры на свойства корня степени (n).

Пример 9
$$(sqrt[5]{7})^5=7;$$
При возведении корня с показателем (n) в степень (n) остается просто подкоренное выражение, так как возведение в степень и извлечение корня это взаимно обратные операции.

Обратите внимание, что неважно, где стоит степень – над корнем или под корнем, результат будет одинаковым.
$$sqrt[5]{7^5}=7$$

Из рассмотренного выше примера следует свойство ((sqrt[n]{a})^k=sqrt[n]{a^k}). Не имеет значения, извлекаете ли вы сначала корень, а потом возводите в степень, или наоборот, сначала возводите в степень подкоренное выражение, и только потом извлекаете корень.

Пример 10
$$sqrt[3]{8^2}=(sqrt[3]{8})^2=2^{2}=4;$$
$$sqrt[3]{8^2}=sqrt[3]{64}=4;$$
Получается одно и тоже.

Более того, показатель корня и степень подкоренного выражения можно домножить на одно и тоже число (p), результат от этого не изменится. Может пригодиться в различных преобразованиях и при сравнении корней между собой.

$$ sqrt[n]{a^k}=sqrt[n*p]{a^{k*p}};$$

Пример 11
$$ sqrt[3]{10^2}=sqrt[3*2]{10^{2*2}}=sqrt[6]{10^{4}}=sqrt[6]{1000};$$

Эту же формулу можно использовать наоборот:
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
То есть можно сокращать показатель корня и степень подкоренного выражения, что существенно упрощает вычисления в некоторых случаях.

Пример 12
$$ sqrt[6]{16}=sqrt[6]{2^4}=sqrt[3]{2^2}=sqrt[3]{4};$$

Рассмотрим применение формул корня от произведения и частного, без которых невозможно решить ни один приличный пример.
Корень степени (n) от произведения равен произведению корней степени (n) от этих множителей.
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
И аналогично корень степени (n) от частного равен частному корней n-й степени.
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$

Пример 13
$$sqrt[3]{125*8}=sqrt[3]{125}*sqrt[3]{8}=5*2=10;$$
$$sqrt[3]{-frac{27}{8}}=frac{-sqrt[3]{27}}{sqrt[3]{8}}=frac{-3}{2};$$

Формулы справедливы не только для двух множителей:

Пример 14
$$sqrt[3]{125*8*27}=sqrt[3]{125}*sqrt[3]{8}*sqrt{27}=5*2*3=30;$$

Пример 15
$$sqrt[4]{frac{16*81}{625}}=frac{sqrt[4]{16*81}}{sqrt[4]{625}}=frac{sqrt[4]{16}*sqrt[4]{81}}{sqrt[4]{625}}=frac{2*3}{5}=frac{6}{5};$$

Обратите внимание! Формулы произведения и частного корней справедливы только для корней с одинаковыми показателями. Нельзя перемножить корни с разными показателями.

$$sqrt[3]{6}*sqrt[4]{7}=?$$

Ничего здесь сделать мы не можем!

И следите за отрицательными числами при использовании корней четной степени. Произведение двух отрицательных чисел может существовать под одним корнем, так как они при умножении дают знак плюс. Но разбивать такое произведение на два корня четной степени ни в коем случае нельзя: выражение теряет всякий смысл.

$$sqrt[4]{-15*(-7)} neq sqrt[4]{-15}*sqrt[4]{-7};$$
$$sqrt[4]{-15*(-7)} = sqrt[4]{15*7}=sqrt[4]{15}*sqrt[4]{7};$$

Арифметический корень второй степени

Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если его возвести во вторую степень (в квадрат).

Не забудем упомянуть, что есть числа, для которых невозможно найти равный этому числу квадрат, который являлся бы действительным числом. Проще говоря, не для всех чисел можно найти действительное число, квадрат которого был бы равен данному числу. 

Арифметический корень второй степени числа a (a≥0) — неотрицательное число, которое становится равным a, если возвести его в квадрат.

Арифметический корень второй степени из числа a имеет следующее обозначение: a. Однако встречается и такое обозначение: a2, но двойку (показатель корня) не нужно прописывать.

Знак арифметического корня «» также имеет название «радикал». Следует запомнить, что «корень» и «радикал» являются полными синонимами (имеют абсолютно одинаковое значение и употребляются и в том, и в том варианте).

Число, стоящее под знаком корня, — это подкоренное число. Если под знаком корня стоит целое выражение, то его принято называть подкоренным выражением, соответственно.

{{banner}}

Далее мы рассмотрим исключительно арифметические корни из неотрицательных чисел и выражений. 

Кубический корень

Арифметический корень третьей степени (кубический корень) — неотрицательное число, которое при условии возведении его в куб, станет равным a. Обозначается как a3.

Число 3 в данной записи — показатель корня. Число или выражение, стоящее под знаком корня — подкоренное.

Опять же, слово «арифметический» чаще всего не используют, а просто говорят: «корень третьей степени из числа a». 

Арифметический корень n-ной степени из числа a≥0 — неотрицательное число, которое, при условии возведения в степень, становится равным числу a и обозначается: an, где a — подкоренное число или выражение, а n — показатель корня.

Арифметический корень можно записать при помощи следующих символов: 

(an)n=a.

Исходя из определения арифметического корня n-ной степени, подкоренным выражением должно являться неотрицательное число или выражение. Если в равенстве (an)n=a обе части умножить на -1, то получатся две равносильные части равенства: -(an)n=-a

Из этого следует, что для нечетных показателей арифметического корня записывают следующее равенство:

-an=-an