Расчет показателей надежности
ПОКАЗАТЕЛЬ
НАДЕЖНОСТИ.
Количественная характеристика одного
или нескольких свойств, составляющих
надежность
объекта.
ЕДИНИЧНЫЙ
ПОКАЗАТЕЛЬ НАДЕЖНОСТИ.
Показатель надежности,
характеризующий одно из свойств,
составляющих надежность
объекта.
КОМПЛЕКСНЫЙ
ПОКАЗАТЕЛЬ НАДЕЖНОСТИ.
Показатель надежности,
характеризующий несколько свойств,
составляющих надежность
объекта.
РАСЧЕТНЫЙ
ПОКАЗАТЕЛЬ НАДЕЖНОСТИ.
Показатель надежности,
значения которого определяются расчетным
методом.
ЭКСПЕРИМЕНТАЛЬНЫЙ
ПОКАЗАТЕЛЬ НАДЕЖНОСТИ.
Показатель
надежности,
точечная или интервальная оценка
которого определяется по данным
эксплуатации.
ЭКСПЛУАТАЦИОННЫЙ
ПОКАЗАТЕЛЬ НАДЕЖНОСТИ.
Показатель
надежности,
точечная или интервальная оценка
которого определяется по данным
эксплуатации.
ВЕРОЯТНОСТЬ
БЕЗОТКАЗНОЙ РАБОТЫ –
P(t).
Вероятность того, что в пределах
заданной
наработки
(или в
интервале времени от 0
до t)
отказ
объекта не возникает:
P(t)=N(t)/N0
,
где
N(t) –
число работоспособных устройств в
момент времени t;
N0
– число
работоспособных устройств в момент
времени t=0
(число
наблюдаемых устройств).
Вероятность
безотказной работы выражается числом
от нуля до единицы (или в процентах). Чем
больше значение вероятности безотказной
работы устройства, тем оно надежнее.
Пример.
При эксплуатации 1000 силовых трансформаторов
типа ОМ за год вышло из строя 15. Имеем
N0
= 1000 шт.,
N(t)
= 985 шт.
P(t)=N(t)/N0
= 985/1000 = 0,985.
ВЕРОЯТНОСТЬ
ОТКАЗА –
q(t).
Вероятность того, что в пределах
заданной
наработки
(или в
интервале времени от 0
до t)
произойдет отказ:
q(t)=n(t)/N0
,
где
n(t) –
число устройств, отказавших к моменту
времени t;
N0
– число
работоспособных элементов устройств
в момент времени t=0
(число
наблюдаемых устройств).
q(t)
= 1 – P(t).
С
РЕДНЯЯ
НАРАБОТКА ДО ОТКАЗА.
Математическое ожидание наработки
объекта до
первого отказа
Тср
(среднее значение продолжительности
работы ремонтируемого устройства до
первого отказа):
где
ti
– продолжительность
работы (наработка) до отказа i-го
устройства;
N0
– число
наблюдаемых устройств.
Пример.
При эксплуатации 10 пускателей выявили,
что первый отказал после 800 переключений,
второй – 1200, далее соответственно –
900, 1400, 700, 950, 750, 1300, 850, 1150.
Тср
=
(800 + 1200 + 900 + 1400 + 700 + 950 + 750 + 1300 + 850 + 1150)/10 =
1000 переключений
СРЕДНЯЯ
НАРАБОТКА НА ОТКАЗ.
Т –
отношение суммарной наработки
восстанавливаемого
объекта к
математическому ожиданию числа его
отказов
в течении этой наработки(среднее
время наработки между отказами).
ИНТЕНСИВНОСТЬ
ОТКАЗОВ.
Условная плотность вероятности
возникновения
отказа
объекта, определяемая при условии, что
до рассматриваемого момента времени
отказ не
возник (среднее число отказов в единицу
времени):
(t)
= n(t)
/ N t
,
где
n(t)
– число
устройств, отказавших в период времени
t
;
N
– число
наблюдаемых устройств;
t
– период
наблюдения.
Пример.
При эксплуатации 1000 трансформаторов в
течение 10 лет произошло 20 отказов
(причем, каждый раз отказывал новый
трансформатор). Имеем: N
=
1000
шт.,
n(t)
= 20 шт., t
= 10 лет.
(t)
= 20/(1000
10) = 0,002 (1/год).
С
РЕДНЕЕ
ВРЕМЯ ВОССТАНОВЛЕНИЯ. Математическое
ожидание времени восстановления
работоспособного состояния
объекта после отказа
Тср
(среднее время вынужденного или
регламентного простоя устройства,
вызванного обнаружением и устранением
отказа).
где
i
– порядковый
номер отказа;
i
– среднее время обнаружения и устранения
i-го
отказа.
КОЭФФИЦИЕНТ
ГОТОВНОСТИ.
КГ
– вероятность того, что объект окажется
в работоспособном
состоянии
в произвольный момент времени, кроме
планируемых периодов, в течении которых
применение объекта по назначению не
предусматривается.
Определяется как отношение наработки
на отказ устройства в единицах времени
к сумме этой наработки и времени
восстановления.
КГ
= Т / (Т + ТВ).
Расчет надежности
Основной метод расчета надежности
основывается на экспоненциальной
математической модели безотказной
работы элементов (наиболее часто
встречающейся при исследовании надежности
систем управления и предполагающей
постоянство интенсивности отказов во
времени):
вероятность
безотказной работы за наработку t:
,
средняя наработка
на отказ (до отказа) равна обратной
величине интенсивности отказов:
,
Допущения,
предопределяемые данным методом:
отказы комплектующих
элементов являются случайными независимыми
событиями;
одновременно два
и более элемента отказать не могут;
интенсивность
отказов элементов в течении срока их
службы в одних и тех же рабочих режимах
и условиях эксплуатации является
постоянной;
отказы элементов
бывают двух видов обрыв (О) и короткое
замыкание (КЗ).
Вероятность
безотказной работы системы, имеющего
в своем составе N
элементов
(блоков):
,
где
Pi(t)
– вероятность безотказной работы элемента
(блока).
Интенсивность
отказов блока, состоящего из M
комплектующих элементов:
.
Интенсивность
отказов элементов, работающих в переменных
режимах на заданном отрезке времени:
,
где
1,
2
– интенсивности отказов на интервалах
t1,
t2
соответственно.
Связь интенсивности отказов с наработкой
и вероятностью безотказной работы:
,
.
Перед началом расчета на основании
логического анализа принципиальных и
структурных схем, функционального
назначения определяется структура
объекта с точки зрения надежности
(последовательное и параллельное
соединение элементов).
Параллельное с точки зрения надежности
соединение элементов – когда устройство
откажет, если откажут все элементы.
Последовательное с точки зрения
надежности соединение элементов –
когда устройство откажет если откажет
хотя бы один элемент.
Причем, элементы, соединенные электрически
последовательно (параллельно) могут с
точки зрения надежности быть наоборот
параллельными (последовательными).
Для разных типов отказов (короткое
замыкание или обрыв) элементы могут с
точки зрения надежности последовательными
для одного типа отказа и последовательными
для другого. Например, гирлянда изоляторов,
электрически соединенные последовательно
для отказа типа короткое замыкание с
точки зрения надежности имеют параллельное
соединение, а для отказа типа обрыв –
последовательное.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
Часть 1.
Введение
Развитие современной аппаратуры характеризуется значительным увеличением ее сложности. Усложнение обуславливает повышение гарантии своевременности и правильности решения задач.
Проблема надежности возникла в 50-х годах, когда начался процесс быстрого усложнения систем, и стали вводиться в действие новые объекты. В это время появились первые публикации, определяющие понятия и определения, относящиеся к надежности [ 1 ] и была создана методика оценки и расчета надежности устройств вероятностно-статистическими методами.
Исследование поведения аппаратуры (объекта) во время эксплуатации и оценка ее качества определяет его надежность. Термин “эксплуатация” происходит от французского слова “exploitation”, что означает получение пользы или выгоды из чего-либо.
Надежность – свойство объекта выполнять заданные функции, сохраняя во времени значения установленных эксплуатационных показателей в заданных пределах.
Для количественного выражения надежности объекта и для планирования эксплуатации используются специальные характеристики – показатели надежности. Они позволяют оценивать надежность объекта или его элементов в различных условиях и на разных этапах эксплуатации.
Более подробно с показателями надежности можно ознакомиться в ГОСТ 16503-70
– “Промышленные изделия. Номенклатура и характеристика основных показателей надежности.”, ГОСТ 18322-73
– “Системы технического обслуживания и ремонта техники. Термины и определения.”, ГОСТ 13377-75
– “Надежность в технике. Термины и определения”.
Определения
Надежность – свойство [далее – (сво-во)] объекта [далее – (ОБ)] выполнять требуемые функции, сохраняя свои эксплуатационные показатели в течение заданного периода времени.
Надежность представляет собой комплексное сво-во, сочетающее в себе понятие работоспособности, безотказности, долговечности, ремонтопригодности и сохранности.
Работоспособность – представляет собой состояние ОБ, при котором он способен выполнять свои функции.
Безотказность – сво-во ОБ сохранять свою работоспособность в течение определенного времени. Событие, нарушающее работоспособность ОБ, называется отказом. Самоустраняющийся отказ называется сбоем.
Долговечность – сво-во ОБ сохранять свою работоспособность до предельного состояния, когда его эксплуатация становится невозможной по техническим, экономическим причинам, условиям техники безопасности или необходимости капитального ремонта.
Ремонтопригодность – определяет приспособляемость ОБ к предупреждению и обнаружению неисправностей и отказов и устранению их путем проведения ремонтов и технического обслуживания.
Сохраняемость – сво-во ОБ непрерывно поддерживать свою работоспособность в течение и после хранения и технического обслуживания.
Основные показатели надежности
Основными качественными показателями надежности является вероятность безотказной работы, интенсивность отказов и средняя наработка до отказа.
Вероятность безотказной работы
P(t) представляет собой вероятность того, что в пределах указанного периода времени
t, отказ ОБ не возникнет. Этот показатель определяется отношение числа элементов ОБ, безотказно проработавших до момента времени
t к общему числу элементов ОБ, работоспособных в начальный момент.
Интенсивность отказов l(t) – это число отказов n(t) элементов ОБ в единицу времени, отнесенное к среднему числу элементов
Nt ОБ, работоспособных к моменту времени
Dt:
l(t)=n(t)/(Nt*Dt), где
Dt – заданный отрезок времени.
Например: 1000 элементов ОБ работали 500 часов. За это время отказали 2 элемента. Отсюда,
l(t)=n(t)/(Nt*Dt)=2/(1000*500)=4*10-6 1/ч, т.е. за 1 час может отказать 4-е элемента из миллиона.
Показатели интенсивности отказов комплектующих берутся на основании справочных данных [ 1, 6, 8 ]. Для примера в
табл. 1 приведена интенсивность отказов
l(t) некоторых элементов.
Табл. 1.
|
|
Наименование элемента |
Интенсивность отказов, *10-5, |
|
1 |
Резисторы |
0,0001…1,5 |
|
2 |
Конденсаторы |
0,001…16,4 |
|
3 |
Трансформаторы |
0,002…6,4 |
|
4 |
Катушки индуктивности |
0,002…4,4 |
|
5 |
Реле |
0,05…101 |
|
6 |
Диоды |
0,012…50 |
|
7 |
Триоды |
0,01…90 |
|
8 |
Коммутационные устройства |
0,0003…2,8 |
|
9 |
Разъемы |
0,001…9,1 |
|
10 |
Соединения пайкой |
0,01…1 |
|
11 |
Провода, кабели |
0,01…1 |
|
12 |
Электродвигатели |
100…600 |
Табл. 2.
|
№ |
Наименование элемента |
Коэффициент надежности |
|
1 |
Резисторы |
1,0 |
|
2 |
Конденсаторы |
0,25…0,83 |
|
3 |
Трансформаторы |
1,3…3,0 |
|
4 |
Катушки индуктивности |
1…2 |
|
5 |
Реле |
1…10 |
|
6 |
Диоды |
1,3…30,0 |
|
7 |
Триоды |
1,3…75,0 |
|
8 |
Электродвигатели |
10…40 |
Надежность ОБ, как системы, характеризуется потоком отказов
L, численно равное сумме интенсивности отказов отдельных устройств:
L=åli
По формуле рассчитывается поток отказов и отдельных устройств ОБ, состоящих, в свою очередь, из различных узлов и элементов, характеризующихся своей интенсивностью отказов. Формула справедлива для расчета потока отказов системы из
n элементов в случае, когда отказ любого из них приводит к отказу всей системы в целом. Такое соединение элементов называется логически последовательным или основным. Кроме, того, существует логически параллельное соединение элементов, когда выход их строя одного из них не приводит к отказу системы в целом. Связь вероятности безотказной работы
P(t) и потока отказов L
определяется:
P(t)=exp(-Dt), очевидно, что 0<P(t)<1 и
0<P(t)<1 и p(0)=1, а p(¥)=0
Средняя наработка до отказа
To – это математическое ожидание наработки ОБ до первого отказа:
To=1/L=1/(åli), или, отсюда: L=1/To
Время безотказной работы равно обратной величине интенсивности отказов.
Например: технология элементов обеспечивает среднюю интенсивность отказов
li=1*10-5 1/ч. При использовании в ОБ
N=1*104 элементарных деталей суммарная интенсивность отказов
lо= N*li=10-1 1/ч. Тогда среднее время безотказной работы ОБ
To=1/lо=10
ч. Если выполнить ОБ на основе 4-х больших интегральных схем (БИС), то среднее время безотказной работы ОБ увеличится в N/4=2500 раз и составит 25000 ч. или 34 месяца или около 3 лет.
Расчет надежности
Формулы позволяют выполнить расчет надежности ОБ, если известны исходные данные – состав ОБ, режим и условия его работы, интенсивности отказов его компонент (элементов). Однако при практических расчетах надежности есть трудности из-за отсутствия достоверных данных о интенсивности отказов для номенклатуры элементов, узлов и устройств ОБ. Выход из этого положения дает применение коэффициентного метода.
Cущность коэффициентного метода состоит в том, что при расчете надежности ОБ используют не абсолютные значения интенсивности отказов
li, а коэффициент надежности ki, связывающий значения
li с интенсивностью отказов lb какого-либо базового элемента:
ki=li/lb
Коэффициент надежности ki практически не зависит от условий эксплуатации и для данного элемента является константой, а различие условий эксплуатации
ku учитывается соответствующими изменениями
lb. В качестве базового элемента в теории и практике выбран резистор. Показатели надежности комплектующих берутся на основании справочных данных [ 1, 6, 8 ]. Для примера в
табл. 2 приведен коэффициенты надежности
ki некоторых элементов. В табл. 3 приведены коэффициенты условий эксплуатации
ku работы для некоторых типов аппаратуры.
Влияние на надежность элементов основных дестабилизирующих факторов – электрических нагрузок, температуры окружающей среды – учитывается введением в расчет поправочных коэффициентов
a. В табл. 4 приведены коэффициенты условий
a работы для некоторых типов элементов. Учет влияния других факторов – запыленности, влажности и т.д. – выполняется коррекцией интенсивности отказов базового элемента с помощью поправочных коэффициентов.
Результирующий коэффициент надежности элементов ОБ с учетом поправочных коэффициентов:
ki’=a1*a2*a3*a4*ki*ku, где
ku – номинальное значение коэффициента условий эксплуатации
ki – номинальное значение коэффициент надежности
a1 – коэффициент учитывающий влияние электрической нагрузки по U, I или P
a2 – коэффициент учитывающий влияние температуры среды
a3 – коэффициент снижения нагрузки от номинальной по U, I или P
a4 – коэффициент использования данного элемента, к работе ОБ в целом
Табл. 3.
|
№ |
Условия эксплуатации |
Коэффициент условий |
|
1 |
Лабораторные условия |
1 |
|
2 |
Аппаратура стационарная: |
|
|
– в помещениях |
2…8 |
|
|
– вне помещений |
10…15 |
|
|
3 |
Подвижная аппаратура: |
|
|
– корабельная |
40…60 |
|
|
– автомобильная |
50…70 |
|
|
– поездная |
60…80 |
Табл. 4.
|
№ |
Наименование элемента и его параметры |
Коэффициент нагрузки |
|
1 |
Резисторы: |
|
|
– по напряжению |
0,7…0,8 |
|
|
– по мощности |
0,3…0,7 |
|
|
2 |
Конденсаторы |
|
|
– по напряжению |
0,7…0,8 |
|
|
– по реактивной мощности |
0,8…0,9 |
|
|
3 |
Диоды |
|
|
– по прямому току |
0,7…0,8 |
|
|
– по обратному напряжению |
0,7…0,85 |
|
|
– по температуре перехода |
0,7…0,8 |
|
|
4 |
Триоды |
|
|
– по току коллектора |
0,7…0,8 |
|
|
– по напряж. коллектор-эмиттер |
0,7…0,8 |
|
|
– по рассеиваемой мощности |
0,7…0,8 |
Порядок расчета состоит в следующем:
1. Определяют количественные значения параметров, характеризующие нормальную работу ОБ.
2. Составляют поэлементную принципиальную схему ОБ, определяющую соединение элементов при выполнении ими заданной функции. Вспомогательные элементы, использующиеся при выполнении функции ОБ, не учитываются.
3. Определяются исходные данные для расчета надежности:
- тип, количество, номинальные данные элементов
- режим работы, температура среды и другие параметры
- коэффициент использования элементов
- коэффициент условий эксплуатации системы
- определяется базовый элемент lb и интенсивность отказов lb‘
- по формуле: ki‘=a1*a2*a3*a4*ki*ku
определяется коэффициент надежности
4. Определяются основные показатели надежности ОБ, при логически последовательном (основном) соединении элементов, узлов и устройств:
- вероятность безотказной работы:
P(t)=exp{-lb*To*[n*å(Ni*ki’)]}, где
Ni – число одинаковых элементов в ОБ
n – общее число элементов в ОБ, имеющих основное соединение - наработка на отказ:
To=1/{lb*[n*å(Ni*ki’)]}
Если в схеме ОБ есть участки с параллельным соединением элементов, то сначала
делается расчет показателей надежности отдельно для этих элементов, а затем для ОБ в целом.
5. Найденные показатели надежности сравниваются с требуемыми. Если не соответствуют, то принимаются меры к повышению
надежности ОБ (см. часть 2).
6. Средствами повышения надежности ОБ являются:
– введение избыточности, которая бывает:
- внутриэлементная – применение более надежных элементов
- структурная – резервирование – общее или раздельное
Пример расчета:
Рассчитаем основные показатели надежности для вентилятора на асинхронном электродвигателе. Схема приведена на
рис. 1. Для пуска М замыкают QF, а затем SB1. KM1 получает питание, срабатывает и своими контактами КМ2 подключает М к источнику питания, а вспомогательным контактом шунтирует SB1. Для отключения М служит SB2.
Рис.1.
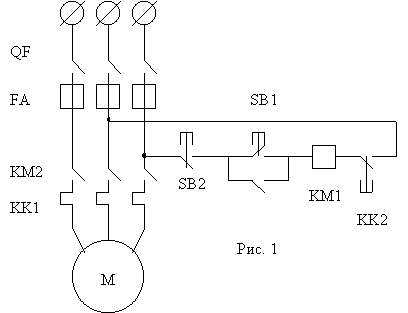
В защите М используются FA и тепловое реле KK1 с КК2. Вентилятор работает в закрытом помещении при T=50 C в длительном режиме.
Для расчета применим коэффициентный метод, используя коэффициенты надежности компонент схемы. Принимаем интенсивность отказов базового элемента
lb=3*10-8. На основании принципиальной схемы и ее анализа, составим основную схему для расчета надежности (см. рис.
2). В расчетную схему включены компоненты, отказ которых приводит к полному отказу устройства. Исходные данные сведем в
табл. 5.
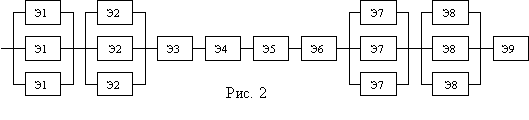
Табл. 5.
|
Базовый элемент, 1/ч |
lб |
3*10-8 |
||||||||
|
Коэф. условий эксплуатации |
ku |
2,5 |
||||||||
|
Интенсивность отказов |
lб’ |
lб* ku=7,5*10-8 |
||||||||
|
Время работы, ч |
t |
5000 |
||||||||
|
Элемент принципиальной схемы |
QF |
FA |
KK2 |
KM1 |
SB1 |
SB2 |
KM2 |
KK1 |
M |
|
|
Элемент расчетной схемы |
Э1 |
Э2 |
Э3 |
Э4 |
Э5 |
Э6 |
Э7 |
Э8 |
Э9 |
|
|
Число элементов |
Ni |
3 |
3 |
1 |
1 |
1 |
1 |
3 |
3 |
1 |
|
Коэф. надежности |
ki |
5 |
25 |
10 |
25 |
5 |
5 |
20 |
18 |
250 |
|
Коэф. нагрузки |
Kn |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,8 |
0,6 |
0,6 |
0,85 |
|
Коэф. электрической нагрузки |
a1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3,5 |
|
Коэф. температуры |
a2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Коэф. нагрузки по мощности |
a3 |
1 |
0,52 |
0,52 |
0,52 |
1 |
1 |
1 |
1 |
0,8 |
|
Коэф. использования |
a4 |
4,4 |
4,2 |
1 |
1 |
4,2 |
0,3 |
4,4 |
4,2 |
4,4 |
|
Произведение коэф. a |
*a |
4,4 |
2,2 |
0,52 |
0,52 |
4,2 |
0,3 |
4,4 |
4,2 |
12,32 |
|
Коэф. надежности |
ki’ |
2,2 |
55 |
5,2 |
13 |
21 |
1,5 |
88 |
75,6 |
3080 |
|
Ni*ki’ |
6,6 |
165 |
5,2 |
13 |
21 |
1,5 |
264 |
226,8 |
3080 |
|
|
S(Ni*ki’) |
3783,9 |
|||||||||
|
Наработка до отказа, ч |
To |
1/[lб’*S(Ni*ki’)]=3523,7 |
||||||||
|
Вероятность |
p(t) |
е[-lб’*To*S(Ni*ki’)]=0,24 |
По результатам расчета можно сделать выводы:
1. Наработка до отказа устройства: To=3524 ч.
2. Вероятность безотказной работы: p(t)=0,24. Вероятность того, что в пределах заданного времени работы t в заданных условиях работы не возникнет отказа.
Часть
2.
Частные случай расчета надежности.
1. Объект (далее ОБ) состоит из n блоков, соединенных последовательно (см. рис.
3). Вероятность безотказной работы каждого блока p. Найти вероятность безотказной работы P системы в целом.
Решение: P=pn
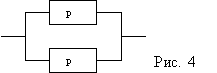
2. ОБ состоит из n блоков, соединенных параллельно (см. рис.
4). Вероятность безотказной работы каждого блока p. Найти вероятность безотказной работы P системы в целом.
Решение: P=1-(1-p)2
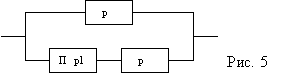
3. ОБ состоит из n блоков, соединенных параллельно (см. рис.
5). Вероятность безотказной работы каждого блока p. Вероятность безотказной работы переключателя (П) p1. Найти вероятность безотказной работы P системы в целом.
Решение: P=1-(1-p)*(1-p1*p)
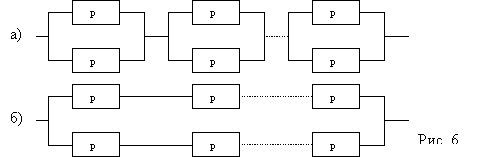
4. ОБ состоит из n блоков (см. рис. 6), с вероятность безотказной работы каждого блока p. С целью повышения надежности ОБ произведено дублирование, еще такими-же блоками. Найти вероятность безотказной работы системы: с дублированием каждого блока Pa, с дублированием всей системы Pb.
Решение: Pa=[1-(1-p)2]n
Pb=[1-(1-p)n]2
5. ОБ состоит из n блоков (см. рис. 7), с вероятность безотказной работы каждого блока p, величина которой условно показаны на рисунке. С целью повышения надежности ОБ произведено дублирование, еще такими-же блоками, наименее надежных блоков. Найти вероятность безотказной работы P системы.
Решение: P=[1-(1-p1)2]*[1-(1-p2)3]*p3*p4*[1-(1-p5)*(1-p6)]
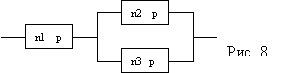
6. ОБ состоит из 3-х узлов (см. рис. 8). В первом узле n1 элементов, во втором узле n2 элементов. В третьем узле n3 элементов. Вероятность безотказной работы каждого элемента p. Найти вероятность безотказной работы P системы.
Решение: P1=pn1
P2=pn2
P3=pn3
P23=1-(1-pn2)*(1-pn3)
P= pn1*[1-(1-pn2)*(1-pn3)]
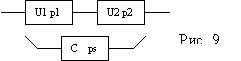
7. ОБ состоит из 2-х узлов U1 и U2, соединенных последовательно, и стабилизатора C (см. рис.
9). При исправном C вероятность безотказной работы U1=p1, U2=p2. При неисправном C вероятность безотказной работы U1=p1′, U2=p2′. Вероятность безотказной работы C=ps. Найти вероятность безотказной работы P системы в целом.
Решение: P=ps*p1*p2+(1-ps)*p’1*p’2
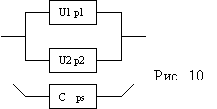
8. ОБ состоит из 2-х узлов U1 и U2, соединенных параллельно, и стабилизатора C
(см. рис. 10). При исправном C вероятность безотказной работы U1=p1, U2=p2. При неисправном C вероятность безотказной работы U1=p1′, U2=p2′. Вероятность безотказной работы C=ps. Найти вероятность безотказной работы P системы в целом.
Решение: P=ps*[1-(1-p1)*(1-p2)]+(1-ps)*[1-(1-p1′)*(1-p2′)]
9. ОБ состоит из 2-х узлов U1 и U2. Вероятность безотказной работы за время t узлов: U1 p1=0.8, U2 p2=0.9. По истечении времени t ОБ несправен. Найти вероятность, что:
– H1 – неисправен узел U1
– H2 – неисправен узел U2
– H3 – неисправны узлы U1 и U2
Решение: Очевидно, имело место H0, когда оба узла исправны.
Событие A=H1+H2+H3
Априорные (первоначальные) вероятности:
– P(H1)=(1-p1)*p2=(1-0.8)*0.9=0.2*0.9=0.18
– P(H2)=(1-p2)*p1=(1-0.9)*0.8=0.1*0.8=0.08
– P(H3)=(1-p1)*(1-p2)=(1-0.8)*0.9=0.2*0.1=0.02
– A=i=1å3*P(Hi)=P(H1)+P(H2)+P(H3)=0.18+0.08+0.02=0.28
Апостерионые (конечные) вероятности:
– P(H1/A)=P(H1)/A=0.18/0.28=0.643
– P(H2/A)=P(H2)/A=0.08/0.28=0.286
– P(H3/A)=P(H3)/A=0.02/0.28=0.071
10. ОБ состоит из m блоков типа U1 и n блоков типа U2. Вероятность безотказной работы за время t каждого блока U1=p1, каждого блока U2=p2. Для работы ОБ достаточно, чтобы в течение t работали безотказно любые 2-а блока типа U1 и одновременно с этим любые 2-а блока типа U2. Найти вероятность безотказной работы ОБ.
Решение: Событие A (безотказная работа ОБ) есть произведение 2-х событий:
– A1 – (не менее 2-х из m блоков типа U1 работают)
– A2 – (не менее 2-х из n блоков типа U2 работают)
Число X1 работающих безотказно блоков типа U1 есть случайная величина, распределенная по биномиальному закону с параметрами m, p1. Событие A1 состоит в том, что X1 примет значение не менее 2, поэтому:
P(A1)=P{X1>2}=1-P(X1<2)=1-P(X1=0)-P(X1=1)=1-(g1m+m*g2m-1*p1),
где
g1=1-p1
аналогично:
P(A2)=1-(g2n+n*g2n-1*p2), где
g2=1-p2
Вероятность
безотказной работы ОБ:
R=P(A)=P(A1)*P(A2)=[1-(g1m+m*g2m-1*p1)]*[1-(g2n+n*g2n-1*p2)],
где
g1=1-p1, g2=1-p2
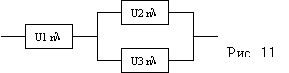
11. ОБ состоит из 3-х узлов (см. рис.
11). В узле U1 n1 элементов с интенсивностью отказов l1. В узле U2 n2 элементов с интенсивностью отказов l2. В узле U3 n3 элементов с интенсивностью отказов l2, т.к. U2 и U3 дублируют друг друга. U1 выходит из строя если в нем отказало не менее 2-х элементов. U2 или U3, т.к. дублируются, выходят из строя если в них отказал хотя бы один элемент. ОБ выходит из строя если отказал U1 или U2 и U3 вместе. Вероятность безотказной работы каждого элемента p. Найти вероятность того, что за время t ОБ не выйдет из строя.
Решение: Вероятность выхода из строя одного элемента U1, U2 или U3 за t равны:
p1=1-e–l1*t
p2=p3=1-e–l2*t
Вероятность выхода из строя U1
за t
равна:
R1=1-(1-p1)n1*n1*p1*(1-p1)n1-1
Вероятности выхода из строя U2
и U3
равны:
R2=1-(1-p2)n2
R3=1-(1-p3)n3
Вероятности выхода из строя всего ОБ:
R=R1+(1-R1)*R2*R3
Литература:
- Малинский В.Д. и др. Испытания радиоаппаратуры, “Энергия”, 1965 г.
- ГОСТ 16503-70 – “Промышленные изделия. Номенклатура и характеристика основных показателей надежности”.
- Широков А.М. Надежность радиоэлектронных устройств, М, Высшая школа, 1972 г.
- ГОСТ 18322-73 – “Системы технического обслуживания и ремонта техники. Термины и определения”.
- ГОСТ 13377-75 – “Надежность в технике. Термины и определения”.
- Козлов Б.А., Ушаков И.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики, М, Сов. Радио, 1975 г.
- Перроте А.И., Сторчак М.А. Вопросы надежности РЭА, М, Сов. Радио, 1976 г.
- Левин Б.Р. Теория надежности радиотехнических систем, М, Сов. Радио, 1978 г.
- ГОСТ 16593-79 – “Электроприводы. Термины и определения”.
И. Брагин 08.2003 г.
Расчёт надёжности — процедура определения значений показателей надёжности объекта с использованием методов, основанных на их вычислении по справочным данным о надежности элементов объекта, по данным о надёжности объектов-аналогов, данным о свойствах материалов и другой информации, имеющейся к моменту расчета.
В результате расчета определяются количественные значения показателей надёжности.
История[править | править код]
Необходимость расчёта надёжности технических устройств и систем существовала с момента начала использования их человеком. Например, в начале 1900-х годов существовала задача оценки среднего времени горения газовых фонарей, а в середине 1930-х, благодаря работам шведского ученого В. Вейбулла, получила известность задача описания среднего времени наработки электронной лампы до её выхода из строя (распределение Вейбулла).
Примером поиска методов расчёта надёжности является история создания ракетных комплексов Фау-1 и Фау-2 Вернером фон Брауном[1]. В лаборатории Брауна тогда работал немецкий математик Эрик Пьеружка (Eric Pieruschka), который доказал, что надёжность ракеты равна произведению надёжности всех компонентов, а не надёжности самого ненадёжного элемента, как считал Браун. Позднее вместе с Брауном в середине 50-х годов в США работал немецкий инженер Роберт Луссер (англ.), который сформулировал основные теоретические положения будущей теории надёжности. Его формула для расчета надёжности системы с последовательным соединением элементов стала известна как «закон Луссера» (англ.).
К первым работам по расчёту надёжности в Советском Союзе можно отнести статью инженера Якуба Б. М. «Показатели и методы расчета надёжности в энергетическом хозяйстве», опубликованную в журнале «Электричество», № 18, 1934 г., и статью профессора Сифорова В. И. «О методах расчёта надёжности работы систем, содержащих большое число элементов» (Известия Академии наук СССР. Отделение технических наук. № 6, 1954 г.) Независимо от закрытых работ немецких ученых, в указанных статьях надёжность систем с последовательным соединением рассчитывалась как произведение надёжности элементов.
Первая в СССР монография по теории и расчёту надёжности — книга И. М. Маликова, А. М. Половко, Н. А. Романова, П. А. Чукреева «Основы теории и расчёта надёжности» (Ленинград, Судпромгиз, 1959 г.).
Цели расчета надёжности[править | править код]
Решение вопросов надёжности и безопасности современных структурно-сложных технических систем и объектов осуществляется на всех стадиях жизненного цикла, от проектирования и создания, производства, до эксплуатации, использования и утилизации. При этом могут преследоваться следующие цели[2]:
- обоснование количественных требований к надёжности объекта или его составным частям;
- сравнительный анализ надёжности вариантов схемно-конструктивного построения объекта и обоснование выбора рационального варианта, в том числе по стоимостному критерию;
- определение достигнутого (ожидаемого) уровня надёжности объекта и/или его составных частей, в том числе расчетное определение показателей надёжности или параметров распределения характеристик надежности составных частей объекта в качестве исходных данных для расчета надёжности объекта в целом;
- обоснование и проверку эффективности предлагаемых (реализованных) мер по доработкам конструкции, технологии изготовления, системы технического обслуживания и ремонта объекта, направленных на повышение его надёжности;
- решение различных оптимизационных задач, в которых показатели надёжности выступают в роли целевых функций, управляемых параметров или граничных условий, в том числе таких, как оптимизация структуры объекта, распределение требований по надёжности между показателями отдельных составляющих надёжности (например, безотказности и ремонтопригодности), расчет комплектов ЗИП, оптимизация систем технического обслуживания и ремонта, обоснование гарантийных сроков и назначенных сроков службы (ресурса) объекта и др.;
- проверку соответствия ожидаемого (достигнутого) уровня надёжности объекта установленным требованиям (контроль надежности), если прямое экспериментальное подтверждение их уровня надёжности невозможно технически или нецелесообразно экономически.
На этапе проектирования технических систем выполняется проектный расчет надёжности.
Проектный расчет надёжности — процедура определения значений показателей надёжности объекта на этапе проектирования с использованием методов, основанных на их вычислении по справочным и другим данным о надёжности элементов объекта, имеющихся к моменту расчета.
Проектный расчет надёжности входит в состав обязательных работ по обеспечению надёжности любой автоматизированной системы и выполняется на основе требований нормативно-технической документации (ГОСТ 27.002-89, ГОСТ 27.301-95, ГОСТ 24.701-86).
На этапе испытаний и эксплуатации расчёт надёжности проводится для оценки количественных показателей надёжности спроектированной системы.
Методы расчёта надёжности[править | править код]
Структурные методы расчета надёжности[править | править код]
Структурные методы являются основными методами расчета показателей надёжности в процессе проектирования объектов, поддающихся разукрупнению на элементы, характеристики надёжности, которых в момент проведения расчетов известны или могут быть определены другими методами.
Расчет показателей надёжности структурными методами в общем случае включает:
- представление объекта в виде структурной схемы, описывающей логические соотношения между состояниями элементов и объекта в целом с учетом структурно-функциональных связей и взаимодействия элементов, принятой стратегии обслуживания, видов и способов резервирования и других факторов;
- описание построенной структурной схемы надёжности объекта адекватной математической моделью, позволяющей в рамках введенных предположений и допущений вычислить показатели надёжности объекта по данным о надёжности его элементов в рассматриваемых условиях применения.
В качестве структурных схем надёжности могут применяться:
- схемы функциональной целостности;
- структурные блок-схемы надёжности;
- деревья отказов;
- графы состояний и переходов.
Логико-вероятностный метод[править | править код]
В логико-вероятностных методах (ЛВМ) исходная постановка задачи и построение модели функционирования исследуемого системного объекта или процесса осуществляется структурными и аналитическими средствами математической логики, а расчет показателей свойств надёжности, живучести и безопасности выполняется средствами теории вероятностей.
ЛВМ являются методологией анализа структурно-сложных систем, решения системных задач организованной сложности, оценки и анализа надёжности, безопасности и риска технических систем. ЛВМ удобны для исходной формализованной постановки задач в форме структурного описания исследуемых свойств функционирования сложных и высокоразмерных систем. В ЛВМ разработаны процедуры преобразования исходных структурных моделей в искомые расчетные математические модели, что позволяет выполнить их алгоритмизацию и реализацию на ЭВМ.
Основоположником научно-технического аппарата ЛВМ и прикладных аспектов их применения, а также создателем и руководителем научной школы является профессор Рябинин И. А..
Общий логико-вероятностный метод[править | править код]
Необходимость распространения ЛВМ на немонотонные процессы привела к созданию общего логико-вероятностного метода (ОЛВМ). В ОЛВМ расчета надёжности аппарат математической логики используется для первичного графического и аналитического описания условий реализации функций отдельными и группами элементов в проектируемой системе, а методы теории вероятностей и комбинаторики применяются для количественной оценки безотказности и/или опасности функционирования проектируемой системы в целом. Для использования ОЛВМ должны задаваться специальные структурные схемы функциональной целостности исследуемых систем, логические критерии их функционирования, вероятностные и другие параметры элементов.
В основе постановки и решения всех задач моделирования и расчета надёжности систем с помощью ОЛВМ лежит так называемый событийно-логический подход. Этот подход предусматривает последовательное выполнение следующих четырёх основных этапов ОЛВМ:
- этап структурно-логической постановки задачи;
- этап логического моделирования;
- этап вероятностного моделирования;
- этап выполнения расчетов показателей надёжности.
Метод деревьев отказов[править | править код]
Метод Марковского моделирования[3][править | править код]
Примеры расчета надёжности систем простой структуры[править | править код]
Последовательная система[править | править код]
В системе с последовательной структурой отказ любого компонента приводит к отказу системы в целом.
Система логических уравнений для приведенной выше последовательной системы:
Пример последовательной системы.

Логическая функция работоспособности (решение системы логических уравнений):
Вероятность безотказной работы:
где 
В общем случае вероятность безотказной работы системы равна:
Параллельная система[править | править код]
Пример параллельной системы.
В системе с параллельной структурой отказ системы в целом происходит только при отказе всех элементов.
Система логических уравнений для приведенной параллельной системы:

Логическая функция работоспособности (решение системы логических уравнений):
Вероятность безотказной работы:
В общем случае вероятность безотказной работы системы равна:
Система типа: «k из n»[править | править код]
Вероятность того, что в системе, состоящей из 

,
где
— вероятность безотказной работы элемента системы;
— биномиальный коэффициент из
по
.
Вероятность того, что в системе, состоящей из 

Вероятность того, что в системе, состоящей из 

Некоторые программные пакеты для расчета надёжности[править | править код]
Программные средства, предназначенные для анализа и расчета надежности, готовности и ремонтопригодности (в алфавитном порядке)[5]
[6]
[7]
[8]:
- отечественные
- АРБИТР[9]
- АРМ Надежности[10]
- АСОНИКА-К[11]
- AnyGraph[12][неавторитетный источник]
- CRISS[13]
- зарубежные
- BlockSim[14]
- ITEM Software[15]
- RAM Commander от Advanced Logistics Development[16]
- Reliability Workbench[17]
- Windchill[18]
См. также[править | править код]
- Надёжность
- Схема функциональной целостности
Примечания[править | править код]
- ↑ Мант Д. И. Почему не летит «Булава». Агентство ПРоАтом (10 июня 2009). Дата обращения: 12 января 2012. Архивировано 4 октября 2006 года.
- ↑ ГОСТ 27.301-95 Архивная копия от 15 мая 2021 на Wayback Machine Надёжность в технике. Расчет надёжности. Основные положения. Минск, 1995. С. 12
- ↑ Дерево отказов, как метод структурного анализа, пример дерева событий и происшествий. Дата обращения: 22 января 2015. Архивировано 22 января 2015 года.
- ↑ 1 2 3
Kuo, W., Zuo, M. J. Optimal Reliability Modeling: Principles and Applications. — NY: Wiley, 2002. — P. 231-280. — ISBN 0-471-29342-3. - ↑ Викторова В.С. , Кунтшер Х.П., Степанянц А.С. Анализ программного обеспечения моделирования надёжности и безопасности систем // Надёжность. — 2006. — № 4(19). — С. 46—57. — ISSN 1729-2646.
- ↑ Строгонов А., Жаднов В., Полесский С. Обзор программных комплексов по расчету надёжности сложных технических систем // Компоненты и технологии. — 2007. — № 5. — С. 183—190. — ISSN 2079-6811.
- ↑ Software — NTNU. Дата обращения: 8 февраля 2012. Архивировано 21 сентября 2012 года.
- ↑ Willis R. Survey of support software for reliability engineering Архивная копия от 3 июля 2012 на Wayback Machine //Society of Reliability Engineers. 2006.
- ↑ АРБИТР. Дата обращения: 8 февраля 2012. Архивировано 8 января 2012 года.
- ↑ АРМ Надежности. Дата обращения: 8 февраля 2012. Архивировано 22 декабря 2015 года.
- ↑ АСОНИКА-К. Дата обращения: 8 февраля 2012. Архивировано 11 февраля 2012 года.
- ↑ AnyGraph. Дата обращения: 8 октября 2019. Архивировано из оригинала 23 октября 2017 года.
- ↑ А.М. Бахметьев, И.А. Былов, А.В. Думов, А.С. Смирнов. Совершенствование программного обеспечения для проведения вероятностного анализа безопасности ядерных установок // Ядерная энергетика. — 2008. — № 2. — С. 21—29. — ISSN 0204-3327. (недоступная ссылка)
- ↑ BlockSim. Дата обращения: 8 февраля 2012. Архивировано 25 февраля 2012 года.
- ↑ ITEM Software. Дата обращения: 8 февраля 2012. Архивировано 9 марта 2012 года.
- ↑ RAM Commander — [[Bee Pitron]]. Дата обращения: 15 марта 2020. Архивировано 10 февраля 2020 года.
- ↑ Reliability Workbench. Дата обращения: 8 февраля 2012. Архивировано 28 декабря 2011 года.
- ↑ Windchill. Дата обращения: 8 февраля 2012. Архивировано из оригинала 7 февраля 2012 года.
Литература[править | править код]
- Барлоу Р., Прошан Ф. Статистическая теория надёжности и испытания на безотказность. -М.: Наука, 1984. – 328 с.
- Барлоу Р., Прошан Ф. Математическая теория надёжности. -М.: Советское радио, 1969.- 485 с.
- Козлов Б. В., Ушаков И. А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. -М.:,Советское радио”, 1975.
- Маликов И. М., Половко А. М., Романов Н. А., Чукреев П. А. Основы теории и расчёта надёжности. — Л.:Судпромгиз, 1959.
- Маликов И. М., Половко А. М., Романов Н. А., Чукреев П. А. Основы теории и расчёта надёжности. Изд. 2-е, доп. — Л.:Судпромгиз, 1960. — 144с.
- Можаев А. С. Общий логико-вероятностный метод анализа надёжности сложных систем. Уч. пос. Л.: ВМА, 1988. — 68с.
- Половко А. М. Основы теории надёжности. — М.:Наука, 1964. — 446с.
- Половко А. М., Гуров С. В. Основы теории надёжности. — СПб.:БХВ-Петербург, 2006. — 702с.
- Половко А. М., Гуров С. В. Основы теории надёжности. Практикум. — СПб.:БХВ-Петербург, 2006. — 560с.
- Рябинин И. А. Надёжность и безопасность структурно-сложных систем. СПб.: Издательство Санкт-Петербургского университета, 2007 г., 278 с.
- Рябинин И. А. Основы теории и расчета надёжности судовых электроэнергетических систем. — Л.: Судостроение, 1967, 1971.
- Рябинин И. А., Черкесов Г. Н. Логико-вероятностные методы исследования надёжности структурно-сложных систем 1981. 264 с.
- Рябинин И. А. Reliability of Engineering Systems. Principles and Analysis. — M.: Mir, 1976.
Ссылки[править | править код]
- MIL-HDBK-217F-Notice2 — Американский военный стандарт расчета надёжности для электронных компонентов.
- Основные положения общего логико-вероятностного метода анализа систем.
- Левин В. И. Логическая теория надёжности сложных систем. М.: Энергоатомиздат, 1985.
- Расчет надёжности и безопасности автоматизированных систем управления — Методические рекомендации.
- Можаев А. С., Скворцов М. С., Струков А. В. «Применение автоматизированного структурно-логического моделирования для проектного расчета надёжности АСУ».
- Рябинин И. А. Надёжность и безопасность структурно-сложных систем.
- Рябинин И. А., Струков А. В. — «Кратко аннотированный список публикаций зарубежный периодический изданий по вопросам оценивания надёжности структурно-сложных систем» в сборнике «Моделирование и Анализ Безопасности и Риска в Сложных Системах: Труды Международной научной школы МА БР — 2011».
- Ушаков И. А. Откуда есть пошла надёжность на Руси.