Как найти показатель преломления материала клина - Сайт, где вы сможете решить свои вопросы

Критерии оценивания выполнения задания Баллы

Приведено полное решение, включающее следующие элементы:

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом;

II) сделаны правильные рисунки, на которых построены изображения двух источников, с указанием хода лучей в линзе;

III) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);

IV) представлены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);

V) представлен правильный ответ с указанием единиц измерения искомой величины

Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеется один или несколько из следующих недостатков.

Записи, соответствующие пунктам II и III, представлены не в полном объёме или отсутствуют.

И (ИЛИ)

В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.

И (ИЛИ)

Отсутствует пункт V, или в нём допущена ошибка (в том числе в записи единиц измерения величины)

Представлены записи, соответствующие одному из следующих случаев.

Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

Сделаны только правильные рисунки, на которых построены изображения двух источников с указанием хода лучей в линзе

Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла

0 Максимальный балл 3

Источник

Министерство образования и науки Российской Федерации Федеральная заочная физико-техническая школа при Московском физико-техническом институте

(государственном университете)

ФИЗИКА

Тонкие линзы

Задание №5 для 8-х классов

(2010 – 2011 учебный год)

г. Долгопрудный, 2011

2010-2011 уч. год., № 5, 8 кл. Физика. Тонкие линзы.

Составитель: В.П. Слободянин, доцент кафедры общей физики МФТИ.

Физика: задания №5 для 8-х классов (2010 – 2011 учебный год). – М.: МФТИ, 2011, 20с.

Дата отправления заданий по физике и математике – 10 апреля 2011 г.

Учащийся должен стараться выполнять все задачи и контрольные вопросы в заданиях. Некоторая часть теоретического материала, а также часть задач и контрольных вопросов являются сложными и потребуют от учащегося больше усилий при изучении и решении. В целях повы-шения эффективности работы с материалом они обозначены символом «*» (звёздочка). Мы рекомендуем приступать к этим задачам и контрольным вопросам в последнюю очередь, разобравшись вначале с более простыми.

Составитель:

Слободянин Валерий Павлович

Подписано 21.01.11. Формат 60×90 1/16.

Бумага типографская. Печать офсетная. Усл. печ. л. 1,25. Уч.-изд. л. 1,11. Тираж 1400. Заказ №5-з.

Федеральная заочная физико-техническая школа при Московском физико-техническом институте (государственном университете)

ООО «Печатный салон ШАНС»

141700, Москов. обл., г. Долгопрудный, Институтский пер., 9. ФЗФТШ при МФТИ, тел/факс (495) 408-5145 – заочное отделение

тел./факс (498) 744-6351 – очно-заочное отделение тел. (498) 744-6583 – очное отделение

e-mail: zftsh@mail.mipt.ru

Наш сайт: www.school.mipt.ru

2010-2011 уч. год., № 5, 8 кл. Физика. Тонкие линзы.

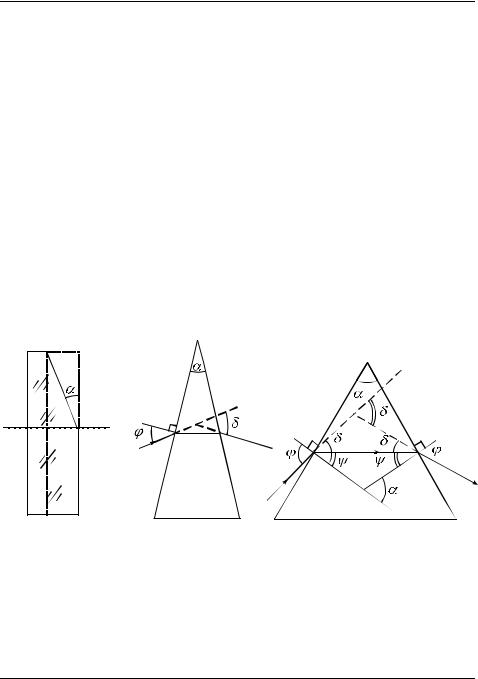
Прежде чем изучать тонкие линзы, давайте решим задачу о прохождении узкого пучка света через тонкий клин. Тонким клином называется стеклянная призма, у которой угол α при вершине мал (α <<1) . Чтобы

изготовить такой клин в заводских условиях, берут стеклянную плоскопараллельную пластинку и на шлифовальном станке часть одной из её граней стачивают под малым углом α (рис. 1.1). Если левую грань клина сошлифовать так, что она уменьшится на толщину плоскопараллельной пластинки ABCD, то угол отклонения узкого пучка света, падающего под малым углом ϕ1 на клин, не изменится. Поэтому договорились изобра-

жать клин так, как показано на рис. 1.2. Пусть n – показатель преломления материала клина. Найдём угол δ отклонения луча от исходного направления. Задачу будем решать в предположении, что углы α и ϕ1 малы. На рис. 1.3 эти углы для наглядности сильно увеличены.

ϕ1 = nψ1 , Приближенный закон Снелла (см. §7 задания 4).

ϕ2 = nψ2 .

A	B
	1	1	2

		1	2
		2
		1
		n	1
D	C

Рис. 1.1	Рис. 1.2	Рис. 1.3
Угол отклонения луча на первой грани δ1	=ϕ1 −ψ1 =(n −1)ψ1 .
Угол отклонения луча на второй грани δ2	=ϕ2 −ψ2 =(n −1)ψ2 .

По теореме о внешнем угле треугольника угол отклонения луча, прошедшего сквозь клин, равен δ =δ1 +δ2 =(n −1)(ψ1 +ψ2 ) .

По той же теореме α1 =ψ1 +ψ2 , а углы α и α1 равны как углы со взаимно перпендикулярными сторонами. В итоге мы получим:

2010-2011 уч. год., № 5, 8 кл. Физика. Тонкие линзы.
		δ =δ1 +δ2 =(n −1)(ψ1 +ψ2 ) =(n −1)α1 =(n −1)α .
Итак, угол отклонения δ пучка параллельных лучей, прошедших сквозь
тонкий клин, не зависит от угла падения и остаётся постоянной ве-
личиной:			δ =(n −1)α.	(1.1)

Иногда у плоскопараллельной пластинки стачивают под малыми угла-
	ми обе половины одной из граней (см. рис. 1.4). Получившееся
	устройство называют бипризмой. Если на бипризму пустить ши-
	рокий пучок параллельных лучей света, то после прохождения
	бипризмы пучки станут сходиться. Рассмотрим
	пример 1.1. На бипризму, изготовленную из стекла с показа-
	телем преломления n = 1,5 и имеющую ширину b = 3 см, пустили
	широкий пучок параллельных лучей света. Углы при вершине
	бипризмы одинаковы и равны α = 0,05 рад. За бипризмой обра-
	зовалось два сходящихся пучка параллельных лучей.
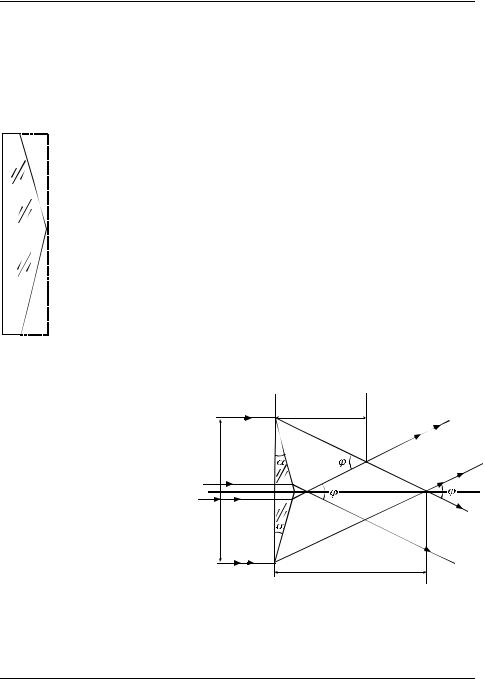
	1) Под каким углом φ будут сходиться лучи?
	Если за бипризмой установить экран, то на нём можно наблю-
	дать область, освещённую обоими пучками.
	2) На каком расстоянии L1 от бипризмы нужно установить
Рис. 1.4 экран, чтобы область перекрытия пучков была максимальной?
	3) На каком максимальном расстоянии L2 от бипризмы пучки
лучей ещё будут пересекать-		L1
ся?				(1)
Решение.	1)	Изобразим

ход	лучей	за	бипризмой		(1)
(рис. 1.5). Верхняя половина
бипризмы отклонит падаю-	b	(2)
щий пучок лучей вниз на
угол				(2)
δ1 =(n −1)α =0,025 рад,
а нижняя – вверх на такой		L2
же по величине угол
	δ2 =(n −1)α.
Следовательно,	пучки будут		Рис. 1.5
сходиться под углом

ϕ= 2δ1 = 2(n −1)α = 0,05 рад.

2)Максимальная область перекрытия пучков находится там, где пере-

2010-2011 уч. год., № 5, 8 кл. Физика. Тонкие линзы.

секаются лучи (1) и (2) (см. рис. 1.5).		b		b
В силу малости угла ϕ искомое расстояние	L ≈	=	= 30 см.
2ϕ	4α(n −1)
	1
3) Из того же рисунка легко видеть,	что максимальное	расстояние
L2 = 2L1 = 60 см.
§2. Тонкая линза

Слово «линза» произошло от латинского lens – чечевица. В оптике под линзой понимают прозрачное тело, ограниченное выпуклыми или вогну- тыми поверхностями и преобразующее форму светового пуч- ка. Одна из поверхностей линзы может быть плоской. Мы бу-

дем рассматривать линзы, находящиеся в воздухе, если иное

специально не оговорено. Если линза преобразует пучок па-

раллельных лучей в сходящийся, её называют собирающей

или положительной. Если после прохождения линзы пучок

параллельных лучей становится расходящимся, линзу называ-

Рис. 2.1 ют рассеивающей или отрицательной. Существует огромное разнообразие типов линз. Так, для решения некоторых научных задач используют цилиндрические линзы (рис. 2.1). Но наиболее широкое распространение получили линзы, обе преломляющие поверхности которых представляют собой части сфер с разными радиусами кривизны.


1 2	3		4	5	6	d		d

		Рис. 2.2.					Рис. 2.3

Такие линзы относительно просты в изготовлении. Собирающие линзы делятся на двояковыпуклые, плоско-выпуклые, вогнуто-выпуклые. Рассеивающие – на двояковогнутые, плоско-вогнутые и выпукло-вогнутые. На рисунке 2.2 дан вид сбоку на такие линзы. Мы с вами рассмотрим основные свойства так называемых тонких линз. Говорят, что линза тонкая, если её толщина d много меньше диаметра D (рис. 2.3).

Рис. 2.4

2010-2011 уч. год., № 5, 8 кл. Физика. Тонкие линзы.

Здесь уместно отметить, что упрощённый подход, который мы будем использовать в нашем исследовании, с одной стороны, позволяет ясно понять основные свойства тонких линз, с другой, – не позволяет учесть некоторые эффекты, например искажения

(их называют аберрациями), неизбежно возникающие при прохождении света через реальные толстые линзы.

Для того чтобы исправить аберрации, при производстве оптических приборов часто используют составные линзы или линзы, поверхность которых имеет специальную форму, например, параболическую.

Заметим, что хороший объектив микроскопа может содержать более десяти линз (рис. 2.4).

§3. Фокусные расстояния плоско-выпуклой линзы

Рассмотрим линзу, представляющую собой кусок стекла, который с од-

ной стороны ограничен плоской

поверхностью, а с другой – сфе-

рической (рис. 3.1). Пусть радиус

сферической поверхности равен

R, а показатель преломления стек-

ла n. Главной оптической осью

такой линзы назовём прямую СX,

перпендикулярную

плоской по-

верхности линзы и

проходящую

через центр кривизны C выпук-

лой поверхности. Предположим,

Рис. 3.1

что слева на плоскую поверхность линзы падает пучок лучей, параллельных главной оптической оси. Выберем из этого пучка произвольный луч AA′, проходящий на расстоянии h от главной оптической оси. Этот луч,

преломившись на сферической поверхности, пересечёт главную оптическую ось на некотором расстоянии F от линзы. Если угол падения φ1 мал, то мы сможем воспользоваться приближённым законом Снелла: n φ1 = φ2.

Угол отклонения
δ = φ2 – φ1 = (n – 1) φ1.	(3.1)

Так как углы δ и φ1 малы, запишем приближенное равенство:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задача 52942 …

Условие

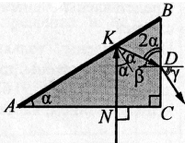
Верхняя грань АВ прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина α = 30°. Луч света падает из воздуха на клин перпендикулярно грани АС, преломляется и выходит в воздух через другую грань под углом γ= 45° к её нормали. Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

физика 10-11 класс
5219

Решение

Поскольку луч падает на грань АС перпендикулярно, он на ней не преломляется, а, падая на грань АВ, согласно закону отражения света отражается под тем же углом α. Следовательно, так как KN || ВС, то β = 90 – 2α.
Закон преломления света в точке D: n sinβ = sinγ, nsin(90-2α) = sinγ.
Получаем: п = sinγ/cos2α ≈1,4.
Ответ: п = 1,4

Написать комментарий

Источник

Макеты страниц

Оптическая деталь с плоскими преломляющими поверхностями 1 и 2, образующими двугранный угол называется преломляющей призмой. Сечение призмы плоскостью, перпендикулярной к ребру двугранного угла, будет главным сечением призмы (рис. 59).

Угол между направлениями входящего и выходящего лучей называется углом отклонения, а угол между преломляющими плоскими гранями — преломляющим углом призмы.

Рассмотрим ход луча в главном сечении призмы. Угол преломления на первой грани определяется из формулы

(призма находится в воздухе).

Рис. 59. Ход луча в преломляющей призме

Из рис. 59 следует

тогда

Угол отклонения луча призмой

Представляет интерес отыскание значения угла падения на первую грань призмы, при котором угол отклонения преломленного луча будет наименьшим.

Для этой цели, пользуясь формулой (121), запишем:

или

Кроме того, из равенства (119) имеем:

Продифференцировав формулы (118) и (120), получим следующие равенства:

из которых, учитывая равенства (122) и (123), найдем выражение

Кроме того, перемножая правые и левые части формул (118) и (120), получим равенство

Одновременное существование равенств (124) и (125) возможно только при условии, когда

Так как вторая производная то равенства (126) определяют условие получения сйщщ при данном преломляющем угле призмы. Из этих же равенств следует, что получается при таком расположении преломленного луча внутри призмы, при котором этот луч перпендикулярен к биссектрисе преломляющего угла

Для определения служит формула (120), из которой с учетом равенств (126) и (119) получаем выражение

используемое при выборе показателя преломления материала призмы измеряются, например, на гониометре).

Рассмотрим влияние изменения показателя преломления материала призмы на угол отклонения преломленного луча. Показатель преломления зависит от длины волны монохроматического излучения. Поэтому, если луч, поступающий в призму, монохроматический, то при преломлении отдельные монохроматические составляющие этого луча будут отклоняться на разные углы (дисперсия призмы).

Угловой дисперсией призмы называется зависимость угла отклонения луча от длины световой волны, равная производной этого угла по длине волны, т. е.

Найдем угловую дисперсию призмы для случая, описываемого формулой (127). В результате ее дифференцирования получим выражение

где дисперсия материала призмы; среднее значение показателя преломления в данном интервале длин волн.

Угловое значение дисперсии вычисляют по формуле

разность показателей преломления на краях данного интервала длин волн

Если (стекло K8), то рад .

Угловая дисперсия призмы и угловое значение дисперсии будут большими, если угол отклонения

Преломляющие призмы в основном применяют в виде диспергирующих элементов в спектральных приборах.

Из формулы (128), которая определяет угловое значение дисперсии, следует, что эта величина тем больше, чем больше преломляющий угол призмы. Ограничение на угол накладывается той же формулой, а именно: где среднее значение показателя преломления материала призмы в заданном диапазоне длин волн.

При невыполнении этого неравенства наблюдается полное внутреннее отражение на второй преломляющей грани призмы. Следует отметить, что формула (128) определяет угловое значение дисперсии при наименьшем угле отклонения. Если угол отклонения то соответственно увеличивается и угловая дисперсия. Однако при этом уменьшается разрешающая сила спектрального прибора, что и определяет использование преломляющих призм в положении наименьшего отклонения.

Наиболее часто преломляющий угол призмы выбирают равным 60°.

Рис. 60. Преломляющие призмы

Преломляющие (диспергирующие) составные призмы спектральных приборов — призмы Резерфорда, Амичи, Аббе и трехпризменная система — показаны на рис. 60.

Отличительной особенностью призмы Резерфорда (рис. 60, а) является большая угловая дисперсия, получаемая за счет увеличения преломляющего угла основной призмы 2, изготовленной из флинта. Вспомогательные призмы 1 и 3 делаются из крона. Следовательно,

Для такой призмы угол спектра [см. вывод формулы (128)] определяется после дифференцирования по равенства гц

После дифференцирования получим:

Формула (129) позволяет вычислить а также сделать вывод о том, что для призмы, помещенной в среду с показателем преломления, большим, чем единица предельное значение преломляющего угла ограничивается неравенством где среднее значение показателя преломления в рассматриваемом диапазоне длин волн для призм то же, для призмы 2.

Угол достигает значения

Призма Амичи (рис. 60, б) называется призмой прямого видения, так как направления падающего и преломленного лучей для определенной длины волны совпадают, что удобно при конструктивном оформлении спектральных приборов. В частном случае обеспечивается совпадение падающего луча и биссектрисы угла

дисперсии. Призмы 1 и 3 изготовляют из крона, призму 2 — из флинта

Из рис. 60, б при использовании условия прямого видения получается следующая зависимость между преломляющими углами и показателями преломления (призма 2 равнобедренная):

Для призмы прямого видения значение угловой дисперсии не достигает максимума.

Призма Аббе (рис. 60, в) относится к призмам постоянного отклонения с углом Для уменьшения поглощения призму с полным внутренним отражением выполняют из крона. На рис. показана система прямого видения из трех преломляющих призм.

Если преломляющий угол призмы мал , то такую призму называют клином. Формула (120) при этом принимает следующий вид:

Используя равенство (121), получим

Из последних двух формул и формулы (118) получим значение угла отклонения луча клином .

Если принять условие, что угол падения мал, откуда следует и малость угла преломления то

Клин, как и призма, имеет дисперсию и соответствующее ей угловое значение дисперсии.

Из формулы (130) следует, что угловое значение дисперсии клина

Например, для диапазона длин волн, границы которого соответствуют синему и красному цветам, где средняя дисперсия материала клина

Оптические клинья в оптических системах используют в качестве компенсаторов при юстировке и измерениях. Однако более часто клиновидность проявляется как ошибка, допущенная при изготовлении плоскопараллельных пластин, предварительная оценка влияния которой обеспечивает задание ее допустимого значения.

Рассмотрим использование клина в качестве компенсатора. При вращении клина (рис. 61) изображение осевой точки описывает окружность радиусом у, который зависит от значения угла отклонения и от расстояния между клином и плоскостью изображения:

К сожалению, движение изображения по окружности в целях измерения и компенсации использовать нельзя. Прямолинейное

движение изображения с достаточной степенью точности может быть обеспечено двумя одинаковыми клиньями, вращаемыми в противоположных направлениях на равные углы (рис. 62).

Наибольший суммарный угол отклонения будет, очевидно, тогда, когда главные сечения клиньев лежат в одной плоскости, а преломляющие углы направлены в одну сторону:

При вращении клиньев угол отклонения в рассматриваемой меридиональной плоскости будет следующим:

С помощью, например, сферической тригонометрии доказывается, что горизонтальной (боковой) составляющей угла отклонения луча можно пренебречь.

Прямолинейное движение изображения может быть получено также при поступательном перемещении клина по направлению падающего луча. В этом случае (рис. 63) перемещение клина из положения 1 в положение 2 на расстояние вызывает смещение изображения:

Из формулы (131) следует, что перемещение клина и смещение изображения прямо пропорциональны.

Поступательно перемещающийся клин в отличие от вращающихся клиньев можно использовать в сходящихся пучках лучей. Для компенсации или измерения малых угловых или линейных величин пользуются парой вращающихся клиньев. Большому углу поворота соответствует малое изменение в положении преломленного луча. Поступательно перемещающийся клин, используемый для компенсации и измерения малых линейных величин, является менее точным.

Рис. 61. Вращение клииа

Рис. 62. Вращение двух клиньев

Рис. 63. Поступательное перемещение клина

Рис. 64. Клин с переменным преломляющим углом

Клин с переменным преломляющим углом может быть выполнен из двух линз: плосковыпуклой и вогнуто-плоской, составляющих плоскопараллельную пластину и подвижно соединенных так, как показано на рис. 64.

Оглавление

ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ
Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
1. Принцип Ферма
2. Показатель преломления
3. Правила знаков
4. Законы преломления и отражения
5. Полное внутреннее отражение
6. Преломляющие и отражающие поверхности
Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
7. Преломление лучей плоской поверхностью
8. Преломление лучей сферической поверхностью
9. Отражение лучей плоской поверхиостью
10. Отражение лучей сферической поверхностью
11. Преломление лучей несферической поверхностью
12. Отражение от несферических поверхностей
Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
14. Кардинальные элементы идеальной оптической системы
15. Зависимости между положениями и размерами предмета и изображения
16. Угловое увеличение. Узловые точки
17. Продольное увеличение
18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
19. Изображение наклонных плоскостей предметов
20. Расчет хода луча через идеальную систему
21. Оптические системы из нескольких компонентов
Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
23. Инвариант Гюйгенса-Гельмгольца
24. Расчет хода нулевых лучей
Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
25. Материалы, применяемые для изготовления оптических деталей
26. Линзы
27. Плоскопараллельные пластины
28. Плоские, сферические и несферические зеркала
29. Отражательные призмы
30. Преломляющие призмы и клинья
31. Световоды и волоконная оптика
32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
34. Входной и выходной зрачки
35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
36. Действующее отверстие входного зрачка
Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
37. Оптическое излучение. Поток излучения
38. Энергетические и световые величины и их единицы
39. Связь между световыми и энергетическими величинами
40. Распространение излучения
41. Коэффициент пропускания оптической системы
42. Прохождение потока излучения через светофильтр
43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
44. Формулы для расчета хода лучей на ЭВМ
45. Формулы для расчета хода бесконечно тонких астигматических пучков
46. Выбор начальных данных для расчета хода лучей
Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
47. Общие положения о вычислении аберраций оптической системы
48. Аберрации третьего порядка
49. Условия нормировки вспомогательных лучей
50. Сферическая аберрация
51. Меридиональная кома
52. Условие синусов и условие изопланатизма
53. Астигматизм и кривизна поверхности изображения
54. Дисторсия
Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
56. Хроматизм увеличения
57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
58. Устройство глаза
59. Основные характеристики глаза
60. Недостатки глаза и их коррекция
Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
61. Назначение и виды осветительных систем
62. Оптическая схема прожектора дальнего действия
63. Зеркальные осветительные системы
64. Линзовые конденсоры
Глава XIII. ЛУПА И МИКРОСКОП
65. Лупа и ее характеристики
66. Оптическая схема микроскопа и его основные характеристики
67. Разрешающая способность микроскопа
68. Глубина изображаемого пространства для микроскопа
69. Объективы и окуляры микроскопа
70. Осветительные системы микроскопов
Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
71. Схема телескопической системы и ее основные характеристики
72. Разрешающая способность телескопической системы
73. Основные сведения об объективах и окулярах телескопических систем
74. Фокусировка окуляра телескопической системы
75. Применение коллектива в зрительной трубе
76. Расчет зрительной трубы Кеплера
77. Схема зрительной трубы Галилея и ее расчет
78. Расчет призменного монокуляра
79. Расчет зрительной трубы с линзовой оборачивакщей системой
80. Основные сведения о зрительных трубах переменного увеличения
81. Стереоскопические телескопические системы
82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
83. Основные характеристики фотообъектива
84. Разрешающая способность и функция передачи модуляции фотографической системы
85. Глубина изображаемого пространства и глубина резкости
86. Определение выдержки при фотографировании
87. Основные типы фотографических объективов
Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
88. Оптические характеристики передающих и приемных телевизионных трубок
89. Объективы передающих телевизионных камер и их основные характеристики
90. Разрешающая способность и ФПМ телевизионной системы
91. Телевизионная система с «бегущим лучом»
Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
92. Виды и особенности проекционных систем
93. Эпископическая проекционная система
94. Диаскопическая проекционная система
95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
96. Некоторые характеристики и параметры приемников излучения
97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
102. Некоторые принципиальные схемы оптических фотоэлектрических систем
Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
105. Оптические системы для концентрации излучения лазера
106. Оптические системы для уменьшения расходимости лазерного пучка
107. Оптическая фотоэлектрическая система с лазером
108. Оптические системы, применяемые в голографии
Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
109. Характеристика трансформированного изображения и его получение
110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
111. Цилиндрическая афокальная система
Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
112. Общие сведения о методах аберрационного расчета оптических систем
113. Допустимые остаточные аберрации в различных оптических системах
114. Связь между параметрами 1-го и 2-го вспомогательных лучей
115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
116. Основные параметры тонких компонентов
117. Аберрации оптических систем с иесферическими поверхностями
118. Расчет оптической системы на минимум сферической аберрации
119. Расчет двухлинзового склеенного объектива
120. Расчет двухливэового несклеенного объектива
121. Расчет светосильного двухкомпоиентного объектива
122. Расчет объектива типа триплета
123. Расчет зеркальных систем
124. Расчет зеркально-линзовых систем
125. Об автоматизированной коррекции оптических систем на ЭВМ
126. Суммирование аберраций
127. О допусках в оптических системах
128. Оценка качества изображения по результатам аберрационного расчета
129. Волновая аберрация оптической системы

Источник

2017-01-22

На стеклянный клин перпендикулярно его грани падает узкий пучок света. Показатель преломления стекла $n = 1,41$, угол при вершине клина $alpha = 10^{ circ}$. Сколько освещенных пятен будет видно на экране, поставленном за клином на некотором расстоянии от него?

Решение:

На рис. показан ход лучей в клине после многократного отражения от его внутренних поверхностей. Как видно из рисунка, угол падения на вторую грань клина при первом попадании луча на нее равен $alpha$, при втором — $3 alpha$, при $n$-м $(2n – 1) alpha $. Лучи выходят из призмы, если угол падения на ее вторую грань меньше угла полного внутреннего отражения $alpha_{0}$, который находится из условия

$sin alpha_{0} = frac{1}{n}$.

Отсюда получаем $alpha_{0} approx 45^{ circ}$, a для углов падения на грань имеем:

$alpha_{1} = alpha = 10^{ circ}; alpha_{2} = 3 alpha = 30^{ circ}; alpha_{3} = 5 alpha = 50^{ circ}$.

Таким образом, уже $alpha_{3} > alpha_{0}$ т. е. уже третий луч испытает полное внутреннее отражение на второй грани клина. Итак, из призмы выйдут только два узких пучка света, которые и дадут два освещенных пятна на достаточно удаленном экране.

Ответ: два пятна.

Источник

§2. Тонкая линза

§3. Фокусные расстояния плоско-выпуклой линзы

Задача 52942 …

Условие

Решение

Написать комментарий

Вам также может понравиться

Как найти каналы на приставки мтс

System may be damaged or reduce its life cycle when overvoltage как исправить

Как составить e mail письмо

Добавить комментарий Отменить ответ