Отчет
ИТМО
Кафедра
физики
Группа
2870
Лабораторная
работа № 2
Определение
показателя преломления материала
плоско-выпуклой линзы.
Цель
работы – вычисление
показателя преломления материала линзы
по радиусу её кривизны и главному
фокусному расстоянию.
Главное фокусное расстояние линзы
связано с радиусами кривизны её
поверхностей зависимостью:
1/f = (n/n – 1)(1/R1
– 1/R2)
(1)
где – главное фокусное расстояние линзы;
n, n,
– показатели преломления материала
линзы и окружающей среды соответственно;
R1 и R2
– радиусы кривизны поверхностей линзы.
Кривизна одной из поверхностей
плоско-выпуклой линзы равна нулю, поэтому
формула (1) принимает более простой вид
1/f
= (n-1)1/R
Для показателя преломления материала
линзы получаем
n = 1+R/f
(2)
Линзу в данной работе считаем тонкой,
поэтому главное фокусное расстояние
будем отсчитывать от оптического центра
линзы.
Описание
лабораторной установки.
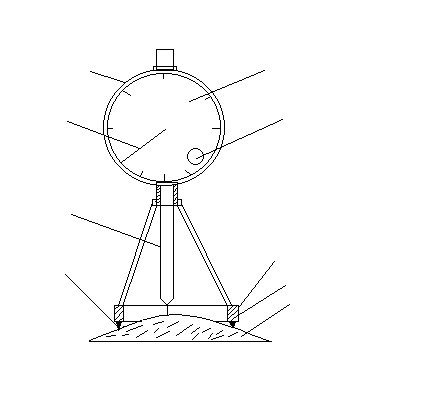
Для измерения радиуса кривизны линзы
R служит прибор, называемый
сферометром. Сферометр состоит из
опорного металлического кольца N
и укреплённой на нём измерительной
головки K. Три ножки Q1,
Q2 и Q3
(на рисунке не показана) сферометра
выполнены в виде металлических шариков,
впрессованных в опорное кольцо с нижней
стороны и расположенных в вершинах
правильного треугольника, центр которого
совпадает с центром опорного кольца.
Измерительная головка прибора снабжена
подвижным штоком S, который
может передвигаться через центр опорного
кольца перпендикулярно его плоскости.
При надавливании на нижний заострённый
конец штока снизу вверх шток поднимается,
вдвигаясь в головку. При снятии давления
шток возвращается в исходное положение,
благодаря пружине, находящейся внутри
головки. Высота поднятия штока определяется
с точностью до сотых долей миллиметра
по показаниям двух стрелок на головке.
Центральная стрелка C
указывает число сотых долей миллиметра,
а стрелка D, более короткая
и расположенная сбоку от центральной,
– число целых миллиметров. При полном
обороте центральной стрелки боковая
стрелка сдвигается на одно деление, что
соответствует смещению штока на 1 мм.
Шкала, по которой определяется положение
центральной стрелки, имеет цену деления
0,01мм. Эту шкалу можно поворачивать,
вращая внешнее кольцо M
с насечкой, охватывающее снаружи
измерительную головку.
С помощью сферометра определяют радиус
кривизны линзы, рассчитывая его по
формуле
R = a2/6h
+ h/2 (3)
где a – расстояние между
ножками сферометра; h –
высота шарового сегмента, отсекаемого
от линзы плоскостью, касательной к
ножкам сферометра.
Параметр a удобно
определять, измеряя миллиметровой
линейкой расстояния между центрами
отпечатков ножек сферометра, оставленных
ими на листе бумаги. По результатам трёх
(так как всего ножек – три) измерений
определяют среднее значение a
и погрешность a.
Главное фокусное расстояние линзы f
измеряется
при помощи зрительной трубы с
автоколлимацион-
ной настройкой на бесконечность.
Исследуемую
линзу L помещают на
оптическую скамью между
экраном P и трубкой B.
Расстояние от экрана до
линзы определяют по оптической скамье.
Порядок
выполнения работы.
-
Установить на сферометре начало отсчёта,
используя плоскую стеклянную пластину.
Для этого сферометр поставить на
пластину и, поворачивая наружное кольцо
с насечкой, совместить нулевую отметку
шкалы с центральной стрелкой. Затем
линзу вместе со штативом снять с рейтера
и положить на стол сфериметрической
поверхностью вверх, положив под неё
лист бумаги, чтобы не поцарапать стекло.
Сверху поставить сферометр и передвигать
его по поверхности линзы. Среднее
значение показаний прибора характеризует
величину h, а их разброс
– погрешность h. -
Измерить главное фокусное расстояние
линзы, предварительно настроив зрительную
трубу на бесконечность, приложив к
входному объективу зрительной трубы
плоское зеркало. Труба построит резкое
изображение перекрестия, которое
находится в окуляре, за счёт отражения
параллельных лучей от плоского зеркала,
что достигается вращением винта
настройки, расположенного на корпусе
трубы слева. В результате в поле зрения
окуляров будут видны два перекрестия.
Между трубой B и экраном
P установить на оптическую
скамью исследуемую линзу L.
Перемещать линзу до тех пор, пока в
трубу не будет видна стрелка на экране.
В этом случае экран будет находиться
в фокальной плоскости линзы. Так как
линза тонкая, то расстояние от неё до
экрана и будет равно главному фокусному
расстоянию. Данную операцию повторить
три-пять раз, каждый раз измеряя
расстояние от линзы до экрана, и
определить среднее значение f
и погрешность f . -
Измерив величины h, a,
f и определив погрешности
h, a, f
, по формулам (1), (2) вычислить показатель
преломления n и рассчитать
погрешность результата n
по формуле, которую следует вывести
заранее.
Вычисления:
h = (80+79.9+79.9+79.9)/4 = 79.925 мм
1/f = (n/n -1)(1/R1-1/R2)
n =
1+R/f
R = a2/6h
+ h/2
h = 32 мм , h = 0.1
мм
f1
= 88
f2
= 87.3
f3
= 86.9
f4
= 87.9
f =
87.525
R = a2/6h
+ h/2= (86.5)2/6*32
+ 32/2 = 54.97 мм
a = 86.5 мм
a = 86.5 мм
n =
1 + R/f = 1+54.97/87.525=1.62
ИЗМЕРЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
СТЕКЛА ЛИНЗЫ
С.И.Федорино
Оборудование: симметричная двояковыпуклая стеклянная линза;
штангенциркуль; линейка измерительная.
Задание
Измерьте показатель преломления стекла, из которого
изготовлена линза.
Метод выполнения
работы
Показатель преломления n
вещества, из которого изготовлена линза, можно определить из формулы:
,
( 1 )
где F — главное фокусное расстояние линзы; R1 и R2 — радиусы сферических поверхностей, образующих линзу; n —
показатель преломления вещества, из которого изготовлена линза. Если линза
симметричная относительно оптического центра и двояковыпуклая, то R1 = R2 = R, и, следовательно:
, (
2 )
откуда
.
( 3 )
Из формулы ( 3 ) видно, что для определения
показателя преломления n вещества линзы нужно измерить фокусное
расстояние F линзы и радиус R её сферических поверхностей.
Фокусное расстояние линзы можно измерить,
получив на экране изображение источника света и измерив расстояние d от
предмета до линзы и расстояния f от линзы до изображения. Из формулы линзы:
( 4 )
следует, что если источник света находится на достаточно большом
расстоянии от линзы ( d ® ¥ ), то:
F » f (
5 )
Радиус кривизны сферических поверхностей линзы можно рассчитать, проведя
измерения геометрических размеров линзы: её толщины Н, диаметра D и
толщины цилиндрического слоя h0 ( рис. 1 ). Для треугольника ОАВ имеем:
R2 = AB2 + OB2 = r2
+ (R – h)2.
Проведя
преобразования, получим:
,
( 6 )
где r = D/2, h = (H – h0)/2.
Следовательно, 
и
окончательно:
(
7 )
Н
 |
|||
 |
r
R
O B O
D R
 |
A
 |
h h0 h
Рис. 1
Порядок выполнения работы
1.
С помощью линзы получите
на экране (листе бумаги или стене) изображение предметов, находящихся за окном
классной комнаты. Измерьте расстояние f от линзы до получившегося изображения и
определите фокусное расстояние F линзы. Исходя из нескольких подобных
измерений вычислите среднее значение фокусного расстояния линзы FСР.
2.
Штангенциркулем измерьте
толщину линзы Н, толщину цилиндрического слоя h0 и диаметр линзы D.
3.
Рассчитайте радиус R
сферических поверхностей линзы по формуле ( 7 ).
4.
Измерения повторите не
менее пяти раз и рассчитайте среднее значение RСР.
5.
Подставив в формулу ( 3 )
найденные средние значения, определите показатель преломления вещества из
которого изготовлена линза.
6.
Результаты измерений и
расчётов занесите в отчётную таблицу:
|
№ п/п |
F, мм |
H, мм |
h0, мм |
D, мм |
R, мм |
n |
e, % |
|
среднее |
7.
Оцените границы
погрешностей измеренной величины по формуле:
( 8 )
Контрольные вопросы:
1.
При каких условиях можно
считать, что фокусное расстояние линзы F приблизительно равно расстоянию f от
линзы до изображения?
2.
Как можно измерить радиусы
кривизны сферических поверхностей линз?
3.
Получите формулу для
расчёта показателя преломления вещества плосковыпуклой линзы.
Формулу (6) можно положить в основу геометрической теории любых центрированных систем в параксиальных лучах. Применяя ее к первой преломляющей поверхности сложной системы, найдем положение изображения, возникающего от преломления на этой поверхности. Полученное изображение играет роль предмета для преломления на второй сферической поверхности. Положение второго промежуточного изображения, возникающего от преломления на второй сферической поверхности, можно найти с помощью той же формулы и т. д. Путем такого применения формулы (6) к каждой из преломляющих поверхностей можно найти положение окончательного изображения, даваемого всей системой.
В качестве примера рассмотрим центрированную систему, состоящую из двух сферических поверхностей, ограничивающих какой-либо прозрачный, хорошо преломляющий материал (стекло, кварц). Такая система представляет обычную линзу. Линза называется Тонкой, если ее толщина мала по сравнению с радиусами кривизны ограничивающих поверхностей. На рис. 3 для ясности линза изображена толстой, но в расчетах будем полагать, что точки О1 и О2 сливаются в точку О, которая носит название оптического центра линзы и от которой отсчитываются все расстояния.
Любой параксиальный луч, проходящий через О, практически не испытывает преломления, так как для этих лучей участки обеих поверхностей линзы можно считать параллельными, и лучи, проходя через них, не меняют направления, а лишь смещаются параллельно самим себе. Так как толщиной линзы мы пренебрегаем, то смещение это ничтожно мало и луч практически проходит без преломления, если с обеих сторон линзы находится одинаковая среда. Луч, проходящий через оптический центр, называется Осью линзы. Ось, проходящая через центры обеих поверхностей, называется Главной, остальные оси называются побочными.
Рис. 3
Преломление на первой сферической поверхности создало бы без второй поверхности в сплошном стекле с показателем преломления N изображение в точке С, расположенной на расстоянии ОС = А, так что
, (11)
Где А1 = ОS,
R1 — радиус кривизны первой поверхности линзы;
N1 — показатель преломления среды, в которой расположен предмет.
Для второй поверхности промежуточное изображение С будет служить предметом. Изображение такого предмета после преломления на второй поверхности, получаемое в точке S1, и будет окончательным изображением источника S, которое дает линза. Здесь опять применима формула (6), которая примет вид:
, (12)
Где R2 — радиус кривизны второй поверхности;
A2 = S1O;
N2 – показатель преломления среды, в которой находится изображение.
Складывая равенства (11) и (12), получим формулу тонкой линзы:
, (13)
Где (N2 – N)/R2 + (N – N1)/R1 — оптическая сила тонкой линзы, равная сумме оптических
Сил обеих преломляющих поверхностей.
Если справа и слева от линзы находится одна и та же среда с показателем преломления N0 ,т. е. n1 = N2 = N0, тогда формула (13) примет вид:
, (14)
Где (N – 1) — относительный показатель преломления. 
Общая формула линзы (13) справедлива для тонких линз любой формы (двояковыпуклых, двояковогнутых и т. д.) при любом расположении предмета и соответствующем расположении фокуса. Нужно только принять во внимание знаки A1, a2, R1, R2, считая их положительными, если они отложены вправо от линзы, по ходу луча, и отрицательными, если они отложены влево от линзы (против хода луча).
Если предмет удаляется от линзы (А1 возрастает по абсолютной величине), то изображение перемещается. Положение изображения, соответствующее предельному случаю, когда источник удален в бесконечность, носит название Фокуса линзы. Фокус линзы есть точка, сопряженная бесконечно удаленной точке главной оси, или – место схождения лучей, параллельных главной оптической оси. Расстояние от линзы до фокуса есть Фокусное расстояние тонкой линзы. Плоскость, проходящая через фокус перпендикулярно к главной оси, называется Фокальной плоскостью.
Для фокусных расстояний с использованием формулы (14) имеем следующие соотношения:
При a1 ® –¥:
; (15)
При a2 ® ¥:
. (16)
Если справа и слева от линзы находится одна и та же среда, то фокусные расстояния линзы равны по величине и противоположны по знаку, т. е. фокусы лежат по разные стороны от линзы.
Если по обе стороны линзы располагаются разные среды (
), то фокусные расстояния F1 и F2 , определяемые из формулы (13), разные и относятся между собой, как –N1/N2, т. е. F1/F2 = –N1/N2.
В зависимости от знака и величины R1 и R2, а также от знака (N – 1), величина F1 может быть положительной либо отрицательной, т. е. Фокус может быть Мнимым или Действительным. То же относится и к F2, причем нетрудно видеть, что если первый фокус мнимый, то и второй тоже будет мнимым и наоборот. Если фокусы действительны, т. е. параллельные лучи после преломления сходятся, то линза называется Собирательной или Положительной. При мнимых фокусах параллельные лучи после преломления в линзе становятся расходящимися. Поэтому такие линзы называются Рассеивающими или Отрицательными.
Если материал тонкой линзы преломляет сильнее, чем окружающая среда (N > N0, N – 1 > 0), то собирательными будут линзы утолщающиеся к середине (двояковыпуклые, плосковыпуклые, вогнуто-выпуклые). К рассеивающим линзам принадлежат Двояковогнутые, плосковогнутые, выпукло—Вогнутые, т. е. линзы утончающиеся к середине. Если материал тонкой линзы преломляет меньше, чем окружающая среда, то линзы меняются свойствами.
Вводя фокусное расстояние линзы, придадим формуле линзы вид:
. (17)
Легко видеть, что изменение величины А1 приводит к изменению а2 того же знака, т. е. изображение сдвигается вдоль оси в том же направлении, что и предмет. Исключение составляет лишь точка A1 = f1, при прохождении которой изображение переходит из A2 = +¥ в A2 = –¥. На рис. 4 показано построение изображений и перемещение их в зависимости от перемещения предмета для положительной (рис. 4А) и отрицательной (рис. 4Б) тонких линз, находящихся в воздухе. Для построения выбраны лучи, ход которых заранее известен. К таким лучам относятся:
1) луч, идущий параллельно оптической оси. В пространстве изображений ему соответствует сопряженный луч, идущий через задний фокус F2;
2) наклонный луч, проходящий через передний фокус F1. Сопряженный ему луч пойдет параллельно оптической оси.
На рис. 4 показано построение изображения для семи положений предмета, заданных расстоянием А1:
1) a1 > 2F; 2) a1 = 2F; 3) a1 > F; 4) a1 = f; 5) a1 < F; 6) A1 = 0;
7) предмет расположен за линзой;
8) предмет находится в переднем фокусе отрицательной линзы.
Рис. 4А
Предметы, расположенные справа от линзы, могут быть только мнимыми, так как они образуются мысленным продолжением падающих на линзу лучей. На рисунке эти предметы изображены штриховыми линиями.
Рис. 4Б
Идеальной оптической называют систему, в которой сохраняется гомоцентричность пучков и изображение оказывается строго геометрически подобно предмету. Каждой точке пространства объектов соответствует в идеальной системе точка пространства изображений. Эти точки носят название Сопряженных точек. Точно также каждой прямой или плоскости пространства объектов должна соответствовать сопряженная прямая или плоскость пространства изображений.
Изложенное раньше показывает, что идеальная оптическая система может быть осуществлена в виде центрированной оптической системы, если ограничиться параксиальными лучами. Как показывает теория, изображение предметов с помощью идеальной оптической системы может быть построено без детального исследования хода лучей внутри системы и требует только знания ряда так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства оптической системы.
Рис. 5
Линия, соединяющая центры сферических поверхностей, представляет собой ось симметрии центрированной системы и называется Главной оптической осью системы.
Пусть MM и NN — крайние поверхности, ограничивающие оптическую систему, а О1О2 — главная оптическая ось (рис. 5). Проведем луч А1В1 параллельный главной оптической оси. Этому лучу соответствует луч C2D2, выходящий из системы. Ход луча внутри оптической системы нас интересовать не будет. Точка F2 пересечения луча C2D2 с главной оптической осью является изображением бесконечно удаленной точки (это легко показать с помощью второго луча, распространяющегося вдоль главной оптической оси). Точку F2 называют задним фокусом системы (Фокусом в пространстве изображений). Плоскость, перпендикулярная к О1О2 и проходящая через F2, называется Фокальной плоскостью. Задний фокус оптической системы не всегда, конечно, лежит справа от нее, как это изображено на рис. 5. Так, в рассеивающих системах этот фокус может лежать и слева от всех поверхностей, входящих в состав системы.
Рассмотрим теперь луч А2В2, входящий в систему справа и лежащий на продолжении луча А1В1. Слева из системы выйдет луч C1D1, сопряженный лучу А2В2. Точку F1 называют передним фокусом системы (Фокусом в пространстве предметов). Исходящие из него лучи в пространстве изображений параллельны оптической оси. Продолжим теперь C1D1 и C2D2 до пересечения с продолжениями А1В1 и А2В2 и отметим точки пересечения R1 и R2. Легко видеть, что эти точки сопряжены, т. е. являются изображением друг друга. Действительно, точка R1 лежит на пересечении лучей А1В1 и С1D1, а точка R2 — на пересечении сопряженных лучей А2В2 и С2D2 (для большей наглядности направление одной пары сопряженных лучей, например, А2В2 и С1D1, можно изменить на противоположное, пользуясь обратимостью световых лучей). Из построения ясно, что точки R1 и R2 лежат на одинаковом расстоянии от главной оптической оси, т. е. R1H1 = R2H2 (линейное поперечное увеличение равно 
). Можно показать, что в идеальной системе все точки плоскости P1, перпендикулярной к главной оптической оси и проходящей через R1, попарно сопряжены точкам плоскости P2, также перпендикулярной к главной оптической оси и проходящей через R2. При этом сопряженные точки находятся на одинаковых расстояниях от оси (например, точки Q1 и Q2 на рис. 5).
Две сопряженные плоскости Р1 и Р2, отражающие друг друга с поперечным увеличением V = + 1, называются Главными плоскостями, а точки H1 и H2 — главными точками системы. Расстояния от главных точек до фокусов называются Фокусными расстояниями: f1 = H1F1; F2 = H2F2. В том случае, когда с обеих сторон системы находится одна и та же среда (например, воздух) 
.
Если известно положение фокусов и главных плоскостей, изображение предмета может быть найдено путем простых геометрических построений с использованием двух лучей, исходящих из одной точки. Рис. 6 иллюстрирует эти построения. Луч 1, проведенный параллельно главной оси, имеет в качестве сопряженного луч 1¢, пересекающий вторую главную плоскость на высоте H2D2 = H1D1 и проходящий через фокус F2. Луч 2, проходящий через фокус F1 и пересекающий главную плоскость на высоте Н1С1, пройдет на той же высоте (Н1С1 = Н2С2) через вторую главную плоскость и пойдет параллельно главной оси.
Оптическая система называется Положительной (Собирающей), если передний фокус F1, лежит левее главной плоскости Р1, а задний фокус F2 — правее главной плоскости Р2. Если же F1 располагается правее Р1, а F2 — левее Р2, система называется Отрицательной или Рассеивающей. Фокусному расстоянию систем приписывается определенный знак: плюс — для собирающих систем и минус — для рассеивающих. Если определить положение предмета и изображения по их расстояниям от соответствующих главных плоскостей, то легко установить соотношение между этими расстояниями (А1 и А2) и фокусным расстоянием системы, которое аналогично формуле (17).
Рис. 6
Положение предмета и его изображения можно определять относительно фокусов F1 И F2 (рис. 6). Обозначая эти расстояния соответственно через X1 и X2 и рассматривая две пары подобных треугольников А1В1F1 F1H1С1 и H2D2F2 F2A2B2, по определению линейного увеличения запишем
, (18)
.
Отсюда следует, что F1/X1 = X2/F2 или
. (19)
Из рис. 6 видно также, что
и .
С учетом последних соотношений формула (19) примет вид:
. (20)
Соотношения (18), (19), (20) наряду с (17), определяющие положение сопряженных точек в данной системе, играют роль формул системы.
Пользуясь правилом знаков, можно описать все свойства как собирательных, так и рассеивающих систем.
Следует подчеркнуть, что главные плоскости и главные точки могут лежать как внутри, так и вне системы и при этом могут располагаться как угодно несимметрично относительно поверхностей, ограничивающих оптическую систему.
Большой практический интерес представляет случай, когда размер системы в направлении главной оптической оси значительно меньше фокусного расстояния. В этом случае оптический луч, проходя внутри системы, мало смещается, так что точки С1 и В1, С2 и В2 (рис. 5) практически совпадают. Главные плоскости (и главные точки Н1,Н2) при этом совмещаются друг с другом и располагаются посредине системы. Такая оптическая система называется Тонкой линзой. Расстояния А1 и А2 и фокусные расстояния можно в этом случае приближенно отсчитывать от центра линзы.
Кроме линейного увеличения, систему можно характеризовать Угловым Увеличением W , понимая под W отношение тангенсов углов U2 и U1, составляемых сопряженными лучами А2M2 и A1M1 С оптической осью (рис. 7), т. е. W = tg U2/tg U1
Из рис. 7 видно, что W = A1/A2 (ибо H1M1 = H2M2), тогда как линейное увеличение V = N1A2/N2A1 (см. раздел 2), т. е.
. (21)
Если предмет и изображение расположены в одной среде (N1 = N2), то W×V = 1.
Как угловое, так и линейное увеличение системы различно для разных точек оси, причем чем больше линейное увеличение, тем меньше угловое.
Сопряженные точки, в которых угловое увеличение системы W = 1, представляют собой особенные точки системы. Эти точки называются Узлами (или Узловыми точками) и характеризуются тем, что сопряженные лучи, проходящие через узлы, параллельны друг другу, ибо U1 = U2.
В каждой системе такой парой точек будут точки N1 и N2, отстоящие от первого и второго фокусов соответственно на расстояния равные X1 = F1×N1 = F2 и X2 = F2×N2 = F1.
Координаты этих точек удовлетворяют уравнению системы (19), т. е. они являются Сопряженными.
Их расстояния относительно главных плоскостей равны соответственно H1N1 = A1¢ = F1 – F2 И H2N2 = A2¢ = F1 – F2 , следовательно, для этих точек угловое увеличение равно 1, т. е. они служат узловыми точками системы.
Плоскости, проходящие через узлы перпендикулярно к оптической оси, называются Узловыми плоскостями. Шесть плоскостей (Две фокальные, две главные и две узловые) и шесть точек главной оси, им соответствующие (Фокусы, главные точки, узлы), называются кардинальными плоскостями и Точками.
Зная свойства кардинальных плоскостей и точек, можно построить изображение предмета в любой системе. На рис. 6 показано, как можно построить изображение, если дано расположение ее главных плоскостей и фокусов.
Рис. 7
На рис. 7 используется еще один луч (луч 3), идущий через узел N1. Ему сопряженный луч 3¢ проходит через узел N2 И параллелен лучу 3.
Для построения изображения предмета можно ограничиться двумя лучами из трех.
Когда по обе стороны системы располагается одна и та же среда, то фокусные расстояния F1 и F2 Равны по абсолютной величине. Узловые точки в этом случае сливаются с главными.
Тонкая линза может рассматриваться как частный случай толстой линзы, в которой точки Н1 и Н2 совпадают, и главные плоскости сливаются. Узловые точки, совмещенные с Н1 и Н2, также совпадут, образуя оптический центр линзы.
В настоящей работе измеряются фокусные расстояния тонких положительных и отрицательных линз, а также определяется фокусное расстояние и положение главных плоскостей сложной оптической системы. Измерения выполняются на оптической скамье, вдоль которой могут перемещаться рейтера с линзами, экранами, масштабами и т. д. Перед началом измерений центры всех линз нужно установить на одной высоте и проследить за тем, чтобы оптические оси линз были параллельны ребру оптической скамьи. Легко убедиться на опыте, что при слабых линзах и небольших увеличениях, которые применяются в данной работе, такая установка может быть произведена на глаз. При измерениях расстояния между деталями оптической системы отсчитываются по линейке, расположенной вдоль оптической скамьи. Отсчет производится по указателям, расположенным на основаниях рейтеров. Наводка изображения на резкость производится на глаз. Чтобы уменьшить роль возникающих при этом неточностей, измерения в каждом случае рекомендуется выполнять несколько раз, а результаты — усреднять.
Применяемые в работе линзы обладают заметной хроматической аберрацией (зависимость фокусного расстояния от длины световой волны). Точность измерений существенно повышается при работе со светофильтром.
