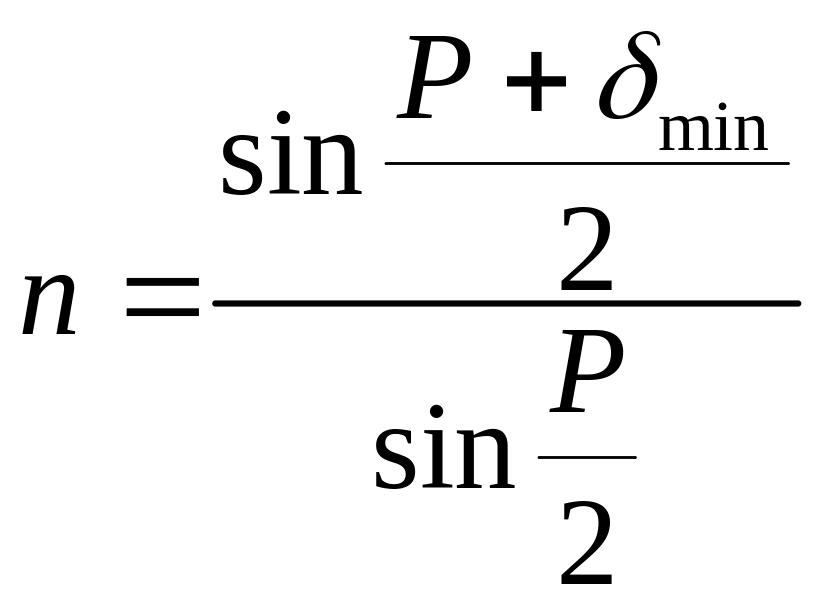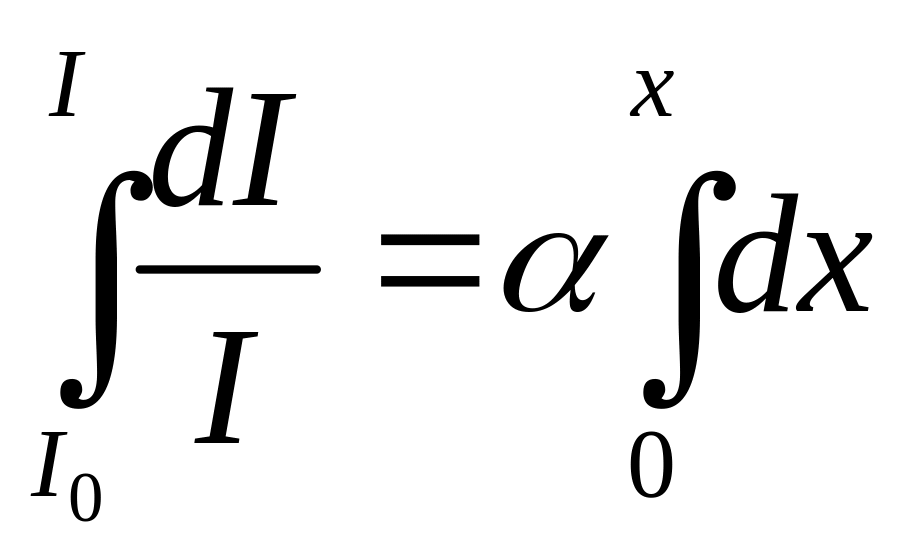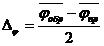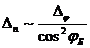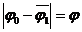Показатель – преломление – материал – призма
Cтраница 1
Показатель преломления материала призмы удобно определять по углу наименьшего отклонения.
[1]
Показатель преломления материала призмы удобно определять по углу наименьшего отклонения. Как известно, минимальное отклонение света получается при симметричном ходе лучей в призме.
[2]
Поскольку показатель преломления материала призмы зависит от длины волны А, угол отклонения 6 будет различным для разных Я, что приводит к пространственному разделению излучений по X.
[4]
Значения показателей преломления материалов призм зависят от температуры; вследствие этого градуировка спектрометров может изменяться с температурой. В конструкциях современных отечественных приборов предусмотрена температурная компенсация смещения градуировки. Как показывает сравнение расчета с опытом, применяемый способ компенсации является вполне удовлетворительным в пределах изменения температуры на 3 С; в этом интервале относительное смещение не превышает собственной погрешности прибора.
[5]
Поскольку значения показателей преломления материалов призм зависят от температуры, то при ее изменении в процессе работы, происходящем главным образом из-за поглощения излучения от источника света внутри прибора, положение полос поглощения может изменяться.
[7]
Благодаря тому, что показатель преломления материала призмы больше показателя преломления контролируемой жидкости, для которой предназначен прибор, всегда можно обеспечить полное внутреннее отражение луча в измерительной призме изменением угла падения входного светового луча.
[8]
Призменные спектральные приборы, в которых используется зависимость показателя преломления материала призмы от длины волны. Эти приборы до последнего времени составляли основную массу спектральных приборов, однако они вытесняются приборами с дифракционными решетками. К недостаткам призменных приборов относится также их относительно невысокая разрешающая способность.
[9]
На рис. 77 представлена схема, поясняющая метод определения показателя преломления материала призмы, преломляющий угол которой известен. Авто коллимационным путем ось трубы устанавливают перпендикулярно к выходной грани призмы и, скрепив столик с трубой, вращают их до тех пор, пока перекрестие трубы не совместится с изображением щели коллиматора. При этом снимают отсчет. Второй отсчет снимают при непосредственной наводке трубы на щель.
[11]
На рис. 11.27 представлена схема, поясняющая метод определения показателя преломления материала призмы, преломляющий угол которой известен. Автоколлимационным путем ось трубы устанавливают перпендикулярно к выходной грани призмы и, скрепив столик с трубой, вращают их до тех пор, пока не совместят перекрестие трубы с изображением щели коллиматора. При этом снимают отсчет.
[13]
Для того чтобы призма диспергировала излучение и возникал спектр, показатель преломления материала призмы должен изменяться с длиной волны. Чем быстрее это происходит, тем выше дисперсия. Так как это условие выполняется вблизи полос поглощения, то наилучшую дисперсию призма имеет как раз на границе пропускания.
[14]
Для того чтобы призма диспергировала излучение и возникал спектр, показатель преломления материала призмы должен изменяться с длиной волны. Чем быстрее это происходит, тем выше дисперсия. Так как это условие выполняется вблизи полос поглощения, то наилучшую дисперсию призма имеет как раз на границе пропускания.
[15]
Страницы:
1
2
3
Показатель преломления призмы.
Если
луч света переходит из одной среды в
другую, то на границе радела этих сред
он претерпевает преломление. При
преломлении
света выполняются следующие законы:
1. Падающий
и преломленный лучи, и перпендикуляр,
восстановленный
к границе раздела двух сред в точке
падения луча, лежат в одной
плоскости.
2
.
Отношение синуса угла падения к синусу
угла преломления для данных
двух сред есть величина постоянная, и
называется относительным
показателем преломления второй среды
относительно первой (рис.4).
(7)
Если
луч падает из вакуума в данную
среду, то показатель преломления
данной среды относительно
вакуума называется абсолютным
показателем преломления.
Показатель преломления зависит
от длины волны падающего света.
Законы
преломления света дают возможность
построить ход луча через
призму.
Пусть
ABC
есть сечение трехгранной призмы
плоскостью, перпендикулярной
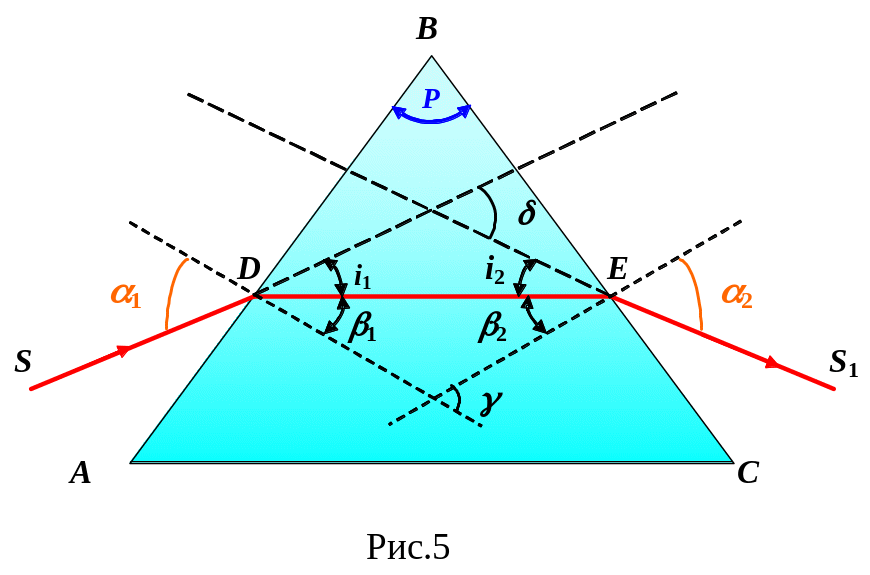
к обеим преломляющим поверхностям (рис.
5). На рис. 5 изображен ход монохроматического
луча через призму. Для этого луча угол
Р
является преломляющим углом призмы.
Луч S
падает на грань АВ
призмы под углом α1.
В точке D
он преломляется в сторону
основания АС
и пойдет внутри призмы по направление
DE,
образуя угол преломления β1.
В
стретив
грань ВС
под углом падения β2,
луч вторично преломится в сторону
основания и выйдет из призмы под углом
преломления
α2
в направлении ES1.
Угол между
направлениями падающего и выходящего
лучей называется углом отклонения δ.
Из построения видно, что:
|
; ; ; |
(8) |
Из соотношения
(8) для угла δ
имеем
|
|
(9) |
Величина угла
отклонения δ
зависит от преломляющего угла призмы
Р
и показателя преломления призмы.
При заданном угле
преломления Р
и показателя преломления n
угол
δ
зависит от угла падения α1
на первую преломляющую
грань.
Если угол падения α1
таков, что преломляющийся луч DE
проходит
внутри призмы перпендикулярно биссектрисе
преломляющего угла
Р,
то угол δ
будет
иметь наименьшее значение. При AB
= BC
луч
DE
проходит через призму параллельно
основанию AC
призмы.
Тогда,
очевидно, α1
=
α2
и β1
=
β2.
Следовательно, из (9) для угла δ
имеем:
|
|
(10) |
а
преломляющий угол Р
из соотношения (8) будет равен:
|
|
(11) |
Если
значение α1
из (10) и β1
из (11) подставить в формулу (7), выражающую
закон преломления, то окончательно
будем иметь:
|
|
(12) |
Формула
(12) является расчетной. Она дает возможность
определить показатель
преломления n
призмы, зная величину преломляющего
угла
Р
(угол Р
обычно равен 450
либо 60°) и измерив с помощью гониометра
наименьший угол отклонения луча
для
любого из семи
основных цветов в сплошном спектре.
Поглощение света.
При прохождении
электромагнитной волны (света) через
вещество
часть энергии волны затрачивается на
возбуждение колебаний электронов,
находящихся внутри атомов вещества.
Частично эта энергия вновь возвращается
излучения в виде вторичных волн,
возбуждаемых электронами; частично же
она переходит в другие виды энергии
(например, во внутреннюю энергию
вещества). Таким образом, интенсивность
света при прохождении через вещество
уменьшается –
свет поглощается
в веществе. Вынужденные колебания
электронов, а, следовательно,
и поглощение света, становятся особенно
интенсивными при
резонансной частоте.
Пусть
через однородное вещество распространяется
пучок параллельных
лучей (рис. 6).
Выделим
в этом веществе бесконечно тонкий слой
толщины dx,
ограниченный
параллельными поверхностями,
перпендикулярными к направлению
распространения света. Опыт показывает,
что изменение интенсивности
света на пути dx
пропорционально величине этого пути
и величине самой интенсивности:
|
|
(13) |
где α
–
коэффициент поглощения, зависящий от
рода вещества.
Пусть
на входе в поглощающий слой (на границе
или в каком-то месте
внутри вещества) интенсивность света
равна I0.
Найдем интенсивность
света I,
прошедшего слой вещества толщины х.
Для этого
проинтегрируем выражение (13), предварительно
разделив переменные:
|
|
Взяв интегралы,
получим:
|
|
откуда
|
|
(14) |
Выражение (14)
называется законом Бугера. Согласно
этому закону интенсивность
света убывает в поглощающем веществе
экспоненциально.
При
интенсивность
оказывается в «
»
раз
меньше,
чем
.
Таким образом, коэффициент поглощения
есть величина, обратная толщине слоя,
при прохождении которого интенсивность
света убывает в «
»
раз.
Коэффициент поглощения зависит от рода
вещества и длины волны (частоты) света.
Так как длина волны
(частота)
определяет цвет света, следовательно,
лучи различных цветов
поглощаются данным веществом по-разному.
Например, оконное стекло
хорошо пропускает видимый свет и почти
полностью поглощает ультрафиолетовые
лучи. Для газов при низком давлении
коэффициент поглощения
для большинства длин волн близок к нулю,
металлы практически
непрозрачны для света.
Как
уже отмечалось, коэффициент поглощения
α
зависит от длины волны λ.
Поэтому выражение (14) можно записать в
виде:
|
|
(15) |
При поглощении
света веществами, растворенными в
практически не поглощающем растворителе
(например, в чистой воде), коэффициент
поглощения пропорционален концентрации
растворенного вещества c.
|
αλ |
(16) |
где
α1λ
коэффициент пропорциональности, также
зависящий от длины волны λ.
Соотношение (16) называют законом Бера.
Для таких растворов закон Бугера
примет вид:
|
|
(17) |
Преобразуем
выражение (17)
|
или |
Переходя к десятичным логарифмам, имеем:
|
|
(18) |
Величина
называется оптической плотностью
раствора. Введя оптическую плотность,
соотношение (18) можно записать:
откуда
,
где
.
Оптическая
плотность D
пропорциональна концентрации раствора
«с»
и
толщине слоя вещества x,
через
который проходит
свет. Коэффициент пропорциональности
ε,
зависящий
от длины
волны λ
и природы растворенного вещества,
называется молекулярной
оптической плотностью (молекулярной
экстинкцией).
Отношение
называется прозрачностью или
светопропуcканием
раствора.
Между
оптической плотностью и светопропусканием
имеется следующая зависимость:
|
|
Следует
отметить, что ослабление света может
происходить за счет
рассеяния световой энергии в стороны
также по экспоненциальному
закону. Однако, в случае прозрачных тел,
рассеянием можно пренебречь.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свет, испускаемый одним элементарным излучателем (атомом, молекулой) в каждом акте излучения всегда поляризован. Но макроскопические источники света состоят из огромного числа таких частиц, которые излучают свет независимо друг от друга, и направления электрических векторов Е при элементарных актах излучения имеют случайный характер. Поэтому направление результирующего вектора Е во времени меняется хаотически. Подобное излучение называют неполяризованным или естественным светом.
Электромагнитное излучение, у которого направление вектора Е остается неизменным, называется плоскополяризованным (или линейно-поляризованным). Частично поляризованный свет – это свет, в котором имеется преимущественное направление вектора Е. Например, лазерное излучение, как правило, является поляризованным, в то время как тепловое излучение почти всегда неполяризовано.
Состояние поляризации света может измениться при отражении, преломлении и при прохождении света через анизотропные вещества. Поляризованный свет можно получить из естественного с помощью специальных приборов, называемых поляризаторами.
Человеческий глаз не способен отличать поляризованный свет от неполяризованного, поэтому для анализа поляризации исследуемое излучение пропускают через поляризатор.
Если направить пучок естественного света на границу раздела двух диэлектриков, то часть света отразится, а часть, преломляясь, будет распространяться во второй среде. В общем случае отраженный и преломленный лучи частично поляризованы. При некотором строго определенном для данной пары сред значении угла падения отраженный от границы раздела свет оказывается полностью поляризованным. Такой угол падения jБ называется углом Брюстера и определяется выражением, называемым законом Брюстера
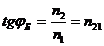
где n1 и n2 – показатели преломления первой и второй среды, соответственно, а n12 – относительный показатель преломления.
Причина этого явления в следующем. Известно, что луч, падающий на границу двух сред возбуждает движение зарядов, которое, в свою очередь, генерирует преломленный и отраженный лучи. Оказывается, что в случае, если отраженный и преломленный лучи образуют прямой угол, а падающий луч поляризован в плоскости падения (плоскость, в которой лежат падающий, преломленный или отраженный лучи и перпендикуляр, восстановленный в точку падения), то отраженного луча не будет совсем. Но в данной лабораторной работе можно пронаблюдать только уменьшение интенсивности отраженного луча, т. к. падающий свет не строго поляризован.
Закон Брюстера лежит в основе метода определения показателя преломления одной из сред, если известен показатель преломления второй.
Относительный показатель преломления n12 можно определить еще одним способом. Согласно закону преломления света (закон Снеллиуса)
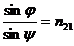
где j — угол падения, а y — угол преломления (рис.1а). Отсюда следует, что при переходе света из оптически более плотной среды (с большим n) в менее плотную, преломленный луч удаляется от нормали к поверхности раздела (рис.1а), т. е. угол преломления становится больше угла падения.

С увеличением угла падения соответственно увеличивается и угол преломления, поэтому при некотором строго определенном для данных сред угле падения jпред, угол преломления станет равным 90° (рис.1б). Если же луч падает под углами (рис.1в), большими предельного jпред, то происходит полное отражение света от границы раздела.:
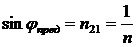
где n – показатель преломления оптически более плотной среды, а показатель преломления менее плотной среды (воздуха) приближенно равен 1.
Имеется случай, когда закон Снеллиуса не выполняется. В лабораторной работе №7 (где рассмотрен закон Малюса), излагается понятие обыкновенного и необыкновенного лучей света в одно- и двуосных кристаллах (кристаллы турмалина). Необыкновенный луч не подчиняется закону Снеллиуса, в то время как обыкновенный луч подчиняется ему.
Поляризованный свет имеет важные аналитические применения. В поляризованном свете в материалах становятся видимыми деформации. Например, линии деформации в стекле можно сделать видимыми если поместить стекло между двумя поляризованными фильтрами.
Описание установки
1. При определении показателя преломления стеклянной призмы с помощью закона Брюстера используется установка, схема которой приведена на рис.2.
Свет лазера 1 падает на грань АС призмы 4. Призма может вращаться на столике 5 вокруг вертикальной оси. В эксперименте угол Брюстера определяется по полному света, отраженного от поверхности АС призмы. Его можно наблюдать на экране 3. Величины углов, необходимых для расчетов, измеряются по шкале поворотного столика (5)

2. Для определения показателя преломления при полном внутреннем отражении призму (4) необходимо установить так, как показано на рис. 3. при этом свет падает на грань призмы ВС и испытывает полное внутреннее отражение на грани АС. Тогда для вычисления показателя преломления материала призмы можно воспользоваться законом преломления (2) применительно к грани ВС и формулой (3) для полного внутреннего отражения на грани АС. Из рис. 3. очевидно, что jпред = 45° — y. Решая совместно эти уравнения, получаем
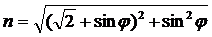
где j — угол падения света на грань ВС призмы 5.
Изменяя угол падения лазерного пучка на эту грань можно определить угол полного внутреннего отражения по появлению прошедшего через грань АС света на экране 3.
Порядок выполнения работы.
Упражнение 1. Определение показателя преломления материала призмы n с помощью закона Брюстера.
1. Установить большую грань призмы АС перпендикулярно лазерному лучу (нормальность падения проверяется по отраженному лучу на экране 4 (рис.2)). Записать значение угла j0 по шкале, соответствующее этому положению.
2. Поворачивая столик против часовой стрелки, добиться максимального гашения отраженного луча. Определить по шкале угол jпр . Поворачивать столик в том же направлении наблюдая усиление отраженного луча. Далее, вращая призму в обратном направлении, снова добиться гашения отраженного луча и определить угол jобр по шкале. Повторить эту процедуру 3-5 раз, занося результаты измерений в таблицу.
|
№ опыта |
j0 |
jпр |
jобр |
|
|
|
1 |
|||||
|
2 |
|||||
|
3 |
|||||
|
4 |
|||||
|
5 |
|||||
|
Среднее |
3. Вычислить среднее значение угла j в прямом и обратном направлении jпр и jобр . Вычислить среднее значение угла Брюстера:
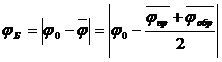
и среднеарифметическое отклонение Dj в радианной мере:
4. Вычислить показатель преломления стекла по формуле (1).
5. Оценить погрешность измерения по формуле
Упражнение 2. Определение n с помощью полного внутреннего отражения.
1. Установить малую грань ВС призмы перпендикулярно лазерному лучу. Записать значение угла j0 по шкале. Пронаблюдать полное отражение луча от грани АС.
2. Повернуть столик так, чтобы на экране появился прошедший через грань АС луч. Определить угол j1, соответствующий появлению прошедшего луча. Провести измерения угла j1 3–5 раз. Данные занести в таблицу. Определить среднее значение .
3. Определить угол поворота призмы, который является углом падения на малую грань ВС при полном внутреннем отражении:
Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.
Геометрическая оптика: призмы
В этой статье решаем задачи с призмами. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1.
Монохроматический луч падает нормально на боковую поверхность призмы, преломляющий угол которой равен . Показатель преломления материала призмы для этого луча равен 1,5. Найдите угол отклонения луча, выходящего из призмы, от первоначального направления.
Так как луч падает нормально на поверхность призмы, то не преломляется на этой поверхности. На вторую же боковую грань он упадет под некоторым углом, и преломится на ней.
К задаче 1
В треугольнике (прямоугольном) угол
по условию, поэтому второй острый угол равен
. Поэтому угол падения луча на вторую грань равен
. Зная показатель преломления, можно найти угол преломления. Нужный нам угол – разность угла преломления и угла падения луча.
По закону преломления
Ответ: .
Задача 2. Луч света входит в стеклянную призму под углом и выходит из призмы в воздух под углом
, причем, пройдя призму, отклоняется от первоначального направления на угол
. Найдите преломляющий угол призмы.
К задаче 2
Рассмотрим рисунок. Угол , смежный с данным углом отклонения луча, равен
. В четырехугольнике
угол
равен
, как вертикальный с углом падения, а угол
равен
как вертикальный с углом преломления. Так как сумма углов четырехугольника равна
, то угол
равен:
Теперь рассмотрим четырехугольник . В нем два угла прямых, поэтому преломляющий угол призмы равен:
Ответ: .
Задача 3.
Световой луч падает по нормали на боковую грань прямой стеклянной призмы, поперечное сечение которой – равнобедренный треугольник, . Показатель преломления материала призмы для этого луча равен 1,5. Определите угол между падающим и вышедшим из призмы лучами.
Рассмотрим два случая падения луча.
К задаче 3
В первом случае ход луча показан рыжим цветом. На боковой грани призмы луч не преломится, так как падает на нее нормально. Найдем угол падения луча на нижнюю поверхность призмы. Угол призмы равен
– так как треугольник равнобедренный. Тогда в треугольнике
угол
. А угол падения луча
равен
. Для данного показателя преломления предельный угол полного отражения равен
То есть луч не преломится, а отразится от нижней грани призмы. Угол отражения также равен , и, следовательно, угол
. Следовательно, треугольник
подобен
и тоже является прямоугольным. Следовательно, на второй боковой грани призмы луч тоже не преломится, и выйдет под углом
по отношению к падающему (угол
, искомый – смежный с ним).
Ответ: .
Теперь рассмотрим второй случай падения луча.
К задаче 3
Снова на первой боковой грани не произойдет преломления. На вторую боковую грань луч упадет под углом , что тоже превышает предельный угол полного отражения, и далее луч попадет на нижнюю грань призмы, падая на нее под углом
. В треугольнике
угол
, угол
. Определим угол
:
Определим угол :
Определим угол отклонения луча: в треугольнике угол
, угол
, следовательно, искомый угол
Ответ: .
Задача 4.
Тонкий световой луч падает на боковую грань стеклянной призмы из воздуха под углом . Угол между боковыми гранями призмы равен
. Показатель преломления воздуха равен 1, а стекла 1,41. Определите угол смещения луча от первоначального направления
.
К задаче 4
Определим угол преломления .
Рассмотрим четырехугольник . В нем два угла – прямые, преломляющий угол призмы –
, тогда угол
(это следует из суммы углов четырехугольника). Следовательно, из суммы углов треугольника можем определить угол
в одноименном треугольнике:
Найденный нами угол – не что иное, как угол падения луча на вторую грань призмы. Тогда данный луч выйдет из призмы, не преломившись, так как падает перпендикулярно границе раздела.
Тогда искомый угол – угол – равен разности угла
и угла преломления
, то есть
.
Ответ: .
Показатель преломления материала — нелинейная величина, зависящая от длины волны падающего излучения. Эта зависимость может быть ключевым свойством материала при изготовлении простейших спектроскопических приборов (к примеру — призм). В то же время зависимость показателя преломления от длины волны бывает губительна в других оптических приборах, в частности там, где важна точная фокусировка лучей. В последнее время появляется всё больше новых материалов и веществ, оптические свойства которых необходимо исследовать. В этой задаче мы попробуем определить зависимость показателя преломления неизвестной жидкости от длины волны, используя жидкость, для которой эта зависимость уже известна.
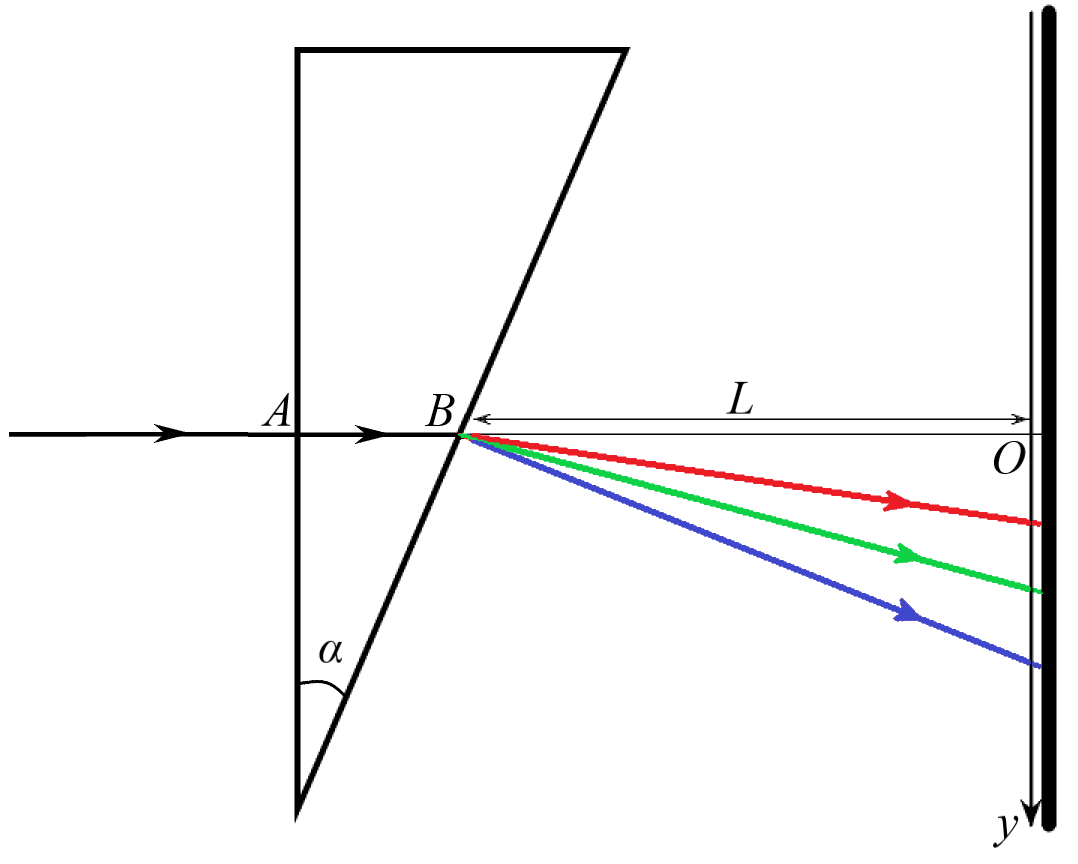
Схема измерений представлена на рисунке ниже. На воздушную призму с тонкими стенками с углом $alpha=30^{circ}$ при вершине, погружённую в исследуемую жидкость, падает тонкий луч источника. Луч падает на одну из граней призмы перпендикулярно в точке $A$ и затем выходит из призмы в точке $B$. Из-за зависимости показателя преломления от длины волны углы, под которыми лучи разной длины волны выйдут из призмы, будут различаться. На расстоянии $L$ от точки $B$ находится экран, перпендикулярный $AO$. Для удобства дальнейшей работы введём безразмерную величину $x=frac yL$. На экране размещено множество светочувствительных элементов, которые измеряют интенсивность $mathcal J_x(x)$ (мощность, падающую на единицу площади поверхности в единицу времени) в точках, в которых они расположены.
Часть А. Спектральные свойства источника (3.77 балла).
Обычный источник света (такой как настольная лампа) характеризуется тем, что излучает свет не одной длины волны (как это делает лазер), а длин волн сразу в некотором диапазоне. Чтобы охарактеризовать его излучение, введём понятие спектральной плотности $mathcal J_lambda(lambda)$. Мы определяем её так, чтобы мощность, излучаемая источником в диапазоне длин волн от $lambda$ до $lambda+Deltalambda$, равнялась $mathcal J_lambda(lambda)Deltalambda$, где $Deltalambda$ — малая величина. В этой части задачи мы исследуем спектральную плотность источника.
Выясним сначала, в какую точку $x$ на экране должен попадать луч, проходящий через призму, в зависимости от показателя преломления жидкости. Применив закон Снеллиуса для лучей получим следующую формулу для зависимости $x$ от $n$:[x=operatorname{tg}alphafrac{sqrt{n^2-sin^2alpha}-cosalpha}{sqrt{n^2-sin^2alpha}+sinalphaoperatorname{tg}alpha}.tag{1}]Чтобы по известному значению $x$ восстановить значение $n$, формулу (1) необходимо “обратить”. В результате несложных вычислений получим:[n=frac{sqrt{1+x^2}}{1-xoperatorname{ctg}alpha}.tag{2}]Показатель преломления большинства прозрачных материалов в видимом диапазоне можно приближённо описать формулой:[n(lambda)=A+frac B{lambda^2},tag{3}]где $A$ и $B$ — некоторые постоянные.
Сначала измерения проводят в известной жидкости, для которой эти постоянные равны $A=1.14$ и $B=8.6cdot10^4 нм^{2}$. В таблице в листе ответов приведены значения интенсивности $mathcal J_x$ в условных единицах в точках с координатой $x$.
A1
0.41
Для каждого $x$ найдите $n$.
A2
0.82
Для каждого $x$ найдите $lambda$.
Чтобы получить формулу для спектральной плотности $mathcal J_lambda$, необходимо провести более сложные расчёты. Ограничимся здесь лишь итоговой формулой для спектральной плотности:[mathcal J_lambda=frac{2Bsqrt{1+x^2}}{lambda^3}frac{(1-xoperatorname{ctg}alpha)^2}{x+operatorname{ctg}alpha}mathcal J_x.tag{4}]
A3
0.82
Для каждого $x$ найдите $mathcal J_lambda$ (в условных единицах на нм). Поскольку для каждого $x$ мы уже вычислили $lambda$, мы получили зависимость $mathcal J_lambda(lambda)$.
A4
0.49
Постройте график $mathcal J_lambda(lambda)$.
В дальнейшем нам также понадобится посчитать, какая доля мощности источника излучается на длинах волн, меньших некоторого значения $lambda$. Обозначим эту величину как $sigma(lambda)$. Для её нахождения надо посчитать площадь под графиком $mathcal J_x$. Это мы будем делать методом трапеций.
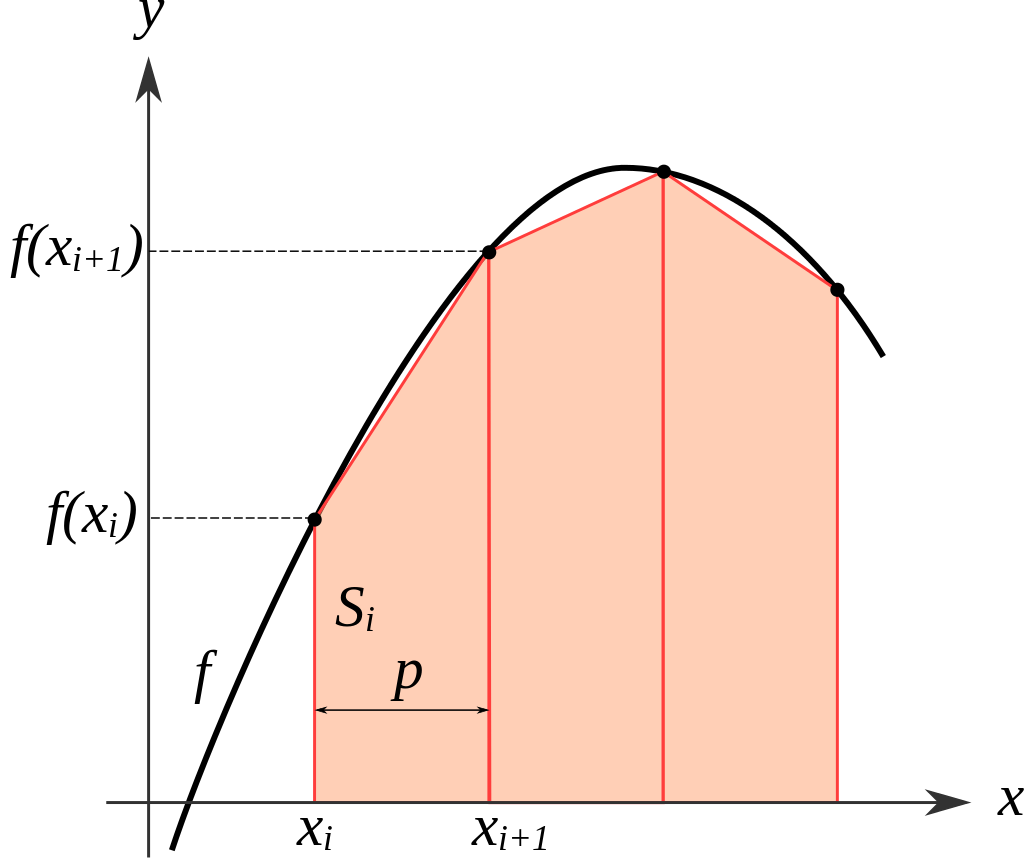
Пусть нам известны значения $f_i$ функции $f(x)$ в точках $x_i$. Тогда площадь под графиком этой функции можно оценить как сумму площадей трапеций, построенных, как показано на рисунке ниже.
Поскольку в нашем случае точки $x_i$ расположены через равные интервалы, формула для итоговой площади $S_k$ под графиком между точками $x_0$ и $x_k$ имеет вид:[S_kapproxleft(frac{f_0+f_k}2+sum_{i=1}^{k-1}f_iright)Delta x,tag{5}]где $Delta x=x_{i+1}-x_i$ — расстояние между соседними точками.
A6
1.23
Найдите для каждого $x$ значение $sigma$. Поскольку для каждого $x$ мы нашли $lambda$, мы получили также зависимость $lambda(sigma)$.
Часть B. Зависимость показателя преломления от длины волны (6.23 балла).
Теперь жидкость, в которую погружена призма, заменим на неизвестную, зависимость показателя которой от длины волны мы хотим найти. Схема эксперимента остаётся той же. В таблице в листе ответов приведены значения интенсивности $mathcal J_x$ в условных единицах в точках с координатой $x$.
B1
0.41
Для каждого $x$ найдите $n$.
B2
1.23
Найдите для каждого $x$ значение $sigma$.
В прошлой части задачи мы получили зависимость $sigma(lambda)$, которая теперь позволит нам восстановить $n(lambda)$ для неизвестной жидкости. Однако значения $sigma$, полученные в предыдущей части, не совпадают со значениями, полученными здесь. Чтобы узнать, каким значениям $lambda$ соответствуют полученные в предыдущем пункте $sigma$, прибегнем к т.н. линейной интерполяции зависимости $lambda(sigma)$.
Суть линейной интерполяции состоит в следующем. Пусть нам известны значения $lambda_1$ и $lambda_2$ функции $lambda(sigma)$ в точках $sigma_1$ и $sigma_2$ соответственно. Если эти точки находятся достаточно близко друг к другу, то с хорошей точностью можно приблизить функцию между этими двумя точками участком прямой. Это позволяет нам приближённо восстановить значения функции для $sigma_1 < sigma < sigma_2$.
Выведем формулу, определяющую $lambda(sigma)$. Поскольку функцию мы приближаем линейной, то искомую зависимость можно записать в виде:[lambda=asigma+b.tag{6}]Для нахождения $a$ и $b$ заметим, что эта прямая должна проходить через точки $(sigma_1,lambda_1)$ и $(sigma_2,lambda_2)$. Подставляя их в уравнение (6), получим систему уравнений:[begin{cases}lambda_1=asigma_1+b,\lambda_2=asigma_2+b.end{cases}tag{7}]Решая эту систему, получим окончательно:[lambda=frac{lambda_2-lambda_1}{sigma_2-sigma_1}sigma+frac{lambda_1sigma_2-lambda_2sigma_1}{sigma_2-sigma_1}.tag{8}]
B3
4.10
С помощью линейной интерполяции найдите, каким значениям $lambda$ соответствуют полученные значения $sigma$. Поскольку $n$ были вычислены в $bf B1$, мы получаем искомую зависимость $n(lambda)$.
B4
0.49
Постройте график $n(lambda)$ в удобном масштабе (кривая должна занимать большую часть графика по обеим осям, оси не обязательно должны начинаться с нуля).