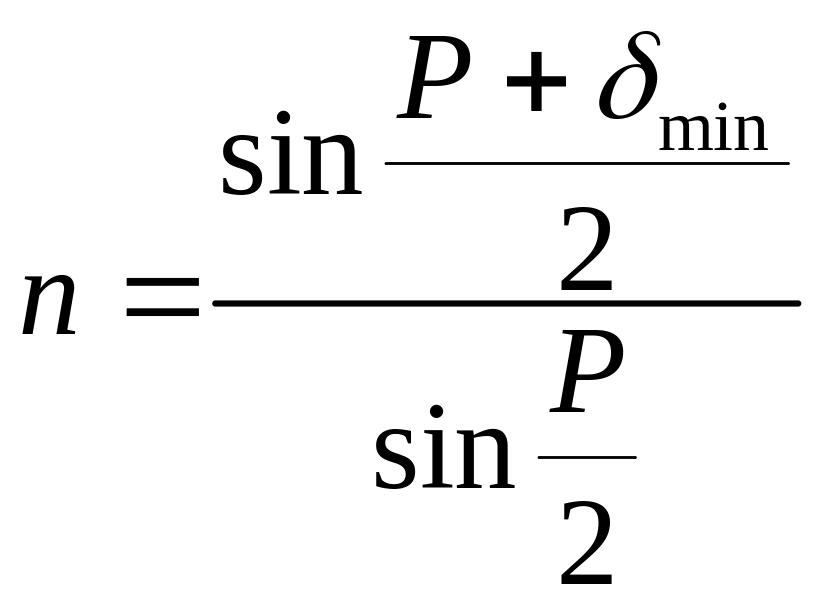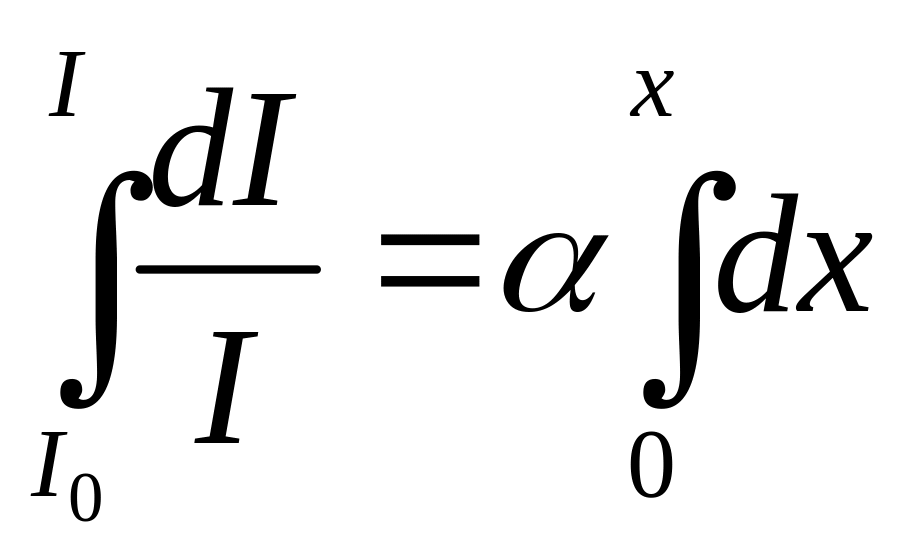Показатель преломления призмы.
Если
луч света переходит из одной среды в
другую, то на границе радела этих сред
он претерпевает преломление. При
преломлении
света выполняются следующие законы:
1. Падающий
и преломленный лучи, и перпендикуляр,
восстановленный
к границе раздела двух сред в точке
падения луча, лежат в одной
плоскости.
2
.
Отношение синуса угла падения к синусу
угла преломления для данных
двух сред есть величина постоянная, и
называется относительным
показателем преломления второй среды
относительно первой (рис.4).
![]()
(7)
Если
луч падает из вакуума в данную
среду, то показатель преломления
данной среды относительно
вакуума называется абсолютным
показателем преломления.
Показатель преломления зависит
от длины волны падающего света.
Законы
преломления света дают возможность
построить ход луча через
призму.
Пусть
ABC
есть сечение трехгранной призмы
плоскостью, перпендикулярной
к обеим преломляющим поверхностям (рис.
5). На рис. 5 изображен ход монохроматического
луча через призму. Для этого луча угол
Р
является преломляющим углом призмы.
Луч S
падает на грань АВ
призмы под углом α1.
В точке D
он преломляется в сторону
основания АС
и пойдет внутри призмы по направление
DE,
образуя угол преломления β1.
В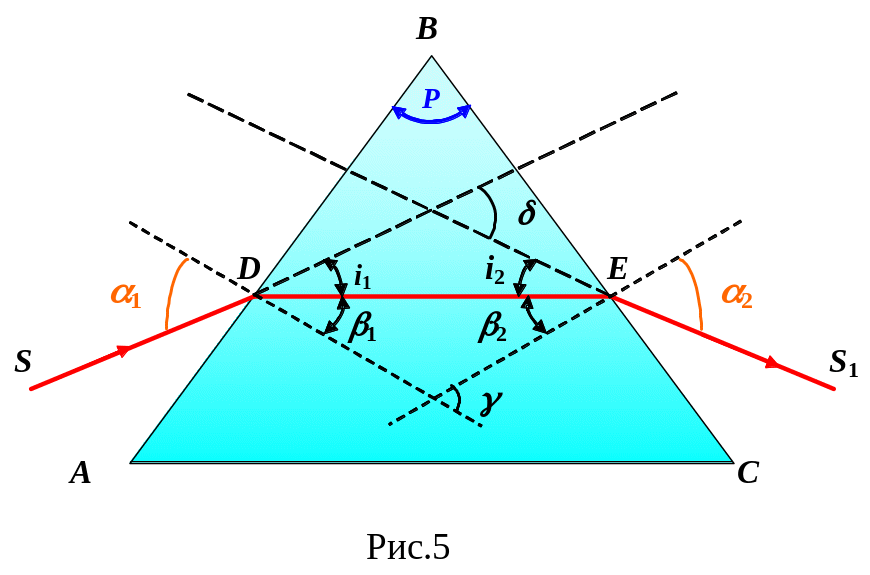
стретив
грань ВС
под углом падения β2,
луч вторично преломится в сторону
основания и выйдет из призмы под углом
преломления
α2
в направлении ES1.
Угол между
направлениями падающего и выходящего
лучей называется углом отклонения δ.
Из построения видно, что:
|
; ; ; |
(8) |
Из соотношения
(8) для угла δ
имеем
|
|
(9) |
Величина угла
отклонения δ
зависит от преломляющего угла призмы
Р
и показателя преломления призмы.
При заданном угле
преломления Р
и показателя преломления n
угол
δ
зависит от угла падения α1
на первую преломляющую
грань.
Если угол падения α1
таков, что преломляющийся луч DE
проходит
внутри призмы перпендикулярно биссектрисе
преломляющего угла
Р,
то угол δ
будет
иметь наименьшее значение. При AB
= BC
луч
DE
проходит через призму параллельно
основанию AC
призмы.
Тогда,
очевидно, α1
=
α2
и β1
=
β2.
Следовательно, из (9) для угла δ
имеем:
|
|
(10) |
а
преломляющий угол Р
из соотношения (8) будет равен:
|
|
(11) |
Если
значение α1
из (10) и β1
из (11) подставить в формулу (7), выражающую
закон преломления, то окончательно
будем иметь:
|
|
(12) |
Формула
(12) является расчетной. Она дает возможность
определить показатель
преломления n
призмы, зная величину преломляющего
угла
Р
(угол Р
обычно равен 450
либо 60°) и измерив с помощью гониометра
наименьший угол отклонения луча
![]()
для
любого из семи
основных цветов в сплошном спектре.
Поглощение света.
При прохождении
электромагнитной волны (света) через
вещество
часть энергии волны затрачивается на
возбуждение колебаний электронов,
находящихся внутри атомов вещества.
Частично эта энергия вновь возвращается
излучения в виде вторичных волн,
возбуждаемых электронами; частично же
она переходит в другие виды энергии
(например, во внутреннюю энергию
вещества). Таким образом, интенсивность
света при прохождении через вещество
уменьшается –
свет поглощается
в веществе. Вынужденные колебания
электронов, а, следовательно,
и поглощение света, становятся особенно
интенсивными при
резонансной частоте.
Пусть
через однородное вещество распространяется
пучок параллельных
лучей (рис. 6).

Выделим
в этом веществе бесконечно тонкий слой
толщины dx,
ограниченный
параллельными поверхностями,
перпендикулярными к направлению
распространения света. Опыт показывает,
что изменение интенсивности
света на пути dx
пропорционально величине этого пути
и величине самой интенсивности:
|
|
(13) |
где α
–
коэффициент поглощения, зависящий от
рода вещества.
Пусть
на входе в поглощающий слой (на границе
или в каком-то месте
внутри вещества) интенсивность света
равна I0.
Найдем интенсивность
света I,
прошедшего слой вещества толщины х.
Для этого
проинтегрируем выражение (13), предварительно
разделив переменные:
|
|
Взяв интегралы,
получим:
|
|
откуда
|
|
(14) |
Выражение (14)
называется законом Бугера. Согласно
этому закону интенсивность
света убывает в поглощающем веществе
экспоненциально.
При
![]()
интенсивность
оказывается в «![]()
»
раз
меньше,
чем
![]()
.
Таким образом, коэффициент поглощения
есть величина, обратная толщине слоя,
при прохождении которого интенсивность
света убывает в «
»
раз.
Коэффициент поглощения зависит от рода
вещества и длины волны (частоты) света.
Так как длина волны
(частота)
определяет цвет света, следовательно,
лучи различных цветов
поглощаются данным веществом по-разному.
Например, оконное стекло
хорошо пропускает видимый свет и почти
полностью поглощает ультрафиолетовые
лучи. Для газов при низком давлении
коэффициент поглощения
для большинства длин волн близок к нулю,
металлы практически
непрозрачны для света.
Как
уже отмечалось, коэффициент поглощения
α
зависит от длины волны λ.
Поэтому выражение (14) можно записать в
виде:
|
|
(15) |
При поглощении
света веществами, растворенными в
практически не поглощающем растворителе
(например, в чистой воде), коэффициент
поглощения пропорционален концентрации
растворенного вещества c.
|
αλ |
(16) |
где
α1λ
коэффициент пропорциональности, также
зависящий от длины волны λ.
Соотношение (16) называют законом Бера.
Для таких растворов закон Бугера
примет вид:
|
|
(17) |
Преобразуем
выражение (17)
|
или |
Переходя к десятичным логарифмам, имеем:
|
|
(18) |
Величина
![]()
называется оптической плотностью
раствора. Введя оптическую плотность,
соотношение (18) можно записать:
![]()
откуда
![]()
,
где
![]()
.
Оптическая
плотность D
пропорциональна концентрации раствора
«с»
и
толщине слоя вещества x,
через
который проходит
свет. Коэффициент пропорциональности
ε,
зависящий
от длины
волны λ
и природы растворенного вещества,
называется молекулярной
оптической плотностью (молекулярной
экстинкцией).
Отношение
![]()
называется прозрачностью или
светопропуcканием
раствора.
Между
оптической плотностью и светопропусканием
имеется следующая зависимость:
|
|
Следует
отметить, что ослабление света может
происходить за счет
рассеяния световой энергии в стороны
также по экспоненциальному
закону. Однако, в случае прозрачных тел,
рассеянием можно пренебречь.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Геометрическая оптика: призмы
В этой статье решаем задачи с призмами. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1.
Монохроматический луч падает нормально на боковую поверхность призмы, преломляющий угол которой равен . Показатель преломления материала призмы для этого луча равен 1,5. Найдите угол отклонения луча, выходящего из призмы, от первоначального направления.
Так как луч падает нормально на поверхность призмы, то не преломляется на этой поверхности. На вторую же боковую грань он упадет под некоторым углом, и преломится на ней.

К задаче 1
В треугольнике (прямоугольном) угол
по условию, поэтому второй острый угол равен
. Поэтому угол падения луча на вторую грань равен
. Зная показатель преломления, можно найти угол преломления. Нужный нам угол – разность угла преломления и угла падения луча.
По закону преломления
Ответ: .
Задача 2. Луч света входит в стеклянную призму под углом и выходит из призмы в воздух под углом
, причем, пройдя призму, отклоняется от первоначального направления на угол
. Найдите преломляющий угол призмы.

К задаче 2
Рассмотрим рисунок. Угол , смежный с данным углом отклонения луча, равен
. В четырехугольнике
угол
равен
, как вертикальный с углом падения, а угол
равен
как вертикальный с углом преломления. Так как сумма углов четырехугольника равна
, то угол
равен:
Теперь рассмотрим четырехугольник . В нем два угла прямых, поэтому преломляющий угол призмы равен:
Ответ: .
Задача 3.
Световой луч падает по нормали на боковую грань прямой стеклянной призмы, поперечное сечение которой – равнобедренный треугольник, . Показатель преломления материала призмы для этого луча равен 1,5. Определите угол между падающим и вышедшим из призмы лучами.
Рассмотрим два случая падения луча.

К задаче 3
В первом случае ход луча показан рыжим цветом. На боковой грани призмы луч не преломится, так как падает на нее нормально. Найдем угол падения луча на нижнюю поверхность призмы. Угол призмы равен
– так как треугольник равнобедренный. Тогда в треугольнике
угол
. А угол падения луча
равен
. Для данного показателя преломления предельный угол полного отражения равен
То есть луч не преломится, а отразится от нижней грани призмы. Угол отражения также равен , и, следовательно, угол
. Следовательно, треугольник
подобен
и тоже является прямоугольным. Следовательно, на второй боковой грани призмы луч тоже не преломится, и выйдет под углом
по отношению к падающему (угол
, искомый – смежный с ним).
Ответ: .
Теперь рассмотрим второй случай падения луча.

К задаче 3
Снова на первой боковой грани не произойдет преломления. На вторую боковую грань луч упадет под углом , что тоже превышает предельный угол полного отражения, и далее луч попадет на нижнюю грань призмы, падая на нее под углом
. В треугольнике
угол
, угол
. Определим угол
:
Определим угол :
Определим угол отклонения луча: в треугольнике угол
, угол
, следовательно, искомый угол
Ответ: .
Задача 4.
Тонкий световой луч падает на боковую грань стеклянной призмы из воздуха под углом . Угол между боковыми гранями призмы равен
. Показатель преломления воздуха равен 1, а стекла 1,41. Определите угол смещения луча от первоначального направления
.

К задаче 4
Определим угол преломления .
Рассмотрим четырехугольник . В нем два угла – прямые, преломляющий угол призмы –
, тогда угол
(это следует из суммы углов четырехугольника). Следовательно, из суммы углов треугольника можем определить угол
в одноименном треугольнике:
Найденный нами угол – не что иное, как угол падения луча на вторую грань призмы. Тогда данный луч выйдет из призмы, не преломившись, так как падает перпендикулярно границе раздела.
Тогда искомый угол – угол – равен разности угла
и угла преломления
, то есть
.
Ответ: .
2017-07-12 ![]()
При каких значениях показателя преломления материала прямоугольной призмы возможен ход луча, изображенный на рисунке? Сечение призмы — равнобедренный прямоугольный треугольник, луч падает на грань АВ перпендикулярно.

Решение:

Угол при вершине призмы $alpha = 45^{ circ}$ . На гранях АС и ВС луч должен испытывать полное внутреннее отражение, т.е. должны выполняться условия:
$begin{cases} sin i geq frac{1}{n}; \ sin i^{ prime} geq frac{1}{n}, end{cases}$
где $n$ — показатель преломления призмы. При отражении света внутри призмы $i = r, i^{ prime} = r^{ prime}$, поэтому
$begin{cases} sin i geq frac{1}{n}; \ sin i^{ prime} = sin left ( frac{ pi}{2} – i right ) geq frac{1}{n} end{cases} Rightarrow begin{cases} sin i geq frac{1}{n}; \ cos i geq frac{1}{n} end{cases} Rightarrow begin{cases} sin^{2} alpha geq frac{1}{n^{2}}; \ cos^{2} alpha geq frac{1}{n^{2}} end{cases} Rightarrow sin^{2} + cos^{2} alpha geq frac{2}{n^{2}}$.
Следовательно, $n geq sqrt{2}$.
Полное условие задачи
Преломляющий угол равнобедренной стеклянной призмы равен 60°. Найти наименьший угол отклонения луча от его первоначального направления. Показатель преломления стекла 1,5.
Краткое условие задачи
Решение задачи
Угол отклонения луча от первоначального направления θ будет минимальным, когда луч выйдет из призмы под тем же углом, под которым упал на призму. Следовательно:
Отсюда следует что:
Для треугольника ABC угол отклонения луча 3 – 4 от первоначального направления 1 – 2 – угол θ – является внешним углом при угле С. Внешний угол равен сумме двух остальных углов треугольника ABC:
Согласно закону преломления можем записать:
откуда получаем:
Теперь рассмотрим равнобедренный треугольник ADB. В нем угол DAB равен:
который, также равен углу DBA, а сумма всех углов в треугольнике ADB равна 180°. Тогда можно записать:
откуда получаем:
Теперь, подставив данный угол в закон преломления получим:
Отсюда имеем:
Выразим угол падения на призму:
Подставляем в формулу для θ:
Подставляем данные и находим численный результат:
Ответ: 38°.
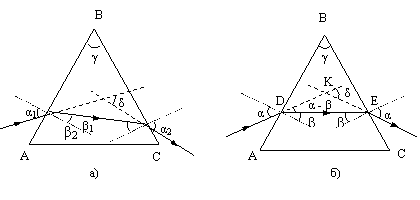
угол δ – угол
отклонения.
угол γ
– преломляющий угол призмы.
Угол
отклонения зависит от угла падения α1, преломляющего угла
призмы γ и показателя преломления материала призмы n.
 |
Основные формулы для расчета показателя преломления света
призмой:

где γ – преломляющий угол призмы,
δ – угол наименьшего
отклонения,
α – угол падения,
n –
показатель преломления материала,
![]() –
–
разность отсчетов.
Формула для расчета погрешности:
![]()
Таблицы измерений:
1 Определение преломляющего угла
призмы Таблица1
|
Номер измерения |
Отсчет слева |
Отсчет справа |
|
|
|
|
1 |
|
|
|
||
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
Среднее значение ![]()