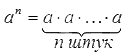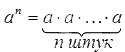Как найти показатель степени зная основание

Степень числа

Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.

Рассмотрим умножение одинаковых чисел, например:

Произведение 5 · 5 · 5 можно записать так: 5 3 (пять в третьей степени). Выражение 5 3 — это степень. Следовательно,

5 · 5 · 5 = 5 3 = 125.

Рассмотрим выражение 5 3 . В этом выражении число 5 — основание степени, а число 3 — показатель степени.

Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.

Степень числа: определения, обозначение, примеры

В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.

Степени с натуральными показателями: понятие квадрата и куба числа

Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).

Степень числа a с натуральным показателем n – это произведение n -ного числа множителей, каждый из которых равен числу а . Записывается степень так: a n , а в виде формулы ее состав можно представить следующим образом:

Например, если показатель степени равен 1 , а основание – a , то первая степень числа a записывается как a 1 . Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a 1 = a .

В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8 · 8 · 8 · 8 можно сократить до 8 4 . Примерно так же произведение помогает нам избежать записи большого числа слагаемых ( 8 + 8 + 8 + 8 = 8 · 4 ) ; мы это уже разбирали в статье, посвященной умножению натуральных чисел.

Как же верно прочесть запись степени? Общепринятый вариант – « a в степени n ». Или можно сказать « n -ная степень a » либо « a n -ной степени». Если, скажем, в примере встретилась запись 8 12 , мы можем прочесть « 8 в 12 -й степени», « 8 в степени 12 » или « 12 -я степень 8 -ми».

Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа 7 ( 7 2 ) , то мы можем сказать « 7 в квадрате» или «квадрат числа 7 ». Аналогично третья степень читается так: 5 3 – это «куб числа 5 » или « 5 в кубе». Впрочем, употреблять стандартную формулировку «во второй/третьей степени» тоже можно, это не будет ошибкой.

Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.

В основании не обязательно должно стоять целое число: для степени ( 4 , 32 ) 9 основанием будет дробь 4 , 32 , а показателем – девятка. Обратите внимание на скобки: такая запись делается для всех степеней, основания которых отличаются от натуральных чисел.

Например: 1 2 3 , ( — 3 ) 12 , — 2 3 5 2 , 2 , 4 35 5 , 7 3 .

Для чего нужны скобки? Они помогают избежать ошибок в расчетах. Скажем, у нас есть две записи: ( − 2 ) 3 и − 2 3 . Первая из них означает отрицательное число минус два, возведенное в степень с натуральным показателем три; вторая – число, соответствующее противоположному значению степени 2 3 .

Иногда в книгах можно встретить немного другое написание степени числа – a ^ n (где а – основание, а n — показатель). То есть 4 ^ 9 – это то же самое, что и 4 9 . В случае, если n представляет собой многозначное число, оно берется в скобки. Например, 15 ^ ( 21 ) , ( − 3 , 1 ) ^ ( 156 ) . Но мы будем использовать обозначение a n как более употребительное.

О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a n -ное число раз. Подробнее об этом мы писали в другой статье.

Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.

Что такое степени с целым показателем

В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.

Степень числа с целым положительным показателем можно отобразить в виде формулы: .

При этом n – любое целое положительное число.

Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:

Равенство a m : a n = a m − n будет верно при условиях: m и n – натуральные числа, m < n , a ≠ 0 .

Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0

Но при этом a n : a n = 1 — частное равных чисел a n и a . Выходит, что нулевая степень любого отличного от нуля числа равна единице.

Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: a m · a n = a m + n .

Если n у нас равен 0 , то a m · a 0 = a m (такое равенство также доказывает нам, что a 0 = 1 ). Но если а также равно нулю, наше равенство приобретает вид 0 m · 0 0 = 0 m , Оно будет верным при любом натуральном значении n , и неважно при этом, чему именно равно значение степени 0 0 , то есть оно может быть равно любому числу, и на верность равенства это не повлияет. Следовательно, запись вида 0 0 своего особенного смысла не имеет, и мы не будем ему его приписывать.

При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.

Разберем пример с конкретными числами: Так, 5 0 — единица, ( 33 , 3 ) 0 = 1 , — 4 5 9 0 = 1 , а значение 0 0 не определено.

После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: a m · a n = a m + n .

Введем условие: m = − n , тогда a не должно быть равно нулю. Из этого следует, что a − n · a n = a − n + n = a 0 = 1 . Выходит, что a n и a − n у нас являются взаимно обратными числами.

В итоге a в целой отрицательной степени есть не что иное, как дробь 1 a n .

Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).

Степень a с целым отрицательным показателем n можно представить в виде дроби 1 a n . Таким образом, a — n = 1 a n при условии a ≠ 0 и n – любое натуральное число.

Проиллюстрируем нашу мысль конкретными примерами:

3 — 2 = 1 3 2 , ( — 4 . 2 ) — 5 = 1 ( — 4 . 2 ) 5 , 11 37 — 1 = 1 11 37 1

В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:

Степень числа a с натуральным показателем z ​​ – это: a z = a z , e с л и z — ц е л о е п о л о ж и т е л ь н о е ч и с л о 1 , z = 0 и a ≠ 0 , ( п р и z = 0 и a = 0 п о л у ч а е т с я 0 0 , з н а ч е н и я в ы р а ж е н и я 0 0 н е о п р е д е л я е т с я ) 1 a z , е с л и z — ц е л о е о т р и ц а т е л ь н о е ч и с л о и a ≠ 0 ( е с л и z — ц е л о е о т р и ц а т е л ь н о е ч и с л о и a = 0 п о л у ч а е т с я 0 z , е г о з н а ч е н и е н е о п р е д е л я е т с я )

Что такое степени с рациональным показателем

Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.

Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа a с дробным показателем m / n , где n – натуральное число, а m – целое.

У нас есть некоторая степень с дробным показателем a m n . Для того, чтобы свойство степени в степени выполнялось, равенство a m n n = a m n · n = a m должно быть верным.

Учитывая определение корня n -ной степени и что a m n n = a m , мы можем принять условие a m n = a m n , если a m n имеет смысл при данных значениях m , n и a .

Приведенные выше свойства степени с целым показателем будут верными при условии a m n = a m n .

Основной вывод из наших рассуждений таков: степень некоторого числа a с дробным показателем m / n – это корень n -ой степени из числа a в степени m . Это справедливо в том случае, если при данных значениях m , n и a выражение a m n сохраняет смысл.

Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.

1. Мы можем ограничить значение основания степени: возьмем a , которое при положительных значениях m будет больше или равно 0 , а для отрицательных – строго меньше (поскольку при m ≤ 0 мы получаем 0 m , а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом:

Степень с дробным показателем m / n для некоторого положительного числа a есть корень n -ной степени из a, возведенного в степень m . В виде формулы это можно изобразить так:

Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.

Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как

0 m n = 0 m n = 0 при условии целого положительного m и натурального n .

При отрицательном отношении m n < 0 степень не определяется, т.е. такая запись смысла не имеет.

Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.

Выражение a m n иногда все же имеет смысл при некоторых отрицательных значениях a и некоторых m . Так, верны записи ( — 5 ) 2 3 , ( — 1 , 2 ) 5 7 , — 1 2 — 8 4 , в которых основание отрицательно.

2. Второй подход – это рассмотреть отдельно корень a m n с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень a , в показателе которой стоит сократимая обыкновенная дробь, считается степенью a , в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись a m · k n · k , то мы можем свести ее к a m n и упростить расчеты.

Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.

Объединим все данные выше определения в одной записи:

Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.

Для любой обыкновенной сократимой дроби m · k n · k степень можно заменить на a m n .

Степень числа a с несократимым дробным показателем m / n – можно выразить в виде a m n в следующих случаях: — для любых действительных a , целых положительных значений m и нечетных натуральных значений n . Пример: 2 5 3 = 2 5 3 , ( — 5 , 1 ) 2 7 = ( — 5 , 1 ) — 2 7 , 0 5 19 = 0 5 19 .

— для любых отличных от нуля действительных a , целых отрицательных значений m и нечетных значений n , например, 2 — 5 3 = 2 — 5 3 , ( — 5 , 1 ) — 2 7 = ( — 5 , 1 ) — 2 7

— для любых неотрицательных a , целых положительных значений m и четных n , например, 2 1 4 = 2 1 4 , ( 5 , 1 ) 3 2 = ( 5 , 1 ) 3 , 0 7 18 = 0 7 18 .

— для любых положительных a , целых отрицательных m и четных n , например, 2 — 1 4 = 2 — 1 4 , ( 5 , 1 ) — 3 2 = ( 5 , 1 ) — 3 , .

В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: — 2 11 6 , — 2 1 2 3 2 , 0 — 2 5 .

Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, 6 / 10 = 3 / 5 . Тогда должно быть верным ( — 1 ) 6 10 = — 1 3 5 , но — 1 6 10 = ( — 1 ) 6 10 = 1 10 = 1 10 10 = 1 , а ( — 1 ) 3 5 = ( — 1 ) 3 5 = — 1 5 = — 1 5 5 = — 1 .

Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.

Таким образом, степень положительного числа a с дробным показателем m / n определяется как 0 m n = 0 m n = 0 . В случае отрицательных a запись a m n не имеет смысла. Степень нуля для положительных дробных показателей m / n определяется как 0 m n = 0 m n = 0 , для отрицательных дробных показателей мы степень нуля не определяем.

В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: 5 1 , 7 , 3 2 5 — 2 3 7 .

При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:

5 1 , 7 = 5 17 10 = 5 7 10 3 2 5 — 2 3 7 = 3 2 5 — 17 7 = 3 2 5 — 17 7

Что такое степени с иррациональным и действительным показателем

Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.

Допустим, что у нас есть иррациональное число a и последовательность его десятичных приближений a 0 , a 1 , a 2 , . . . . Например, возьмем значение a = 1 , 67175331 . . . , тогда

a 0 = 1 , 6 , a 1 = 1 , 67 , a 2 = 1 , 671 , . . . , a 0 = 1 , 67 , a 1 = 1 , 6717 , a 2 = 1 , 671753 , . . .

и так далее (при этом сами приближения являются рациональными числами).

Последовательности приближений мы можем поставить в соответствие последовательность степеней a a 0 , a a 1 , a a 2 , . . . . Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.

Возьмем для примера a = 3 , тогда a a 0 = 3 1 , 67 , a a 1 = 3 1 , 6717 , a a 2 = 3 1 , 671753 , . . . и т.д.

Последовательность степеней можно свести к числу, которое и будет значением степени c основанием a и иррациональным показателем a . В итоге : степень с иррациональным показателем вида 3 1 , 67175331 . . можно свести к числу 6 , 27 .

Степень положительного числа a с иррациональным показателем a записывается как a a . Его значение – это предел последовательности a a 0 , a a 1 , a a 2 , . . . , где a 0 , a 1 , a 2 , . . . являются последовательными десятичными приближениями иррационального числа a . Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом 0 a = 0 Так, 0 6 = 0 , 0 21 3 3 = 0 . А для отрицательных этого сделать нельзя, поскольку, например, значение 0 — 5 , 0 — 2 π не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и 1 2 , 1 5 в 2 и 1 — 5 будут равны 1 .

Как узнать степень числа?

Самое разумное разложить число на простые множители, тогда можно найти и основание и показатель степени.
Если известно основание, то показатель можно найти логарифмированием, например,
2^x=8
Чтобы найти x нужно прологарифмировать обе части по основанию 2
x = log по основанию 2 от 8 = ln 8 / ln 2 (так можно на калькуляторе посчитать) = 3
Если известен показатель, то основание находится извлечением корня, например,
x^3=8
извлекаем корень кубический из обоих частей
x=корень кубический из 8 = 2

Если же неизвестно ни то ни другое разложи число на простые множители, это делается последовательным делением числа на простые множители
614656 / 2 = 307328
307328 / 2 = 153664
153664 / 2 = 76832
76832 / 2 = 38416
38416 / 2 = 19208
19208 / 2 = 9604
9604 / 2 = 4802
4802 / 2 = 2401
2401 не делится на 2, на 3, на 5 (последовательно перебираем простые числа)
2407 / 7 = 343
343 / 7 = 49
49 / 7 = 7
7 / 7 = 1
Итого мы делили на 2 восемь раз и на 7 четыре раза, следовательно
614656 = 2^8 * 7^4
Если мы хотим найти представление в виде a^b с натуральными a и b и b должно быть максимальным, то в качестве b нужно брать НОД степеней полученных в разложении на простые множители, то есть в данном случае b=НОД (8,4)=4
основанием степени a будет служить 2^(8/b) * 7^(4/b) = 2^2 * 7^1 = 4*7=28

Аналитического способа не существует. То бишь формулы для нахождения степени и числа, которое возводят в эту степень — нет.

Так для общего развития скажу, что даже нахождение достаточно больших простых чисел — занятие затруднительное и очень хорошо оплачиваемое. А для решения вашей задачи (как минимум) нужно знать что это число уже не простое. :)))

Здравствуйте, уважаемый Максим Сальников !

Общей методики для задач такого типа, как мне известно, нет .

Самый простой способ — разложить данное число на простые множители .

В приведённом Вами примере это будет выглядеть так :

614656 = ( 2 x 2 x2 x 2 x 2 x 2 x 2 x 2 ) x ( 7 x 7 x 7 x 7 )

Из 7 x 7 x 7 x 7 следует, что » вероятная степень » равна 4 : 7 x 7 x 7 x 7 = 7 ^ 4 ( 1 )

Тогда из 2 x 2 x2 x 2 x 2 x 2 x 2 x 2 образуем ( 2 x 2 ) x ( 2 x 2 ) x( 2 x 2 ) x ( 2 x 2 ) = 4 ^ 4 ( 2 )

Согласно ( 1 ) и ( 2 ) можем записать : 614656 = ( 4 ^ 4 ) x ( 7 ^ 4 ) = ( 4 x 7 ) ^ 4 = 28 ^ 4 !